Towards Multi-objective Optimisation of Quantitative Goal Models using

Constraint Programming

Christophe Ponsard

and Robert Darimont

CETIC Research Centre, Charleroi, Belgium

Respect-IT SA, Louvain-la-Neuve, Belgium

Keywords:

Multi-objective Optimisation, Goal-oriented Requirements Engineering, Search-based Software Engineering,

Quantitative Reasoning, Pareto Front, Tool Support.

Abstract:

Goal Model are widely used to capture system goals and reﬁne them into operational requirements assigned

to human, hardware or software. Such models support alternative goal reﬁnements resulting in a potentially

large design space to explore. A given design can be quantitatively evaluated in terms of its fulﬁlment of a

set of non-functional requirements (e.g. reliability, performance) or business goals (e.g. costs, stakeholder

satisfaction). Optimisation techniques can be used to explore the design space to determine an optimal design

according to a single objective like the cost but also according to multi-objective techniques to propose a set

of Pareto-optimal solutions in which a best solution can be selected. In this paper, we show how to translate

a goal-oriented requirements model, expressed in the KAOS notation, into a constraint programming (CP)

problem. The OscaR.CP engine is used to get, from all alternatives co explored, either global or Pareto-

optimal solutions. Our method is implemented as a tool plugin of a requirements engineering platform and is

benchmarked on the classical meeting scheduler case study.

1 INTRODUCTION

Requirements Engineering (RE) is concerned with

the elicitation, evaluation, speciﬁcation, consolida-

tion, and evolution of the objectives, functionalities,

qualities, and constraints of a software-based system

(van Lamsweerde, 2009). It is a crucial phase as

many project failures can be traced back to ﬂaws in re-

quirements. In addition to dealing with completeness

and consistency issues, RE also allows one to take

various high-level design decisions related to several

ways to reach the system goals using different com-

binations of software/hardware/human agents, gener-

ally also resulting in different trade-offs among Non-

Functional Requirements (NFR), i.e. qualities like

performance, usability or security. Such alternative

designs can be precisely modelled using Goal- Ori-

ented Requirements Engineering (GORE) notations

like KAOS (Dardenne et al., 1993), i* (Yu and My-

lopoulos, 1997) or GRL (ITU, 2012).

Complex systems can contain many alternatives

with various constraints restricting how they can be

combined and also complex impacts on different

kinds of properties, especially NFR. The process to

select an adequate design can actually be described

as an optimisation problem over the system design

space (Mogk, 2014). More precisely, it is a multi-

objective optimisation problem given the many, so

different qualities of a system needs to simultaneously

met. Translating such problems into a single optimi-

sation problem is not recommended because it is difﬁ-

cult to assess the relative importance of those qualities

and therefore to combine them into a unique objec-

tive function. An alternative approach is to compute a

set of solutions known as Pareto-optimal from which

trade-offs can be explicitly evaluated (Zhang et al.,

2008). Search-based software engineering (SBSE)

(Harman, 2007) is a specialised ﬁeld of software en-

gineering concerned with the application of optimisa-

tion tools to this kind of problems. A famous one is

the Next Release Problem which is known to be NP-

Hard (Bagnall et al., 2001).

The aim of this paper is to explore how to use

SBSE to tackle the problem of alternative selections

in a multi-objective context by computing the Pareto

front containing all solutions explicitly. To support

this work, the KAOS notations have been used. How-

ever, the same concepts and methods can be applied to

the other GORE notations mentioned above. On the

SBSE side, we will consider the use of constraint pro-

286

Ponsard, C. and Darimont, R.

Towards Multi-objective Optimisation of Quantitative Goal Models using Constraint Programming.

DOI: 10.5220/0009357602860292

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 286-292

ISBN: 978-989-758-396-4; ISSN: 2184-4372

gramming, more speciﬁcally using the Open Source

OscaR library which provides, among others, power-

ful support to multi-objective problems (OscaR Team,

2012). In order to illustrate our approach, we have

focused on a well-known RE case study: the meet-

ing scheduler (van Lamsweerde et al., 1995) which

has already been used for multi-objective reasoning

(Nguyen et al., 2018).

Our paper is structured as follows. First, Section 1

reviews existing work in this area. Then Section 2

presents the goal modelling notation used here and il-

lustrates it on our meeting scheduler case study. Sec-

tion 3 details our mapping of the variability part of the

model into a CP model using OscaR.CP. Section 4 ex-

ploits the model to perform single and multi-objective

searches and illustrate the result on our case study. Fi-

nally, Section 5 concludes and identiﬁes some future

work.

2 LITERATURE OVERVIEW

This section reviews different reported works investi-

gating the use of CP to reason about GORE models.

Looking at other standard goal modelling nota-

tions, GRL support quantitative reasoning, especially

through Key Performance Indicators (KPI) (Barone

et al., 2011). A mapping on constraint programming

was also developed using the JaCoP library (Luo and

Amyot, 2011). However the work is more directed to-

wards the deﬁnition of a better declarative semantics

of GRL. The exploitation seems limited to the propa-

gation on trees without alternatives designs and does

not investigate the possibility to explore the design

space as we do.

Related to i*, an extensive multi-objective frame-

work is available (Nguyen et al., 2018). It formalises

the notion of Constraint Goal Models (CGM) to sup-

ports different kinds of requirements (nice-to-have,

preferences, optimisation, constraints,..). It exploits

automated reasoning SMT-based solvers to support

sound and complete reasoning on such goal models.

An Eclipse-based CGM tool is available. However,

its optimisation capabilities are limited to a lexico-

graphic approach, i.e. with priority ranking among

goals. A special attention is devoted to ensuring the

reasoning scales on large models derived from the

meeting scheduler also used in our work.

Another tool called WebREd-Tool was developed

for the i* method (Aguilar et al., 2011; Calderon et al.,

2012). It is a set of Eclipse plugins assisting the de-

signer in the early phases of a Web application de-

velopment process. It helps the designer to compare

different conﬁgurations of functional requirements,

while balancing and optimising non-functional re-

quirements. The algorithm relies on Pareto efﬁciency

and provides both tabular and radar based visualisa-

tions. The algorithm itself does not seem efﬁcient and

scalable as it explicitly stores all possible conﬁgura-

tions. However, the authors performed a controlled

experiment that conﬁrm requirement engineers may

perform better at the task of selecting FRs while op-

timising and balancing NFRs using the proposed ap-

proach and visualisation (Zubcoff et al., 2018).

Feature models are quite close to goal models in

terms of structure, attributes, constraints. Complete

mapping of feature models over constraint logic pro-

gramming have been deﬁned, e.g. (Karatas¸ et al.,

2010) and enable to perform operations such as prop-

agation, emptiness check or enumeration of products.

However, they do not relate to requirements and do no

answer the problem we tackle here.

Finally, another KAOS approach has been devel-

oped to deal with uncertainty in goals (Heaven and

Letier, 2011). It relies on a simulation approach us-

ing a genetic algorithm which also results in a multi-

objective analysis. This approach requires a more

complex modelling in which probability distributions

must be speciﬁed and is more computation intensive.

It can be seen as complementary to the present work

and can be used to introduce a more realistic goal

modelling.

3 GOAL MODELLING OF THE

MEETING SCHEDULER

Goals prescribe, at different levels of abstraction, key

properties the considered system should achieve. In

this paper, the focus is only put on modelling goals

although it is usually combined with other models to

structure the domain and agent interactions.

KAOS uses several abstraction levels to express

goals starting from high-level strategic goals. In

the meeting scheduler case study (van Lamsweerde

et al., 1995) used as running example, it can be a

goal like “Achieve[EfﬁcientSchedulingOfMeetings]”

as depicted in Figure 1 as a light blue parallelograms.

In KAOS, high-level goals progressively reﬁned into

more concrete and operational ones through reﬁne-

ment relationships. A reﬁnement relationship links

a parent goal to several subgoals with different ful-

ﬁlment conditions using either AND-reﬁnement (all

subgoals need to be satisﬁed) or OR-reﬁnement (a sin-

gle subgoal is enough, i.e. possible alternatives). The

“WHY” and “HOW” questions can be used to conve-

niently navigate from subgoals to parent goals (why)

and from parent goals to subgoals (how).

Towards Multi-objective Optimisation of Quantitative Goal Models using Constraint Programming

287

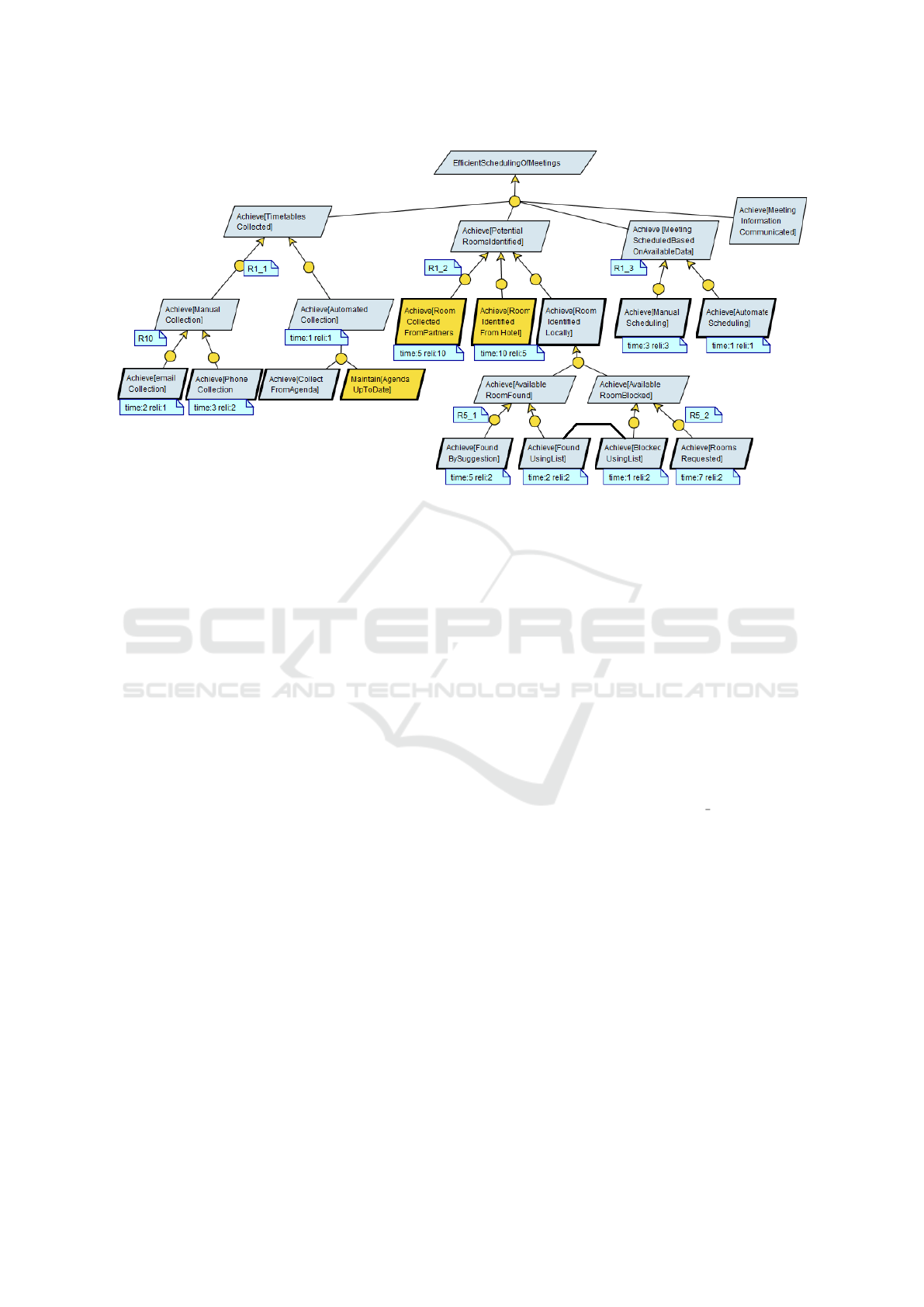
Figure 1: Goal graph for the Meeting Scheduler.

In our case study modelled in Figure 1,

the top reﬁnement decomposes the goal “Ef-

ﬁcientSchedulingOfMeetings” into the follow-

ing goals: “Achieve[TimetablesCollected]”,

“Achieve [PotentialRoomsIdentiﬁed]”, “Achieve

[MeetingScheduledBasedOnAvailableData]” and

“Achieve[Meeting InformationCommunicated]”.

This is an AND-reﬁnement of the top level goal: the

set of subgoals forms a chain of milestones that yields

our top level goal. Such reﬁnements are spotted with

yellow circular connectors in our model.

As depicted in Figure 1, the ﬁrst level of reﬁne-

ment for our case study is is composed of the goals:

“Achieve[TimetablesCollected]”, “Achieve [Poten-

tialRoomsIdentiﬁed]”, “Achieve [MeetingScheduled-

BasedOnAvailableData]” and “Achieve[Meeting In-

formationCommunicated]”. Those goals form a

AND-reﬁnement of the higher level goal: the set of

subgoals forms a chain of milestones that yield our

top level goal. Such a reﬁnement can be spotted by a

yellow circular connectors in our model.

Our model contains many OR-reﬁnements that

can be detected as yellow circular connectors de-

parting from the same parent goal. For exam-

ple, the goal “Achieve[TimetablesCollected]” can be

satisﬁed either by “Achieve[ManualCollection]” or

“Achieve[AutomatedCollection]”. Goals may also

have more than two alternatives. For example, the

goal ”Achieve[PotentialRoomsIdentiﬁed]” has three

alternatives. Some alternatives may be restricted

to speciﬁc choice done in another one. For exam-

ple, the alternatives ”Achieve[FoundUsingList]” and

”Achieve[BlockedUsingList]” need to be selected to-

gether.

In this paper, we will assume only one al-

ternative can be selected in a conﬁguration and

will discuss this again towards the end of our pa-

per. A design conﬁguration can then be repre-

sented as a vector D = {R

, ..R

} where R

an integer in the range 0..N

that represents the

selected alternative. 0 means no alternative se-

lected and is only relevant for a sub-alternative that

is not in the scope (i.e. subtree) of a selected

alternative, e.g. “Achieve[EmailCollection]” and

“Achieve[PhoneCollection]” is not relevant when se-

lecting “Achieve[AutomatedCollection]”. The identi-

ﬁcation number of each alternative is captured in the

model. They are graphically represented in Figure 1

from left to right. For example, R1 1 has two alter-

natives: #1 is “Achieve[ManualCollection]” and #2 is

“Achieve[AutomatedCollection]”.

The functional goal decomposition stops when

reaching a goal controllable by an agent, i.e. answer-

ing the “WHO” question about responsibility assign-

ment. These goals are either requirements (depicted

like goals but with a thicker border) on the software

or expectations on the behaviour of agents in the envi-

ronment (depicted as requirements but with a yellow

background).

The satisfaction of goals can be assessed by

their contribution to different several qualities usu-

ally modelled as non-functional requirements (NFR)

using fulﬁlling standard classiﬁcations such as (ISO,

2011). Each functional requirement can contribute to

one or several NFR. This should be preferably mea-

sured in a well-deﬁned domain units, either generic

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

288

(e.g. reliability of a goal can be measured as the ratio

of number of failures vs. total number of occurrences)

or problem-speciﬁc (e.g. usability can be assessed as

the amount of manual work that needs to be done).

NFR satisfaction on higher goals can usually be as-

sessed as a combination of the contribution of lower

level nodes (eventually possibly leaf requirements)

using propagation rules. For an OR-reﬁnement, the

maximal value is selected as we look for the optimal

(as maximum). For an AND-reﬁnement, it will depend

on the type of quality assessed:

• many properties related to resources usage can be

additive on such reﬁnements, e.g. our usability

metric measured in hours.

• reliability is not additive but multiplicative, espe-

cially when considering chains of tasks as in our

model structure

• user satisfaction will generally be reﬂected by the

minimal level of satisfaction of a goal reﬁnement.

A more complete framework to reason about the par-

tial satisfaction of goals was also developed by (Letier

and van Lamsweerde, 2004).

Figure 1 shows two quality attributes: time and re-

liability for leaf-level goals. From there we can infer

higher level values using the above rules. For exam-

ple, at top level the total cost will be the sum of the

cost of R1 1, R1 2 and R1 3.

4 TRANSLATING GOAL

VARIANTS INTO A CP MODEL

Translating the KAOS model into an OscaR.CP

model requires three main steps

• extracting all alternatives from the model

• generating speciﬁc constraints across alternatives

• for each target quality: producing an objective

function

Note the target CP model is written is the same lan-

guage as OscaR, i.e. the Scala programming language

which is a very expressive general-purpose program-

ming language providing support for functional pro-

gramming (Odersky, 2004).

4.1 Extracting Alternatives

Alternatives are extracted by querying our model

repository. In our experimental setting, we are us-

ing the Objectiver tool which can be queried us-

ing OQL (Respect-IT, 2005). We also use some

post-processing to only keep goals with more than

one AND-reﬁnement, that is, goals with an OR-

reﬁnement. Such queries can easily be adapted to

other contexts. The result is shown in Listing 1. Each

OR-reﬁnement is given a unique identiﬁer R1 1, etc.),

is labelled with the parent goal, and decorated with

the size of the AND-reﬁnement set composing the OR-

Reﬁnement (named in short in the following, the size

of the OR-Reﬁnement).

Listing 1: Listing of alternatives with fan-out.

R1 1 Ach ieve [ T i m e t a b l e s C o l l e c t e d ] 2

R1 2 Ach ieve [ P o t e n t i a l R o o m s I d e n t i f i e d ] 3

R1 3 Ach ieve [ Me eti ngS che duledBasedOnAvailab leD . ] 2

R5 1 Ach ieve [ AvailableRoomFound ] 2

R5 2 Ach ieve [ Availa bleRoomBlocked ] 2

R10 Achieve [ M a n u a l C o l l e ction ] 2

In the following, each OR-reﬁnement in the goal

graph will have a state. The values of the states are:

• Disabled: the OR-reﬁnement has been discarded

and none of its alternatives can be selected in the

design

• Enabled: the OR-reﬁnement is not discarded and

one of its alternatives may be selected in the de-

sign (but none is currently selected

• Selected: the OR-Reﬁnement is enabled and one

alternative is selected in the design

Based on this, for each alternative, a variable is de-

clared, with the identiﬁer of an OR-Reﬁnement as a

name and with a domain ranging from 0 to the size

of the OR-reﬁnement as computed in the previous

step. A special kind of variable called CPIntVar cap-

turing the speciﬁed range is used. A strictly posi-

tive value means the OR-reﬁnement is enabled and the

value tells the alternative that is selected. A “0”-value

means the alternative is disabled.

4.2 Generating Speciﬁc Constraints

In what follows, we will call sub − alternative, an al-

ternative in the subtree of another alternative.

The following speciﬁc constraints express that at

the end of the computation a complete and consistent

design has been built:

• completeness: all top level alternatives OR-

reﬁnements are enabled selected (i.e. all associ-

ated variables ?!==0)

• consistency#1: if an alternative is not selected, all

its sub- alternatives should must be disabled (by

recursion, it is enough to disable the closest sub-

alternatives using reﬁnement links)

Towards Multi-objective Optimisation of Quantitative Goal Models using Constraint Programming

289

• consistency#2: if an alternative is selected, its

sub-alternatives should be enabled (again the

same recursion remark holds)

• domain speciﬁc: e.g. if some alternatives need

to be selected together or if two alternatives are

mutually exclusive.

The computation of those constraints is quite easy to

translate using Boolean equality/equivalence ? ===,

difference ?! ==, implication ==>, conjunction &&

and disjunction || operators as depicted in Listing 2.

Listing 2: CP model for goal variants and constraints.

va l R1 1 = CPIntVar (0 t o 2 )

va l R1 2 = CPIntVar (0 t o 3 )

va l R1 3 = CPIntVar (0 t o 2 )

va l R5 1 = CPIntVar (0 t o 2 )

va l R5 2 = CPIntVar (0 t o 2 )

va l R10 = CPIntVar ( 0 t o 2)

/ / t o p l e v e l a l t e r n a t i v e s

add ( R1 1 ?!== 0)

add ( R1 2 ?!== 0)

add ( R1 3 ?!== 0)

/ / e na b l i n g and d i s a b l i n g c o n s t r a i n t s

add ( ( R1 2 ?!== 3 )

==> ( ( R5 1?===0) && ( R5 2 ? == =0 )) )

add ( ( R1 2 ?=== 3 )

==> ( ( R5 1 ?! ==0 ) && ( R5 2 ? ! = = 0 ) ) )

/ / domain s p e c i f i c c o n s t r a i n t s

add ( ( R1 1 ?!== 1 ) ==> ( R10?===0))

add ( ( R1 1 ?=== 1 ) ==> ( R10 ? ! = =0 ) )

Based on this set of constraints, the list of alternatives

can be easily produced using the commands of Listing

3. It generates 24 different conﬁgurations.

Listing 3: Optimisation search.

s e a r c h {

b i n a r y S t a t i c (

Seq ( R1 1 , R1 2 , R1 3 , R5 1 , R5 2 , R10 ) )

} on S o l u t i o n {

p r i n t l n ( ” R1 1 : ”+R1 1+ . . . )

} s t a r t ( )

4.3 Objective Function

Objective functions are also encoded as CPIntVar

and can be expressed using expressions involving our

variables. The rules described in Section 2 are ap-

plied to produce evaluation at all levels enabling leaf

values to propagate up to the top level based on the

selected alternatives. The alternative selection opera-

tor is simply the truth value (RX?===expected value)

which will evaluate to 0 when false and to 1 when

true. Note that we consider only reﬁnements without

any shared goals which deserve a special attention and

are discussed at the end of this section.

For example, our time quality can be encoded as

shown in Listing 4.

Listing 4: Optimisation search.

def ti me R 1 1 : CPIntVar =

( R1 1 ? === 1)∗ (( R10?===1)∗2+(R10?===2)∗3)

+( R1 1?===2)∗1

def ti me R 1 2 : CPIntVar =

( R1 2?===1)∗5+

( R1 2?===2)∗10+

( R1 2 ? === 3)∗ (( R5 1?===1)∗5+( R5 1?===2)∗2

+( R5 2?===1)∗1+( R5 2?===2)∗7)

def ti me R 1 3 : CPIntVar =

( R1 3?===1)∗3+( R1 3?===2)∗1

va l t ime =( t ime R1 1+ tim e R1 2+ tim e R 1 3 )

At this point, it is easy to perform a single objective

search, for example minimising the time can be done

inserting the command minimize(time) before the

search. It will yield the result of Listing 5

Listing 5: Optimisation search.

o b j e c t i v e t i g h t e n e d t o 10 l b :−1

R1 1 :1 R1 2 : 1 R1 3 : 1 R5 1 : 0 R5 2 : 0 R10 : 1

o b j e c t i v e t i g h t e n e d t o 8 l b :−1

R1 1 :1 R1 2 : 1 R1 3 : 2 R5 1 : 0 R5 2 : 0 R10 : 1

o b j e c t i v e t i g h t e n e d t o 6 l b :−1

R1 1 :1 R1 2 : 3 R1 3 : 2 R5 1 : 2 R5 2 : 1 R10 : 1

o b j e c t i v e t i g h t e n e d t o 5 l b :−1

R1 1 :2 R1 2 : 3 R1 3 : 2 R5 1 : 2 R5 2 : 1 R10 : 0

5 MULTI-OBJECTIVE

OPTIMISATION

Performing a multi-objective search is also quite

easy thanks to the multi-objective search function

and Pareto visualisation contributed by (Hartert and

Schaus, 2014). After deﬁning a second objective

function, the optimisation command before the search

becomes paretoMaximize(obj1, obj2) as shown

in Listing 6. Note that the ﬁrst objective function was

turned into a maximisation by computing 20 − time

(i.e. time resource left) just to ensure both functions

need to be maximised.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

290

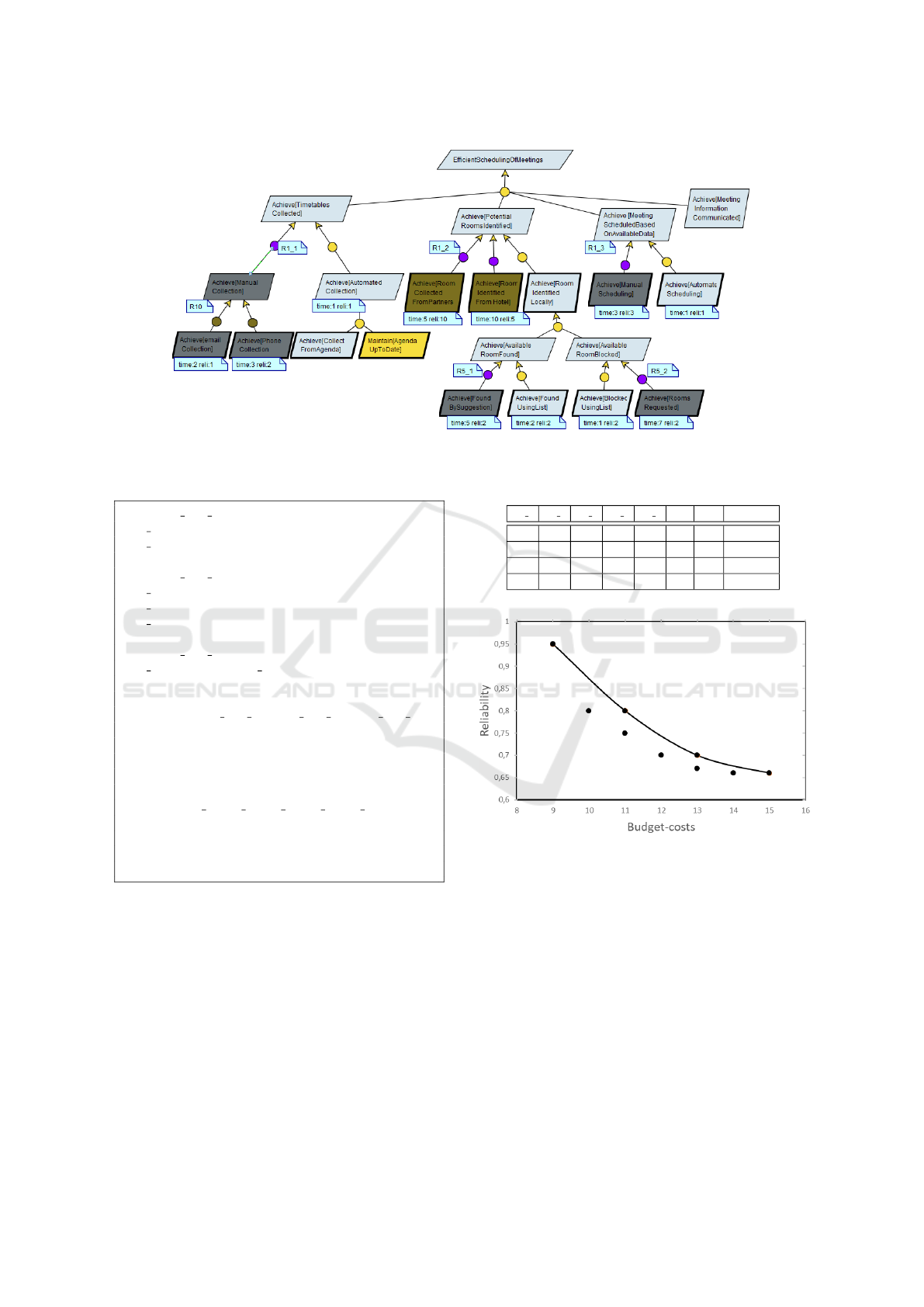
Figure 3: Visual representation of the selected design.

Listing 6: Multi-objective search (for costs see Listing 6).

def r e l i R 1 1 : CPIntVar =

( R1 1 ? === 1)∗ (( R10?===1)∗1+(R10?===2)∗2)+

( R1 1?===2)∗1

def r e l i R 1 2 : CPIntVar =

( R1 2?===1)∗10+

( R1 2?===2)∗5+

( R1 2?===3)∗2

def r e l i R 1 3 : CPIntVar =

( R1 3?===1)∗3+( R1 3?===2)∗1

va l o bj1 =t im e ∗( −1)+20

va l o bj2 = r e l i R 1 1 ∗ r e l i R 1 2 ∗ r e l i R 1 3

cp . pa reto Maxi miz e ( obj1 , ob j2 )

s e a r c h {

b i n a r y S t a t i c (

Seq ( R1 1 , R1 2 , R1 3 , R5 1 , R5 2 , R10 ) )

} on S o l u t i o n {

p a r e t o P l o t . i n s e r t ( obj 1 . v alu e ,

ob j2 . v a lue )

} s t a r t ( )

Figure 2 depicts both the complete search as a cloud

of points and the resulting Pareto front which can also

be presented in tabular form with more information

enabling the selection (see Table 1). The reliability

information has been normalised to a real value be-

tween 0 and 1 without impacting the solutions but to

better match conventional representation for this at-

tribute. The plot and the table can be used to guide

the analyst in selecting a right solution, e.g. by ruling

out too costly alternatives, unreliable ones or making

sure a speciﬁc OR-reﬁnement is selected.

Table 1: Tabular view of Pareto solutions.

R1 1 R1 2 R1 3 R5 1 R5 2 R10 Cost Reliability

1 1 1 0 0 2 9 0,95

2 1 1 0 0 0 11 0,8

2 1 2 0 0 0 13 0,7

2 3 2 2 1 0 15 0,66

Figure 2: Pareto front.

The tool also provides a ﬁltering mechanism to grey

out the part of the model not covered by the selected

alternative. Figure 3 highlights the instance selected

by the time minimisation reported earlier.

5.1 Discussion

Shared goals require some extra processing in order

to avoid counting them twice. Actually, a shared goal

may have a contribution of its own to be counted once

and a contribution for being involved in one or more

reﬁnements. Making sure the goal is counted once

can be encoded through selection checking operators

referring to the other alternatives involving it.

Towards Multi-objective Optimisation of Quantitative Goal Models using Constraint Programming

291

About the readability of the constraints, although

the generated code is meant to be executed by an

optimisation engine, the selection operators could

be stated in more user-friendly form, e.g. using

isSelected(alt) rather than ”alt?! == 0. Operators for

checking other states can also be introduced.

The current mapping is limited to the selection of

a single alternative which is usual for goal reﬁnements

but not for the dual of goals, i.e. obstacles. In this

case, making sure an obstacle is managed may require

to select multiple OR-reﬁnements. The current map-

ping cannot cope with this but could be adapted, e.g.

an array of CPBoolVar, and speciﬁc constraints for

imposing no, one or some alternatives. This results in

the generation of far larger design spaces which also

raises the need for better guidance.

6 CONCLUSION & NEXT STEPS

In this paper, we developed an approach to deal with

the exploration of the design space at requirements

engineering time. As multiple qualities need to be

assessed simultaneously, a multi-objective approach

computing a Pareto front was used to provide the an-

alyst with a candidate set of solutions which can then

be reviewed more carefully. Our translation from the

KAOS notation to the OscaR.CP was tested on the

meeting scheduler benchmark.

Our work is still quite in early phase. Our next

steps are to cover the different extensions identi-

ﬁed such as better language primitives, dealing with

shared goals and allowing the selection of multiple

alternatives. We also plan to improve usability and to

validate on larger models and with external analysts.

ACKNOWLEDGEMENTS

Thanks to Respect-IT for giving access to the Objec-

tiver tool and to the OscaR team for its Open Source

optimisation library.

REFERENCES

Aguilar, J., Garrig

os, I., and Maz

on, J.-N. (2011). A goal-

oriented approach for optimizing non-functional re-

quirements in web applications. pages 14–23.

Bagnall, A., Rayward-Smith, V., and Whittley, I. (2001).

The next release problem. Information and Software

Technology, 43(14):883 – 890.

Barone, D., Jiang, L., Amyot, D., and Mylopoulos, J.

(2011). Reasoning with key performance indicators.

volume 92, pages 82–96.

Calderon, A. et al. (2012). Webred: A model-driven tool

for web requirements speciﬁcation and optimization.

In Web Engineering.

Dardenne, A., van Lamsweerde, A., and Fickas, S. (1993).

Goal-directed requirements acquisition. Sci. Comput.

Program., 20(1-2):3–50.

Harman, M. (2007). The current state and future of search

based software engineering. In Future of Software En-

gineering (FOSE ’07), pages 342–357.

Hartert, R. and Schaus, P. (2014). A support-based algo-

rithm for the bi-objective pareto constraint. In Proc.

28th AAAI Conf. on A.I., July 27-31, Qu

ebec, Canada.

Heaven, W. and Letier, E. (2011). Simulating and optimis-

ing design decisions in quantitative goal models. In

IEEE 19th Int. Requirements Engineering Conference.

ISO (2011). System and Software Quality Requirements

and Evaluation (SQuaRE). https://iso25000.com.

ITU (2012). Z.151 (10/12), User Requirements Notation

(URN) - Language Deﬁnition.

Karatas¸, A. S., O

guzt

un, H., and Do

gru, A. (2010). Map-

ping extended feature models to constraint logic pro-

gramming over ﬁnite domains. In Proc. of the 14th

Int. Conf. on Software Product Lines: Going Beyond.

Letier, E. and van Lamsweerde, A. (2004). Reasoning about

partial goal satisfaction for requirements and design

engineering. SIGSOFT Softw. Eng. Notes, 29(6).

Luo, H. and Amyot, D. (2011). Towards a declarative,

constraint-oriented semantics with a generic evalua-

tion algorithm for GRL. In Proc. of the 5

Interna-

tional i* Workshop, Trento, Italy, August 28-29.

Mogk, N. W. (2014). A requirements management system

based on an optimization model of the design process.

Procedia Computer Science, 28:221 – 227.

Nguyen, C. M. et al. (2018). Multi-objective reasoning with

constrained goal models. Requir. Eng., 23(2).

Odersky, M. (2004). Scala Programming Language. https:

//www.scala-lang.org.

OscaR Team (2012). OscaR: Operational Research in

Scala. Available under the LGPL licence from https:

//bitbucket.org/oscarlib/oscar.

Respect-IT (2005). The Objectiver Goal-Oriented Require-

ments Engineering Tool. http://www.objectiver.com.

van Lamsweerde, A. (2009). Requirements Engineering -

From System Goals to UML Models to Software Spec-

iﬁcations. Wiley.

van Lamsweerde, A., Darimont, R., and Massonet, P.

(1995). Goal-directed elaboration of requirements for

a meeting scheduler: problems and lessons learnt. In

Proc. of IEEE Int. Symposium on Req. Eng. (RE’95).

Yu, E. S. K. and Mylopoulos, J. (1997). Enterprise mod-

elling for business redesign: The i* framework. SIG-

GROUP Bull., 18(1):59–63.

Zhang, Y., Finkelstein, A., and Harman, M. (2008). Search

based requirements optimisation: Existing work and

challenges. In Requirements Engineering: Founda-

tion for Software Quality.

Zubcoff, J. et al. (2018). Evaluating different i*-based ap-

proaches for selecting functional requirements while

balancing and optimizing non-functional require-

ments: A controlled experiment. Information and

Software Technology.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

292