Weighted Scoring of Multiple-choice Questions based Exams: Expert

and Empirical Weighting Factors

Panagiotis Photopoulos

, Odysseus Tsakiridis

, Ilias Stavrakas

and Dimos Triantis

Department of Electrical and Electronic Engineering, University of West Attica, Athens, Greece

Keywords: Multiple-choice Questions, Weighted Scoring, Electronic Examination, Expert Weighting, Empirical

Weighting.

Abstract: The increasing number of students per class and the limited teaching resources are important factors for

increasing the popularity of multiple-choice questions based (MCQ) exams amongst the academic tutors.

Weighted grading of MCQ items is compatible with a wide range of options, therefore it can reward those

students who have successfully answered the most demanding items. In the case of weighted scoring of a

MCQ based exam, the weighting factor of each item can be obtained a priori from an expert of the domain,

usually the lecturer, or a posteriori by some empirical method. The overall score of a student is calculated as

the weighted average of the items successfully answered. This publication presents an iterative method for

scoring MCQ based examinations. The proposed method attempts to achieve the best possible congruence of

the overall student scores calculated as the weighted average based on expert and empirical weighting.

1 INTRODUCTION

Multiple-choice questions (MCQs) are increasingly

used in higher education (Bjork 2015) for

supplementing or even replacing traditional

assessment practices despite the fact that they have

been criticized for assessing factual knowledge only

(Freeman and Lewis 1998). If appropriately designed,

MCQ exams can effectively asses a wide range of

abilities e.g. the depth of understanding of the subject

matter under consideration (Simkin & Kuechler,

2005) and the ability to reason analytically (Scharf, E.

M.; Baldwin, 2007). Computer networks enable more

flexibility in the delivery of MCQs at times and places

which are in tune with students’ needs. Marking can

be automated providing feedback to the students

within a few seconds after the end of the examination.

When marking is done by a computer, it appears to be

free of human intervention or judgment and in that

sense it fosters amongst the examinees the idea of a

thoroughly objective process (Freeman and Lewis,

1998). Compared to paper-based MCQs, the use of

online computer-assisted assessment (CAA) can

https://orcid.org/0000-0001-7944-666X

https://orcid.org/0000-0002-6014-1783

https://orcid.org/0000-0001-8484-8751

https://orcid.org/0000-0003-4219-8687

significantly reduce the burden associated with

testing large student cohorts (Bull & McKenna, 2004;

Donnelly, 2014). It is anticipated that because of their

greater efficiency, computerized exams will be more

widely used in the years to come (Hiller, 2014)

A MCQ based exam presents students with a task,

which has to be both important and clear and can be

answered correctly, by those students who have

achieved the desired level of knowledge and

understanding. Rules in accordance with the above

mentioned conditions for preparing MCQs, have

already been proposed (Hansen, 1997).

MCQ tests are usually constructed by tutors

themselves (Carroll, and Moody 2006), formal

training and support is rather lacking (Rudner and

Schafer 2002). Tutors use their past experience to

carry out present assessment practices (Siri, Freddano

2011).

MCQ exams are popular among the students

(Ventouras et al., 2010) presumably because they

consider that they are easier to take (Chan and

Kennedy, 2002). Nonetheless, Struyven, K., Dochy,

F., and Janssens, S., (2005) found that students

382

Photopoulos, P., Tsakiridis, O., Stavrakas, I. and Triantis, D.

Weighted Scoring of Multiple-choice Questions based Exams: Expert and Empirical Weighting Factors.

DOI: 10.5220/0009358303820387

In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 1, pages 382-387

ISBN: 978-989-758-417-6

consider them as being less fair, since MCQ exams

are not homogeneous (Dascalua, et.al. 2015) as far as

the difficulty of the various items is concerned.

Attributing equal marks to each item regardless of its

difficulty, certainly raises questions related to the

fairness of the overall score. A number of

publications have attempted to tackle this criticism by

suggesting strategies, which are meant to increase

fairness by employing weighted grading (McCoubrie,

2004; Hameed, 2016).

Weights per item can be obtained a priori from an

expert, usually the examiner herself, or by means of

some empirical method. When an empirical method

is employed the weighting factors are obtained from

some mathematical function of the average success or

difficulty ratios (i.e. the percentage of the examinees

who failed to answer the item correctly) of the

examinees for each specific item (Cross et al., 1980;

Hameed, 2016)

We will call the first way of assigning weighting

factors ‘expert weighting’ and the second ‘empirical

weighting’.

Fairness of an examination is related to factors

such as diligent construction of the MCQs, precision,

clarity, lingual simplicity and clear pass-fail standards

(McCoubrie, 2005). Fairness is also related to the

distribution of marks amongst the various multiple-

choice questions. Usually in MCQ based exams, all

items carry equal marks regardless of how demanding

they are. All the correct answers are counted, then the

incorrect answers are also counted and the final mark

results as the difference of the correct minus the

incorrect answers. Students who have answered the

same number of questions get the same score

regardless of the difficulty of the questions they

attempted. Fairness implies correct replies for more

demanding items to get higher marks.

MCQ items differ according to their importance,

difficulty and complexity (Hameed, 2016).

Importance of a question is related to how essential it

is within the curriculum. Difficulty is related to the

amount of effort needed to answer the question.

Complexity has to do with the background knowledge

and the kind of thinking required to answer a question

(Hameed, 2011). Fair scoring is calling for taking into

consideration the aforementioned factors (Saleh and

Kim, 2009)

Experts can provide fast and self-consistent

weighting factors. On the other hand empirical

weighting factors are perceived to be immune to

human intervention and thus they obtain an aura of

objectivity. Hameed (2016) proposed a fuzzy system

evaluation approach, to obtain weighted scores taking

account of the difficulty of each item.

2 METHOD USED

This section provides a description of the method

employed.

2.1 Variables Used

The variables employed in the proposed method are

the following:

N: is the number of the multiple choice questions

(items) included in each test.

M: is the number of students who sat the test.

: is the ‘expert weighting’ factor of the ith item. It

is a number estimate showing the degree of difficulty

of the ith out of the N questions within a suitable

scale. It is a subjective weighting factor determined

by an expert, the tutor in this case, prior to the

examination. There are various options for assigning

values to each item. For example, W

may range

from 0.1 to 1 giving the freedom of 10 levels of

difficulty amongst the MSQ items. In this case the N

questions of the test will be divided in ten subgroups

, n

,…, n

, of difficulty 0.1, 0.2,… respectively. In

another option the tutor may consider 5 levels of

difficulty i.e. very easy, easy, intermediate difficulty,

difficult and very difficult. As the number of

difficulty levels increase it becomes more difficult to

the tutor to set a number of comprehensive criteria in

order to decide which item belongs to which level of

difficulty (Gower and Daniels, 1980).

In the present study, the N items of each test were

divided into three groups of n

, n

items each,

where:

items were assigned an expert weighting factor

equal to 1, n

items of W

=2 and for the rest n

items

=3, where

=N (1)

: is the score of the ith item of the test. q

takes two

possible values: q

=1 if the question has been

correctly answered and q

=0, otherwise. i=1,...,N

: is the overall score for each student calculated as

the weighted average of the actual performance in

each question (q

values) weighted by the set of the

expert weighting factors W



Ti i









(2)

: is the percentage of the examinees who answered

the ith question correctly

Weighted Scoring of Multiple-choice Questions based Exams: Expert and Empirical Weighting Factors

383

: is the percentage of the students who failed to

answer the ith item correctly. i.e.

=1-P

The proposed methods employs the N values of P

order to calculate the respective ‘empirical’ waiting

factors W

which are used to calculate the actual

score of each student.

: is related to the difficulty ratio of each item

through the equation

= P

+α (3)

where α is an empirical correction factor ranging

between 0.24± 0.04

The actual overall score of each examinee E

calculated from the equation:











iSi

(4)

2.2 Two Scores per Examinee

In the proposed method two overall scores are

calculated for each examinee:

: which is a “dummy” overall score for each

individual student. It is calculated as the weighted

average of the successful answers given by the

examinee, weighted by the W

factors defined by the

tutor-expert. E

scores are not announced to the

students but they do influence the final marks

indirectly as it is explained below. Additionally, they

emerge as a key element for comparing the expert

weighting to the empirical weighting factors.

: is the overall score of each individual student.

It is the weighted average of the successful answers

given by the examinee, weighted by the W

factors,

= P

+α. E

is the overall score, which is given as

feedback to the student as the final mark of the

examination taken.

The value of the empirical parameter α results by

the condition of achieving the best possible

congruence between the E

and E

values, j=1,...,M.

The mathematical criterion for fulfilling the

abovementioned condition is the value of the quantity









SjTj

to be minimum.

The proposed method unfolds like that:

M students sit the exam. Each student is presented

with N MCQs. Before the examination the tutor sets

the values W

. As soon as the examination is finished,

the E

scores are calculated using equation (2).

Also the P

values are calculated. The











iSi

, scores are calculated by setting







FiSi

with an initial value of α=0. Next, the

quantity









SjTj

is calculated. The parameter α

is allowed to take successively increasing values in

order to determine the value of α which minimizes









SjTj

. Say that this value is α*. After the

value of α* has been obtained, the overall score for

each one of the M students is calculated from the

equation











, where





For the five examinations presented here, it was found

that the respective α values obtained –one for each

examination- which rendered



min







SjTj

ranged from 0,20 to 0,28 approximately, i.e

04,024,0







3 APPLYING THE METHOD

This section presents the findings of applying the

proposed method in the case of 5 examinations for the

following courses: Physics of Semiconductor

Devices (PSD) and Nanoelectronic devices (NED)

included in the curriculum of the Department of

Electrical and Electronic Engineering of the

University of West Attica. Tables 1 and 2 include the

relative information for these examinations.

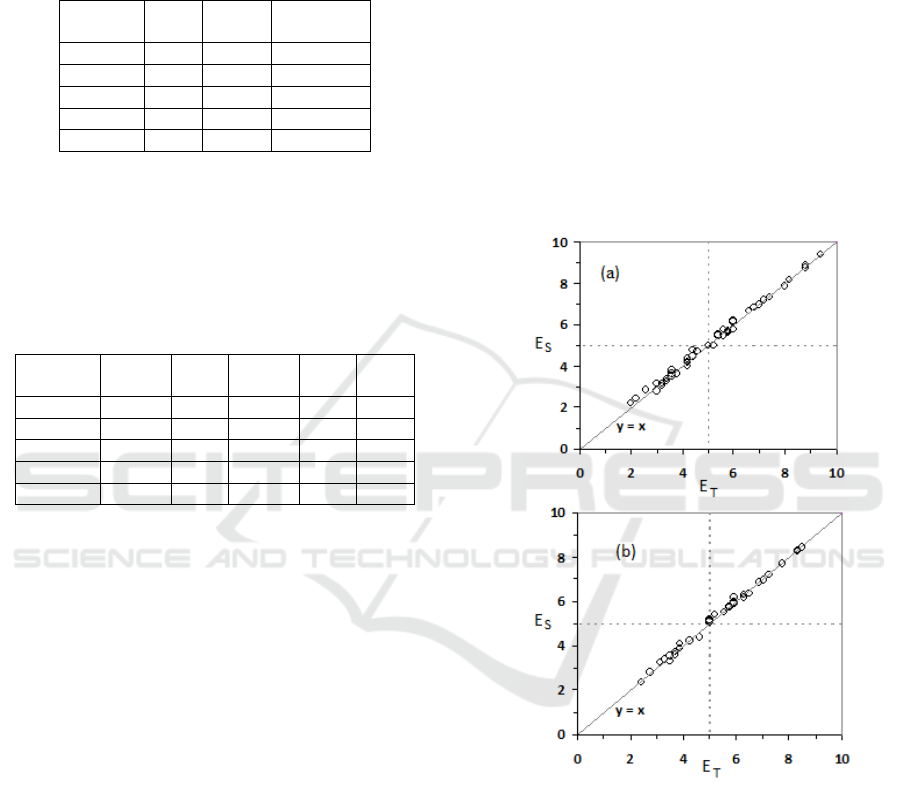
Figure 1 shows, for indicative only purposes, the

congruence of the E

and E

values and it refers to

two out of the five MCQ based exams presented here

(PSD-02 and NED-01). The α value for both of these

exams was 0,25.

Weighted scoring of MCQ exams is considered to

improve fairness. The expert determined weighting

factors are meant to reflect the complexity of each

question. Nonetheless this strategy may give rise to

concerns and complaints by the students and fuel

what has been characterized as ‘paranoia over points’

CSEDU 2020 - 12th International Conference on Computer Supported Education

384

(Cross et al., 1980) canceling thus the intended

fairness.

Table 1. Exam Details: N: number of items, M: number of

students, n

-n

are bundles of MCQ items with W

values 1, 2 and 3 respectively.

Exam

code

N M

-n

(Eq. 1)

PSD-01 28 46 10-10-8

PSD-02 25 44 7-11-7

PSD-03 25 40 9-9-7

NED-01 28 35 10-10-8

NED-02 30 36 10-11-9

Table 2: The various results of the 5 examinations. <E

) stand for the average score and % of the students who

passed the exam respectively, when marks are calculated

based on tutor defined weighting factors equation (2).

>, (E

) stand for the average score and % of the students

who passed the exam respectively, when marks are

calculated based on empirical weighting factors equation

(4).

Exam

code

)

(%)

)

(%)

PSD-01 5.46 57 5.48 57 0,24

PSD-02 5.17 55 5.16 52 0,25

PSD-03 4.65 45 4.66 45 0,22

NED-01 5.32 60 5.32 60 0,25

NED-02 5.36 53 5.37 56 0,27

Appealing to the difficulty ratio of each question

), which is a quantity derived from the actual

performance of the students, appears as a more

objective or at least less examiner-dependent set of

quantities which enhances the perceived fairness of

scoring.

The parameter α is an intervention parameter

which brings closer the E

and E

values. The

criterion for calculating α focuses on the actual final

overall score of each student. It does not examine the

score achieved in each individual question since the

latter would make things unreasonably complicated.

Other researchers have used a similar line of

reasoning (Hameed, 2016). Additionally, it is fairness

of the overall final mark which is all important and

matters to the students.

The empirical parameter α has the effect of

smoothing down the big differences in the relative

influence of the weighting factors to the overall score.

Setting W

is a very stringent and demotivating

condition as it is explained below.

Consider for example the case when a large

number of the students have successfully answered a

certain number of items. Then the contribution of

these items to the overall score of each student will be

minimal, making thus the students feel that their

effort was in vain and therefore demotivating them.

By the same token, items answered by very few

examinees, i.e. high P

, will have a very high relative

influence to the final score. In this case those

questions which were meant to discriminate high

performers will actually be the punishers of the non-

high achievers, which undermines any intention of

fairness. (Omari, 2013). Finally, allowing the

empirical weighting factor to be equal to P

would be

overly individualistic since it would equate the

success of the few to the failure of the many. The

success of the many will lead to very few marks and

the success of the few to very high gains. Hence,

smoothing the distribution of the empirical weighting

factors is important to ensure fairness of the scores.

Figure 1: Congruence of the E

and E

scores for two of the

MCQ based exams: PSD-02-44-25 (a) and NED-01-35-28

(b).

Say that in a MCQ based examination the items k

and l have been answered correctly by the 90% and

the 60% of the examinees respectively. Then the

difficulty factors will be P

=0.1 and P

=0.4, i.e. the

item l will be considered as 4 times more difficult

compared to the item k. According to the proposed

method the empirical weighting factors will be

=0.1+α and W

=0,4+α. It is easily seen that the

ratio W

is less than P

. Hence, adding the

Weighted Scoring of Multiple-choice Questions based Exams: Expert and Empirical Weighting Factors

385

quantity α to the difficulty factor, rationalizes the

relative influence of each item to the overall score.

When α is added to P

, the resulting value W

leads to a decrease of the relative influence of the

high-end weighting factors and a respective increase

of the influence of lower-end ones. The merit of the

proposed method lies in the fact that the weighting

factors which influence the final marks are mainly

determined by the performance of the students who

sat the examination.

Table 2 compares the results of 5 MCQ based

examinations. <E

> stands for the average marks of

the students who sat each examination, when the

mark of each individual student is given according to

equation (2) (W

, tutor defined weighting factors).

> stands for the average marks of the students

who sat each examination, when the mark of each

individual student is given according to equation (4)

, empirical weighting factors). The last column at

the right of Table 2 shows the value of the parameter

α for each one of the examinations. It is seen that, for

a suitable value of α there is good agreement between

the <E

> and <E

> values as well as the percentage

of students who passed the examination (E

and E

Our method serves as a tool for sending an alarm

to the examiner in the following two cases: The first

comes from the direct comparison of the expert

weighting factors W

to the average difficulty ratio

of the ith item. In case when the difficulty ratio P

roughly follows the discreet values of W

, then this

can be considered as a sign of success on behalf of the

tutor. Low W

when P

is high for a certain item, is

an indication of either luck of clarity or poor language

use (McCoubrie, 2005).

Low divergence between E

and E

, is also an

indication of an adequate agreement between the

judgment of the tutor and the actual performance of

the students (Fig.1). In cases when there is a

considerable divergence between E

and E

, then

this is an indicator for action to be taken by the tutor.

4 CONCLUSIONS

The present publication suggests, as a proof of

concept, a method for scoring MCQ based

examinations. The score of each student is obtained

as a weighted average of the items correctly

answered. Expert and empirical weighting factors are

both employed. The empirical weighting factor

depends on the difficulty ratio of each item, which

practically equals the percentage of students who

failed to answer a specific item. For each student two

scores are calculated: for the first, the expert

weighting factors are used and for the second, the

empirical ones. The mathematical condition imposed

to ensure best possible congruence between the two

sets of scores, was minimization of the sum of the

squared distances between the two scores over all the

examinees.

A more thorough study of the differences between

expert weighting factors and a posteriori difficulty

ratios is required in order to gain a better

understanding of the factors affecting the congruence

of the experts’ and empirical weighting overall

scores.

REFERENCES

Benvenuti, S., 2010. “Using MCQ-based assessment to

achieve validity, reliability and manageability in

introductory level large class assessment”, HE Monitor

No 10 Teaching and Learning beyond Formal Access:

Assessment through the Looking Glass, 21-33.

Freeman, R., and R. Lewis., 1998. Planning and

Implementing Assessment. London: Kogan Page.

Bjork, E.L., Soderstrom, N.C., and Little, J.L., 2015. “Can

multiple-choice testing induce desirable difficulties?

Evidence from the laboratory and the classroom”, The

American Journal of Psychology, 128(2), 229-239.

Bull, J., & McKenna, C., 2004. Blueprint for computer-

assisted assessment : London, RoutledgeFalmer

Carroll, T., and Moody, L., 2006. “Teacher-made tests”,

Science Scope, 66-67.

Chan, N., and Kennedy, P.E., 2002. “Are Multiple-Choice

exams easier for economics students? A comparison of

multiple-choice and ‘equivalent’ constructed-response

exam questions”, Southern Economic Journal, 68 ( 4),

957-971.

Cross, L.H., Ross, F. K., and Scott Geller E., 1980. “Using

Choice-Weighted Scoring of Multiple-Choice Tests for

Determination of Grades in College Courses”, The

Journal of Experimental Education, 48(4), 296-301.

Dascalua, C.G., Enachea, A.M., Radu Bogdan Mavrua,

R.B., Zegana, G., 2015. “Computer-based MCQ

Assessment for Students in Dental Medicine –

Advantages and Drawbacks”, Procedia - Social and

Behavioral Sciences 187, 22– 27.

Donnelly, C., 2014. “The use of case based multiple choice

questions for assessing large group teaching:

implications on student’s learning”, Irish Journal of

Academic Practice, 3(1), 1-15.

Freeman, R. & Lewis, R. 1998. Planning and Implementing

Assessment: London: Kogan Page.

Gower, D.M., Daniels, D.J., 1980. ‘Some factors which

influence the facility index of Objective test items in

school Chemistry’, Studies in Educational Evaluation,

6, 127-136.

Hameed, I.A., 2011. “Using Gaussian membership

functions for improving the reliability and robustness of

CSEDU 2020 - 12th International Conference on Computer Supported Education

386

students’ evaluation systems” Expert systems with

Applications: 38(6), 7135-7142.

Hameed, I.A., 2016 “A Fuzzy System to Automatically

Evaluate and Improve Fairness of Multiple-Choice

Questions (MCQs) based Exams”, Proceedings of the

8th International Conference on Computer Supported

Education (CSEDU), 476-481.

Hansen, JD., 1997. “Quality multiple-choice test questions:

item-writing guidelines and an analysis of auditing

testbanks”. J. Educ Bus. 73, 94–97.

Hillier, M. 2014. “The very idea of e-Exams: student (pre)

conceptions Research context. Rhetoric and Reality:

Critical perspectives on educational technology”,

Proceedings ASCILITE, Dunedin, 77-88.

McCoubrie, P., 2005. “Improving the fairness of multiple-

choice questions: a literature review” Medical Teacher,

Vol. 26(8), 709–712.

Omari, A., 2013. An Evaluation and Assessment System for

Online MCQ's Exams. International Journal of

Electronics and Electrical Engineering, 1(3), 219-222

Rudner L, Schafer W., 2002. What teachers need to know

about assessment: National Education Association,

Washington, DC.

Saleh, I., Kim, S.-I., 2009. A fuzzy system for evaluating

students’ learning achievement. Expert systems with

Applications, 36(3), 6236-6243.

Scharf, E. M., & Baldwin, L. P., 2007, “Assessing multiple

choice questions (MCQ) tests - a mathematical

perspective”. Active Learning in Higher Education, 8,

31-47.

Simkin, M.G. and Kuechler, W.L., 2005. “Multiple-Choice

tests and student understanding: what is the

connection?” Decision Sciences - Journal of Innovative

Education: 3(1), 73-98.

Siri, A., Freddano M., 2011. “The use of item analysis for

the improvement of objective examinations” Procedia -

Social and Behavioral Sciences 29,188 – 197.

Struyven, K., Dochy, F., and Janssens, S., (2005)

“Students’ Perceptions about Evaluation and

Assessment in Higher Education: A Review”,

Assessment and Evaluation in Higher Education 30(4),

325–341.

Ventouras, Ε. Triantis, D. Tsiakas, P. Stergiopoulos, C.,

2010, “Comparison of examination methods based on

multiple-choice questions and constructed-response

questions using personal computers”, Computers &

Education, 54, 455-451.

Weighted Scoring of Multiple-choice Questions based Exams: Expert and Empirical Weighting Factors

387