Classiﬁcation of Students’ Conceptual Understanding in STEM

Education using Their Visual Attention Distributions: A Comparison of

Three Machine-Learning Approaches

Stefan K

uchemann, Pascal Klein, Sebastian Becker, Niharika Kumari and Jochen Kuhn

Physics Department - Physics Education Research Group, TU Kaiserslautern,

Erwin-Schr

odinger-Strasse 46, 67663 Kaiserslautern, Germany

Keywords:

Eye-tracking, Machine Learning, Deep Learning, Performance Prediction, Total Visit Duration, Problem-

solving, Line-graphs, Adaptive Learning Systems.

Abstract:

Line-Graphs play a central role in STEM education, for instance, for the instruction of mathematical con-

cepts or for analyzing measurement data. Consequently, they have been studied intensively in the past years.

However, despite this wide and frequent use, little is known about students’ visual strategy when solving line-

graph problems. In this work, we study two example line-graph problems addressing the slope and the area

concept, and apply three supervised machine-learning approaches to classify the students performance using

visual attention distributions measured via remote eye tracking. The results show the dominance of a large-

margin classiﬁer at small training data sets above random decision forests and a feed-forward artiﬁcial neural

network. However, we observe a sensitivity of the large-margin classiﬁer towards the discriminatory power

of used features which provides a guide for a selection of machine learning algorithms for the optimization of

adaptive learning environments.

1 INTRODUCTION

In times of increasing heterogeneity between learn-

ers, it becomes increasingly important to respond to

the needs of individuals and to support learners indi-

vidual learning process. One possibility is to person-

alize learning environments via adaptive systems that

are able to classify the learner’s behavior during the

learning or problem-solving process and potentially

include the knowledge of individual answers to pre-

vious questions which can produce a sharper picture

of learner characteristics over time and can thus of-

fer a tailored support or provide targeted feedback. In

this context, the learners eye movements during prob-

lem solving or learning are a promising data source.

This paper examines the problem-solving process of

learners while solving two kinematics problems using

their visual attention distribution and the answer cor-

rectness. Using machine-learning algorithm, we aim

to obtain an accurate prediction of the performance

based on behavioral measures, so that in a second step

an adaptive system can react to the data with tailored

support (feedback, cues, etc). For the subject topic,

we chose students’ understanding of line graphs in the

context of kinematics. This can be motivated by the

fact that many problems in physics and other scientiﬁc

disciplines require students to extract relevant infor-

mation from graphs. It is also well known that graphs

have the potential to substantially promote learning of

abstract scientiﬁc concepts. Dealing with (kinemat-

ics) graphs also requires the ability to relate mathe-

matical concepts to the graphical representation - such

as the area under the curve or the slope of the graph.

Since these cognitive processes are closely linked to

perceptual processes, e.g. extracting relevant infor-

mation from graphs, this subject is particularly acces-

sible for the eye-tracking method.

In this work we address the question how the spa-

tiotemporal gaze pattern of students is linked to the

correct problem-solving strategy. Speciﬁcally, we

different machine-learning based classiﬁcation algo-

rithms to predict the response correctness in physics

line-graph problems based on the gaze pattern. To

optimize the predictability, we compare the classiﬁ-

cation performance of three different machine learn-

ing algorithms, namely a support vector machine, a

random forest and a deep neural network (multilayer

perceptron).

Küchemann, S., Klein, P., Becker, S., Kumari, N. and Kuhn, J.

Classiﬁcation of Students’ Conceptual Understanding in STEM Education using Their Visual Attention Distributions: A Comparison of Three Machine-Learning Approaches.

DOI: 10.5220/0009359400360046

In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 1, pages 36-46

ISBN: 978-989-758-417-6

2 THEORETICAL BACKGROUND

2.1 Line-graphs in STEM Education

Scientiﬁc information is represented in different

forms of visual representation, ranging from natu-

rally visual ones like pictures in textbooks to more

abstract ones like diagrams or formulas. A widely

used form of representation in STEM education are

line-graphs. These representations depict the covari-

ation of two variables and thus the relationship be-

tween physical quantities. In this context, the ability

to interpret graphs can be considered as a key com-

petence in STEM education. Despite the great impor-

tance for STEM learning, many studies have shown

that it is difﬁcult for students to use line-graphs in a

competent way (Glazer, 2011), especially in physics

(Beichner, 1994; Ceuppens et al., 2019; Forster, 2004;

Ivanjek et al., 2016; McDermott et al., 1987). In par-

ticular, the determination of the slope of a line-graph

as well as the area below causes great difﬁculties for

learners in the subject area of kinematics, to which

Beichner, 1993 could identify ﬁve fundamental difﬁ-

culties of students with kinematic graphs (Beichner,

1993).

1. Graph as Picture Error: Students consider the

graph not as an abstract mathematical represen-

tation, but as a photograph of the real situation.

2. Slope/Height Confusion: Students misinterpret

the slope as the height (y-ordinate) in the graph.

3. Variable Confusion: Students do not distinguish

between distance, velocity and acceleration.

4. Slope Error: Students determine the slope of a

line with non-zero y-axis intersection in the exact

same way as if the line passes through the origin.

5. Area Difﬁculties: Students cannot establish a re-

lationship between the area below the graph and

a corresponding physical quantity. For example,

they relate the word ”change” automatically to the

slope rather than to the area.

In order to enable researchers and teachers to de-

tect the presence of these difﬁculties in learners, Be-

ichner (1994) developed the Test for Understanding

Graphs in Kinematics (TUG-K), which has found

widespread use in didactic research in particular (Be-

ichner, 1994).

2.2 Visual Attention as an Indicator of

Cognitive Processes during Problem

Solving

Investigating learning processes has been in the scope

of a considerable number of studies in the ﬁeld of

STEM (Posner et al., 1982; Schnotz and Carretero,

1999). The most important and commonly used

method to study cognitive activity during learning or

problem solving is the student interview with think-

ing aloud protocols (LeCompte and Preissle, 1993;

Champagne and Kouba, 1999). This method suf-

fers from validity problems, as interaction effects be-

tween interviewer and interviewee can falsify the re-

sults. For this reason, in recent years educational re-

searchers have resorted to a research method typically

used by psychologists in other academic disciplines

to study basic cognitive processes in reading and

other types of information processing: eye-tracking

(Rayner, 1998; Rayner, 2009). The eye movements

are classiﬁed by ﬁxations (eye stop points) and sac-

cades (jumps between ﬁxations). The basis for the

interpretation of eye-movement data is the eye-mind

hypothesis, which was developed by (Just and Car-

penter, 1976) and later validated by neuropsychol-

ogy (Kustov and Robinson, 1996). According to the

eye-mind hypothesis, a ﬁxation point of the eye also

corresponds to a focus point of mental attention, so

that the eye movements map the temporal-spatial de-

coding of visual information (Hoffman and Subrama-

niam, 1995; Salvucci and Anderson, 2001). Thus, the

eye movements represent a valid indirect measure of

the distribution of attention associated with cognitive

processes. In other words, ﬁxations reﬂect the atten-

tion and contains information about the cognitive pro-

cesses at speciﬁc locations and they are determined

by the perceptual and cognitive analysis of the infor-

mation at that location. Eye tracking thus provides

a non-intrusive method to obtain information about

visual attention and cognitive processing while stu-

dents read instructions or solve problems, particularly

where visual strategies are involved.

Constructing a visual understanding of line graphs

requires the learner to extract information from the

graph to combine them with prior knowledge. We

refer to the cognitive theory of multimedia learning

(CTML) (Mayer, 2009) which allows us to interpret

the functions and mechanisms of extracting infor-

mation and constructing meaning with graphs. The

CTML identiﬁes three distinct processes (selection,

organization, and integration) involved in learning

and problem-solving. Selection can be described as

the process of accessing pieces of sensory information

from the graph. Eye-tracking measures such as the

Classiﬁcation of Students’ Conceptual Understanding in STEM Education using Their Visual Attention Distributions: A Comparison of

Three Machine-Learning Approaches

visit duration on certain areas (so-called areas of in-

terest, AOIs) provide information that students attend

to that information. Organization describes structur-

ing the selected information to build a coherent in-

ternal representation, involving, for example, com-

parisons and classiﬁcations. As mentioned above,

Rayner addressed the idea that eye-movement param-

eters such as number of ﬁxations, ﬁxation duration,

duration time, and scan paths are especially relevant

to learning. In particular, it has been shown in sev-

eral studies that ﬁxation duration and number of ﬁxa-

tions on task-relevant areas are indicators of expertise

(Gegenfurtner et al., 2011). Integration can be consid-

ered as combining internal representations with acti-

vated prior knowledge (long-term memory). In the

context of line graphs, learners need to integrate ele-

ments within graphs, such as the different axis values

or axis intervals. In summary, it is widely agreed that

ﬁxations (their counts and their duration) are associ-

ated with processes of the selection and organization

of information extracted from the text or the illustra-

tion, while transitions between different AOIs are re-

lated to integration processes (Alemdag and Cagiltay,

2018; Scheiter et al., 2019; Sch

uler, 2017).

2.3 Eye-tracking Research in the

Context of (Line) Graphs

Eye tracking has proven to be a powerful tool for

studying students’ processes during graphical prob-

lem solving, complementing the existing research

with a data resource consisting of students’ visual

attention (Klein et al., 2018). In the context of

kinematic graphs, previous eye-tracking research pro-

vided evidence that the visual-spatial abilities have

a strong correlation with students’ response correct-

ness during problem-solving. Students who solve

problems with line graphs correctly focus longer on

the axes (Madsen et al., 2012), which was also sup-

ported by previous work et al. (Klein et al., 2019a),

whereas students with low spatial abilities tend to in-

terpret graphs literally (Kozhevnikov et al., 2007). In

general, Susac et al. found that students who an-

swer qualitative and quantitative line-graph problems

in different contexts correctly, in average focus longer

the graph area (Susac et al., 2018) We also anticipate

that above-mentioned learning difﬁculties and mis-

conceptions (see Section 2.1) may be observed in our

study and may be reﬂected in certain gaze patterns.

For instance, it is likely that students who inhibit cer-

tain misunderstandings focus longer on conceptual-

irrelevant areas of the graph or require longer to

identify the relevant areas in comparison to experts

(Gegenfurtner et al., 2011). In this work, we studied

the eye-movement patterns of high-school students

when solving the test of understanding graphs in kine-

matics (TUG-K). Previous eye-tracking research of

this test by Kekule observed different strategies of stu-

dents who performed best and those who performed

worst (Kekule, 2015; Kekule, 2014), but the author

found no difference in the average ﬁxation duration

between the best and the worst performers (Kekule,

2015). The reason for this inconclusive result might

be that the response conﬁdence also has a strong in-

ﬂuence on the visual attention duration of students, as

pointed out by K

uchemann et al. (K

uchemann et al.,

2019), and was not considered in the previous TUG-

K study. In another study of visual attention distri-

bution of students while solving the TUG-K, Klein et

al. found that students focus signiﬁcantly longer on

the answer they choose which implies that students

who gave the correct answer also focus longer on it in

comparison to students who answer incorrectly (Klein

et al., 2019b). In general, the conclusions of eye-

tracking studies have the potential to identify misun-

derstandings and learning difﬁculties when combined

with other evaluations which can be used to develop

speciﬁc instructions that facilitate learning for stu-

dents.

2.4 Machine-Learning Classiﬁcation of

Response Correctness

In this work, we use three different machine-learning

classiﬁers which each of them inhibit a number of ad-

vantages in order to identify the most suitable algo-

rithm for classifying the response correctness based

on the eye-tracking metrics during the students’ so-

lution process of line-graph problems, namely the to-

tal visit duration (TVD) in speciﬁc areas of interest

(AOIs). Here, the intention is not to maximize the pre-

diction performance but to compare the performance

of different classiﬁers under similar conditions.

The three algorithms are a Support Vector Ma-

chine (SVM), a Random Forest (RF) and a Multilayer

Perceptron (MLP). The SVM is a large margin classi-

ﬁer which means that it creates a kernel-based multi-

dimensional decision boundary and aims to maximize

its margin to the training instances (G

eron, 2019).

The RF consists of an ensemble of decision trees

which each of them classiﬁes a random subset of the

training data, particularly, it searches for the best fea-

ture among a subset of features to classify an instance.

It also has the advantage of a measure of the feature

importance by evaluating how much the tree nodes re-

duce the Gini impurity on average (G

eron, 2019). The

MLP is a deep neural network which assigns a weight

to each input and classiﬁes the instance according to

CSEDU 2020 - 12th International Conference on Computer Supported Education

threshold logic units which are artiﬁcial neurons that

calculate the sum of all weighted inputs and apply a

step function to determine the output. In this case, the

training instances optimize the weight of each feature

by a backpropagation algorithm called Gradient De-

scent (G

eron, 2019).

3 METHODS

3.1 Participants

The sample consisted of N=115 German and Swiss

high school students (11th grade, 58 female, 57 male;

all with normal or correct-to-normal vision). In the

school libraries we set up several identical eye track-

ing systems and the pupils participated in data col-

lection in groups of up to four persons either in their

free time or in regular classes (with permission of the

teachers). The participants received no credit or gift

for participating.

3.2 Problem-solving Task

The TUG-K is as standardized inventory for assess-

ing student understanding of graphs, consisting of 26

items in total. All of them were presented to the stu-

dents in two sets of 13 items with a short break in be-

tween the two sets. In this work, we restrict our analy-

sis to two quantitative items, question 4, and question

5. Question 5 addresses the slope concept in context

of the velocity of an object determined via the tempo-

ral derivative of the position. Question 4 requires the

inverse mathematical calculation, viz. integrating the

velocity graph to obtain the change in position.

3.3 Eye-Tracking Procedure and

Apparatus

The items were presented on a 22-in. computer screen

(1920x1080; refresh rate 75 Hz) equipped with an

eye tracker (Tobii X3-120 stationary eye-tracking sys-

tem). A nine-point calibration procedure was per-

formed before each set of 13 questions. The stu-

dents then worked on the material without interrup-

tion from the researcher. The students could spend

as much time as necessary answering the questions.

Students received no feedback after completing a task

and could not return to previous tasks. For the assign-

ment of the eye-movement types (ﬁxations, saccades),

an I-VT (Identiﬁcation by Velocity Threshold) algo-

rithm was adopted (thresholds: 8500

◦

for the ac-

celeration, and 30

◦

/s for the velocity).

3.4 Machine Learning

For the preprocessing of the data, we included a num-

ber of standard procedures to improve the perfor-

mance which are outlined in the following(G

eron,

2019). We performed a log transformation of the data

which was followed by a standardization. Those TVD

values which have a z-score>4 were replaced by the

mean of that feature for that speciﬁc class. A feature

selection was applied using F-regression and the fea-

tures were ranked on basis of their signiﬁcance.

We considered three non-linear classiﬁcation al-

gorithms: A Random Forest (RF), a kernel based Sup-

port Vector Machine (SVM) and a Deep Neural Net-

work (Multilayer Perceptron - MLP).

We split the data randomly into

1 − x/x, with the testing set size x =

[0.1,0.2,0.3, 0.4,0.5,0.6, 0.7,0.8,0.9] and the

training set size of 1 − x. For every train-test split we

performed a cross validation on the training set. To

split the training data into K-folds, we used Stratiﬁed

K-fold. This process was performed 10 times and an

average accuracy was obtained for every split. The

output labels were 0 (incorrect answer selection) and

1 (correct answer selection). The best parameters

for Random Forest and SVM where obtained using

RandomizedSearchCV which we used because of

the efﬁcient and reliable results provided by this

algorithm.

For the Deep Neural Network, we used three

dense layers, we applied a ”Relu” activation function

for hidden layers and a sigmoid for the output layer.

For the loss, a binary cross entropy was used. To pre-

vent overﬁtting, we included early stopping with a pa-

tience of 100. Apart from that, 300 epochs were taken

with a learning rate of 0.005. The Neural Network

gave a least accuracy comparable to SVM and RF.

3.5 Position and Size of AOIs

Figure 1 shows the analyzed AOIs of item 4 (panel a)

and item 5 (panel b). In both problems, the analyzed

AOIs cover only the graphical area because we are in-

terested in the visual problem-solving strategy of the

students and the prediction probability based on this

data. It was previously shown that the students who

choose the correct answer focus signiﬁcantly longer

on this answer option than students who do not choose

an incorrect answer (Klein et al., 2019b). Therefore,

it is likely to have a strong effect on the prediction

probability of the algorithm when including this op-

tion and the performance of the algorithm could not

unambiguously be assigned to the problem-solving

strategy. We also did not include the text area in the

Classiﬁcation of Students’ Conceptual Understanding in STEM Education using Their Visual Attention Distributions: A Comparison of

Three Machine-Learning Approaches

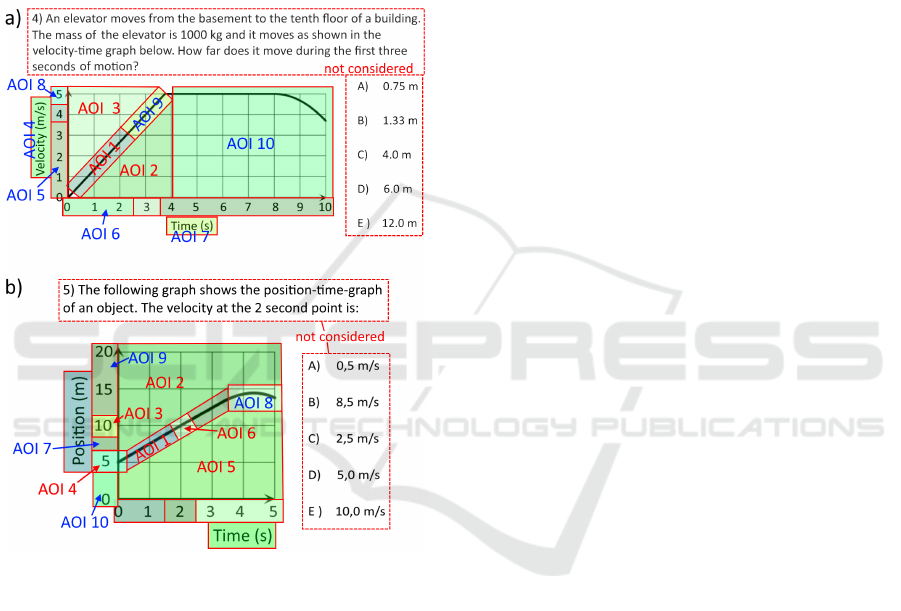
analysis because the total visit duration on the text is

likely to be attributed to reading speed which would

also cause a confusion with our focus on the graphical

problem-solving strategy of the students.

Item 4 addresses the area concept which needs to

be applied to extract information about the position

from the v(t) graph. One way to determine the area

of this graph in the ﬁrst three seconds is that the y-

axis interval [0,4] is multiplied with the x-axis inter-

val [0, 3] and the result is divided by 2 since the graph

is linear and starts at the origin. Item 5 addresses the

Figure 1: Quantitative Items of the TUG-K Analyzed in

This Work Which Address the Area Concept in Item 4

(Panel a) and the Slope Concept in Item 5 (Panel B). AOIs

Which Exhibit a Signiﬁcant Difference in the TVD between

Students with Correct and Incorrect Answers Are Labeled

in Red. Those AOI with an Insigniﬁcant Difference in the

TVD Are Labeled in Blue.

slope concept which needs to be applied to extract the

velocity from a x(t)- graph (where x(t) means the po-

sition of an object at time t.). Here, the graph does not

pass through the origin, so it is necessary to calculate

the fraction of the size of the y-axis interval [5,10] and

the size of the x-axis interval [0,2].

The position, orientation and size of AOIs are

motivated by the Information-Reduction Hypothesis

which states that experts visually select conceptual-

relevant areas more efﬁciently (Haider and Frensch,

1996) and the previous work by Klein et al. who

found that students which solve a problem correctly

focus longer on areas along the graph and on the axes

(Klein et al., 2019a).

In this line, we ﬁrst isolated the point directly

mentioned in the question text, here ”the ﬁrst three

seconds” (item 4) and ”the 2 second point” (item 5),

which we call the surface feature, and all areas which

are directly linked to it, which is the point on the graph

(item 4: x = 3, y = 4 (AOI 9); item 5: x = 2, y = 10

(AOI 6);) and the associated point on the y-axis (item

4: y = 4 (no label); item 5: y = 10 (AOI 3)). There-

fore, we separated the area along the linear part of the

graph into two (item 4) and three (item 5) sections

in order to isolate the area that is directly related to

the surface feature. Additionally, we selected the end

point of one possible y-axis interval y = 5 (AOI4 in

item 5). The remaining areas along the axes, around

the graph and the axes labels are considered individu-

ally.

4 RESULTS

In Figure 1, the AOIs are ordered according to the

ascending order of p-values which result from the F-

statistics (see Table 1 and 2). Those AOIs in which

there is a signiﬁcant relation of the response correct-

ness (coded as 1=correct and 0=incorrect) on the total

visit duration within the F-statistics are labeled in red

(signiﬁcance level p < 0.05). In item 4, the answer

correctness exhibits a signiﬁcant dependence on the

TVD in three AOIs, namely the lower section of the

graph (AOI 1), the area underneath the graph (AOI 2)

and the area above the graph (AOI 3).

In item 5, the answer correctness is also signiﬁ-

cantly related to the lower graph section (AOI 1) as

well as the area underneath (AOI 5) and above the

graph (AOI 2). Additionally, there is a signiﬁcant dif-

ference in the TVD between students who gave a cor-

rect and an incorrect answer in the areas around the

points on the y-axis y = 5 (AOI 4) and y = 10 (AOI

5) and the point on the graph (AOI 6: x = 2, y = 10)

which is linked to the surface feature.

Overall, in both items, the surface feature does not

show a signiﬁcant difference in the TVD between stu-

dents with correct and incorrect answers but the lower

graph area and the areas below and above the graph

indeed shows a signiﬁcant difference in the TVD be-

tween students with correct and incorrect answers.

The statistical difference in the TVD between stu-

dents who gave a correct and an incorrect answer is

also visible in the heat map of the relative attention

duration in Figure 2. In comparison of the total visit

duration in item 4 between students who answered

CSEDU 2020 - 12th International Conference on Computer Supported Education

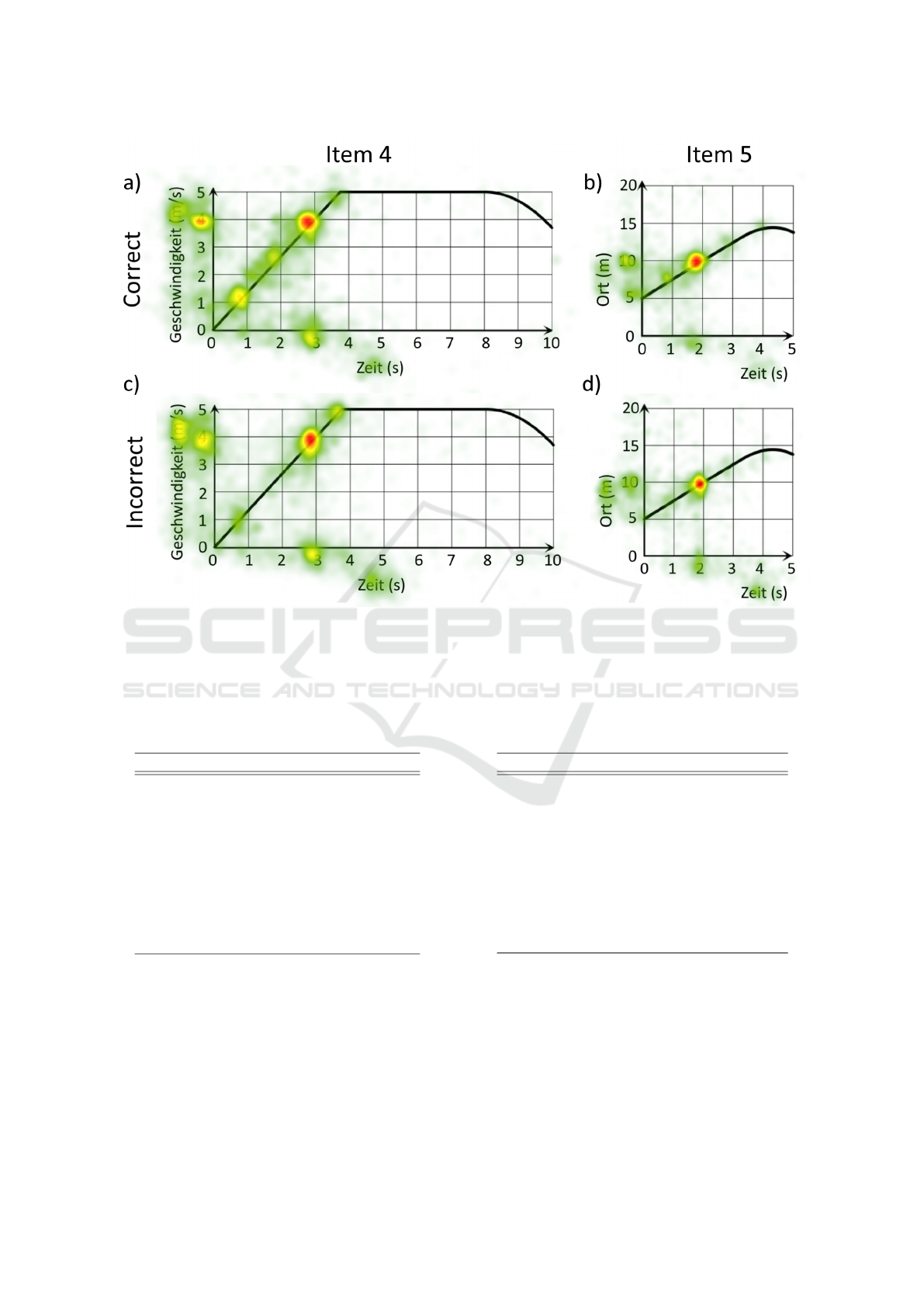
Figure 2: Heat Maps of the Relative Attention Duration for Item 4 (Left Panels) and 5 (Right Panels) for Students Who

Answered Correctly (Top Panels) and Students Who Answered Incorrectly (Bottom Panel).

Table 1: AOIs of Item 4 including the Statistical Compar-

ison (Effect Size in Terms of the p-Value) of the TVD be-

tween Students Who Answered Correctly and Those Who

Answered Incorrectly for Each AOI. The First Three AOIs

Are below the Signiﬁcance Level of p < 0.05.

Area p-value Label

Lower graph section < 10

−4

AOI 1

Below graph 0.0083 AOI 2

Above graph 0.0163 AOI 3

y-axis label 0.3677 AOI 4

y-axis interval: [0, 3] 0.4109 AOI 5

x-axis interval: [0, 2] 0.4409 AOI 6

x-axis label 0.4919 AOI 7

y-value: y = 5 0.5672 AOI 8

Upper graph section 0.6301 AOI 9

Remaining graph area 0.6474 AOI 10

this question correctly (panel a) and those who an-

swered it incorrectly (panel b), it is noticeable that

students with a correct answer pay more visual at-

tention on the lower section of the linear part of the

graph as well as below the graph and the y-axis tick

labels for y < 4. In contrast, students with an incor-

rect answer allocate more relative attention to the end

of the linear region and the units of the y-axis. In this

illustration, it seems that both student groups focus

Table 2: AOIs of Item 5 including the Statistical Compar-

ison (Effect Size in Terms of the p-Value) of the TVD be-

tween Students Who Answered Correctly and Those Who

Answered Incorrectly for Each AOI. The First Six AOIs Are

below the Signiﬁcance Level of p < 0.05.

Area p-value Label

Lower graph section 0.0002 AOI 1

Above graph 0.0006 AOI 2

y-value: y = 10 0.0046 AOI 3

y-value: y = 5 0.0117 AOI 4

Below graph 0.0387 AOI 5

Point: x = 2, y = 10 0.0453 AOI 6

y-value: y = 7.5 0.2086 AOI 7

Non-linear part 0.2098 AOI 8

y-axis interval: [15, 20] 0.3791 AOI 9

y-value: y = 0 0.4227 AOI 10

similarly on the surface feature (x = 3) and the areas

which are linked to the surface feature, i.e. the point

(x = 3, y = 4) and yaxis tick label y = 4.

Similarly, the heat maps of the relative durations

of item 5 show that the students who gave a correct

answer (Figure 2b) seem to focus on distinct points

on the graph where the graph intersects with the ver-

tical grid lines whereas the students with an incorrect

answer (Figure 2b) show a more scattered visual at-

Classiﬁcation of Students’ Conceptual Understanding in STEM Education using Their Visual Attention Distributions: A Comparison of

Three Machine-Learning Approaches

tention. In this way, it is visible that students with

a correct answer focus longer on the lower section of

the graph and on the y-axis tick value y = 5. Contrary,

students who gave an incorrect answer seem to focus

more on the x-axis and y-axis labels. It seems that

above the graph, there is a particular difference in the

area between the graph and the y-axis for 5 < y < 10.

Comparably to item 4, in item 5, both student groups

seem to pay a similar amount of visual attention to

the surface feature (x = 2) and the areas which are

linked to it ((x = 2, y = 10) and y = 10). To ana-

0.0 0.2 0.4 0.6 0.8 1.0

0.5 0.6 0.7 0.8 0.9

Item 4: 4 Features

Testing set size

Prediction Probability

SVM

MLP

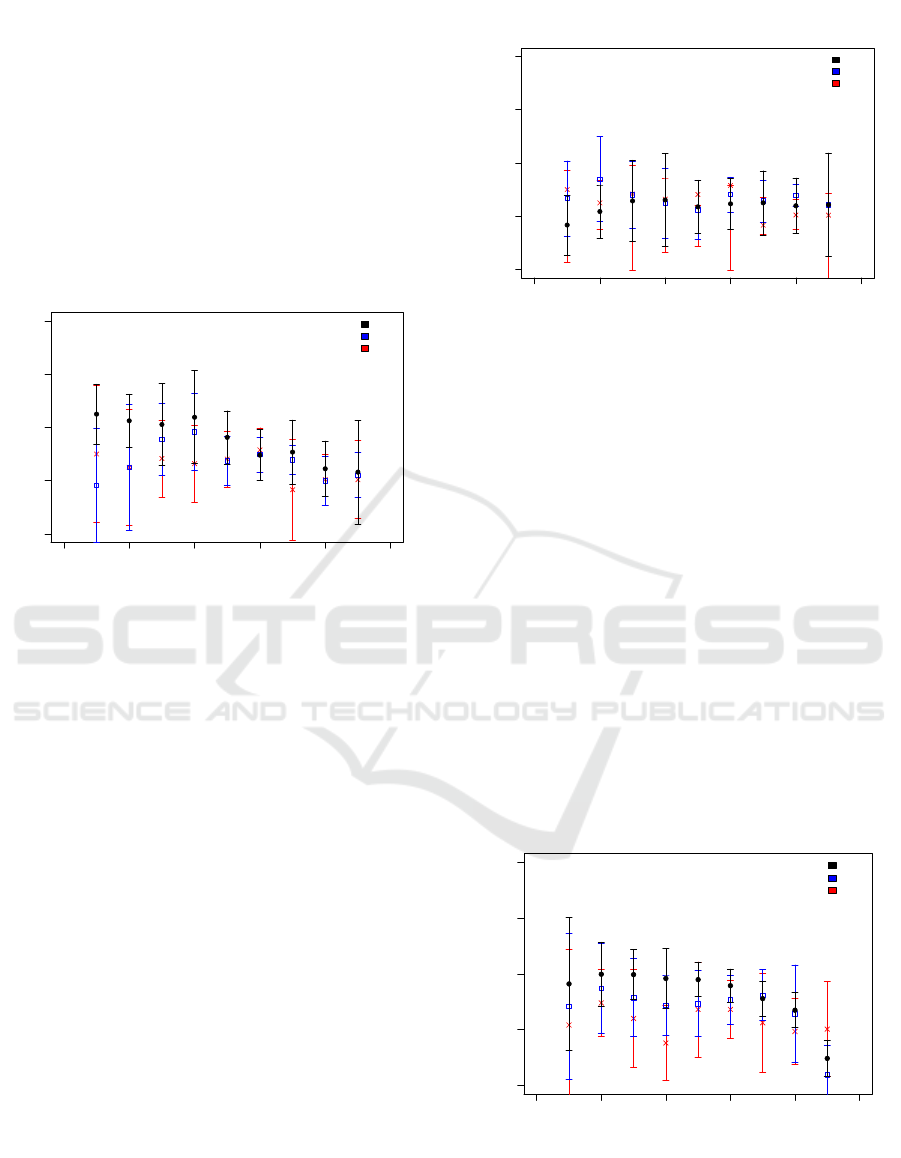
Figure 3: Probability of a Correct Prediction of Three Dif-

ferent Machine Learning Algorithms for the Response Cor-

rectness of Item 4 as a Function of Test Set Size for 4 Fea-

tures. The Data Points Represent the Average of 10 Inde-

pendent Runs and the Error Bars Reﬂect the Standard De-

viation of These Runs.

lyze the predictability of the identiﬁed AOIs in the

item 4, addressing the area concept, and item 5, tar-

geting the slope concept, we trained three different

algorithms with different number of features. Figure

3 displays the performance of the three algorithms us-

ing a small number of features. In this case, the best

performance among three, four and ﬁve features were

obtained when using four features. Please keep in

mind that the training set and the test set are disjoint

data sets. This means that the training set size is 1− x

(where x is the testing set size).

In Figure 3, it is noticeable that the prediction

probability of the SVM is increasing with test set sizes

(i.e. with decreasing training set sizes) whereas the

MLP remains unaffected by the change in test set size

within the error bars and the RF even exhibits a max-

imum at a testing set size of 0.4. At large test set

sizes (> 0.5), the prediction performance of the re-

sponse correctness of the three algorithms is more or

less comparable whereas the SVM exceeds the per-

formance of the other two algorithms at small test set

sizes.

0.0 0.2 0.4 0.6 0.8 1.0

0.5 0.6 0.7 0.8 0.9

Item 4: 9 Features

Testing set size

Prediction Probability

SVM

MLP

Figure 4: Prediction Probability for the Response Correct-

ness of Item 4 as a Function of Test Set Size for 9 Features.

The Data Points Represent the Average of 10 Independent

Runs and the Error Bars Reﬂect the Standard Deviation of

These Runs.

Figure 4 shows the prediction probability of the

three algorithms using the TVD of 9 AOIs for testing

and training. Here, we show the results of 9 features

because it performs best among 8, 9 or 10 features for

testing and training and we intended to contrast the

algorithm’s performance for a small and large num-

ber of features. In comparison to 4 features, the per-

formance of the deep neural network (MLP) with 9

features is the same at small and at large test set sizes.

The prediction probability of the RF is comparable

between 4 and 9 features at large test set sizes (> 0.4)

and, at small test set sizes (< 0.3), it is enhanced. The

predictive power of the SVM also shows a similar per-

formance at large test set sizes (≥ 0.6) and a clearly

decreased performance at small test set sizes (≤ 0.5).

0.0 0.2 0.4 0.6 0.8 1.0

0.5 0.6 0.7 0.8 0.9

Item 5: 3 Features

Testing set size

Prediction Probability

SVM

MLP

Figure 5: Prediction Probability for the Response Correct-

ness of Item 5 as a Function of Test Set Size for 3 Features.

As before, the Data Points Represent the Average of 10 In-

dependent Runs and the Error Bars Represent the Standard

Deviation of These Runs.

CSEDU 2020 - 12th International Conference on Computer Supported Education

0.0 0.2 0.4 0.6 0.8 1.0

0.5 0.6 0.7 0.8 0.9

Item 5: 10 Features

Test set size

Prediction Probability

SVM

MLP

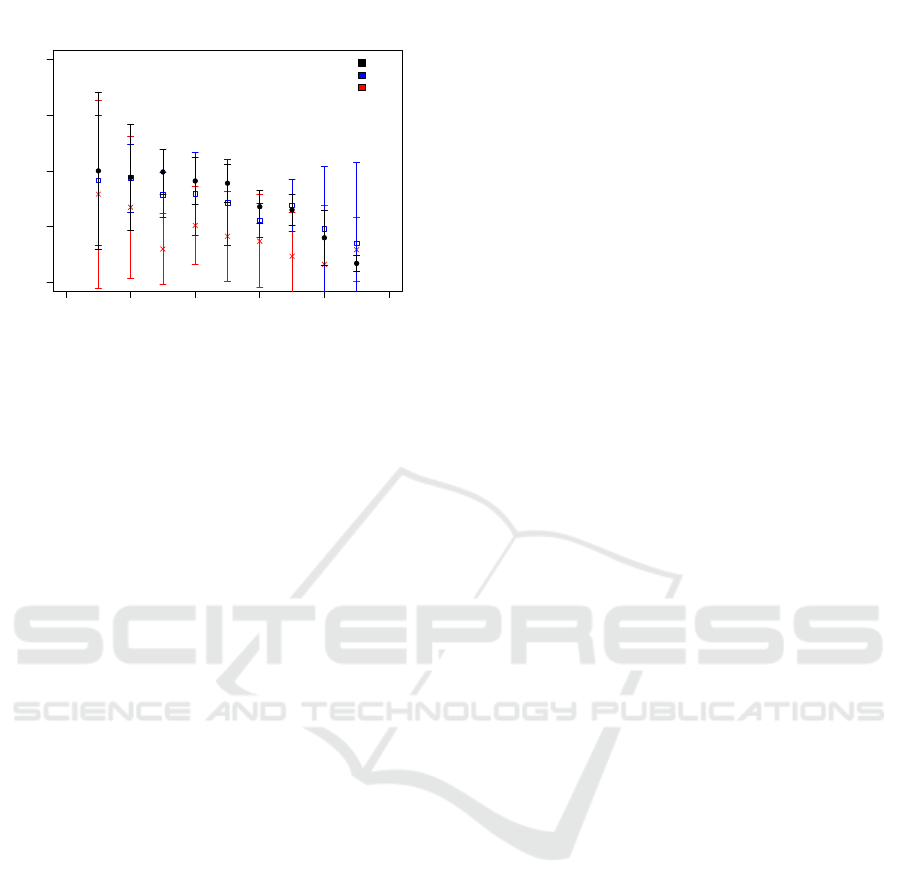
Figure 6: Prediction Probability for the Response Correct-

ness of Item 5 as a Function of Test Set Size for 10 Features.

As before, the Data Points Represent the Average of 10 In-

dependent Runs and the Error Bars Represent the Standard

Deviation of These Runs.

For item 5, we also selected the best performance

of the three algorithms to predict the response correct-

ness for a small number of features (here, the TVD of

3 AOIs) and a large number of features (the TVD of

10 AOIs). Figure 5 shows the probability of a cor-

rect prediction using three features. In this case, there

is a constant performance for the three algorithms for

small and medium test set sizes (< 0.7) and decreas-

ing trend of the SVM and RF with increasing test set

size for large test set sizes (≥ 0.7) whereas the MLP

remains constant. Among small and medium test set

sizes there is a similar hierarchy among the three al-

gorithms: The deep neural network shows the lowest

performance with a maximum performance of 65% at

a test set size of 0.2, the RF shows a higher predic-

tion probability at nearly all test set size and reaches

a maximum of 68% at a test set size of 0.2, and the

SVM outperforms the other two algorithms at small

and medium test set sizes with a maximum performs

of 70% at a test set size of 0.2. At large test set

sizes, the performance of the SVM and RF decrease

most strongly, even below the value of the MLP at the

largest test set size.

In comparison to 3 features, Figure 6 shows the

probability of a correct response prediction using 10

features. It is noticeable that the predictive power of

the MLP is most strongly decreased for all test set

sizes, so the performance difference in comparison

to the other two algorithms. Here, the performance

of the SVM got slightly reduced at nearly all test set

sizes except for the smallest test set size (). In con-

trast to the other algorithms, the performance of the

RF remains unaffected at nearly all test set size. De-

spite the changes in performance when increasing the

number of features, the performance of the SVM still

exceeds the performance of the other two algorithms

at small and medium test set sizes (≤ 0.6). At large

test set sizes the average prediction probability of the

RF is slightly higher than the one of the other two al-

gorithms.

5 DISCUSSION

In this work, we studied the probability of an accurate

prediction of students’ response correctness during

physics line-graph problems of three machine learn-

ing algorithms when trained by different eye-tracking

data sets. We analyzed the TVD as a measure of the

visual attention distribution during problem-solving

of physics line-graph items addressing the slope (item

5) and the area concept (item 4) from the TUG-K.

In item 4, we found that the TVD in three AOIs is

signiﬁcantly higher for students with correct answers

in comparison to those with incorrect answers, which

is the lower graph area, the area underneath and above

the graph. This means that students which determine

the area underneath the graph correctly also focus

longer on this area. In this problem, there are sev-

eral ways to determine the area underneath the graph.

One way would be to calculate the area of the rectan-

gle (3s · 4m/s) and divide it by two, since the graph

is the diagonal in this rectangle. When applying this

strategy, it is not obvious why the students would fo-

cus longer on the area underneath or above the graph

because it does not contain procedure-relevant infor-

mation. Another way to determine the area would

be to count the squares underneath (or above) the

graph. This strategy, in fact, requires the student to

focus on this area in order to extract the number of

squares. At this point, we cannot unambiguously con-

clude which strategy the students apply who solved

this item correctly. To solve this open question and to

understand more about the relation between problem-

solving strategy and eye-tracking data, future research

needs to include students’ comments such as a retro-

spective think aloud study.

In item 5, we found that students who solve this

quantitative problem correctly also focus longer on

the lower graph area. This observation is in agreement

with Klein et al. who observed that students who

answer qualitative slope items correctly have more

ﬁxations along the graph than students who give the

wrong answer (Klein et al., 2019a). In this item, stu-

dents also focus longer on the area underneath and

above the graph. In this case, we assume that it might

be a part of the slope determination. One approach

to calculate the slope is to mentally construct a right-

Classiﬁcation of Students’ Conceptual Understanding in STEM Education using Their Visual Attention Distributions: A Comparison of

Three Machine-Learning Approaches

angled triangle underneath (or alternatively on top of)

the graph in the way that the hypotenuse is parallel to

the graph and the right-angled sides are parallel to the

axes. The slope results from the fraction of the right-

angled sides (∆y/∆x). The visual attention could be

attributed to the mental construction of this slope tri-

angle. Additionally, there is also a higher attention on

the speciﬁc points on the y-axis (y = 5 and y = 10).

These two points are the two most likely points to be

used as end points of an y-axis interval because only

at these two y-values the graph overlaps with an inter-

section of the grid.

Furthermore, we analyzed the probability of a cor-

rect prediction of the students’ response of three dif-

ferent algorithms. Overall, it is noticeable that the

SVM performs best in several of the cases, such as

at small numbers of features (4 features in item 4; 3

features in item 5) at small and medium test set size

(< 0.6) or performs as good as other algorithms, for

instance, at a small number of features (4 features in

item 4; 3 features in item 5) at large test set sizes

(> 0.6) or with 9 features in item 4 at medium to

large test set sizes (> 0.4). However, the SVM also

seems to have some weaknesses. When the number

of features increases, for instance in item 4 from 4 to

9 features or in item 5 from 3 to 10 and to 13 (see

Appendix) features, the performance of the SVM de-

creases noticeably at small test set sizes (in item 4)

and at medium test set sizes (in item 5). Similarly,

the performance of the deep neural network decreases

with increasing number of features. In contrast to

that, for the studied area and slope concept, the perfor-

mance of the RF seems to be the most consistent when

changing the number of features. Here, an increase in

the number of features means that there are features

added in which the TVDs in the AOIs do not exhibit

a signiﬁcant difference between students who answer

correctly and incorrectly. It seems that this causes a

problem, particularly for the SVM and the MLP. The

performance of the RF is not affected when additional

features are added.

Here, we anticipate that an important factor which

causes the dependence of the algorithms on the num-

ber of features is the discriminatory power of the

features between students who answer correctly and

those who answer incorrectly. The creation of the

kernel-based multidimensional decision boundary in

the SVM seems to cause a better prediction than

the feature selection-process in the RF and weight-

adjustment process in the MLP when trained with dis-

criminating data. When including features with p-

values larger than 0.05, we found a decreasing per-

formance of the SVM. It seems that the creation of

the decision boundary is largely compromised when

including data which does not discriminate well. The

advantage of the RF here is that the algorithm selects

the relevant features and does not include unneces-

sary features. This explains why an increasing num-

ber of features, even adding non-discriminating fea-

tures does not seem to affect the performance of the

RF. This selection process also seems to outperform

the weight-adjusting process during the training of the

MLP.

In most of the cases, the algorithms show an in-

creasing trend with decreasing test set size. This

means, when the algorithms are trained with a larger

number of instances, the classiﬁcation of the test set

improves. In those cases, the performance of the algo-

rithms would beneﬁt from a larger number of training

instances. To optimize the performance of the algo-

rithms apart from using a larger number of training

data, one could, for instance, improve the feature se-

lection process, particularly with identifying and in-

cluding more features which show a signiﬁcant dif-

ference between students with correct and incorrect

answers. Apart from that, one could include a dimen-

sionality reduction or optimize the impurity level in

the case of decision trees. However, the identiﬁcation

of the optimal tree is a time consuming task (G

eron,

2019).

6 CONCLUSION

In this work, we used remote eye tracking to study

the visual strategies of students to solve physics line-

graph problems targeting the area and the slope con-

cept. We evaluated a large data set of 115 high school

students who solved the TUG-K and found that stu-

dents who solve an exemplary quantitative area prob-

lem correctly focus signiﬁcantly longer on the area

along the graph, not only on areas which are linked

to the surface, and on the area underneath and above

the graph. This gaze behavior can be explained with

speciﬁc mathematical problem-solving strategies but

further research is required to support this hypothe-

sis. Similarly, students who solve a quantitative line-

graph problem addressing the area concept also pay

more visual attention to the area along the graph, un-

derneath and above the graph and, additionally, they

focus longer on speciﬁc points on the y-axis which are

likely to be end points of a y-axis interval.

Using a small and a large number of eye-tracking

features, we trained three different machine learning

algorithms to classify the students’ response correct-

ness. We found that in several cases the SVM ex-

hibits the best and the MLP shows the lowest perfor-

mance. However, we found that the performance of

CSEDU 2020 - 12th International Conference on Computer Supported Education

the SVM depends on the discriminatory power of the

features and the decreases if the algorithm is trained

with features which do not discriminate well between

students with correct and incorrect answers. In such

cases, the RF shows the most consistent performance

and reaches the same performance levels as the SVM

or even outperforms the SVM.

REFERENCES

Alemdag, E. and Cagiltay, K. (2018). A systematic review

of eye tracking research on multimedia learning. Com-

puters & Education, 125:413–428.

Beichner, R. J. (1993). Third misconceptions seminar pro-

ceedings (1993).

Beichner, R. J. (1994). Testing student interpretation of

kinematics graphs. American journal of Physics,

62(8):750–762.

Ceuppens, S., Bollen, L., Deprez, J., Dehaene, W., and

De Cock, M. (2019). 9th grade students’ under-

standing and strategies when solving x (t) problems

in 1d kinematics and y (x) problems in mathemat-

ics. Physical Review Physics Education Research,

15(1):010101.

Champagne, A. and Kouba, V. (1999). Written products

as performance measures. In Mintzes, J., Wandersee,

J., and Novak, J., editors, Assessing science under-

standing: A Human constructivist view, pages 224–

248. New York: Academic Press.

Forster, P. A. (2004). Graphing in physics: Processes and

sources of error in tertiary entrance examinations in

western australia. Research in science Education,

34(3):239–265.

Gegenfurtner, A., Lehtinen, E., and S

alj

o, R. (2011). Ex-

pertise differences in the comprehension of visualiza-

tions: A meta-analysis of eye-tracking research in pro-

fessional domains. Educational Psychology Review,

23(4):523–552.

eron, A. (2019). Hands-On Machine Learning with Scikit-

Learn, Keras, and TensorFlow: Concepts, Tools, and

Techniques to Build Intelligent Systems. O’Reilly Me-

dia.

Glazer, N. (2011). Challenges with graph interpretation: A

review of the literature. Studies in Science Education,

47(2):183–210.

Haider, H. and Frensch, P. A. (1996). The role of informa-

tion reduction in skill acquisition. Cognitive psychol-

ogy, 30(3):304–337.

Hoffman, J. E. and Subramaniam, B. (1995). The role of

visual attention in saccadic eye movements. Attention,

Perception, and Psychophysics, 57:787–795.

Ivanjek, L., Susac, A., Planinic, M., Andrasevic, A., and

Milin-Sipus, Z. (2016). Student reasoning about

graphs in different contexts. Physical Review Physics

Education Research, 12(1):010106.

Just, M. A. and Carpenter, P. (1976). Eye ﬁxations and cog-

nitive processes. Cognitive Psychology, 8:441–480.

Kekule, M. (2014). Students’ approaches when dealing

with kinematics graphs explored by eye-tracking re-

search method. In Proceedings of the frontiers in

mathematics and science education research confer-

ence, FISER, pages 108–117.

Kekule, M. (2015). Students’ different approaches to solv-

ing problems from kinematics in respect of good

and poor performance. In International Conference

on Contemporary Issues in Education, ICCIE, pages

126–134.

Klein, P., K

uchemann, S., Br

uckner, S., Zlatkin-

Troitschanskaia, O., and Kuhn, J. (2019a). Student

understanding of graph slope and area under a curve:

A replication study comparing ﬁrst-year physics and

economics students. Physical Review Physics Educa-

tion Research, 15(2):020116.

Klein, P., Lichtenberger, A., K

uchemann, S., Becker, S.,

Kekule, M., Viiri, J., Baadte, C., Vaterlaus, A., and

Kuhn, J. (2019b). Visual attention while solving the

test of understanding graphs in kinematics: An eye-

tracking analysis. European Journal of Physics.

Klein, P., Viiri, J., Mozaffari, S., Dengel, A., and Kuhn, J.

(2018). Instruction-based clinical eye-tracking study

on the visual interpretation of divergence: How do

students look at vector ﬁeld plots? Physical Review

Physics Education Research, 14(1):010116.

Kozhevnikov, M., Motes, M. A., and Hegarty, M. (2007).

Spatial visualization in physics problem solving. Cog-

nitive science, 31(4):549–579.

uchemann, S., Klein, P., Fouckhardt, H., Gr

ober, S., and

Kuhn, J. (2019). Improving students’ understanding

of rotating frames of reference using videos from dif-

ferent perspectives. arXiv preprint arXiv:1902.10216.

Kustov, A. A. and Robinson, D. L. (1996). Shared neural

control of attentional shifts and eye movements. Na-

ture, 384(6604):74.

LeCompte, M. D. and Preissle, J. (1993). Ethnography and

qualitative design in educational research. San Diego,

California: Academic Press.

Madsen, A. M., Larson, A. M., Loschky, L. C., and Re-

bello, N. S. (2012). Differences in visual attention

between those who correctly and incorrectly answer

physics problems. Physical Review Special Topics-

Physics Education Research, 8(1):010122.

Mayer, R. E. (2009). Multimedia learning. New York:

Cambridge University Press, 2 edition.

McDermott, L. C., Rosenquist, M. L., and Van Zee, E. H.

(1987). Student difﬁculties in connecting graphs and

physics: Examples from kinematics. American Jour-

nal of Physics, 55(6):503–513.

Posner, G. J., Strike, K. A., Hewson, P. W., and Gertzog,

W. A. (1982). Accommodation of a scientiﬁc concep-

tion: Toward a theory of conceptual change. Science

education, 66(2):211–222.

Rayner, K. (1998). Eye movements in reading and informa-

tion processing: 20 years of research. Psychological

bulletin, 124(3):372.

Rayner, K. (2009). Eye movements and attention in read-

ing, scene perception, and visual search. The quar-

Classiﬁcation of Students’ Conceptual Understanding in STEM Education using Their Visual Attention Distributions: A Comparison of

Three Machine-Learning Approaches

terly journal of experimental psychology, 62(8):1457–

1506.

Salvucci, D. D. and Anderson, J. R. (2001). Automated

eye-movement protocol analysis. Human-Computer

Interaction, 16:39–86.

Scheiter, K., Schubert, C., Sch

uler, A., Schmidt, H., Zim-

mermann, G., Wassermann, B., Krebs, M.-C., and

Eder, T. (2019). Adaptive multimedia: Using gaze-

contingent instructional guidance to provide person-

alized processing support. Computers & Education,

139:31–47.

Schnotz, W., V. S. and Carretero, M. (1999). New perspec-

tives on conceptual change. Pergamon.

Sch

uler, A. (2017). Investigating gaze behavior during pro-

cessing of inconsistent text-picture information: Ev-

idence for text-picture integration. Learning and In-

struction, 49:218–231.

Susac, A., Bubic, A., Kazotti, E., Planinic, M., and Pal-

movic, M. (2018). Student understanding of graph

slope and area under a graph: A comparison of

physics and nonphysics students. Physical Review

Physics Education Research, 14(2):020109.

APPENDIX

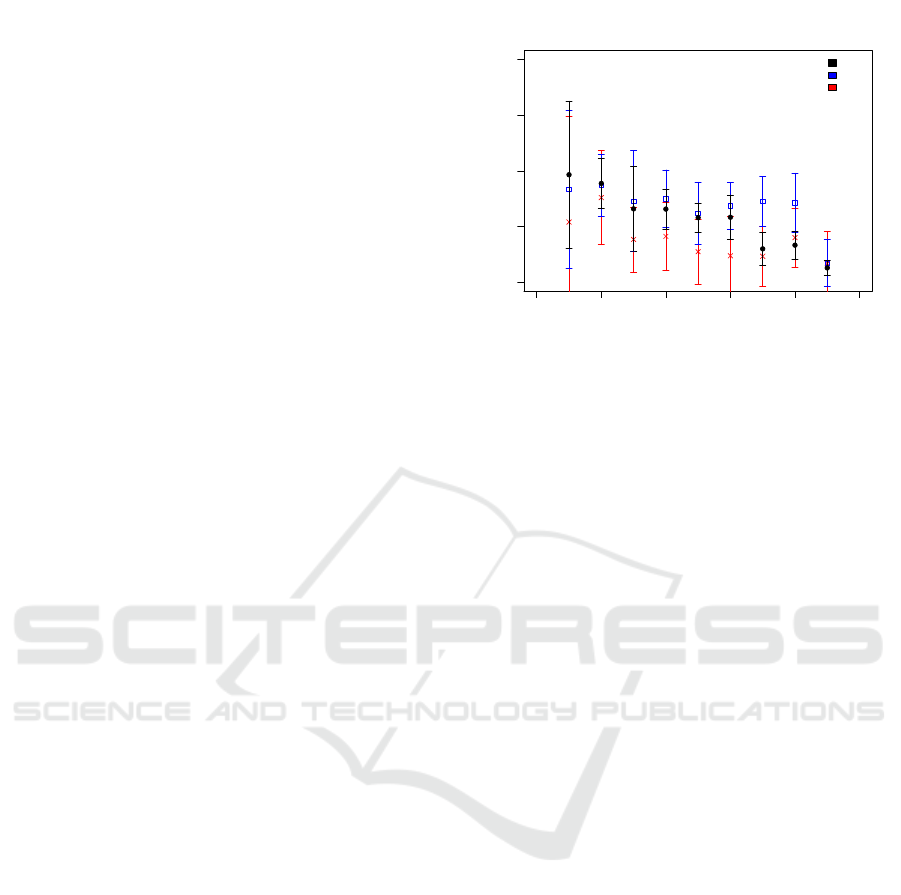
Figure 7 shows the prediction probability for the re-

sponse correctness of the three algorithms for students

while solving item 5. In this case we used 13 fea-

tures for testing and training. It is noticeable that the

RF achieves the highest prediction probability at all

test set sizes except the smallest test set size. In com-

parison to the results with 3 and with 10 features the

prediction probability of the SVM has signiﬁcantly

decreased, particularly at medium and large test set

sizes (≥ 0.3) so that it does not make the best predic-

tion anymore. At large test set sizes the SVM reaches

similar prediction probabilities as the MLP.

0.0 0.2 0.4 0.6 0.8 1.0

0.5 0.6 0.7 0.8 0.9

Item 5: 13 Features

Test set size

Prediction Probability

SVM

MLP

Figure 7: Prediction Probability for the Response Correct-

ness of Item 5 as a Function of Test Set Size for 13 Features.

As before, the Data Points Represent the Average of 10 In-

dependent Runs and the Error Bars Represent the Standard

Deviation of These Runs.

CSEDU 2020 - 12th International Conference on Computer Supported Education