
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver
Monitoring Systems
Juan Diego Ortega
1,2 a
, Marcos Nieto
1 b
, Luis Salgado
3 c
and Oihana Otaegui
1 d
1
Vicomtech Foundation, Basque Research and Technology Alliance (BRTA), Donostia-San Sebastián, Spain
2
Departamento de Señales, Sistemas y Radiocomunicaciones, ETS Ingenieros de Telecomunicación,
Universidad Politécnica de Madrid (UPM), Madrid, Spain
3
Grupo de Tratamiento de Imágenes, Information Processing and Telecommunications Center (IPTC)
and ETS Ingenieros de Telecomunicación, Universidad Politécnica de Madrid (UPM), Madrid, Spain
Keywords:
Eyelid Aperture, Blink Detection, Driver Monitoring, Computer Vision, ADAS.
Abstract:
This paper presents a new method for eyelid aperture estimation, suitable to be used in Driver Monitoring
Systems (DMS) to measure blink patterns such as microsleeps and any other metric that assess the fatigue
level of the driver. The method has been designed to work real-time and in continuous operation, by intro-
ducing a novel online Exponential Weighted Moving Average (EWMA)-based Bayesian estimation process,
which ensures dynamic adaptability to drivers with different physiognomy features, and also to changes due
to physiological states (e.g. drowsiness). Our method has been implemented in the framework of a DMS,
to take advantage of existing facial landmark detection and tracking mechanisms, and to provide real-time
functionality for driving platforms (such as the NVIDIA Drive PX 2). The method is evaluated against a
large labelled dataset, and compared to baseline and previous existing methods, showing an excellent balance
between adaptability, performance, and robustness.
1 INTRODUCTION
Drowsy driving is an important cause of road acci-
dents. Studies have shown that up to 6% of all mo-
tor vehicle crashes were related to drivers whose per-
formance was impaired by fatigue. More dramati-
cally, in the EU, 20% of truck-involved fatal crashes
were related with fatigued drivers (SafetyNet, 2009).
Therefore, the automobile industry is pushing forward
the development of fully autonomous vehicles whose
aim is to reduce crashes due to driver errors, eventu-
ally achieving the desired zero-accident road scenario
(European Commission, 2011).
While Level-5 of driving automation is the ulti-
mate goal, Levels-1, 2, and 3 still consider the active
presence of a human driver in the car (SAE Interna-
tional, 2018). Therefore, modern Advanced Driver
Assistance Systems (ADAS) developers have increas-
ingly consider to include Driver Monitoring Systems
(DMS) to achieve a holistic understanding of the
a
https://orcid.org/0000-0001-5539-106X
b
https://orcid.org/0000-0001-9879-0992
c
https://orcid.org/0000-0002-5364-9837
d
https://orcid.org/0000-0001-6069-8787
scene. DMS are crucial to analyse the driver status
for an enhanced and safer mode transfer between au-
tonomous and manual operation (Cabrall et al., 2016).
Over the past decade, works on DMS have pro-
posed methods to determine fatigue and distraction
attending to the type of inputs from the driver. Tra-
ditionally, DMSs had relied on vehicular features to
determine driver inattention (e.g. steering wheel an-
gle, pedal action, lane deviation, etc.) (Boyle et al.,
2008). However, when using highly autonomous ve-
hicles, these features will not be available as the driver
is not manipulating the vehicle, making it difficult to
continuously monitor the driver state.
Other works studied biological features of the
driver (e.g. heart, brain, skin signals) (Borghini et al.,
2014) using devices attached to the driver. These
methods require expensive intrusive sensors which
make them unfeasible for real applications in vehi-
cles.
Drivers also exhibit certain observable behaviour
such as eyelid and head movements that correlate sig-
nificantly with distraction and drowsiness. Besides,
the advances in computer vision research have made
it possible to robustly extract observable features from
342
Ortega, J., Nieto, M., Salgado, L. and Otaegui, O.
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver Monitoring Systems.
DOI: 10.5220/0009369003420352
In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2020), pages 342-352
ISBN: 978-989-758-419-0
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the driver face with unobtrusive sensors (Sikander and
Anwar, 2019).
One of the most reliable physiological indicator
for determining the driver status is the eyelid aperture
level (Danisman et al., 2010). In addition, the use of
ocular dynamics are proven to be the most robust and
meaningful method for drivers’ fatigue and distrac-
tion assessment (Sikander and Anwar, 2019). The
eyelid aperture level is the basic measure to obtain
more complex and discriminative indicators such as
blink duration, blink frequency or PERCLOS. The
last being widely used in the literature (Kaplan et al.,
2015) to determine the fatigue state of the driver.
Scientific works on blink detection could be cat-
egorised in tree main groups: (i) appearance-based
methods, (ii) motion-based methods and (iii) shape-
based methods. Appearance based methods deter-
mine the eye state by either using templates for open
and closed eyes (González-Ortega et al., 2013) or
trained classifiers using machine learning (Han et al.,
2016; Mandal et al., 2017). In (Danisman et al., 2010)
visual changes in eye states are detected using the
horizontal symmetry feature of eyes, while (Daniluk
et al., 2014) computes horizontal and vertical filters to
detect eyelids. Moreover, motion-based methods typ-
ically require to first detect the face and eye regions
within the image by means of statistical classifiers.
Then, motion in the eye area is estimated from optical
flow (Fogelton and Benesova, 2016; Drutarovsky and
Fogelton, 2015). Finally, a decision is made whether
the eyes are or are not covered by the eyelids.
A major drawback of the previous two groups is
that they determine a discrete number of eye states
(i.e. close/open or close/transition/open), instead of
measuring a continuous value of aperture, which can
be used to extract more complex information about
blinking patterns, such as the closing and opening du-
ration of blinks.
Shape-based method, on the other hand, obtain the
contour of the eyelid borders and compute an indica-
tor of the degree of eye aperture. Then, thresholds
for the eyelid aperture (Schmidt et al., 2018), classi-
fication algorithms (Soukupová and Cech, 2016) or
rule-based methods (Baccour et al., 2019) are used to
detect blinks.
The signals to compute the contour of the palpe-
bral fissure can be obtained by image processing al-
gorithms such as the adjustment of an Active Shape
Model (ASM) (Yang et al., 2012) or a Regression
Landmark Model (Gou et al., 2017). These meth-
ods are suitable and practical in the context of real
DMS solutions where face landmark detection is re-
quired for several functions, such as blink analysis,
head pose estimation, or gaze estimation refinement
(Fridman et al., 2016; Goenetxea et al., 2018).
Different approaches have been used to compute
the eyelid aperture measurement. For instance, (Fuhl
et al., 2017) approximate the upper and bottom eye-
lids contours by fitting two intersected parabolic func-
tions, one per eyelid border. The eyelid aperture is
estimated by using the distance from the upper and
lower eyelid curves.
In (Wang et al., 2009) an 8-point eye deformable
model is proposed. The eyelid aperture level degree
is obtained by computing the ratio of the maximum
vertical distance and the intra-ocular distance (IOD)
for each eye. Eye blink detection is determined by
applying an heuristic threshold determined by a set of
evaluation face data. Similarly, in (Yang et al., 2012),
a face tracker based on ASM is computed to obtain a
first position of eye landmarks. Then the eye contour
is refined by fitting a deformable template of two in-
tersected parabolic sections to a distance map based
on the distance of each pixel to the distribution of the
skin colours. The final eye closure score is evaluated
from the converged eye shape.
Blink detectors face three main challenges. First,
it is difficult to reliably distinguish between eye
blink events and gaze-related eyelid closure, spe-
cially glances to the dashboard (Friedrichs and Yang,
2010). Second, the inter-individual differences in
palpebral fissure of the drivers make it difficult to de-
tect blinks when fixed thresholds are used for all in-
dividuals (Schmidt et al., 2018). Third, driver arousal
state, such as drowsiness, has a strong impact in the
eyelid aperture signal (Ebrahim et al., 2013) mak-
ing it necessary to introduce an adaptive algorithm
to overcome the intra-individual variability of eyelid
aperture.
Past works have included some strategies to over-
come these challenges. For instance, in (Nopsuwan-
chai et al., 2008) they apply an statistical ASM to
fit a set of 20 points corresponding to the outline of
upper and lower eyelids. The eyelid aperture level
is defined as the ratio between the maximum verti-
cal distance (height, H) and the maximum horizontal
distance (width, W ) of the eye. To cope the inter-
individual variability, the eyelid aperture measure-
ment is normalised. The eyelid aperture measurement
at frame t, A
t
, is normalised to A
n,t
by:
A
n,t
=
A
t
− A
c,t
A
o,t
− A
c,t
(1)
where A
o,t
and A
c,t
is the average value of open-eye
aperture and closed-eye apertures, respectively. The
maximum opening and closing aperture level is com-
puted by averaging a ground truth data for ’standard’
blinks for each individual driver. Therefore, these
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver Monitoring Systems
343

methods do not automatically compute the normali-
sation parameters (A
o,t
and A
c,t
).
The method proposed in (Sukno et al., 2009) is
based on ASM with Invariant Optimal Features (IOF-
ASM). The quantification of eyelid aperture is de-
termined by the average of vertical distance of eye
landmarks. Then, the aperture value is normalised by
statistics estimated by observing a longer sequence.
The main drawback of these methods is that the
user-dependant signals used to normalise the eyelid
aperture metrics are computed taking a set of data
before-hand, which make these methods not suitable
for online applications.
In (Soukupová and Cech, 2016) facial landmark
detectors are used to localise the eyes and eyelid
contours combined with a classifier that is trained
to recognise eye blinks. The eye aspect ratio com-
puted from the landmarks is used as an estimate of
the degree of eyelid openness. An SVM classifier
of fixed temporal windows is trained to detect eye
blinks. However, using a fixed temporal window for
all subjects may produce mistakes in blink detection
since different individuals with different attentiveness
states could show different blink patterns. Moreover,
in (Gou et al., 2017) a joint cascaded framework for
simultaneously detect eye landmarks and eye open-
ness probability is proposed. The method rely on
the availability of a large labelled dataset to achieve
good results which could limit the applicability of the
method if such database is not available.
In some recent methods such as (Baccour et al.,
2019), a rules-based method is proposed. The steps
to define blink features is obtained by analysing the
properties of blinks. The method uses a filtered signal
of the eye closure and its derivative to calculate the
start and end of blinks. The method defines standard
steps for regular blinks and special cases are consid-
ered. Nevertheless, the computation of some of the
design thresholds are done taking a temporal windows
of several minutes which prevents it to be used in con-
tinuous driving monitoring.
To overcome the different challenges of eye blink
detection, in this paper we present a method for on-
line eyelid aperture normalisation, based on robust fa-
cial landmark points, which is invariant to image scale
and adapts to driver physiological features. A learn-
ing process based on eye state-balanced cost function
is applied to obtain the optimal model parameters us-
ing a training set composed of several subjects with
different attentiveness states. Our method can be cat-
egorised as a shape-based eyelid detection method,
which overcomes the rigidness inherent to previous
works which do not adapt online to each individual,
or to different physiological states.
Our method improves other blink detection ap-
proaches as it outputs a driver-adaptive eyelid
aperture signal, meaning that, for two individuals with
different eye physiognomy, the palpebral fissure am-
plitude will be always retrieve an equivalent eyelid
aperture value between 0 and 1, being 0 a totally
closed eye and 1 when the eye is completely open.
We have implemented the proposed method in the
context of a DMS framework, which works online
in different platforms and is compatible with existing
third-party libraries. Experimental results of our pro-
posed method support our claims, including a com-
parison with other baseline methods and implementa-
tion on different hardware setups: our method shows
improved accuracy in a binary classification of eye
states, making it suitable for integration in complex
real-time DMS pipelines.
The paper is organised as follows. Section 2 de-
tails the proposed method for eyelid aperture normal-
isation. Section 3 describes the method to select the
parameters of our algorithm. Section 4 Describes the
platforms in which our method was integrated. Sec-
tion 5 reviews evaluation of our method based on a
defined cost function and accuracy of the classifica-
tion of opened and closed (blink) states.
2 EYELID APERTURE
ESTIMATION METHOD
It is well known that the shape of human eye varies
between individuals. Different factors such as ethnic-
ity, age and gender can make the individuals to have
this variability. Then, the method that characterises
the palpebral fissure should learn from observations
what is the current degree of eye aperture based on
the maximum and minimum eyelid aperture levels for
the opened and closed eye states, respectively. This
dynamic information allows the method to normalise
the eyelid aperture level to be user-agnostic.
Note that we distinguish between eyelid amplitude
and normalised eyelid aperture. In this work the eye-
lid amplitude is referred as a value obtained from ra-
tios of eye dimensions; while the normalised eyelid
aperture, or simply the eyelid aperture is the degree
of openness of an eye. It is described as a value be-
tween 0 (closed-eye) to 1 (open-eye).
The applications of eyelid aperture detection are
many. For instance, to detect eye blinks and measure
their duration, amplitude, frequency or PERCLOS.
DMS applications can use this valuable information
to learn and predict drowsiness and fatigue state of
drivers.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
344

2.1 Definition of Eyelid Amplitude
We choose to use facial landmarks models to extract
eye dimensions. There are robust real-time facial
landmark detectors available in the literature (Asthana
et al., 2014; Kazemi and Sullivan, 2014) and as open-
source libraries: DLib ERT (King, 2009) or OpenFace
(Baltrusaitis et al., 2016)) that allows to obtain the eye
dimensions. Besides, the information of the facial
landmarks could be used by other driver monitoring
methods such as head pose estimation and gaze esti-
mation, reducing the computational overhead of algo-
rithms in complex systems, obtaining real-time inte-
grated DMS applications.
Face alignment methods compute the eye shape as
a connected set of feature points. Therefore, a mea-
sure of the eyelid amplitude is necessary to obtain
the final eye aperture level. In the literature differ-
ent methods for measuring the eyelid amplitude from
landmarks are proposed.
In (Sukno et al., 2009) the amplitude is mea-
sured as the mean distance between vertically cor-
responding landmarks. Similarly, in (García et al.,
2012) the eye amplitude is defined as the height be-
tween eyelids. However, these methods will not tol-
erate changes of scale. In contrast, other authors
(Soukupová and Cech, 2016; Mandal et al., 2017)
suggest to use scale-independent metrics where the
measure involves using a ratio of a vertical and hori-
zontal distance.
Moreover, in (Baccour et al., 2019), the eye clo-
sure is obtained from the ratio between the vertical
distance between eyelids and a fixed diameter of the
iris. However, to obtain real dimensions of the eye
this method should need to have a calibrated camera
which could not be possible in all DMSs.
In our approach the eye amplitude A
t
is set as the
eye aspect ratio (EAR) between height and width. We
take the eye contour landmarks provided by our fa-
cial landmark model and compute the eye aspect ra-
tio using the maximum height H
t
and width W
t
of the
contour of the facial points as shown in Figure 1.
The eye usually has an rectangular shape (i.e. the
width is larger that height); therefore, to obtain values
closer to one when the EAR is maximum, we propose
to use the double of the EAR as the value of eye am-
plitude to be normalised by our method (eq. 2).
A
t
= min
1,
2H
t
W
t
(2)
The eye amplitude A
t
saturates to 1 for eyes whose
height is half the width, which is something that may
occur for very round eyes. Depending on the phys-
iological state and the facial physiognomy of indi-
Figure 1: Eye landmark fitting and estimation of the height
(H) and width (W) of the eye.
viduals, the nominal amplitude level for opened and
closed eye may be different between each others.
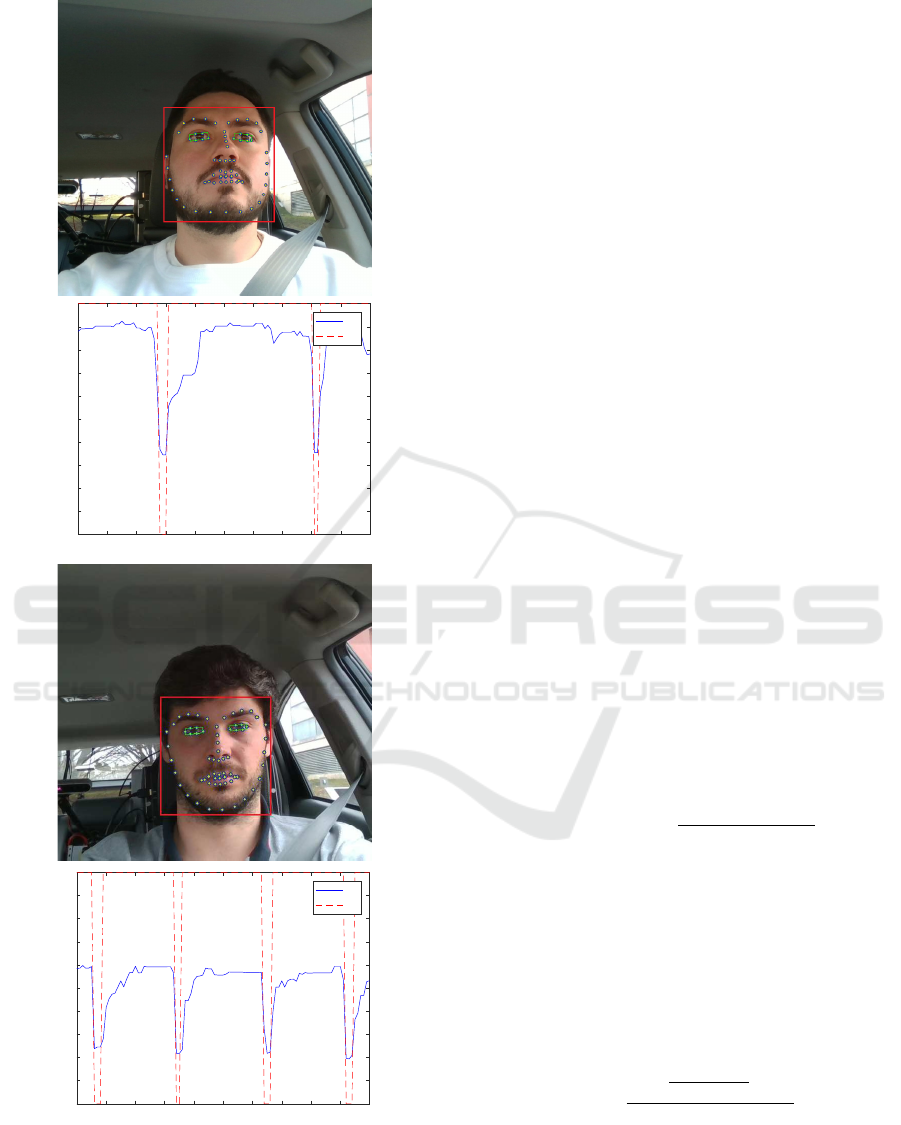
Figure 2 illustrates this difference: we can observe
that different individuals have different maximum and
minimum A values.
2.2 Normalised Aperture Estimation
The eyelid amplitude A
t
value (eq. 2) should be nor-
malised to obtain an aperture level, which is robust to
changes of subject facial characteristics. The compu-
tation of the normalised eyelid aperture A
n,t
, for each
time frame t is achieved using an online probabilistic
approach, which computes the posterior probability
of the event where eye is open E
o,t
and closed E
c,t
,
such as A
n,t
= P(E
o,t
|A
t
).
Using the Bayesian formulation we have the fol-
lowing expressions:
P(E
o,t
|A
t
) =
p(A
t
|E
o,t
)P(E
o,t
)
P(A
t
)
; (3)
P(E
c,t
|A
t
) =
p(A
t
|E
c,t
)P(E
c,t
)
P(A
t
)
(4)
where p(A
t
|E
o,t
) and p(A
t
|E
c,t
) are the probability
density functions that represent the likelihood of ob-
serving the eye in open and closed states, respectively.
P(E
o,t
) and P(E
c,t
) are the a priori probability of each
event, and P(A
t
) is the evidence, a normalisation fac-
tor to ensure
∑
s∈{o,c}
P(E
s,t
|A
t
) = 1, which is com-
puted as P(A
t
) =
∑
s∈{o,c}
p(A
t
|E
s,t
)P(E
s,t
).
The likelihood models are derived from two bal-
anced distributions, truncated at their extremes:
p(A
t
|E
o,t
) = ω
g
(A
t
)g(A
t
|A
o,t−1
;Var(A
o,t−1
)) +
ω
u
(A
t
)u(A
t
|A
o,t−1
,1)
(5)
where g(A
t
|A
o,t−1
;Var(A
o,t−1
)) is the normal distri-
bution with mean equal to A
o,t−1
and variance equal
to the variance of A
o,t−1
; and u(A
t
|A
o,t−1
,1) is a uni-
form distribution in the interval (A
o,t−1
,1), scaled
to g(A
o,t−1
). The factors ω
g
and ω
u
are step func-
tions which determine the application of functions g
and u, respectively: ω
g
(A
t
) = 1 for A
t
≤ A
o,t−1
and
ω
u
(A
t
) = 1 for A
t
> A
o,t−1
. The likelihood of A
t
of
event E
c,t
, p(A
t
|E
c,t
) can be expressed analogously.
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver Monitoring Systems
345
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
A
t
E
o,t
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
A
t
E
o,t
1470 1480 1490 1500 1510 1520 1530 1540 1550 1560 1570
Frame
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
A
t
E
o,t
2280 2290 2300 2310 2320 2330 2340 2350 2360 2370 2380
Frame
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
A
t
E
o,t
Figure 2: Differences in eyelid amplitude for two differ-
ent individuals blinking normally. The graphs below each
user’s frame show the corresponding amplitude A
t
com-
puted as in eq. 2.
Updating the values of A
o,t
and A
c,t
makes the en-
tire process recursive. For that purpose, we propose to
estimate these values as Exponential Weighted Mov-
ing Averages (EWMA) (Friedrichs and Yang, 2010)
whose learning factors are updated at each frame ac-
cording to a function which determines the local vari-
ability of the signal in a temporal window:
A
o,t
= ω
o
A
o,t−1
+ (1 − ω
o
)A
t
(6)
A
c,t
= ω
c
A
c,t−1
+ (1 − ω
c
)A
t
(7)
The learning factors, ω
o
and ω
c
, are not static, but
defined as dynamic values to increase the impact of
a new measurement A
t
according to its distance to
A
o,t−1
and A
c,t−1
, i.e. when A
t
is very close to A
o,t−1
then its impact on A
o,t
update is higher (by decreasing
ω
o
).
Therefore, we build signal A
s,t
, which is the
EWMA of measurement A
t
.
A
s,t
= α A
s,t−1
+ (1 − α)A
t
(8)
where α is the averaging factor of A
s,t
.
Under the hypothesis that the time eyes are open
is higher than the time eyes are closed, then A
s,t
is
always closer to A
o,t
than to A
c,t
. Therefore, we can
use A
s,t
to define the value of ω
o
. A way to imple-
ment this idea, and also provide a mechanism to de-
fine ω
c
is to create a sigmoid function (which returns
a value between 0 and 1) on the difference between A
t
and A
s,t−1
(higher values of this sigmoid corresponds
to situations the eye is more likely open, and lower
values correspond to closed eye measurements). The
sigmoid function is defined as:
Φ(A
s,t
− A
t
) =
1
1 + e
−a(A
s,t
−A
t
−c)
(9)
where variables a and c can be selected to make the
sigmoid function be centred at c = (A
o,t
− A
c,t
)/2
(i.e. the expected mid-way between the eye ampli-
tudes at open and closed states), and to reach a sig-
nificant value at the maximum possible difference,
e.g. Φ(A
o,t
− A
c,t
) = 0.95 (note the sigmoid func-
tion asymptotically approaches to 1 but without never
reaching it):
a = −
log
1
Φ(A
o,t
−A
c,t
)
− 1
A
o,t
− A
c,t
− c
(10)
Figure 3 details the evolution of the involved func-
tions in the computation of the normalised aperture.
Note in second row, the values of the sigmoid range
from 0 to 1, following the variability of A
t
. In
practice, this variability is counterproductive for an
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
346

EWMA learning factor (i.e. it makes the EWMA not
smooth). Therefore, the learning factor update equa-
tion needs to be regularised as follows:
ω
o
= β + (1 − β)Φ(A
s,t
− A
t
) (11)
ω
c
= β + (1 − β)(1 − Φ(A
s,t
− A
t
)) (12)
These learning factors leads to smoother evolution
of A
o,t
and A
c,t
. Parameter β is a user-defined param-
eter that balances the impact of Φ.
In addition, Figure 4 illustrates the values of the
computed amplitudes on a sample 500 frames se-
quence. As we can observe, the EWMA is slowly
learning the average of A
t
, while A
o,t
and A
c,t
adapt to
the observed open and closed-eye amplitudes (a full
discussion on the learning rates for each signal is pro-
vided in section 3). For this example the following
constants were used: α = 0.999 and β = 0.99. It is
possible to see that Φ determines how likely the mea-
surement belongs to the open and closed states, and
the learning factors ω
o
and ω
c
are updated according
to Φ. In other words, the average closed-eye ampli-
tude A
c,t
is updated with significant weight, assigned
to the current measurement A
t
proportionally to ω
c
,
which corresponds to the situations where the eye is
likely closed.
3 PARAMETER LEARNING
3.1 Manual Parameter Selection
The two design parameters of the our method are
α and β. On the one hand, α determines how fast
the EWMA A
s,t
learns from observed measurements,
while β determines the amount of impact function Φ
can have on the estimation of the amplitude values for
open and closed-eye states, A
o,t
and A
c,t
.
It is noteworthy to mention that the learning pa-
rameters of the EWMA expressions are inversely pro-
portional to the learning speed of the function, i.e.
values closer to 1 (e.g. 0.9999) express slower learn-
ing rates than smaller values. Therefore, their selec-
tion is critical to get the expected behaviour.
We can select values for this parameters by defin-
ing what is the expected learning period for the esti-
mated magnitudes. For that purpose, we can rewrite
the EWMA equation (eq. 8) as time series:
A
s,t
= α
t
A
s,0
+ (1 − α)
t
∑
i=1
α
t−i
A
i
(13)
From this expression, and considering an extreme
case where EWMA is initialised to 1.0, and then all
subsequent measurements are 0.0, we can define the
equivalent time period to decrease x% as:
T
x
=
log(1 − x)
log(α)
(14)
and reversely,
α = exp
log(1 − x)
T
x
(15)
This equation can be used to obtain a guess on
the required value of the learning parameter α for a
certain period, e.g. T
95
. For instance, α should be
at least 0.999 to get a period of about 1000 frames,
which corresponds to 40 seconds at 25 fps, because
the average value of the eyelid amplitude A
s,t
should
not change faster than that (physiologically, average
eyelid amplitude changes slowly due to fatigue fac-
tors (Sikander and Anwar, 2019)). Similar procedure
can be done over eq. 11 to obtain an estimation of β.
Therefore, β should be around 0.99 to get faster adap-
tion (T
95
(0.99) = 50) to the expected value of open
and closed-eye amplitudes, A
o,t
, A
c,t
, which can dy-
namically change due to face gestures, gaze patterns
(e.g. looking to the dashboard), etc.
3.2 Parameter Training
However, to improve the adaptability of the method
to the data of each user, the selection of the values for
α and β should be done automatically. We propose to
defining a cost function and using a training set which
covers a variety of subjects and blinking situations.
Let us consider E
o,t
, a binary signal whose value
is 1 and 0 when the eye is in open and closed, re-
spectively, and O the set of time indexes for which
A
n,t
> 0.5 (i.e. the method is classifying the eye as
open) and C the set of tie indexes for which A
n,t
≤ 0.5
(i.e. classified as closed). Then, we define a cost func-
tion which penalises the errors between the predicted
normalised eyelid aperture and the ground truth la-
bels. The objective is to obtain the values for α and β
that minimize the following cost function:
J =
1
|O|
∑
t∈O
ρ(A
n,t
,E
o,t
) +
1
|C |
∑
t∈C
ρ(A
n,t
,E
o,t
)
+
1
|O ∪ C |
∑
t
γ(A
n,t
,E
o,t
,τ)
(16)
where |O| and |C | are the cardinalities of sets O and C
respectively, and ρ() is a M-estimator of the squared
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver Monitoring Systems
347

100 150 200 250 300 350 400 450 500 550 600
0
0.2
0.4
0.6
0.8
A
t
A
s,t
100 150 200 250 300 350 400 450 500 550 600
0
0.5
1
(A
s,t
-A
t
)
100 150 200 250 300 350 400 450 500 550 600
0.99
0.995
1
w
o,t
w
c,t
100 150 200 250 300 350 400 450 500 550 600
0.2
0.4
0.6
0.8
A*
o
A*
c
Figure 3: Values of the different parameters involved in the computation of the normalised aperture for a sample sequence.
100 150 200 250 300 350 400 450 500 550 600
Frame
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
A
t
A
s
A
o
A
c
A
n
Figure 4: Sample values of eyelid closure A
t
, EWMA A
s,t
, open and closed-eye estimated amplitudes A
o,t
and A
c,t
, and
normalised aperture A
n,t
.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
348

difference:
ρ(A
n,t
,E
o,t
) =
(A
n,t
− E
o,t
)
2
,i f |A
n,t
− E
o,t
| < ε
ε
2
,otherwise
(17)
where ε can be selected as a suitable maximum ex-
pected error of a classifier (e.g. ε = 0.3) so that larger
errors are considered as outliers by the M-estimator.
The factor γ() provides temporal smoothness to
the measurement, by applying a running window fac-
tor with length τ (i.e. τ = 5 frames):
γ(A
n,t
,E
o,t
,τ) =
1
2τ + 1
i=t+τ
∑
i=t−τ
ρ(A
n,t
,E
o,t
) (18)
For the training process, we have labelled 12 video
sequences 5000 frames long each (60000 labelled
frames), of 3 subjects with different physiological
facial attributes (and thus different eyelid amplitude
values), each of them in 4 different blinking states:
(awake blinking, no-blinking, long blinks, drowsy).
The sequences were captured using a real vehicle (see
Figure 2 for examples). The amplitude value A
t
is ob-
tained using the face alignment method in the litera-
ture (Kazemi and Sullivan, 2014).
To learn the differences between users we com-
pute the cost maps for each subject as shown in
Figure 5 (summing the cost of all sequences of each
subject). As we can see the shapes of the cost map
are slightly different, but showing similar minimum
values (except subject 3). For a online version of the
algorithm we can start with global parameters and as
more values are available, we can fine tune the param-
eters for each user, using the proposed method.
Moreover, we have collected all the cost values
spanning α and β from 0 to 1, and as a result we have
the cost map summed to all sequences is illustrated in
Figure 6. The minimum cost is obtained when α gets
closer to 1.0, and β is kept behind at around 0.98. This
is well aligned with the approximate values reasoned
in section 3.1. However, this automatic process allows
a better fine tuning adjustment of the parameters to
real driving sequences.
0.035
1
0.04
0.045
1
0.8
0.05
EWMA cost total
0.5
0.6
0.055
0.4
0.2
0
Figure 6: Map of the cost function J for α and β values
spanning from 0.0 to 1.0 in steps of 0.01.
4 IMPLEMENTATION
The proposed method has been implemented in C++
as part of a DMS library. This library is built as a set
of modules to address specific functions, such as face
detection, facial landmark tracking, face recognition,
eyelid closure measurement, gaze estimation, etc. An
API allows to connect complex systems with third-
party libraries such as OpenCV, DLib, OpenFace, etc.
The DMS pipeline with eyelid aperture estimation
was integrated into three different machines, includ-
ing a standard PC (Intel i5, 8GB RAM), an embedded
platform (NXP i.MX6 ARM Cortex A9, 1GB RAM),
and the NVIDIA Drive PX 2 platform (2XTegra X2
SoCs). Table 1 shows the average processing time
on the test sequences. As we can see, the algorithm
runs in real-time for both PC and NVIDIA Drive PX
2, while still provides about 10 fps for the embedded
platform, which is enough to run the application. The
normalisation method consumes only a small fraction
of the entire pipeline (most of the computation goes
to previous stages, such as facial landmark analysis).
0.05
1
0.06
0.07
1
0.08
EWMA cost user 1
0.5
0.09
0.5
0
0.02
1
0.025
1
0.03
EWMA cost user 2
0.5
0.035
0.5
0
0.03
1
0.035
1
EWMA cost user 3
0.04
0.5
0.5
0
Figure 5: Map of cost function J for each user and for α and β values spanning from 0.0 to 1.0 in steps of 0.01.
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver Monitoring Systems
349

Table 1: Average computing time of the entire pipeline (in-
cluding face detection and facial landmark), and the eyelid
aperture estimation method alone.
PC Embedded Drive PX 2
Pipeline 32.5 ms 87.7 ms 23.2 ms
Eyelid 3.1 ms 6.7 ms 2.1 ms
5 TESTS & DISCUSSION
To validate the benefits of normalising the eyelid am-
plitude, we compute the normalised eyelid aperture
A
n,t
and define a threshold of 0.8 to determine binary
blink events. Since the signal is normalised for each
user, the threshold is applicable to all the tested se-
quences and will not suffer of accuracy loss when de-
tecting blinks (Schmidt et al., 2018). We set this value
to correctly include the closing and opening phases of
the blinks (i.e. eye states with eyelid aperture lower
than 80% are considered as blinks).
Ground truth annotations on blink patterns in the
driving context is not easily available. Therefore, to
test our algorithm, we have collected sequences of
three users and two arousal state with different blink-
ing patterns (awake and drowsy). Test sequences were
obtained in real driving conditions at different times
of day, with volunteers inside a real car. A total of
10000 frames were captured for each user. Manual la-
belling of the open and blinking states was performed
on the sequences.
A first evaluation of the proposed method was
done using the cost function in eq. 16 and compar-
ing it with other baseline methods. The cost function
is suitable to evaluate different algorithms as it re-
flects the error produced with respect to a ground truth
dataset. We implemented two baseline methods based
on simple calculations: the envelope function and a
Gaussian Mixture Model (GMM) of the eye ampli-
tude signal A
t
(eq. 2 to obtain the open, A
o
and closed
A
c
signals; then, using eq. 1 the normalised eyelid
aperture A
n,t
is obtained. The purpose of this eval-
uation is to assess whether our normalisation method
reduces the estimation error compared to basic signal
processing alternatives.
As we can see in Table 2, the proposed method
provides the average lowest cost, and homogeneous
costs for all users and type of blinking patterns. This
is due to its enhanced capability to adapt to eyelid am-
plitude variations, which is more robust than simple
metrics such as GMM or envelope computations.
A second evaluation was done based on a bi-
nary classification approach. Our aim is to compare
our method’s ability to correctly classify the eyes as
open or closed. Therefore, we defined two eye states
(classes): open and closed (blink). Accuracy val-
ues were computed for both classes (see Table 3).
Other related works results are included for compari-
son. These methods use different evaluation datasets
which were not available for our evaluation. How-
ever, our testing set share similar characteristics with
their data which make our experimentation represen-
tative and comparable. In addition, further validation
with common data should be done to complement the
provided results.
The results in Table 3 show that the application
of a user-based normalisation method before a simple
threshold-based classification achieves results com-
parable to other more sophisticated eye state clas-
sification methods. Moreover, our method is accu-
rate enough to classify different types of sequences
of awake (normal blinks) and drowsy (microsleeps)
users.
Table 3: Comparison for frame classification accuracy of
open and close states. For our method α and β with the
lowest average cost was selected.
Accuracy (%) Open Closed All
Sukno et al. (2009) 99.5 80.5 97.1
Qin et al. (2012) 97.0 88.7 91.6
Gou et al. (2017) - - 91.4
Ji et al. (2018) 96.8 96.2 97.6
Our Method (Awake) 97.3 92.1 97.8
Our Method (Drowsy) 99.1 95.9 98.9
Our Method (Total) 98.5 95.3 98.1
The results show lower accuracy for the awake
sequences, specially when classifying closed (blink)
eyes. These errors could be produced due to the fast
transitions between open and closed eyes in normal
blinks and the capturing rate of the camera (≈ 30 f ps).
In these situations one or two-frames error has a
Table 2: Cost of different methods for the 3 users and 2 blinking patterns (Normal and Drowsy). Our method (EWMA) with
α = 0.999 and β = 0.99 obtains the lowest average cost.
User 1 User 2 User 3
Normal Drowsy Normal Drowsy Normal Drowsy Mean
Envelope 0.16 0.08 0.31 0.15 0.18 0.17 0.17
GMM 0.10 0.11 0.24 0.11 0.03 0.10 0.11
Our Method 0.03 0.06 0.07 0.04 0.06 0.04 0.05
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
350

greater impact on the accuracy values compared to the
drowsy sequences, where blink intervals are longer.
Nevertheless, the overall accuracy is higher than other
results reported in related state-of-the-art methods.
Finally, the presented results suggest that in-
cluding our method in more complex blink de-
tection pipelines within Driver Monitoring Systems
(DMS) improves the overall detection accuracy with-
out adding significant computational overhead.
6 CONCLUSIONS
In this paper we have presented a method to obtain
an eyelid aperture signal, based on online amplitude
analysis, which enables driver-adaptive normalisation
of eye amplitudes obtained with face alignment meth-
ods. Its parameters have been trained using manually
labelled sequences and a proposed cost function with
minimisation mechanisms. The method has been im-
plemented within the framework of a Driver Monitor-
ing System (DMS) library. Experimental results show
real-time performance in different platforms used in
automation applications, which make it feasible for
integration in complex ADAS systems without signif-
icant computational overhead.
The method was evaluated using the proposed cost
function, which makes use of manually labelled data
samples. Comparison with simple baseline methods
was provided showing lower error cost. In addition,
the results of the classification problem for open and
closed eyes show higher accuracy and adaptability
to driver-specific visual features compared to other
state-of-the-art methods.
Our method can be incorporated into blink de-
tection pipelines to improve the estimation of blink
parameters while it also produces adaptive eyelid
aperture estimates valuable for subsequent driver’s
arousal state analysis. Future work include the valida-
tion of the method under a wide variety of use cases
and conditions, extending our current database.
ACKNOWLEDGEMENTS
This work has received funding from the European
Union’s H2020 research and innovation programme
(grant agreement n
o
690772, project VI-DAS).
REFERENCES
Asthana, A., Zafeiriou, S., Cheng, S., and Pantic, M.
(2014). Incremental face alignment in the wild. IEEE
Conference on Computer Vision and Pattern Recogni-
tion, CVPR, pages 1859–1866.
Baccour, M. H., Driewer, F., Kasneci, E., and Rosenstiel,
W. (2019). Camera-Based Eye Blink Detection Al-
gorithm for Assessing Driver Drowsiness. In IEEE
Intelligent Vehicles Symposium, pages 866–872.
Baltrusaitis, T., Robinson, P., and Morency, L. P. (2016).
OpenFace: An open source facial behavior analysis
toolkit. In 2016 IEEE Winter Conference on Applica-
tions of Computer Vision, WACV 2016.
Borghini, G., Astolfi, L., Vecchiato, G., Mattia, D., and Ba-
biloni, F. (2014). Measuring neurophysiological sig-
nals in aircraft pilots and car drivers for the assessment
of mental workload, fatigue and drowsiness. Neuro-
science and Biobehavioral Reviews, 44:58–75.
Boyle, L. N., Tippin, J., Paul, A., and Rizzo, M. (2008).
Driver performance in the moments surrounding a mi-
crosleep. Transportation Research Part F: Traffic Psy-
chology and Behaviour, 11(2):126–136.
Cabrall, C., Janssen, N., Goncalves, J., Morando, A., Sass-
man, M., and de Winter, J. (2016). Eye-based driver
state monitor of distraction, drowsiness, and cogni-
tive load for transitions of control in automated driv-
ing. 2016 IEEE International Conference on Systems,
Man, and Cybernetics (SMC), pages 001981–001982.
Daniluk, M., Rezaei, M., Nicolescu, R., and Klette, R.
(2014). Eye Status Based on Eyelid Detection : A
Driver Assistance System. In International Confer-
ence on Computer Vision and Graphics.
Danisman, T., Bilasco, I. M., Djeraba, C., and Ihaddadene,
N. (2010). Drowsy driver detection system using eye
blink patterns. In International Conference on Ma-
chine and Web Intelligence, ICMWI, pages 230–233.
Drutarovsky, T. and Fogelton, A. (2015). Eye blink detec-
tion using variance of motion vectors. In Proceed-
ings of 2th workshop on Assistive Computer Vision
and Robotics in ECCV 2014, volume 8927.
Ebrahim, P., Stolzmann, W., and Yang, B. (2013). Eye
movement detection for assessing driver drowsiness
by electrooculography. Proceedings - 2013 IEEE In-
ternational Conference on Systems, Man, and Cyber-
netics, SMC 2013, pages 4142–4148.
European Commission (2011). Roadmap to a Single Euro-
pean Transport Area–Towards a competitive and re-
source efficient transport system. Technical report,
European Commission.
Fogelton, A. and Benesova, W. (2016). Eye blink detection
based on motion vectors analysis. Computer Vision
and Image Understanding, 148:23–33.
Fridman, L., Lee, J., Reimer, B., and Victor, T. (2016).
Owl and Lizard: Patterns of Head Pose and Eye Pose
in Driver Gaze Classification. IET Computer Vision,
10(4):1–9.
Friedrichs, F. and Yang, B. (2010). Camera-based drowsi-
ness reference for driver state classification under real
driving conditions. In IEEE Intelligent Vehicles Sym-
posium, volume 4, pages 101–106.
Fuhl, W., Santini, T., and Kasneci, E. (2017). Fast & robust
eyelid outline & aperture detection in real-world sce-
User-adaptive Eyelid Aperture Estimation for Blink Detection in Driver Monitoring Systems
351

narios. In IEEE Winter Conference on Applications of
Computer Vision.
García, I., Bronte, S., Bergasa, L. M., Almazán, J., and
Yebes, J. (2012). Vision-based drowsiness detector
for real driving conditions. In IEEE Intelligent Vehi-
cles Symposium, Proceedings, pages 618–623.
Goenetxea, J., Unzueta, L., Elordi, U., Ortega, J. D., and
Otaegui, O. (2018). Efficient monocular point-of-gaze
estimation on multiple screens and 3D face tracking
for driver behaviour analysis. In 6th Int. Conf. on
Driver Distraction and Inattention, pages 1–8.
González-Ortega, D., Díaz-Pernas, F. J., Antón-Rodríguez,
M., Martínez-Zarzuela, M., and Díez-Higuera, J. F.
(2013). Real-time vision-based eye state detection for
driver alertness monitoring. Pattern Analysis and Ap-
plications, 16(3):285–306.
Gou, C., Wu, Y., Wang, K., Wang, K., Wang, F. Y., and Ji,
Q. (2017). A joint cascaded framework for simulta-
neous eye detection and eye state estimation. Pattern
Recognition, 67:23–31.
Han, W., Yang, Y., Huang, G. B., Sourina, O., Klanner, F.,
and Denk, C. (2016). Driver Drowsiness Detection
Based on Novel Eye Openness Recognition Method
and Unsupervised Feature Learning. In IEEE Interna-
tional Conference on Systems, Man, and Cybernetics,
SMC, pages 1470–1475.
Ji, Y., Wang, S., Lu, Y., Wei, J., and Zhao, Y. (2018). Eye
and mouth state detection algorithm based on con-
tour feature extraction. Journal of Electronic Imaging,
27(05):1.
Kaplan, S., Guvensan, M. A., Yavuz, A. G., and Karalurt, Y.
(2015). Driver Behavior Analysis for Safe Driving: A
Survey. IEEE Transactions on Intelligent Transporta-
tion Systems, 16(6):3017–3032.
Kazemi, V. and Sullivan, J. (2014). One millisecond face
alignment with an ensemble of regression trees. Pro-
ceedings of the IEEE Computer Society Conference
on Computer Vision and Pattern Recognition, pages
1867–1874.
King, D. E. (2009). Dlib-ml: A Machine Learning Toolkit.
Journal of Machine Learning Research, 10:1755–
1758.
Mandal, B., Li, L., Wang, G. S., and Lin, J. (2017). Towards
Detection of Bus Driver Fatigue Based on Robust Vi-
sual Analysis of Eye State. IEEE Transactions on In-
telligent Transportation Systems, 18(3):545–557.
Nopsuwanchai, R., Noguchi, Y., Ohsuga, M., Kamakura,
Y., and Inoue, Y. (2008). Driver-independent assess-
ment of arousal states from video sequences based on
the classification of eyeblink patterns. In IEEE Con-
ference on Intelligent Transportation Systems, Pro-
ceedings, ITSC, pages 917–924.
Qin, H., Liu, J., and Hong, T. (2012). An eye state identifi-
cation method based on the embedded hidden Markov
model. IEEE International Conference on Vehicular
Electronics and Safety, ICVES, pages 255–260.
SAE International (2018). Taxonomy and Definitions for
Terms Related to Driving Automation Systems for
On-Road Motor Vehicles. Technical report, SAE In-
ternational.
SafetyNet (2009). Fatigue. Technical report, European
Comission Project.
Schmidt, J., Laarousi, R., Stolzmann, W., and Karrer-Gauß,
K. (2018). Eye blink detection for different driver
states in conditionally automated driving and manual
driving using EOG and a driver camera. Behavior Re-
search Methods, 50(3):1088–1101.
Sikander, G. and Anwar, S. (2019). Driver Fatigue Detec-
tion Systems: A Review. IEEE Transactions on Intel-
ligent Transportation Systems, 20(6):2339–2352.
Soukupová, T. and Cech, J. (2016). Real-Time Eye Blink
Detection using Facial Landmarks. In 21st Computer
Vision Winter Workshop.
Sukno, F. M., Pavani, S. K., Butakoff, C., and Frangi,
A. F. (2009). Automatic assessment of eye blink-
ing patterns through statistical shape models. In In-
ternational Conference on Computer Vision Systems.
ICVS., volume 5815 LNCS, pages 33–42.
Wang, L., Ding, X., Fang, C., Liu, C., and Wang, K. (2009).
Eye blink detection based on eye contour extraction.
In Proceedings of SPIE - The International Society for
Optical Engineering, volume 7245.
Yang, F., Yu, X., Huang, J., Yang, P., and Metaxas, D.
(2012). Robust eyelid tracking for fatigue detection.
In IEEE, editor, 19th IEEE International Conference
on Image Processing (ICIP), pages 1829–1832.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
352
