
Verifying Sanitizer Correctness through Black-Box Learning:
A Symbolic Finite Transducer Approach
Sophie Lathouwers
1 a
, Maarten Everts
2 b
and Marieke Huisman
1 c
1
Formal Methods and Tools, University of Twente, Enschede, The Netherlands
2
Services and Cybersecurity, University of Twente & TNO, Enschede, The Netherlands
Keywords:
Automata Learning, Sanitizers, Symbolic Finite Transducers, Injection Attacks, Software Verification.
Abstract:
String sanitizers are widely used functions for preventing injection attacks such as SQL injections and cross-
site scripting (XSS). It is therefore crucial that the implementations of such string sanitizers are correct. We
present a novel approach to reason about a sanitizer’s correctness by automatically generating a model of the
implementation and comparing it to a model of the expected behaviour. To automatically derive a model of the
implementation of the sanitizer, this paper introduces a black-box learning algorithm that derives a Symbolic
Finite Transducer (SFT). This black-box algorithm uses membership and equivalence oracles to derive such a
model. In contrast to earlier research, SFTs not only describe the input or output language of a sanitizer but
also how a sanitizer transforms the input into the output. As a result, we can reason about the transformations
from input into output that are performed by the sanitizer. We have implemented this algorithm in an open-
source tool of which we show that it can reason about the correctness of non-trivial sanitizers within a couple
of minutes without any adjustments to the existing sanitizers.
1 INTRODUCTION
Injection flaws have been identified as the most se-
rious web application security risk by the OWASP
Top Ten project (OWASP Foundation, 2017). Some
examples of injection vulnerabilities include cross-
site scripting (XSS), code injection, command injec-
tion and SQL injection. Injection vulnerabilities oc-
cur when untrusted data is interpreted by the system,
which can result in the execution of a user-given com-
mand or the injection of malicious data into the sys-
tem. This may have consequences such as disclo-
sure of personal information, modification of data and
even deletion of data. To prevent exploitation of injec-
tion vulnerabilities one can aim to detect vulnerabil-
ities on time and repair them, reject malicious input,
limit the privileges of users or modify the given input.
This research focuses on the approach where input,
given by the user to the system, is modified such that
dangerous characters are removed.
Sanitizers, also called string manipulating pro-
grams, are programs that remove or replace
a
https://orcid.org/0000-0002-7544-447X
b
https://orcid.org/0000-0002-5302-8985
c
https://orcid.org/0000-0003-4467-072X
such unwanted characters. For example, the
FILTER SANITIZE EMAIL function in PHP (The PHP
Group, 2018b) removes all characters that are not
allowed in email addresses. Sanitizers are widely
used in practice, however, writing them is quite diffi-
cult. This is because sanitizers are used in a security-
sensitive environment where a small mistake can al-
ready introduce a vulnerability in the application. To
address this problem, we investigate how we can eas-
ily verify the correctness of existing sanitizers.
Figure 1 gives an overview of the methodology
that we use to reason about the correctness of sanitiz-
ers. We developed a black-box learning algorithm that
can automatically deduce a model, called a Symbolic
Finite Transducer (SFT), from a sanitizer by inspect-
ing the input and output. We compare the learned
model to a specification written by the user to rea-
son about the correctness of a sanitizer. As far as we
are aware, this is the first approach to automatically
derive a model that reasons about the input-output be-
haviour in a black-box manner. Moreover, aside from
writing the specification, the approach is fully auto-
matic and can be applied to existing sanitizers written
in any language. We have evaluated this approach by
analysing the correctness of existing real-world san-
itizers. We identify what types of sanitizers can be
784
Lathouwers, S., Everts, M. and Huisman, M.
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach.
DOI: 10.5220/0009371207840795
In Proceedings of the 6th International Conference on Information Systems Security and Privacy (ICISSP 2020), pages 784-795
ISBN: 978-989-758-399-5; ISSN: 2184-4356
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Specification
Learning
algorithm
Check
consistency
User
Learned model
Specification
Distinguishing
input or ‘OK’
Sanitizer
Figure 1: An overview of the methodology that we use to
reason about the correctness of sanitizers. We use a black-
box learning algorithm to derive a model from the sanitizer
which is compared to a specification written by the user. Af-
terward, any discrepancies between the models are reported
to the user.
learned using this approach and what the bottlenecks
of the current implementation are.
Contributions:
1. A novel approach to study the correctness of san-
itizers by comparing learned models to a specifi-
cation.
2. A black-box SFT learning algorithm that uses
equivalence and membership queries.
3. Implementation of the black-box SFT learning al-
gorithm and evaluation of its performance and ap-
plicability.
2 SYMBOLIC FINITE
AUTOMATA AND
TRANSDUCERS
For this research we used automata to represent san-
itizers. Mealy machines are unfortunately not suit-
able to represent sanitizers because it would need one
transition per input character per state in the automa-
ton. If this is applied in a setting with strings, with
many possible input characters, this would result in
very large and cluttered automata. For example, if
we only reason about the generic alphabet (a-z), this
would already lead to 26 transitions per state. To
make the automata more concise, we turn to symbolic
finite automata (SFAs) and symbolic finite transduc-
ers (SFTs) which can concisely represent similar tran-
sitions for many different input characters. For exam-
ple, all characters that are not changed by a sanitizer
can be represented by a single transition per state in
an SFT. SFAs can be used to reason about behaviour
that is only related to the input or the output language.
q
0
x != '>' ^ x != '&' ^ x != '<' / [x]
x == '>' / [&, g, t, ;]
x == '&' / [&, a, m, p, ;]
x == '<' / [&, l, t, ;]
Figure 2: An SFT that encodes <, > and & into their
HTML references <, > and &. This describes the
behaviour of the python method escape with the optional
flag set to False (Python Software Foundation, n.d.).
SFTs can be used to reason about the relation between
the input and the output.
A Symbolic Finite Transducer (SFT) can be de-
scribed using the tuple (Q, q
0
,F, ι, o, ∆) (Bjørner and
Veanes, 2011) where:
• Q is the finite set of states
• q
0
∈ Q is the initial state
• F ⊆ Q is the set of accepting states
• ι is the input sort
• o is the output sort
• ∆ is a function consisting of ∆
ε
∪ ∆
¯
ε
:
– ∆
ε
denotes all transitions in the automaton la-
belled with a first-order predicate (which is the
input condition) and the set of output functions.
The output functions describe what output is
generated when this transition is taken.
– ∆
¯
ε
denotes all transitions in the automaton la-
belled with ε as the input condition and the set
of output functions. ε-transitions are transitions
that can be taken without consuming an input at
any point in time.
An example of an SFT can be seen in Figure 2.
Each transition is labelled y/z where y denotes the
input condition and z denotes the set of output func-
tions. The initial state is indicated by an arrow and
accepting states are encircled twice in the figure. To
check whether an SFT accepts a certain input, we
start in the initial state. For each character of the in-
put, denoted by x in the input condition, we evaluate
the predicates of the transitions starting in the cur-
rent state. We will then follow the transition whose
predicate evaluates to true for this input character and
generate the corresponding output. If we end in an
accepting state, then the input is accepted.
An SFA is an SFT that produces empty outputs
(Bjørner and Veanes, 2011). Thus, an SFA looks sim-
ilar to an SFT, the only difference is that there are no
output functions for transitions.
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach
785

3 SPECIFICATIONS
To reason about the correctness of sanitizers, we es-
tablish what behaviour is considered correct by writ-
ing a specification which describes how the sanitizer
is supposed to behave. In this section, we there-
fore first discuss what types of specifications can be
checked with our approach (see Section 3.1). Fol-
lowed by Section 3.2 which describes how the cor-
rectness of the specifications can be checked.
Instead of comparing the specification and imple-
mentation, it is also possible for the user to inspect
the learned model itself without writing a specifica-
tion. However, we think that writing a specification
is important since it forces the user to think about
what correct behaviour would be. Moreover, it is easy
to overlook mistakes in a model. Aside from that,
specifications can also be reused for similar sanitiz-
ers whereas manual inspection would be required for
each new implementation.
3.1 Type of Specifications
To discover the type of behaviours that users are in-
terested in, we looked at the literature (Hooimeijer
et al., 2011) and organised a brainstorming session
with employees of a security company called North-
wave (Northwave, n.d.), that specialises in, among
other things, security testing.
The following type of specifications can be
checked with our approach:
• Blacklisting: Specify which (sequences of) char-
acters are not allowed in the input or output.
• Whitelisting: Specify which (sequences of) char-
acters are allowed in the input or output.
• If z then x → y: If condition z is satisfied, then all
occurrences of x are replaced by y. Note that this
can also be used to specify that something must
not change, in that case, you specify “if z then x →
x”. If z is replaced by True then the specification
means that x should always be changed into y.
• Length: Specify the allowed length of the input or
output.
• Equivalence, Idempotency and Commutativity:
Check whether two sanitizers behave the same,
whether a sanitizer is idempotent or whether a
sanitizer commutes with another sanitizer.
• Bad Output: Given a bad output, search for an
input that leads to this output.
We can divide these types of specifications into
two categories: input/output-only and input-output
related.
q
8
q
0
x != '<'
x != 's' ^ x != '<'
q
1
x == '<'
x == '<'
x != 'c' ^ x != '<'
q
2
x == 's'
x != 'r' ^ x != '<'
q
3
x != 'i' ^ x != '<'
q
4
x == 'c'
x != 'p' ^ x != '<'
q
5
x != 't' ^ x != '<'
q
6
x == 'r'
x != '>' ^ x != '<'
q
7
x == 'i'
x == '<'
x == '<'
x == 'p'
x == '<'
x == '<'
x == 't'
x == '<'
x == '<'
true
x == '>'
Figure 3: An SFA that accepts all inputs that contain
<script>.
Input/output-only Specifications are specifications
that only reason about the input language or the output
language. Specifications that are input/output-only,
and should be expressed with SFAs, include: black-
listing, whitelisting and length specifications.
Input-output Related Specifications reason about
the transformation from the input into the output.
Input-output related specifications, that should be ex-
pressed with SFTs, include: If z then x → y, equiv-
alence, idempotency, commutativity and bad output
specifications.
3.2 Checking Specifications
Next, we explore what users need to specify to check
each type of specification mentioned in the previous
section. It also explains how each specification is
compared to the learned model using the information
provided by the user. It is important that if a specifi-
cation is in the form of an SFT, then the SFT needs
to be single-valued, i.e., it always produces the same
output upon a given input. This is necessary in order
to determine equivalence. While determinism of the
SFT implies that it is single-valued, nondeterministic
SFTs can also be single-valued (Veanes et al., 2012).
In case the specification is in the form of an SFA, we
can compare this to an SFA of the input or output lan-
guage which can be derived from an SFT.
Blacklisting: The user needs to construct an SFA that
accepts all unacceptable inputs or outputs as specified
on the blacklist. To check the specification, compute
the union of the specified SFA with the SFA that rep-
resents the input or output language. If the union is
equal to the empty automaton, then no disallowed in-
put or output is accepted. For example, if the text
“<script>” is disallowed, then we specify an automa-
ton that accepts everything containing this text (see
ForSE 2020 - 4th International Workshop on FORmal methods for Security Engineering
786
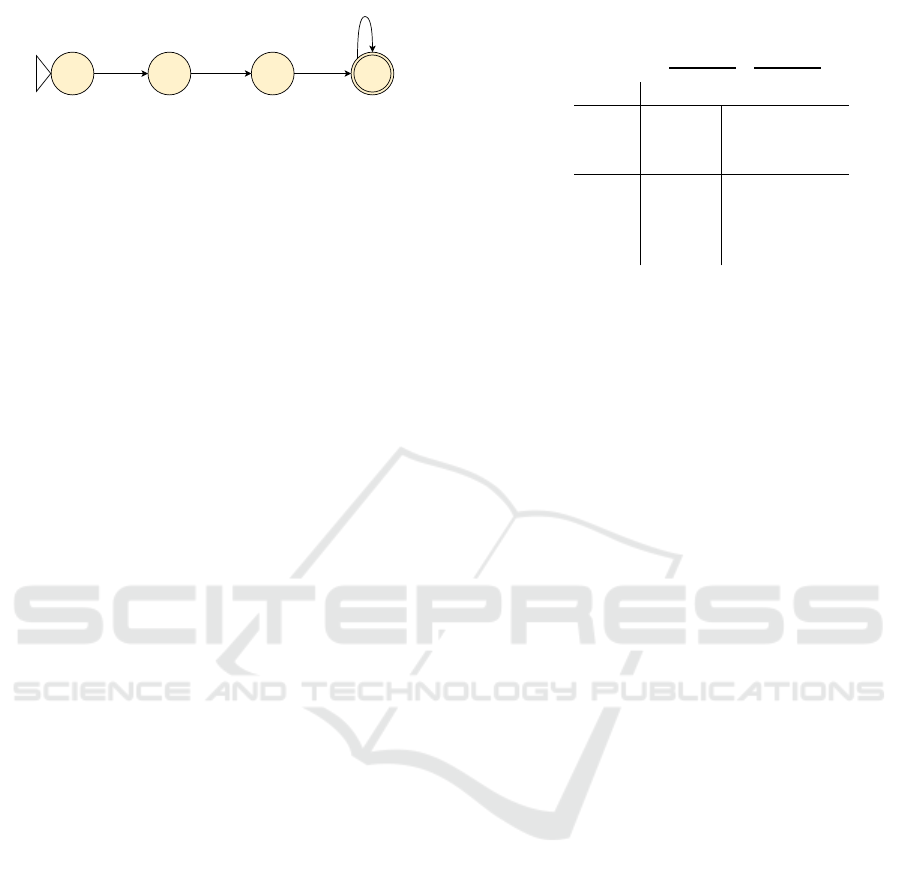
q
0
q
1
true
q
2
true
q
3
true
true
Figure 4: An SFA that accepts all inputs that consist of at
least three characters.
Figure 3).
Whitelisting: The user needs to construct an SFA that
accepts all acceptable inputs or outputs as specified
in the whitelist. The specification can be checked in
one of the following two ways: (1) check if the two
SFAs are equivalent, if so, then they accept the same
inputs or outputs, or (2) check if the learned SFA is
a subset of the specified SFA, if so, then the sanitizer
accepts some, perhaps all, inputs or outputs from the
whitelist.
Length: The user needs to specify an SFA that ac-
cepts all words of length x. To check the specifica-
tion, first, compute the complement of the specified
automaton. Next, compute the union of the comple-
ment and the SFA that represents the input or output
language. If the union is non-empty, then there ex-
ists a word with a length that is not x. Otherwise, all
words have length x. The user can also specify an
SFA that accepts all words of length < x, ≤ x, > x,
≥ x to check whether all words have the correspond-
ing length. For example, if we only allow text which
consists of at least three characters, then we specify
the automaton in Figure 4.
If z then x → y: For this, the user needs to specify
the complete system in the form of an SFT. To check
the specification, we check for equivalence between
the learned model and the specification. For exam-
ple, if the characters <, > and & are translated into
their HTML references, we write a specification as in
Figure 2.
Equivalence, Idempotency and Commutativity:
For equivalence, the user needs to specify which sani-
tizers should be compared. To check equivalence, we
check whether domain and partial equivalence hold
(Hooimeijer et al., 2011). To check for idempotency,
we compose the learned SFT that represents the san-
itizer with itself. If the composed SFT is equivalent
to the SFT that represents the sanitizer, then the san-
itizer is idempotent. When checking commutativity,
the user needs to specify between which two sanitiz-
ers, A and B, (s)he wants to check for commutativity.
Then, we compute the composition of A with B as
well as the composition of B with A. If the composi-
tions are equal, then the sanitizers A and B commute.
Bad Output: The user needs to specify the bad out-
put in the form of a string. For example, the user
might be looking for an input that leads to the out-
Table 1: Example of an SOT. ID is an abbreviation of the
IDENTITY function type.
W
z }| {
Input ε
S
ε f = ε T = [ID]
\ f =\\ T = [ID, ID]
\\ f = T = [ ]
Λ
a f = a T = [ID]
\a
f = a T = [ID]
\\\ f = \\ T = [ID, ID]
\\a f = a T = [ID]
put “<script>”. To find such an input, we use a pre-
image computation over the SFT that represents the
sanitizer. This can be implemented with a backward
breadth-first search.
4 LEARNING ALGORITHM FOR
SFTs
In this section, the black-box learning algorithm for
SFTs is explained. This algorithm allows us to derive
a model of the sanitizer’s implementation to which the
specification can be compared.
Firstly, some necessary background information
is introduced in Section 4.1. Secondly, the main al-
gorithm for learning SFTs is shown in Section 4.2.
Thirdly, details about the hypothesis generation in the
main algorithm are discussed in Section 4.3. Finally,
the implementation of the equivalence oracle that is
used in the algorithm is discussed in Section 4.4.
4.1 Preliminaries
The automata-based string analysis technique that we
have developed is a black-box learning algorithm in-
spired by Angluin’s L* algorithm (Angluin, 1987).
Our algorithm learns the behaviour of the System Un-
der Learning (SUL) without needing access to the im-
plementation. In order to do this, the algorithm can
ask two types of questions:
• Membership Queries: What is the output of the
SUL when it is given the string s?
• Equivalence Queries: Given a hypothesis automa-
ton, either obtain a confirmation that it is a correct
hypothesis automaton or obtain a counterexample
that distinguishes the hypothesis and the SUL.
We store the results of these queries in a Symbolic
Observation Table (SOT). The SOT is represented by
the tuple (S,W,Λ, f , T ). In this definition we also use
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach
787

Σ and Γ which represent the input and output alphabet
respectively:
• S ⊆ Σ
∗
is a set of access strings (Argyros et al.,
2016).
• W ⊆ Σ
∗
is a set of distinguishing strings (Argyros
et al., 2016).
• Λ ⊆ S · Σ is a set of one-step extensions of S, i.e.,
this is a (sub)set of access strings which are con-
catenated with a character from the input alpha-
bet.
• f : Σ
∗
×Σ
∗
→ Γ
∗
is a partial function that results in
the suffix of the output. The suffix is equal to the
output corresponding to the input string sd when
we have removed the largest common prefix of the
output corresponding to the input string s. sd con-
sists of some input string s followed by a single
character d from the input alphabet.
• T : Σ
∗
× Σ
∗
→ {IDENTITY,CONSTANT}
∗
is a
partial function that results in a set of types of
output functions. It corresponds to an encoding
of the output found in f . For each character in the
output, T specifies whether it corresponds to an
identity function or a constant (compared to the
input character).
Note that this is a different SOT as used by Ar-
gyros et al. (Argyros et al., 2016). The difference is
that we store the output in f and its encoding in T
whereas Argyros et al. only store the output for their
SFA learning algorithm. This encoding is necessary
to ensure that similar inputs are represented by one
state in the SFT.
Next, we discuss an example of an SOT for a sani-
tizer that escapes all (unescaped) backslashes with an-
other backslash. In Table 1, you can see the final SOT
that was generated when learning. Consider the input
“\a”. When giving this to the sanitizer, this should
result in “\\a” as output. In the SOT we store the out-
put that was generated for the last character, in this
case “a”, in f . As output we generated the same char-
acter as the input character, therefore the stored en-
coding is ID (which represents the identity function)
in T . If you want to deduce the complete output, we
would need to have a look at all prefixes of the input
“\a”: {ε, \, \a} and their corresponding generated
output functions. For ε the generated output is the
identity function, which is equal to the empty string.
This is then followed by twice the identity function
for \which results in the output \\. And finally, the
identity function corresponding to the last character
a generates a as output. If we concatenate all these
outputs, then we get that the final output is “\\a”.
Function Types: Note that an important design
choice for this algorithm is to use the function types
{IDENTITY,CONSTANT} to identify different out-
put characters. The minimal set of function types
which can represent all outputs would consist of only
CONSTANT. This would, however, not allow us to
effectively group transitions since each different in-
put character would need a different output function.
Therefore, we have chosen to add the type IDENTITY
which represents all characters that are not modified.
Using many different function types would result in
SFTs with more states therefore we limited our num-
ber of function types to two for our experiments. It
is, however, possible to define other function types.
For example, if you want to learn a model of a sani-
tizer that shifts all letters with an offset of 1, then one
could define the function type OFFSET + 1.
The black-box algorithm also uses the concept of
closedness of the observation table. Let OT be an ob-
servation table. Then OT is closed if, for all t ∈ S · Σ,
there exists an s ∈ S such that all entries in the rows
of s and t in the OT are equal (Angluin, 1987).
4.2 The SFT Learning Algorithm
The SFT learning algorithm is described in
Algorithm 1. More details on this algorithm, in-
cluding an example of how the algorithm works
and more specification examples, can be found in
the Master’s thesis on which this paper is based
(Lathouwers, 2018).
4.3 From SOT to Hypothesis
Automaton
Line 12 of the SFT learning algorithm calls an al-
gorithm to generate a hypothesis automaton from the
SOT. This algorithms is described in Algorithm 2.
Final States: We observe that different sanitizer
implementations can handle rejecting an input dif-
ferently, e.g., returning “null” or returning an empty
string. Considering that we are using a black-box al-
gorithm, the user would not know how the program
acts upon an unacceptable input. Therefore, as in
other research (Botin
ˇ
can and Babi
´
c, 2013; Shahbaz
and Groz, 2009), we assume that all states of the SFT
are final.
Generating Guards: On line 9 of the hypothesis
generation algorithm, a guard generating algorithm is
used. This algorithm generates guards, also called in-
put conditions, for all transitions that start in the same
state q
s
. To generate the guards, it uses a set of ev-
idence and the corresponding outputs. The evidence
is the input character upon which a transition is taken
to move to a next state in the automaton. The guard
generator works as follows:
ForSE 2020 - 4th International Workshop on FORmal methods for Security Engineering
788

Algorithm 1: The SFT Learning algorithm.
Data: SUL to which we can pose
membership and equivalence queries
Result: SFT that represents the SUL
1 SOT = (S = {ε},W {ε},Λ =
/
0,T =
/
0, f =
/
0)
2 Fill the SOT with entries by posing
membership queries to the SUL.
3 while no equivalent hypothesis automaton has
been found do
4 while SOT is not closed do
5 Find the shortest t ∈ Λ such that for all
s ∈ S it holds that row(s) 6= row(t).
6 Let S = S ∪ {t}
7 if there is no b ∈ Σ such that
t · b ∈ S ∪ Λ then
8 add t · b to Λ
9 end
10 Fill the missing entries in T and f by
posing membership queries.
11 end
12 Create hypothesis automaton from the
SOT.
13 Pose equivalence query for the generated
hypothesis automaton.
14 if there exists a counterexample z then
15 Let i
0
∈ {0,1,...,|z| − 1} such that the
response of the target machine is
different for the strings s
i
0
z
>i
0
and
s
i
0
+1
z
>i
0
+1
.
16 Define the distinguishing string d as
z
>i
0
+1
.
17 Let b be an arbitrary character from
the input language
18 if row(s
i
0
b) = row(s
j
) when d is
added to W for some j 6= i
0
+ 1. then
19 Add s
i
0
b to Λ
20 else
21 Add d to W .
22 end
23 Update the missing entries in T and f .
24 end
25 end
26 Return the hypothesis automaton
• If the set of evidence is empty, generate one tran-
sition with the guard True. The set of output
functions of this transition will consist only of the
identity function.
• If the set contains one piece of evidence, then
one transition will be generated with the guard
True. The set of output functions will be gener-
ated based on the output associated with the evi-
dence. It will generate either the identity function
Algorithm 2: Algorithm that describes how a hy-
pothesis automaton is derived from a closed SOT.
Data: Closed SOT
Result: Hypothesis automaton
1 for s ∈ S do
2 Create a final state q
s
3 end
4 Set the initial state to q
ε
, which is the state
corresponding to the empty string
5 foreach q
s
do
6 Find its one-step extensions in Λ in the
rows of the SOT
7 end
8 foreach q
s
do
9 (φ,ψ,q) = guardGeneratingAlgorithm(...)
/* Call the guard generating
algorithm with all one-step
extensions of q
s
*/
10 Add transition q
s
φ/ψ
−−→ q to the set of
transitions
11 end
or a constant for each character in the output. The
identity function will be generated if the character
is the same as the evidence, otherwise a constant
with the value of the output character is generated.
• Otherwise, the set contains multiple pieces of evi-
dence. Pieces of evidence are grouped together if
they lead to the same state. The largest group of
evidence is chosen to act as a sink transition. This
means that all characters for which no evidence
exists will be grouped into this sink transition. For
each generated guard, the term generator is called.
Generating Terms: The term generator is a novel
addition to the algorithm that generates terms, i.e.,
output functions, for all transitions. It takes a pred-
icate, i.e., a guard, and the starting state of the transi-
tion as an argument (see Algorithm 3).
4.4 Equivalence Oracle
In practice, there is no all-knowing entity that can
check whether a hypothesis automaton is equivalent
to the specified black-box system because we assume
that the user cannot access the implementation of the
system. Therefore, an equivalence oracle, as used
in step 5 of the learning algorithm, is approximated
using membership queries. If no counterexample is
found, then we assume that the hypothesis automaton
is a correct description of the program’s behaviour.
Some ways in which an equivalence oracle can be im-
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach
789

Algorithm 3: Algorithm that describes how terms
are generated for a specific guard and state.
Data: State q
s
and a guard g
Result: (Set of) guards with corresponding
terms.
1 for all one-step extensions of q
s
that satisfy
guard g do
2 Let s be the string that represents state q
s
3 Let s · b the string that represents state
q
s
· b.
4 Compute the suffix of the output such that
it is equal to o
s·b
− o
s
where o
s
denotes
the output of the automaton upon
input s. /* The suffix
represents the output that is
generated for character b.
*/
5 Let T = {}
6 foreach c ∈ suffix do
7 if c == b then
8 Extend T with the identity
function
9 else
10 Extend T with the constant
function c
11 end
12 end
13 end
14 if T is the same for all one-step extensions
then Return T
15
/* There exist two one-step
extensions, q
s
· b and q
s
· c, of q
s
for
which the set of term functions
differ, therefore the predicate
needs to be split. */
16
17 Split the predicate into two predicates such
that q
s
· b satisfies only one of the two
predicates and q
s
· c satisfies only the other
predicate.
18 foreach generated predicate do
19 termGenerator(q
s
, generated predicate)
20 end
plemented include the following (which are all imple-
mented in our tool):
• Random testing (Hamlet, 2002): Generate strings
of a specified length randomly.
• Random prefix selection (Smeenk, 2012): Take
the access string of a randomly chosen state as a
prefix and append a suffix of randomly generated
characters.
• State coverage (Simao et al., 2009): Generate a
set of strings such that each state in the automaton
is visited at least once.
• Transition coverage (Simao et al., 2009): Gen-
erate a set of strings such that each transition is
taken at least once.
• Predicate coverage (Offutt et al., 2003): Generate
a set of strings such that each predicate, including
sub-predicates, is satisfied at least once.
5 RESULTS
5.1 Validation of SFT Learning
Algorithm
To validate our approach, we have tried to learn mod-
els of existing real-world sanitizers. The following
sanitizers have been chosen to evaluate our approach:
1. Encode (from the he project (Bynens, 2018))
2. Escape (from the cgi python module (Python Soft-
ware Foundation, 2018))
3. Escape (from the escape-string-regexp project
(Sorhus, 2016))
4. Escape (from the escape-goat project (Sorhus,
2017))
5. Unescape (from the escape-goat project (Sorhus,
2017))
6. Unescape (from the postrank-uri project (Pos-
tRank Labs, 2017))
7. To Lowercase (from the CyberChef project
(GCHQ (Government Communications Head-
quarters), n.d.))
8. htmlspecialchars (built-in PHP function (The PHP
Group, 2018a))
9. filter sanitize email (built-in PHP function (The
PHP Group, 2018b))
10. Remove tags (from the govalidator project (Saske-
vich, 2018))
These specific sanitizer implementations have been
found by searching on GitHub among all projects
for the keywords “escape”, “encode”, and “sanitize”,
which are keywords often used to describe sanitizers.
The results on GitHub were sorted by “Most stars”
after which the top 20 repositories have been cho-
sen. Then, the repositories have been filtered so that
only string sanitizers were left which had clear docu-
mentation on how they should work, which could be
used and for which we could write a specification in
ForSE 2020 - 4th International Workshop on FORmal methods for Security Engineering
790

at most 10 minutes. Aside from sanitizers that have
been found this way, three other sanitizers have also
been tested of which two have been written in PHP
and one in Python. These have been added so that we
tested sanitizer implementations written in different
languages.
An implementation of the algorithm, as well
as all tested programs and corresponding specifica-
tions, are available at: https://github.com/Sophietje/
SFTLearning.
The tests have been run on a MacBook Pro, run-
ning Mojave 10.14.2 with a 2.3GHz Intel Core i5 (4
cores) and 16 GB of memory available. We have cho-
sen the input alphabet consisting of the Unicode char-
acters represented by the decimals 32 up to 400 (un-
less stated otherwise). This includes the Basic Latin
alphabet, the Latin-1 Supplement, Latin Extended-A
and part of Latin Extended-B. We used an equivalence
oracle that guarantees predicate coverage; it generates
3000 tests per (sub-)predicate. Also, a time-out was
set that interrupts the process if it did not deduce a
model within 10 minutes. See Table 2 for the results
of the SFT learning algorithm on existing sanitizers.
The learned models have all been compared to a
specification of the program to check whether they are
correct. No mistakes were found in these implemen-
tations.
Most of the sanitizers could be automatically in-
ferred with our SFT learning algorithm within two
minutes. Overall, the sanitizers can be divided into
two main categories:
• Sanitizers that act based on the occurrence of a
single character (sanitizers 1, 2, 3, 4, 7, 8, 9).
• Sanitizers that act based on the occurrence of mul-
tiple characters (sanitizers 5, 6, 10).
From the results we conclude that we can fully
automatically learn models of existing sanitizers that
act based on occurrences of single characters within
a couple of minutes. Learning models of sanitizers
that act based on the occurrence of multiple characters
is not yet feasible with this approach. This is what
we expected since the underlying model, SFT, cannot
represent these.
To explain why SFTs cannot represent sanitizers
that act based on the occurrence of multiple charac-
ters, we have a look at an example. Consider a specifi-
cation for a sanitizer that encodes the character &, if it
is not yet encoded, into its HTML reference ”&”
(see Figure 5). This specification does not perfectly
model the behaviour of the sanitizers. If a string ends
with ”&a”, ”&am” or ”&” then it will only output
the encoding of & and ignore the characters after this.
We need to recognize the end of the input to be able to
Table 2: Results of the SFT learning algorithm on exist-
ing sanitizers. a means that the model has been correctly
derived for the Basic Latin alphabet. b means that we are
only able to learn this model when acting as an equivalence
oracle ourselves. When automatically learning this automa-
ton, the counterexamples are not minimal, thus resulting in
a timeout because the automaton becomes too complex.
Sanitizer Total
running
time(s)
Time spent in
mem. oracle
(ms)
Time spent in
eq. oracle (ms)
# mem.
queries
# eq.
queries
# states
learned
# states
specified
# transitions
learned
# transitions
specified
Can be
learned?
1. Encode (he) 7 3919 4870 129733 336 3 1 21 7 Yes
a
2. Escape (cgi) 4 1971 2635 88442 241 3 1 12 4 Yes
a
3. Escape (escape-string-regexp) 75 18945 27137 680560 1328 3 1 14 2 Yes
4. Escape (escape-goat) 40 13882 21138 536243 1121 5 1 30 6 Yes
5. Unescape (escape-goat) - - - - - 14 - 22 - No
6. Unescape (postrank-uri) - - - - - 7 - 40 - No
7. To Lowercase (CyberChef) 23 8087 9079 192865 919 2 1 54 27 Yes
a
8. htmlspecialchars (php) 20 8581 16392 484277 316 4 1 20 5 Yes
9. filter sanitize email (php) - - - - - 1 - 12 - No
b
10. Remove tags (govalidator) - - - - - 8 - 18 - No
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach
791

q
0
q
1
q
2
x == '&' / [encode(x)]
q
3
x == ';' / [ ]
x != ';' / ['a', 'm', 'p', x]
q
4
x == 'a' / [ ]
x != 'a' / [x]
x != 'm' / ['a', x]
x == 'm' / [ ]
x != 'p' / ['a', 'm', x]
x == 'p' / [ ]
x != '&' / [x]
Figure 5: An SFT which encodes & into its HTML refer-
ence ”&”, unless it is part of an encoded &. Note that
this SFT does not precisely model the sanitizer.
solve this problem. This can be modelled by adding ε-
transitions to the automaton, which are currently not
inferred. This would, however, result in an automa-
ton that is not single-valued. Therefore, we would be
unable to check whether the automaton is equivalent
to another automaton which is necessary to compare it
to specifications. Another solution would be to extend
this algorithm to deduce SFTs with lookback, looka-
head or registers, which is an extension we leave for
future work.
5.2 Finding Bugs in Sanitizers
We also wanted to evaluate whether our method can
be used to automatically find errors in the implemen-
tations of sanitizers (since no bugs were found in pre-
vious experiments). To do this, we have asked an indi-
vidual with a security and programming background
to implement the sanitizers that we were able to au-
tomatically learn from the previous section. He pro-
vided us with two implementations for each sanitizer,
one that was intended to be correct, and one in which
he (might have) introduced mistakes on purpose. He
wrote down which errors have been introduced such
that we could, after learning and (possibly) identify-
ing errors, check whether we found all mistakes.
We learned models from his provided implemen-
tations
1
using our SFT learning algorithm. This learn-
ing process has been done with the same settings,
namely input alphabet, equivalence oracle implemen-
tation, and time-out, as were used for the previous
experiments. Then, we checked for any mistakes
in these implementations by comparing the learned
1
Available at https://github.com/Sophietje/
SFTLearning/tree/master/Sanitizers/implementationsJ
models to the specification that we had already writ-
ten for the previous experiment. If these were not
equal then a counterexample was produced for which
the two models behave differently. Such a counterex-
ample gives an idea of what the error in the program
is, which can then be used to perform a detailed man-
ual inspection of the learned model to identify the
problem.
We identified the following errors in the imple-
mentations that were supposed to be correct:
• Encode (he): Wrong first output function for sev-
eral characters and incorrect encodings of all char-
acters.
• Escape (Escape-string-regexp): Two characters
(\, $) should have been escaped and one character
(-) should not have been escaped.
• Escape (escape-goat): Wrong order in applying
the encodings.
• htmlspecialchars (php): Character encoding of ”
misses the character ;.
Next, we tried to find errors in the programs in
which mistakes were introduced on purpose. The fol-
lowing errors were found:
• Encode (he): Wrong first output function for sev-
eral characters and a wrong encoding of & and <.
• Escape (cgi): Double substitution of &.
• Escape (escape-string-regexp): Two characters
(\, $) should have been escaped and one character
(-) should not have been escaped.
• Escape (escape-goat): Wrong order in applying
encodings.
• htmlspecialchars (php): Two single quotes are
wrongly encoded instead of encoding a double
quote.
We compared the errors found with the list de-
scribing the intended errors. We correctly identified
the cause of all mistakes.
There were two cases in which the error that we
identified was not completely accurate. Firstly, in the
case of escape (cgi), we identified that the charac-
ter & was substituted twice. In the actual implemen-
tation the characters < and > were also substituted
twice. However, these second substitutions do not
change the string because the first substitution already
removed all < and > characters. So, while the dou-
ble substitution of the & character results in incorrect
output, which we identified correctly, the double sub-
stitution of < and > does not result in incorrect out-
put. Secondly, the model could not accurately repre-
sent the error that was introduced in htmlspecialchars
because the sanitizer’s behaviour for the character ’
ForSE 2020 - 4th International Workshop on FORmal methods for Security Engineering
792

depended on the character that followed. Therefore,
although we misinterpreted the error, we were still
able to identify the cause of the problem.
6 DISCUSSION
As shown previously, our approach for reasoning
about the correctness of sanitizers can effectively be
used to find errors in the implementations of sanitiz-
ers. There are, however, a number of limitations one
should be aware of.
For instance, no black-box learning algorithm has
access to an exact equivalence oracle, i.e., we cannot
precisely determine equivalence between the imple-
mentation and the model. Such an equivalence ora-
cle is therefore simulated by testing a large number
of test cases. If all test cases succeed, we assume
that the model correctly represents the implementa-
tion. However, if the number of test cases is too small,
then the model will not accurately represent the sani-
tizer. As a result, any analysis done on such a model
may also not accurately reflect the behaviour of the
sanitizer. We have shown that we can deduce correct
models when using enough test cases. Users of the
tool should, however, be aware that if it is used to
analyse more complex sanitizers, then a larger num-
ber of test cases is likely required to deduce correct
models.
Also, when learning a sanitizer, the user needs to
specify which input alphabet (s)he considers. This
means that if an error occurs outside of the specified
alphabet, then this cannot be found using our method.
Fortunately, our approach can handle large input al-
phabets.
Additionally, the user is asked to write a speci-
fication that accurately describes the sanitizer’s be-
haviour. If the user makes any mistakes in this spec-
ification, then the corresponding errors in the sani-
tizer may not be uncovered. Moreover, writing such
a specification can take a lot of time and may not be
feasible for larger models. It is, however, also possi-
ble for the user to inspect a graphical representation of
the learned model to find errors. We leave it as future
work to minimise these graphical representations.
Finally, we note that the proposed SFT learning
algorithm cannot accurately represent all sanitizers.
Specifically, it is unable to precisely represent sanitiz-
ers whose behaviour depends on multiple characters.
Thus, if our approach is used to reason about sanitiz-
ers whose behaviour depends on multiple characters,
then the results will be inaccurate. One could reason
about such sanitizers by extending the current algo-
rithm to SFTs with lookahead.
7 RELATED WORK
Black-box automata learning was first introduced by
Angluin with the L* algorithm (Angluin, 1987). L*
derives deterministic finite automata using equiva-
lence and membership queries. A similar approach,
using such queries, has been developed for many
other types of automata such as: Mealy machines
(Shahbaz and Groz, 2009), register automata (Cassel
et al., 2014), and SFAs (Argyros et al., 2016; Drews
and D’Antoni, 2017). We extend this list by devel-
oping a learning algorithm for SFTs. Moreover, au-
tomata learning has shown to be a valuable technique
to derive models from large real-world systems by
several case studies (Smeenk et al., 2015; Bohlin and
Jonsson, 2008).
Automata learning has also been used to detect
vulnerabilities in TLS implementations (De Ruiter
and Poll, 2015). Similar to how we reason about
input-output behaviour, De Ruiter and Poll reason
about TLS implementations using messages between
a client and server. They use Mealy machines to
represent the implementations which use one transi-
tion per input per state. As the input and output al-
phabet they use an abstraction of the possible mes-
sages, which amounts to 12 messages for servers and
13 messages for clients. After they have inferred a
Mealy machine, they minimise the representation by
combining similar transitions and then the model is
inspected manually to find errors. In the case of sani-
tizers, we are interested in much larger alphabets; for
our experiments we reasoned about ±370 possible in-
put characters. Due to the size of the input alphabet,
Mealy machines are not an ideal representation be-
cause the automata would be very large. Therefore,
rather than minimising afterwards, we try to learn a
symbolic finite transducer immediately. And while
manual inspection of the model is possible, we advo-
cate writing specifications which can be reused and
automatically checked.
This work is an extension of the work by Argyros
et al. (Argyros et al., 2016) who presented a black-
box learning algorithm that infers SFAs from sanitiz-
ers. Unfortunately, SFAs can only describe the input
or output language and not the relation between the
input and the output language. Argyros et al. mention
that their SFA learning algorithm can be adapted to
learn SFTs. In our research, we have developed and
implemented such an algorithm for deducing SFTs
which allows us to reason about the correctness of
transformations between the input and the output lan-
guage. We allow the user to check types of speci-
fications such as blacklisting or length whereas Ar-
gyros et al. only allow the checks that are provided
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach
793

for BEK (Hooimeijer et al., 2011) programs such as
equivalence, idempotency and commutativity, which
are included in our tool as well.
BEK (Hooimeijer et al., 2011) is a language that
can be used to develop sanitizers and analyse their
correctness. However, this cannot be used to reason
about the correctness of existing sanitizers without re-
implementing them.
Botin
ˇ
can and Babi
´
c (Botin
ˇ
can and Babi
´
c, 2013)
present a technique Sigma* that learns symbolic look-
back transducers from programs. This model can
represent more sanitizers than the SFTs that we use.
However, they use a white-box learning technique,
meaning that they need access to the source code
whereas we only need to be able to observe the input
and output of the program. Extending the algorithm
that we present in this paper to symbolic lookback
transducers that Botin
ˇ
can and Babi
´
c use is a topic for
future work.
There exist several other methods to reason about
sanitizers’ correctness most of which focus on detect-
ing vulnerabilities (Balzarotti et al., 2008; Moham-
madi et al., 2015; Shar and Tan, 2012). Our approach
can be used to detect vulnerabilities similar to these
methods. However, we are also able to reason about
their input-output behaviour in terms of, e.g. idempo-
tency and commutativity.
Aside from correct implementation of sanitizers,
the placement of sanitizers also influences the correct-
ness of an application. If sanitizers are not placed
correctly then applications may still be vulnerable.
Several researchers have therefore focused on either
repairing the placement of sanitizers, or automati-
cally placing sanitizers (Saxena et al., 2011; Weleare-
gai and Hammer, 2017; Yu et al., 2011). These ap-
proaches are considered complementary research to
the ideas discussed in this paper.
Aside from sanitization, there are also
sanitization-free defences. For example, Scholte
et al. (Scholte et al., 2012) show that automatically
validating input can be a good alternative to output
sanitization for preventing XSS and SQL injection
vulnerabilities. Similarly, Costa et al. (Costa et al.,
2007) have presented the tool Bouncer which pre-
vents exploitation of software by generating input
filters that drop dangerous inputs.
8 CONCLUSION AND FUTURE
WORK
To conclude, we have presented a new approach to
reason about the correctness of sanitizers. First of
all, we developed a new learning algorithm, which
uses equivalence and membership queries, to auto-
matically derive SFTs of existing sanitizers. This au-
tomaton describes how the sanitizer transforms an in-
put into its corresponding output. Then, we wrote a
specification of the sanitizer, in the form of an SFA
or SFT. This specification is compared to the learned
model of the sanitizer in order to find any discrepan-
cies between the models. With a case study, we have
shown that we can use our approach to automatically
reason about real-world existing sanitizers within a
few minutes.
As future research, we think that extending the
learning algorithm to support epsilon transitions and
SFTs with lookahead, lookback or registers is most
important. This would allow us to reason about more
complex sanitizers. One can also look into improving
the user experience of the approach by letting users
write the specifications in ways that are more familiar
to them such that they do not need to understand how
SFTs work. Another option is to present users with
a minimised graphical representation of the learned
models for manual correctness inspection.
REFERENCES
Angluin, D. (1987). Learning regular sets from queries
and counterexamples. Information and computation,
75(2):87–106.
Argyros, G., Stais, I., Kiayias, A., and Keromytis, A. D.
(2016). Back in black: towards formal, black box
analysis of sanitizers and filters. In 2016 IEEE Sym-
posium on Security and Privacy, pages 91–109. IEEE.
Balzarotti, D., Cova, M., Felmetsger, V., Jovanovic, N.,
Kirda, E., Kruegel, C., and Vigna, G. (2008). Saner:
Composing static and dynamic analysis to validate
sanitization in web applications. In 2008 IEEE Sym-
posium on Security and Privacy, pages 387–401.
IEEE.
Bjørner, N. and Veanes, M. (2011). Symbolic transduc-
ers. Technical Report MSR-TR-2011-3, Microsoft
Research.
Bohlin, T. and Jonsson, B. (2008). Regular inference
for communication protocol entities. Technical re-
port, Technical Report 2008-024, Uppsala University,
Computer Systems.
Botin
ˇ
can, M. and Babi
´
c, D. (2013). Sigma*: symbolic
learning of input-output specifications. In ACM SIG-
PLAN Notices, volume 48, pages 443–456. ACM.
Bynens, M. (2018). he. https://github.com/mathiasbynens/
he. Accessed on: 19-12-2019.
Cassel, S., Howar, F., Jonsson, B., and Steffen, B. (2014).
Learning extended finite state machines. In Interna-
tional Conference on Software Engineering and For-
mal Methods, pages 250–264. Springer.
Costa, M., Castro, M., Zhou, L., Zhang, L., and Peinado, M.
(2007). Bouncer: Securing software by blocking bad
ForSE 2020 - 4th International Workshop on FORmal methods for Security Engineering
794

input. In ACM SIGOPS Operating Systems Review,
volume 41, pages 117–130. ACM.
De Ruiter, J. and Poll, E. (2015). Protocol state fuzzing
of tls implementations. In Proceedings of the
24th USENIX Security Symposium, pages 193–206.
USENIX Association.
Drews, S. and D’Antoni, L. (2017). Learning symbolic
automata. In International Conference on Tools and
Algorithms for the Construction and Analysis of Sys-
tems, pages 173–189. Springer.
GCHQ (Government Communications Headquarters)
(n.d.). Cyberchef. https://github.com/gchq/
CyberChef. Accessed on: 19-12-2019.
Hamlet, R. (2002). Random testing. Encyclopedia of soft-
ware Engineering.
Hooimeijer, P., Livshits, B., Molnar, D., Saxena, P., and
Veanes, M. (2011). Fast and precise sanitizer anal-
ysis with BEK. In Proceedings of the 20th USENIX
Security Symposium. USENIX Association.
Lathouwers, S. (2018). Reasoning about the correctness
of sanitizers. Master’s thesis, University of Twente,
Enschede, the Netherlands.
Mohammadi, M., Chu, B., and Ritcher Lipford, H. (2015).
POSTER: Using unit testing to detect sanitization
flaws. In Proceedings of the 22nd ACM SIGSAC Con-
ference on Computer and Communications Security,
pages 1659–1661. ACM.
Northwave (n.d.). https://northwave-security.com/. Ac-
cessed on 19-12-2019.
Offutt, J., Liu, S., Abdurazik, A., and Ammann, P.
(2003). Generating test data from state-based speci-
fications. Software testing, verification and reliability,
13(1):25–53.
OWASP Foundation (2017). Owasp top 10 application se-
curity risks - 2017. https://www.owasp.org/index.php/
Top 10-2017 Top 10. Accessed on 19-12-2019.
PostRank Labs (2017). PostRank URI. https://github.
com/postrank-labs/postrank-uri. Accessed on: 19-12-
2019.
Python Software Foundation (2018). 20.2. cgi — common
gateway interface support. https://docs.python.org/2/
library/cgi.html. Accessed on: 19-12-2019.
Python Software Foundation (n.d.). 20.1. html — Hyper-
Text Markup Language support. https://docs.python.
org/3/library/html.html#html.escape. Accessed on 19-
12-2019.
Saskevich, A. (2018). govalidator. https://github.com/
asaskevich/govalidator/. Accessed on: 19-12-2019.
Saxena, P., Molnar, D., and Livshits, B. (2011). SCRIPT-
GARD: automatic context-sensitive sanitization for
large-scale legacy web applications. In Proceedings
of the 18th ACM conference on Computer and com-
munications security, pages 601–614. ACM.
Scholte, T., Robertson, W., Balzarotti, D., and Kirda, E.
(2012). Preventing input validation vulnerabilities
in web applications through automated type analysis.
In Computer Software and Applications Conference
(COMPSAC), 2012 IEEE 36th Annual, pages 233–
243. IEEE.
Shahbaz, M. and Groz, R. (2009). Inferring mealy ma-
chines. In International Symposium on Formal Meth-
ods, pages 207–222. Springer.
Shar, L. K. and Tan, H. B. K. (2012). Mining input saniti-
zation patterns for predicting sql injection and cross
site scripting vulnerabilities. In Proceedings of the
34th International Conference on Software Engineer-
ing, pages 1293–1296. IEEE Press.
Simao, A., Petrenko, A., and Maldonado, J. C. (2009).
Comparing finite state machine test coverage criteria.
IET software, 3(2):91–105.
Smeenk, W. (2012). Applying automata learning to com-
plex industrial software. Master’s thesis, Radboud
University Nijmegen.
Smeenk, W., Moerman, J., Vaandrager, F., and Jansen, D. N.
(2015). Applying automata learning to embedded con-
trol software. In International Conference on Formal
Engineering Methods, pages 67–83. Springer.
Sorhus, S. (2016). escape-string-regexp. https://github.com/
sindresorhus/escape-string-regexp. Accessed on: 19-
12-2018.
Sorhus, S. (2017). escape-goat. https://github.com/
sindresorhus/escape-goat. Accessed on: 19-12-2019.
The PHP Group (2018a). htmlspecialchars. http://php.net/
manual/en/function.htmlspecialchars.php. Accessed
on: 19-12-2019.
The PHP Group (2018b). Sanitize filters. http://php.net/
manual/en/filter.filters.sanitize.php. Accessed on: 19-
12-2019.
Veanes, M., Hooimeijer, P., Livshits, B., Molnar, D., and
Bjorner, N. (2012). Symbolic finite state transducers:
Algorithms and applications. In ACM SIGPLAN No-
tices, volume 47, pages 137–150. ACM.
Welearegai, G. B. and Hammer, C. (2017). Idea: Optimized
automatic sanitizer placement. In International Sym-
posium on Engineering Secure Software and Systems,
pages 87–96. Springer.
Yu, F., Alkhalaf, M., and Bultan, T. (2011). Patching vul-
nerabilities with sanitization synthesis. In Proceed-
ings of the 33rd International Conference on software
engineering, pages 251–260. ACM.
Verifying Sanitizer Correctness through Black-Box Learning: A Symbolic Finite Transducer Approach
795
