
Learning Domain-specific Grammars from a Small Number of Examples
Herbert Lange
a
and Peter Ljungl
¨
of
b
Computer Science and Engineering, University of Gothenburg and Chalmers University of Technology, Sweden
Keywords:
Computational Linguistics, Sub-grammar Extraction, Constraint Solving.
Abstract:
In this paper we investigate the problem of grammar inference from a different perspective. The common
approach is to try to infer a grammar directly from example sentences, which either requires a large training
set or suffers from bad accuracy. We instead view it as a problem of grammar restriction or sub-grammar
extraction. We start from a large-scale resource grammar and a small number of examples, and find a sub-
grammar that still covers all the examples. To do this we formulate the problem as a constraint satisfaction
problem, and use an existing constraint solver to find the optimal grammar. We have made experiments with
English, Finnish, German, Swedish and Spanish, which show that 10–20 examples are often sufficient to learn
an interesting domain grammar. Possible applications include computer-assisted language learning, domain-
specific dialogue systems, computer games, Q/A-systems, and others.
1 INTRODUCTION
The mainstream trend in NLP is towards general pur-
pose language processing for tasks such as informa-
tion retrieval, machine translation and text summar-
isation. But there are use cases where we do not want
to handle language in general, but instead restrict the
language that our systems can recognise or produce.
The reason for restricting the language can be very
high precision, e.g., in safety-critical systems, or in
order to build domain-specific systems, e.g., special-
purpose dialogue systems.
For our experiments we use the Grammatical
Framework (GF) (Ranta, 2009b; Ranta, 2011) as the
underlying grammar formalism, but the main ideas
are transferable to other formalisms such as HPSG,
LFG or LTAG. The main requirement is that there is
a general purpose resource grammar, such as the Re-
source Grammar Library (RGL) (Ranta, 2009a) for
GF.
1.1 Use Case: Language Learning
One use case is language learning – to create a tool
that can help language teachers create grammar exer-
cises for their students. We want a system that can
suggest new exercises based on a certain grammatical
topic. One exercise topic could focus on gender and
a
https://orcid.org/0000-0002-1450-5486
b
https://orcid.org/0000-0002-1625-2793
number agreement, another topic on relative clauses,
while yet another could focus on inflecting adjectives
or adverbs.
Each exercise topic is defined by a specialised
grammar that can recognise and generate examples
that showcase that topic. Creating those grammars
directly requires experience in grammar writing and
knowledge of the grammar formalism. However, lan-
guage teachers usually lack these skills. So, our idea
is to let the teacher write down a set of example sen-
tences that show which kind of sub-language they
have in mind, and the system will automatically in-
fer a suitable grammar.
The optimal final grammar should cover and gen-
eralise from the given examples, but at the same time
it should not over-generate and should instead reduce
the ambiguity as much as possible. These are contra-
dictory requirements, so the best we can hope for is a
good compromise.
1.2 Use Case: Domain-specific
Applications for Interlingual
Communication
Another use case for our research is domain spe-
cific applications, such as dialog systems, expert sys-
tems and apps to support communication in situations
where participants do not share a common language.
These situations are common in healthcare, especially
when involving immigrants. Here misunderstandings
422
Lange, H. and Ljunglöf, P.
Learning Domain-specific Grammars from a Small Number of Examples.
DOI: 10.5220/0009371304220430
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 422-430
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

can cause serious problems.
In the development of such systems, the com-
putational linguists who are specialists on the tech-
nological side have to collaborate with informants
who have deep knowledge of the language. The do-
main is established by discussing example sentences.
These sentences can be automatically translated into
a domain-specific grammar, which can be refined by
generating new example sentences based on the gram-
mar and receiving feedback about them from the in-
formants.
Such an iterative, example-based, development of
application-specific grammars allows for close col-
laboration between the parties involved. The result
is a high quality domain-specific application.
2 BACKGROUND
We cannot claim independence from related work
both from past and current research. There is a long
history of grammar development and grammar learn-
ing. Furthermore, using constraint solving for related
problems is not an uncommon approach.
2.1 Previous Work on Grammar
Inference
Grammar Inference. There has been a lot of work
on generic grammar inference, both using supervised
and unsupervised methods (see, e.g., overviews by
(Clark and Lappin, 2010) and (D’Ulizia et al., 2011)).
Most of these approaches focused on context-free
grammars, but there has also been work on learning
grammars in more expressive formalisms (e.g., (Clark
and Yoshinaka, 2014)).
Data-oriented Parsing. (DOP) (Bod, 1992; Bod,
2003; Bod, 2006) is an alternative approach. The
grammar is not explicitly inferred, but instead a tree-
bank is seen as an implicit grammar which is used by
the parser. It tries to combine subtrees to find the most
probable parse tree. The DOP model is interesting be-
cause it has some similarities with our approach (see
Section 7 for a more in-depth discussion).
Sub-grammar Extraction. We do not want to hide
the fact that there has been previous work on sub-
grammar extraction (Henschel, 1997; Ke
ˇ
selj and Cer-
cone, 2007). Both articles present approaches to
extract an application-specific sub-grammar from a
large-scale grammar focusing on more or less ex-
pressive grammar formalisms: CFG, systemic gram-
mars (equivalent to typed unification based gram-
mars) and HPSG. However, both approaches are sub-
stantially different from our approach, either in the
input they take or in the constraints they enforce on
the resulting grammar.
Logical Approaches. To our knowledge, there have
been surprisingly few attempts to use logical or
constraint-based approaches, such as theorem prov-
ing or constraint optimisation, for learning grammars
from examples. One exception is (Imada and Na-
kamura, 2009) who experiment with SAT solvers to
learn context-free grammars.
2.2 Abstract Grammars and Resources
Grammatical Framework (GF) (Ranta, 2009a; Ranta,
2011) is a multilingual grammar formalism based
on a separation between abstract and concrete syn-
tax. The abstract level is meant to be more or less
language-independent, and every abstract syntax can
have several associated concrete syntaxes, which act
as language-specific realisations of the abstract rules
and trees. This means that a multilingual GF grammar
can be used as a simple machine translation system
where the abstract syntax is used as an interlingua.
In this paper we only make use of the high-level ab-
stract syntax, which makes it possible to transfer our
approach to other grammar formalisms with a com-
parable high-level abstraction.
Abstract Syntax. is closely related to context-free
grammars. To be able to identify individual rules,
every abstract rule has a unique label. This means
that there can be several rules with the same argu-
ments and result categories, but different labels. Lex-
ical items are represented as constant functions, i.e.,
functions without parameters, on the abstract level.
Formally, an abstract grammar is a tuple G =
(C, L, R, S) where
C is a set of syntactic categories
L is a set of labels
R ⊆ L × C × C
∗
is a set of syntactic rules
S ∈ C is the start symbol of the grammar
An abstract syntax tree is a tree where all nodes are
labels which are type-correct according to the gram-
mar. There is no formal difference between leaves
and internal nodes, but a leaf is just a node without
any children. The trees are therefore similar to ab-
stract syntax trees as they are used in, e.g., computer
science (Ranta, 2012, Chapter 2.5).
Learning Domain-specific Grammars from a Small Number of Examples
423

Resource Grammar. The GF Resource Grammar
Library (RGL) (Ranta, 2009a) is a general-purpose
grammar library for 30+ languages which covers most
common grammatical constructions. Its main purpose
is to act as an API when building domain-specific
grammars. It provides high-level access to the lin-
guistic constructions, facilitating the development of
specific applications. The inherent multilinguality
also makes it easy to create and maintain multilingual
applications.
However, it is necessary to learn the GF formalism
to use the RGL to write GF grammars, limiting the
user group. In contrast, the methods presented in this
paper allow non-grammarians to create grammars for
their own domain or application.
2.3 Constraint Satisfaction Problems
(CSP)
Many logical satisfiability problems can be formu-
lated as constraint satisfaction problems (CSP) (Rus-
sell and Norvig, 2009, chapter 6). In a CSP we want
to find an assignment of a number of variables that
respect some given constraints. CSPs are classified
depending on the domains of the variables, and the
kinds of constraints that are allowed. In this paper
we formulate our problem based on Boolean variables
in the constraints but require integer operations in the
objective functions. An objective function is the func-
tion whose value has to be maximised or minimised
while solving the constraints. We use the IBM ILOG
CPLEX Optimization Studio
1
to find solutions to this
restricted kind of integer linear problem (ILP).
3 PROBLEM FORMULATION
We can describe the problem we want to solve as
the following: given one large, expressive, but over-
generating, grammar (called the resource grammar),
and some example sentences, we want to infer a sub-
grammar that covers the examples and is optimal with
respect to some objective function. One possible ob-
jective function would be to reduce the number of am-
biguous analyses.
3.1 Definition of the Problem
We assume that we already have a parser for the re-
source grammar that returns all possible parse trees
for the example sentence. That means we can start
1
http://www.cplex.com/
from a set of sets of trees. Then we can formulate our
problem in a formal way:
• Given: F = {F
1
, . . . , F
n
}, a set of forests where
each forest F
k
= {T
k1
, ..., T
kt
k
}, t
k
is the number of
trees in F
k
and each forest F
k
represents the ex-
ample sentence s
k
.
• Problem: select at least one T
ki
k
from each F
k
,
while minimising the objective function
• Possible objective functions:
rules: the number of rules in the resulting gram-
mar (i.e., reducing the grammar size)
trees: the number of all initial parse trees T
ki
that
are, intended or not, valid in the resulting gram-
mar (i.e., reducing the ambiguity)
rules+trees: the sum of rules and trees
weighted: is a modification of rules+trees where
each rule is weighted by the number of occur-
rences in all F
k
If every tree T
ki
only consisted of one single node
(which they usually do not), then the problem would
be equivalent to the Hitting Set problem (Garey and
Johnson, 1979, section A3.1), which is NP-complete
(Karp, 1972). Since our problem is a generalisation
of the Hitting Set problem, it is NP-complete too.
3.2 Modelling as a CSP
Even though there exist other solutions for the related
class of set covering problems, a natural approach to
this problem seems to lie in modelling it as a con-
straint satisfaction problem.
Given the set of forests F = {F
1
. . . F
n
} with
F
k
= {T
k1
, . . . , T
kt
k
}, there are various possible ways
to model the problem, depending on the choice of the
atomic units we want to represent by the logic vari-
ables. This can range from subtrees of size 1, i.e.,
single nodes, to different sizes of subtrees as well as
different ways to split a tree into these units. In the
following we use subtrees of size 1, which is equival-
ent to the labelled nodes of an abstract syntax tree, but
see Section 7 for a discussion of other alternatives.
This means we can represent a tree T
ki
in the forest
F
k
as the set of labels in the tree, T
ki
= {l
ki
1
, . . . l
ki
m
ki
}.
This results in a loss of structural information but does
not have any negative effect on the outcome of our
approach. Another possible representation would be
multi-sets, but it can be easily shown that this would
not result in any improvement, given that we trans-
late trees into conjunctions of variables and repetition
within a conjunction can easily be eliminated.
As the next step we translate our problem into lo-
gic. We want to guarantee that our set of forests F is
covered. To do so, we need to cover at least one of
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
424
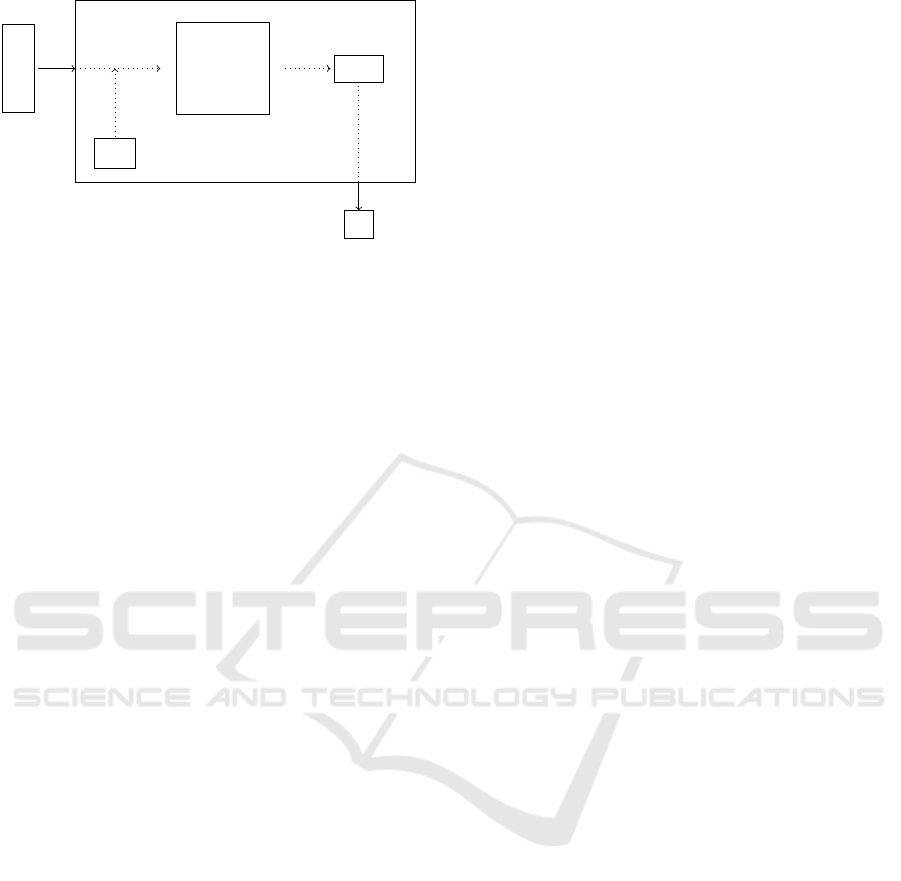
parse
extract
grammar
S
1
.
.
.
S
n
G
R
T
11
. . . T
1t
1
.
.
.
T
n1
. . . T
nt
n
CSP
G
Figure 1: Learning component for inferring a grammar
G from example sentences S
1
. . . S
n
and resource grammar
G
R
.
the trees in each forest F
k
∈ F . To cover a tree T
ki
,
we need to cover the set of labels {l
ki
1
, . . . l
ki
m
ki
} repres-
enting the tree. The set can be turned into a logical
formula by converting it into a conjunction of logical
variables representing labels. The result is the logical
formula:
T
ki
=
m
ki
^
j=1
l
ki
j
To cover a forest we need to cover at least one tree,
leading to the disjunction:
F
k
=
t
k
_
i=1
T
ki
=
t
k
_
i=1
m
ki
^
j=1
l
ki
j
Finally to cover the set of forests we construct the
conjunction:
F =
n
^
k=1
F
k
=
n
^
k=1
t
k
_
i=i
m
ki
^
j=i
l
ki
j
In addition to this complex Boolean constraint, we
want to minimise the value of one of the objective
functions from Section 3.1. For this optimisation we
need to be able to sum and multiply integers, which
makes the whole problem an instance of ILP.
4 IMPLEMENTATION
We have implemented a learning component that in-
fers a grammar, shown in Figure 1. It can be treated
as a black box that takes a set of sentences S
1
. . . S
n
as
an input and produces a grammar G as output, doing
so by relying on a resource grammar (labeled G
R
).
First the sentences are parsed using the resource
grammar G
R
and the syntax trees translated into lo-
gical formulas, in the way described in Section 3.2.
The resulting constraints are handed to the constraint
solver, which returns a list of rule labels that form the
basis for the new restricted grammar G. The output of
the solver is influenced by the choice of the objective
function (candidates are described in Section 3.1).
In fact the solver does not necessarily only return
one solution. In case of several solutions, they are
ordered by the objective value. Choosing the one with
the best value is a safe choice even though there might
be a solution with a slightly worse score that actually
performs better on the intended task.
4.1 Bilingual Grammar Learning
If our example sentences are translated into another
language, and the resource grammar happens to be
bilingual, we can use that knowledge to improve the
learning results.
For each sentence pair (S
i
, S
0
i
), we parse each sen-
tence separately using the resource grammar into the
forests F
i
= {T
i1
. . . T
it
i
} and F
0
i
= {T
0
i1
. . . T
0
it
0
i
}. We
then only keep the trees that occur in both forests, i.e.,
F
i
∩ F
0
i
. These filtered tree sets are translated into lo-
gical formulas, just as for monolingual learning.
The reason for doing bilingual learning is to re-
duce the ambiguity. A sentence can be more ambigu-
ous in one language than in another. The intersection
of the trees selects the disambiguated reading. The
disambiguation makes the constraint problem smaller
and the extracted grammar more likely to be the in-
tended one.
5 EVALUATION
Related literature (D’Ulizia et al., 2011) presents
several measures for the performance of grammar
inference algorithms, most prominently the meth-
ods “Looks-Good-To-Me”, “Rebuilding-Known-
Grammar” and “Compare-Against-Treebank”. Our
first learned grammars passed the informal “Looks-
Good-To-Me” test, so we designed two experiments
to demonstrate the learning capabilities of our
approach following the other two approaches.
5.1 Rebuilding a Known Grammar
The process is shown in Figure 2. To evaluate our
technique in a quantitative way we start with two
grammars G
R
and G
0
, where G
0
is a sub-grammar
of G
R
. We use G
0
to generate random example sen-
tences. These examples are then used to learn a new
grammar G as described in Section 4. The aim of the
experiment is to see how similar the inferred gram-
mar G is to the original grammar G
0
. To measure this
we compute precision and recall in the following way,
Learning Domain-specific Grammars from a Small Number of Examples
425

generate
sentences
Learning
component
compare
grammars
S
1
.
.
.
S
n
G
0
G
R
G
Figure 2: Evaluating by rebuilding a known grammar G
0
into G.
compare
trees
parse
sentences
Learning
component
G
R
(S
1
, T
1
)
.
.
.
(S
n
, T
n
)
T
1
.
.
.
T
n
S
1
.
.
.
S
n
T
0
11
. . . T
0
1t
1
.
.
.
T
0
n1
. . . T
0
nt
n
G
Figure 3: Evaluating by comparing to a treebank.
where L
0
are the rules of the original grammar and L
the rules of the inferred grammar:
Precision =
|L
0
∩ L|
|L|
Recall =
|L
0
∩ L|
|L
0
|
We can analyse the learning process depending on,
e.g., the number of examples, the size of the examples
and the language involved.
We conducted this experiment for Finnish, Ger-
man, Swedish, Spanish and English. For each of these
languages we used the whole GF RGL as the resource
grammar G
R
and a small subset containing 24 syn-
tactic and 47 lexical rules as our known grammar G
0
(Listing 1).
We tested the process with an increasing num-
ber of random example sentences (from 1 to 20), an
increasing maximum depth of the generated syntax
trees (from 6 and 10) and our four different objective
functions.
5.2 Comparing against a Treebank
Our second approach to evaluate our grammar learn-
ing technique, depicted in Figure 3, had a more
manual and qualitative focus. Instead of starting with
a grammar which we want to rebuild, we start from
a treebank {(S
1
, T
1
). . . (S
n
, T
n
)}, i.e., a set of example
abstract R ule s = {
fun
Us e N : N -> CN ;
Us e N2 : N2 -> CN ;
Ad j CN : AP -> CN -> CN ;
Us e PN : PN -> NP ;
Us eP r on : P ron -> NP ;
De t CN : De t -> CN -> NP ;
Ad v NP : NP -> Adv -> NP ;
Co njN P : C onj -> ListNP -> NP ;
Ba seN P : NP -> NP -> ListNP ;
Po sit A : A -> AP ;
Pr epN P : P rep -> NP -> Adv ;
Us e V : V -> VP ;
Co mp lS l as h : VP S la sh -> NP -> VP ;
Sl as h V2 a : V2 -> VPSlash ;
Co mp l VA : VA -> AP -> VP ;
Ad v VP : VP -> Adv -> VP ;
Pr edV P : NP -> VP -> Cl ;
Us e Cl : T emp -> Pol -> Cl -> S ;
Ut t S : S -> Utt ;
Ad v S : Ad v -> S -> S ;
Us eC o mp : C omp -> VP ;
Co mpA P : AP -> Comp ;
TT A nt : T ens e -> Ant -> Temp ;
De tQ u an t : Q uan t -> Num -> Det ;
}
Listing 1: The subgrammar used in “rebuild-grammar” ex-
periment.
sentences in a language and one gold-standard tree for
each sentence.
We use the plain sentences S
1
. . . S
n
from the tree-
bank to learn a new grammar G, using the GF RGL
extended with the required lexicon as the resource
grammar G
R
. Then we parse the sentences with the
resulting grammar G, and compare the resulting trees
with the original trees in our gold standard. If the ori-
ginal tree T
i
for sentence S
i
is among the parsed trees
T
0
i1
. . . T
0
it
i
, we report that as a success.
If the gold standard tree is not covered, we could
compute a more fine-grained similarity score, such as
labelled attachment score (LAS) or tree edit distance.
However, because of the limited size of the treebanks
we decided against this extension.
The data we used for testing the grammar learning
consists of hand-crafted treebanks for the following
languages: Finnish, German, Swedish and Spanish
(see Table 1 for statistics and Listing 4 for examples).
5.3 Comparing against a Bilingual
Treebank
Our final experiment was to do the same “compare-
against-treebank” experiment, but using a bilingual
treebank instead of a monolingual one.
We translated all the treebank sentences
into English to get four bilingual treebanks
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
426

min
¨
a sy
¨
on leip
¨
a
¨
a
I eat bread
PhrUtt NoPConj (UttS (UseCl (TTAnt TPres ASimul) PPos (PredVP (UsePron i_Pron)
(ComplV2 eat_V2 (MassNP (UseN bread_N)))))) NoVoc
min
¨
a en sy
¨
o leip
¨
a
¨
a
I don’t eat bread
PhrUtt NoPConj (UttS (UseCl (TTAnt TPres ASimul) PNeg (PredVP (UsePron i_Pron)
(ComplV2 eat_V2 (MassNP (UseN bread_N)))))) NoVoc
sy
¨
o leip
¨
a
¨
a
eat bread
PhrUtt NoPConj (UttImpSg PPos (ImpVP (ComplSlash (SlashV2a eat_V2)
(MassNP (UseN bread_N))))) NoVoc
sy
¨
ok
¨
a
¨
a leip
¨
a
¨
a
eat bread
PhrUtt NoPConj (UttImpPl PPos (ImpVP (ComplSlash (SlashV2a eat_V2)
(MassNP (UseN bread_N))))) NoVoc
...
min
¨
a haluan laulaa laulun suihkussa
I want to sing a song in the shower
PhrUtt NoPConj (UttS (UseCl (TTAnt TPres ASimul) PPos (PredVP
(UsePron i_Pron) (ComplVV want_2_VV (AdvVP (ComplSlash
(SlashV2a sing_V2) (DetCN (DetQuant IndefArt NumSg) (UseN song_N)))
(PrepNP in_Prep (DetCN (DetQuant DefArt NumSg) (UseN shower_N)))))))) NoVoc
Figure 4: Excerpt from the Finnish treebank used in the “comparing-against-treebank” experiment. The Finnish example is
followed by the English translation and the abstract syntax tree.
{(S
1
, S
0
1
, T
1
). . . (S
n
, S
0
n
, T
n
)}. Then we used the
bilingual learning component described in Sec-
tion 4.1, using the GF RGL as the bilingual resource
grammar.
6 RESULTS
We ran the experiments from the previous Section and
the results indicate that this direction of research is
promising. In the following Sections we will discuss
the results in detail.
6.1 Results: Rebuilding a Known
Grammar
We ran the first experiment, described in Section 5.1,
and a selection of the results can be seen in Figures 5–
7. We report precision and recall for a sequence of
experiments, where for each experiment we generated
sets of random sentences with increasing size.
All three graphs (Figure 5, 6 and 7) resemble typ-
ical learning curves where the precision stays mostly
stable while the recall rises strongly in the beginning
and afterwards approaches a more or less stable level.
The precision rises slightly between 1 and 5 input sen-
tences. The recall rises a lot in the beginning and
remains almost constant after input of about 5 sen-
tences. With larger input the precision starts to drop
slightly when we learn additional rules that are not
part of the original grammar. These curves are pretty
much stable across all languages (see Figure 5), ob-
jective functions (see Figure 6) and maximum tree
depth used in sentence generation (see Figure 7), al-
though there are some exceptions.
As can be seen in Figure 6, the curve for the
two objective functions “trees” and “weighted” don’t
really match this general description of an ideal learn-
ing curve. Instead the precision decreases signific-
antly after about 10 sentences, which means the al-
gorithm adds unnecessary rules. This shows that not
all objective functions work similarly well with all
languages.
Additionally, in Figure 7 we can see that with a
maximum tree depth of 5 we can only achieve a recall
of about 0.8, which means that for this tree depth we
do not encounter all grammar rules.
These results confirm that our method is very gen-
eral and provides good results, especially for really
small training sets of only a few to a few dozen
sentences. By starting from a linguistically sound
source grammar, which we recover by extracting a
sub-grammar, we can show that the learned grammar
is sound in a similar way.
Learning Domain-specific Grammars from a Small Number of Examples
427

Figure 5: Results for objective function rules and various
languages.
Figure 6: Results for Finnish and various objective func-
tions.
6.2 Results: Comparing against a
Treebank
We used the treebanks and the process described in
Section 5.2 to further evaluate our learning method.
Table 1 shows the results of running our experiment
on monolingual and bilingual treebanks of four dif-
ferent languages, and with two objective functions,
rules+trees and weighted. The table columns are:
Size the number of sentences in the treebank
Acc. the accuracy, meaning the percentage of sen-
tences where the correct tree is among the
parse trees for the new grammar
Amb. the ambiguity, i.e., the average number of
parse trees per sentence
We can cover all the sentences from the treebank with
our learned grammar and, as the table shows, in most
cases we cover the gold standard tree. We inspec-
ted more closely the sentences where the grammar
Figure 7: Results for English with objective function rules
and various generation depths.
fails to find the gold standard tree, and found that the
trees usually differ only slightly, so if we used attach-
ment scores instead of accuracy we would get close
to 100% accuracy in every case.
A clear exception is the case of the monolingual
Finnish treebank. When we use the rules+trees ob-
jective function, we have serious problems learning
the correct grammar, with only 1 correct sentence out
of 22. This is due to a high level of ambiguity among
Finnish word forms. If we instead use the weighted
objective function, we get a decent accuracy, but the
grammar becomes highly ambiguous with 115 parse
trees per sentence on average. The second part of the
experiment, using a bilingual treebank, solves most of
the problems involving Finnish.
6.3 Results: using Bilingual Treebanks
When we repeated the experiment using translation
pairs as described in Section 5.3 we got similar res-
ults. The main difference is that the resulting gram-
mars are more compact for the weighted objective
function, resulting in fewer analyses. Notably, for
Finnish the average number of trees per sentence
drops by one order of magnitude. This is because
the high ambiguity of Finnish sentences is reduced
when disambiguated using the English translations.
The resulting rules of the sub-grammar for Finnish
can be seen in Listing 2.
7 FUTURE WORK
The work described here is only the beginning of an
interesting line of research. We did the first steps in
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
428

Table 1: Results for comparing against a treebank. Acc(uracy) means the percentage of sentences where the correct tree is
found, and Amb(iguity) means the average number of parse trees per sentence.
monolingual bilingual
rules+trees weighted rules+trees weighted
Size Acc. Amb. Acc. Amb. Acc. Amb. Acc. Amb.
Finnish 22 5% 1.0 91% 115 86% 4.9 96% 8.7
German 16 75% 1.1 100% 2.0 94% 1.1 100% 1.5
Swedish 10 100% 1.1 100% 2.8 100% 1.1 100% 1.2
Spanish 13 100% 1.2 92% 3.7 100% 1.2 100% 2.3
AS imu l : A nt ;
Ad v VP : VP -> Adv -> VP ;
Co mp lS l as h : VP S la sh -> NP -> VP ;
Co mp l VV : V V -> VP -> VP ;
De fAr t : Quan t ;
De t CN : D et -> CN -> NP ;
De tQ u an t : Qua n t -> Num -> Det ;
Im p VP : VP -> Imp ;
In de f Ar t : Qua n t ;
Ma ssN P : CN -> NP ;
No PC o nj : PC onj ;
No V oc : V oc ;
Nu m Sg : N um ;
PN e g : P ol ;
PP o s : P ol ;
Ph rUt t : PCon j -> Utt -> Voc -> Phr ;
Pr edV P : NP -> VP -> Cl ;
Pr epN P : Prep -> NP -> Adv ;
Sl as h V2 a : V 2 -> VPSlash ;
TP r es : Te n se ;
TT A nt : Te n se -> Ant -> Temp ;
Us e Cl : Tem p -> Pol -> Cl -> S ;
Us e N : N -> CN ;
Us eP r on : Pr o n -> NP ;
Ut tI m pP l : Pol -> Imp -> Utt ;
Ut tI m pS g : Pol -> Imp -> Utt ;
Ut t S : S -> Utt ;
br ea d _N : N ;
ea t_V 2 : V2 ;
i_ Pro n : Pron ;
in _P r ep : Pr e p ;
ki tc he n _N : N ;
mu st _ VV : V V ;
sh ow e r_ N : N ;
si ng _ V2 : V 2 ;
so ng_ N : N ;
wa nt _2 _ VV : VV ;
Listing 2: Extracted abstract syntax rules for the bilingual
treebank experiment.
describing the initial problem and a feasible approach
for solving it. Based on this we see potential for many
relevant extensions.
Atomic Units. In Section 3.2 we translate the parse
trees to a constraint satisfaction problem in a very
straightforward way: every tree label is translated into
one logical variable. This is the same as splitting the
tree into its smallest possible pieces – subtrees of size
one. The idea is similar to DOP, but DOP does not
limit itself to only size one subtrees. The accuracy
of the DOP parsing model increases if we allow lar-
ger subtrees, so that is an obvious next step for our
algorithm too.
One effect of allowing logical variables to refer to
subtrees rather than labels is that the resulting gram-
mar rules will not be a subset of the original resource
grammar rules. Instead some combinations of re-
source grammar rules might be merged into one rule,
which makes the final grammar even more specialised
towards the example sentences.
Negative Examples. Another extension of our cur-
rent approach would be the use of negative examples
to give a more fine-grained control over the resulting
grammar. Instead of saying we want to be able to
cover sentences S
1
, . . . , S
n
we also want to be able to
say that we definitely want to exclude a set of sen-
tences S
0
1
, . . . , S
0
m
. This approach would not require
any additional technical knowledge from the person
authoring the examples.
This idea can best be implemented in an iterative
manner where we first generate a grammar, which is
used to generate example sentences, and then the au-
thor decides which of the examples are acceptable and
which are not. These decisions are fed back into the
learning module, which extracts a new grammar.
Multilingual Learning. There are many further
possible experiments to investigate the influence of
bilingual and multilingual grammar learning. This
seems most interesting in connection with the use of
large-scale lexicons because they introduce an addi-
tional source of lexical ambiguity. The results for the
Finnish treebank suggest that using translation pairs
instead of monolingual sentences can improve the res-
ults a lot.
Learning Domain-specific Grammars from a Small Number of Examples
429

Handling Larger Problem Sizes. Our implement-
ation does not have any problems with efficiency
– all experiments run within less than a minute on
an ordinary laptop. But since the problem itself is
NP-complete, we will potentially run into difficulties
when we increase the number of logical variables,
either by increasing the number of example sentences,
making the sentences longer (and therefore more am-
biguous), or by allowing larger subtrees in the CSP.
One main problem is the number of parse trees,
which can grow exponentially in the length of the
sentences. If we also split the trees into all possible
subtrees, the number grows even more. One possible
solution we want to explore is to move away from the
formulation of our problem in terms of parse trees and
instead refer to the states in the parse chart. The chart
has a polynomial size, compared to the exponential
growth of the trees, and it should be possible to trans-
late the chart directly to a complex logical formula
instead of having to go via parse trees.
Other Grammar Formalisms. Currently our al-
gorithm uses the GF resource grammar library, but
there are other formalisms and resource grammars for
which we hope the method can prove useful, such as
the HPSG resource grammars developed within the
DELPH-IN collaboration,
2
or grammars created for
the XMG metagrammar compiler.
3
8 CONCLUSION
In this paper we have shown that it is possible to learn
a grammar from a very limited number of example
sentences, if we can make use of a large-scale re-
source grammar. In most cases only around 10 ex-
ample are enough sentences to get a grammar with
good coverage.
There is still work left to be done, including per-
forming more evaluations on different kinds of gram-
mars and example treebanks. But we hope that this
idea can find its uses in areas such as computer-
assisted language learning, domain-specific dialogue
systems, computer games, and more. We will espe-
cially focus on ways to use this method in Computer-
Assisted Language Learning. However, a thorough
evaluation of the suitability of the extracted grammars
has to be conducted for each of these applications and
remains as future work.
2
http://www.delph-in.net/wiki/index.php/Grammars
3
http://xmg.phil.hhu.de/
REFERENCES
Bod, R. (1992). A computational model of language per-
formance: Data oriented parsing. In COLING’92,
14th International Conference on Computational Lin-
guistics, Nantes, France.
Bod, R. (2003). An efficient implementation of a new DOP
model. In EACL’03, 10th Conference of the European
Chapter of the Association for Computational Lin-
guistics, Budapest, Hungary.
Bod, R. (2006). Exemplar-based syntax: How to get
productivity from examples. The Linguistic Review,
23(3). Special issue on exemplar-based models in lin-
guistics.
Clark, A. and Lappin, S. (2010). Unsupervised learning and
grammar induction. In Clark, A., Fox, C., and Lap-
pin, S., editors, The Handbook of Computational Lin-
guistics and Natural Language Processing, chapter 8,
pages 197–220. Wiley-Blackwell, Oxford.
Clark, A. and Yoshinaka, R. (2014). Distributional learning
of parallel multiple context-free grammars. Machine
Learning, 96(1-2):5–31.
D’Ulizia, A., Ferri, F., and Grifoni, P. (2011). A survey of
grammatical inference methods for natural language
learning. Aritifical Intelligence Review, 36:1–27.
Garey, M. R. and Johnson, D. S. (1979). Computers
and Intractability: A Guide to the Theory of NP-
Completeness. W. H. Freeman & Co, New York, USA.
Henschel, R. (1997). Application-driven automatic sub-
grammar extraction. In Computational Environments
for Grammar Development and Linguistic Engineer-
ing.
Imada, K. and Nakamura, K. (2009). Learning context free
grammars by using SAT solvers. In 2009 Interna-
tional Conference on Machine Learning and Applic-
ations, pages 267–272.
Karp, R. M. (1972). Reducibility among combinatorial
problems. In Miller, R. E., Thatcher, J. W., and Bo-
hlinger, J., editors, Complexity of Computer Compu-
tations, pages 85–103. Plenum, New York, USA.
Ke
ˇ
selj, V. and Cercone, N. (2007). A formal approach to
subgrammar extraction for nlp. Mathematical and
Computer Modelling, 45(3):394 – 403.
Ranta, A. (2009a). The GF Resource Grammar Library.
Linguistic Issues in Language Technology, 2(2).
Ranta, A. (2009b). Grammatical Framework: A Multilin-
gual Grammar Formalism. Language and Linguistics
Compass, 3(5):1242–1265.
Ranta, A. (2011). Grammatical Framework: Program-
ming with Multilingual Grammars. CSLI Publica-
tions, Stanford.
Ranta, A. (2012). Implementing Programming Languages.
An Introduction to Compilers and Interpreters. Col-
lege Publications.
Russell, S. and Norvig, P. (2009). Artificial Intelligence: A
Modern Approach. Prentice Hall, 3rd edition.
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
430
