
Security for Distributed Smart Meter: Blockchain-based Approach,
Ensuring Privacy by Functional Encryption
Artem Yurchenko
1
, Mahbuba Moni
1
, Daniel Peters
1
, Jan Nordholz
1,2
and Florian Thiel
1
1
Physikalisch-Technische Bundesanstalt, Berlin and Brunswick, Germany
2
Institute of Software Engineering and Theoretical Computer Science, Technical University of Berlin, Germany
Keywords:
Legal Metrology, Smart Meter, Functional Encryption, Distributed Ledger Technology, Blockchain.
Abstract:
Today the trend towards a completely distributed measuring device is progressing and increasing numbers of
measuring instruments have already a cloud connection. This development requires new solutions to cover the
requirements laid down by legal metrology. These new challenges could be tackled by designing innovative
solutions which extend and merge novel technologies. The aim of this publication is to use blockchain tech-
nology and functional encryption to develop a model of a secure smart metering system, demonstrating the
capabilities and limitations of these technologies in a practical scenario in the framework of legal metrology.
1 INTRODUCTION
The trend towards networking and distribution of sys-
tem components is increasingly affecting broad sec-
tors of the economy: terms such as IoT, SmartMeter,
SmartHome, SmartFabric are often used in this con-
text. The field of legal metrology is affected by these
changes as well. An increasing number of measuring
instruments are connected to the internet, the mea-
surement data is partially stored in the cloud and
the device operation could even be controlled via a
browser interface.
All these developments expose legal metrology to
new challenges to guarantee a level of metrological
security comparable to a concentrated measuring de-
vice. The example case of a smart meter shows im-
pressively what efforts have to be made to guaran-
tee the required level of metrological security with
conventional means, leading to a rather complex sys-
tem, e.g. in Germany (BSI, 2019). This publica-
tion presents an alternative model of a smart meter-
ing system based on the use of blockchain technol-
ogy and functional encryption. This approach aims at
reducing the complexity of the system while achiev-
ing the required adequate level of metrological se-
curity. Therefore, the goal of this publication is to
examine the limits and possibilities of blockchain
and functional encryption on a simplified smart me-
ter model. The model presented contains measuring
sensors, consumer and service provider entities.While
the customer is entitled to entire measurement data,
the service provider is only allowed to see the accu-
mulated consumption. Our aim is to guarantee the
data authenticity and privacy as well as the integrity
of the algorithm by using a combination of blockchain
and functional encryption establishing confidence in
the correctness of measurements, which is one of the
main goals of the legal metrology. But first the con-
text of legal metrology should be described in more
detail.
2 CONTEXT OF LEGAL
METROLOGY
Legal metrology establishes confidence in the correct-
ness of measurements and protects the users of mea-
suring instruments and their customers (Thiel, 2018).
There are more than 130 million of measurement in-
struments in Germany which are employed for com-
mercial or administrative purposes, such as water me-
ters, gas meters, weighing instruments, taximeters,
thermal energy meters and electricity meters (Esche
and Thiel, 2015). About 345 million measurement in-
struments (7 billion in sales) are sold annually in the
EU, with most of them being subject to legally regu-
lations (Thiel, 2018).
292
Yurchenko, A., Moni, M., Peters, D., Nordholz, J. and Thiel, F.
Security for Distributed Smart Meter: Blockchain-based Approach, Ensuring Privacy by Functional Encryption.
DOI: 10.5220/0009377702920301
In Proceedings of the 10th International Conference on Cloud Computing and Services Science (CLOSER 2020), pages 292-301
ISBN: 978-989-758-424-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2.1 The Framework of Legal Metrology
The International Organization of Legal Metrology
(OIML) was founded to harmonize the regulations
across national borders and thus to reduce barriers
to trade and innovation. For this purpose, the orga-
nization publishes various guides and recommenda-
tions. From the perspective of metrological software,
the document OIML D31 plays the most important
role (OIML, 2008). The WELMEC Software Guide
7.2 (WELMEC, 2018) is mostly used on the European
level, as it contains practical recommendations for im-
plementing the requirements of the Measuring Instru-
ments Directive (2014/32/EU). This directive serves
as the basis of national legislation for measuring in-
struments in the European Union.
The WELMEC 7.2 Software Guide defines six risk
classes, which vary in terms of the necessary software
protection, software examination and software con-
formity. Software examination is usually done by no-
tified bodies prior to market launch. Thereafter, veri-
fication is periodically carried out by market surveil-
lance. Often, this verification process is limited to vi-
sual inspection of hardware seals, verification of the
software identifier, and sample measurements.
In the process of software conformity assessment,
a distinction between the legally relevant and non-
legally relevant software must be made. According to
WELMEC 7.2 all software modules that contribute to
or influence measurement results are legally relevant.
This not only includes software modules that generate
and process, but also those that transfer, store and dis-
play the measurement data. This makes a large part of
the software legally relevant, which could, potentially,
lead to an increased testing effort and corresponding
market launch delay.
WELMEC and OIML propose the use of modulariza-
tion and clear software separation to increase the se-
curity and simplify the software assessment. Works
such as (Peters et al., 2015) substantiate and extend
this approach and seek to achieve the highest level
of security using separation kernels and virtualiza-
tion technologies. Such solutions typically require
the presence of a full-fledged operating system on
the measurement instruments and require secure hard-
ware.
2.2 Current State in Software
Verification and Future Challenges
The current methods to establish confidence in the
correctness of measurements are based on system in-
tegrity. The hardware is physically sealed, and the
software integrity is verified by calculating check-
sums over all relevant files and modules. This ap-
proach provides a temporal security which holds until
a software or hardware vulnerability suitable to ex-
ploit the security system is found.
For measurement instruments not connected to net-
works the exploitation of the vulnerability requires
the physical presence of the attacker, but with de-
vices connected to the internet the situation is radi-
cally changing since the circle of potential attackers
gets significantly larger. The network connectivity
increases the complexity of the overall system and
thus expands the possible attack surface. It also of-
fers a new way of influencing the device so that even
the calculation of the checksum might be manipu-
lated without breaking any seal. To prevent this situa-
tion measurement instruments need to undergo regu-
lar updates. However, each update itself constitutes a
(deliberate) manipulation of the software, which usu-
ally requires recertification and is inconvenient for all
stakeholders. On the other hand, outfitting measuring
devices with an internet connection allows completely
new usage scenarios and business models which range
from connecting to the manufacturer’s cloud infras-
tructure to creating a fully distributed measuring de-
vice.
These usage scenarios lead to the emergence of new
device architectures whose software integrity can-
not be adequately secured by checksum methods. It
would therefore be desirable to have a verification
method which does not verify the binary image it-
self, but the functionality contained therein. Since the
functionality to be tested so far can be very extensive
and complex, it makes sense to subject these to a log-
ical separation. Essentially, a distinction can be made
between the core measuring algorithm, which is re-
sponsible for the conversion of the raw sensor data
into the displayed measured value, and the remaining
software. The guarantee of correct execution of the
core algorithm thus fulfills the basic requirement for
the correctness of a measurement, even if the struc-
tural integrity of the software image is not present.
The indispensable prerequisite for this is the correct-
ness of the result display as well as the authenticity of
the raw sensor data.
Another aspect, which is not yet part of the metro-
logical requirements, but which plays a central role,
especially for the customer, is the data privacy. The
current encryption methods only guarantee security
during transport and storage of the data. Since the
data often has to be further processed on its way, the
processing system has to decrypt the data, process it
and re-encrypt the result. If no separate cryptographic
hardware is used the secret keys and data are exposed
at least to the system operator. It would therefore be
Security for Distributed Smart Meter: Blockchain-based Approach, Ensuring Privacy by Functional Encryption
293

advantageous to be able to do calculations with en-
crypted data without first having to decrypt them first.
The above considerations result in the following mini-
mum security requirements for a distributed measure-
ment device to establish confidence in the correctness
of measurements:
• Privacy and authenticity of measurement data
• Authenticity (implying integrity) of the core mea-
surement algorithm
Based on these requirements, possible building blocks
for a solution are presented below. Finally, a simple
model of a smart metering system based on selected
blocks is presented and evaluated.
3 OVERVIEW OF SECURITY
PRIMITIVES
The usual way to ensure privacy and authenticity is
the use of cryptography. The purpose of this section
is to give the overview of the existing cryptographi-
cal primitives which can be utilized in our smart me-
ter example to ensure the authenticity and privacy of
measurement data as well as the authenticity and in-
tegrity of the core measurement algorithm.
3.1 Re-execution of Core Algorithm by
Trusted Third Party
The simplest way to verify the correctness of a cal-
culation result is to re-execute it. At first glance, the
re-execution of the core algorithm appears to be an
elegant and simple solution, but a closer look reveals
some serious issues. The re-executing party must be
supplied with a copy of the manufacturer’s algorithm
as well as the relevant measurement data, thus it has
to be trusted by all stakeholders which is not easy to
achieve. Assuming the use of encryption and signa-
tures to provide data authenticity and transport pri-
vacy this platform also contains all the secret keys.
This combination makes the platform a popular target
for cyberattacks. If this platform is operated by the
device manufacturer, the question arises if the core
algorithm on the re-execution platform and the mea-
surement device are the same as that has been certi-
fied by the notified body. It can be summed up that
this simple approach has some structural and practi-
cal vulnerabilities that cannot be easily circumvented.
Therefore, this approach has no practical relevance
and can be discarded.
3.2 Homomorphic Encryption
Homomorphic encryption allows calculations to be
performed on encrypted data without having to de-
crypt it first which primarily addresses the problem
of data privacy mentioned before. Formally homo-
morphic encryption could be described as a tuple of
algorithms [Gen, Enc, Dec, Eval]:
• (pk, sk, evk) ← Gen(1
λ
, α) is the key generation
algorithm, λ the unary security parameter and α
denotes auxiliary inputs. The result of key gener-
ation is a key-triple, where pk is the public key, sk
is a secret key and evk is an evaluation key. Usu-
ally the evaluation key is considered to be part of
the public key.
• c ← Enc(m, pk) describes the encryption algo-
rithm, where m ∈ P is the plain text message and
c ∈ X is the ciphertext, where P and X are the cor-
responding plaintext and ciphertext spaces.
• c
R
← Eval(c
1
...c
n
, evk, f ) is the evaluation algo-
rithm. It takes as inputs a tuple of encrypted val-
ues and the evaluation key and produces an en-
crypted result C
R
∈ X . The input f formally de-
fines the function to be evaluated.
• m ← Dec(c, sk) defines the decryption function
While some ciphers have homomorphic properties re-
lated to a single arithmetic operation, such as (un-
padded) RSA, Paillier, and ElGamal cryptosystems,
for a long time there was no fully homomorphic en-
cryption that theoretically enabled the execution of ar-
bitrary functions. The situation changed in 2009 as
Craig Gentry proposed the first fully homomorphic
encryption scheme(Gentry, 2009). Since then, nu-
merous other schemes have been proposed and suc-
cessfully implemented, for instance(Brakerski et al.,
2012) and (Smart and Vercauteren, 2010). From a
practical perspective, two classes of homomorphic
encryption schemes could be distinguished, the lev-
elled and bootstrapped schemes. In the first case, the
depth of the circuit (function) cannot be subsequently
changed, so that the number of operations to be per-
formed is limited in advance. In the second case, the
circuit depth is theoretically unlimited, but requires an
additional computationally expensive operation, the
bootstrapping, which renews the encryption on a reg-
ular basis. One possible application of a bootstrapped
scheme is privacy protection in the area of cloud com-
puting. An example would be a distributed measur-
ing instrument consisting of several sensors, a cloud-
based computing unit and secure displays. The en-
tire calculation in the processing unit is encrypted and
the secure display has the only secret key to decrypt
the result.(Oppermann et al., 2017) While this method
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
294

ensures the anonymity of the measurement data, no
statement can be made regarding the integrity of the
algorithm.
3.3 Proof Systems
The verification of correctness in case of outsourced
computations is an important general distributed com-
puting issue. One possible solution is provided by
proof systems, whereby the server executing the com-
putation provides proof of its correctness in addition
to the result of the computation. Formally, such a
proof system can be generally described as a tuple of
probabilistic polynomial-time algorithms:
• (vk, sk, evk) ← Gen(1
λ
, f ) is the key generation
algorithm, λ the unary security parameter and f
denotes the algorithm to be proven. The result of
key generation is a key-triple, where vk is the ver-
ification key, sk is a secret key and evk is a public
evaluation key.
• σ
x
← InputEncode(x, sk) describes the process of
encoding a given input x.
• σ
y
← Prove(σ
x
, evk) is the proof generation algo-
rithm, which generates a proof of correctness for
the calculation determined by ek and encoded in-
put data.
• y or ⊥← Veri f y(σ
y
, pk) confirms or refutes the
correctness of the calculation.
Roughly, such proof systems can be differenti-
ated into interactive and argument-based systems.
While interactive systems assume a super-polynomial
prover, the argument-based systems establish a
polynomial-bound prover and are thus more practice-
oriented. The argument-based approaches can also
be realized as non-interactive proof systems, which is
important from a practical point of view, since the ad-
ditional communication between the verifier and the
prover can ideally be limited to sending the proof.
Especially the efficiency of such processes plays an
important role in their practical application. In this
context, the literature distinguishes between absolute
efficiency and amortized efficiency. In the first case,
the total computation time for calculating and evalu-
ating the proof is set in relation to the computational
time required by the algorithm to be verified. In the
second case, only the time necessary for verification
is considered. Many practical implementations there-
fore distinguish between the setup phase, which is ex-
ecuted once for each algorithm and involves a high
computational effort and the proof and verification
phase, which is set in relation to the computation time
of the algorithm to be tested and serves as an impor-
tant efficiency measure. Some of the approaches have
already gained practical importance and offer imple-
mentation evaluations such as Pinocchio(Parno et al.,
2016), SNARKS for C(Ben-Sasson et al., 2013) and
Geppetto(Costello et al., 2015). The main purpose
of such proof systems is to prove the correctness of
the (unencrypted) execution of an algorithm, there-
fore they could serve as a replacement to the soft-
ware integrity hashes, especially in cloud environ-
ments. Even if they solve the problem of algorithm
integrity checking, the core algorithm must continue
to run with unencrypted data in the distributed system,
which will not solve the privacy problem.
It is conceivable to combine such a proof method (in-
put privacy assumed) with homomorphic encryption
in order to take advantage of the benefits of both ap-
proaches. From a practical point of view, it must be
said that proof methods and homomorphic encryp-
tion require considerable computational resources and
generally have a strong dependency on the depth of
the circuit which represents the core algorithm. How-
ever, in environments where computing power does
not matter much, such a solution may be applicable.
3.4 Functional Encryption
Functional encryption, similar to homomorphic en-
cryption, allows calculations to be performed on en-
crypted data. The main difference, however, is that
the functional encryption provides a plaintext result
of the calculation. Formally, a functional encryption
can be defined as a tuple of probabilistic polynomial
time algorithms:
• (pk, sk) ← Setup(1
λ
) is the key generation algo-
rithm, λ the unary security parameter. The result
of key generation is a key tuple, where pk is the
public key and sk is a secret key.
• ek ← Gen(sk, f ) generates an evaluation key with
respect to a function f
• c ← Enc(x, pk) encrypts a value x
• f (x)or ⊥← Dec(c, ek) computes f (x) and pro-
vides the decrypted result.
The functional encryption was proposed in 2005 (Sa-
hai and Waters, 2005) and formalized in 2011 (Boneh
et al., 2011). Theoretically, the functional encryption
allows execution of arbitrary functions on encrypted
data, but in practice there are only a few implemen-
tations with a strong limitation on the functions to be
performed. In contrast to homomorphic encryption,
the calculations cannot be cascaded because the result
is decrypted directly after an (albeit complex) opera-
tion, which also undermines output privacy.
Nevertheless, such a method offers many advantages.
First, it guarantees privacy of the input data, if we as-
Security for Distributed Smart Meter: Blockchain-based Approach, Ensuring Privacy by Functional Encryption
295

sume that the function f (x) is difficult to invert. At
the same time, it guarantees the integrity of the algo-
rithm because the evaluation key is tied to the func-
tion. Thus, it combines the properties of homomor-
phic encryption and the proof systems. Another ad-
vantage is that the input data can only be decrypted
in the context of functions for which the evaluation
keys have been generated. If the secret key is securely
deleted after a single use, the encrypted data cannot be
used for purposes other than the specific function(s).
All these features serve to create trust between the
executing party and the data provider. A key weak-
ness of functional encryption for its use in distributed
computation lies in the fact that the calculation result
is unencrypted. Thus, the executing party can falsify
the result. However, there is the possibility of sepa-
rating the calculation execution and the result decryp-
tion, depending on the scheme used. In our construc-
tion, such a separation is possible, but not necessary.
An essential class of functional encryption is offered
by the inner-product schemes (Abdalla et al., 2015),
(Agrawal et al., 2016). They allow the calculation of
a scalar product of two vectors, where one of the vec-
tors is encrypted and the second represents the func-
tion f (x). In the following, the scheme based on De-
cisional Diffie-Hellman from the Cifer library (Cifer,
2019) is used: due to its relatively simple implemen-
tation of the encryption and a relatively small cipher-
textsize it is a viable candidate even for the integration
on resource-limited devices.
3.5 Blockchain Technology
Recent years have seen the evolution from central-
ized computational storage to decentralized architec-
tures and systems. Distributed ledger technology in-
novation is one of the key developments making this
move conceivable which includes smart contracts and
blockchain technologies. Smart contracts are the self-
executing software into the ledger. As a peer-to-
peer electronic cash system, the blockchain technol-
ogy first came up with the Bitcoin cryptocurrency,
published by an author under the pseudonym Satoshi
Nakamoto (Nakamoto, 2008).
In blockchain technology, blocks are linked in se-
quential order and having a valid network since each
block contains the cryptographic hash of previous
block. To authenticate and verify the data, each block
holds a permanent timestamp. There can be two
forms of blockchain platform named as permission-
less and permissioned. In permissionless blockchain,
anybody can join and take part in the network consen-
sus while in permissioned blockchain consensus can
be achieved by known identifiers. For achieving bet-
ter transaction latency and throughput, permissioned
blockchain consensus protocol needs less computa-
tional resources (Melo et al., 2019). This enables
blockchain technology to store not only data but also
to define inter-participant roles and rules. The im-
mutability feature makes the blockchain more useful
once a transaction is written onto the blockchain and
cannot be erased or, at least, it would be extremely
difficult to change.
Our blockchain implementation setup will take ad-
vantages of these features. Taking the specific con-
straints of legal metrology into consideration we
have chosen the permissioned blockchain Hyper-
ledger Fabric (Hyperledger Project) for our proof of
concept implementation. Hyperledger Fabric has a
modular architecture that enables the configuration of
smart contracts (called also chaincode in Hyperledger
terminology) which are then executed within the
Docker containers. In our experiments we have used
version 1.4 of Hyperledger Fabric (Fabric, 2019).
4 SMART METER MODEL
A classic smart metering system consists of several
sensors that produce measurement values in given
time intervals. The sensors are connected to a gate-
way, which is used for storing and further processing
of the measurement data. The gateway thus repre-
sents a central unit for which special security precau-
tions must be taken. Customers as well as the energy
provider are able to make requests to the gateway. A
special role in this construct is the gateway adminis-
trator, who has privileged access to the gateway and
can change the configuration.
4.1 Proposed Approach
Figure 1: Proposed Smart Metering Model.
The proposed model (see Fig. 1) closely follows the
existing smart metering model but has a different dis-
tribution of the component roles. The central assump-
tion is that the customer is a proprietor of the gener-
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
296

ated measurement data and that the energy provider is
only interested in learning the total consumption for
billing purposes in a given time period. The sensors
are classified as trustworthy and are regularly checked
for manipulation by market surveillance. The distri-
bution and storage of measurement data is done on the
blockchain. In the following, the entire process is out-
lined as an example in order to clarify the functioning
of the proposed overall system.
Figure 2: FE-Key Setup Procedure.
In an initial setup step the consumer securely gen-
erates a key pair consisting of a secret (SK) and
a public functional key (PK). The public functional
key is transmitted to the sensor via a secure chan-
nel (provided by the gateway). In the second step
the consumer and the provider agree on a suitable
tariff model, according to which the consumer gen-
erates an evaluation functional key (EK). This key is
transferred to the provider by means of another secure
channel (see Fig. 2). In the last step the sensor is reg-
istered on the blockchain and on the gateway.
The blockchain plays the role of a central distributed
storage for encrypted measurement data. The sen-
sors periodically encrypt their measurements using
their public key (PK) and store the result into the
blockchain. After a fixed period of time, these en-
crypted consumption values are read by the energy
supplier from the blockchain and the total sum is cal-
culated with the aid of the corresponding evaluation
key (EK). If the function specified by the evaluation
key differs from that used by the manufacturer for the
calculation and decryption of the sum, the decryp-
tion fails. This ensures that both the customer and
the provider reach consensus about the function to be
performed. The provider has no knowledge of the
individual measured values, while the customer can
decrypt the individual values and calculate the total
consumption on his own. The application of the de-
scribed method ensures confidence in the algorithm
to be executed between the customer and the provider.
At the same time, the privacy of the customer is main-
tained.
In addition to data storage, calculations can be de-
fined to take place within the scope of the blockchain;
such programs are generally called smart contracts.
These can also be statistical surveys, whereby the cus-
tomer would have to be asked explicitly each time to
generate a corresponding evaluation key. Similar ap-
proaches already exist for solutions based on homo-
morphic encryption (Stan et al., 2018). Also, the up-
date process of existing tariff models can be realized
much more easily by using smart contracts and issu-
ing new functional keys, as this does not require any
updates of the actual gateway software. The gateway
must accommodate less functionality and can there-
fore be made simpler and possibly with relaxed secu-
rity requirements while still providing its interfaces to
the customer and the energy provider. The adminis-
tration of the blockchain network can still be done by
the original gateway administrator.
The public and redundant nature of the blockchain
provides transparency and data authenticity, while the
use of functional encryption guarantees data privacy
and algorithm authenticity.
4.2 Threat Model
Our approach protects the privacy of customer mea-
surement data and establishes trust between the cus-
tomer and the service provider regarding the use of the
data. In our threat model, service providers are con-
sidered to run a trustworthy security infrastructure, in-
cluding the PKI, but are potentially curious to learn
individual usage numbers of their customers, mak-
ing them attackers on the ”privacy” aspect. Further-
more, we consider the network and third parties as un-
trusted, so we have to choose a protocol scheme that
is resistant to eavesdropping, message manipulation
and replay from others. Indeed, our chosen functional
encryption scheme is secure under the s-IND-CPA as-
sumption; however, careless generation of evaluation
keys may allow third parties to gather information
through means of statistical inference. Thus the re-
sponsibility of maintaining the security of the mea-
surement data lies with the customer who holds the
secret key and is not restricted in any use of his mea-
surement data.
5 IMPLEMENTATION DETAILS
To evaluate the performance, we ran our experiments
on an Intel Server S2600CW with 256 GB RAM and
two Xeon E5-2650 v4 CPUs running at 2,2 GHz with
Security for Distributed Smart Meter: Blockchain-based Approach, Ensuring Privacy by Functional Encryption
297

24 physical and 48 virtual cores in total. Our soft-
ware environment is based on Ubuntu Bionic Beaver
(18.04.1 LTS). This server hosts the blockchain net-
work along with the client application.
The functional tests were performed on top of Docker
containers as Hyperledger Fabric is using docker for
containerization and network virtualization. The sys-
tem was configured as minimal setup with 1 peer, 1
orderer container with solo-orderer service which de-
rives solo consensus mechanism.
Peer (peer0 container) used in our experimental setup
was configured both as an endorser and a commit-
ter. Therefore, for executing the transaction’s required
chaincode, an additional chaincode container (dev) is
used. The Orderer container is necessary to order
transactions and create new blocks establishing con-
sensus. CouchDB has been used to keep the peer
ledger state. Additionally, we have created a CLI
(command line interface) container to interact with
the network.
For both the customer and provider application, we
have used one of the available APIs (fabric-java-sdk)
to generate a transaction proposal. The SDK sends
the transaction proposal to peer0. peer0 plays the spe-
cial role as the trusted peer which is able to execute
smart contracts. It also verifies whether the transac-
tion proposal is well-formed and has not been sub-
mitted already in the past (replay-attack protection),
and checks the authorization of the customer and
provider to perform the proposed operation (Fabric,
2019). The peer0 instance and the peer ”dev” (which
executes the chaincode) gets assigned one CPU core
each. Orderer peers and our client applications are
freely distributed over remaining CPU cores.
Such a configuration makes it possible to explore the
limits of the smallest possible Hyperledger installa-
tion, which in principle can be implemented on a
middle-class consumer computer.
In addition to the blockchain installation, there are
two applications developed by us (Java) that simu-
late measuring instruments and the provider applica-
tion. Both applications are multithreaded, which al-
lows multiple parallel instances to be simulated. Each
meter (instance) generates random measurement val-
ues, which are then individually encrypted and writ-
ten to the blockchain. To simulate maximum utiliza-
tion of the system, the encryption and sending of the
data is not done in a 15-minute cycle (BSI, 2019), but
directly after receiving the confirmation that the pre-
vious data was written to the blockchain. The number
of parallel application instances (threads) is varied ac-
cordingly, as well as the key length of the functional
encryption, which directly affects the size of the ci-
phertext.
6 RESULTS
When evaluating the results, it should be noted that
the generation of each key is a one-time process and
therefore not time-critical. The calculation and the
decryption of the result takes place monthly and is
therefore also less time-critical. The encrypting and
storing a single measurement value in the blockchain
should not exceed the sensor reading intervall (e.g. 15
minutes for electricity meters) (BSI, 2019), which is
a natural limit to the number of possible sensors. The
evaluation of the results is done in the order of the
processes and is structured according to the respec-
tive of an active participant (consumer, measurement
sensor and provider client).
6.1 Setup Step
The first initial step concerns the commissioning of
the device and is carried out once. The generation of
functional key us carried out by customer and takes
most of the time in the registration procedure for the
sensor(fig. 3). Depending on the size of the key, the
time increases significantly. Since this process runs
only once, this effort is acceptable, but requires at
least a consumer-grade computer (mobile platforms
would be less suitable).
Figure 3: Keygeneration Time.
6.2 Measurement Instrument
The measurement instrument calculates the actual
measurement value, encrypts it with functional public
key and puts the value on the blockchain using REST
protocol. From the figure 4 it can be seen that the en-
cryption time in relation to the time necessary to store
the value on the blockchain does not play a significant
role.
It should be taken into account that encryption is done
on a relatively low-computing device, so the encryp-
tion times could be significantly higher. However, the
figure 4 shows that the current encryption time could
increase by up to the factor 20,000, without exceeding
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
298
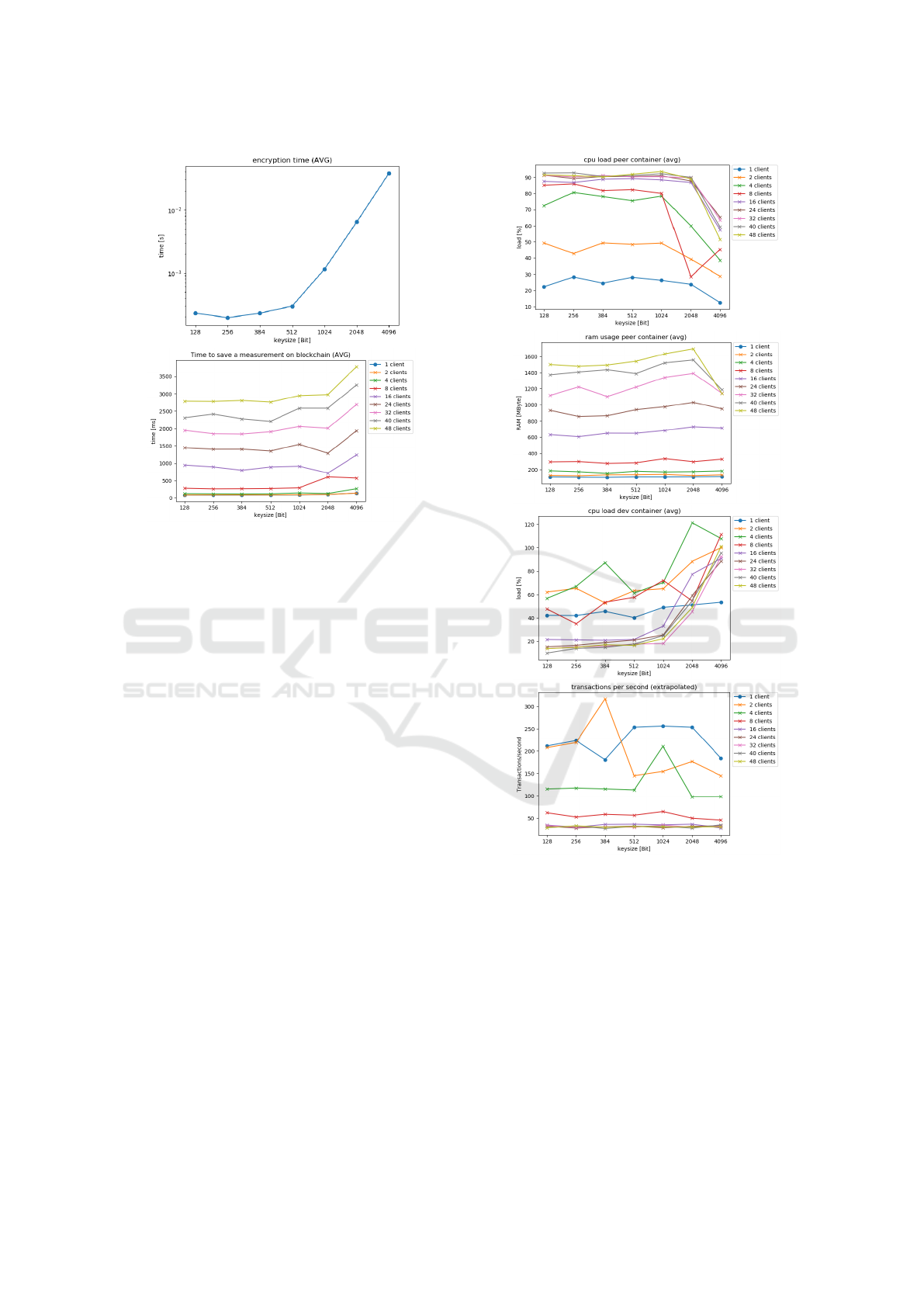
Figure 4: Encryption Time and Time to Store the Value on
the Blockchain.
the interval of 15 minutes between successive read-
outs. The time required for a value to be stored on the
blockchain depends heavily on the utilization of the
blockchain and does not show any significant depen-
dence on the size of the value to be stored (key size).
Considering the performance data of the two contain-
ers peer0 and dev (fig. 5), a clear dependency on the
number of connected measurement devices (clients)
could be seen. While the utilization of the peer in-
creases with increasing number of measuring devices,
the utilization of the dev container decreases, which
indicates a bottleneck in the peer container.
It can be concluded that an increase in the number of
peers would have a positive effect on the overall per-
formance. At the same time there is a dependency
on the value size in the dev container, so that a larger
key size might require more dev containers. Similar
statements can be made when considering the num-
ber of transactions per second. The transaction rate
seems to break down from at least 8 simultaneous
client applications, which can primarily be explained
by the high load of the peer container. Nevertheless,
in case of optimal system utilization with 8 simultane-
ous blockchain transactions and assuming the transac-
tion time of 500 ms 1800 measurement sensors could
be served at the same time without violating the max-
imum sensor reading intervall of 15 minutes (cf. fig.
4). Admittedly, it is an ideal case that requires perfect
synchronization, in reality the limit would be corre-
spondingly lower.
Figure 5: Blockchain Statistics.
6.3 Provider Client
The provider client application is used to collect all
the measurement values for each of the measurement
instrument at the end of a billing period and to de-
crypt the overall consumption. Since this operation
is performed only at the end of a billing cycle, it is
less time-critical and the provider usually has access
to higher computing capacity than the customer. At
the same time, the blockchain allows parallel access,
so billing can be done on multiple parallel instances.
Nonetheless, efficiency also plays an important role.
Security for Distributed Smart Meter: Blockchain-based Approach, Ensuring Privacy by Functional Encryption
299
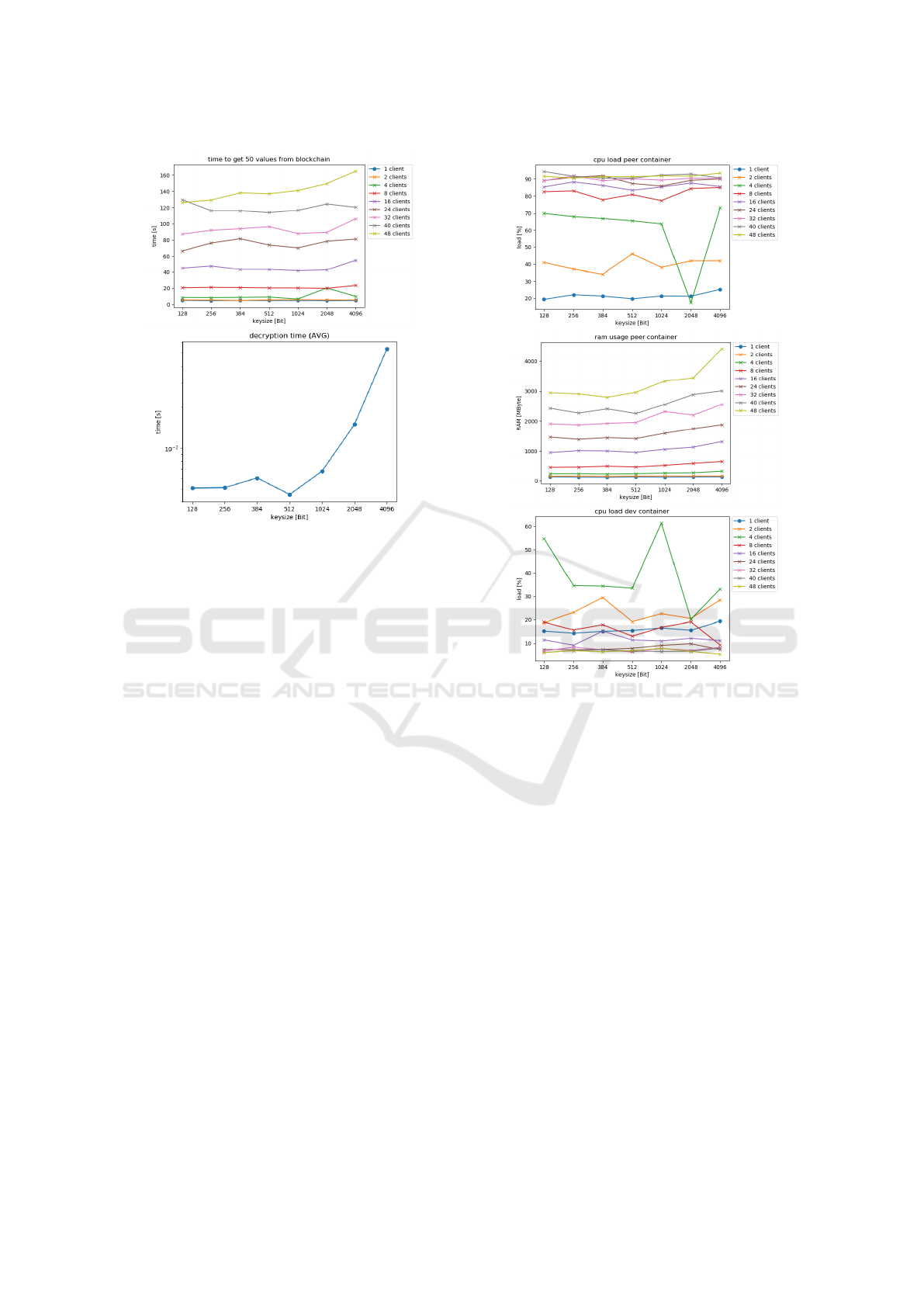
Figure 6: Provider Application (Time to Get All Values and
Decryption Time).
The decryption time is short in relation to the time
it takes to read a value from the blockchain and the
latter has an approximately linear dependence on the
number of measured values. We have determined a
number of measured values to be 50 to reduce the
simulation time (fig. 7). Especially the peer serves
as a performance bottleneck as the number of par-
allel instances increases. Similarly to the cpu load
the memory consumption in the peer increases signif-
icantly compared to the consumption caused by me-
ter accesses (fig. 7 ), while the memory consump-
tion of dev container remains below 500 MByte. It is
therefore worth increasing the capacity of the peer to
ensure optimal throughput and utilization of the dev
container.
7 CONCLUSION
It can generally be concluded that the application of
functional encryption in combination with blockchain
technology opens new perspectives in the field of le-
gal metrology. It allows the customer to determine
the use of his data while at the same time giving him
the security and confidence in the correctness of mea-
surement results, thereby fulfilling the basic require-
ments of legal metrology. By using the logical sep-
aration presented in this publication, it is possible to
define the protected algorithm core, which gets cryp-
tographically secured to provide algorithm authentic-
Figure 7: Blockchain Statistics Provider Application.
ity as well as privacy and data authenticity. The con-
cept presented in this publication uses a combination
of functional encryption and blockchain technology
to achieve these goals. The results of the simulations
show the advantages and limitations of both technolo-
gies. Furthermore, we have proven that a practical,
energy efficient system can be designed even with re-
stricted computing capacity of intelligent sensors and
without requiring high computing power from the ser-
vice provider.
REFERENCES
Abdalla, M., Bourse, F., Caro, A. D., and Pointcheval, D.
(2015). Simple Functional Encryption Schemes for
Inner Products. In Lecture Notes in Computer Science,
pages 733–751. Springer Berlin Heidelberg.
Agrawal, S., Libert, B., and Stehl
´
e, D. (2016). Fully Se-
cure Functional Encryption for Inner Products, from
Standard Assumptions. In Advances in Cryptology –
CRYPTO 2016, pages 333–362. Springer Berlin Hei-
delberg.
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
300

Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., and
Virza, M. (2013). SNARKs for C: Verifying Program
Executions Succinctly and in Zero Knowledge. In Ad-
vances in Cryptology – CRYPTO 2013, pages 90–108.
Springer Berlin Heidelberg.
Boneh, D., Sahai, A., and Waters, B. (2011). Functional
Encryption: Definitions and Challenges. In Theory of
Cryptography, pages 253–273. Springer Berlin Hei-
delberg.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2012).
(Leveled) Fully Homomorphic Encryptionwithout
Bootstrapping. In ITCS Proceedings of the 3rd Inno-
vations in Theoretical Computer Science Conference.
BSI (2019). Technische Richtlinie BSI TR-03109-1: An-
forderungen an die Interoperabilit
¨
at der Kommunika-
tionseinheit eines intelligenten Messsystems.
Cifer (2019). https://github.com/fentec-project/CiFEr re-
trieved 28. oct. 2019.
Costello, C., Fournet, C., Howell, J., Kohlweiss, M.,
Kreuter, B., Naehrig, M., Parno, B., and Zahur, S.
(2015). Geppetto: Versatile Verifiable Computation.
In 2015 IEEE Symposium on Security and Privacy.
IEEE.
Esche, M. and Thiel, F. (2015). Software Risk Assessment
for Measuring Instruments in Legal Metrology. Fed-
CSIS, Vol. 5.
Fabric, H. (2019). https://hyperledger-
fabric.readthedocs.io/en/release-1.4/txflow.html
retrieved 9. dec. 2019.
Gentry, C. (2009). Fully homomorphic encryption using
ideal lattices. In Proceedings of STOC.
Melo, W. S., Bessani, A., Neves, N., Santin, A. O., and
Carmo, L. F. R. C. (2019). Using Blockchains to
Implement Distributed Measuring Systems. IEEE
Transactions on Instrumentation and Measurement,
68(5):1503–1514.
Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic
Cash System. Bitcoin: A Peer-to-Peer Electronic
Cash System.
OIML (2008). General requirements for software con-
trolled measuring instruments, OIML, 2008.
Oppermann, A., Grasso-Toro, F., Yurchenko, A., and
Seifert, J. P. (2017). Secure Cloud Computing: Com-
munication Protocol for Multithreaded Fully Homo-
morphic Encryption for Remote Data Processing. In
IEEE International Symposium on Parallel and Dis-
tributed Processing with Applications (IEEE ISPA
2017).
Parno, B., Howell, J., Gentry, C., and Raykova, M. (2016).
Pinocchio. Communications of the ACM, 59(2):103–
112.
Peters, D., Thiel, F., Peter, M., and Seifert, J.-P. (2015).
A secure software framework for Measuring Instru-
ments in legal metrology. In IEEE International In-
strumentation and Measurement Technology Confer-
ence (I2MTC) Proceedings.
Sahai, A. and Waters, B. (2005). Fuzzy Identity-Based En-
cryption. In Lecture Notes in Computer Science, pages
457–473. Springer Berlin Heidelberg.
Smart, N. P. and Vercauteren, F. (2010). Fully Homomor-
phic Encryption with Relatively Small Key and Ci-
phertext Sizes. In Public Key Cryptography – PKC
2010, pages 420–443. Springer Berlin Heidelberg.
Stan, O., Zayani, M.-H., Sirdey, R., Hamida, A. B.,
Leite, A. F., and Mziou-Sallami, M. (2018). A
New Crypto-classifier Service for Energy Efficiency
in Smart Cities. In Proceedings of the 7th Interna-
tional Conference on Smart Cities and Green ICT Sys-
tems. SCITEPRESS - Science and Technology Publi-
cations.
Thiel, F. (2018). Digital transformation of legal metrology
- the European Metrology Cloud. OIML Bulletin, Vol.
LIX, Nr. 1.
WELMEC, . (2018). WELMEC 7.2 Software Guide (Mea-
suring Instruments Directive 2014/32/EU1), 2018.
Security for Distributed Smart Meter: Blockchain-based Approach, Ensuring Privacy by Functional Encryption
301
