
Unsupervised Statistical Learning of Context-free Grammar
Olgierd Unold
1 a
, Mateusz Gabor
1 b
and Wojciech Wieczorek
2 c
1
Department of Computer Engineering, Wrocław University of Science and Technology, Poland
2
Faculty of Science and Technology, University of Silesia in Katowice, Poland
Keywords:
Formal Languages, Grammar Inference, Weighted Context-free Grammar, Unsupervised Learning, Statistical
Methods, ADIOS.
Abstract:
In this paper, we address the problem of inducing (weighted) context-free grammar (WCFG) on data given.
The induction is performed by using a new model of grammatical inference, i.e., weighted Grammar-based
Classifier System (wGCS). wGCS derives from learning classifier systems and searches grammar structure
using a genetic algorithm and covering. Weights of rules are estimated by using a novelty Inside-Outside
Contrastive Estimation algorithm. The proposed method employs direct negative evidence and learns WCFG
both form positive and negative samples. Results of experiments on three synthetic context-free languages
show that wGCS is competitive with other statistical-based method for unsupervised CFG learning.
1 INTRODUCTION
Grammatical inference is a part of symbolic Artifi-
cial Intelligence and deals with the induction of for-
mal structures like grammars or trees from data (de la
Higuera, 2010). Among different types of grammars,
the weighted context-free grammars (weighted CFG,
WCFGs) or equally expressive probabilistic context-
free grammars (PCFGs) (Smith and Johnson, 2007)
play a unique role and have found use in many areas
of syntactic pattern matching or broadly natural lan-
guage processing.
The task of learning WCFGs/PCFGs from data
consists of two subproblems: determining a dis-
crete structure of the target grammar and estimating
weighted/probabilistic parameters in the grammar.
In the task of estimating grammar parameters, a
structure of CFG is fixed. Bayesian approach (John-
son et al., 2007) or maximum likelihood estimation
(Baker, 1979; Lari and Young, 1990) are typically
here applied.
Taking into account the kind of presentation
and the type of information, methods of learning
CFG’s topology can be divided into informant-based
and text-based methods, and supervised, unsuper-
vised, and semi-supervised methods, respectively
a
https://orcid.org/0000-0003-4722-176X
b
https://orcid.org/0000-0002-5397-0655
c
https://orcid.org/0000-0003-3191-9151
(D’Ulizia et al., 2011). In unsupervised learning there
is no knowledge of the structure of the language, like
a treebank or structured corpus.
Unsupervised structure learning CFG is known to
be a hard task (de la Higuera, 2010; Clark and Lap-
pin, 2010), and from a theoretical point of view im-
possible from positive examples only (Gold, 1967).
However, Gold’s theorem does not cover all kinds of
CFGs, such for example, PCFGs and finite grammars
(Horning, 1969; Adriaans, 1992). Despite its diffi-
culty, unsupervised PCFG/WCFG grammar induction
seems to be still an important task and even more
practical than supervised learning due to the lack of
annotated data.
From several unsupervised methods available we
may mention here ADIOS (Solan et al., 2005),
EMILE (Adriaans and Vervoort, 2002), Synapse
(Nakamura, 2003), e-GRIDS (Petasis et al., 2004),
or LS (Wieczorek, 2010) and GCS (Unold, 2008).
Grammar-based Classifier system (GCS) (Unold,
2005; Unold, 2008) is one of the few induction sys-
tems learning both structure and grammar parameters.
Initially, GCS was dedicated to learning crisp context-
free grammar, in (Unold, 2012) was extended to a
fuzzy version, in (Unold and Gabor, 2019b) some pre-
liminary results on a weighted version were recently
obtained.
According to (D’Ulizia et al., 2011), there
are many computational techniques to be applied
in grammatical inference, like statistical methods,
Unold, O., Gabor, M. and Wieczorek, W.
Unsupervised Statistical Learning of Context-free Grammar.
DOI: 10.5220/0009383604310438
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 1, pages 431-438
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
431

evolutionary-based methods, heuristic methods, min-
imum description length, greedy search methods, and
clustering techniques. WCFG can be classified as an
example of the statistical method, same as ADIOS ap-
proach (Solan et al., 2005), where statistical informa-
tion to derive regularities from sentences is used.
Our main contribution is to present a novel algo-
rithm for unsupervised learning of WCFG. Follow-
ing ideas from (Smith and Eisner, 2005b), the algo-
rithm employs direct negative evidence to estimate
weights of induced grammar. The proposed approach
was tested over three artificial context-free languages
and compared to ADIOS - the other unsupervised,
statistical-based method for CFG induction.
2 PRELIMINARIES
2.1 Probabilistic/Weighted Context-free
Grammar
A Probabilistic Context Free Grammar (PCFG)
G consists of (1) a Context–Free Grammar CFG
(V,T, R,S) with no useless productions, where V - a
finite set of non-terminals disjoint from T , T - a finite
set of terminals, R - a finite set of productions, S ∈ V
is called the start symbol, and (2) production proba-
bilities p(A → β) = P(β|A) for each A → β ∈ R, the
conditional probability of an A replaced by β.
A production A → β is useless iff it is not used in
any terminating derivation, i.e., there are no deriva-
tions of the form S ⇒
γAδ ⇒ γβδ ⇒
∗
w for any
γ,δ ∈ (V ∪ T )
and w ∈ T
.
If r
1
... r
n
is a sequence of productions used to
generate a tree ψ, then P
G
(ψ) = p(r
1
).. . p(r
n
) =
∏
r∈R
p(r)
f
r
(ψ)
, where f
r
(ψ) is the number of times
r is used in deriving ψ.
In PCFG
∑
ψ
P
G
(ψ) = 1 if p satisfies suitable con-
straints, whereas in WCFG all constraints are re-
leased. Note that a PCFG is a special case of WCFG,
moreover, it has been shown that weighted and proba-
bilistic context-free grammars are equally expressive
(Smith and Johnson, 2007).
CFG is in Chomsky Normal Form when each rule
takes one of the three following forms: S → ε where
S is the start symbol; X → Y Z where Y and Z are
non-terminals; or X → t where t is a terminal.
2.2 Estimating Production Probabilities
Having established the topology of grammar, one can
find the set of rules probabilities. This task can be
solved by the Inside-Outside (IO) algorithm (Baker,
1979; Lari and Young, 1990), which tries to maximize
the likelihood of the data given the grammar.
ˆ
t(W ) = arg max
t∈T (W)
p(t), where t - left-most deriva-
tion, W - sentence (w
1
w
2
... w
n
),
ˆ
t(W ) - the most
likely left-most derivation for sentence W , T(W ) - set
of left-most derivations for sentence W, p(t) - proba-
bility of left-most derivation.
The IO algorithm starts from some initial param-
eters setting, and iteratively updates them to increase
the likelihood of the data (the training corpus). To es-
timate the probability of the rule, the algorithm counts
the so-called inside and outside probability.
The inside probability is the probability of de-
riving a particular substring from the given sen-
tence w
i
... w
j
from a given left-side symbol α
i j
(A) =
P(A −→ w
i
... w
j
), where A is any non-terminal
symbol. The outside probability is the proba-
bility of deriving from the start symbol of the
substring w
i
... w
i−1
Aw
j+1
... w
n
β
i j
(A) = P(S −→
w
1
... w
i−1
Aw
j+1
... w
n
).
Having the inside α and outside β probabilities for
every sentence w
i
in the training corpus, the occur-
rences of a given rule for a single sentence is calcu-
lated for non-terminal symbols: c
ϕ
(A −→ BC,W ) =
ϕ(A−→BC)
P(W )
∑
1≤i≤ j≤k≤n
β
ik
(A)α
i j
(B)α
j+1,k
(C),
and for terminal symbols: c
ϕ
(A −→ w,W ) =
ϕ(A−→w)
P(W )
∑
i≤1
β
ii
(A), where P(W ) = P(S −→
w
1
w
2
... w
n
) is the probability of deriving a sentence.
For each rule A −→ α the number c
ϕ
(A −→
α,W
i
) is added to the total count count(A −→ α) =
∑
n
i=1
c
ϕ
(A −→ α,W
i
) and then proceed to the next sen-
tence.
After processing each sentence in this way the pa-
rameters are re-estimated to obtain new probability of
the rule (maximization) ϕ
0
(A −→ α) =
count(A−→α)
∑
λ
count(A−→λ)
,
where count(A −→ λ) is as rule with the same left-
hand symbol.
3 THE WEIGHTED
GRAMMAR-BASED
CLASSIFIER SYSTEM
The weighted Grammar-based Classifier System be-
longs to the family of Learning Classifier Systems
(Urbanowicz and Moore, 2009) and is based on
the previous version (Unold, 2005) operating only
on context-free grammar without probabilities or
weights. According to the idea of grammatical in-
ference, wGCS receives as the input data set in the
form of positive and negative labeled sentences, as
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
432
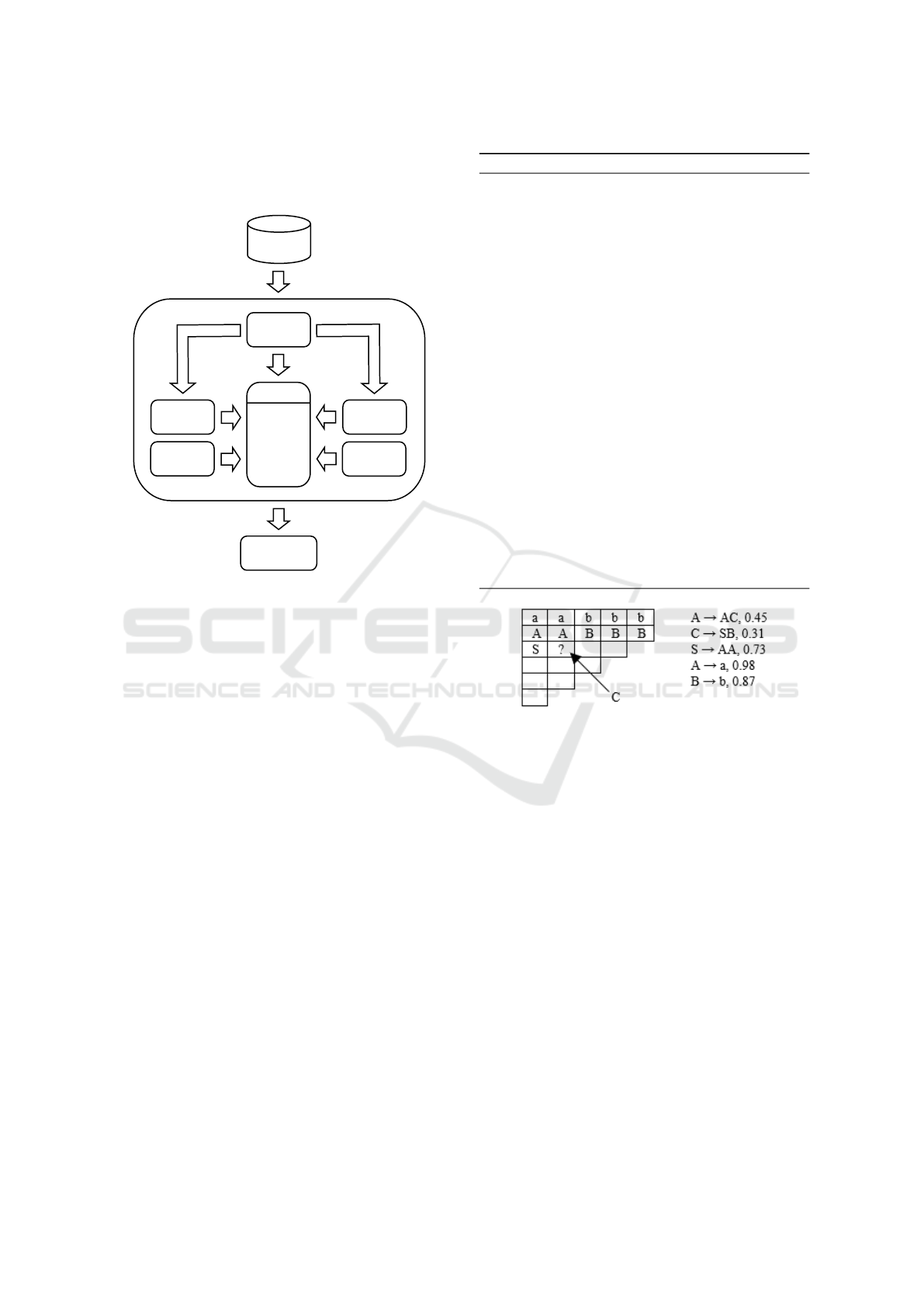
the output the WCFG is induced. All grammar rules
in wGCS are in Chomsky Normal form. The general
architecture of wGCS is given in Fig.1.
Train /
Validation
CKY
Population
Rule 1
Rule 2
Rule 3
...
Genetic
algorithm
Grammar
initialization
Stochastic
module
Correction
module
Grammar
Figure 1: The overall architecture of wGCS.
3.1 CKY Parser
The core of the system is CKY (Cocke-Kasami-
Younger) parsing algorithm that classifies whether a
sentence belongs to grammar or not. CKY oper-
ates under the idea of dynamic programming, and its
computational complexity is O(n
3
|G|), where n is the
length of the sentence and |G| is the size of grammar
(Hopcroft et al., 2001).
For a CFG in Chomsky Normal Form, the CKY
algorithm operates on a table of size n× n, where n is
the length of the input sentence (see Algorithm 1).
3.2 Grammar Initialization
The initial grammar is generated in two phases.
Firstly, based on the training set, the symbols and ter-
minal rules are matched with the symbols found in
the data set, while the non-terminal rules are created
randomly from the symbols of the terminal rules and
the start symbol S. Secondly, all positive sentences
are parsed with the help of a mechanism called cover-
ing, which adds to the grammar lacking non-terminal
rules.
Let us illustrate how the covering algorithm works
using the example (see Figure 2). Analyzing the cells
of CKY table, in turn, we come across an empty cell
marked by ?. None of the grammar rules have a string
Algorithm 1: CKY Parsing.
1: function CKY-PARSE(sentence,grammar)
2: Initialize table to the upper half of an n × n
matrix
3: for k in 1 to LEN(sentence) do
4: for i in k − 1 to 0, incrementing in step
size −1 do
5: if i == k − 1 then
6: for rule X → t such that
sentence[k]==t do
7: Put X in table[i,k]
8: end for
9: else
10: for j in i + 1 to j − 1 do
11: for rule X → Y Z such that Y ∈
table[i, j] and Z ∈ table[ j,k] do
12: Put X in table[i,k]
13: end for
14: end for
15: end if
16: end for
17: end for
18: return table
19: end function
Figure 2: Exemplary covering over CKY table. The cover-
ing inserts an additional rule C → AB to allow parsing go
further.
of non-terminals AB at the right-hand side. This string
is necessary so that parsing can continue. In this case,
the covering algorithm inserts one of the available
non-terminal symbols A, B, C or S into the empty cell.
This inserting increases the grammar by an additional
rule e.g., C → AB, and enables the parsing go further.
Due to the use of covering, we parse all positive
sentences and provide the system with maximum re-
call equals to one but also generate an excess of non-
terminal rules that are successively removed with the
help of a correction module.
3.3 Genetic Algorithm
To discover new non-terminal rules in a grammar, a
genetic algorithm (GA) was engaged. GA takes two
non-terminal rules as individuals, then in the process
of genetic operations, creates a new pair of rules that
is added to the grammar. The genetic algorithm is
Unsupervised Statistical Learning of Context-free Grammar
433

run once in each evolutionary step. Two individu-
als with the highest fitness are taken for reproduction.
The model adopts the selection of one pair due to the
high interdependence (so-called epistasis) of individ-
uals from each other, forming rules in grammar. In
general, the various available methods for a crossover
can be adopted.
The fitness measure for each rule is calculated as:
f
c
=
U
p
U
p
+U
n
if U
p
+U
n
> 0
0 if U
p
+U
n
= 0
(1)
where: U
p
- number of uses of rule while parsing cor-
rect sentence, U
n
- number of uses of rule while pars-
ing incorrect sentence.
Each selected individual for reproduction is sub-
jected to two genetic operations: crossover and muta-
tion.
• Crossover
Crossover involves the exchange of one of the
right-hand symbols between the rules - in half of
the cases, the first symbol is changed; in other
situations, the second. This operation runs every
evolutionary step with a probability of 1. Rule
weights are not exchanged. Getting two rules as
input:
A → BC,0.4,
D → EF,0.3,
(2)
the crossover operator can create the following
rules:
– if the random probability does not exceed 50%,
the first right-hand symbol will be replaced:
A → EC,0.4,
D → BF,0.3,
(3)
– if the random probability is higher 50%, the
second right-hand symbol will be replaced:
A → BF,0.4,
D → EC,0.3.
(4)
• Mutation
During the mutation, each of the production sym-
bols may be replaced by another non-terminal
symbol. This operation is performed for every
symbol with every evolutionary step with a prob-
ability of 0.7. For the rule:
A → BC,0.6, (5)
the result of the mutation operator can be, e.g.:
A → DC,0.6, or
A → DD,0.6,or
D → BD,0.6.
(6)
3.4 Stochastic Module
The wGCS, contrary to other approaches, makes use
of direct negative evidence in learning WCFGs. Di-
rect negative evidence is derived from language ac-
quisition theory and depicts all ungrammatical sen-
tences exposed to a language learner. Inspired by
the research of Smith and Eisner (Smith and Eis-
ner, 2005b; Smith and Eisner, 2005a), we extended
the idea of the Inside-Outside algorithm by introduc-
ing negative sentences into the estimation mechanism,
calling this method Inside-Outside Contrastive Esti-
mation (IOCE). The main idea of Contrastive Esti-
mation (CE) is to move probability mass from the
neighborhood of an observed sentence N (s) to s it-
self, where the neighborhood N (s) contains exam-
ples that are perturbations of s. We explore the idea of
CE using randomly generated sentences not belong-
ing to the target language in the task of learning pro-
duction weights.
Recently, CE factor of the rule was introduced in
(Unold and Gabor, 2019a):
ψ
CE
(A −→ α) =
count(A −→ α)
count(A −→ α) + count
ng
(A −→ α)
, (7)
where count
ng
(A −→ α)–the estimated counts that
a particular rule is used in a neighborhood.
The new weight of the rule is calculated as fol-
lows:
ϕ
0
(A −→ α) =
count(A −→ α)
∑
β
count(A −→ β)
· ψ
CE
(A −→ α). (8)
3.5 Correction Module
The purpose of this module is to remove non-terminal
rules with low weight. In our experiments, we remove
rules with a weight determined experimentally lower
than 0.001.
Note that the learned weights are not used in a fur-
ther classification but only to prune the induced gram-
mar.
3.6 Induction Algorithm
The first step in grammar induction with wGCS (see
Algorithm 2) is to initialize the grammar. During each
evolutionary step, new rules are added to grammar
through the operation of a genetic algorithm. Then
the stochastic module tunes the weight values of all
rules in grammar. We end the evolutionary step by
cleansing the grammar of the rules with low weights.
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
434

Algorithm 2: Induction algorithm.
Input: Training and validation set
Output: Weighted context-free grammar
1: Initialize the grammar
2: for i ← 1 to Evolutionary Steps do 500
3: Run genetic algorithm
4: for j ← 1 to IOCE iterations do 10
5: Run the stochastic module on the training
set
6: end for
7: Run the correction module
8: Evaluate grammar on the validation set
9: end for
10: return WCFG
4 TEST ENVIRONMENT
4.1 Experimental Protocol
The experiments with wGCS were carried out ac-
cording to the experimental protocol described in
Algorithm 3, using jGCS library (Unold, 2019).
Each induction cycle in the wGCS, like in other
evolutionary approaches, is repeated many times
(ExperimentRuns = 10) to avoid an accidental action.
Algorithm 3: Experimental protocol.
Input: Test set
Output: Metrics
1: for i ← 1 to Experiment Runs do 10
2: Run the Induction Algorithm 2
3: Evaluate grammar on the test set
4: end for
5: Calculate the metrics
6: return metrics
4.2 Benchmarks
The experiment for WGCS were performed over not-
overlapping datasets in proportions 60% for the train
set, 20 % for the validation set, and 20 % for the
test set. For the ADIOS approach, the validation
set was included in the train set, and the test set re-
mained the same. Each set contains both positive and
negative sentences taken from three context–free lan-
guages (Keller and Lutz, 1997), i.e. ab - the language
of all strings consisting of equal numbers of as and bs,
bra1 - the language of balanced brackets, and pal2 -
palindromes over {a,b}. All sentences were limited
to the length of 17 in sets ab, pal2 and 19 in set bra1.
Metrics of training, validation, and test sets are given
in Tab 1, Tab 2, and Tab 3 respectively.
Table 1: Training sets metrics.
Set Size
Positive
sentences
Negative
sentences
ab 299 157 142
bra1 299 157 142
pal2 198 99 99
Table 2: Validation sets metrics.
Set Size
Positive
sentences
Negative
sentences
ab 102 54 48
bra1 102 54 48
pal2 68 34 34
Table 3: Test sets metrics.
Set Size
Positive
sentences
Negative
sentences
ab 102 54 48
bra1 102 54 48
pal2 68 34 34
The training sets were used for inducing gram-
mars; the validation sets were applied to evaluate the
grammar during the induction process, while the com-
parison of methods has been performed based on the
test sets.
To evaluate the quality classification of the com-
pared methods, we use the following four scores de-
fined as tp, fp, fn, and tn, representing the numbers
of true positives (correctly recognized positive sen-
tences), false positives (negatives recognized as pos-
itives), false negatives (positives recognized as nega-
tives), and true negatives (correctly recognized nega-
tives), respectively. Based on these values, we calcu-
late the widely used Precision, Recall, and combined
metric F1-score.
Precision is defined as P = t p/(t p + f p), Recall
as R = t p/(t p+ f n), F1 as the harmonic mean of Pre-
cision and Recall F1 = 2 · (P ·R/(P + R)).
To reduce bias in evaluating the learning, we cal-
culate the average of the classification metrics of the
10 independent runs of compared methods over train-
ing and test sets. The inner loop of expectation-
maximization steps in wGCS was repeated 10 times.
4.3 A Brief Description of ADIOS
Approach
ADIOS (for Automatic Distillation of Structure) uses
statistical information present in sentences to iden-
tify significant segments and to distill rule-like reg-
ularities that support structured generalization (Solan
et al., 2005). It also brings together several crucial
conceptual components; the structures it learns are
Unsupervised Statistical Learning of Context-free Grammar
435
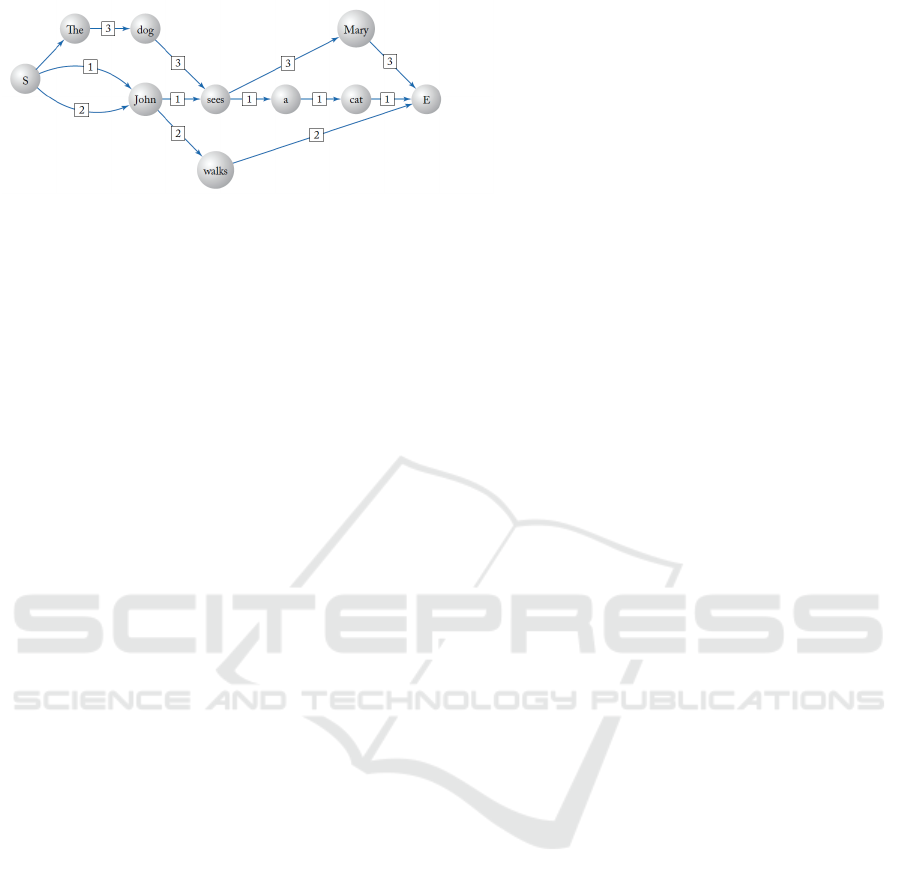
Figure 3: Initial ADIOS directed graph for three exemplary
positive input sentences: John sees a cat, John walks, and
The dog sees Mary. Each sentence has own path in the
graph, words are aligned with each other (figure taken from
(Heinz et al., 2015).
(i) variable-order, (ii) hierarchically composed, (iii)
context-dependent, (iv) supported by a previously un-
documented statistical-significance criterion, and (v)
dictated solely by the corpus at hand. The ADIOS al-
gorithm has been tested on a variety of language data,
as well as on DNA and protein sequences from several
species with auspicious.
ADIOS starts from building a directed graph from
input (positive only) sentences, where each sentence
has its own path in the graph, and words are aligned
with each other (Figure 3). Next, the learning
step starts. It iterative searches for significant pat-
terns, where significance is measured according to
a context-sensitive probabilistic criterion defined in
terms of local flow quantities in the graph. At the end
of each iteration, the most significant pattern is added
to the lexicon as a new unit, the some substitutable
subpaths are merged into a new vertex, and the graph
is compressed accordingly. The search for patterns is
repeated until no new significant paths are found.
5 RESULTS
In all experiments, we used Intel Xeon CPU E5-2650
v2, 2.6 GHz, under Ubuntu 16.04 operating system
with 190 GB RAM.
Table 4 summarizes the performance of the three
compared methods: wGCS using of direct nega-
tive evidence, wGCS employing the standard Inside–
Outside method and therefore using in learning only
positive sentences (denoted as wGCS positive), and
ADIOS, which also uses a set of only positive sen-
tences in induction of CFG.
Note that the wGCS with IOCE gained the high-
est Precision among tested methods and languages,
and thanks to that also the highest F1 metric. wGCS
with the standard IO and limited to positive sentences
achieved similar but better results than the ADIOS
method.
In order to compare the classification performance
of the methods statistically, we decided to choose F1
as the measure of quality, which is often used in the
field of information retrieval and machine learning.
Because our sample is small (ten independent runs for
each dataset) and the obtained variance, especially be-
tween ADIOS and wGCS, are not equal, Welsh’s t test
is best suited for finding out whether obtained means
are significantly different (Salkind, 2010, pp. 1620–
1623). As we can see from Table 5, p value is low
in all cases, so we can conclude that our results did
not occur by chance and that using wGCS method is
likely to improve classification performance for pre-
pared benchmarks. The wGCS positive also outper-
formed ADIOS but to a lesser degree.
Results analysis prompts us to draw the follow-
ing conclusions: (a) all compared methods, includ-
ing ADIOS, have 100% Recall, i.e. all methods build
grammars that recognise perfectly positive sentences,
(b) wGCS in all his variants has noticeable higher
Precision (and consistently F1) than ADIOS, which
means it better recognizes negative sentences, (c) the
presence of negative sentences can improve the learn-
ing of CFG in statistical-based wGCS.
6 CONCLUSIONS
We have presented a novel approach for unsupervised
learning of WCFG. The proposed method, based on
some principles of learning classifier systems, seeks
the output grammar consistent with the training set
of labeled sentences combining covering initializa-
tion, genetic algorithm, and new Inside-Outside Con-
trastive Estimation algorithm for estimating produc-
tion weights. The wGCS induces both the structure
and weights of induced grammar. The proposed ap-
proach was tested over three artificial context-free
languages.
The results of our experiments show that wGCS is
competitive with the state of the art method ADIOS
for unsupervised statistical learning CFG, and learn-
ing from negative sentences can improve the quality
of the statistical-learned grammar.
Future work should investigate more grammar-
dedicated heuristic algorithm, like split-merge ap-
proach (e.g., (Stolcke and Omohundro, 1994; Hogen-
hout and Matsumoto, 1998)). There are natural ways
to improve the covering algorithm, at least by consid-
ering how often particular non-terminal symbols ap-
pear in the rules set. Finally, the induction method we
have introduced should apply to real tasks, like bio-
data mining (Wieczorek and Unold, 2016).
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
436

Table 4: Average Precision (P), Recall (R), and F-measure (F1) with the standard deviation for the compared methods.
Dataset
wGCS wGCS positive ADIOS
P R F1 P R F1 P R F1
ab 0.87 ± 0.00 1.00 ±0.00 0.93 ±0.00 0.84 ±0.00 1.00 ± 0.00 0.92 ± 0.00 0.65 ± 0.10 1.00 ± 0.00 0.78 ±0.07
bra1 1.00 ± 0.00 1.00 ±0.00 1.00 ±0.00 0.90 ±0.00 1.00 ± 0.00 0.95 ± 0.00 0.70 ± 0.10 1.00 ± 0.00 0.82 ±0.07
pal2 0.89 ±0.02 0.99 ±0.01 0.94 ± 0.01 0.73 ± 0.00 1.00 ± 0.00 0.85 ± 0.02 0.61 ±0.09 1.00 ±0.00 0.75 ± 0.07
Table 5: Obtained p values for F1 from Welch’s t test.
Datasets wGCS vs. ADIOS wGCS positive vs. ADIOS wGCS vs. wGCS positive
ab 9.35e-05 1.56e-04 6.63e-127
bra1 2.48e-05 2.82e-04 3.39e-133
pal2 1.39e-05 2.39e-03 1.23e-10
ACKNOWLEDGEMENTS
The research was supported by the National Sci-
ence Centre Poland (NCN), project registration no.
2016/21/B/ST6/02158.
REFERENCES
Adriaans, P. and Vervoort, M. (2002). The EMILE 4.1
grammar induction toolbox. In International Col-
loquium on Grammatical Inference, pages 293–295.
Springer.
Adriaans, P. W. (1992). Language learning from a catego-
rial perspective. PhD thesis, Universiteit van Amster-
dam.
Baker, J. K. (1979). Trainable grammars for speech recog-
nition. The Journal of the Acoustical Society of Amer-
ica, 65(S1):S132–S132.
Clark, A. and Lappin, S. (2010). Unsupervised learning and
grammar induction. The Handbook of Computational
Linguistics and Natural Language Processing, 57.
de la Higuera, C. (2010). Grammatical Inference: Learn-
ing Automata and Grammars. Cambridge University
Press.
D’Ulizia, A., Ferri, F., and Grifoni, P. (2011). A survey of
grammatical inference methods for natural language
learning. Artificial Intelligence Review, 36(1):1–27.
Gold, E. M. (1967). Language identification in the limit.
Information and control, 10(5):447–474.
Heinz, J., De la Higuera, C., and Van Zaanen, M. (2015).
Grammatical inference for computational linguistics.
Synthesis Lectures on Human Language Technologies,
8(4):1–139.
Hogenhout, W. R. and Matsumoto, Y. (1998). A fast method
for statistical grammar induction. Natural Language
Engineering, 4(3):191–209.
Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2001). In-
troduction to automata theory, languages, and compu-
tation. Acm Sigact News, 32(1):60–65.
Horning, J. J. (1969). A study of grammatical inference.
Technical report, Stanford Univ Calif Dept of Com-
puter Science.
Johnson, M., Griffiths, T., and Goldwater, S. (2007).
Bayesian inference for pcfgs via markov chain monte
carlo. In Human Language Technologies 2007: The
Conference of the North American Chapter of the As-
sociation for Computational Linguistics; Proceedings
of the Main Conference, pages 139–146.
Keller, B. and Lutz, R. (1997). Evolving stochastic context-
free grammars from examples using a minimum de-
scription length principle. In Workshop on Automatic
Induction, Grammatical Inference and Language Ac-
quisition.
Lari, K. and Young, S. J. (1990). The estimation of stochas-
tic context-free grammars using the inside-outside al-
gorithm. Computer speech & language, 4(1):35–56.
Nakamura, K. (2003). Incremental learning of context
free grammars by extended inductive CYK algorithm.
In Proceedings of the 2003rd European Conference
on Learning Context-Free Grammars, pages 53–64.
Ruder Boskovic Institute.
Petasis, G., Paliouras, G., Karkaletsis, V., Halatsis, C., and
Spyropoulos, C. D. (2004). e-GRIDS: Computation-
ally efficient gramatical inference from positive exam-
ples. Grammars, 7:69–110.
Salkind, N. J. (2010). Encyclopedia of Research Design.
SAGE Publications, Inc.
Smith, N. A. and Eisner, J. (2005a). Contrastive estimation:
Training log-linear models on unlabeled data. In Pro-
ceedings of the 43rd Annual Meeting on Association
for Computational Linguistics, pages 354–362. Asso-
ciation for Computational Linguistics.
Smith, N. A. and Eisner, J. (2005b). Guiding unsupervised
grammar induction using contrastive estimation. In
Proc. of IJCAI Workshop on Grammatical Inference
Applications, pages 73–82.
Smith, N. A. and Johnson, M. (2007). Weighted and proba-
bilistic context-free grammars are equally expressive.
Computational Linguistics, 33(4):477–491.
Solan, Z., Horn, D., Ruppin, E., and Edelman, S.
(2005). Unsupervised learning of natural languages.
Proceedings of the National Academy of Sciences,
102(33):11629–11634.
Stolcke, A. and Omohundro, S. (1994). Inducing prob-
abilistic grammars by bayesian model merging. In
Unsupervised Statistical Learning of Context-free Grammar
437

International Colloquium on Grammatical Inference,
pages 106–118. Springer.
Unold, O. (2005). Context-free grammar induction with
grammar-based classifier system. Archives of Control
Sciences, 15(4):681–690.
Unold, O. (2008). Grammar-based classifier system: a uni-
versal tool for grammatical inference. WSEAS Trans-
actions on Computers, 7(10):1584–1593.
Unold, O. (2012). Fuzzy grammar-based prediction of amy-
loidogenic regions. In International Conference on
Grammatical Inference, pages 210–219.
Unold, O. (2019). jGCS. https://github.com/ounold/jGCS.
Unold, O. and Gabor, M. (2019a). How implicit neg-
ative evidence improve weighted context-free gram-
mar induction. In International Conference on Artifi-
cial Intelligence and Soft Computing, pages 595–606.
Springer.
Unold, O. and Gabor, M. (2019b). Weighted context-free
grammar induction– a preliminary report. In PP-
RAI
´
2019, pages 319–322. ISBN 978-83-943803-2-8.
Urbanowicz, R. J. and Moore, J. H. (2009). Learning clas-
sifier systems: a complete introduction, review, and
roadmap. Journal of Artificial Evolution and Applica-
tions, 2009:1.
Wieczorek, W. (2010). A local search algorithm for gram-
matical inference. In Jose M. Sempere, P. G., edi-
tor, Grammatical Inference: Theoretical Results and
Applications: 10th International Colloquium, ICGI
2010, Valencia, Spain, September 2010. Proceedings,
volume 6339 of Lecture Notes in Computer Science,
pages 217–229, Berlin, Heidelberg. Springer-Verlag.
Wieczorek, W. and Unold, O. (2016). Use of a novel gram-
matical inference approach in classification of amy-
loidogenic hexapeptides. Computational and mathe-
matical methods in medicine, 2016.
NLPinAI 2020 - Special Session on Natural Language Processing in Artificial Intelligence
438
