
An Improvement of Genetic Algorithm based on Dynamic Operators
Rates Controlled by the Population Performance
Beatriz Flamia Azevedo
1,3 a
, Ana I. Pereira
1,2 b
and Glaucia Maria Bressan
3 c
1
Research Centre in Digitalization and Intelligent Robotics (CeDRI), Instituto Polit
´
ecnico de Braganc¸a, Braganc¸a, Portugal
2
Algoritmi Research Centre, University of Minho, Campus de Gualtar, Braga, Portugal
3
Federal University of Technology - Paran
´
a, Corn
´
elio Proc
´
opio, Paran
´
a, Brazil
Keywords:
Genetic Algorithm, Genetic Operators, Dynamic Rates, Hybrid Approach.
Abstract:
This work presents a hybrid approach of genetic algorithm with dynamic operators rates that adapt to the
phases of the evolutionary process. The operator’s rates are controlled by the amplitude variation and standard
deviation of the objective function. Besides, a new stopping criterion is presented to be used in conjunction
with the proposed algorithm. The developed approach is tested with six optimization benchmark functions
from the literature. The results are compared to the genetic algorithm with constant rates in terms of the
number of function evaluations, the number of iterations, execution time and optimum solution analysis.
1 INTRODUCTION
Optimization is a mathematics field that studies the
identification of functions’ extreme points, either
maximal or minimal. In the last decade, the use of
optimization methods has become an essential tool
for management, decision making, as well as improv-
ing and developing technologies as it allows gaining
competitive advantages (Mitchell, 1998; Haupt and
Haupt, 2004).
Inspired by Darwin natural selection theory, op-
timization techniques had considerable progress in
the area of population algorithms. J. H. Holland
(Holland, 1992) and his collaborators tightly studied
the natural optimization mechanisms and mathemati-
cally formalized the natural process of evolution and
adaptation of living beings. These researchers devel-
oped artificial systems inspired in natural optimiza-
tion mechanisms (Mitchell, 1998), that can be used
to solve real optimization problems that arise from
industrial fields. Genetic Algorithms (GA) are the
most famous example of this methodology and they
are used in wide fields, such as image processing,
pattern recognition, financial analysis, industrial opti-
mization, etc (Ghaheri et al., 2015; Haupt and Haupt,
2004; Xu et al., 2018).
a
https://orcid.org/0000-0002-8527-7409
b
https://orcid.org/0000-0003-3803-2043
c
https://orcid.org/0000-0001-6996-3129
The several applications of GA led to numerous
computational implementations and algorithm varia-
tions. Many works propose strategies to improve the
GA and consequently the optimization problem solu-
tion. However, in most works, these improvements
are restricted to specific applications that cannot be
extended to optimization problems in general.
Knowing that GA performance depends on the op-
timization problem, this work consists of exploring
strategies to automatically adapt the GA to the op-
timization problem and proposes a variation of the
Genetic Algorithm to be used in general optimization
problems.
The traditional version of GA uses constant val-
ues in the genetic operator’s rates for the evolution-
ary process. In this paper is presented a dynamic GA
that considers three phases, where different operators
rates are used and they are dynamically controlled by
the amplitude and standard deviation of the objective
function. Besides this, a new stopping criterion is pro-
posed that depends on the algorithm behavior in the
last phase. This approach is tested by six optimiza-
tion test function and the results are compared with
the Genetic Algorithm with constant rates.
This paper is organized as follows: in Section 2,
GA concepts are introduced, highlighting the behav-
ior of the genetic operators. In Section 3 some stud-
ies and variations of GA are presented. In Section 4
the dynamic GA proposed in this work is described,
388
Azevedo, B., Pereira, A. and Bressan, G.
An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance.
DOI: 10.5220/0009385403880394
In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 388-394
ISBN: 978-989-758-396-4; ISSN: 2184-4372
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

while the numerical results are presented in Section 5.
Finally, the conclusion and future work proposed are
presented in Section 6.
2 GENETIC ALGORITHM
The Genetic Algorithm is composed of a set of in-
dividuals, usually named as chromosomes, that are
considered solutions for the optimization problem.
This set of individuals is known as the population,
and they have a fixed number of individuals in each
generation (iteration). The population is represented
by N
pop
individuals distributed in the feasible region,
which is the space where each variable can have val-
ues (Sivanandam and Deepa, 2008).
Thereby, the basic idea of GA is to create an initial
population P
0
of feasible solutions, to evaluate each
individual using the objective function and to select
some individuals to define the optimum subset of in-
dividuals N
keep
, and to modify them by the crossover
and mutation operators, in order to create new indi-
viduals (offspring).
The value provided by the objective function de-
fines how adapted an individual is to solve the opti-
mization problem. The most adapted individuals have
a greater chance of surviving for the next generation,
while the less adapted are eliminated; similar to what
is proposed by Darwin’s theory. This is an iterative
process in which at the end of each iteration all in-
dividuals are evaluated and ordered according to the
objective function value until a stopping criterion be
achieved (Haupt and Haupt, 2004; Sivanandam and
Deepa, 2008).
Some genetic algorithms variants are combined
with a local search method to present the global so-
lution with better precision. These algorithms are
considered hybrid genetic algorithms. In this work,
the Nelder Mead method (Nelder and Mead, 1965) is
used to improve the solution precision. The Hybrid
Genetic Algorithm is represented in the Algorithm 1.
A Genetic Algorithm depends substantially on the
efficiency of genetic operators. These operators are
responsible for new individuals creation, diversifi-
cation and maintenance of adaptation characteristics
acquired in previous generations (Sivanandam and
Deepa, 2008). The most useful operators are the se-
lection, crossover and mutation which are used in this
work and described below.
The selection operator selects elements of the cur-
rent population in order to produce more individuals
(offspring). It has the mission to guide the algorithm
for promising areas, where the probability to find
the optimum solution is higher (Pham and Karaboga,
Algorithm 1 : Hybrid Genetic Algorithm with Constant
Rates Operators.
Generates a randomly population of individuals,
P
0
, with dimension N
pop
.
Set k = 0.
Set the operators rates.
while stopping criterion is not met do
Set k = k +1.
P
0
= Apply selection procedure in N
pop
.
P
00
= Apply crossover procedure in N
keep
.
P
000
= Apply mutation procedure in N
keep
.
P
k+1
= N
pop
best individuals of {P
k
∪ P
00
∪
P
000
}.
Apply the local search method in the best solution
obtained by genetic algorithm.
2000; Sivanandam and Deepa, 2008). This procedure
is based on the survival probability that depends on
the objective function value for each individual.
The crossover operator is used to create new in-
dividuals from surviving individuals selected through
the selection operator. The crossover procedure is re-
sponsible for recombining the individuals characteris-
tic during the reproduction process, with this process
it is possible for the offspring to inherit characteristics
of previous generations (Pham and Karaboga, 2000;
Sivanandam and Deepa, 2008).
The mutation operator is responsible for diversify-
ing the existing population allowing the search for the
solution in promising areas and avoiding premature
convergence in local points. This process helps the al-
gorithm to escape from local optimum points because
it slightly modifies the search direction and introduces
new genetic structures in the population (Pham and
Karaboga, 2000; Sivanandam and Deepa, 2008).
Each genetic operator has a specific rate that de-
termined how many individuals will be used and gen-
erated in each genetic procedure. In the traditional
GA the rates are constant values for all evolutionary
process. However, there is not a consensus in the lit-
erature about which value should be used on each op-
erator. On the other hand, many works in literature
assert the intuitive idea that crossover and mutation
rates should not be constant throughout the evolution-
ary process (Vannucci and Colla, 2015), but should
rather vary in the different phases of the search. Once
again there is no consensus on the values of the rates
and how to calculated them. For these reasons the de-
termination of operators rates is normally defined by
individual problem analysis or they are calculated by
means of trial-and-error (Lin et al., 2003).
An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance
389

3 RELATED WORKS
Several versions of genetic operators are described in
the literature and many studies have been done to im-
prove these operators’ performance, see for example
(J
´
ano
ˇ
s
´
ıkov
´
a et al., 2017; Xu et al., 2018; Das and
Pratihar, 2019). The problem of operator rates calcu-
lation is considered a challenging problem in the liter-
ature either for constant rates or dynamic approaches.
The optimal rates setting is likely to vary for differ-
ent problems (Pham and Karaboga, 2000), but it is a
time consuming task. For these reasons, some studies
focused on determining good control rates values for
the genetic operators.
For constants rates and binary individuals rep-
resentation, (De Jong, 1975) recommends a range
of [50,100] individuals in the population size, 60%
for crossover rate and 0.1% for mutation rate. The
(Schaffer et al., 1989) suggests a range of [20-30] in-
dividuals in the population, [75% - 95%] for crossover
rate and [0.5% - 1%] for mutation rate, while (Grefen-
stette, 1986) uses a population of 30 individual, 95%
for crossover and 1% for mutation. As it is possi-
ble to see, these ranges have large variations, being
inconclusive and strongly dependent on the research
knowledge and the problem variations.
On the other hand, some studies concentrate ef-
forts on adapting the control parameters during the
optimization process. These techniques involve ad-
justing the operators’ rates according to problems
characteristic as the search process, the trend of the
fitness, stability (Vannucci and Colla, 2015), fitness
value (Priya and Sivaraj, 2017; Pham and Karaboga,
2000), or based on experiments and domain expert
opinions (Li et al., 2006).
In order to adjust the mutation and crossover rates,
(Vannucci and Colla, 2015) uses a fuzzy inference
system to control the operators’ variation. Accord-
ing to the authors, this method also accelerates the at-
tainment of the optimal solution and avoid premature
stopping in a local optimum through a synergic effect
of mutation and crossover.
Another approach is presented in (Xu et al., 2018),
which uses the GA method to solve the traveling
salesman problem optimizing the mutation charac-
ters. In this case, a random cross mapping method and
a dynamic mutation probability are used to improve
the algorithm. In the approach, the crossover op-
eration varies according to the randomly determined
crossover point and the mutation rate is dynamically
changed according to population stability.
In (Das and Pratihar, 2019) the crossover operator
guided by the prior knowledge about the most promis-
ing areas in the search region is presented. In this
approach four parameters are defined to control the
crossover operator: crossover probability, variable-
wise crossover probability, multiplying factor, direc-
tional probability. It was noted the use of the direc-
tional information helps the algorithm to search in
more potential regions of the variable space.
In (Whitley and Hanson, 1989) is proposed an
adaptive mutation through monitoring the homogene-
ity of the solution population by measuring the Ham-
ming distance between the parents’ individuals during
the reproduction. Thereby, the more similar the par-
ents, the higher mutation probability.
In study of (Fogarty, 1989) adopts the same mu-
tation probability for all parts of an individual and
then decreased to a constant level after a given num-
ber of generations. Another strategy is presented in
(Pham and Karaboga, 2000), upper and lower limits
are chosen for the mutation rate and within those lim-
its the mutation rate is calculated for each individual,
according to the objective function value.
According to (Pham and Karaboga, 2000) in the
first 50 generations there are few good solutions in
the population, so in the initial stage high mutation
rate is preferable to accelerate the search. In contrast,
(Shimodaira, 1996) supports high mutation rates at
the end of the process, in order to come out from lo-
cal optima where the algorithm can be stuck. For the
references presented is possible to verify that there is
no consensus on the values of the rates. For this rea-
son, in this work the rates are dynamically established
by the analysis of population performance throughout
the evolutionary process.
4 DYNAMIC GENETIC
ALGORITHM
This study presents a dynamic Genetic Algorithm
with continuous variable individual representation
that is initially randomly generated (Haupt and Haupt,
2004). Through analysis of the GA behavior, it was
noted that the objective function standard deviation
of the beginning evolutionary process is higher, as ex-
pected because the generation of the initial population
is random. For this reason, the individuals are very
dispersed in the search region. For the same reason,
in the first iterations, the population amplitude is also
very higher. As the search process evolves, the popu-
lation tends to concentrate in specific feasible regions,
in which the chance to find the optimum solution is
higher (promising regions). This causes a decrease in
the standard deviation and amplitude of the objective
function value. At the end of the evolutionary pro-
cess, both amplitude and standard deviation tend to
ND2A 2020 - Special Session on Nonlinear Data Analysis and Applications
390
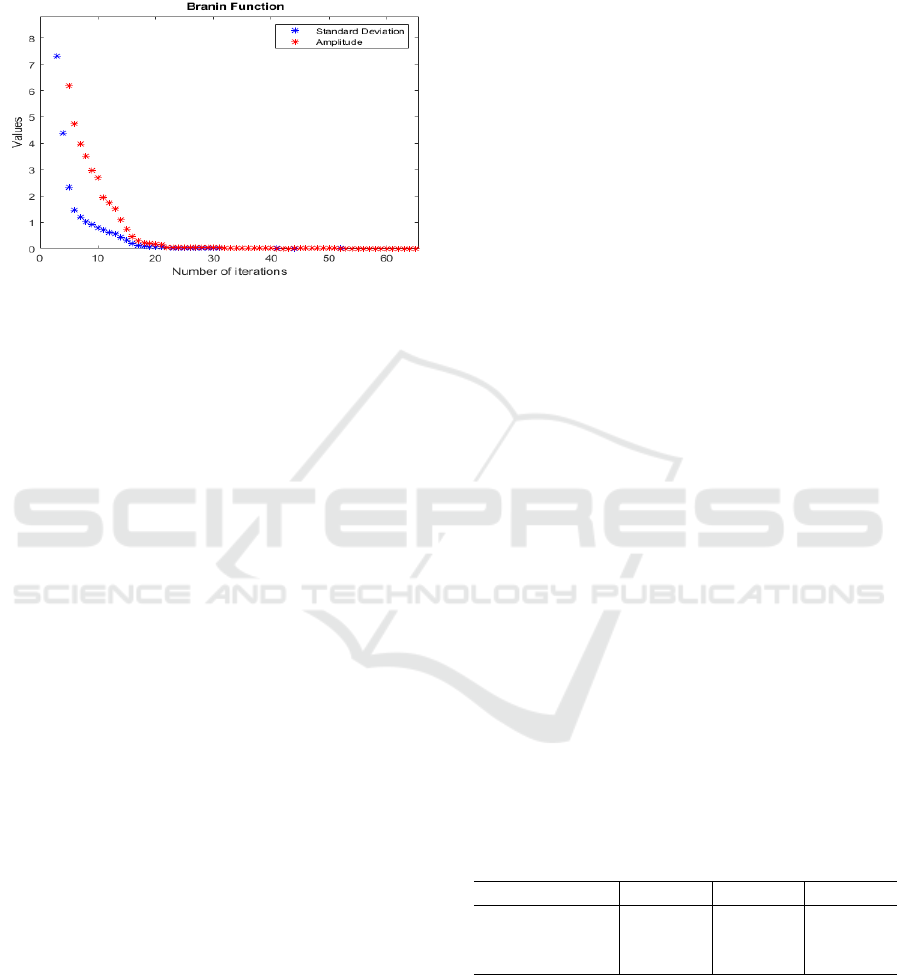
zero, due to the population convergence to the opti-
mum solution point. An example of this behavior is
presented in Figure 1, for the Branin function, consi-
dering an approximation in the initial interactions.
Figure 1: Standard deviation and amplitude of Branin func-
tion.
In this work the individuals are randomly selected
for the crossover and mutation procedures. The two-
point crossover and continue mutation procedures are
used, similar as in (Bento et al., 2013). The rates
variations are controlled by the amplitude and the
standard deviation of each generation and the ampli-
tude differences between successive populations. Be-
sides, a new stopping criterion is also proposed to be
used in conjunction with the traditional ones.
The results of the proposed algorithm are com-
pared with the executions of a hybrid Genetic Algo-
rithm presented in (Bento et al., 2013), considering
the Nelder Mead method, as local search. In (Bento
et al., 2013) the continuous representation is used, and
the follow constants rates are suggested: population
size equal 100 individuals, 0.5 × N
pop
individuals in
selection procedure and 0.25 × N
pop
individuals for
crossover and mutation procedures.
4.1 Determination and Control of the
Operators Rates
By the algorithm analysis is easy to note that the al-
gorithm has different properties throughout the evolu-
tionary process. For this reason, three different phases
were identified according to the amplitude and stan-
dard deviation patterns observed in the algorithm and
by literature review and described in the following
condition
| f (x
1
) − f (x
N
pop
)| ≤ ε ∧ s
f
≤ ε,
where f (x
1
) and f (x
N
pop
) are the best and the worst
objective values in the current population, s
f
is the
standard deviation of the current population and ε ∈
{ε
i
, e
d
}. The three search phases are described in de-
tail as follows.
• Phase 1 - Initial: in this phase the population
amplitude and standard deviation are higher and
there are few good solutions in the population.
For these reasons, higher rates are considered to
accelerate the search. This phase initiates when
the algorithm starts and stops when the population
standard deviation and amplitude be smaller than
ε
i
, and a condition of k
i
iterations be exceeded.
• Phase 2 - Development: the Development phase
starts immediately after Phase 1 and ends when
the population amplitude and standard deviation
are smaller than ε
d
and exceed at least k
d
itera-
tions. The condition of k
d
iteration was defined
to avoid the algorithm remain too short time at
this phase, because depending on the problem the
ε
d
value is quickly reached and consequently the
possible solutions are not so well explored. In this
second phase the operator parameters should not
be so higher as in the initial phase because the
search is concentrated in the promising areas ob-
tained in the first phase. At the end of this phase
the algorithm has already found the optimum re-
gion, but needs to refine the optimum solution.
• Phase 3 - Refinement: this phase has the aim to
refine the solution. The amplitude and standard
deviation are small, that is possible to conclude
that the optimum solution is very close to being
achieved. The rates used in this phase are smaller
than in the other phases because few modifica-
tions are needed. This phase starts immediately
after Phase 2, and continues until a stopping
criterion be achieved.
This work not established constants parameters in
the different phases. Thus, an initial value for each
operator rate is determined in the beginning of each
phase as presented in Table 1.
Table 1: Initial operator rates for each phase.
Genetic Operator Phase 1 Phase 2 Phase 3
Selection 0.7 × N
pop
0.6 × N
pop
0.5 × N
pop
Crossover 0.5 × N
pop
0.4 × N
pop
0.3 × N
pop
Mutation 0.4 × N
pop
0.3 × N
pop
0.2 × N
pop
In the second and third phases, the rate values can
vary 10% considering the initial value. This decision
is based on the amplitude difference between succes-
sive populations. Thereby, if the amplitude difference
between k and k − 1 iterations is smaller than ε
ph2
in the second phase, or smaller than ε
ph3
in the third
phase, the rates increase 1%, otherwise decrease 1%.
An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance
391

This strategy is designed to stimulate small modifi-
cations in the algorithm search and prevent it from
getting stuck at local points. The codification of the
proposed algorithm is shown in the algorithm 2.
Algorithm 2: Hybrid Genetic Algorithm with Dynamic Op-
erators Rates.
Generates a randomly population of individuals,
P
0
, with dimension N
pop
.
Set k = 0.
while stopping criterion is not met do
Set k = k +1.
Identify the Phase and update the operator rates
if necessary
P
0
= Apply selection procedure in N
pop
.
P
00
= Apply crossover procedure in N
keep
.
P
000
= Apply mutation procedure in N
keep
.
P
k+1
= N
pop
best individuals of {P
k
∪ P
00
∪
P
000
}.
Apply the local search method in the best solution
obtained by genetic algorithm.
4.2 Stopping Criterion
In the third phase, the algorithm is very close to the
optimum solution and few modifications are done at
each iteration in order to preserve the good results al-
ready found. For this reason, it not useful to waste ex-
ceeding time in this phase. In this sense, the following
criterion is proposed that can be used in conjunction
with the other criterion already used, as the maximum
number of generation, time limit, number of function
evaluation, minimum error, etc.
This proposed stopping criterion consists of ana-
lyzing the population evolution in the Phase 3. There-
fore, if the standard deviation and amplitude differ-
ences are smaller than 10
−10
in a N
pop
× n in succes-
sive iterations, the algorithm stops. With this strategy,
the stopping criterion adapts to different optimization
problems.
5 NUMERICAL RESULTS
The dynamic Genetic Algorithm variant and the stop-
ping criterion proposed in this study are validated us-
ing six benchmark functions defined in the literature:
Branin function (dimension 2), Easom function (di-
mension 2), Ackley Function (dimension 3), Rosen-
brock function (dimension 3), Sum Squares function
(dimension 4) and Levy function (dimension 5) (Gra-
macy and Lee, 2012; Jamil and Yang, 2013; Sur-
janovic and Bingham, ).
These benchmark functions have several proper-
ties that can be truly useful to test the algorithm per-
formance in an unbiased way (Jamil and Yang, 2013).
Besides, the results are compared with the Genetic Al-
gorithm with constant rates proposed in (Bento et al.,
2013).
The numerical results were obtained using a In-
tel(R) Core (TM) i3 CPU M920 @2.67GHz with 6
GB of RAM. It was considered the following parame-
ters k
i
= 50, ε
i
= 1, k
d
= 150, ε
d
= 10
−3
, ε
ph2
= 10
−3
,
ε
ph3
= 10
−6
, N
pop
= 100 individuals at each genera-
tion, and each problem was executed 100 times, since
the Genetic Algorithm is a stochastic method.
The average of the objective function value, f
∗
,
the number of iterations needed, k, the number of
function evaluation f un.eval and the time needed in
seconds, T, are presented in the Tables 2 and 3 for the
Genetic Algorithm with constants rates and dynamic
rates, respectively.
Table 2: GA with constant rates algorithm results.
Function f ∗ k f un.eval T
Branin 3.9789 × 10
−1
1040 54131 2.18
Easom −9.9900 × 10
−1
1080 56191 2.29
Ackley 1.5100 × 10
−4
2765 143848 5.88
Rosenbrock 1.5120 × 10
−9
5404 281145 11.28
S. Squares 1.7937 × 10
−6
1526 79397 3.31
Levy 4.6310 × 10
−10
872 45499 2.34
Table 3: GA with dynamic rates algorithm results.
Function f ∗ k f un.eval T
Branin 3.9789 × 10
−1
410 36439 1.36
Easom −9.9900 × 10
−1
415 36789 1.39
Ackley 1.0500 × 10
−4
881 75030 2.80
Rosenbrock 1.5945 × 10
−9
1936 161748 5.88
S. Squares 2.1476 × 10
−6
803 68618 2.59
Levy 4.5925 × 10
−10
448 39389 1.87
Analyzing Tables 2 and 3 is possible to conclude
that the optimum solution obtained by both algo-
rithms is very similar. However, the performance of
the GA with dynamic rates is higher because the opti-
mum solution for all problems tested was found using
fewer iterations, function evaluations in a short time
than the Genetic Algorithm with constant rates.
In order to compare the accuracy of the proposed
approach, the Euclidean distance was evaluated and
compared between the results obtained and the opti-
mum solution presented in the literature (Literature).
Table 4 presents the numerical results.
It is possible to observe in Table 4 that the op-
timum solution obtained by both algorithms is very
ND2A 2020 - Special Session on Nonlinear Data Analysis and Applications
392
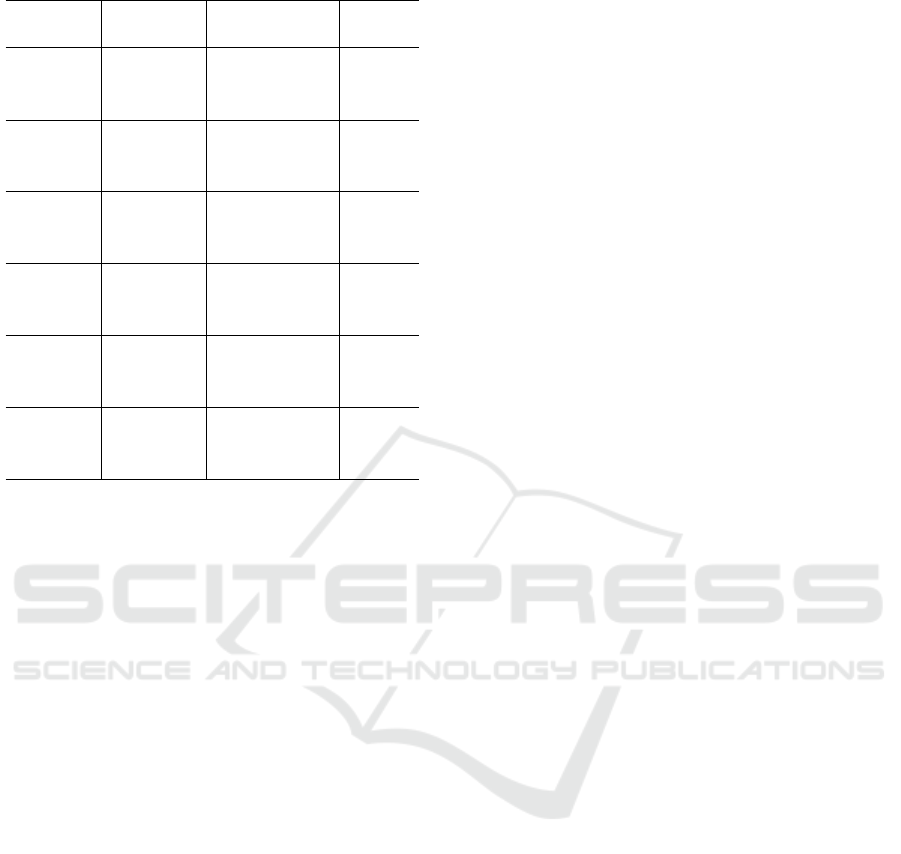
Table 4: Average of euclidean distances comparison.
Function Method
Optimum
Solution
Euclidean
Distance
Branin
Literature 3.9789 × 10
−1
0
Constant rates 3.9789 × 10
−1
1 × 10
−3
Dynamic rates 3.9789 × 10
−1
1 × 10
−3
Easom
Literature -1 0
Constant rates−9.9900 × 10
−1
3 × 10
−2
Dynamic rates−9.9900 × 10
−1
3 × 10
−2
Ackley
Literature 0 0
Constant rates 1.5100 × 10
−4
3 × 10
−4
Dynamic rates 1.0500 × 10
−4
2 × 10
−4
Rosenbrock
Literature 0 0
Constant rates 1.5120 × 10
−9
3 × 10
−5
Dynamic rates 1.5945 × 10
−9
3 × 10
−5
S. Squares
Literature 0 0
Constant rates 1.7937 × 10
−6
9 × 10
−4
Dynamic rates 2.1476 × 10
−6
8 × 10
−4
Levy
Literature 0 0
Constant rates 4.6310 × 10
−10
5 × 10
−5
Dynamic rates 4.5925 × 10
−10
5 × 10
−5
close to the optimum solution presented in the litera-
ture, which proves the efficiency of the proposed ap-
proach.
6 CONCLUSION AND FUTURE
WORK
This work presents a new variation of hybrid Ge-
netic Algorithm considering dynamic operators rates.
The obtained results were very satisfactory since
the Genetic Algorithm combined with dynamic rates
demonstrated excellent ability to found the optimal
solution and when compared to the Genetic Algo-
rithm with constant rates, the approach stands out
since it requires less computational effort. Since it
was used benchmark functions with different proper-
ties, the Genetic Algorithm with dynamic rates can be
applied to different optimization problems. As future
work, it is intended to use machine learning, as Fuzzy
Systems and Artificial Neural Networks, to identify
patterns in the Genetic Algorithm and use this infor-
mation to improve the dynamic rates.
ACKNOWLEDGEMENTS
This work has been supported by FCT — Fundac¸
˜
ao
para a Ci
ˆ
encia e Tecnologia within the Project Scope:
UIDB/5757/2020.
REFERENCES
Bento, D., Pinho, D., Pereira, A. I., and Lima, R. (2013).
Genetic algorithm and particle swarm optimization
combined with powell method. In 11th International
Conference of Numerical Analysis and Applied Math-
ematics, volume 1558, pages 578–581. ICNAAM
2013.
Das, A. K. and Pratihar, D. K. (2019). A directional
crossover (dx) operator for real parameter optimiza-
tion using genetic algorithm. Applied Intelligence,
49:1841––1865.
De Jong, K. A. (1975). An analysis of the behavior of a
class of genetic adaptive systems. PhD thesis, Univer-
stity of Michigan, Ann Arbor, Michigan.
Fogarty, T. C. (1989). Varying the probability of mutation in
the genetic algorithm. In Proceedings of the Third In-
ternational Conference on Genetic Algorithms, pages
104–109, San Francisco, CA, USA. Morgan Kauf-
mann Publishers Inc.
Ghaheri, A., Shoar, S., Naderan, M., and Hoseini, S. S.
(2015). The applications of genetic algorithms in
medicine. Oman Medical Journal, 30(6):406–416.
Gramacy, R. B. and Lee, H. K. (2012). Cases for the
nugget in modeling computer experiments. Statistics
and Computing, 22(3):713–722.
Grefenstette, J. (1986). Optimization of control parameters
for genetic algorithms. IEEE Trans. Syst. Man Cy-
bern., 16(1):122–128.
Haupt, R. and Haupt, S. E. (2004). Practical Genetic Algo-
rithms. John Wiley & Sons, 2 edition.
Holland, J. H. (1992). Adaptation in natural and artificial
systems: an introductory analysis with applications to
biology, control, and artificial intelligence. University
of Michigan Press, Cambridge, MA, USA.
Jamil, M. and Yang, X. (2013). A literature survey of bench-
mark functions for global optimization problems. In-
ternational Journal of Mathematical Modelling and
Numerical Optimisation, 4(2):150–194.
J
´
ano
ˇ
s
´
ıkov
´
a, L., Herda, M., and Haviar, M. (2017). Hybrid
genetic algorithms with selective crossover for the ca-
pacitated p-median problem. Central European Jour-
nal of Operations Research, 25(1):651–664.
Li, Q., Tong, X., Xie, S., and Liu, G. (2006). An im-
proved adaptive algorithm for controlling the proba-
bilities of crossover and mutation based on a fuzzy
control strategy. In Sixth International Conference on
Hybrid Intelligent Systems (HIS’06), Rio de Janeiro,
Brazil. IEEE.
Lin, W., Lee, W., and Hong, T. (2003). Adapting crossover
and mutation rates in genetic algorithms. Journal
of Information Science and Engineering, 19(5):889–
903.
Mitchell, M. (1998). An Introduction to Genetic Algo-
rithms. MIT Press, Cambridge, MA, USA, 1 edition.
Nelder, J. A. and Mead, R. (1965). A simplex method
for function minimization. The Computer Journal,
7(4):308–313.
An Improvement of Genetic Algorithm based on Dynamic Operators Rates Controlled by the Population Performance
393

Pham, D. and Karaboga, D. (2000). Intelligent optimisa-
tion techniques: genetic algorithms, tabu search, sim-
ulated annealing and neural networks. Springer, 1
edition.
Priya, R. D. and Sivaraj, R. (2017). Dynamic ge-
netic algorithm-based feature selection and incom-
plete value imputation for microarray classification.
Current Science, 112(1):126–131.
Schaffer, J. D., Caruana, R. A., Eshelman, L. J., and Das, R.
(1989). A study of control parameters affecting online
performance of genetic algorithms for function opti-
mization. In Proceedings of the Third International
Conference on Genetic Algorithms, pages 51–60, San
Francisco, CA, USA. Morgan Kaufmann Publishers
Inc.
Shimodaira, H. (1996). A new genetic algorithm using
large mutation rates and population-elitist selection
(galme). In Proceedings of the 8th International Con-
ference on Tools with Artificial Intelligence, ICTAI
’96, pages 25–32, Washington, DC, USA. IEEE Com-
puter Society.
Sivanandam, S. N. and Deepa, S. N. (2008). Introduction to
Genetic Algorithms. Springer, 1 edition.
Surjanovic, S. and Bingham, D. Virtual library of simula-
tion experiments: Test function and datasets.
Vannucci, M. and Colla, V. (2015). Fuzzy adaptation of
crossover and mutation rates in genetic algorithms
based on population performance. Journal of Intel-
ligent & Fuzzy Systems, 28(4):1805–1818.
Whitley, D. and Hanson, T. (1989). Optimizing neural net-
works using faster, more accurate genetic search. In
Proceedings of the Third International Conference on
Genetic Algorithms, pages 391–396, San Francisco,
CA, USA. Morgan Kaufmann Publishers Inc.
Xu, J., Pei, L., and Zhu, R. (2018). Application of a ge-
netic algorithm with random crossover and dynamic
mutation on the travelling salesman problem. Proce-
dia Comput. Sci., 131:937–945.
ND2A 2020 - Special Session on Nonlinear Data Analysis and Applications
394
