A Graph-based Approach for Process Robustness in Unreliable

Communication Environments

Frank Nordemann

, Ralf T

onjes

, Elke Pulverm

uller

and Heiko Tapken

Faculty of Engineering and Computer Science, Osnabr

uck University of Applied Sciences, Osnabr

uck, Germany

Institute of Computer Science, University of Osnabr

uck, Osnabr

uck, Germany

Keywords:

Business Process, Process Robustness, Unreliable Communication Environments, BPMN, DAG, rBPMN.

Abstract:

The Business Process Model and Notation (BPMN) is broadly used to model and execute process deﬁnitions.

Many processes include different participants and require reliable communication to operate properly. How-

ever, BPMN is used in a growing number of use cases taking place in unreliable communication environments.

Intermittent or broken connectivity potentially interrupts or breaks down process operation. Methods for the

veriﬁcation of process robustness are missing. This paper presents a graph-based approach to automatically

identify robust process path conﬁgurations. Using process-to-graph transition rules and robustness metrics,

graph-based search algorithms allow to ﬁnd robust process paths and to rate their level of robustness. Pro-

cess examples show that well-known shortest-path algorithms not necessarily identify the most appropriate

path. Comparing all paths using metrics for the path robustness level and robustness probability is a promising

choice for most scenarios. Inspired by maximum-ﬂow algorithms, a combined-path analysis may optimize

robustness by combining process paths based on different communication technologies.

1 INTRODUCTION

Aside from traditional business process domains like

banks, shops, the supplier- and shipping industry, the

Business Process Model and Notation 2.0 [BPMN,

(OMG, 2011)] is applied in a growing number of non-

traditional domains. BPMN is being used due to its

expressiveness, ﬂexibility, mature tool support, ability

to execute process models and to model collaborative

processes including different participants.

Non-traditional use cases may take place in un-

reliable communication environments not addressed

by BPMN. Areas such as Cyber Physical Systems

(CPS), agriculture, road-side construction, environ-

mental and wildlife monitoring as well as scenarios

located in undeveloped or disaster affected regions

often encounter intermittent or broken connectivity.

However, connectivity-related issues should not lead

to interrupted or failed process executions.

The BPMN meta-model extension rBPMN

(Nordemann et al., 2020) has been designed to

enable robust process execution even in the case of

intermittent or broken connectivity. rBPMN ensures

robustness by providing alternatives for possibly fail-

ing message ﬂows, by moving functionality between

participants and by dynamically integrating partic-

ipants and their functionality at process runtime.

Calculations based on connectivity estimations allow

to evaluate the robustness of individual message

ﬂows at design time. However, rBPMN misses

mechanisms and metrics to analyze and evaluate the

robustness of an entire process.

This paper introduces a graph-based approach to

automatically identify and rank robust paths in a pro-

cess. The approach may be used at design time to

verify process robustness and at runtime to optimize

process execution. The main research contributions

of the paper include:

1. Process-to-Graph transition rules for BPMN and

rBPMN process elements in terms of communi-

cation robustness,

2. Robustness metrics allowing to identify robust

process paths and to rate their level of robustness,

3. A graph analysis heuristic for dynamically chang-

ing scenarios and a graph analysis procedure for

the combination of process path segments,

4. A comparison of graph-based search algorithms

for robust path identiﬁcation and

5. Use-case-Driven recommendations for the selec-

tion and utilization of robustness metrics and

search algorithms.

Nordemann, F., Tönjes, R., Pulvermüller, E. and Tapken, H.

A Graph-based Approach for Process Robustness in Unreliable Communication Environments.

DOI: 10.5220/0009389100970107

In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2020), pages 97-107

ISBN: 978-989-758-421-3

The remainder of the paper is as follows: First, re-

lated work (Section 2) and rBPMN (Section 3) are

presented, followed by the process-to-graph transi-

tion (Section 4) and the robustness analysis based on

search algorithms (Section 5). Lastly, results are dis-

cussed (Section 6) before a summary concludes the

paper (Section 7).

2 RELATED WORK

BPMN has been used and extended for various use

cases and application areas (Braun and Esswein,

2014). Worth mentioning are the diverse activ-

ities in the areas of the Internet of Things (IoT)

(Meyer et al., 2013), (Chiu and Wang, 2013) and

CPS (Graja et al., 2016), (Bocciarelli et al., 2017),

aiming to include new physical entities as resources

for business processes. IoT resources may differenti-

ate from each other by Quality of Information (QoI)

aspects, including the reliability of physical entities.

This topic is addressed by several publications,

allowing to integrate and observe QoI aspects in

business processes (Martinho and Domingos, 2014),

(Domingos et al., 2020).

Reliability and performance of BPMN processes

is discussed in (Bocciarelli and D’Ambrogio, 2011).

A meta-model extension adds metadata descriptions

about process / task reliability (e.g. mean time be-

tween failure for a task) and performance character-

istics (e.g. time required for a task). Further elabo-

rations in (Bocciarelli et al., 2014) allow to simulate

processes prior to runtime.

Process reliability is also discussed in (Resp

ıcio

and Domingos, 2015). Using an added reliabil-

ity value for each activity, the overall process re-

liability is calculated. Effects of human and non-

human resources on process reliability are addressed

in (Domingos et al., 2016).

A BPMN extension to integrate Wireless Sen-

sor Networks (WSN) is illustrated in (Sungur et al.,

2013). The extension enhances usage of sensor-based

data by adding a WSN task, WSN pool and perfor-

mance annotations.

The reliability of ambient assisted living systems

is handled in (Martinho et al., 2016). By integrat-

ing reliability information about various used compo-

nents into BPMN, the overall reliability may be eval-

uated for appropriate resource allocation.

In (Mazzola et al., 2017), a mechanism based

on semantically annotated process models allows to

compensate faulty tasks for process service plan exe-

cution in cloud environments.

Some publications use BPMN in conjunction with

Directed Acyclic Graphs [DAG’s, (Even, 2011)]. (Di-

jkman et al., 2007) introduce formal semantics in

terms of mapping BPMN to Petri nets, allowing to ap-

ply existing analysis methods to process deﬁnitions.

The authors continue their work in (Dijkman et al.,

2009) to check BPMN processes for similarities in

relation to tasks and control ﬂows. (Ceballos et al.,

2015) use DAG’s to model and advice on human ac-

tivities. In contrast, (Gounaris, 2016) apply perfor-

mance optimization methods (reordering and paralyz-

ing tasks) on DAG’s originating from reduction strate-

gies for data-intensive queries and ﬂows.

The process-to-graph-transition presented in this

paper has similarities with the previously listed pub-

lications. For instance, all publications map activities

to graph vertices and sequence ﬂows / message ﬂows

to graph edges. However, the objectives of the pub-

lications differ, resulting in differences of the graph

mapping. Some concepts rely on probabilistic models

and statistics for the graph mapping. Others avoid the

use of edge weights. Signiﬁcant differences exist in

mapping BPMN gateways due to focusing on differ-

ent aspects (e.g. performance, similarity, human ac-

tivities, communication robustness) and varying anal-

ysis methods and algorithms.

To the best of the authors’ knowledge, no publica-

tion focuses on evaluating process reliability / robust-

ness with regards to unreliable communication envi-

ronments. Due to different objectives, no literature

contribution outlines a process-to-graph transition as

required for communication robustness. Identiﬁca-

tion and comparison of robust process paths are miss-

ing. Besides, no publication provides a graph map-

ping for rBPMN’s extension elements.

3 RESILIENT BPMN (rBPMN)

This section introduces rBPMN (Nordemann et al.,

2020), a BPMN extension for robust process model-

ing in unreliable communication environments.

The motivation for rBPMN’s development orig-

inates from the growing use of BPMN in environ-

ments featuring intermittent or broken connectivity.

Since communication is not in the focus of BPMN,

rBPMN extends its meta-model allowing domain ex-

perts to include alternatives for failing connectivity,

to move functionality between participants, to check

robustness at design time and to dynamically adapt a

process at runtime.

rBPMN realizes robustness by introducing new

process elements presented in Figure 1. Opportunistic

Message Flows (abbreviated: OppMessageFlows) de-

scribe possibly failing message transfers between par-

ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering

MovTask

(moveable)

OppTask

OppDynTask

Autonomy

attribute

MovSubProc.

(moveable)

OppMessageFlow

MessageFlow (BPMN)

OppPriorityFlow

OppDecisionFlow

MovParticipant

(moveable)

Figure 1: rBPMN message ﬂows, activities and attributes.

ticipants. The ﬂows’ metadata includes information

about the message to be transferred and an estimated,

scenario-based connectivity. OppMessageFlows may

be grouped by non-graphical OppMessageGroups to

deﬁne sets of alternatives for different topics or con-

cerns. In an OppMessageGroup, only one alterna-

tive needs to communicate successfully to establish

robustness. The decision for one of the alternatives

can be priority-based (OppPriorityFlows) or criteria-

based (OppDecisionFlows).

The addition of moveable tasks and participants

(MovTasks, MovSubProcesses, MovParticipants) en-

ables a movement of (limited) functionality or ser-

vices from one participant to another. In case of fail-

ing connectivity, a process may continue its operation

by executing the moved functionality locally using an

OppTask. Locally moved functionality is indicated by

the autonomy attribute (cf. Figure 1). An OppDyn-

Task allows to integrate dynamically appearing par-

ticipants at process runtime. Here, appearing partici-

pants that offer functionality required by an OppMes-

sageGroup dynamically extend the group as an addi-

tional alternative. Typical use cases for OppDynTasks

are applications in Mobile Ad-Hoc Networks, Delay-

Tolerant Networks and Opportunistic Networks.

rBPMN is able to check the robustness of mes-

sage ﬂows at design time. Robustness calculations

examine the required message size, available band-

width, failure probability and given time frame to

state whether or not a message ﬂow is robust. The

reader is referred to (Nordemann et al., 2020) for

more information about technical insights.

Since rBPMN is only able to evaluate the ro-

bustness of individual message ﬂows between partic-

ipants, it motivates this paper to address and evaluate

robustness of an entire process.

4 PROCESS-TO-GRAPH

TRANSITION

The application of graph-based search algorithms for

the robustness analysis requires to translate a process

into an acyclic graph ﬁrst. This section introduces a

procedure to map BPMN processes to DAG’s with re-

spect to communication robustness.

Ex1

Figure 2: Process example Ex1.

Ex1

Ex1'

P1 T1'

Figure 3: Robustness graph of Ex1.

4.1 Creation of Robustness Graph

Figure 2 depicts a simple process example Ex1 featur-

ing exclusive gateways (XOR) and a participant P1.

As indicated by the OppMessageFlows, communica-

tion of task T1 with P1 may be interfered. In contrast,

path segment including T2 requires no communica-

tion and is always robust. Only one of the two paths

including T1 or T2 is chosen depending on the param-

eters instructing the exclusive gateway with its deci-

sion.

The related robustness graph G

Ex1

= (V,E) in-

cludes a set of vertices V representing BPMN ac-

tivities / participants and several edges E reﬂecting

sequence ﬂows and message ﬂows. As shown in

Figure 3, G

Ex1

has a starting vertex Ex1 and an ending

vertex Ex1’. Accordingly, communication of T1 with

P1 is arranged by T1 → P1 → T1’. A second graph

path represents the use of T2 instead of T1.

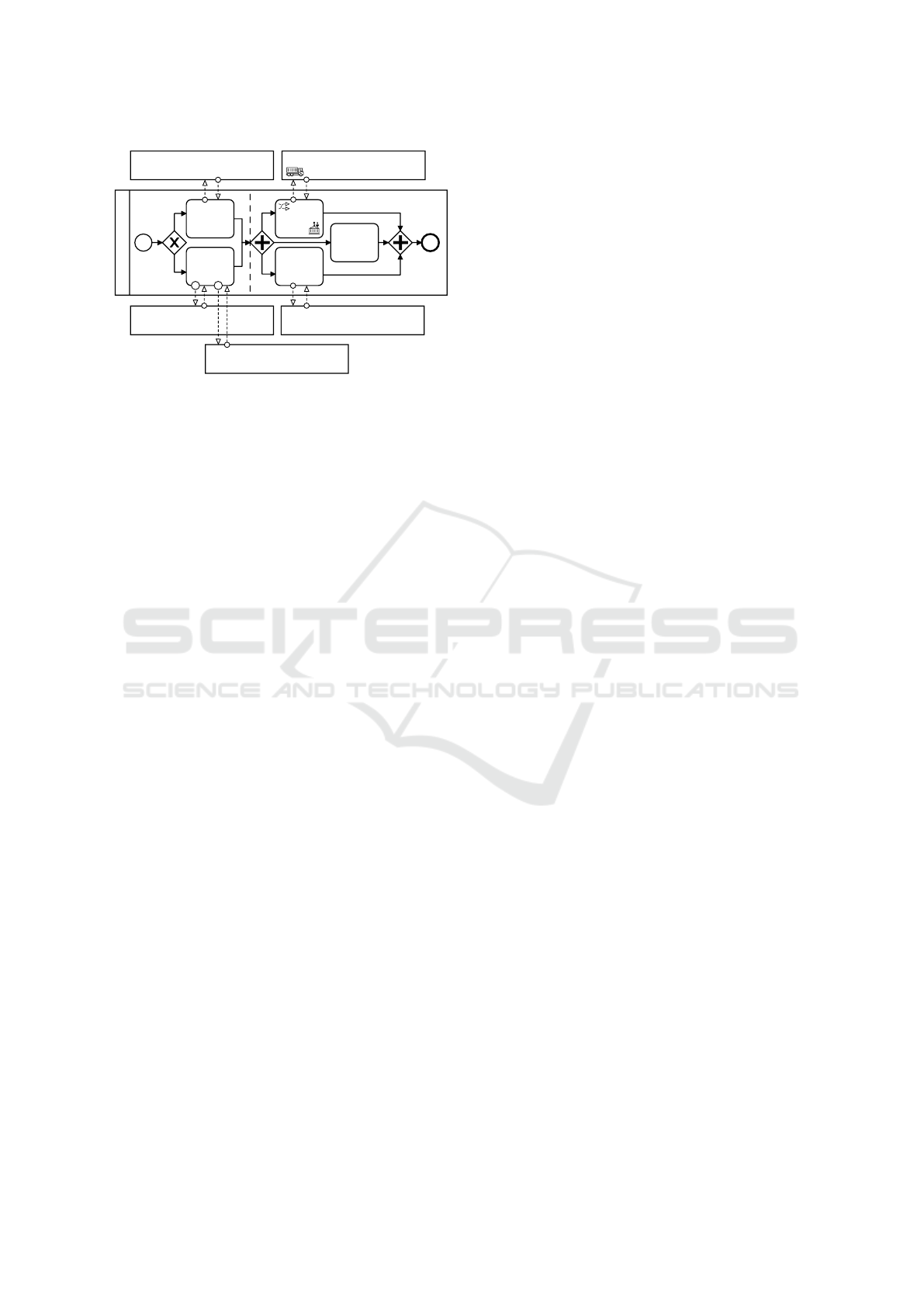
A second process example Ex2 is illustrated in

Figure 4, featuring exclusive and parallel gateways.

Communication with all participants is unreliable.

The associated robustness graph in Figure 5 has been

created using transition rules summarized in Table 1.

The transition is explained in detail subsequently.

In the ﬁrst part of the process (Ex2a in Figure 4,

Ex2 → G in Figure 5), the paths of T1 and T2 are sep-

arated by an exclusive gateway. Since only one of the

two paths is chosen, the graph reﬂects this by adding

separate paths for T1 and T2 and merging them after-

wards.

At T2, communication with P2a and P2b is re-

alized by OppDecisionFlows belonging to the same

OppMessageGroup, labeled with the character a. Ei-

ther communication with P2a or P2b has to work for

a robust process. Hence, T2 connects P2a and P2b

by separate paths, resulting in three path options for

robustness in Ex2a. The vertex G is used as a glue ver-

tex, since there is no BPMN activity element merging

A Graph-based Approach for Process Robustness in Unreliable Communication Environments

Table 1: Rules for the transition of BPMN and rBPMN process elements to graph segments.

Process Element Graph Segment Explanation

BPMN Gateways (GW’s)

Exclusive GW,

Event-based GW

Separated paths X Only one of the GW options is chosen and needs to be part of

the process path.

Parallel GW Extended path X Robustness depends on all summarized GW options.

Inclusive GW,

Parallel event-based GW

Separated and

extended paths

X One or more GW options can be chosen. Possible GW option

combinations need to be reﬂected in the graph.

Complex GW Separated paths and /

or extended path(s)

X No general rule can be provided, depends on concrete GW op-

tions. In practice often replaced by other GW’s.

BPMN Path Merging by Exclusive GW

Splitting GW:

parallel, inclusive, complex,

parallel event-based

Separated and

extended paths

X Splitting GW and merging exclusive GW results in multiple

executions of the merged process segment. The number of

executions depends on the number of combined options.

BPMN Flows / Events

Conditional sequence ﬂow X Different way to model GW options. GW transition rules are

applied.

Message ﬂow a) Extended path

b) Remove element

X* a) If robustness requires a successful message ﬂow.

b) If robustness is not affected by message ﬂow.

Event X If relevant for robustness, the event is initiated by a message

ﬂow. Message ﬂow transition rules are applied.

Interrupting event / signal Separated paths X Event / signal occurrence modiﬁes process path. Robustness

depends on the alternative path initiated by the event / signal.

BPMN Activities / Participants

Sub-process,

Call activity

Extended path X Robustness depends on activities within the sub-process / call

activity. Graph may be extended by a subgraph.

Pool

Collapsed pool

X Represent a (summarized) subgraph. Transition rules of mes-

sage ﬂow are applied.

rBPMN Flows

OppMessageFlow,

OppPriorityFlow,

OppDecisionFlow

a) Extended path

b) Remove element

X* a) If robustness requires a successful message ﬂow.

b) If robustness is not affected by message ﬂow.

OppMessageGroup Separated paths X OppMessageGroups deﬁne sets of alternative ﬂows. Hence,

every ﬂow results in a separate path in the robustness graph.

Multiple OppMessageGroups Extended path X Multiple OppMessageGroups separate alternatives for differ-

ent concerns, resulting in an extended path.

rBPMN Activities / Participants

OppTask

(moved functionality)

a) Separated paths

b) Extended path

X* OppTasks allow to execute functionality of other participants.

A local functionality a) adds an alternative to an existing

OppMessageGroup or b) stands for itself.

OppDynTask

(dynamic participants)

Separated paths X OppDynTasks allow to integrate dynamically appearing partic-

ipants as alternatives for existing OppMessageGroups.

MovTask, MovSubProcess,

MovParticipant

Separated paths X One path for executing functionality on a remote participant.

Another path for local execution of functionality.

Declaration: Xautomatable X* requires process context information to be automated

ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering

100

Ex2

P2a

P2b

Figure 4: Process example Ex2.

the different process paths.

The second process part Ex2b executes T3, T4 and

T5 in parallel. T3 and T4 are inﬂuenced by unreliable

communication, T5 includes no communication and

is always robust. All three tasks need to be executed

for a robust process due to the parallel gateway. To

reﬂect this in the graph, the path of T3 is extended by

the paths of T4 and T5.

T3 needs to call a functionality offered by P3.

This can be done by i) calling P3 and receiving the

desired result or by ii) moving (limited) functionality

from P3 to T3 and execute it locally (P3l). The ro-

bustness graph integrates this by two separate paths

between T3 and T3’.

T4’s communication with P4 may interrupt or

break. Since there are no decisions, its representa-

tion in the graph is a single path T4 → P4 → T4’.

Lastly, T5 is robust since it is not involved in any com-

munication. By extending the path of T3 / T4 with

a vertex for T5, the robustness graph of Figure 5 is

complete. The next subsection explains the x-labeled

graph edges and why the inclusion of T5 is dispens-

able in this scenario.

There is no need to translate BPMN processes to

robustness graphs manually. Transition can be auto-

mated following the rules of Table 1. As denoted,

some elements require additional semantics to clarify

the meaning of the modeled process segment. This

may be done by BPMN text annotations or metadata.

4.2 Reduction of Robustness Graph

The robustness graph in Figure 5 relates to the BPMN

process illustrated in Figure 4. However, only a subset

of edges and vertices included in the graph is exposed

to unreliable communication and its consequences for

robustness. The affected edges have been labeled

with an x, representing process parts where unreliable

communication or moving of functionality occurs.

Figure 6 illustrates a simpliﬁed version of the robust-

ness graph shown in Figure 5. Unlabeled edges have

been removed. Where necessary, vertices have been

removed or combined. The outcome is a compact

DAG, ready to be assigned with edge weights and to

serve as a basis for the graph analysis.

In general, process elements affected by robust-

ness need to be part of the graph. In the area of unreli-

able communication environments, this requires con-

sideration of:

• Possibly failing message ﬂows (OppMessage-

Flows, OppPriorityFlows, OppDecisionFlows),

• moveable activities (MovTasks, MovSubPro-

cesses, MovParticipants),

• locally executable functionality (OppTasks) and

• dynamic alternatives (OppDynTaks).

It is important to include all possible process paths

in the graph after simpliﬁcation. If a path segment

between gateways is robust due to avoidance of com-

munication, it may be combined to a single vertex but

still needs to be part of the graph. For instance, it is

not allowed to remove T2 from the graph of Ex1 in

Figure 3.

4.3 Further Transition Elaborations

Not all transition rules listed in Table 1 have been ap-

plied in the transitions of process examples Ex1 and

Ex2. This section provides concluding examples for

signiﬁcant transition aspects based on (reduced) ro-

bustness graphs.

4.3.1 Path Merging by Exclusive Gateways

Parallel and inclusive gateways split the BPMN pro-

cess token into as many tokens as outgoing gateway

options apply. When the tokens arrive at a merg-

ing point realized by a parallel or inclusive gateway,

the process is synchronized by merging all previously

created token copies. However, if merging is realized

by an exclusive gateway, no synchronization takes

place and all token copies continue their way to the

process’ end. This is also affecting robustness, since

the merged segment of the process will be executed

multiple times.

Process example Ex3 (Figure 7) illustrates process

merging by an exclusive gateway. In Ex3a, a paral-

lel gateway splits the process into two path segments

calling services at participants P1 / P2. The related

robustness graph shown by Figure 8 has been created

using parallel gateway transition rules by extending a

common graph path (cf. Table 1). After an exclusive

gateway merging P3 is executed twice, since the two

A Graph-based Approach for Process Robustness in Unreliable Communication Environments

101

Ex2

Ex2'

T1'

P2a

P2b

T2'

P3l

T3' T4 P4

T4' T5

Figure 5: Robustness graph of Ex2.

Ex2

P2a

P2b

Ex2'T3

P3l

T4 P4

Figure 6: Reduced robustness graph of Ex2.

Ex3

Figure 7: Process example Ex3 featuring a merging exclu-

sive gateway.

process tokens created by the parallel gateway have

not been synchronized.

The parallel gateway has been replaced by an in-

clusive gateway in Ex3b. One, some or all outgo-

ing process segments may be chosen by the inclusive

gateway, depending on process variables. The robust-

ness graph in Figure 9 reﬂects this by three separate

paths for i) P1, ii) P2, iii) P1 and P2. Here, each path

continues to the end of Ex3b and includes the merged

process segment as many times as gateway options

have been combined. The path including both P1 and

P2 combines two options and the common path exe-

cutes P3 twice.

4.3.2 Integration of Subgraph Segments

Pools represent participants in BPMN. A participant

may be an actor or system part of a different organiza-

tion, resulting in Service Level Agreements (SLA’s)

taking care about the robustness of offered services

or functionalities. However, a participant may also

be part of the same organization accepting robustness

conﬁguration demands. In the latter case, relevant ro-

bustness graph segments of the service offering par-

ticipant can be integrated into the graph of the calling

participant.

This has been done for the graph of P1, which was

inserted into the graph of Ex1 in Figure 10. P1 in-

Ex3a P1 Ex3a'P2 P3 P3

2-times P3

Figure 8: Robustness graph of Ex3a.

P1 P3

P2 P3

P1 P2 P3

Ex3b'

Ex3b

x-times P3x gateway options

Figure 9: Robustness graph of Ex3b.

cludes two separate paths for calling P6 / P7 and is

now part of Ex1’s robustness calculation. Ex1 may

choose the service for P1 to enhance robustness. The

same procedure allows to integrate graphs of sub-

processes.

4.3.3 Integration of Dynamic Participants

rBPMN allows to enhance robustness by dynamically

integrating participants at process runtime. Using

OppDynTasks, dynamic participants add an option to

an existing OppMessageGroup that needs to be re-

ﬂected in the robustness graph. The illustration pro-

vided in Figure 11 is based on process example Ex1 of

Figure 2. Besides calling a service at P1, T1 may call

a service located at the dynamically appearing partic-

ipant Pd. Typical use cases for dynamic participants

are ad-hoc, delay-tolerant or opportunistic networks

[cf. (Fall, 2003), (Pelusi et al., 2006)].

Ex1

Ex1'

T1'

P6 P1'

Subgraph of P1

Figure 10: Integrated path segment of P1 into robustness

graph of Ex1.

T1'P1

Ex1

Ex1'

Figure 11: Dynamic participant Pd in the robustness graph

of Ex1.

ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering

102

Table 2: Robustness metrics.

Semantic Symbol & Formula P*

Number of path edges n ∈ N X

Robustness of path edge R

∈ R

(Total) robustness of path R

∑

i=1

Robustness level of path R

= min(R

,...,R

) X

Average robust. of path R

= R

/n X

Median robust. of path R

= median(R

,...,R

) X

Range of path R

= max(R

,...,R

) − R

P* ⇒ also applicable to probability-based graphs

5 ROBUSTNESS GRAPH

ANALYSIS

Based on the robustness graphs of Section 4, this

Section deﬁnes robustness metrics and applies graph-

based search algorithms to ﬁnd robust process conﬁg-

urations.

5.1 Robustness Metrics

Multiple metrics to measure robustness are introduced

subsequently. A distinction is made between the ap-

plication of edge weights based on estimated connec-

tivity and based on probabilities.

5.1.1 Estimated Connectivity Weights

rBPMN introduced a mechanism to calculate the ro-

bustness of a message ﬂow at design time. The calcu-

lation includes parameters such as estimated message

size, protocol overhead, available bandwidth, and fail-

ure probability. In (Nordemann et al., 2020), the

mechanism has been used to specify whether or not

a message ﬂow is robust. However, the resulting ro-

bustness R

∈ R|R

≥ 0 of the calculation includes ad-

ditional information. R

basically describes, how of-

ten a message can be sent in an available time period

(cf. Equation 1).

< 1 : Message can be sent only partly

= 1 : Message can be sent exactly once

> 1 : Message can be sent more than once

(1)

The calculated robustness R

for a message ﬂow is

used as a weight for the corresponding edge in the

robustness graph. This way, it is not only possible to

ﬁnd a robust process path, but to rank the robustness

of different paths. Identiﬁed process paths may be

compared by metrics of Table 2.

Table 3: Metrics exclusive to probability-based graphs.

Semantic Symbol & Formula

Probability of path edge P

∈ R|0 ≤ P

≤ 1

Probability of path P

∏

i=1

Boolean prob. of path P

= 0 (∀ P

< 1)

= 1 (∀ P

= 1)

Calculations are based on estimated parameters and

may differ from real-world connectivity. Raising the

minimum robustness level R

allows to include a con-

nectivity safety margin for robust process paths. For

instance, a scenario may deﬁne a minimum R

= 2.0

for robust process paths. A path with R

= 1.5 would

be rated as not robust, since it is not able to provide

the requested connectivity safety margin.

5.1.2 Probability Weights

Estimating use case connectivity by detailed parame-

ters may be challenging for domain experts unfamiliar

with communication technologies. It may be easier

for them to describe connectivity based on probabili-

ties. Alternatively, used applications may record con-

nectivity by logging successful and failing message

transfers. In these cases, evaluations may be done

by applying the identiﬁed probabilities as robustness

probability P

∈ R|0 ≤ P

≤ 1 to appropriate edges.

Applicable metrics are listed in Table 2 and Table 3.

5.2 Shortest-path / Longest-path

Analysis

Shortest-path algorithms such as Dijkstra (Even,

2011) and Bellman-Ford (Bellman, 1958) ﬁnd the

path with lowest total weight (or cost) from a source

to a destination. Since not minimum cost, but

maximum robustness is desired here, edge weights

need to be adjusted by i) inverting positive weights

new

= (R

old

− R

max

) ∗ −1) or by ii) applying nega-

tive weights (R

new

= R

old

∗−1), if supported. Or else,

a longest-path analysis with maximum total weight is

applied, leading to the same result. While the longest-

path problem is NP-hard in general, it can be solved

in polynomial time in DAG’s applied here (Sedgewick

and Wayne, 2011). If calculation effort is not critical,

implementations may be based on the Breadth-First

Search [BFS, (Even, 2011)]. Since the following sub-

sections apply positive edge weights, the longest-path

method is used subsequently.

Figure 12 shows the result of a longest-path anal-

ysis on process example Ex2 with the chosen path as

a dashed line. While the path with highest robustness

from Ex2 → Ex2’ has been chosen, the path is not

robust because of the path robustness level R

= 0.8.

A Graph-based Approach for Process Robustness in Unreliable Communication Environments

103

6.0

Ex2

0.8

P2a

1.5

P2b

2.1

Ex2'

1.4

P3l

3.0

T4 P4

2.01.7

2.3

1.6

2.3

3.0

Figure 12: Longest-path analysis on Ex2 using estimated

connectivity weights.

3.0

Ex2

P2a

1.5

P2b

2.1

Ex2'

1.4

P3l

3.0

T4 P4

2.01.7

2.3

1.6

2.3

3.0

Figure 13: Longest-path analysis on Ex2 after removal of

non-robust edges (R

max

= 3.0).

This is due to the impact of an edge with a weight

of 6.0, which guides the algorithm to include P1 into

the path. The mechanism might help for maximizing

the total weight, but certainly not for ﬁnding robust

process paths.

Removing all non-robust edges R

< 1 (cf.

Equation 1) from a graph enables the analysis to ﬁnd

only robust paths. Furthermore, it is suggested to limit

the maximum weight of an edge R

max

to avoid over-

weighting graph edges. R

max

is also applied to edges

representing locally moved functionality (e.g., edges

connected to P3l of Ex2) and edges that have no ro-

bustness inﬂuence. Figure 13 presents an adjusted

process graph and the resulting path with highest ro-

bustness of a longest-path analysis.

Figure 14 illustrates a longest-path analysis using

exemplary probability values as edge weights. The

analysis summarizes edge weights to choose the path

with highest total weight

∑

i=1

. Especially when

using probabilities, this might not identify the most

appropriate path. It is important to include other met-

rics such as the probability of the path P

. Further-

more, adjusting the graph by removing all edges not

fulﬁlling a deﬁned minimum robustness level R

may

be useful.

5.3 Maximum-step Analysis

With the maximum-step analysis, a straightforward

heuristic for ﬁnding robust process paths is introduced

in this paper. Based on the Depth-First Search (DFS,

(Tarjan, 1972)), the algorithm chooses the edge with

the highest weight at each separation point (or step)

until the end vertex is reached. The algorithm in-

cludes an optional parameter for a minimum path ro-

bustness level R

. If it has to choose an edge not meet-

ing the desired robustness level, the algorithm returns

to the last separation point and chooses the next high-

est ranked edge to continue the path to the end vertex.

The analysis will present no outcome if no path with

the required robustness level exists.

Applying the maximum-step heuristic to the Ex2

1.0

Ex2

0.7

P2a

0.8

P2b

0.9

Ex2'

0.8

P3l

1.0

T4 P4

0.90.9

0.9

1.0

Figure 14: Longest-path analysis on Ex2 using probability

edge weights.

P1 P3

1.3

Ex4

1.7

1.5

Ex4'

2.0

1.4

2.3

1.4

2.5

Figure 15: Challenging robustness graph for maximum-step

heuristic.

graphs of Figure 13 and Figure 14 leads to the same

chosen paths as depicted in the Figures. However,

facing conditions as shown by Figure 15 is challeng-

ing for the maximum-step analysis and will not re-

sult in ﬁnding the most robust path. In the graph of

Figure 15, the heuristic is unable to notice the more

robust path including P2 / P4 / P6. However, the

algorithm may be an appropriate choice for highly

dynamic scenarios, where graph edge values show a

level of uncertainty or do change rapidly.

5.4 All-path Analysis

Evaluating robustness graphs using the all-path

method is a versatile type of analysis. All pos-

sible process paths between source and destination

are identiﬁed (e.g. using BFS or DFS). The differ-

ent paths are compared by use-case-driven metrics.

For instance, the robustness level of a path R

is of

main interest for many scenarios, especially when dis-

tinguishing between different robust process paths.

When working with non-robust process paths and

edge weights based on probabilities, the probability

of the path P

might be the main relevant factor.

Table 4 compares the paths for process example

Ex2 with different metrics. The estimated connec-

tivity and probability weights of Figure 12 and Fig-

ure 14 are used for the calculations. Evaluating esti-

mated connectivity edges by path robustness R

leads

to chose the path including P1 / P3l, a non-robust pro-

cess path. Focusing on the robustness level of the

path R

corrects the evaluation by choosing the path

including P2b / P3l. The same result is presented by

the probability of the path P

. Metrics may be prior-

itized or combined to decide on the most appropriate

process path.

5.5 Combined-path Analysis

Finding the most robust conﬁguration for a process

does not necessarily mean to ﬁnd the path with high-

est robustness R

or highest probability P

. A pro-

cess may utilize hybrid networks to combine different

ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering

104

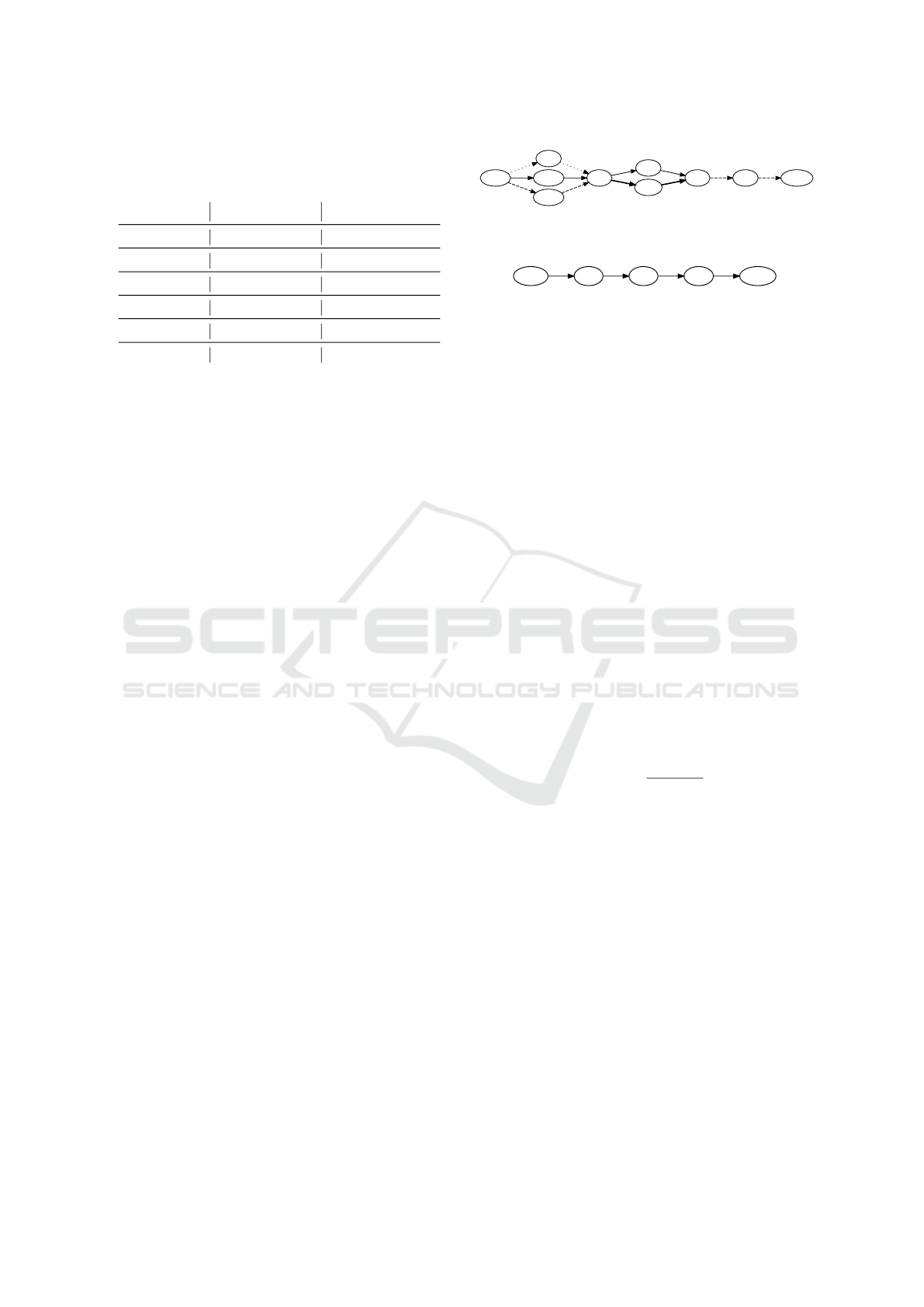
Table 4: Comparison of different process paths using an all-

path analysis and selected metrics.

Path variation Est. edge weights Prob. edge weights

Ex2 → Ex2’

P1 / P3 0.8 14.1 2.35 5.2 0.41 0.7 0.87 0.3

P1 / P3l 0.8 17.1 2.85 5.2 0.57 0.7 0.92 0.3

P2a / P3 1.4 10.5 1.75 0.9 0.42 0.8 0.87 0.1

P2a / P3l 1.5 13.5 2.25 1.5 0.58 0.8 0.92 0.2

P2b / P3 1.4 11.7 1.95 0.9 0.47 0.8 0.88 0.1

P2b / P3l 2.0 14.7 2.45 1.0 0.66 0.9 0.93 0.1

technologies for communication (Mayer, 2012). For

instance, the combination of infrastructure-based (e.g.

Cellular, WiFi in access-point mode, LoRaWAN) and

infrastructure-free (e.g. WiFi in ad-hoc mode) tech-

nologies multiplies communication opportunities, es-

pecially in environments with unreliable communica-

tion.

The combined-path analysis introduced in this

subsection allows to combine process paths realized

by different communication technologies to enhance

robustness of a process. The analysis is inspired by

maximum-ﬂow algorithms of network graphs such as

(Ford and Fulkerson, 2009) and (Dinic, 1970), ﬁnding

the maximum amount of ﬂow able to be transferred

from a source to a sink in a capacity-restricted net-

work. While robustness graphs already represent net-

work graphs, maximum-ﬂow algorithms are not ap-

plicable here. Robustness graphs do not use capacity-

labeled edges required by the algorithms, but edge

weights based on estimated connectivity or probabil-

ities. The meaning of edge weights is not equiva-

lent and application of maximum-ﬂow algorithms will

not necessarily result in enhanced robustness. For

instance, a combination of non-robust connectivity

weights of different paths does not result in a robust

path. However, the maximum-ﬂow principle may be

adapted for robustness as shown subsequently. Pre-

requisite for using a combined-path analysis on a ro-

bustness graph is to only include separate path seg-

ments that use different communication technologies

compared to each other.

Figure 16 illustrates the use of different technolo-

gies to communicate with participants in Ex2 with

probability edge weights. A combination of paths

is possible for segments Ex2 → T3 and T3 → T4.

Combining m different paths to a joint edge P

be-

tween separation points results in summarizing the

probabilities of each separate path, as illustrated by

Equation 2.

= min

∑

j=1

∏

i=1

j,i

, 1

(2)

1.0

Ex2

0.7

P2a

0.8

P2b

0.9

Ex2'

0.8

P3l

1.0

T4 P4

0.90.9

0.9

1.0

Cellular

Locally

LoRaWAN

WiFi

Ad-Hoc

moved functionality

Figure 16: Enhancing robustness by combining communi-

cation technologies.

Ex2 T3

1.0

Ex2'T4

1.0

0.9 0.9

Figure 17: Summarized robustness of different communi-

cation technologies.

Consequently, a graph with combined segments as

shown by Figure 17 is created. The summarized val-

ues for Ex2 → T3 (2.23) and T3 → T4 (1.72) have

been limited to 1 by Equation 2, since probability

edge weights P

> 1 are not allowed (cf. Table 3).

Based on the combined graph, other metrics such

as the path probability P

and the path robustness

level P

may be applied to evaluate effectiveness

of path combinations. For instance, evaluation of

the path probability P

of the most robust path of

Figure 16 (including P2b and P3l) and the individ-

ual path of Figure 17 illustrates an enhancement from

F16

= 0.66 to P

F17

= 0.81.

When using the combined-path analysis on graphs

with estimated connectivity weights, calculation of a

combined path segment is based on Equation 3. The

calculation summarizes the average weight of every

path segment to a joint edge weight R

. Combina-

tions need to be done carefully, since the joint weight

might not indicate that path segments may include

a weak or unstable edge (cf. Ex2 → P1 → T3 in Fig-

ure 12). The robustness level R

of the different paths

may help to identify the number of non-robust paths.

∑

j=1

∑

i=1

j,i

(3)

6 DISCUSSION

The presented graph-based approach proves to be able

to identify and rank robust paths in a process. Using

the approach, process robustness may be veriﬁed at

design time and optimized during runtime. The in-

troduced metrics and methods for the application of

graph edge weights allow to design the robustness

analysis ﬂexible and use-case-oriented.

Creating robustness graphs is guided by process-

to-graph transition rules. While the transition is ex-

plicit for most process elements, certain elements re-

quire context information to be translated automati-

cally. Integrating segments of other participants / sub-

processes as subgraphs allows to completely inﬂuence

the process path according to robustness demands.

A Graph-based Approach for Process Robustness in Unreliable Communication Environments

105

Depending on the objectives of the robustness

analysis and the available connectivity knowledge,

edge weights based on connectivity estimations or

based on probabilities may be used. Additional con-

nectivity knowledge may be gained by using process

mining techniques (Van Der Aalst, 2011) on past pro-

cess data (event logs).

If robust process paths shall be found and ranked,

connectivity estimations should be applied as edge

weights. Likewise, integrating a connectivity safety

margin to compensate differences between estima-

tions and real-world connectivity requires to use es-

timated weights. However, estimated connectivity

weights require detailed knowledge or statistics about

the scenario’s connectivity. If limited knowledge

or only simple connectivity statistics exist, robust-

ness probabilities might be the right choice as edge

weights. Furthermore, probability edge weights are

not subjected to over-weighting and are perfectly suit-

able for combined-path analyses.

Evaluation of graph-based search algorithms indi-

cates that the application of shortest-path / longest-

path algorithms may not be optimal due to their fo-

cus on total weight. A promising choice is the all-

path analysis combined with a use-case-driven selec-

tion of appropriate robustness metrics. Most scenar-

ios may operate well by focusing on a preferably high

robustness of the weakest element of the path (path

robustness level R

) or a high path probability P

. If

accuracy of edge weights is uncertain or weight val-

ues change rapidly due to scenario-related circum-

stances (e.g. at runtime), utilization of the maximum-

step heuristic is considerable. Finally, in scenar-

ios featuring different communication technologies, a

combined-path analysis may optimize robustness by

combining process paths. A graph preparation (e.g.

limiting maximum edge weight, removing edges not

fulﬁlling required robustness) has shown to be useful

prior to analysis.

7 CONCLUSION

Operation of processes taking place in unreliable

communication environments is exposed to the risk of

intermittent or failing connectivity, resulting in pro-

cess interruptions or complete break downs. While

rBPMN provides extensions to support robust process

modeling in BPMN, mechanisms and metrics to ver-

ify and optimize robustness of an entire process are

missing.

This paper introduces a graph-based approach to

identify the most robust conﬁguration of a process re-

garding the applied use case. Process-to-graph transi-

tion rules for BPMN and rBPMN process elements al-

low to automatically generate robustness graphs. Ro-

bustness metrics based on connectivity estimations

and alternatively based on probabilities allow ﬁnding

robust process paths and to rank their robustness.

As illustrated by process examples, shortest-path

and longest-path algorithms may not identify the most

robust process conﬁguration. An all-path graph anal-

ysis using metrics for the path robustness level and

the path robustness probability is a promising choice

for most scenarios. An additional combined-path

analysis may enhance robustness by combining paths

which use different communication technologies.

ACKNOWLEDGEMENTS

The presented work is part of the OPeRAte project

(OPeRAte, 2019). OPeRAte is supported by funds

of the Federal Ministry of Food and Agriculture

(BMEL) based on a decision of the Parliament of the

Federal Republic of Germany via the Federal Ofﬁce

for Agriculture and Food (BLE) under the innovation

support program.

REFERENCES

Bellman, R. (1958). On a routing problem. Quarterly of

applied mathematics, 16(1):87–90.

Bocciarelli, P. and D’Ambrogio, A. (2011). A BPMN

extension for modeling non functional properties of

business processes. In Proceedings of the 2011 Sym-

posium on Theory of Modeling & Simulation, pages

160–168. Society for Computer Simulation Interna-

tional.

Bocciarelli, P., D’Ambrogio, A., Giglio, A., and Paglia, E.

(2014). Simulation-based performance and reliabil-

ity analysis of business processes. In Proceedings of

the 2014 Winter Simulation Conference, pages 3012–

3023. IEEE Press.

Bocciarelli, P., D’Ambrogio, A., Giglio, A., and Paglia,

E. (2017). A BPMN extension for modeling cyber-

physical-production-systems in the context of Indus-

try 4.0. In 14th International Conference on Network-

ing, Sensing and Control (ICNSC), pages 599–604.

IEEE.

Braun, R. and Esswein, W. (2014). Classiﬁcation of

domain-speciﬁc BPMN extensions. In IFIP Working

Conference on The Practice of Enterprise Modeling,

pages 42–57. Springer.

Ceballos, H. G., Flores-Solorio, V., and Garcia, J. P. (2015).

A probabilistic bpmn normal form to model and ad-

vise human activities. In International Workshop

on Engineering Multi-Agent Systems, pages 51–69.

Springer.

ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering

106

Chiu, H.-H. and Wang, M.-S. (2013). A study of IoT-aware

business process modeling. International Journal of

Modeling and Optimization, 3(3):238.

Dijkman, R., Dumas, M., and Garc

ıa-Ba

nuelos, L. (2009).

Graph matching algorithms for business process

model similarity search. In International confer-

ence on business process management, pages 48–63.

Springer.

Dijkman, R. M., Dumas, M., and Ouyang, C. (2007). For-

mal semantics and automated analysis of bpmn pro-

cess models. preprint, 7115.

Dinic, E. A. (1970). Algorithm for solution of a problem of

maximum ﬂow in networks with power estimation. In

Soviet Math. Doklady, volume 11, pages 1277–1280.

Domingos, D., Resp

ıcio, A., and Martinho, R. (2016). Us-

ing resource reliability in BPMN processes. Procedia

Computer Science, 100:1280–1288.

Domingos, D., Resp

ıcio, A., and Martinho, R. (2020). Re-

liability of IoT-aware BPMN healthcare processes. In

Virtual and Mobile Healthcare: Breakthroughs in Re-

search and Practice, pages 793–821. IGI Global.

Even, S. (2011). Graph algorithms. Cambridge University

Press.

Fall, K. (2003). A delay-tolerant network architecture for

challenged internets. In Proceedings of the 2003 con-

ference on Applications, technologies, architectures,

and protocols for computer communications, pages

27–34. ACM.

Ford, L. R. and Fulkerson, D. R. (2009). Maximal ﬂow

through a network. In Classic papers in combina-

torics, pages 243–248. Springer.

Gounaris, A. (2016). Towards automated performance op-

timization of bpmn business processes. In East Euro-

pean Conference on Advances in Databases and In-

formation Systems, pages 19–28. Springer.

Graja, I., Kallel, S., Guermouche, N., and Kacem, A. H.

(2016). BPMN4CPS: A BPMN extension for mod-

eling Cyber-Physical Systems. In 25th International

Conference on Enabling Technologies: Infrastructure

for Collaborative Enterprises (WETICE), pages 152–

157. IEEE.

Martinho, R. and Domingos, D. (2014). Quality of informa-

tion and access cost of IoT resources in BPMN pro-

cesses. Procedia Technology, 16:737–744.

Martinho, R., Domingos, D., and Resp

ıcio, A. (2016). Eval-

uating the reliability of ambient-assisted living busi-

ness processes. In ICEIS (2), pages 528–536.

Mayer, C. P. (2012). Hybrid Routing in Delay Tolerant Net-

works. KIT Scientiﬁc Publishing.

Mazzola, L., Kapahnke, P., Waibel, P., Hochreiner, C.,

and Klusch, M. (2017). FCE4BPMN: On-demand

QoS-based optimised process model execution in the

cloud. In 2017 International Conference on Engineer-

ing, Technology and Innovation (ICE/ITMC), pages

305–314. IEEE.

Meyer, S., Ruppen, A., and Magerkurth, C. (2013). In-

ternet of Things-aware process modeling: integrating

IoT devices as business process resources. In Interna-

tional Conference on Advanced Information Systems

Engineering, pages 84–98. Springer.

Nordemann, F., T

onjes, R., and Pulverm

uller, E. (2020).

Resilient BPMN: Robust process modeling in unre-

liable communication environments. In 8th Interna-

tional Conference on Model-Driven Engineering and

Software Development (MODELSWARD). Scitepress.

OMG (2011). Object Management Group: Business Pro-

cess Model and Notation (BPMN) 2.0 Speciﬁcation,

www.omg.org/spec/BPMN/2.0/About-BPMN (2019-

09-03).

OPeRAte (2019). Osnabrueck University of Ap-

plied Sciences: OPeRAte research project,

http://operate.edvsz.hs-osnabrueck.de (2019-09-

03).

Pelusi, L., Passarella, A., and Conti, M. (2006). Oppor-

tunistic networking: data forwarding in disconnected

mobile ad hoc networks. IEEE Communications Mag-

azine, 44(11):134–141.

Resp

ıcio, A. and Domingos, D. (2015). Reliability of

BPMN business processes. Procedia Computer Sci-

ence, 64:643–650.

Sedgewick, R. and Wayne, K. (2011). Algorithms.

Addison-Wesley Professional, 4th edition.

Sungur, C. T., Spiess, P., Oertel, N., and Kopp, O. (2013).

Extending BPMN for wireless sensor networks. In

2013 IEEE 15th Conference on Business Informatics,

pages 109–116. IEEE.

Tarjan, R. (1972). Depth-ﬁrst search and linear graph algo-

rithms. SIAM journal on computing, 1(2):146–160.

Van Der Aalst, W. (2011). Process mining: discovery,

conformance and enhancement of business processes,

volume 2. Springer.

A Graph-based Approach for Process Robustness in Unreliable Communication Environments

107