
Particle Swarm Optimization for Performance Management in
Multi-cluster IoT Edge Architectures
Shelernaz Azimi
1
, Claus Pahl
1
and Mirsaeid Hosseini Shirvani
2
1
Free University of Bozen-Bolzano, Bolzano, Italy
2
Department of Computer Engineering, Sari branch, Islamic Azad University, Sari, Iran
Keywords:
Internet of Things, Edge Computing, Cloud Computing, Particle Swarm Optimization, PSO, Performance.
Abstract:
Edge computing extends cloud computing capabilities to the edge of the network, allowing for instance
Internet-of-Things (IoT) applications to process computation more locally and thus more efficiently. We aim
to minimize latency and delay in edge architectures. We focus on an advanced architectural setting that takes
communication and processing delays into account in addition to an actual request execution time in a per-
formance engineering scenario. Our architecture is based on multi-cluster edge layer with local independent
edge node clusters. We argue that particle swarm optimisation as a bio-inspired optimisation approach is an
ideal candidate for distributed load processing in semi-autonomous edge clusters for IoT management. By
designing a controller and using a particle swarm optimization algorithm, we can demonstrate that processing
and propagation delay and the end-to-end latency (i.e., total response time) can be optimized.
1 INTRODUCTION
Edge computing provides an intermediate layer for
computation and storage at the ’edge’ of the network,
often between Internet-of-Things devices and central-
ized data center clouds (Mahmud et al., 2019; Pahl
et al., 2018). Edge computing promises better per-
formance through lower latency since computation is
moved closer to application. Reducing data transfer
time by avoiding the transfer of large volumes of data
to remote clouds has also the effect of reducing secu-
rity risks. Localization is here the key principle.
Performance and load management in edge archi-
tectures has been addressed in the past (Baktyan and
Zahary, 2018; Minh et al., 2019), but often the ar-
chitectures referred to do not reflect the often geo-
graphically distributed nature of edge computing. We
expand here on works like (Gand et al., 2020; Tata
et al., 2017) that have considered single autonomous
clusters only. We propose here a solution for a multi-
cluster solution, where each cluster operates semi-
autonomously, only being coordinated by an orches-
trator that manages load distribution. Another direc-
tion that we add is a realistic reflection of performance
concerns. In our performance model, we consider de-
lays caused by communication and queueing (prop-
agation delays) as well as processing delays of con-
trollers and edge execution nodes into a comprehen-
sive end-to-end latency concept that realizes the re-
sponse time from the requestor’s perspective.
Thus, our approach extends the state-of-the-art by
combining an end-to-end latency optimization frame-
work with a multi-cluster edge architecture. We pro-
pose Particle Swarm Optimization (PSO) for the op-
timization here. PSO is a bio-inspired evolutionary
optimization method (Saboori et al., 2008) to coordi-
nate between autonomous entities such as edge clus-
ters in our case. PSO distinguishes personal (here lo-
cal cluster) best fitness and global (here cross-cluster)
best fitness in the allocation of load to clusters and
their nodes – which we use to optimize latency. Our
orchestrator takes local cluster computation, but also
centralised cloud processing as options on board. We
demonstrate the effectiveness of our performance op-
timization by experimentally comparing it with other
common load distribution strategies.
2 RELATED WORK
(Gu et al., 2017) have studied the link between the
distribution of work and virtual machine assignment
in cyber-physical systems based on edge computing
principles. They looked at minimizing the final cost
and satisfying service quality requirements. Process-
328
Azimi, S., Pahl, C. and Shirvani, M.
Particle Swarm Optimization for Performance Management in Multi-cluster IoT Edge Architectures.
DOI: 10.5220/0009391203280337
In Proceedings of the 10th International Conference on Cloud Computing and Services Science (CLOSER 2020), pages 328-337
ISBN: 978-989-758-424-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ing resources at the edge of the network is introduced
as a solution. The paper did not, however, refer to re-
alistic IoT and cloud scenarios. In (Meng et al., 2017),
energy-delay computing is addressed in a workload
allocation context. Given the importance of cost and
energy in delay-sensitive interactions for requesting
and providing processing resources, an optimal strat-
egy for delay-sensitive interactions is presented. The
scheme seeks to achieve an energy-delay compromise
at the edge of the cloud. The authors formalize task
allocation in a cloud-edge setting, but only used sim-
ple models to formulate energy loss and delay.
(Sarkar et al., 2018) also focuses on modeling de-
lay, energy loss and cost. Our aim is to use an evolu-
tionary algorithm for edge orchestration and to obtain
the optimal response times. In (Wang et al., 2018),
a PSO and game theoretic based task allocation for
MEC was designed. First, to ensure the closeness of
nodes in each group, the maximizing minimum dis-
tance clustering algorithm was designed. Then, they
proposed a multi-task assignment model based on
Nash equilibrium and then they used the PSO to find
the Nash equilibrium point, minimizing the all tasks
execution time and saving the energy cost and find the
tasks that need to be offloaded to the group. We use
the priority setting algorithm to sort tasks and then
upload tasks to the group in a certain order, thereby
confirming the order of tasks uploaded on the device,
which jointly considers the calculation time in base
station and mobile device and transmission time.
In (Manasrah and Ali, 2018) a Hybrid GA-PSO
Algorithm in Cloud Computing is used to allocate
tasks to the resources efficiently. The Hybrid GA-
PSO algorithm aims to reduce the makespan and the
cost and balance the load of the dependent tasks over
the heterogeneous resources in cloud computing en-
vironments. We have used a similar approach with
only PSO in the edge layer. In (Rolim et al., 2010),
the performance management solution is based on a
wireless sensor network. The purpose of the proposed
method is ultimately to identify the delays-sensitive
requests and take action when faced with them. Dif-
ferent kinds of genetic algorithm have been used for
different scheduling problems in the cloud (Omara
and Arafa, 2010) and (Wang et al., 2001).
3 PARTICLE SWARM
OPTIMIZATION
Particle Swarm Optimization (PSO) is the central so-
lution to our performance optimization strategy. This
section introduces important concepts as well as spe-
cific tools and technologies that are combined here.
The particle swarm optimization (PSO) method
is a global minimization method that can deal with
problems whose solution is a point or surface in an
n-dimensional space. In such a space, an elementary
velocity is assigned to particles in the swarm, as well
as the channels of communication between particles.
• Particles in our research are edge nodes that pro-
vide computing resources.
• Velocity links to processing load / performance.
These nodes then move through the response space
and the results are calculated on the basis of a merit
criterion after each time interval. Over time, nodes
accelerate toward nodes of higher capacity that are in
the same communication group.
To update the location of each node when moving
through the response space, we use these equations:
V
i
(t) = w ∗ v
i
(t − 1)+c
1
∗ rand
1
∗ (P
i.best
− X
i
(t − 1)+
c
2
∗ rand
2
∗ (P
g.best
− X
i
(t − 1))
(1)
and
X
i
= x
i
(t − 1) +V
i
(t) (2)
where w is the inertial weight coefficient (moving in
its own direction) indicating the effect of the previous
iteration velocity vector (V
i
(t)) on the velocity vector
in the current iteration (V
i
(T + 1)). c
1
is the constant
training coefficient (moving along the path of the best
value of the node examined). c
2
is the constant train-
ing coefficient (moving along the path of the best node
found among the whole population). rand
1
and rand
2
are random numbers with uniform distribution in the
range 1 to 2. V
i
(t-1) is the velocity vector in iteration
(t-1). X
i
(t-1) is the position vector in iteration (t-1).
The random generation of the initial population is
simply the random determination of the initial loca-
tion of the nodes by a uniform distribution in the so-
lution space (search space). The random population
generation stage of the initial population exists in al-
most all probabilistic optimization algorithms. How-
ever, in this algorithm, in addition to the initial ran-
dom location of the nodes, a certain amount of initial
node velocity is also assigned. The initial proposed
range for node velocity results from Equation (3).
X
min
− X
max
2
≤ V ≤
X
max
− X
min
2
(3)
Select the Number of Primary Nodes. Increasing
the number of primary nodes reduces the number
of iterations required for the algorithm to converge.
However, this reduction in the number of iterations
does not mean reducing the runtime of the program
to achieve convergence. An increase in the number of
primary nodes does results in a decrease in the num-
ber of repeats. The increase in the number of nodes
Particle Swarm Optimization for Performance Management in Multi-cluster IoT Edge Architectures
329

causes the algorithm to spend more time in the node
evaluation phase, which increases the time it takes to
run the algorithm until it achieves convergence, de-
spite decreasing the number of iterations. So, increas-
ing the number of nodes cannot be used to reduce the
execution time of the algorithm. It should be noted
that decreasing the number of nodes may cause lo-
cal minima to fall and the algorithm fails to reach the
original minimum. If we consider the convergence
condition as the number of iterations, although de-
creasing the number of initial nodes decreases the ex-
ecution time of the algorithm, the solution obtained
would not be the optimal solution to the problem.
Thus, the initial population size is determined by the
problem. In general, the number of primary nodes
is a compromise between the parameters involved in
the problem. Selecting an initial population of 2 to 5
nodes is a good choice for almost all test problems.
Evaluation of the Objective Function (Cost or Fit-
ness Calculation) of Nodes. We need to evaluate
each node that represents a solution to the problem
under investigation. Depending on this, the evaluation
method is different. For example, if it is possible to
define a mathematical function for the purpose, sim-
ply by placing the input parameters (extracted from
the node position vector) into this mathematical func-
tion, it is easy to calculate the cost of the node. Note
that each node contains complete information about
the input parameters of the problem that this informa-
tion is extracted from and targeted to. Sometimes it
is not possible to define a function for node evalua-
tion., e.g. when we have linked the algorithm to other
software or used experimental data. In such cases,
information about software input or test parameters
should be extracted from the node position vector and
placed in the software associated with the algorithm
or applied to the relevant test. Running software or
performing tests and observing/measuring the results
determines the cost of each node.
Record the Best Position for Each Node (P
i.best
) and
the Best Position among All Nodes (P
g.best
). There
are two cases: If we are in the first iteration (t = 1),
we consider the current position of each node as the
best location for that node – see Eq. (4) and (5).
P
i.best
= X
i
(t), i = 1, 2,4,..., d (4)
cost(P
i.best
) = cost(X
j
(t)) (5)
In other iterations, we compare the cost for the nodes
in Step 2 with the value of the best cost for each node.
If this cost is less than the best recorded cost for this
node, then location and cost of this node replace the
previous one. Otherwise there is no change in location
and cost recorded for this node – see Eq. (6):
(
if cost(X
i
(t)) < cost(P
i.best
)
else no change
⇒
(
cost(P
i.best
) = cost(X
j
(t)) i = 1, 2,..., d
P
i.best
= x
i
(t)
(6)
The global best P
g.best
is the best local P
i.best
value.
4 CLUSTER PERFORMANCE
OPTIMIZATION
We now apply the PSO method in order to opti-
mize processing times in our multi-cluster edge sce-
nario. We present a new way to minimize total delay
and latency in edge-based clusters. Our optimization
method shall be defined in four steps: (i) the edge
cluster architecture is defined, (ii) the edge controller
is designed, (iii) the optimization problem is defined,
(iv) the PSO optimization algorithm is implemented.
In the following, each of these steps will be explained.
4.1 Request Management
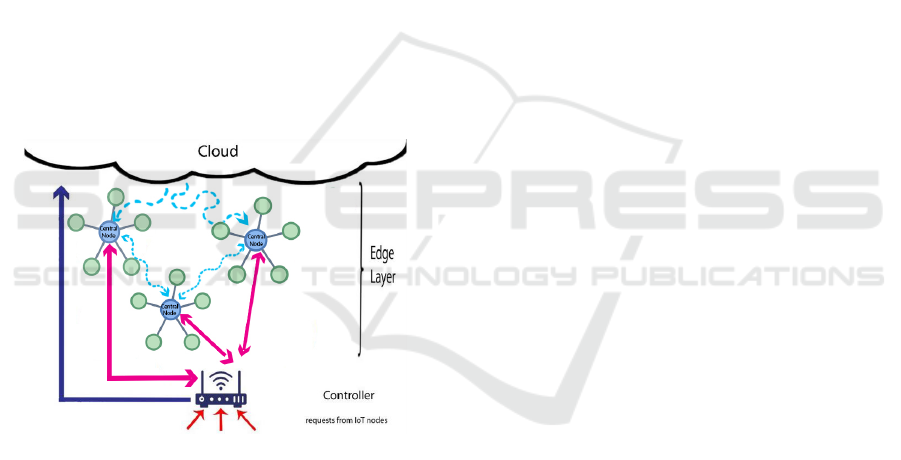
In our architecture, there are three layers: the things
layer, where the objects and end users are located; the
edge layer, where the edge nodes for processing are
located; and finally the cloud layer, where the cloud
servers are provided (González and Rodero-Merino,
2014). We assume the edge nodes to be clustered.
That is, there are multiple clusters of edge nodes,
where each has a local coordinator.
Request Processing. The communication between
IoT, edge and cloud nodes happens as follows. IoT
nodes can process requests locally or send them to
the controller for processing in the edge or the cloud.
Edge nodes can process incoming requests or, if un-
available, pass them to another edge node or the con-
troller. Cloud nodes process the allocated requests
and return the result to the IoT nodes, see Figure
1. The purpose of this study is to minimize total
execution time for IoT nodes in a proposed frame-
work based on edge computing.A controller decides
to which edge (or cloud) node to allocate a request.
The transfer time and the waiting (e.g., queueing
time) at the controller incur a delay.
Definition 1. A delay is the time spent by transfer-
ring a request to the next node and waiting there to be
processed. Thus, we typically have controller delays
D
C
, edge node delays D
E
and IoT node delays D
I
.
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
330
The processing time is the time for execution at
a node, i.e., either a controller processing time P
C
or
an edge node processing time P
E
.
Definition 2. The response time R for an IoT node
is the time it takes to get a request processed, i.e., the
time between sending a request for processing until
receiving the result.
RT = D
C
+ P
C
+ D
E
+ P
E
+ D
I
This is also known as end-to-end latency in net-
worked environments.
The requests are generated by the IoT nodes with a
given deadline DL for processing and they are sent to
the controller for allocation of processing nodes. The
requests transferred from different IoT nodes get into
a queue until they finally get to the controller. The
controller will consider the total waiting time of all
edge nodes from their availability tables taking into
account the request deadline and will then allocate
the request to the best edge node with the lowest total
waiting time by applying PSO principles. The archi-
tectural framework of the edge-based system used in
this study is shown in Figure 1.
Figure 1: The IoT-Edge-Cloud architecture.
4.2 Controller Design
The controller is embedded as an orchestrator be-
tween the things layer and the edge. All requests from
the things layer will first be transferred to the con-
troller and then sent to either the best edge node or
directly to the cloud. As said, the controller performs
the decision process based on the total waiting time
(delay) of the entire request in different edge nodes.
Upon receiving the new request, the controller deter-
mines the best node and allocates the request to that
node according to the deadline of the request and the
lowest total waiting time of all the edge nodes using
the particle optimization algorithm PSO. The status
of the selected node’s queue and it’s execution status
are updated in an availability table. If no appropriate
node is found in the edge layer for a received request,
the controller sends the request directly to the cloud
for processing as a backup.
Types of Cluster Coordination. Two types of in-
teraction for edge nodes can be implemented (Shin
and Chang, 1989): coordinated, in which some dedi-
cated nodes control the interactions of their surround-
ing nodes, fully distributed, in which each edge node
interacts with any other node. In the coordinated
method, the edge layer is divided into smaller clus-
ters, with a central coordinating node in each of these
clusters, which is directly interacting with the con-
troller and which controls the other nodes in its clus-
ter. This coordinator is aware of the queue status of
those nodes and stores all the information in the avail-
ability table. The central coordinating nodes are also
processing nodes which aside from their processing
responsibility, can manage the other nodes in their
clusters too. These central coordinators have 3 dif-
ferent connections, 2 direct connections and 1 pub-
lic connection. The central coordinators are directly
connected to their cluster’s nodes and the controller
and they communicate with other central coordina-
tors with public announces. When a request is sent
to the controller, the cluster coordinators announce
their best node in their area (personal best) publicly
and support the lead controller in determining the best
node in the layer (global best). This step is repre-
sented in Equation (6).
4.3 Optimization
In the third step, the PSO-based edge performance
optimization problem is defined. In our method,
the optimization problem has one main objective and
one sub-objective so that the realization of the sub-
objective will lead to the fulfilling the main objective.
In the following, each of these goals will be defined.
• Main objective: to minimize the total response
time R. In the proposed method, two elements,
the controller and the particle optimization algo-
rithm, have been used to accomplish this goal.
• Secondary objective: to reduce delay D. Delays in
each layer must be considered separately to calcu-
late the total delay.
We use (Yousefpour et al., 2017) to calculate delays.
Delay in Things Layer. Note that thing nodes can
both process requests themselves or send them to the
edge or cloud for processing. If an IoT node decides
to send their request to the edge or cloud for process,
the request will be sent to the controller first. Con-
sidering the number of the IoT nodes and the num-
ber of the requests, the sent request will get into a
Particle Swarm Optimization for Performance Management in Multi-cluster IoT Edge Architectures
331

queue before reaching the controller and after reach-
ing the controller, the request should wait until the
controller finds the best edge node for allocation. In
other words, this is the delay before allocation.
Note, we adopt the notational settings as follows:
The subscript indexes i, j and k refer to processing
nodes at IoT, Edge and Cloud layer, respectively. The
superscripts I, E and C refer to source or destination
of transferred requests or responses at IoT, Edge or
Cloud level, respectively. For example, EC refers to
an edge-to-cloud transfer.
Definition 3. The delay in the IoT node i is repre-
sented by D
i
and is calculated as follows:
D
i
= P
I
i
× (A
i
) + P
E
i
× (X
IE
i j
+Y
IE
i j
+ L
i j
) + P
C
i
× (X
IC
ik
+Y
IC
ik
+ H
k
+ X
CI
ki
+Y
CI
ki
)
(7)
• P
I
i
is the probability that the things node will pro-
cess the request itself in the things layer, P
E
i
is
the probability of sending the request to the edge
layer, and P
C
i
is the probability of sending the re-
quest directly to the cloud; with P
I
i
+P
E
i
+P
C
i
= 1.
• A
i
is the average processing delay of node i when
processing its request. X
IE
i j
is the propagation de-
lay from object node i to node jj, Y
IE
i j
is the sum
of all delays in linking from object node i to node
j. Likewise, X
IC
ik
delays propagation from object
node i to cloud k server and Y
CI
ki
is the sum of
all delays in sending a link from object node i
to cloud server k. X
CI
ki
and Y
CI
ki
are broadcast and
send delays from the k server to the node i.
• H is the average delay for processing a request
on the cloud server k, which includes the queue
waiting time on the cloud server k plus the request
processing time on the cloud server k.
There is no specific distribution for P
I
i
, P
E
i
and P
C
i
,
because their values will be defined by separate ap-
plications based on service quality requirements and
rules. In other words, their values will be given as
input to this framework.
Delay in Edge Layer. We now define a recursive re-
lation for calculating L
i j
.
Definition 4. L
i j
is a delay for processing IoT node
i’s requests in the edge. After allocation, the re-
quest will be queued at the chosen edge node. This is
the delay after allocation. L
i j
is calculated as follows:
L
i j
= P
j
.(W
j
+ X
EI
ji
+Y
EI
ji
)
+ (1 + p
j
.[[1 − φ(x)][X
EE
j j
0
+Y
EE
j j
0
+ L
i j
0
(x + 1)]
+ φ(x)[X
EC
jk
+Y
EC
jk
+ (H
k
+ X
CI
ki
+Y
CI
ki
]]
j
0
= best( j), k = h( j)
(8)
Here, W
j
refers to the mean waiting time at node j
and φ(x) is also a discharge function.
Delayed transmission from the cloud layer to the
object layer will be considered in L
i j
, as the request
edge later be unloaded to another node in the edge
layer. L
i j
is the processing delay of the node i request
in the edge layer or even the cloud layer, if it is un-
loaded from the edge node to the cloud server, so that
the node j edge be the first node in the edge layer
to which the node request of object i is sent. All the
other variables already have been defined.
4.4 PSO Algorithm Implementation
In the final step, the performance optimization algo-
rithm is specified. The particle swarm optimization
algorithm is used to solve the optimization problem.
Our PSO algorithm consists of several steps, which
will be discussed now.
• Establish an Initial Population and Evaluate it.
The particle swarm optimization algorithm starts
with an initial random population matrix like
many evolutionary algorithms such as genetic al-
gorithms. This algorithm, unlike genetic algo-
rithms however, has no evolutionary operator such
as a mutant. Each element of the population is
called a node. In fact, the particle swarm opti-
mization algorithm consists of a finite number of
nodes that randomly take the initial value.
Here, the edge layer is divided into different clus-
ters and in each cluster consists of a central coor-
dinator node and its dependent nodes. For each
node, two states of location and velocity are de-
fined, which are modeled with a location vector
and a velocity vector, respectively. These vectors
assist the controller in finding the best available
node. The location vector helps in finding the
position of the local best and the velocity vector
leads the controller towards the global best.
In Equations (7) and (8), all edge nodes j are pro-
cessing nodes. Selected nodes are also local co-
ordination nodes for the clusters. However, these
are not singled out in the equations since they also
have processing capacity.
• The Fitness Function. The fitness function is
used for evaluating the initial population. Since
the problem is a two-objective optimization, both
goals must be considered in the fitness function.
– The first objective is to minimize the total re-
sponse time (latency) in the edge-based archi-
tecture indicated by RT .
To achieve the first goal, we define a metric
called T
E
= P
E
+ D
E
that represents the total
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
332

execution time of the request at the edge node,
which is the sum of the processing time P
E
of the request and the waiting time D
E
of the
request in the edge node’s queue. TimeFinal
(T F) is the maximum time T
E
that is allowed
for the execution at the edge node in other to
meet the required deadline DL with
T F = DL − (D
C
+ P
C
+ D
I
) (9)
i.e., Max(T
E
) = T F or T
E
∈ [0 . . . T F ].
– The second objective is to reduce the delay of
the edge-based architecture D.
The second goal relates to the sum of the delays
in the IoT layer and the delay in the edge layer:
D = D
C
+ D
E
+ D
I
(10)
Both goals are defined as minimization. Ulti-
mately, fitness is calculated as follows:
Fitness = T F + D (11)
• Determine the Best Personal Experience and the
Best Collective Experience. The nodes move in
the solution space at a dynamic rate based on the
experience of the node itself and the experience
of the neighbors in the cluster. Unlike other evo-
lutionary algorithms, particle swarm optimization
does not use smoothing operators (such as inter-
sections in the frog algorithm). Thus, the answers
remain in the search space to share their infor-
mation and guide the search to the best position
in the search space. So, here the coordinating
nodes search for the best experience within their
own and their neighbor’s domain. To update the
node’s velocity and position, first the best position
of each node and then the best position among all
nodes in each step must be updated.
• Location and Velocity Updates. The dimension
of the problem space is equal to the number of
parameters in the function to optimize. The best
position of each node in the past and the best po-
sitions of all nodes are stored. Based on this, the
nodes decide how to move next. At each itera-
tion, all the nodes move in the next n-dimensional
space of the problem to find the general optimum
point. The nodes update their velocities and their
position according to the best absolute and local
solutions. Here, the coordinating nodes read the
availability table of their cluster nodes and pub-
lish their best nodes to the controller. In this way,
they move towards the overall best node.
• Check the Termination Condition. Finally, the ter-
mination condition is checked. If this condition
is not met, we return to the stage of determining
the best personal experience and the best collec-
tive experience. There are several types of termi-
nation conditions:
– Achieve an acceptable level of response,
– Reach a specified number of repetitions/time,
– Reach a certain number of iterations or a time
specified without seeing an improvement,
– Check a certain number of responses.
Here, the termination condition is to achieve an
acceptable level of response.
Implementation. The proposed PSO Performance
Optimization is presented in Algorithm 1.
Algorithm 1: PSO-based Edge Performance.
1: function SCHEDULE(PSO,DAG)
2: Input: PSO and DAG characteristics
3: Output: Optimal Request Scheduling
4: Initial First Parameters
5: loop
6: Initial Population
7: Calculate Fitness
8: if Fitness < PBest then
9: PBest ← Fitness
10: GBest ← PBest
11: loop
12: Compute Velocity via Equation (1)
13: Compute Position via Equation (2)
14: Calculate Fitness via Equation (11)
15: if Fitness < PBest then
16: PBest ← Fitness
17: GBest ← PBest
18: Return: Optimal Schedule
5 EVALUATION
Our aim is to reduce the total response time – or end-
to-end latency. We chose a comparative experimental
approach to evaluate our solution.
The particle swarm optimization algorithm and a
so-called BAT algorithm (Yang, 2012) are used to es-
tablish the controller and compare. The BAT algo-
rithm was chosen due to its similarity to the particle
swarm optimization. Thus, it allows meaningful per-
formance comparisons. Furthermore, its wide-spread
use in different optimization situations make it a suit-
able benchmark. The BAT algorithm is an algorithm
inspired by the collective behavior of bats in the natu-
ral environment proposed in (Yang, 2012). This algo-
rithm is based on the use of bat reflection properties.
We used the MATLAB software to evaluate our
solution. The concepts presented earlier are fully
Particle Swarm Optimization for Performance Management in Multi-cluster IoT Edge Architectures
333

coded and implemented in MATLAB.
5.1 PSO & BAT Parameter Adjustment
In order to obtain meaningful results, this algorithm is
implemented with the dual-objective evaluation func-
tion according to Equation (11) with 200 iterations.
The initial parameters specified in this implementa-
tion are shown in Table 1. Using the values in Table 1
Table 1: Initial parameters - PSO Edge Optimization.
Parameters Values
Population number 50
Number of Repeats 200
Value w 1
Decrease coefficient w 0.99
c1,c2,c3 2
for initialization, the particle swarm optimization al-
gorithm is executed and the graph in Figure 2 shows
the result of the implementation of this algorithm in
terms of fitness values for the respective iterations.
As shown in Figure 2, with the increase of iterations,
Figure 2: Fitness results for the PSO algorithm.
the results of the fitness evaluation function for the
two objectives (runtime and delay) is reduced. Our
PSO performance optimization algorithm is a two-
objective algorithm that reduces execution time and
delay in execution of requests. The objective function
value in the implementation of the particle swarm op-
timization algorithm is approximately 233 as a bench-
mark for the BAT comparison. It should be noted that
due to the random structure of the evolutionary algo-
rithms, the results per run may be different from the
previous ones.
In order to comparatively evaluate our proposed
method, an evolutionary BAT algorithm has been im-
plemented in order to compare correctly with the
same conditions. Thus, the BAT algorithm has been
implemented with the same two-objective evaluation
function and with 200 iterations as the particle opti-
mization algorithm. The initial parameters specified
in this implementation are shown in Table 2. Using
Table 2: Initial parameters - BAT Optimization.
Parameters Values
Population number 50
Number of Repeats 200
Minimum frequency 0
Maximum frequency 100
Sound intensity coefficient 0.1
Pulse rate coefficient 0.1
the above values for the BAT strategy initialization,
the BAT algorithm is executed and the diagram in Fig-
ure 3 shows the result of the implementation of this al-
gorithm. In Figure 3, the motion diagram of the BAT
Figure 3: Fitness results for the BAT algorithm.
algorithm is shown. The conditions are the same for
both particle swarm and bat optimization algorithms
and the objective function in both algorithms has been
implemented and evaluated with respect to both run-
time and delay reduction. As can be seen, the BAT
algorithm has reached the target function of 237.5,
while in the particle swarm optimization algorithm
this value is 233. These results indicate that our algo-
rithm is better than the evolutionary BAT algorithm.
5.2 Scenario-based Comparison
In order to deepen the analysis, the proposed solution
was tested for 3 different scenarios: once with differ-
ent number of requests, once with different number of
edge layer nodes, once with identical parameters, but
in different iterations.
Scenario 1 – Request Variation. In the first scenario,
a number of requests and nodes in the edge layer are
used to compare the results. In this scenario, we fixed
the number of edge layers nodes and assumed vari-
able and incremental user requests. Table 3 shows the
details of this scenario configuration.
Figure 4 shows the results of different user re-
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
334

Table 3: The initial parameters in first scenario.
Parameters Values
Number of user requests 30/60/100/150/200/250
Number of edge layer nodes 20
Processing power of each edge node 4 G Ram / 8 Mips Processor
Amount of time each user requests Randomized in range [1,20]
Amount of CPU per user request Random in the interval [2,8]
quests with 20 nodes in the edge layer. Here, the num-
ber of edge layer nodes is 20 and the number of user
requests are 30, 50, 100, 150, 200 and 250. Equation
(11) is used to calculate the fitness function.
Figure 4: Result of 1st scenario: fitness over no. of requests.
As can be seen in Figure 4, our PSO-based op-
timization algorithm produces far better results than
the BAT algorithm. As the number of requests in-
creases, the value of the target function (execution
time + delay time) increases. Increasing the number
of requests will increase the execution time, as well
as increase the execution time, as more nodes will be
involved. This increases the value of the target func-
tion, which is the sum of the execution time and de-
lay. In all cases, our PSO algorithm shows better re-
sults. Despite the increase in the objective function
value in both algorithms, the growth rate of the ob-
jective function value in the particle swarm optimiza-
tion algorithm is lower than the BAT algorithm, which
means that our algorithm outperforms BAT.
In order to compare under different conditions, the
next step is to increase the number of layer nodes in
order to observe the effect of this increase in a graph.
Scenario 2 – Edge Node Variation. In the second
scenario, unlike the previous scenario, now the num-
ber of requests is fixed, but the number of edge layer
nodes is assumed to be variable. Increasing the num-
ber of nodes has been done as a trial-and-error exper-
iment and no special algorithm is used. Full details of
the second scenario are given in Table 4.
For this experiment, 100 input requests are consid-
ered. In this scenario, the number of user requests is
considered to be fixed, but the number of edge layer
nodes is considered to be 5, 10, 15, 20, 30 and 50.
Table 4: The initial parameters in second scenario.
Parameters Values
Number of user requests 100
Number of edge layer nodes 5/10/15/20/30/50
Processing power of each edge node 4 G Ram / 8 Mips Processor
Amount of time each user requests Randomized in range [1,20]
Amount of CPU per user request Random in the interval [2,8]
Figure 5: 2nd scenario: fitness over no. of requests.
Equation (11) is used to calculate the fitness function.
By increasing the number of layer nodes in the
edge, the fitness function decreases due to the pos-
sibility of executing requests on more nodes. The
higher the number of edge layer nodes, the more
likely it is that requests will be processed using nodes
whose latency is lower. In other words, with the in-
crease in the number of edge layer nodes the con-
troller’s options for allocating more requests are in-
creased and thus the chances of finding a suitable
node with low latency increases. As the conditions
change, the way in which requests are executed is also
varied, which reduces execution time. For the par-
ticle optimization algorithm, the greater the number
of edge layer nodes, the lower the objective function.
Furthermore, for PSO algorithm, the reduction of the
target function is much faster than the BAT algorithm,
which is evident in Figure 5. Each algorithm was run
multiple times to better compare the algorithms.
Scenario 3 – Iteration Variation. In the third sce-
nario, several iterations assume both the user requests
and the number of nodes in the edge layer fixed. In
this scenario, each algorithm was run 5 times with the
same inputs and the results were obtained. It should
be noted that in this experiment, the number of re-
quests is 100 and the number of edge layer nodes is
50, which were constant at all 5 times. Equation (11)
is used to calculate the fitness function. Table 5 shows
the full configuration details of the third scenario. Ac-
cording to Figure 6, in different iterations we can see
different results despite not changing input values at
each iteration. There are no identifiable rules or ex-
planations detectable by analysing the algorithm out-
Particle Swarm Optimization for Performance Management in Multi-cluster IoT Edge Architectures
335

Table 5: The initial parameters in third scenario.
Parameters Values
Number of user requests 100
Number of Edge Layer Nodes 50
Processing power of each edge node 4 G Ram / 8 Mips Processor
Amount of time each user requests Randomized in range [1,20]
Amount of CPU per user request Random in the interval [2,8]
puts. For example, the value of the fitness function
in the first step with one iteration is less than that of
the BAT algorithm in PSO, and the value of this func-
tion in the second step with two iterations in both al-
gorithms decreased, while in the next step with three
iterations, the value is increased in both.
In general, it can be concluded that the node
swarm optimization algorithm in executing requests
using the dual-fitness function (execution time + ex-
ecution delay) yields significantly better results than
the evolutionary BAT algorithm. This is because in
most iterations, the objective function value in the
particle swarm optimization algorithm was lower than
for the BAT algorithm. A PSO feature is faster con-
vergence. In addition, the particle swarm optimiza-
tion algorithm yields overall good performance re-
sults that reduce orchestration and response time.
Figure 6: 2nd scenario: fitness over number of requests.
6 CONCLUSIONS
Edge computing promises low latency due to local
processing. However, a closer look reveals distributed
and independently managed clusters of processing
edge nodes that need be considered in a performance-
oriented load allocation strategy. Furthermore, delays
occur as the result of transmission delays and waiting
times at orchestration and processing nodes.
In our performance optimization method, we used
an evolutionary algorithm based on particle swarm
optimization, adopted to the multi-cluster architecture
and focusing on delay and end-to-end latency reduc-
tion. We compared our solution with an evolution-
ary BAT algorithm, another method to optimize and
reduce the mean objective function (delay and ex-
ecution latency) of processing requests. Evolution-
ary algorithms are among the best optimization algo-
rithms, and the particle swarm optimization algorithm
we adopted here is less complex than some other evo-
lutionary algorithms. These advantages made the par-
ticle swarm optimization a suitable core of a method
for reducing the total execution time and delay.
As part of our future work, we plan to consider
other algorithm bases such as the firefly algorithm in-
stead of the node swarm optimization for edge perfor-
mance optimization. The firefly algorithm is a com-
mon algorithm in optimization problems that does not
have the limitations of genetic algorithms selecting
the required parameters, which is the most effective
choice for these operations. We could also consider
the ant colony algorithm or linear optimization in-
stead of PSO. The ant colony algorithm is very ef-
ficient, often used in routing problems and the linear
optimization is a good method to achieve the best out-
come in a mathematical model whose requirements
are represented by linear relationships. Apart from the
algorithmic side, we also plan to refine the model by
more precisely separating origins of propagation de-
lay in communication and buffering times. Also dif-
ferent coordination principles from fully centralised
to peer-to-peer management can be considered. And,
we aim to combine this with an auto-scaling con-
troller (Gand et al., 2020), which we implemented so
far only for a single cluster environment.
REFERENCES
Baktyan, A. A. and Zahary, A. T. (2018). A review on cloud
and fog computing integration for iot: Platforms per-
spective. EAI Transact on Internet of Things, 4(14).
Fang, D., Liu, X., Romdhani, I., Jamshidi, P. and Pahl, C.
(2016). An agility-oriented and fuzziness-embedded
semantic model for collaborative cloud service search,
retrieval and recommendation. In Future Generation
Computer Systems, 56, 11-26.
Gand, F., Fronza, I., Ioini, N. E., Barzegar, H. R., Azimi,
S., and Pahl, C. (2020). A fuzzy controller for self-
adaptive lightweight container orchestration. In Intl
Conf on Cloud Computing and Services Science.
Gand, F., Fronza, I., El Ioini, N., Barzegar, H. R. and Pahl,
C. (2020). Serverless Container Cluster Management
for Lightweight Edge Clouds. In Intl Conference on
Cloud Computing and Services Science CLOSER.
Gand, F., Fronza, I., El Ioini, N., Barzegar, H. R. and Pahl,
C. (2020). A Lightweight Virtualisation Platform for
Cooperative, Connected and Automated Mobility. In
6th Intl Conference on Vehicle Technology and Intelli-
gent Transport Systems (VEHITS).
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
336

González, L. M. V. and Rodero-Merino, L. (2014). Finding
your way in the fog: Towards a comprehensive def-
inition of fog computing. Computer Communication
Review, 44(5):27–32.
Gu, L., Zeng, D., Guo, S., Barnawi, A., and Xiang, Y.
(2017). Cost efficient resource management in fog
computing supported medical cyber-physical system.
Trans on Emerging Topics in Computing.
El Ioini, N., Pahl, C. and Helmer, S. (2018). A decision
framework for blockchain platforms for IoT and edge
computing. IoTBDS’18.
Jamshidi, P., Pahl, C., Chinenyeze, S. and Liu, X. (2015).
Cloud Migration Patterns: A Multi-cloud Service Ar-
chitecture Perspective. In Service-Oriented Comput-
ing - ICSOC 2014 Workshops. 6–19.
Jamshidi, P., Pahl, C. and Mendonca, N. C. (2016). Man-
aging uncertainty in autonomic cloud elasticity con-
trollers. IEEE Cloud Computing, 50-60.
Jamshidi, P., Pahl, C. and Mendonca, N. C. (2017). Pattern-
based multi-cloud architecture migration. Software:
Practice and Experience 47 (9), 1159-1184.
Mahmud, R., Srirama, S. N., Ramamohanarao, K., and
Buyya, R. (2019). Quality of experience (qoe)-aware
placement of applications in fog computing environ-
ments. J. Parallel Distrib. Comput., 132:190–203.
Manasrah, A. and Ali, H. (2018). Workflow scheduling
using hybrid ga-pso algorithm in cloud computing.
Wireless Comm and Mobile Comp, 2018:1–16.
Mendonca, N. C., Jamshidi, P., Garlan, D. and Pahl, C.
(2020). Developing Self-Adaptive Microservice Sys-
tems: Challenges and Directions. In IEEE Software.
Meng, H., Zhu, Y., and Deng, R. (2017). Optimal comput-
ing resource management based on utility maximiza-
tion in mobile crowdsourcing. Wireless Communica-
tions and Mobile Computing, 2017.
Minh, Q. T., Nguyen, D. T., Le, V. A., Nguyen, D. H., and
Pham, T. V. (2019). Task placement on fog computing
made efficient for iot application provision. Wireless
Communications and Mobile Computing.
Omara, F. A. and Arafa, M. M. (2010). Genetic algorithms
for task scheduling problem. Journal of Parallel and
Distributed Computing, 70(1):13 – 22.
Pahl, C., Jamshidi, P., and Zimmermann, O. (2018). Archi-
tectural principles for cloud software. ACM Transac-
tions on Internet Technology (TOIT), 18(2):17.
Pahl, C., El Ioini, N., Helmer, S. and Lee, B. (2018). An ar-
chitecture pattern for trusted orchestration in IoT edge
clouds. Intl Conf Fog and Mobile Edge Computing.
Pahl, C., Fronza, I., El Ioini, N. and Barzegar, H. R. (2019).
A Review of Architectural Principles and Patterns for
Distributed Mobile Information Systems. In 14th Intl
Conf on Web Information Systems and Technologies.
Pahl, C., Jamshidi, P. and Zimmermann, O. (2020). Mi-
croservices and Containers. Software Engineering
SE’2020.
Rolim, C. O., Koch, F. L., Westphall, C. B., Werner, J.,
Fracalossi, A., and Salvador, G. S. (2010). A cloud
computing solution for patient’s data collection in
health care institutions. eTELEMED.
Saboori, A., Jiang, G., and Chen, H. (2008). Autotuning
configurations in distributed systems for performance
improvements using evolutionary strategies. In Intl
Conf on Distributed Computing Systems.
Samir, A. and Pahl, C. (2020). Detecting and Localizing
Anomalies in Container Clusters Using Markov Mod-
els. Electronics 9 (1), 64.
Sarkar, S., Chatterjee, S., and Misra, S. (2018). Assessment
of the suitability of fog computing in the context of
internet of things. Trans. Cloud Computing.
Scolati, R., Fronza, I., El Ioini, N., Samir, A. and Pahl,
C. (2019). A Containerized Big Data Streaming Ar-
chitecture for Edge Cloud Computing on Clustered
Single-Board Devices. International Conference on
Cloud Computing and Services Science.
Shin, K. G. and Chang, Y. (1989). Load sharing in dis-
tributed real-time systems with state-change broad-
casts. IEEE Trans. Computers, 38(8):1124–1142.
Tata, S., Jain, R., Ludwig, H., and Gopisetty, S. (2017).
Living in the cloud or on the edge: Opportunities and
challenges of iot application architecture. In Intl Conf
on Services Computing (SCC).
von Leon, D., Miori, L., Sanin, J., El Ioini, N., Helmer,
S. and Pahl, C. (2018). A Performance Exploration
of Architectural Options for a Middleware for Decen-
tralised Lightweight Edge Cloud Architectures. Intl
Conf Internet of Things, Big Data & Security.
von Leon, D., Miori, L., Sanin, J., El Ioini, N., Helmer, S.
and Pahl, C. (2019). A Lightweight Container Mid-
dleware for Edge Cloud Architectures. Fog and Edge
Computing: Principles and Paradigms, 145-170.
Wang, Z., Shi, B., and Zhao, E. (2001). Bandwidth-
delay-constrained least-cost multicast routing based
on heuristic genetic algorithm. Computer Communi-
cations, 24:685–692.
Wang, Z., Zhao, Z., Min, G., Huang, X., Ni, Q., and Wang,
R. (2018). User mobility aware task assignment for
mobile edge computing. Future Gen Comp Systems.
Yang, X.-S. (2012). Bat algorithm for multi-objective opti-
misation. arXiv preprint arXiv:1203.6571.
Yousefpour, A., Ishigaki, G., and Jue, J. P. (2017). Fog
computing: Towards minimizing delay in the internet
of things. In Intl Conf on Edge Computing EDGE’17.
Particle Swarm Optimization for Performance Management in Multi-cluster IoT Edge Architectures
337
