Dynamic Control System Design for Autonomous Car

Shoaib Azam

, Farzeen Munir

and Moongu Jeon

School of Electrical Engineering and Computer Science, Gwangju Institute of Science and Technology,

Gwangju, South Korea

Keywords:

Longitudinal Control, Lateral Control, Model Predictive Control, Pure Pursuit.

Abstract:

The autonomous vehicle requires higher standards of safety to maneuver in a complex environment. We focus

on control of the self-driving vehicle that includes the longitudinal and lateral dynamics of the vehicle. In

this work, we have developed a customized controller for our KIA Soul self-driving car. The customized

controller implements the PID control for throttle, brake, and steering so that the vehicle follows the desired

velocity proﬁle, which enables a comfortable and safe ride. Besides, we have also catered the lateral dynamic

model with two approaches: pure pursuit and model predictive control. An extensive analysis is performed

between pure pursuit and its adversary model predictive control for the efﬁcacy of the lateral model.

1 INTRODUCTION

The 4

industrial revolution brings about the cyber-

physical system into the 21

century. Among the

fascinating technologies, the autonomous vehicle has

captured the center stage, which promises to bring

about the potential metamorphic impact on automo-

tive transportation, environment, and social beneﬁt

(Lee et al., 2018). The progress of an autonomous

vehicle is evaluated on the level of autonomy. The

Society of Automation Engineering (SAE) has distin-

guished six levels of autonomy (SAE, ). Level 0 is

manual control, and level 5 is the fully autonomous

mode, where the car is self-aware of the environment

and intelligent enough to make sensible decisions.

The increase in the level of automation is directly pro-

portional to the ability of the autonomous vehicle to

demonstrate precise control in the complex urban sce-

nario.

The successful automation of the vehicle demands

a perfect synchronization of environmental mapping

for perception to the execution of the control com-

mands(Thomanek and Dickmanns, 1995). Humans

conscious do this job effortlessly, but developing this

behavior in the vehicle requires additional sensors like

camera, Lidar, GNSS, IMU, and Radar to be installed.

In addition to the sensors, advanced machine learning

algorithms are implemented that solve the problem

https://orcid.org/0000-0003-3521-5098

https://orcid.org/0000-0002-6760-4373

https://orcid.org/0000-0002-2775-7789

Figure 1: Our Self-Driving Car Equipped with State-of-the-

Art Sensors That Includes Lidar, IMU, GNSS, Camera and

Radar.

of localization, object detection, object recognition,

motion planning, path planning, and automatic con-

trol (Ziegler et al., 2014)(apo, ) (Munir et al., 2018)

(Acosta et al., 2017).

The problem of automatic control, focuses on ma-

nipulating the actuators such that the vehicle navi-

gates with the desired speed and follows the path de-

ﬁned by the planning module (Rupp and Stolz, 2017).

Therefore, the accuracy of automatic control is vital

to safety and substantial to the autonomous vehicle.

The automatic control of the autonomous vehicle con-

sists of lateral control and longitudinal control(Jiang

and Astolﬁ, 2018). The lateral control commands the

steering angle of the vehicle that controls the head-

456

Azam, S., Munir, F. and Jeon, M.

Dynamic Control System Design for Autonomous Car.

DOI: 10.5220/0009392904560463

In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2020), pages 456-463

ISBN: 978-989-758-419-0

ing direction, whereas the longitudinal control is con-

cerned with regulating the speed of the vehicle, which

is represented by a ﬁrst-order system. The lateral con-

trol dynamics are modeled by the kinematic bicycle

model or dynamic bicycle model(Jun et al., 2018).

In literature, the researchers have utilize the

classical controller such as Proportional-Integral-

Derivative (PID) control (P

erez et al., 2011) (Al-

lou and Zennir, 2018), fuzzy logics(Kodagoda et al.,

2002), sliding mode control(Cristi et al., 1990), opti-

mal state feedback controllers(Moriwaki, 2005), and

model predictive control(Borrelli et al., 2005) for lat-

eral and longitudinal control of the vehicle. Earli-

est autonomous vehicles such as Sandstrom used a

simple geometric model for steering control (Urmson

et al., 2006), whereas famous Stanley had their steer-

ing control model based on kinematic vehicle model

(Thrun et al., 2006). Boss used model predictive con-

trol to perform vehicle control(Urmson et al., 2008).

We have developed our self-driving car, shown in

Figure. 1. It is equipped with state-of-the-art sensors,

including Lidar, GPS, IMU, camera, and radar. The

architecture of our self-driving car consists of 4 lay-

ers: 1) sensor layer that perceives the data from the

environment. 2) Perception layer, which consists of

localization and detection. We have used data from

the Lidar sensor to localize our self-driving car using

NDT matching (Munir et al., 2019). The object de-

tection is performed in image and Lidar data individ-

ually, and the results are fused and transformed into

the world frame. 3) The planning layer takes informa-

tion from the perception layer to determines the path

followed by the self-driving car. It takes into account

the geometry of the world and ﬁnds the safest path

to follow while obeying the trafﬁc rules and 4) The

control layer receives the direction and speed infor-

mation from planning and converts it into the control

signal for car actuators, which enables it to drive au-

tonomously.

In this work, we have proposed a vehicle dynam-

ics model that plays an integral role in the execution

of desired actions required by the autonomous car to

follow the speciﬁed path. The planning module gen-

erates the velocity proﬁle and trajectory that is needed

to be followed. In order to ensure the velocity proﬁle

is properly followed, we have designed a customized

PID controller for longitudinal control. For the lateral

control, we have utilized both Pure Pursuit and Model

Predictive Control based path follower and analyzed

their behavior on the lateral dynamics model. The

operation of longitudinal control is tested with two

different speed ranges: low (0 − 10km/h) and high

(10 − 30km/h).

Figure 2: Kinematic Bicycle Model.

2 VEHICLE MODEL

Vehicle model provides the essential foundation for

studying the characteristics of vehicle control, and

therefore, a proper model of vehicle leads to robust

and deﬁnite modeling of vehicle control(Limebeer

and Massaro, 2018). In this work, we have investi-

gated two types of vehicle models i) kinematic bicy-

cle model and ii) dynamic bicycle model for our self-

driving car. These models are necessary for vehicle

analysis in order to model the controller.

2.1 Kinematic Bicycle Model

The kinematic bicycle model is widely used for the

analysis of vehicle characteristics (Rajamani, 2011)

(Zhang et al., 2018). Figure.2 shows the kinematic bi-

cycle model. In this model, the front two wheels and

as well as the back two wheels are lumped into a sin-

gle wheel, respectively. The front lumped wheel is lo-

cated at the center of the front axle, and similarly, the

rear lumped wheel has center at the rear axle. With the

assumption, that the front wheel can only be steered,

the kinematic model is given by equation(1)-(5)

˙x = v cos(ψ+β) , (1)

˙y = vsin(ψ + β) , (2)

ψ =

(β) , (3)

˙v = a , (4)

β = arctan(

+ l

+ tan(δ

))) , (5)

where, x and y corresponds to the coordinates of the

center of mass in the inertial frame (X,Y ). v is the

Dynamic Control System Design for Autonomous Car

457

Figure 3: Dynamic Bicycle Model.

speed of the vehicle, and ψ denotes the heading of

the vehicle. l

and l

represent the distance of lumped

front wheel to the center of mass and vice versa. In

this model, the control inputs are acceleration (a) and

the steering angle (δ). For simplicity and, in general,

practice the δ

= 0 because the only front wheel is

considered to be steered.

This kinematic model is simple as compared to

other models that include the forces (air resistance,

the weight of the body) and friction. The kinematic

model needs only two parameters (l

and l

) to be

identiﬁed, and this makes it portable for both longi-

tudinal and lateral control.

2.2 Dynamic Bicycle Model

The kinematic bicycle model only includes planar ve-

hicle motions. The effect of forces acting on the body

of the vehicle is overlooked in the simple kinematic

model, which may impact the mild maneuvers. In or-

der to address this problem, a 6 degree-of-freedom

(DOF) dynamic vehicle model is formulated (Raja-

mani, 2011) (Zhou et al., 2019) . Figure. 3 shows

the free body diagram of the vehicle. The governing

equations for this model is shown from equation (6)-

(10).

¨x =

ψ ˙y + a

, (6)

¨y = −

ψ ˙x +

cos(δ

) + F

) , (7)

ψ =

− l

) , (8)

X = ˙x cos(ψ) − ˙y sin(ψ) , (9)

Y = ˙x sin(ψ) + ˙ycos(ψ) , (10)

where, the longitudinal and lateral speed is rep-

resented by ˙x and ˙y, respectively, with respect to the

body frame. The lateral forces on the rear and front

wheel are denoted by F

and F

, respectively. The

yaw rate, vehicle’s mass, and yaw inertia are denoted

ψ, m, and I

, respectively. For the linear tire model,

the F

is deﬁned by the equation (11).

= −C

, (11)

where, i ∈ f , r and α

is the slip angle given by equa-

tion (12)-(13) and C

is the tire cornering stiffness.

= arctan(

+ l

) − δ , (12)

= arctan(

− l

) , (13)

3 LONGITUDINAL CONTROL

The longitudinal vehicle model is responsible for gen-

erating the velocity proﬁle for the autonomous vehi-

cle (Gao et al., 2017). In classical control theory,

feedback controllers are used for compensating the er-

ror between the desired and observed measurements.

Proportional-Integral-Derivative is one such kind of

feedback controller that works on the propagation of

error and minimizes it to achieve the desired response

(Zakia et al., 2019) (Gambier, 2008). The control law

for the PID control is given by equation (14).

u(t) = k

˙e + k

e + k

edt , (14)

where, k

, k

and k

are the proportional, integral and

derivative gain for the PID controller and e is the error.

In our case, the velocity proﬁle of the longitu-

dinal vehicle control includes throttle, brake, and

torque. For the vehicle to follow the velocity pro-

ﬁle, a PID controller is used to minimize the error be-

tween current and target values of the throttle, brake,

and torque. The current values are from the vehicle

Controller-Area-Network (CAN) bus, and target val-

ues are from the planning module. This PID control

is the customized longitudinal controller for our self-

driving car because of the proprietary laws of KIA

Company not sharing the CAN bus IDs, and the CAN

bus IDs have been empirically found by implement-

ing a can-sniffer algorithm.

The PID controller is designed in such a way that

for each throttle, brake, and torque, two separate con-

trol parameters (values of K

, K

, and K

) are used.

The advantage of using this kind of framework gives

the leverage of controlling the vehicle on high and

low speed for throttle and also for the fast and slow

application of torque to the steering wheel. Figure.4

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

458

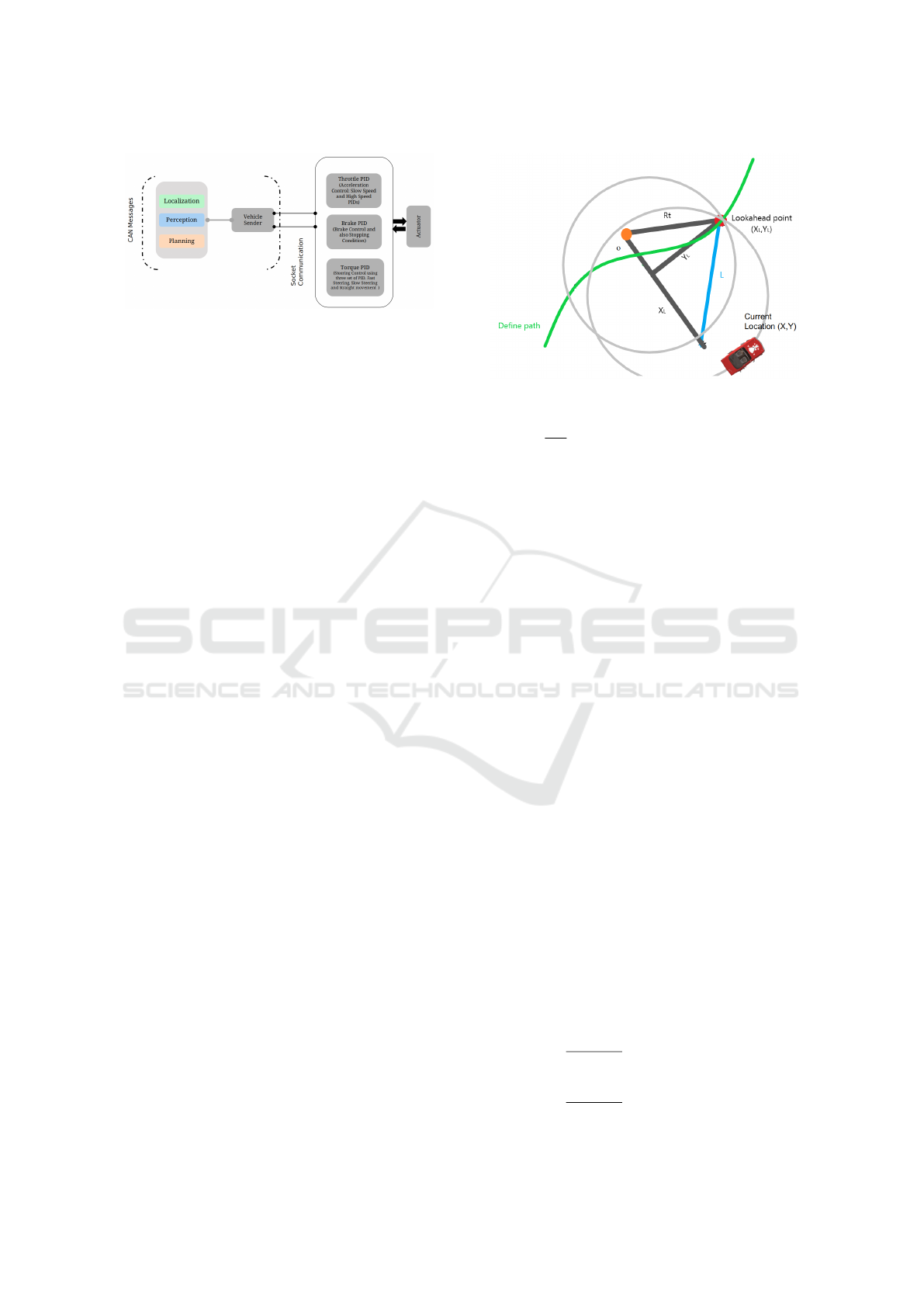
Figure 4: The Longitudinal Control Is Composed of Throt-

tle/brake and Torque Pids. The Controller Receives the In-

formation from Vehicle Sender over Socket of Perception

and Planning Modules.

show the framework for a PID controller that includes

three components (i) Vehicle Sender (ii) Customized

PID controller and (iii) Actuator. The vehicle sender

serves as a communication bridge between the soft-

ware stack and hardware stack and sends the plan-

ning commands over the socket to the customized

controller.

4 LATERAL CONTROL

4.1 Pure Pursuit

Pure Pursuit is a path tracking algorithm that calcu-

lates the curvature from the current position to some

goal position. The goal point is chosen such that it

is always a constant distance ahead of vehicle cur-

rent position (Coulter, 1992). In simpler terms, pure

pursuit chase a moving goal points some distance

ahead, called look-ahead distance. Figure.5 illustrate

the basic principle of pure Pursuit. The current posi-

tion of the vehicle is shown by (X ,Y). The constant

look-ahead distance denoted by L, goal point (X

)

chased by the algorithm on the path. The radius R

the arc that joins the current position to the look-ahead

point (X

). Based on two triangles, the following

equation (15)-(17) are satisﬁed.

= L

, (15)

= R

, (16)

+ o = R

. (17)

The a in equation (17) is put into equation (16), re-

sulting in:

− x

)

= R

, (18)

− 2R

+ X

= R

, (19)

Figure 5: Basic Principle of Pure Pursuit Algorithm.

. (20)

The R

the arc radius determines the path followed by

the vehicle.

4.2 Model Predictive Control

Model predictive control (MPC) incorporates the dy-

namics of the vehicle and controls the lateral motion

of a vehicle while satisfying a set of constraints (Liu

et al., 2017) (Sun et al., 2018). Model predictive con-

trol ﬁnds the optimal trajectory by solving an opti-

mization problem at each time step and generates an

actuator signal based on the ﬁnite horizon. The opti-

mization formulation of MPC for lateral control us-

ing the kinematic and dynamic bicycle model after

converting to the discrete model is given in equation

(21)-(22).

min

∑

i=0

[(z

− z

re f ,i

)

Q(z

− z

re f ,i

)]+

−1

∑

i=0

[(u

− u

i−1

)

R(u

− u

i−1

) + u

] ,

(21)

s.t

= z(t),u

−1

= u(t −t

) ,

i+1

= f (z

),i = 0,..., H

− 1 ,

min,i

6 u

max,i

,∀i ,

min,i

− u

i−1

max,i

,∀i/0 ,

min,i

− u

i−1

max,i

,i = 0 ,

Dynamic Control System Design for Autonomous Car

459

Figure 6: The PID Tuned Graphs for Throttle/brake and Torque. (a) the Command Velocity Is from the Planning and Current

Velocity Is from the CAN Bus of Vehicle. The Throttle Pedal and PID Parameters (K

and K

) Are Also Shown. The

Graph Also Shows the Variation of Each Term (k

˙e , k

E and k

EDt) of PID Controller with Respect to Current and Target

Velocity. (B) Torque PID Tuned Graph Shows the Torque Value Applied to Vehicle after Parameters Are Tuned.

where Q ∈ R

4x4

, R ∈ R

2x2

R ∈ R

2x2

, H

is the hori-

zon prediction. The cost weights is represented by the

diagonal matrices Q, R,

R. The sampling time of the

controller is t

. The system dynamics after discretiz-

ing the vehicle kinematics model is given by f (z

)

where u

−1

is the input given to previous sampling step

u(t −t

). The constraints variables are represented for

lower and upper bound are given by u

min

max

and

max

respectively. The reference trajectory is

given by z

re f

The MPC formulation to cater the vehicle dy-

namic model is given in equation (22).

min

∑

i=0

[(z

− z

re f ,i

)

Q(z

− z

re f ,i

)]+

−1

∑

i=0

[R(4(F

(k + i))

+ Wε

] , (22)

where, 4F

= [4F

(k), 4F

(k +

1),..,4F

(k + H

p−1

)]. ε

is the non-negative

slack variable. Q, R and W are the weighting

matrices.

5 EXPERIMENTATION AND

RESULTS

In this section, we have experimented and evaluated

the longitudinal and lateral control on our self-driving

car.

5.1 Longitudinal Control

The vehicle longitudinal control is responsible to

cater the throttle, brake, and torque (for the steering

Table 1: Quantitative Comparison between Cohen-Coon

Method and Genetic Algorithm.

Controller Parameters

Throttle Torque

Cohen-Coon Method Genetic Algorithm Cohen-Coon Method Genetic Algorithm

0.085 0.003 0.0009 0.0005

0.0045 0.0001 0.0001 0.0002

0.01 0.09 0.0005 0.0008

wheel) applied to the self-driving car. This is achieved

by designing a PID controller. The PID controller is

based on three parameters, given by equation (14),

that are optimized for the robustness of the controller.

These three parameters are proportional (K

), inte-

gral (K

) and derivative (K

). The optimized tuning

of these parameters is essential for the working of the

controller. In our work, we have used two approaches

for tuning the parameters of the PID i) Cohen-Coon

method and ii) Genetic Algorithm.

In the Cohen-Coon method, ﬁrst, the K

parameter

is tuned while the rest two parameters K

and K

are

kept at zero. The other two parameters are tuned when

the K

parameter is optimized. Figure.6 shows the

tuned PID graphs for throttle, brake, and torque.

The parameter’s tuning using the Cohen-Coon

method requires human supervision and tedious to do

manually. In order to tune the parameters dynam-

ically, we used the genetic algorithm for parameter

tuning. The parameter tuning problem is formulated

as an optimization problem with the focus on mini-

mizing the error between current and target values for

each throttle, brake, and torque. Table.1 shows the

quantitative analysis of PID parameters tuned with the

genetic algorithm and Cohen-Coon method. The PID

parameter tuned using genetic algorithm approaches

to the same values as obtained using the Cohen-coon

method; hence it veriﬁes the mathematical formula-

tion of PID using the genetic algorithm, which pro-

vides dynamic tuning of PID parameters.

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

460

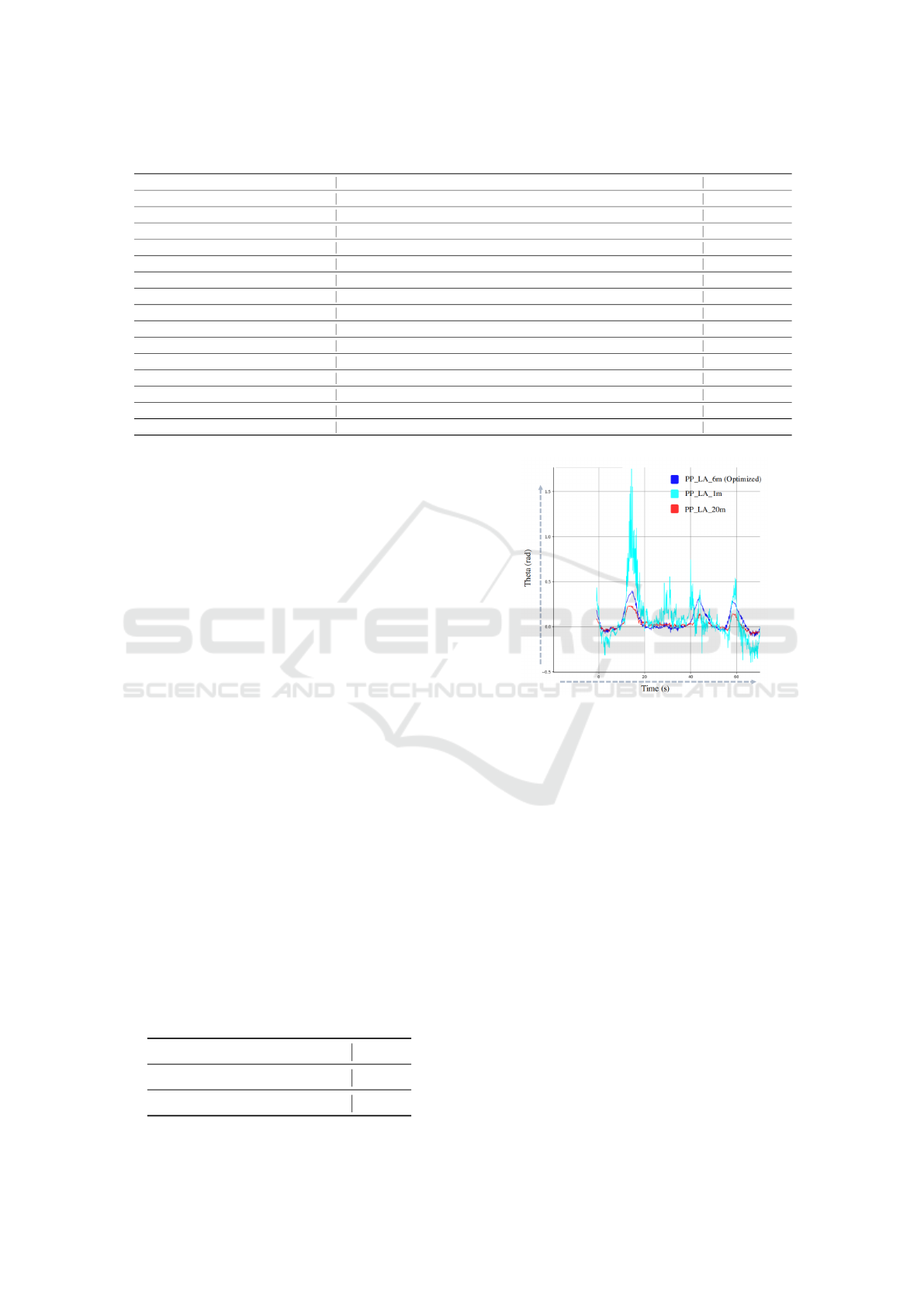
Table 2: Model Predictive Control Based Path Follower Design Parameters.

MPC parameters Description Value

QP solver type used for optimization QP solver option Unconstraint-fast

QPoases(solver) max iteration maximum iteration number for convex optimiaztion with qpoases. 500

Vehicle Model type vehicle model option. described below in detail. Kinematics/Dynamic

Prediction horizon total prediction step for MPC 70

Prediction sampling time prediction period for one step [s] 0.1

Lateral weight error Weight for lateral error in matrix Q 0.1

Heading weight error Weight for heading error in matrix Q 0

Weight heading Error squared velocity coefﬁcient Lateral Heading Error * Velocity 5

Steering Weight Input Steering weight error in matrix R (steer command - reference steer) 1

Weight Steering Input squared velocity coefﬁcient Steering error (steer command - reference steer) * velocity 0.25

Lateral Weight Jerk Weight for lateral jerk (steer(i) - steer(i-1)) * velocity 0

Wheel base Wheel base length for the vehicle model (meters) 2.95

Steering tau Steering dynamics time constant (1d approximation) for vehicle model 0.3

Steering Limit Steering angle limit (deg) 35

Steering Gear Ratio Ratio between the turn of the steering wheel (in degree) to the turn of the wheel (in degree) 15

5.2 Lateral Control

For the lateral control of the self-driving car, we

have used two path tracking controller i) pure pur-

suit and ii) MPC-based path follower. The robust-

ness of these two controllers relies on the proper tun-

ing of parameters based on the vehicle model. In

the case of pure pursuit, the tuned parameters are

shown in Table.3. As pure pursuit mainly depends

on the look-ahead distance, we evaluated the perfor-

mance of pure pursuit by changing the look-ahead

distance. Figure.7 shows the result of the effect of

look-ahead distance on the lateral control using pure

pursuit. The closer look-ahead distance in pure pur-

suit leads to more noise and disturbance in the lat-

eral control, whereas the greater look-ahead distance

provides more deviation of the car from the speciﬁed

ground-truth path. Similarly, the MPC parameters are

optimized, as shown in Table.2.

In order to make a comparative analysis between

the pure pursuit and MPC-based path follower, both

the algorithms are applied to the vehicle at a speed

of 30Km/h. Figure.8 shows the comparison result

qualitatively. It can be seen that in the case of pure

pursuit, the vehicle over-cuts the predeﬁned (ground-

truth) path at corner points, besides the MPC based

path follower follows the ground-truth path more ac-

curately. The quantitative analysis is done by ﬁnd-

ing the lateral error between both pure pursuit and

MPC based path follower. Figure.9 shows the graph

Table 3: Pure Pursuit Tuned Parameters for 30 Km/h Speed.

Pure Pursuit Parameters Values

Look-ahead ratio 2

Minimum Look-ahead Distance 6

Figure 7: Effect of Look-Ahead Distance in Pure Pursuit.

The Legends of the Graph Shows the Look-Ahead Dis-

tances, for Instance PP-LA-1m Is 1m Look-Ahead Distance

in the Pure Pursuit. The 1m Look-Ahead Distance Is More

Prone to Noise and Produce More Vibrations in the Lat-

eral Model of Vehicle. Similarly the the 20m Look-Ahead

Distance Deviates from Original Track and Overlook the

Ground-Truth Waypoints. The Optimized Look-Ahead Dis-

tance Gives the Result with Minimal Error in Contrast to

Other Look-Ahead Distance. Theta (Rad) Shows the Steer-

ing Angle for Lateral Control.

of lateral error between pure pursuit and MPC based

path follower. The difference between pure pursuit

and MPC can be signiﬁcantly observed at the curved

roads; the MPC does not overshoot and accurately

follows the predeﬁned (ground-truth) path. This en-

sures the safety of the car when making turns at nar-

row roads.

6 CONCLUSIONS

The control of the self-driving car plays a monumen-

tal role in the execution of decision commands to the

Dynamic Control System Design for Autonomous Car

461

Figure 8: Qualitative Comparison between Pure Pursuit and Mpc Path Follower. The Red Color Line Shows the Pure Pursuit

and the Green Color Corresponds to Mpc Path Follower. The Ground-Truth Path Is Shown by White Color. The Difference

in Corners (a) and (B) Are Shown in (B) and (C) Respectively.

Figure 9: The Graphs Show the Difference between MPC

and Pure Pursuit. The Difference between the Graphs

Shows the Lateral Error. Theta (Rad) Shows the Steering

Angle for Lateral Control in Case of Both MPC and Pure

Pursuit.

vehicle. In this work, we have exploited the control

of the self-driving car and implemented two control

models i) longitudinal and ii) lateral control based on

the kinematic and dynamic bicycle model. For the

longitudinal control, a customized PID control is de-

veloped, and two approaches are discussed in tuning

the parameters of this controller. Pure pursuit con-

troller and model predictive control-based path fol-

lower are analyzed in the context of lateral control.

The parameters of both controls are optimized in re-

gard to our self-driving car.

ACKNOWLEDGMENT

This work is in part supported by GIST Research In-

stitute (GRI) grant funded by the GIST in 2020.

REFERENCES

Apollo. http://apollo.auto/index.html.

SAE J3016. https://www.sae.org/news/2019/01/sae-

updates-j3016-automated-driving-graphic.

Acosta, M., Kanarachos, S., and Fitzpatrick, M. E. (2017).

A hybrid hierarchical rally driver model for au-

tonomous vehicle agile maneuvering on loose sur-

faces. In Proceedings of the 14th International Con-

ference on Informatics in Control, Automation and

Robotics - Volume 2: ICINCO,, pages 216–225. IN-

STICC, SciTePress.

Allou, S. and Zennir, Y. (2018). A comparative study of

pid-pso and fuzzy controller for path tracking control

of autonomous ground vehicles. In Proceedings of the

15th International Conference on Informatics in Con-

trol, Automation and Robotics - Volume 1: ICINCO,,

pages 306–314. INSTICC, SciTePress.

Borrelli, F., Falcone, P., Keviczky, T., Asgari, J., and Hrovat,

D. (2005). Mpc-based approach to active steering for

autonomous vehicle systems. International Journal of

Vehicle Autonomous Systems, 3(2):265–291.

Coulter, R. C. (1992). Implementation of the pure pursuit

path tracking algorithm. Technical report, Carnegie-

Mellon UNIV Pittsburgh PA Robotics INST.

Cristi, R., Papoulias, F. A., and Healey, A. J. (1990). Adap-

tive sliding mode control of autonomous underwater

VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems

462

vehicles in the dive plane. IEEE journal of Oceanic

Engineering, 15(3):152–160.

Gambier, A. (2008). Mpc and pid control based on multi-

objective optimization. In 2008 American Control

Conference, pages 4727–4732. IEEE.

Gao, H., Zhang, X., Liu, Y., and Li, D. (2017). Longitudi-

nal control for mengshi autonomous vehicle via gauss

cloud model. Sustainability, 9(12):2259.

Jiang, J. and Astolﬁ, A. (2018). Lateral control of an au-

tonomous vehicle. IEEE Transactions on Intelligent

Vehicles, 3(2):228–237.

Jun, N., Jibin, H., et al. (2018). Autonomous driving system

design for formula student driverless racecar. In 2018

IEEE Intelligent Vehicles Symposium (IV), pages 1–6.

IEEE.

Kodagoda, K., Wijesoma, W. S., and Teoh, E. K.

(2002). Fuzzy speed and steering control of an agv.

IEEE Transactions on control systems technology,

10(1):112–120.

Lee, M., Yun, J., Pyka, A., Won, D., Kodama, F., Schi-

uma, G., Park, H., Jeon, J., Park, K., Jung, K., et al.

(2018). How to respond to the fourth industrial revolu-

tion, or the second information technology revolution?

dynamic new combinations between technology, mar-

ket, and society through open innovation. Journal of

Open Innovation: Technology, Market, and Complex-

ity, 4(3):21.

Limebeer, D. J. and Massaro, M. (2018). Dynamics and

optimal control of road vehicles. Oxford University

Press.

Liu, C., Lee, S., Varnhagen, S., and Tseng, H. E. (2017).

Path planning for autonomous vehicles using model

predictive control. In 2017 IEEE Intelligent Vehicles

Symposium (IV), pages 174–179. IEEE.

Moriwaki, K. (2005). Autonomous steering control for

electric vehicles using nonlinear state feedback h con-

trol. Nonlinear Analysis: Theory, Methods & Appli-

cations, 63(5-7):e2257–e2268.

Munir, F., Azam, S., Hussain, I., Sheri, A. M., and Jeon,

M. (2018). Autonomous Vehicle: The Architecture

Aspect of Self Driving Car.

Munir, F., Azam, S., Sheri, A., Ko, Y., and Jeon, M.

(2019). Where Am I: Localization and 3d Maps for

Autonomous Vehicles. In 5th International Confer-

ence on Vehicle Technology and Intelligent Transport

Systems (VEHITS), pages 452–457.

erez, J., Milan

es, V., and Onieva, E. (2011). Cascade ar-

chitecture for lateral control in autonomous vehicles.

IEEE Transactions on Intelligent Transportation Sys-

tems, 12(1):73–82.

Rajamani, R. (2011). Vehicle dynamics and control, ser.

Mechanical Engineering Series. Springer, page 26.

Rupp, A. and Stolz, M. (2017). Survey on Control Schemes

for Automated Driving on Highways, pages 43–69.

Springer International Publishing, Cham.

Sun, C., Zhang, X., Xi, L., and Tian, Y. (2018). Design

of a path-tracking steering controller for autonomous

vehicles. Energies, 11(6):1451.

Thomanek, F. and Dickmanns, E. D. (1995). Autonomous

road vehicle guidance in normal trafﬁc. In Asian Con-

ference on Computer Vision, pages 499–507. Springer.

Thrun, S., Montemerlo, M., Dahlkamp, H., Stavens, D.,

Aron, A., Diebel, J., Fong, P., Gale, J., Halpenny,

M., Hoffmann, G., et al. (2006). Stanley: The robot

that won the darpa grand challenge. Journal of ﬁeld

Robotics, 23(9):661–692.

Urmson, C., Anhalt, J., Bagnell, D., Baker, C., Bittner, R.,

Clark, M., Dolan, J., Duggins, D., Galatali, T., Geyer,

C., et al. (2008). Autonomous driving in urban envi-

ronments: Boss and the urban challenge. Journal of

Field Robotics, 25(8):425–466.

Urmson, C., Ragusa, C., Ray, D., Anhalt, J., Bartz, D.,

Galatali, T., Gutierrez, A., Johnston, J., Harbaugh, S.,

“Yu” Kato, H., et al. (2006). A robust approach to

high-speed navigation for unrehearsed desert terrain.

Journal of Field Robotics, 23(8):467–508.

Zakia, U., Moallem, M., and Menon, C. (2019). Pid-smc

controller for a 2-dof planar robot. In 2019 Interna-

tional Conference on Electrical, Computer and Com-

munication Engineering (ECCE), pages 1–5. IEEE.

Zhang, R., Abraham, A., Dasgupta, S., and Dauwels, J.

(2018). Constrained model predictive control using

kinematic model of vehicle platooning in vissim sim-

ulator. In 2018 15th International Conference on

Control, Automation, Robotics and Vision (ICARCV),

pages 721–726. IEEE.

Zhou, S., Liu, Z., Suo, C., Wang, H., Zhao, H., and Liu, Y.-

H. (2019). Vision-based dynamic control of car-like

mobile robots. In 2019 International Conference on

Robotics and Automation (ICRA), pages 6631–6636.

IEEE.

Ziegler, J., Bender, P., Schreiber, M., Lategahn, H., Strauss,

T., Stiller, C., Dang, T., Franke, U., Appenrodt, N.,

Keller, C. G., et al. (2014). Making bertha drive—an

autonomous journey on a historic route. IEEE Intelli-

gent transportation systems magazine, 6(2):8–20.

Dynamic Control System Design for Autonomous Car

463