
Time-series Approaches to Change-prone Class Prediction Problem
Cristiano Sousa Melo, Matheus Mayron Lima da Cruz, Ant
ˆ
onio Diogo Forte Martins,
Jos
´
e Maria da Silva Monteiro Filho and Javam de Castro Machado
Department of Computing, Federal University of Cear
´
a, Fortaleza-Cear
´
a, Brazil
Keywords:
Change-prone Class, Machine Learning, Deep Learning, Recurrent Algorithm, Time-series.
Abstract:
During the development and maintenance of a large software project, changes can occur due to bug fix, code
refactoring, or new features. In this scenario, the prediction of change-prone classes can be very useful in
guiding the development team since it can focus its efforts on these pieces of software to improve their quality
and make them more flexible for future changes. A considerable number of related works uses machine
learning techniques to predict change-prone classes based on different kinds of metrics. However, the related
works use a standard data structure, in which each instance contains the metric values for a particular class in a
specific release as independent variables. Thus, these works are ignoring the temporal dependencies between
the instances. In this context, we propose two novel approaches, called Concatenated and Recurrent, using
time-series in order to keep the temporal dependence between the instances to improve the performance of the
predictive models. The Recurrent Approach works for imbalanced datasets without the need for resampling.
Our results show that the Area Under the Curve (AUC) of both proposed approaches has improved in all
evaluated datasets, and they can be up to 23.6% more effective than the standard approach in state-of-art.
1 INTRODUCTION
During the development phase of a large software
project, it can have multiple versions due to changes
that are necessary, like bug fix or refactoring, for ex-
ample. The distribution of a specific version of an
application is called release. In general, along this
process, the number of classes increases, making ar-
duous software maintenance over the years.
In this context, a change-prone class is a piece
of software that probably will change in the next re-
lease. Overall, a new software release contains previ-
ously existing classes that have been changed, besides
new and dropped classes. The change-prone classes
require a particular attention (Malhotra and Khanna,
2013). Identifying those classes can enable the devel-
opers to focus preventive action on testing, inspect-
ing, and restructuring efforts (Koru and Liu, 2007).
Also, when a new development team needs to main-
tain a software code, it necessary a considerable effort
to find the most important classes, that is, those that
change more frequently.
Several empirical studies deal with the change-
prone class prediction problem. Altogether, these
works usually propose different kind of metrics, i.e.,
independent variables, such as: oriented object met-
rics (Zhou et al., 2009), C&K metrics (Chidamber and
Kemerer, 1994), code smells (Khomh et al., 2009),
design patterns (Posnett et al., 2011) and evolution
metrics (Elish and Al-Rahman Al-Khiaty, 2013), in
order to maximize performance metrics in Machine
Learning algorithms.
However, as a real-world problem, most of the
studied datasets are imbalanced. Thus, they can skew
the predictive model if not handled correctly (Prati
et al., 2009). The most recent works use two differ-
ent approaches to avoid this problem: oversampling
and undersampling. The former generates synthetic
data of the minority dependent variable while the lat-
ter removes data of the majority dependent variable.
Nevertheless, both change the real data history.
Besides, the related works use a standard struc-
ture for the dataset, in which each instance contains
the metric values for a particular class in a specific
release as independent variables. Figure 1 illustrates
an example of this standard structure. Note that each
line, i.e., instance, represents a class from the soft-
ware project in a particular release, and its columns
contain k metrics, independent variables, M, and one
last column representing the dependent variable D.
Observe that in this example, the C
a
class has three
instances, one for each release in which it appears. In
practice, the Machine Learning algorithms use the k
columns M and the dependent variable D to generate
122
Melo, C., Lima da Cruz, M., Martins, A., Filho, J. and Machado, J.
Time-series Approaches to Change-prone Class Prediction Problem.
DOI: 10.5220/0009397101220132
In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 2, pages 122-132
ISBN: 978-989-758-423-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

their models, ignoring the class identifier C and the
release number R. It means this usual approach is just
engaging in learn a pattern to predict which class will
suffer modification in the next release, ignoring their
history, i.e., the temporal dependence between the in-
stances.
Figure 1: A single instance from a usual dataset.
Thus, to the best of the authors’ knowledge, although
many works are studying the change-prone class pre-
diction problem, none of them take the temporal de-
pendence between the instances into account to gen-
erate predictive models.
In this work, motivated by these issues previ-
ously mentioned, we have proposed two time-series
approaches, called Concatenated and Recurrent, in
order to investigate the importance of keeping the
temporal dependence between the instances to im-
prove the quality of the performance metrics of the
predictive models. A time-series is simply a series
of data points ordered in time, usually for a single
variable. However, in our experiments, the time-
series is multi-variable, i.e., all independent variables
have their time-series to generate the predictive mod-
els. These proposed time-series approaches have been
compared to the standard structure for designing the
dataset. The Recurrent Approach works for imbal-
anced datasets without the need for resampling. With
the purpose of validating the proposed approaches, we
have used four open-source projects: a C# project pre-
sented by (Melo et al., 2019), and three JAVA Apache
projects: Ant, Beam, and Cassandra. Classification
models are built using in the standard structure, and
both the time-series approach proposed in this work.
The performance of the predictive models was mea-
sured using the Area Under the Curve (AUC).
2 RELATED WORKS
A considerable amount of works in the change-prone
class prediction problem has been proposed involving
different aspects, like the predictive model for imbal-
anced or unlabeled datasets, novel predictive metrics,
or guidelines in order to support the set of steps.
(Yan et al., 2017) have proposed a predictive
model on unlabeled datasets. They have tackled this
task by adopting the unsupervised method, namely
CLAMI. Besides, they have proposed CLAMI+ by
extending CLAMI. CLAMI+, compared to state-of-
art, aims to learn from itself. They have tested their
experiments in 14 open source projects, and they have
shown that CLAMI+ slightly improves the results
compared to CLAMI.
The work presented by (Malhotra and Khanna,
2017) shows that most datasets in change-prone class
prediction problems are imbalanced since they have
a minority dependent variable. Then, they evalu-
ate many strategies for handling imbalanced datasets
using some resample techniques in six open-source
datasets. The results have shown that resample tech-
niques tend to improve the quality of performance
metrics.
(Catolino et al., 2018) investigate the use of
developer-related factors approach. For this, they use
these factors as predictors and compare them with ex-
isting models. It has shown the improvement of the
performance metrics. Besides, combining their pro-
posal with Evolution metrics (Elish and Al-Rahman
Al-Khiaty, 2013) can improve up to 22% more effec-
tive than a single model. Their empirical study has
been executed in 20 datasets of public repositories.
(Choudhary et al., 2018) have proposed the use
of new metrics in order to avoid the commonly used
independent variable to generate models in change-
prone class prediction problems, like (Chidamber and
Kemerer, 1994) metrics or Evolution Metrics. These
newly proposed metrics are execution time, frequency
or method call, run time information of methods, pop-
ularity, and class dependency. They have evaluated
their proposed metrics using various versions of open-
source software.
(Melo et al., 2019) have proposed a guideline in
order to support the change-prone class prediction
problem. This guideline helps in decision making
related to designing datasets, doing statistical analy-
sis, checking outliers, removing dimensionality with
feature engineering, resampling imbalanced datasets,
tuning, showing the results, and become them re-
producible. They have shown that careful decision
making can harshly improve performance metrics like
the Area Under the Curve. Furthermore, they have
shown that a predictive model that uses an imbalanced
dataset has the worst results compared to resampled
datasets.
All these studies aforementioned confirm the im-
Time-series Approaches to Change-prone Class Prediction Problem
123

portance of creating different strategies to improve the
quality of performance metrics. However, none of
them take the temporal dependence between the in-
stances into account during the development phase of
models. In the next section, we describe two time-
series approaches in order to keep the temporal his-
tory of each class in their respective release order.
3 TIME-SERIES APPROACHES
TO CHANGE-PRONE CLASS
PREDICTION PROBLEM
As previously mentioned, the related works use a
standard structure for the dataset, in which each in-
stance contains the metric values for a particular class
in a specific release as independent variables. So,
it ignores the temporal dependence between the in-
stances, since the same class can change in different
releases. Thus, by convention, we are going to refers
to the standard structure as One Release per Instance
(ORI).
In this work, we have proposed two time-series
approaches, called Concatenated and Recurrent, in or-
der to exploit the temporal dependence between the
instances to improve the quality of the performance
metrics of the predictive models. In these new time-
series approaches, depending on window size, each
instance will contain the total - or partial - history of
the metrics values of a class, following its release or-
der.
Thus, initially, to design a dataset according to
those novel proposed approaches is necessary to de-
fine a window size. The value of the window size
parameter will be fixed and will define the number of
releases that will compose each instance. In general,
we do not know which is the best value for this hy-
perparameter, so the recommended is to try a range
of values and check their performance metrics in or-
der to investigate what window size retrieves the best
results. During the dataset building, if the number
of releases that a certain class C appears is less than
the window size, the data about this class C will be
dropped. However, the opposite is not true. If the
number of releases that a certain class C appears is
greater than the window size, the data about class C
will be split, as shown in Figure 2. Note that, in Fig-
ure 2, there is a class C that appears in three different
releases. Now, suppose that the window size was set
as two. In this scenario, the data about class C will be
split into two instances, i.e., from release i to release
i + 1 and from release i + 1 to release i + 2. For our
experiments, the window size is sliding.
Figure 2: The Split Process for Window Size equals two.
The following subsections will present in detail the
two time-series approaches proposed in this work,
called Concatenated Approach (CA) and Recurrent
Approach (RA). The former refers to a structure in
which the dataset must be used in Machine Learn-
ing algorithms to generate predictive models, while
the latter refers to a structure in which must be
used in recurrent algorithms, like Gated Recurrent
Units (GRU) (Cho et al., 2014), an advanced neu-
ral network derived from Long Short-Term Memory
(LSTM) (Hochreiter and Schmidhuber, 1997) in Deep
Learning algorithms.
3.1 Concatenated Approach (CA)
To generate a dataset according to the Concatenated
Approach is necessary, initially, to compute the values
of the k metrics for each release R in which a specific
class C appears. So, this process will produce R in-
stances, each one with k columns. After that, for each
class C, it needs to concatenate its n sequential in-
stances, where n is the window size, according to the
split process. Note that in this step, the produced in-
stances will contain n ∗k columns, as the independent
variable. For example, if a class C appears in R = 4
releases and the window size n = 3, two instances,
each one with k ∗ 3 columns will be generated.
Figure 3 illustrates a dataset built according to the
Concatenated Approach. Note that M represents the
chosen metrics (they can be Oriented Object, Evo-
lution, or Code Smells). Thus, an instance in this
dataset contains n ∗ k columns, i.e., independent vari-
ables, respecting the releases order i, i + 1, ..., n to en-
sure the use of time-series information.
3.2 Recurrent Approach (RA)
The Recurrent Approach consists of storage the par-
tial or total history into a single instance of a class,
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
124

Figure 3: Concatenated Structure.
forming a three-dimensional matrix (x, k, n), where x
means the number of classes, k means the number of
metrics, and n means the window size.
Figure 4 depicts an example of the data structure
used in the recurrent approach. R represents the re-
leases of a certain class C, and it will follow the re-
lease order i, i + 1, ..., n. Each one of these releases
contains k metrics M. In short, this dataset contains
x classes C, i.e, there are x instances of window size
n, where each release has k metrics. Note that if the
window size is less than the number of the release of
a class C, this last one will be split, generating more
instances into the dataset.
Figure 4: Recurrent Structure.
The recurrent approach differs from the concatenated
one because, in the former, the recurrent algorithms
contain cell state, i.e., it keeps the temporal depen-
dence between the independent variables. In the lat-
ter, although the window size increases the number of
independent variables into an instance, the Machine
Learning algorithms treat each one of them indepen-
dently.
4 EXPERIMENTAL SETTING
Our research methods consist of developing different
kinds of predictive models and compare them. For
this, we have generated predictive models using three
different approaches: one release per instance (ORI),
concatenated approach (CA) and recurrent approach
(RA), as defined in Section 3.
4.1 Designing the Datasets
In order to evaluate the Time-Series Approaches pro-
posed in this work, we have chosen four software
projects. The first dataset was presented in (Melo
et al., 2019), and it results from a large C# project. It
was used to evaluate a guideline designed to support
the different tasks involved in the change-prone class
prediction problem. The remaining datasets were
built from three JAVA open-source projects: Apache
Ant, Apache Beam, and Apache Cassandra, respec-
tively. Each one of these datasets was modeled fol-
lowing three different approaches: one release per in-
stance (ORI), concatenated approach (CA), and recur-
rent approach (RA).
4.1.1 Independent Variable
In this work, we have chosen as independent vari-
ables the same metrics used in (Melo et al., 2019):
C&K metrics (Chidamber and Kemerer, 1994), Cy-
clomatic Complexity (McCabe, 1976), and Lines of
Code. Logically, these independent variables were
used in all used datasets. To collect all these ori-
ented object metrics, we have used Scitools Under-
stand. The definition of each chosen metric follows:
• Class Between Object (CBO): It is a count of the
number of non-inheritance related couples with
other classes. Excessive coupling between objects
outside of the inheritance hierarchy is detrimental
to modular design and prevents reuse. The more
independent an object is, the easier it is to reuse it
in another application;
• Cyclomatic Complexity (CC): It has been used
to indicate the complexity of a program. It is a
quantitative measure of the number of linearly in-
dependent paths through a program’s source code;
• Depth of Inheritance Tree (DIT): It is the length
of the longest path from a given class to the root
class in the inheritance hierarchy. The deeper a
class is in the hierarchy, the higher the number
of methods it is likely to inherit making it more
complex;
• Lack of Cohesion in Methods (LCOM): It is
the methods of the class that are cohesive if they
use the same attributes within that class, where
0 is strongly cohesive, and one is lacking cohe-
sive. The cohesiveness of methods within a class
Time-series Approaches to Change-prone Class Prediction Problem
125

is desirable since it promotes encapsulation of ob-
ject, meanwhile, lack of cohesion implies classes
should probably be split into two or more sub-
classes;
• Line of Code (LOC): It is the number of line of
code, except blank lines, imports or comments;
• Number of Child (NOC): It is the number of im-
mediate sub-classes subordinated to a class in the
class hierarchy. It gives an idea of the potential
influence a class has on the design. If a class has
a large number of children, it may require more
testing of the methods in that class;
• Response for a Class (RFC): It is the number of
methods that an object of a given class can exe-
cute in response to a received message; if a large
number of methods can be invoked in response to
a message, the testing and debugging of the object
becomes more complicated;
• Weighted Methods per Class (WMC): The
number of methods implemented in a given class
where each one can have different weights. In this
dataset, each method has the same weight (value
equal to one), except getters, setters and construc-
tors, which have weight equal to zero. This vari-
able points that a larger number of methods in an
object implies in the greater the potential impact
on children since they will inherit all the methods
defined in the object.
4.1.2 Dependent Variable
In this work, we have adopted as the dependent vari-
able the metric proposed by (Lu et al., 2012). Thus,
following its definition, an instance, i.e., an oriented
object class, will be labeled as 1 if in the next release
occurs alteration in its LOC independent variable, and
0 otherwise.
4.1.3 Software Projects Overview
An overview of the software projects used to build the
datasets that were employed in order to evaluate the
time-series approaches proposed in this work can be
seen in Table 1. It shows (i) the project names, (ii) the
period in which these projects were developed, (iii)
the average percentage of change-prone classes, (iv)
the number of releases, and (v) the number of object-
oriented classes present in the first and in last releases.
The ratio of the imbalanced dataset is calculated
by the cardinality of minority class over the major-
ity class. In this problem, the minority class tends
to be that we want to predict. According to Table 1,
Apache Ant is the only balanced dataset, while the
other datasets are imbalanced.
4.2 Generating One Release per
Instance (ORI) Models
In order to generate and evaluate predictive models
using the One Release per Instance (ORI) approach,
we have followed the guideline proposed by (Melo
et al., 2019). Initially, we have split each dataset into
training and test sets. The following tasks were per-
formed only on the training set. Lastly, we have used
the test set to check if the generated models were
overfitted.
Four different classification algorithms were used
to evaluate the ORI models: Logistic Regression
(LR), Decision Tree (DT), Random Forest (RF), and
MLP. The source code was developed in Python with
the support of the Scikit-Learn libraries (Pedregosa
et al., 2012), besides it can be found in our public
GitHub repository, which will be detailed in Section
7.
The following subsections will describe in de-
tail the tasks performed over each dataset in order
to generate the predictive models based on the ORI
approach and following the guideline proposed by
(Melo et al., 2019).
4.2.1 Descriptive Statistics
Tables 2, 3, 4, and 5 show the descriptive statis-
tics of the (Melo et al., 2019), Apache Ant, Apache
Beam, and Apache Cassandra datasets, respectively.
All these tables show the minimum, maximum, mean,
median, and standard deviation for each chosen inde-
pendent variable.
4.2.2 Outlier Detection
Outliers are extreme values that deviate from other
observations on the dataset. Outliers are candidates
for aberrant data, which may lead to model misspec-
ification, biased parameter estimation, and incorrect
results (Liu et al., 2004).
In this work, we have used the Interquartile Range
(IQR) to detect outliers. The IQR is the length of the
box in the boxplot, i.e., Q3 - Q1. Here, outliers are
defined as instances that are below Q1 − 1.5 ∗ IQR or
above Q3 + 1.5 ∗ IQR.
Table 6 shows an overview of the datasets before
and after outliers removal.
4.2.3 Normalization
The goal of normalization is to put the values of each
column in the same scale. It is essential to avoid that
the gradients may end up taking a long time to find the
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
126
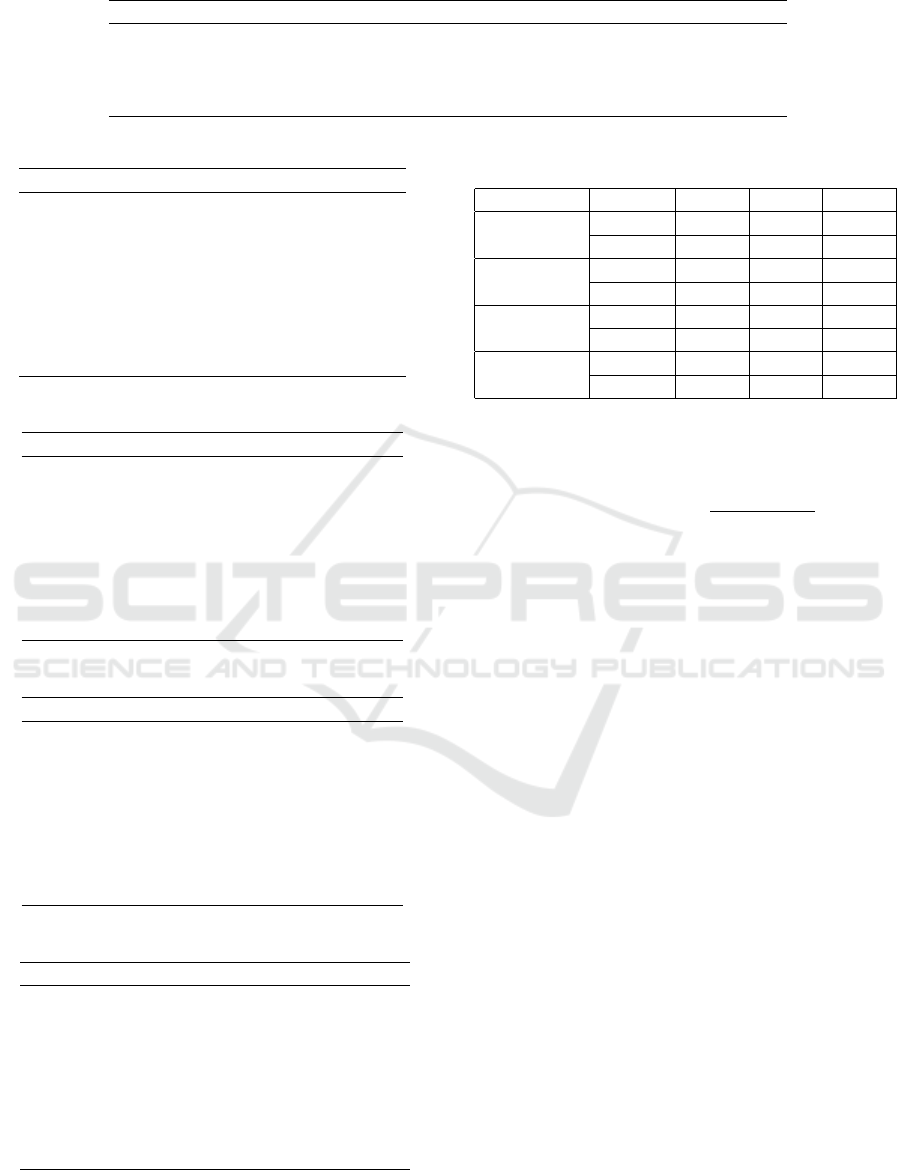
Table 1: Characteristics of the Software Projects Used to Generate the Datasets.
Software Project Period Imb. Rate Releases Classes
(Melo et al., 2019) Jan 2013 - Dec 2018 7.8% 8 762-1693
Apache Ant Jan 2016 - May 2019 70.1% 10 1020-19611
Apache Beam Oct 2017 - Jun 2019 22.4% 15 36595-73923
Apache Cassandra Mar 2010 - Feb 2019 30.3% 49 4244-30308
Table 2: Descriptive Statistics for (Melo et al., 2019).
Metric Min Max Mean Med SD
LOC 0 1369 36.8 12 91.2
CBO 0 162 7.10 3 12.3
DIT 0 7 0.78 0 1.76
LCOM 0 100 0.17 0 0.28
NOC 0 189 0.61 0 6.54
RFC 0 413 9.96 1 25.6
WMC 0 56 1.55 0 4.24
CC 0 488.0 15.9 8 30.3
Table 3: Descriptive Statistics for Apache Ant.
Metric Min Max Mean Med SD
LOC 0 1586 79.4 37 127
CBO 0 40 3.21 2 4.26
DIT 0 7 2.16 2 1.14
LCOM 0 100 32.5 19 35.2
NOC 0 166 0.52 0 4.99
RFC 0 210 23.4 12 27.6
WMC 0 125 7.79 4 10.0
CC 0 99 36.2 33 29.7
Table 4: Descriptive Statistics for Apache Beam.
Metric Min Max Mean Med SD
LOC 0 2749 57.7 22 117
CBO 0 106 5.33 5.33 7.23
DIT 0 6 1.62 1 0.75
LCOM 0 100 17.5 0 28.5
NOC 0 901 0.44 0 11.2
RFC 0 100 8.67 6 8.96
WMC 0 100 4.28 2 5.61
CC 0 179 5.89 3 9.42
Table 5: Descriptive Statistics for Apache Cassandra.
Metric Min Max Mean Med SD
LOC 0 45517 103 32 754
CBO 0 145 5.7 3 8.65
DIT 0 6 1.6 2 0.74
LCOM 0 100 20.5 0 30.6
NOC 0 116 0.27 0 2.3
RFC 0 294 10.9 4 17.9
WMC 0 294 6.5 3 12.0
CC 0 843 13.7 5 31.1
Table 6: Overview of the Datasets Before and After Outliers
Removal.
Dataset Outlier #0 #1 Total
Melo
Before 3871 312 4183
After 3637 287 3924
Apache
Ant
Before 4954 2582 7536
After 4551 2340 6891
Apache
Beam
Before 58599 11849 70448
After 56196 11283 67479
Apache
Cassandra
Before 75616 15925 91541
After 68047 14712 82759
global/local minimum. In this work, we have used the
min-max normalization presented in equation1.
x
0
= λ
1
+ (λ
2
− λ
1
)
x − min
A
max
A
− min
A
(1)
In the equation 1, λ
1
and λ
2
are values to adjust the
data domain to a desired range. The min
A
and max
A
are the minimum, and the maximum values of the fea-
ture A. The original and the normalized value of the
attribute are represented by x and x
0
, respectively. The
standard range is [0,1].
4.2.4 Resample Techniques
In real-world problems, some datasets can be imbal-
anced, i.e., a majority class containing most samples
while the other class contains few samples, this
one generally of our interest (Prati et al., 2009).
Using imbalanced datasets to train models leads to
higher misclassifications for the minority class. It
occurs because there is a lack of information about
it. Some strategies to avoid this misclassification are
resampling techniques, categorized into:
Undersampling (US): refers to the process of
reducing the number of samples in the majority
class. Three US techniques used in this work are
Random Under-Sampler (RUS) (Batista et al., 2004),
which consists of randomly choose an instance from
the majority class and remove it. Tomek’s Link
(TL) (Tomek, 1976), which consists of finding two
instances, one from the majority class and the other
from the minority class, that are the nearest neighbor
of each other and then remove one of the instances.
Edited Nearest Neighbours (ENN) (Wilson, 1972),
Time-series Approaches to Change-prone Class Prediction Problem
127

which consists in removing the nearest instances that
do not belong to the class of the instance.
Oversampling (OS): consists of generating synthetic
data in the minority class in order to balance the pro-
portion of data. Three OS techniques used in this
work are Random Over-Sampler (ROS) (Batista et al.,
2004), which consists of randomly choose an instance
from the minority class and repeat it. Synthetic Mi-
nority Oversampling Technique (SMOTE) (Chawla
et al., 2002), which consists of generating new syn-
thetic instances obtained by combining the features
of an instance and its k-nearest neighbors. Adaptive
Synthetic (ADASYN) (He et al., 2008), which con-
sists in creating synthetic instances of the minority
class considering the difficult to classify this instance
with a KNN algorithm, then it will focus on the harder
instances.
4.2.5 Cross-validation
In order to validate the stability of the generated pre-
dictive models, we use a cross-validation technique to
give information on how well the learner will gener-
alize to an unseen dataset (Arlot and Celisse, 2009).
As specified before, the model will be generated over
the train set, and cross-validation will split it into train
and validation sets. In the end, the test set will serve
as data that represents the real scenario. The test set is
original, i.e., outlier removal or resamples techniques
were not performed on it.
The cross-validation technique used in this work
was stratified k-fold since some datasets are imbal-
anced. Hence, a proportional amount of minority la-
bels is necessary during the phase of the split in k-
fold. According to (James et al., 2013), a suitable k
value in k-fold is k = 5 or k = 10.
4.2.6 Performance Metrics
A confusion matrix gives an overview of output were
sorted correctly and incorrectly, classifying them as
True Positive (TP), True Negative (TN), False Posi-
tive (FP), or False Negative (FN). The following met-
rics are widely used to validate performance results:
accuracy =
T P + T N
T P + T N + FP + FN
(2)
precision =
T P
T P + FP
(3)
sensitivity or recall =
T P
T P + FN
(4)
speci f icity =
T N
T N + FP
(5)
To evaluate a predictive model for the classification
problem is necessary to select the appropriate perfor-
mance metrics according to two possible scenarios:
for a balanced or imbalanced dataset. Since most of
our datasets are imbalanced, metrics like accuracy can
lead to dubious results (Akosa, 2017).
The more suitable metrics for imbalanced datasets
is the Area Under the Curve (AUC) and F-score
(Equation 6). These performance metrics are suitable
because they take the minority classes correctly clas-
sified into account, unlike the accuracy.
F
β
= (1 + β) ·
precision · recall
β
2
· precision + recall
(6)
For these reasons, we have compared the predictive
models using AUC. However, we have also provided
other performance metrics like accuracy, specificity,
sensitivity, and F1 (F-Score).
4.3 Generating Time-series Models
In this subsection, we are going to detail the process
performed to obtain our best results in the concate-
nated and recurrent approaches, presented in Section
3.
4.3.1 Concatenated Approach
For concatenated approach, we have evaluated three
different values for the window sizes: 2, 3, and 4.
Thus, for each previously selected dataset, we have
generated three distinct versions, according to the
window size. Next, we have performed the guideline
proposed by (Melo et al., 2019). However, for the
concatenated approach, we neither perform the out-
lier detection nor the feature selection steps.
Besides, four different classification algorithms
were used to evaluate the concatenated approach: Lo-
gistic Regression (LR), Decision Tree (DT), Random
Forest (RF), and MLP. The source code was devel-
oped in Python with the support of the Scikit-Learn
libraries (Pedregosa et al., 2012), besides it can be
found in our public GitHub repository, which will be
detailed in Section 7.
4.3.2 Recurrent Approach
For recurrent approach, we have evaluated three dif-
ferent values for the window sizes: 2, 3, and 4. Thus,
for each previously selected dataset, we have gener-
ated three distinct versions, according to the window
size. However, unlike the concatenated approach, we
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
128

did not use the guideline proposed by (Melo et al.,
2019). We have just built the data structure into a
Tensor using Keras and uses it with the Gated Recur-
rent Unit (GRU) algorithm. So, we have used imbal-
anced datasets. The GRU structure used in recurrent
approach is presented next:
Begin
model = Sequential()
model.add(GRU(256, input_shape=input_shape,
return_sequences=True))
model.add(Dropout(0.3))
model.add(GRU(128, return_sequences=True))
model.add(Dropout(0.3))
model.add(GRU(64))
model.add(Dropout(0.3))
model.add(Dense(output_dim,
activation=’softmax’))
model.summary()
End
In this approach, we have used three layers of
GRU, from 256 entry to 1, and its activation function
is softmax. We also added three Dropout layers (set
as 0.3) in order to avoid overfitting. The number of
epochs was set by 20, the number of batches was set
by 512, and the number of k, in stratified k-fold, was
set by 5.
5 EXPERIMENTAL EVALUATION
In order to evaluate the proposed approaches, they
have been compared to the one release per instance
(ORI) approach. Classification models are built using
the four selected datasets and three different values
for the window size (2, 3, and 4). The performance of
the predictive models was measured using the Area
Under the Curve (AUC).
5.1 Analyzing ORI Approach vs
Time-veries Approaches
Table 7 shows the best predictive model found for
each dataset, Melo (Melo et al., 2019), Apache Ant,
Apache Beam, and Apache Cassandra, using the One
Release per Instance (ORI) Approach. So, Table 7
illustrates the (i) resample technique used, (ii) the al-
gorithm performed, (iii) if outlier removal was used,
(iv) the spent time for the execution, and (v) the values
of performance metrics. For the (Melo et al., 2019)
dataset, only AUC has been provided in their paper,
so the other performance metrics are missing. Note
that, for each dataset was necessary to run some re-
sample technique since an imbalanced dataset tends
to provides the worst results. Besides, another inter-
esting result was that no dataset presented the best re-
sult using outlier removal.
Table 8 shows the best predictive model found for
each dataset using the Concatenated Approach (CA).
It is important to note that for (Melo et al., 2019)
dataset, the window size 4 was not used due to the
small number of C# classes present in 4 or more re-
leases.
Table 9 depicts the best predictive model found
for each dataset and for each window size using the
Recurrent Approach (RA). In this scenario, we have
used only the imbalanced datasets and a recurrent al-
gorithm.
5.2 Discussion of Results
One of the goals of this research is to experimentally
evaluate how time-series approaches tend to improve
the performance metrics of predictive models used to
solve the change-prone class prediction problem over
imbalanced datasets.
Given the results discussed in the last subsection,
we have decided to get the best AUC metric obtained
from each dataset and compare them according to dif-
ferent approaches. Figure 5 shows the results of this
comparison, which x-axis means the AUC and y-axis
means the best scenario from each dataset in different
approaches.
For all evaluated datasets, the proposed time-
series approaches outperformed the ORI approach.
Note that, in Apache Cassandra, we had the best per-
formance in the ORI approach with the AUC 0.7432
using SMOTE resample with MLP while the Recur-
rent Approach provided the AUC 0.9188, up to 23.6%
more effective than the standard approach in litera-
ture. Besides this improvement, we highlight the re-
duction of execution time in this dataset. For the ORI
approach, the execution time was 37 minutes while in
CA we spent nearly 34 minutes, and RA only took 8
minutes.
We want to highlight the difference of AUC be-
tween the baselines in all approaches, i.e., neither in
ORI nor in Concatenated we perform outlier detection
or resample technique. According to Figure 6, time-
series approaches have the best result overall ORI ap-
proach. In this figure, the x-axis means the AUC
and y-axis means the best scenario from each dataset
in different approaches. The results in the ORI ap-
proach have been the worst since no treatment was
performed. It shows that time-series approaches, spe-
cially Recurrent ones, deal with imbalanced scenar-
ios.
Time-series Approaches to Change-prone Class Prediction Problem
129
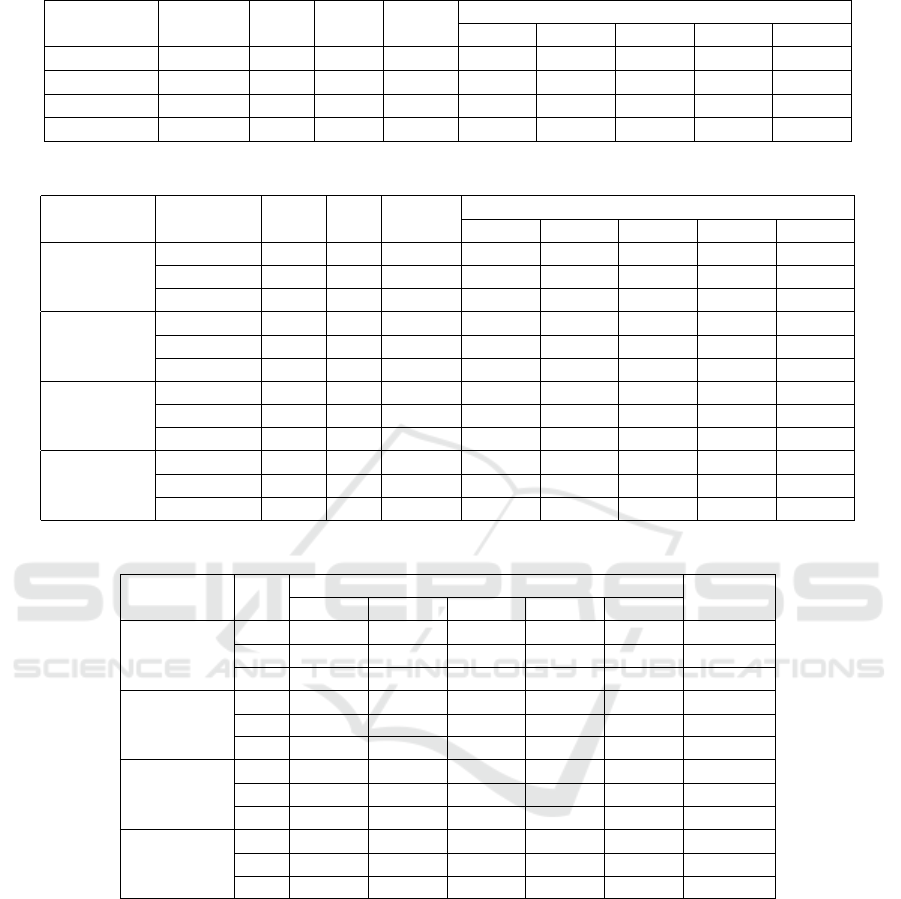
Table 7: Best Results for each Dataset Using the One Release per Instance (ORI) Approach.
Dataset Sample Alg.
Out.
Rem.
Time
Performance Metrics
Acc Spec Sens F1 AUC
Melo SMOTE LR N - - - - - 0.703
Ant ROS MLP N 37.7 s 0.6725 0.6636 0.6886 0.6789 0.6761
Beam ROS RF N 45.4 s 0.7229 0.7599 0.5370 0.7493 0.6484
Cassandra SMOTE MLP N 37min 0.7214 0.7096 0.7767 0.7525 0.7432
Table 8: Best Results for Different Window Size (WS) Using the Concatenated Approach (CA).
Dataset Sample Alg.
WS Time
Performance Metrics
Acc Spec Sens F1 AUC
Melo
ADASYN LR 2 0.27 s 0.7562 0.7593 0.6914 0.8256 0.7254
SMOTE LR 3 0.20 s 0.7807 0.7846 0.7066 0.8404 0.7456
- - 4 - - - - - -
Ant
ROS MLP 2 45.8 s 0.8092 0.8160 0.8007 0.8094 0.8083
ROS MLP 3 14.8 s 0.7985 0.8000 0.7967 0.7989 0.7983
- MLP 4 8.84 s 0.7899 0.7537 0.8269 0.7897 0.7903
Beam
ROS MLP 2 39.0 s 0.7112 0.7584 0.5260 0.7296 0.6422
ROS DT 3 4.61 s 0.7522 0.8237 0.4872 0.7579 0.6554
ADASYN MLP 4 9.5min 0.6841 0.7230 0.5505 0.7034 0.6368
Cassandra
ROS RF 2 33.0 s 0.9106 0.9323 0.8157 0.9124 0.8740
ROS RF 3 1min 0.9060 0.9347 0.7806 0.9071 0.8576
SMOTE RF 4 2min 0.8858 0.8970 0.8377 0.8909 0.8673
Table 9: Best Results for Different Window Size (WS) Using the Recurrent Approach (RA).
Dataset
WS
Performance Metrics
Time
Acc Spec Sens F1 AUC
Melo
2 0.7737 0.7942 0.7390 0.7656 0.7737 29.54 s
3 0.7318 0.6874 0.8503 0.7602 0.7318 38.33 s
4 - - - - - -
Ant
2 0.7753 0.7580 0.8090 0.7827 0.7753 28.81 s
3 0.7586 0.7558 0.7640 0.7599 0.7586 35.42 s
4 0.7371 0.7374 0.7363 0.7369 0.7371 39.78 s
Beam
2 0.6714 0.6430 0.7706 0.7011 0.6714 3min56s
3 0.7003 0.6514 0.8617 0.7419 0.7003 4min48s
4 0.6549 0.6670 0.6186 0.6419 0.6549 5min
Cassandra
2 0.8687 0.8848 0.8478 0.8659 0.8687 5min15s
3 0.9188 0.9287 0.9073 0.9179 0.9188 6min8s
4 0.9152 0.9308 0.8972 0.9137 0.9152 8min4s
6 THREATS TO VALIDITY
We identify some threats to validity in this experimen-
tal analysis:
1. Amount of releases. For our experiments, all
datasets described in Table 1 contain a reasonable
amount of releases. It allowed us to test different
window sizes. When we have decided to use time-
series approaches, it is interesting to check more
than one window size to investigate different val-
ues.
2. Dropped releases. It is necessary to keep in
mind that when we have a large window size, all
classes that contain less release that window size
is dropped. Even that the result can be harshly im-
proved, the large window size can drop a consid-
erable amount of releases, and it can compromise
the history of the project.
3. Amount of datasets. In our experiment, we test our
novel approaches in four datasets. We cannot gen-
eralize the results of using these four datasets to
ensure that time-series is always going to retrieve
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
130

Figure 5: Comparison of the best results between different
approaches.
Figure 6: Baselines comparison between different ap-
proaches.
the best results. Also, we have used only one dif-
ferent dataset besides our generated by Apache
repositories. It has happened mainly due to the
lack of dataset available, or some dataset did not
have enough information about the class to gener-
ate the time-series structure.
7 REPRODUCIBILITY
To reproduce all experiments presented in this re-
search, we provide public access in a GitHub reposi-
tory
1
. All scripts have used Jupyter Notebook in order
to keep track of how this research was designed, run,
and analyzed. We set random seed as 42, in order
to fix the randomness. Besides, we also available the
following content:
1. Scripts to generate raw datasets from Apache
repositories.
2. All generated datasets (release-by-release or final
versions) in CSV.
Information containing the exact version of all li-
braries or external programs used in this research is
available in a README file in our repository.
1
https://github.com/cristmelo/time-series-approaches
8 CONCLUSIONS
In this work, we presented two novels time-series ap-
proaches, called Concatenated and Recurrent, to solve
the change-prone class prediction problem over im-
balanced datasets. The former aims to concatenate
releases side by side in order to generate predictive
models using ordinary Machine Learning algorithms,
and the latter designs a data structure into a tensor
to generate predictive models using recurrent algo-
rithms. The Recurrent Approach uses the concept of
cell state to keep the dependencies between the re-
leases. Besides, the Recurrent Approach works well
for imbalanced datasets without the need for resam-
pling.
In order to evaluate the proposed time-series ap-
proaches, they have been compared to the one release
per instance (ORI) approach. Classification models
are built using the four large open-source projects and
three different values for the window size (2, 3, and
4). The performance of the predictive models was
measured using the Area Under the Curve (AUC).
The experimental results show that the Area Under
the Curve (AUC) of both proposed approaches has
improved in all evaluated datasets, and they can be up
to 23.6% more effective than the standard approach
in state-of-art. Furthermore, in some cases, the exe-
cution time harshly fell. We highlight that for the re-
current approach, resample techniques have not been
performed, i.e., besides the gain in execution time, we
can keep the original data history.
As future works, we plan to perform an extensive
experimental analysis of the proposed approaches us-
ing a wide range of public imbalanced and balanced
datasets. Moreover, we will investigate other data lay-
outs that can be used in recurrent or deep learning al-
gorithms, like Long Short-Term Memory (LSTM), in
order to improve the performance metrics.
ACKNOWLEDGEMENTS
This research was funded by LSBD/UFC.
REFERENCES
Akosa, J. S. (2017). Predictive accuracy : A misleading
performance measure for highly imbalanced data. In
SAS Global Forum.
Arlot, S. and Celisse, A. (2009). A survey of cross vali-
dation procedures for model selection. Statistics Sur-
veys, 4.
Time-series Approaches to Change-prone Class Prediction Problem
131

Batista, G., Prati, R., and Monard, M.-C. (2004). A study of
the behavior of several methods for balancing machine
learning training data. SIGKDD Explorations, 6:20–
29.
Catolino, G., Palomba, F., Lucia, A. D., Ferrucci, F., and
Zaidman, A. (2018). Enhancing change prediction
models using developer-related factors. Journal of
Systems and Software, 143:14 – 28.
Chawla, N. V., Bowyer, K. W., Hall, L. O., and Kegelmeyer,
W. P. (2002). Smote: Synthetic minority over-
sampling technique. Journal of Artificial Intelligence
Research, 16:321–357.
Chidamber, S. and Kemerer, C. (1994). A metrics suite for
object oriented design. IEEE Transaction on Software
Engineering, 20(6).
Cho, K., van Merri
¨
enboer, B., Gulcehre, C., Bougares, F.,
Schwenk, H., and Bengio, Y. (2014). Learning phrase
representations using rnn encoder-decoder for statisti-
cal machine translation.
Choudhary, A., Godara, D., and Singh, R. K. (2018). Pre-
dicting change prone classes in open source software.
Int. J. Inf. Retr. Res., 8(4):1–23.
Elish, M. O. and Al-Rahman Al-Khiaty, M. (2013). A
suite of metrics for quantifying historical changes to
predict future change-prone classes in object-oriented
software. Journal of Software: Evolution and Process,
25(5):407–437.
He, H., Bai, Y., Garcia, E. A., and Li, S. (2008). Adasyn:
Adaptive synthetic sampling approach for imbalanced
learning. In 2008 IEEE International Joint Confer-
ence on Neural Networks (IEEE World Congress on
Computational Intelligence), pages 1322–1328.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural computation, 9:1735–80.
James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013).
An Introduction to Statistical Learning with Applica-
tions in R. Springer.
Khomh, F., Penta, M. D., and Gueheneuc, Y. (2009). An
exploratory study of the impact of code smells on soft-
ware change-proneness. In 2009 16th Working Con-
ference on Reverse Engineering, pages 75–84.
Koru, A. and Liu, H. (2007). Identifying and characterizing
change-prone classes in two large-scale open-source
products. Journal of Systems and Software, 80:63–73.
Liu, H., Shah, S., and Jiang, W. (2004). On-line outlier
detection and data cleaning. Computers & Chemical
Engineering, 28(9):1635 – 1647.
Lu, H., Zhou, Y., Xu, B., Leung, H., and Chen, L.
(2012). The ability of object-oriented metrics to pre-
dict change-proneness: a meta-analysis. Empirical
Software Engineering, 17(3).
Malhotra, R. and Khanna, M. (2013). Investigation of rela-
tionship between object-oriented metrics and change
proneness. International Journal of Machine Learn-
ing and Cybernetics, 4(4):273–286.
Malhotra, R. and Khanna, M. (2017). An empirical study
for software change prediction using imbalanced data.
Empirical Software Engineering, 22.
McCabe, T. J. (1976). A complexity measure. IEEE Trans-
action on Software Engineering.
Melo, C. S., da Cruz, M. M. L., Martins, A. D. F., Matos,
T., da Silva Monteiro Filho, J. M., and de Cas-
tro Machado, J. (2019). A practical guide to support
change-proneness prediction. In Proceedings of the
21st International Conference on Enterprise Informa-
tion Systems - Volume 2: ICEIS,, pages 269–276. IN-
STICC, SciTePress.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,
Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,
Cournapeau, D., Brucher, M., Perrot, M., Duchesnay,
E., and Louppe, G. (2012). Scikit-learn: Machine
learning in python. Journal of Machine Learning Re-
search, 12.
Posnett, D., Bird, C., and D
´
evanbu, P. (2011). An em-
pirical study on the influence of pattern roles on
change-proneness. Empirical Software Engineering,
16(3):396–423.
Prati, R. C., Batista, G. E. A. P. A., and Monard, M. C.
(2009). Data mining with imbalanced class distribu-
tions: concepts and methods. In IICAI.
Tomek, I. (1976). Two modifications of cnn. IEEE Trans.
Systems, Man and Cybernetics, 6:769–772.
Wilson, D. L. (1972). Asymptotic properties of nearest
neighbor rules using edited data. IEEE Transactions
on Systems, Man, and Cybernetics, SMC-2(3):408–
421.
Yan, M., Zhang, X., Liu, C., Xu, L., Yang, M., and Yang,
D. (2017). Automated change-prone class prediction
on unlabeled dataset using unsupervised method. In-
formation and Software Technology, 92:1 – 16.
Zhou, Y., Leung, H., and Xu, B. (2009). Examining the po-
tentially confounding effect of class size on the asso-
ciations between object-oriented metrics and change-
proneness. IEEE Transactions on Software Engineer-
ing, 35(5):607–623.
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
132
