Learning Recursion: Insights from the ChiQat Intelligent Tutoring

System

Omar Alzoubi

1 a

, Barbara Di Eugenio

2 b

, Davide Fossati

3 c

, Nicholas Green

and

Mehrdad Alizadeh

Jordan University of Science and Technology, Jordan

University of Illinois at Chicago, U.S.A.

Emory University, U.S.A.

Keywords:

Recursion, Intelligent Tutoring Systems, Computer Science Education.

Abstract:

Recursion is a difﬁcult concept to teach, and novice programmers struggle Learning it. The reasons include

unfamiliarity with activities associated with analyzing recursion, such as visualizing program execution and

difﬁculty understanding its back ﬂow of control. In this paper we discuss approaches to teaching recursion that

includes conceptual and program visualization methods. We also describe the recursion module of our ChiQat-

Tutor system which relies on ideas from both approaches. We designed several activities that allow students

to work on recursive problems: answering questions, animations, code tracing, validation, and construction

tasks. We conducted four evaluation experiments at two different institutions, with a total of 89 students tak-

ing introductory Computer Science courses. We hypothesized that ChiQat-Tutor can help novice Computer

Science students learn recursion, develop accurate mental models of recursion, and serve as an effective visu-

alization tool with which hidden features of recursion can become evident. Our results showed some evidence

that the animation, answering questions, code tracing, and validation tasks exhibit a trend towards signiﬁcant

learning gains.

1 INTRODUCTION

Recursion is an important concept in computer sci-

ence, whether seen as a problem-solving approach, a

way of expressing an algorithm, a mathematical con-

cept, or a programming technique (McCauley et al.,

2015; Hamouda et al., 2019). It is a powerful and es-

sential computational problem solving technique that

involves breaking down of a problem into smaller

sub-problems of the same kind. Thus said, such de-

composition is not easily comprehended by novice

students learning recursion (Dann et al., 2001). Some

computer science educators suggest that recursion is

an inherently difﬁcult concept to master, and it is one

of the most difﬁcult concepts to teach (Pirolli and An-

derson, 1985). This is because it is a method to deﬁne

subprogram, in which the subprograms being deﬁned

is applied within its own deﬁnition.

A key explanation why recursion is seen as a difﬁ-

https://orcid.org/0000-0002-7978-1633

https://orcid.org/0000-0003-1706-2577

https://orcid.org/0000-0003-3587-8860

cult concept because it is traditionally taught after stu-

dents have developed preconceptions based on their

learning of repetition (Turbak et al., 1999). Addition-

ally, students sometimes have difﬁculty recognizing

different invocations of the same function, and they

get confused by the bookkeeping required for tracing

each recursive call (Tessler et al., 2013). In particular,

they struggle with unfamiliarity with activities asso-

ciated with analyzing recursion, the visualization of

the program execution, the back-ﬂow of control after

reaching the base case, comparison to loop structures,

and the lack of everyday analogies for recursion.

It is acknowledged that in order to understand the

process of recursion and be able to write recursive

code, one must be able to visualize the nature of a

problem and how solutions to smaller sub-problems

are combined to solve the original problem (Bower,

1998). In a comprehensive review conducted by

(McCauley et al., 2015), a number of successful ap-

proaches to teaching recursion were cited. It included;

providing students with variety of analogies and ex-

amples, introducing repetition before recursion, trac-

ing methods, teaching students problem solving tech-

336

Alzoubi, O., Di Eugenio, B., Fossati, D., Green, N. and Alizadeh, M.

Learning Recursion: Insights from the ChiQat Intelligent Tutoring System.

DOI: 10.5220/0009413903360343

In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 2, pages 336-343

ISBN: 978-989-758-417-6

niques to break problems into small sub-problems,

identifying base and recursive cases, and providing

modiﬁable code templates.

The focus of this paper is about the strategies for

teaching recursion which we implemented and eval-

uated in ChiQat-Tutor. We carried out four experi-

ments in two locations: Carnegie Mellon University

in Qatar (CMUQ), and the University of Illinois at

Chicago (UIC), over a period of one year. We ana-

lyzed students’ interactions with the recursion module

of ChiQat-Tutor, looking for further insights on suit-

able approaches for recursion learning. In the next

section we review some of the approaches to teaching

recursion, discussing the advantages and limitations

of each approach. We also introduce our approach to

teaching recursion in ChiQat tutor.

The remainder of this paper is organized as fol-

lows. Section 2 reviews related literature. Section 3

provides an overview of the ChiQat system. Section 4

explains our experimental protocol and data collec-

tion. Section 5 discusses our results; and Section 6

provides concluding remarks.

2 RELATED WORK

A number of approaches to teaching recursion was

discussed in (Tessler et al., 2013). These include con-

ceptual models of recursion and control ﬂow, and the

use of visual aids. Conceptual models are deﬁned

by teachers and are used as tools for understanding

or teaching of a system. Conceptual models used

for teaching recursion include mathematical induc-

tion, abstract and conceptual discussions of recursion,

process tracing, and structure templates of recursive

code (Wu et al., 1998). On the other hand, the visual

aids approach relies on the use of algorithms anima-

tion, program visualizations using video games of an-

imated characters.

Some researchers advocated the use of program

visualizations to introduce recursion. For example,

(Dann et al., 2001) experimented with program visu-

alization technique to introduce recursion to students.

They utilized a software system named Alice which

allowed students to gain intuitive sense and mathe-

matical insight into the recursive process. However,

(Edgington, 2007) cited a number of limitations with

the Alice system.

Algorithm animation are also commonly used as

an aid to teaching recursion. The instructor pro-

grams an animation for commonly used algorithms

(e.g. quick sort, factorial). The student runs the pre-

pared animation observing the behavior using differ-

ent inputs. It is suggested that students should be able

to manipulate the animations, not just watch them, in

order to learn (Bower, 1998). It appears that there

is no consensus on the beneﬁts of algorithm anima-

tion as a learning aid. (Stasko et al., 1993) found no

signiﬁcant result suggesting that algorithm animators

assist learning. They suggested that future research

should focus on allowing students to construct their

own animations. On the other hand, a meta-analysis

of 24 experimental studies on the use of algorithm

visualization (AV) as an aid for learning algorithms

was conducted by (Hundhausen et al., 2002). Their

results showed that the effectiveness of AV is deter-

mined by how students use the AV technology rather

than what the AV technology shows them. Other re-

search showed that animation seems to make a chal-

lenging algorithm more accessible, thus leading to en-

hanced learning (Kehoe et al., 2001).

Recursion Graphs (RGraph) is a visual tool used

to aid the introduction of recursion to students (Sa

and Hsin, 2010). RGraph is similar to recursion trees

in that it shows the invocation sequence. However it

adds the detailed calling sequences from one layer to

another including the intermediate results for each re-

cursive call. An RGraph is a directed graph with two

sets of vertices (oval for a recursion call, and square

for post/pre processing statements of recursion calls).

The RGraph is built layer by layer from top to bot-

tom (i.e. breadth-ﬁrst) with directed edges indicating

the processing sequence. One particular feature of an

RGraph is that it is traceable as it shows the detailed

invocation sequence from one layer to another. Re-

sults showed that the use of RGraphs helped improv-

ing student learning of recursion by providing ﬂexi-

bility in demonstration and more focused pedagogical

interactions from students.

On the other hand, conceptual models for teach-

ing recursion are tools that aim at helping students

formulate accurate mental models of the concept of

recursion (G

otschi et al., 2003; Wu et al., 1998). It is

believed that if a person has a mental model of a pro-

cess, s/he will then be able to make predictions about

the behavior of that process, although perhaps inac-

curately sometimes (Kahney, 1983). Moreover, pos-

session of a model will allow a person to debug the

model when s/he is faced with counter-examples.

Early research on teaching recursion embraced

the use of the mathematical induction model (Ford,

1984). In this model students are taught recursion

through the theory of recurrence relations (Wilcocks

and Sanders, 1994). However, a possible limita-

tion with this approach is that novice computer sci-

ence students might not possess the necessary level

of mathematical skills required to develop a clear un-

derstanding of recursion (Ford, 1984; Wilcocks and

Learning Recursion: Insights from the ChiQat Intelligent Tutoring System

337

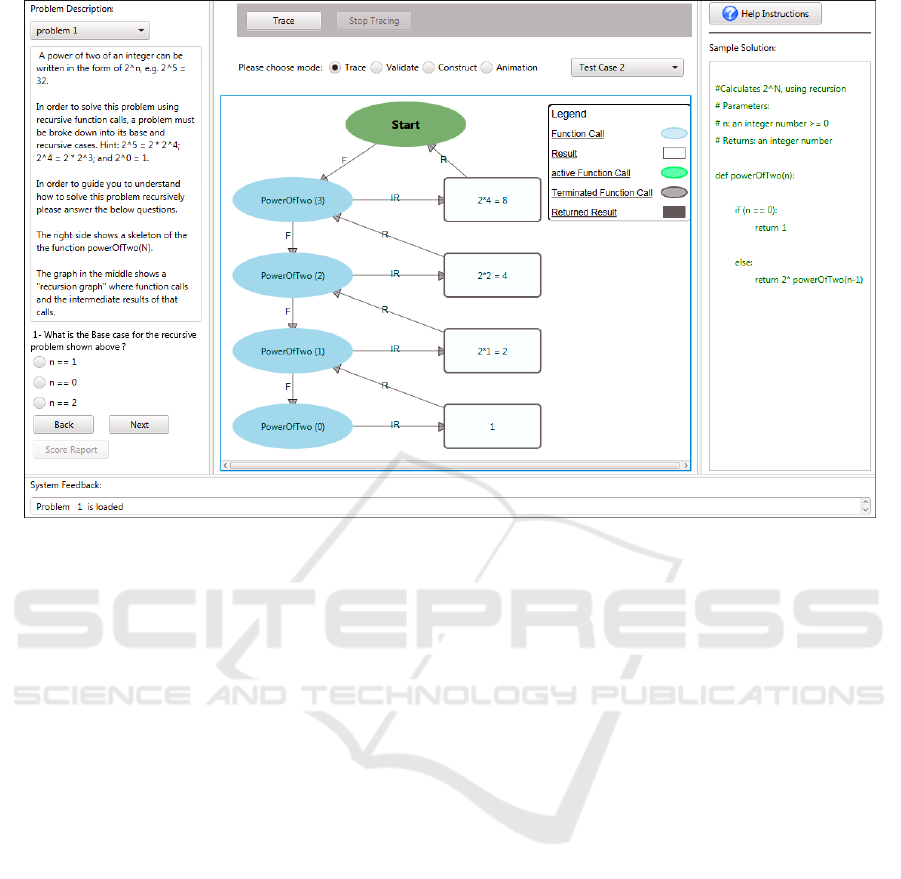
Figure 1: Interface of ChiQat-Tutor Recursion Module. Left: A Problem, Its Explanation, and Questions. Center: Task List

and Recursion Graph. Right: Help Button and Recursive Code. Bottom: System’s Feedback.

Sanders, 1994).

Some researchers believe that more emphasis

should be put on the declarative, abstract level of

problem decomposition rather than on the computa-

tional model and program visualization (Ford, 1984;

Ginat and Shifroni, 1999). A divide-and-conquer

strategy is applied at the problem level, regardless

of the machine implementation. (Ginat and Shifroni,

1999) found that the use of such model signiﬁcantly

enhanced recursive programs formulation ability of

students in comparison to establishing comprehension

via understanding of the process of recursion execu-

tion. On the other hand, (Wu et al., 1998) found that

concrete conceptual model, which provide an appro-

priate level of details of the process of recursion, is

better than abstract conceptual models for teaching

recursion.

A number of mental models of recursion pos-

sessed by both novices and expert programmers in

the context of SOLO programming was identiﬁed

(Kahney, 1983). These include; 1) The Loop model:

novices are hypothesized to possess this model. They

view recursive procedures as a single object instead

of a series of new instantiations. 2) The Odd model:

students acquired the notion that the ﬂow of control

statement, rather than the results of pattern matching,

acts as the stopping condition for recursion. 3) The

Syntactic ”Magic” model: a student is able to match

on syntactic elements and their positions, and make

predictions about the behavior of the recursive pro-

grams on this basis, but has no clear understanding of

how recursion works. 4) The Copies model: students

view recursive instantiations of a recursive procedure

as copies, as opposed to a single object, as in the Loop

model. It is interesting point that novices have the

Loop mental model of recursion. Some research sug-

gested that it is important to teach recursion before

loops not vice versa (Turbak et al., 1999).

The work of (Kahney, 1983) was extended by

(Wilcocks and Sanders, 1994). A number of con-

ceptual models to teaching recursion was evaluated.

These include the mathematical, tree, copies, analo-

gies, and graphical recursive structure models. They

found that the Copies Model is more viable than the

other models. It is believed that this Copies Model is

what expert programmers have of recursion (Kahney,

1983). However, (Kahney, 1983) cautioned that hav-

ing acquired the Copies mental model is not sufﬁcient

to determining what students really know about recur-

sion. Since students can make predictions about re-

cursive procedures behavior without fully understand-

ing recursion.

There has been some previous research on us-

ing structured templates and worked-out examples for

teaching recursion in the context of LISP program-

ming (Pirolli and Anderson, 1985; Hamouda et al.,

2019). It was found that learning is facilitated by

using abstract representations of the structure of re-

CSEDU 2020 - 12th International Conference on Computer Supported Education

338

cursion examples to guide initial coding attempts of

students. The type of information exploited by this

mechanism is an example or demonstration supplied

by some source. However, (Rinderknecht, 2014)

mentioned that although examples can be used to de-

velop analogical problem solving skills, care should

be taken not to rely on them too early. This is in or-

der to prevent students from developing the magic or

syntactic model, identiﬁed by (Kahney, 1983).

3 SYSTEM OVERVIEW

ChiQat-Tutor is a modular tutoring system whose

goal is to facilitate learning of core CS data struc-

tures (e.g., linked lists, trees, stacks) and algorithmic

strategies (e.g., recursion). The interface of ChiQat is

shown in Figure 1. The use of RGraph is extended

in our system by implementing several interactive

tasks; described in Table 1. Students are able to inter-

act with RGraph representation of different recursive

problems (e.g., factorial, palindrome). The RGraph-

based interactive tasks can help students identify the

recursive structure of problems, understand recursive

processes and identify critical features of recursive so-

lutions to these problems. These tasks were designed

with different levels of difﬁculty, which will allow

users to progress from one task to another.

In ChiQat-Tutor we developed an approach to

teaching recursion that is based on the visual model

of RGraph; which is a clever visual representation of

recursive execution. It also uses ideas from the con-

ceptual model of teaching recursion in the form of

code structured templates. We believe that our ap-

proach, mixing ideas from both the conceptual mod-

els and visual aids approaches will help students learn

recursion more effectively. Capitalizing on the advan-

tages of both approaches, and avoiding misconcep-

tions presented by either of them. A similar approach

is followed by RecTutor (Hamouda et al., 2019). It

is found that student performance in learning recur-

sion was enhanced by doing more tracing and writing

exercises practice that addresses common recursion

misconceptions.

Previous research has shown the importance of us-

ing graphical representations, in the form of diagram-

matic traces and animations of recursive problems,

which allowed novice programmers develop correct

mental models of recursion (Wilcocks and Sanders,

1994). The tasks that can be carried on RGraphs in

ChiQat combine characteristics from different con-

ceptual models of teaching recursion. These include

Stack Simulation, the Copies Model, and Tree Model

(Wu et al., 1998). For example, the animation task

represents a stack simulation approach to teaching re-

cursion. Tracing, validating, and constructing RGrahs

tasks can enforce the Copies and tree mental models

of learning recursion. This allows students to look

at recursion solutions from different angles. We be-

lieve that the use of RGraphs coupled with the differ-

ent tasks that students can perform on them can help

students develop the Copies Model that expert pro-

grammers are hypothesized to possess.

Our approach for teaching recursion also embodies

a much widely used strategy of using structure tem-

plates of recursive code and worked-out examples as

an instructional material (Pirolli and Anderson, 1985;

Hamouda et al., 2019). The cognitive processes re-

quired to learn from a solved example are well un-

derstood. The learner must: (a) store in procedural

memory the steps in the example; (b) interpolate the

missing steps, since solved examples are necessarily

incomplete to some extent; (c) infer the purpose of at

least the main steps in the example; and (d) generalize

over the speciﬁcs of the example. Working through

examples is pervasive in instructional situations, and

much appreciated by students. The ChiQat-Tutor will

serve as an effective visualization tool with which hid-

den effects of nested function calls would become ev-

ident when applied to a whole range of problems that

can be solved recursively.

4 DATA AND METHODS

The recursion module was evaluated using multi-

ple experiments conducted at both UIC and CMUQ.

Ethical approvals were obtained from IRB ofﬁces at

CMUQ and UIC prior to the conducting of experi-

ments. Table 1 provides a summary of number of stu-

dents who participated in these experiments. First, a

general description of the experiments is given. Sec-

ond,experiments at both CMUQ and UIC experiments

are discussed separately. Finally, an analysis of the

two groups of students which relate to the correla-

tions between tasks performed with learning gain is

presented.

4.1 Experimental Protocol

All students were asked to complete a consent form.

Then they were asked to complete a pre-test. The

test included problems that involved recursive prob-

lem decomposition, utilizing RGraphs, as tutored in

ChiQat. The consent form and pre-test time was

capped at 10 minutes. Then, they were asked to solve

problems using ChiQat-Tutor, the allotted time was

30 minutes. For each of the problems, all of the

Learning Recursion: Insights from the ChiQat Intelligent Tutoring System

339

Table 1: Task Description.

Task Name Description

Answering questions Students answer multiple choice questions related to the current recursive problem. This task is designed to

test learners’ understanding of the recursive problem and recursion in general.

Animating Learners play a prepared animation and observe the execution order of the recursive code. The node’s color

changes as the animation progresses; green indicates an active function call; gray indicates a terminated call

or an intermediate result, which is explained in a legend next to the RGraph.

Tracing Users click on the nodes of the RGraph and follow the right order of execution. The nodes’ color will

change as users make progress.

Validating Students work on two types of RGraph: an incomplete RGraph, and an RGraph that contains errors. Given

a sample code, students are required to ﬁll the partial RGraph, and then validate their solution. Similarly,

they are required to correct the errors in the ﬂawed RGraph, and then validate their solution.

Constructing Learners build an RGraph for a given recursive code. The ﬁrst few nodes of the RGraph are provided to

them. Students need to validate their solution after ﬁnishing constructing the RGraph.

tasks described in Table 1 were presented. Students

were asked to complete the three recursion problems

Power-of-two, Factorial, and is-Palindrome, but they

were allowed to peruse them in whatever order they

wanted , and no mechanism was used to enforce

completion of any of the problems, or of the activi-

ties. Students were then asked to complete a post-test

(identical to the pre-test) after ﬁnishing working on

the problems. The time allotted for the post-test was

also 10 minutes.

Each question of the pre and post tests was graded

by two graders on a scale from 0 to 5 following a

written guideline. There were two questions per test,

which brings the total of each test to 10 points. Scores

were then rescaled between 0 and 1. Hake’s normal-

ized learning gain (g) was then computed according

to the formula in equation 1. It is deﬁned as the ratio

of the difference in total score to the maximal possi-

ble increase in score (Hake, 1998). We also computed

and used of absolute learning gain as deﬁned in equa-

tion 2.

g =

post − pre

1 − pre

(1)

g = post − pre (2)

4.2 Experiments at CMU Qatar

The students from CMUQ were a mix of Informa-

tion Systems, Biology, and Business majors. They

were exposed to recursion while taking the 15-112

class Fundamentals of Programming and Computer

Science, which is an introductory Python program-

ming course. This class devoted two weeks to recur-

sion, and the experiments were conducted during the

second week, when the students were still being ex-

posed to these concepts. Both CMUQ experiments

took place in two single lab sessions. The differ-

ence between pre-test (µ = 5.27, σ = 1.87) and post-

Table 2: Recursion Experiments - Student Distribution.

Semester & School No. of Students

Fall 14, CMUQ 16

Fall 15, CMUQ 21

Fall 14, UIC 37

Spring 15, UIC 21

Total 95

test (µ = 6.26, σ = 1.79) is signiﬁcant (t = 3.9, d f =

36, p < .001) for the two combined CMUQ students

experiments. However, analyzing the two CMUQ

experiments separately, no signiﬁcant difference be-

tween pre- and post-test for Fall 14 is observed. On

the other hand, there is a signiﬁcant difference be-

tween pre- and post-test for the Fall 15 experiments

(p = 0.004,t = 3.29).

4.3 Experiments at UIC

Recursion is introduced to students at UIC while they

enrolled in the CS151 Mathematical Foundations of

Computing class. The CS151 class is required of CS

and Computer Engineering majors. The CS151 class

devoted four weeks to induction and recursion. In Fall

2014, the experiments took place about two weeks af-

ter the end of the lectures on recursion. But in Spring

2015, they took place about seven weeks later towards

the end of the semester (15 weeks semester).

In Fall 2014, the experiment took place in two

lab sessions during the same day. The difference

between pre-test (µ = 6.74, σ = 2.59) and post-test

(µ = 7.19, σ = 3.01) is only marginally insigniﬁcant

(t = 1.98, d f = 36, p < .055). In Fall 2015, the exper-

iment was conducted in three laboratory sessions, and

no signiﬁcant difference between pre-test and post-

test scores can observed. There is also no signiﬁ-

cant difference between pre-test and post-test scores

for combined populations of both UIC experiments.

CSEDU 2020 - 12th International Conference on Computer Supported Education

340

Table 3: Recursion Experiments Test Scores and Learning Gains.

Semester and school

Pre-test Post-test Absolute Gain Normalized Gain

µ σ µ σ µ σ µ σ

Fall 14, CMUQ 5.43 1.71 6.03 1.33 0.6 1.43 0.09 0.3

Fall 15, CMUQ 5.14 2.01 6.43 2.09 1.29 1.75 0.21 0.41

Fall 14, UIC 6.74 2.59 7.46 1.90 0.72 2.20 0.01 0.54

Spring 15, UIC 7.19 3.01 7.05 2.16 -0.14 2.89 -0.28 1.28

Table 4: Tasks - Derived Variables.

Task Derived Variable Description

Answering Qs

No of Answering Qs Number of questions attempted

Answering Correct Number of correct answers out of all answers given

Animating No of animation Number of Animations attempted

Tracing

No of Tracing Number of tracing tasks attempted

Tracing Correct Number of tracing tasks correctly completed

Node Tracing Correct Number of nodes students clicked in correct order

Node Tracing Errors Number of nodes students clicked in incorrect order

Validating

No of Validating Number of Validating tasks attempted

Validating Correct Number of validating tasks correctly completed

Constructing

No of Constructing Number of Constructing tasks attempted

Constructing Correct Number of constructing tasks correctly completed

Constructing Validation Attempts Number of validation attempts while constructing RGraphs

However, if all students scores from both CMUQ and

UIC are combined, a signiﬁcant difference between

pre- (µ = 6.27, σ = 2.55) and post-test (µ = 6.9, σ =

1.97) can be observed ( p < 0.006, t = 2.79). The next

section will analyze these experiments in terms of the

correlation of activities students performed and their

learning gains.

5 RESULTS AND DISCUSSION

The focus now is on analyzing features of interaction

of students with the ChiQat system. This is in order to

shed light on which tasks are conductive to learning.

For this analysis, few subjects (4 from the UIC Fall

14 group, and 2 from the CMU Fall 15 group) were

excluded. These students took pre- and post-test, and

did use the system, but for some unforeseen reason,

their logs could not be matched. This leaves us with

89 students in total, of which 35 at CMUQ and 54 at

UIC.

The pre-tests of the two groups of students at

CMUQ (µ = 0.52, σ = 0.19) and UIC (µ = 0.68, σ =

0.28) still signiﬁcantly differ (unpaired t-test, p <

0.0023,t = 7.5050, d f = 87); however the two groups

do not differ as gains, or normalized gains are con-

cerned.

We decided to examine the correlation between

the activities the students perform in the system and

learning, to inform future research on which activities

should be emphasized in the system. In this type of

analysis, new variables are added to well-known vari-

ables that often have an effect on learning such as time

(because of the practice effect) and pre-test (previous

knowledge). Indeed, through a simple linear regres-

sion, we ﬁrst analyzed the effect of time on task on

learning (this is the total time students interacted with

the system.

The reason time is explored as a predictive vari-

able is that a signiﬁcant difference is found in time

spent on system between students at CMUQ (µ =

25.30, σ = 4.06) and UIC (µ = 14.26, σ = 6.01) (un-

paired t-test, p < 0.0001, t = 9.1412, d f = 87). Stu-

dents at both CMU and UIC were given 30 minutes

to work on the system, however, the different ex-

perimental settings clearly had an effect. The CMU

experiments took place during formal lectures of 75

minutes long. While the UIC experiments took place

during laboratory sessions which are 50 minutes long,

exactly the length of the whole experiment (10 min-

utes pre-test + 30 minutes system usage + 10 minutes

post-test). The time on system did not correlate with

learning gains, or normalized learning gains. A linear

Learning Recursion: Insights from the ChiQat Intelligent Tutoring System

341

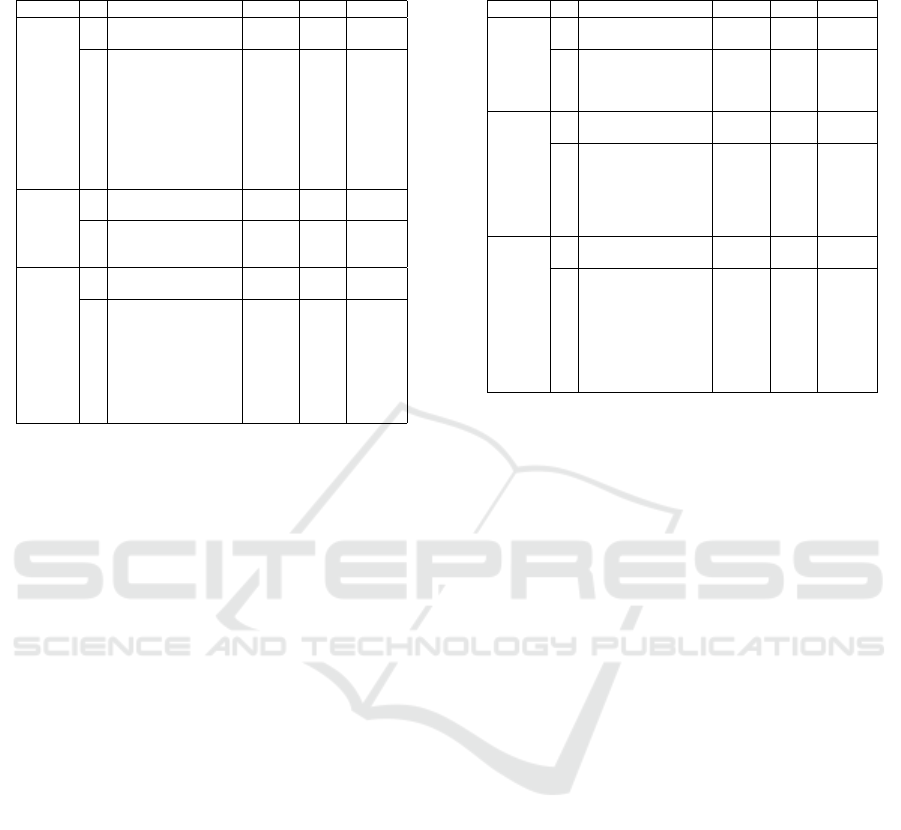
Table 5: Regression Models: Absolute Gain as Dependent

Variable.

Students M Predictor β R

All

Time 0.003

0.421

Pre-test −0.573 < 0.001

Time 0.019

0.421

Pre-test −0.599 < 0.001

Answering questions 0.033 ns

Animations −0.219 0.051

Tracing −0.233 ns

Node Tracing Correct 0.020 ns

Node Tracing Errors 0.056 ns

Validating −0.096 ns

Validating Correct −0.096 ns

CMUQ

Time 0.052

0.212

Pre-test −0.439 0.004

Time 0.055

0.223

Pre-test −0.411 0.004

Answering questions −0.058 ns

UIC

Time 0.043

0.496

Pre-test −0.653 < 0.001

Time 0.049

0.564

Pre-test −0.675 < 0.001

Answering questions 0.154 0.014

Animations −0.218 ns

Tracing −0.083 ns

Node Tracing Errors 0.063 ns

Validating −0.160 0.086

Validating Correct 0.312 ns

regression analysis between time on system and learn-

ing gain/normalized learning gain was not signiﬁcant.

After ascertaining that time was not explanatory,

a systematic multiple linear regressions was run. It

included time, pre-test, and number and type of tasks

attempted by students. The tasks are deﬁned in Ta-

ble 1. We also deﬁne derived variables of the original

tasks which are listed in Table 4. In this regression

analysis, collinear variable with VIF (Variance Inﬂa-

tion Factor) value greater than 5 was excluded.

Tables 5 and 6 report the results of our regression

analyses. We report the smallest signiﬁcant model

(A) which always includes time on task and pre-test.

Then the best signiﬁcant model (B) that includes other

variables, in addition to the pre-test, that are signiﬁ-

cantly correlated with absolute, or normalized, learn-

ing gain. Models B have higher adjusted R

(other

than for absolute gain, for all students in Table 5) and

highlight which speciﬁc tasks are signiﬁcantly corre-

lated with learning. For absolute gains, the alternative

models B are not signiﬁcantly different from the sim-

pler models A, whereas for normalized learning gains,

models B are always signiﬁcantly better than their A

counterparts, for all groups of students (all together,

only CMUQ, only UIC). The two tables 5 and 6 al-

low us to draw some tentative conclusions on which

tasks may be effective for learning. The conclusions

are tentative because they do not generalize across the

two groups of students (CMUQ and UIC) and because

the β coefﬁcients are small.

First, pre-test is always included, as a measure of

previous knowledge. It may be surprising to see that

pre-test is included in the analysis of normalized gain,

Table 6: Regression Models: Normalized Gain as Depen-

dent Variable.

Students M Predictor β R

All

Time 0.007

0.137

Pre-test −0.105 < 0.001

Time 0.010

0.155

Pre-test −0.111 < 0.001

Answering questions 0.022 ns

Animations −0.043 ns

CMUQ

Time 0.023

0.191

0.069

Pre-test −0.075 0.023

Time 0.009

0.269

Pre-test −0.093 0.008

Answering questions −0.007 ns

Animations −0.061 0.046

Tracing −0.026 ns

Node Tracing Correct 0.014 0.033

UIC

Time 0.007

0.103

Pre-test −0.118 0.023

Time −0.014

0.212

Pre-test −0.145 0.002

Answering questions 0.073 0.012

Animations −0.032 ns

Tracing −0.015 ns

Node Tracing Errors 0.027 ns

Validating −0.058 ns

Validating Correct 0.237 0.012

since the deﬁnition itself of normalized gain takes pre-

test into account. However, in this particular case,

pre-test functions as a negative confounder, or sup-

pressor, that hides the (weak) effect of other indepen-

dent variables on learning. As concerns the tasks that

appear in the model we reported, the constructing task

never appears in any of the models. This may be due

to the lengthy nature of the construction task itself.

Students needed more time working on this task, and

consequently small number of students managed to

attempt an complete the task. If we look at all students

together, the only task that trends towards signiﬁcance

is the number of animations; this task is negatively

correlated with absolute gains, but not with normal-

ized gains.

For CMUQ students, no tasks correlate with abso-

lute gains, but as concerns normalized gains, the num-

ber of animations negatively correlates, and the num-

ber of tracing tasks correctly completed positively

correlates with gains. The models for UIC students,

for absolute gains, have the most explanatory power,

with an adjusted R

= 0.564. For this model, an-

swering questions positively correlates with learning

gains; the number of validating tasks exhibits a trend

towards signiﬁcance, but a negative correlation with

gains. For UIC students, for normalized gains, the

model is not as strong, but still answering questions is

positively correlated with gains, and so is the number

of correctly completed validating tasks.

CSEDU 2020 - 12th International Conference on Computer Supported Education

342

6 CONCLUSIONS

We discussed the importance and difﬁculty of teach-

ing recursion to novice computer science students.

Different approaches to teaching recursion were also

discussed, with a focus on conceptual and visual mod-

els. Our approach to teaching recursion in ChiQat-

Tutor was then introduced. Results from our exper-

iments showed that answering questions, animation,

tracing tasks have signiﬁcant correlation with learn-

ing. The validating task has a trend towards signiﬁ-

cant. The constructing task didn’t have a signiﬁcant

effect on learning, and this may due the small number

of students who managed to attempt the task. These

results suggest that interactive visual representation of

recursion algorithms may help students learn. More

work is needed in order to help students develop ac-

curate mental models of recursion. Future work will

be focused on adding structured templates for writing

code, scripting capabilities, intelligent feedback, and

student modeling.

ACKNOWLEDGEMENTS

This work is supported by award NPRP 5–939–1–155

from the Qatar National Research Fund, and is partly

supported by a UIC University Scholar award to Di

Eugenio.

REFERENCES

Bower, R. W. (1998). An investigation of a manipulative

simulation in the learning of recursive programming.

Dann, W., Cooper, S., and Pausch, R. (2001). Using visual-

ization to teach novices recursion. In Proceedings of

the 6th annual conference on Innovation and technol-

ogy in computer science education, pages 109–112.

Edgington, J. (2007). Teaching and viewing recursion as

delegation. J. Comput. Sci. Coll., 23(1):241–246.

Ford, G. (1984). An implementation-independent ap-

proach to teaching recursion. ACM SIGCSE Bulletin,

16(1):213–216.

Ginat, D. and Shifroni, E. (1999). Teaching recursion in

a procedural environment—how much should

we emphasize the computing model? SIGCSE Bull.,

31(1):127–131.

otschi, T., Sanders, I., and Galpin, V. (2003). Mental mod-

els of recursion. SIGCSE Bull., 35(1):346–350.

Hake, R. R. (1998). Interactive-engagement versus tra-

ditional methods: A six-thousand-student survey of

mechanics test data for introductory physics courses.

American journal of Physics, 66(1):64–74.

Hamouda, S., Edwards, S. H., Elmongui, H. G., Ernst, J. V.,

and Shaffer, C. A. (2019). Recurtutor: an interactive

tutorial for learning recursion. ACM Transactions on

Computing Education (TOCE), 19(1):1.

Hundhausen, C. D., Douglas, S. A., and Stasko, J. T.

(2002). A meta-study of algorithm visualization effec-

tiveness. Journal of Visual Languages & Computing,

13(3):259–290.

Kahney, H. (1983). What do novice programmers know

about recursion. In Proceedings of the SIGCHI Con-

ference on Human Factors in Computing Systems,

CHI ’83, pages 235–239, New York, NY, USA. ACM.

Kehoe, C., Stasko, J., and Taylor, A. (2001). Rethink-

ing the evaluation of algorithm animations as learning

aids: an observational study. International Journal of

Human-Computer Studies, 54(2):265–284.

McCauley, R., Grissom, S., Fitzgerald, S., and Murphy,

L. (2015). Teaching and learning recursive program-

ming: a review of the research literature. Computer

Science Education, 25(1):37–66.

Pirolli, P. L. and Anderson, J. R. (1985). The role of

learning from examples in the acquisition of recursive

programming skills. Canadian Journal of Psychol-

ogy/Revue canadienne de psychologie, 39(2):240.

Rinderknecht, C. (2014). A survey on teaching and learn-

ing recursive programming. Informatics in Education,

13(1):87–119.

Sa, L. and Hsin, W.-J. (2010). Traceable recursion with

graphical illustration for novice programmers. In-

Sight: A Journal of Scholarly Teaching, 5:54–62.

Stasko, J., Badre, A., and Lewis, C. (1993). Do algorithm

animations assist learning?: An empirical study and

analysis. In Proceedings of the INTERACT ’93 and

CHI ’93 Conference on Human Factors in Computing

Systems, CHI ’93, pages 61–66, New York, NY, USA.

ACM.

Tessler, J., Beth, B., and Lin, C. (2013). Using cargo-bot to

provide contextualized learning of recursion. In Pro-

ceedings of the Ninth Annual International ACM Con-

ference on International Computing Education Re-

search, ICER ’13, pages 161–168, New York, NY,

USA. ACM.

Turbak, F., Royden, C., Stephan, J., and Herbst, J. (1999).

Teaching recursion before loops in cs1. Journal of

Computing in Small Colleges, 14(4):86–101.

Wilcocks, D. and Sanders, I. (1994). Animating recur-

sion as an aid to instruction. Computers & Education,

23(3):221 – 226.

Wu, C.-C., Dale, N. B., and Bethel, L. J. (1998). Concep-

tual models and cognitive learning styles in teaching

recursion. SIGCSE Bull., 30(1):292–296.

Learning Recursion: Insights from the ChiQat Intelligent Tutoring System

343