Intelligent Regulation System to Optimize the Service Performance of

the Public Transport

Nabil Morri

1,3 a

, Sameh Hadouaj

2,3 b

and Lamjed Ben Said

IT Department, Emirates College of Technology, Abu Dhabi, U.A.E.

Computer Information Systems Department, Higher Colleges of Technology, U.A.E.

SMART Lab., Institut Supérieur de Gestion de Tunis, Université de Tunis, Tunisia

Keywords: Multi-agent Systems, Public Transportation, Regulation System, Optimization, Key Performance Indicators.

Abstract: The urban public transport systems deal with dynamic environments and evolve over time. Frequently, we

dispose of a lot of correlated information that is not well exploited to improve the public transport quality

service, especially in perturbation cases where a regulation system should be used in order to maintain the

public transport scheduled time table. The quality service should be measured in terms of public transport key

performance indicator (KPI) for the wider urban transport system and issues like regularity, punctuality and

correspondence criteria. In fact, in the absence of a set of widely accepted performance measures and

transferable methodologies, it is very difficult for public transport to objectively assess the effects of specific

regulation system and to make use of lessons learned from other public transport systems. Unfortunately,

most of the existing traffic regulation systems do not take into consideration part or most of the performance

criteria when they propose a regulation maneuver. Therefore, the applicability of these models is restricted

only to specific contexts. This paper sets the context of performance measurement in the field of public traffic

management and presents the regulation support system of public transportation (RSSPT). The aim of this

regulation support system is (i) to detect the traffic perturbation by distinguishing the non-equability of

scheduled and the current time table of vehicle passage at the station (ii) and to find the regulation action by

optimizing the performance of the service quality of the public transportation. We adopt a multi-agent

approach to model the system. The validation of our model is done by simulating two scenarios on Abu Dhabi

transport system and shows the efficiency of our system when we want to use many performance indicators

to regulate a disturbance situation.

1 INTRODUCTION

The study of public transportation systems has

changed significantly during recent years in modeling

and simulation. In particular, the increasing use of the

vehicle and the amplification of the public transport

system, make traffic management more complex.

This complexity is due to the difficulty of respecting

the scheduled timetable of vehicle passage and the

emergence of random phenomena that disturbs the

network traffic of vehicle. Thus, to improve the

quality service of public transport, we have to design

and build a regulation support system that detects

disturbances and regulates the traffic of public

https://orcid.org/0000-0002-1642-9309

https://orcid.org/0000-0002-6743-4036

https://orcid.org/0000-0001-9225-884X

transport. The quality service should be measured in

terms of public transport key performance indicators

(KPIs).

Against this perspective, modeling and simulating

such systems show real problems because there is no

clear knowledge of the notion of KPIs and no

common framework standard of quality in public

transport.

Moreover, the current methods and simulation

tools don’t combine various KPI measures into a

single performance value, potentially covering

multiple dimensions or goal categories. Nowadays,

several types of research have been carried out in the

field of the regulation of public transport; (Newell

416

Morri, N., Hadouaj, S. and Ben Said, L.

Intelligent Regulation System to Optimize the Service Performance of the Public Transport.

DOI: 10.5220/0009416104160427

In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 416-427

ISBN: 978-989-758-423-7

 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

and Potts, 1964) studied for the first time the

management of bus disturbances. On the basis of a

simplified model, the authors proved the instability of

a line by the approximation of the buses without

studying the coordination between the vehicles of

different lines.

The regulation strategies are usually based on

scheduling control and try to reduce the number of

buses by adjusting bus schedules. This is based on an

analysis of the cause of the disturbance (Moreira-

Matias et al., 2012) (Verbich et al., 2016), as well as

its impact on calendar-based traffic (Newell, 1977)

(Zhao et al., 2006) (Feng and Figliozzi, 2011)

investigated the main causes of the disturbance and

recommended switching from static regulation based

on a scheduled time table (TMT) to a dynamic

regulation based on the frequency of buses of the

same line. An important problem of this approach is

to find a compromise between the regularity and the

optimal frequency of the service.

The regulation strategies have become more

interesting with the availability of real-time data

provided, such as the Automatic Vehicle Locator

(AVL) systems. Previous to this, most control

methods used decision models that included only bus

arrival times at stops. The works of regulation

systems made in real-time differ in the techniques and

data used. The regulations of this strategy can be

divided into two categories: regulation at stations and

inter-station regulation.

In the first category, the action is carried out at the

station as waiting at a station to regulate only

punctuality. Other criteria like regularity or taking

account of the transfer time in changing the line for

the passenger are neglected. For example, the

research by (Gershenson and Pineda, 2009) is based

on the static exploitation of time and minimum and

maximum waiting time and (Newell, 1974)

(Zolfaghari et al., 2004) (Bartholdi and Eisenstein,

2012) which are based on the dynamic exploitation of

boarding times and the limitation of downtime

(Dwell: time spent by the vehicle at station). Dynamic

strategies are advantageous over static strategies. We

found that dynamic strategies may require up to 40%

less downtime in the schedule (Xuan et al., 2011),

which increases the scheduled commercial speed of

the trip based on AVL data in real-time.

However, in the second category, the control is

done on the links between stations, like the control of

the speed of bus (Pilachowski, 2009) (Daganzo and

Pilachowski, 2011) (He, 2015), the overtaking of

buses or priority mechanisms for traffic signals for

public transit (Albright and Figliozzi, 2012) (Bhouri

et al., 2011). These approaches do not take into

account the real cause of the disturbance.

Based on the above analysis we can conclude that

most of the existing traffic regulation systems do not

take into consideration part or most of the

performance criteria when they propose a regulation

maneuver. Therefore, the applicability of these

models is restricted only to specific contexts.

This paper sets the context of performance

measurement in the field of public traffic

management and presents the regulation support

system of public transportation (RSSPT). The aim of

this regulation support system is to detect the traffic

perturbation by verifying the adequacy between the

planned and the current performance measures and

find the most appropriate regulation action by

optimizing the performance of the service quality of

the public transportation. We adopt a multi-agent

approach to model the system.

This paper is organized as follows. Section 2

introduces and discusses the state of the art of

performance measures. Section 3 describes our

regulation process and the Multi-Agents System

design. Section 4 defines the optimization problem.

Section 5 validates our model by providing

experimentation and result of two reels scenarios

happened in Abu Dhabi transport system. In section 6

we conclude and give some perspectives.

2 STATE OF THE ART OF

PERFORMANCE MEASURES

2.1 Literature Review

The performance of the public transport service is

considered one of the main issues influencing the

level of passengers’ satisfaction. There is abundant

literature on various aspects of key performance

indicators. This review describes selected papers that

focus on the models of passengers’ waiting time at the

station and the suggested regulation strategies for

improving the performance service. Several

publications offer quantitative measures of

performance in regard to the public transportation

service.

(Mark Trompet et al. 2011) evaluates the

performance by the excess waiting time (EWT:

Excess wait time). This indicator is defined as the

difference between the actual waiting time (AWT)

and the scheduled waiting time (SWT). Moreover, in

(M. Napiah et al., 2015) and (Mark Trompet, 2010),

this performance is defined by the average waiting

Intelligent Regulation System to Optimize the Service Performance of the Public Transport

417

time expected by passengers. This indicator

calculates the perceived regularity that measures the

average additional waiting time of passengers. In fact,

the low EWT means that the performance of the

service is fairly regular.

(Oded Cats et al., 2010) defines the performance

by the deviations of the time intervals observed

between the trips of the same line with respect to the

regular frequency of the vehicles during a given

period. This indicator is calculated as a standard

deviation between the observed frequency and the

programmed frequency. In addition, in other specific

projects, to give more meaning to the evolution of the

performance during abrupt changes in the transport

traffic state, (M. Napiah et al., 2015), (Mark Trompet,

2010) and (Oded Cats et al., 2010) provide another

complementary definition for performance. This

performance is defined as a percentage of deviations

that no longer deviate from a quantity in absolute

minutes. It represents the coefficient of variation.

(Neila Bhouri et al., 2016) and (Gay H. et al.,

1991) describe the Gini index as another indicator by

regularity index. Economists and sociologists use the

Gini ratio to measure the degree of income inequality

within groups of people. By analogy in the field of

public transport, the authors measure by this ration

the degree of inequality of performance within a

group of trips of the same line to quickly detect the

abnormal phenomena that disturb the traffic. (S.

Carosi a, et al., 2015) describes regularity as an index

based on vehicle entries at stations. This indicator is

specific to a line. Its formula is expressed as a

percentage of unpunctual vehicle entries in relation to

the total number of planned entries at the stations.

Other projects define the punctuality as another

indicator that determines the performance.

(Noorfakhriah Y. and Madzlan N., 2011) defines the

punctuality as a comparison of the actual departure

times and scheduled departure times at the station. In

(Xumei Chen et al., 2009) the authors distinguish

three types of punctuality measures: the Punctuality

Index based on Routes (PIR), the Deviation Index

based on Stops (DIS) and the Evenness Index based

on Stops (EIS). The PIR is defined as the probability

that a bus will arrive at the terminals during a given

period. The DIS is the ability to maintain distances

and minimize the typical waiting time of a passenger

at the stop, while the EIS is the ability to determine

the consistency and balance of the distance between

the vehicles. However, in (Vaniyapurackal, 2015),

the author considers the punctuality index for a race,

P = 0 if the bus arrives on time in all the stations of its

trip and P = 1 if the bus does not arrive on time at all

stations. For convenience, the punctuality index, P

can be converted to percent for as in P (%) = (1 - P) ×

100 to define the proportion of the trip that was

punctual.

In (Saberi, Meead, et al., 2013), three alternative

performance measures are proposed: Earliness Index

(EI), Width Index (WI), and Second-Order Stochastic

Dominance Index (SSD). These indices are used in

two forms to capture the characteristics of the

unreliability of bus service: (i) the distribution of the

time interval deviations of trips for frequent services,

(ii) the distribution of delays for non-frequent

services.

(Ceder, 2007) adds the transfer time as another

indicator. This indicator covers the time spent when

the passenger is waiting for the vehicle in changing

the line at a connecting station. Other authors add the

running time (time needed to change stop by walking

in the transfer station) in the calculation of the transfer

time.

(Zhenliang, 2013) details and explains the

formula of the Headway Buffer Time. This indicator

indicates the additional travel time required to allow

passengers to arrive on time. It can be used to capture

the additional unreliability caused by an incident.

The authors of (Kenneth et al., 2004) (TRT, 2017)

and (Levinson, Herbert, 1983) examine another

indicator called "Dwell" which is the bus downtime

at stations including terminuses. This indicator refers

to the time a vehicle, such as a bus or a train, goes to

a stop without moving. In general, this time is spent

onboarding or on embarking passengers, but it can

also be used to wait for traffic to be restored (Vu The

Tran et al., 2012) (Cats et al., 2011). For example

when the regulator wants to coordinate between trips

in the transfer station or to be equal as possible to the

scheduled time table.

2.2 Discussion

According to the literature review presented above,

there is no standard significance of the key

performance indicators. The challenge in defining

KPIs is to select the right ones that will give a

sufficient accepting of overall performance on public

transportation. To define KPIs, four strategic themes

in the urban traffic management and the Intelligence

Transportation System (traffic efficiency, traffic

safety, pollution reduction, and social inclusion and

land use) are presented in the white papers by the

European Commission’s strategy on the future of

transport (European Commission, 2011). Also, these

indicators are classified according to objectives in

(Theuns Henning et al, 2011). For benchmarking

purposes, a number of KPIs must be chosen to cover

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

418

the most critical aspects of public transport from a

user's point of view. In the context of this study, we

tackle only KPIs of traffic efficiency. The index of

traffic efficiency represents three major KPIs: (i)

punctuality for the respecting theoretical schedules at

stations, (ii) the regularity for the respecting of the

scheduled headway, and (iii) the correspondence for

the respecting of the scheduled transfer time of the

passengers in the transfer station. Consequently, we

standardize all performance criteria presented in the

literature into three main KPIs: punctuality,

regularity, and correspondence. We describe the

formulas of these performances in section 4.

Moreover, goals and objectives should be clear,

concise, and achievable, in order to model the good

performance formula for the regulation process.

Indeed, the performance of public transport is an

abstract term. In order to include performance

considerations in a detailed engineering public

transportation design and to evaluate the differences

between existing and suggested service alternatives,

it is necessary to describe it in mathematical terms. In

fact, with a mathematical function, we can apply an

optimization approach to the performance formula to

reach the target. In addition, the main drawback of

possible real-time performance regulation actions is

the lack of prudent modeling and software that can

activate automatically or semi-automatically these

actions. Hence, build a regulation system to optimize

the service performance based on key performance

indicators in case of perturbation becomes an absolute

necessity.

3 THE REGULATION SYSTEM

OF PUBLIC TRANSPORT

3.1 Regulation Process

The below figure 1 describes the regulation process

of our system.

Figure 1: Regulation process in our RSSPT.

This process involves five steps:

 Operations supervision: In this step, races are

monitored to see if everything is going as

planned. The same thing happens for boarding

passengers. the surveillance is done on route

and at station after gartering information from

(i) the Automatic vehicle location Module

(AVLM) that is the GPS vehicle tracking

system that continuously records and

automatically transmits the geographic location

and the speed of a vehicle, and (ii) detectors or

loops to provide the properties of roads (length,

speed max, density max, and current density)

and station (passenger embarking and

passenger boarding flow).

 Disturbance identification and evaluation: If an

event occurs, for example, if an accident or

works take place on a road, a rapid assessment

is performed to determine if a regulation action

is required. Otherwise, monitoring continues.

The detection is based on the impact of the

performance variability of the KPIs.

 Evaluation of possible regulation actions: the

system selects the possible regulation actions

from the existing list by using a classification

method. This list is defined and updated by

experts. An example of this list can be found in

(Froloff et al., 1989).

 Decision making: After filtering out possible

solutions, a decision must be made by using an

optimization resolution then, the system

chooses the adequate action.

 Implementation of Decision: After choosing

the decision, it must be applied to the

environment with the update of the operational

plan.

3.2 Multi-agent Design

3.2.1 Multi Agents System for Regulation

Support System Modeling

Multi-agent modeling can give a suitable solution to

public transport network activities where autonomous

entities, called agents, interact with each other in a

distributed, open, heterogeneous and dynamic

environment. We note that multi-agent systems are

increasingly present in the field of traffic regulation.

The following is a short description of the main

characteristics for public transport regulation system:

 Distributed: the information is geographically

dispersed over the network requires distributed

agents.

Deviation

Yes

More actions

Operations

supervision

Disturbance

identification and

evaluation

Conflict?

Evaluation of

possible

regulation

Decision

making

Implementation

of Decision

Intelligent Regulation System to Optimize the Service Performance of the Public Transport

419

 Dynamic: there is a daily change of

information, for example, a vehicle can move

forward, slow down, accelerate and

communicate its passage with other agents like

stations. As well, when the operator detects

perturbation, a new state should be introduced

in the traffic network and derive the bus to

another route as regulation action.

 Open: the vehicles can enter or exit the traffic

network.

 Heterogeneous: The actors of the system are

varied with different natures: vehicle, station,

regulator, etc.

These entities can reason, communicate via

messages to solve conflicts and reach the best

solution. These characteristics demonstrate that the

use of the multi-agents system in regulation support

system modeling has the advantages of introducing

more flexible and efficient representation in the

processes that it models.

3.2.2 Knowledge Components Modeling

The proposed system provides a baseline modeling to

the system knowledge components independently of

the performance model. In order to construct the

system as a whole, we explore separately each agent

with its both interactions “agent-agent” and “agent-

environment”; this will also make it easier to define

the system’s elements. The proposed multi-agent

model is composed of the following agents: vehicle,

link, station, criteria, and regulator. We describe the

behavior and the interactions of each agent in the

following figure (figure 2).

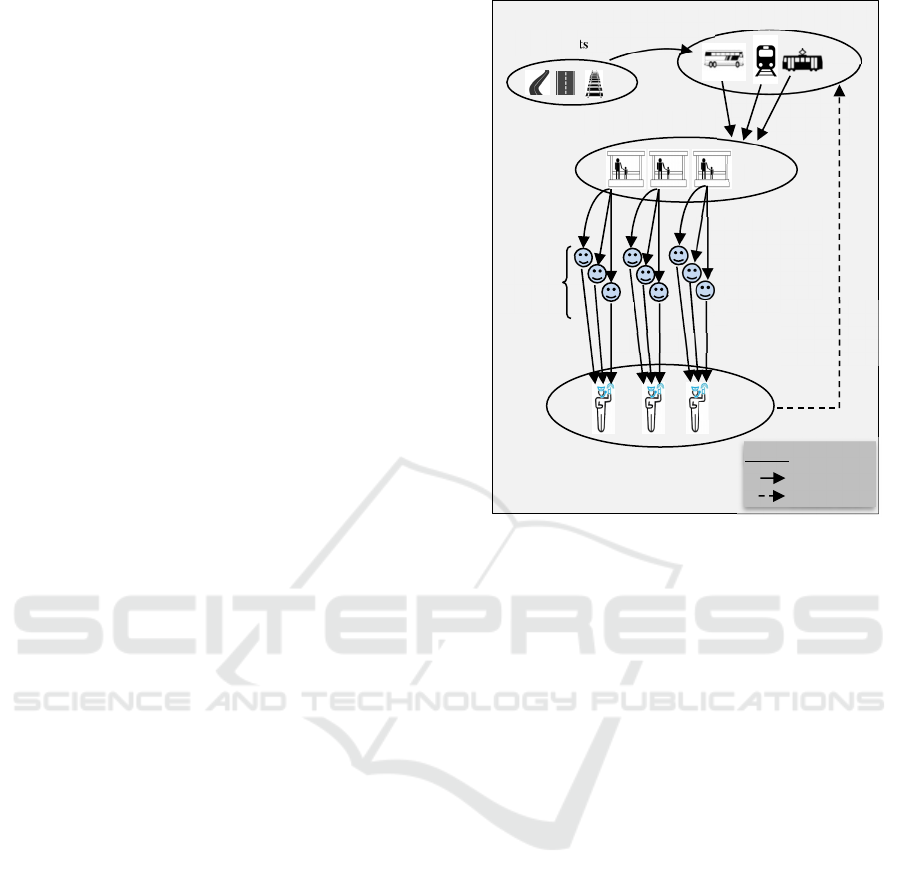
The agents are described as follows:

 Vehicle: Vehicle agent memorizes all its

properties such as position, type (bus, metro,

and tramway), speed, capacity, number of

passengers, line, mission (school bus, special,

and passenger), driver, and the properties of the

current link. Then, these data are sent to the

concerned agents: Station.

 Station: It represents a departure or arrival of

one or more links. It must memorize all

scheduled and real passage hours of vehicle. It

calculates the delayed time for the arrived

vehicle. Then it creates the necessaries KPI

agents for each coming vehicle and sends to

them the calculated delayed time and the

waiting passenger number to calculate the key

performance criteria value.

Figure 2: Multi-agent architecture of RSSPT.

 Link: It represents the connection between two

consecutive stations. It should be related at

least to one line. It memorizes two types of

information: static properties (length, speed

max, and density max) and dynamic properties

(average of vehicle speeds and current density).

These data are sent to the Station agent to

estimate the needed time of the delayed vehicle

to reach the station.

 KPI: It calculates the value of the Key

Performance Indicator and sends it to the

regulator agent.

 Regulator: Each "regulator" agent is

responsible for a geographical area of the

network. It receives the KPI values of each

disturbed vehicle. Then it defines the

perturbation cause (vehicle breakdown, exceed

parking time, driver uneasiness, an accident on

the road, etc.) and follows an optimization

process to find the regulation action. The

optimization process is explained in section 5.

A unique characteristic of this model is that the

same agents are used to ensure the detection and the

regulation process. This makes the model simpler and

solves the problem of data duplication. The KPIs used

in the regulation process can be adjusted according to

the needs of the optimization problem.

Vehicle Agents

Station Agents

Vehicle and link

properties

Delays, scheduled

Time table,

Waiting time

KPI

Agents

Link Agents

Static & dynamic

properties

Regulation

action

Legend

Data flow

Control flow

Criteria

Regulator Agents

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

420

4 OPTIMIZATION RESOLUTION

4.1 Linear Programming Optimization

This section introduces the notion of optimization,

using operations research (OR) principles and

methods. Optimization usually means finding the best

solution to some problem from a set of alternatives

respecting constraints. Formally, an optimization

problem can be described by a set U of potential

solutions, a set L



U of feasible solutions, and an

objective function F: L → IR. In the regulation

problem, we are looking for regulation maneuver x

∗

∈

L that minimizes the value of the objective function

F overall feasible solutions. There is a list of feasible

regulation actions that can be used to handle public

transport traffic. This list should respect the

constraints of the optimization problem.

In an existing problem, F is arbitrary and the

question is whether the set of feasible solutions is

nonempty. The optimization should take into account

all KPIs and constraints fixed by experts of the traffic.

We present a method that can be applied to regulate

different traffic perturbations. This method is inspired

by the work of

(Hartani, 1995)

In the RSSPT, a linear program with n criteria

(KPIs) and m constraints is a minimization problem

defined on a vector x=(x

,...,x

) of real-valued KPIs.

The objective function is a linear function F of x, i.e.

F : IR

→ IR with F(x)=c*x, (1)

Where c = ( c1,..., cn ) is called cost vector. It is

relative to the importance of different KPIs. E.g.

punctuality criteria for buses of low-frequency lines

(large headways) is more important than regularity

while regularity for buses of high-frequency lines

(large headways) is more important than punctuality,

against keeping good transfer time criteria is more

interesting for lines presented transfer stations with a

high passengers’ crowding. The variables are

constrained by m linear constraints of the form:

⋈

, Where

⋈

∈

{≤,≥,=}, a

= (a

,...,a

)

∈

, and b

∈

or i

∈

1..m.

(2)

Consequently, the vector of criteria values of the

feasible solutions is given by:

L={x

∈

∀

∈

1..m and j

∈

1..n: x

≥

∧

⋈

}

(3)

4.2 Optimization Formulas

4.2.1 Formulation of the Optimization

Function

We establish the three KPIs related to traffic

efficiency: punctuality, regularity, and

correspondence for the delayed vehicle.

They are

based on

passengers’ waiting time at the station.

These measures are applicable essentially when it is

assumed that passengers go to the station without

expectations of boarding a particular vehicle at a

particular time (i. e., those passenger arrivals are

Poisson distributed) We formulate the objective

function as follows:

𝐹𝑊



.𝑉



𝑊



.𝑉



𝑊



.𝑉





(4)

Here, the W



, W



and W



represent the

weight (cost) of the criteria in the calculation of the

performance value. It is necessary that: W







 W



1. To calculate the weights, an

experimental method is suggested capable of

achieving a twofold objective: (i) to provide a

methodology for constructing a measure of

performance that can be adapted to any plan or

transport program, and (ii) providing a methodology

that can be transferred between projects. The

technique chosen by the experts is the Delphi method

(Linstone HA and Turrof M, 1975) .

Punctuality criteria: Punctuality is defined in

(Noorfakhriah Y. and Madzlan N., 2011) as a

comparison of actual departure times with expected

departure times at the station. Its formula is:

𝑉

















with

𝑆







𝑛

∑

𝑡

𝑖

𝑡

𝑡



𝑛

𝑖1

(5)

 n: the number of vehicles of the same line

arriving at the station in a defined period.

 h







∑

t



t









the average headway for

n vehicles.

 t



: the actual arrival time of the i-th vehicle.

 t



: the scheduled arrival time of the i-th vehicle.

Regularity criteria: It measures the differences in the

time intervals observed between successive vehicles

of the same line with respect to the scheduled

headway. Its formula is:

𝑉

















with

𝑆











∑

ℎ



ℎ











(6)

 n: the number of vehicles of the same line

arriving at the station in a defined period.

 h

: t

– t

i-1

(i=2,…I), the current headway of the

i-th vehicle.

 h



: the scheduled headway of the i-th vehicle.

Intelligent Regulation System to Optimize the Service Performance of the Public Transport

421

Correspondence criteria: The correspondence

criterion signifies the differences between the

observed correspondence values with those of the

scheduled correspondence. His formula is as follows:

𝑉















wit

𝑆











∑

𝑐



𝑐











(7)

 n: the number of vehicles of the same line

arriving at the station in a defined period.

 c



: the current correspondence of the i-th

vehicle.

 c



: the scheduled correspondence of the i-th

vehicle.

 𝑐̅ : the average of the correspondence for the n

vehicles.

The current correspondence value 'c

' (or the

scheduled 'c

') of the i-th vehicle is the sum of the

waiting time between the vehicle 'i' and all coming

vehicles to the transfer station. It is equal to:

𝐶





𝑓















(8)

𝑓



determines the importance factor of the vehicle

'j' which is in connection with the vehicle 'i'. This

factor is calculated by experts according to the

passengers waiting time of in the connection station

for the vehicle in connection "j"[19]. It is necessary

that:



𝑓



||



1

(9)

And





represents the gap time in relation to the

scheduled waiting time of i-th connecting vehicle. It

is equal to:





𝑡



𝑡



(10)

𝑡



is the current arrival time for the vehicle 'i',

while 𝑡



is the current departure time for the vehicle

in connection 'j'.

4.2.2 Formulation of the Constraints

The following constraints, based on (Ceder, 2007),

are accompanied by the following data notations and

assumptions.

 H





: minimum headway in the i station.

 H





: maximum headway in station i.

 t



: t



t



time between the departure time t



of station j and the departure time t



of station

i. i and j represent respectively the two

successive stations of the link l



 T



: estimated total travel time i.

 T



: scheduled total travel time i.

 N



: number of performed trips in station i.

 V





: punctuality value in station i.

 V





: permitted punctuality max value in

station i.

 V





: regularity value in station i.

 V





: permitted regularity max value in

station i.

The problem is feasible under the following

constraints:





I





(11)





minI











(12)



N







(13)









1







(14)



T



with T



 T





n∗







(15)

These constraints are mandatory in order to verify

the following:

 not to exceed the maximum regularity value

permissible limit (equation 11).

 the next trip does not catch up with the

regulated trip (equation 12).

 the departure time at each station i does not

exceed the maximum hour allowed during a

regulation (equation 13).

 respect the minimum regularity between the

vehicles of the same line (equation 14).

 not to exceed the maximum time allowed for a

given trip (equation 15).

As a hypothesis, it is assumed that the first

departure for each trip must take place in the interval

[0, 𝐼





] in order to have not a conjunction of two

consecutive trips in the starting station.

4.3 Regulation Algorithm

The regulation process begins after the detection of

perturbation. In the following algorithm, pre-

conditions are defined which correspond to the

optimization constraints:

Algorithm 1: Regulation.

Iutput:

- Actual status of traffic network,

scheduled and real timetable of

public transport.

Output:

- Regulation action

begin

repeat

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

422

- Station Agent receives the

necessaries information from Vehicle

and link Agents

- Station Agent calculates the waiting

time of each coming vehicle

- Each KPI Agent receives the waiting

time of its corresponding vehicle

- Each KPI Agent calculates its

criteria value

- Each Regulator Agent receives all

criteria value of the corresponding

vehicle

- Each Regulator Agent calculates the

performance function “UF” of the

corresponding vehicle

until “F” falls down in the critical

area

- The Regulator Agent fixes the type

of vehicle with their properties

- The Regulator Agent fixes the

incident /*vehicle breakdown,

congestion, driver malaise*/.

- Optimization Module

end

We describe the optimization module in the

following algorithm:

Algorithm 2: Optimization module.

Iutput:

- Vehicle with their properties and

incident

Output:

- Regulation action

begin

switch (Type of vehicle and Incident)

case

- The Regulator Agent checks its

Knowledge Base /* familiar

perturbation, expressed by Basic

facts and Basic rules. */

if (incident exists) then

 The Regulator Agent extracts

the list of feasible regulation

actions // use decision tree

 The Regulator Agent calculates

the objective function “F” of

each regulation action

 The Regulator Agent chooses the

optimal regulation maneuver.

else // new situation

 the Regulator Agent produces a

new regulation action using its

expertise

 the Regulator Agent updates his

knowledge base.

end

5 TESTING AND RESULT

5.1 Description

To validate the regulation strategy of our system, we

tested our model on a real traffic network of Abu

Dhabi. The resolution is expressed by an optimization

problem with the objective function F using linear

programming presented below. We used AnyLogic to

simulate traffic scenarios and estimate measures

needed to calculate The KPIs values. AnyLogic is a

program for computer-aided transport planning,

which determines the impacts of existing or planned

supply that can encompass public transportation by

simulating traffic scenarios

(https://www.anylogic.com/). In addition, AnyLogic

combines a dynamic simulation engine for animation

and analytical tools for optimization. By combining

these techniques, it provides models, which allow

both to visualize the animation of the model and its

logical analysis.

The scheduled data are collected from the

department of transport of Abu Dhabi, as well as the

map and the observed data are collected from the

OpenStreetMap as OSM files to model the public

transportation map data like lines, links, stations, and

vehicles.

As described above, the regulation process will be

activated only when F value falls down into a critical

zone. The critical zone is defined by experts of public

transport according to the treated zone of the network

traffic. To prove the efficiency of our system in

different situations, we tested results on two scenarios

of perturbation.

Figure 3: Traffic Network

zone of scenario 1.

Figure 4: Traffic Networ

zone of scenario 2.

The first scenario presents perturbation detected

in a station without correspondence (no transfer

station) and the second one presents perturbation

detected in a transfer station. We describe the two

scenarios in the sections below:

Intelligent Regulation System to Optimize the Service Performance of the Public Transport

423

5.2 Scenario 1

Scenario 1 presents traffic congestion in Al Falah

Street due to a school entrance: peak hour (see figure

3). The station represents stop for three lines 008, 009

and 010 that have the same next station in the two

directions. This means that there is no transfer time to

calculate the correspondence KPI. Consequently,

𝑊



0 . In addition, the distribution of criteria

weight gives more importance to the punctuality

criteria. It is due to the existence of many schools in

this area and there is a large main headway (20 min).

After calculating the objective function F of the

coming bus for each line, the regulator detects, at

different times, perturbation for each line 008, 009

and 010 (see table 1).

The system starts its optimization phase by using

the initial objective function value F

start

(see table 2).

Each regulator for each coming bus wants to find the

optimal regulation action with F

opt

value. For each

bus, the list of the feasible regulation actions was

extracted and simulated to let each regulator estimate

the objective function of each feasible regulation

action of each coming bus.

Table 1: Buses Information at Al Bateen Station.

Line

Frequency

Theoretical

time at

Station

Detecting

perturbation

time



REG

PUN

COR

08 20 07h: 33 a

07h: 38 a

8 0.25 0.75 0

09 20 07h: 37 a

07h: 42 a

10 0.25 0.75 0

10 20 07h: 37 a

07h: 42 a

10 0.25 0.75 0

After optimization, the regulator chooses the

derive maneuver for the three later buses of the three

lines, and accelerates after departure from the station

to reduce the delays and improve the travel time of

the busses (see table 2).

Table 2: Result Values in Regulation Process of Scenario 1.

Line

Detect.

Opt.

Detect.

Opt.

Detect.

Opt.

before

start

opt

08 25 33 5 13 7 7 4.25 1.25 8.26 6.15

09 25 35 5 15 6.5 6.5 4.13 1.88 9.13 6.63

10 25 35 5 15 7.5 22.5 4.13 1.88 9.13 6.63

In this case, the disturbed bus of line 08 comes 5

minutes earlier with F

opt

=6.15. The F

opt

return

progressively to the target value F

before

(value

corresponding to the theoretical value before

perturbation) and the disturbance was fully regulated

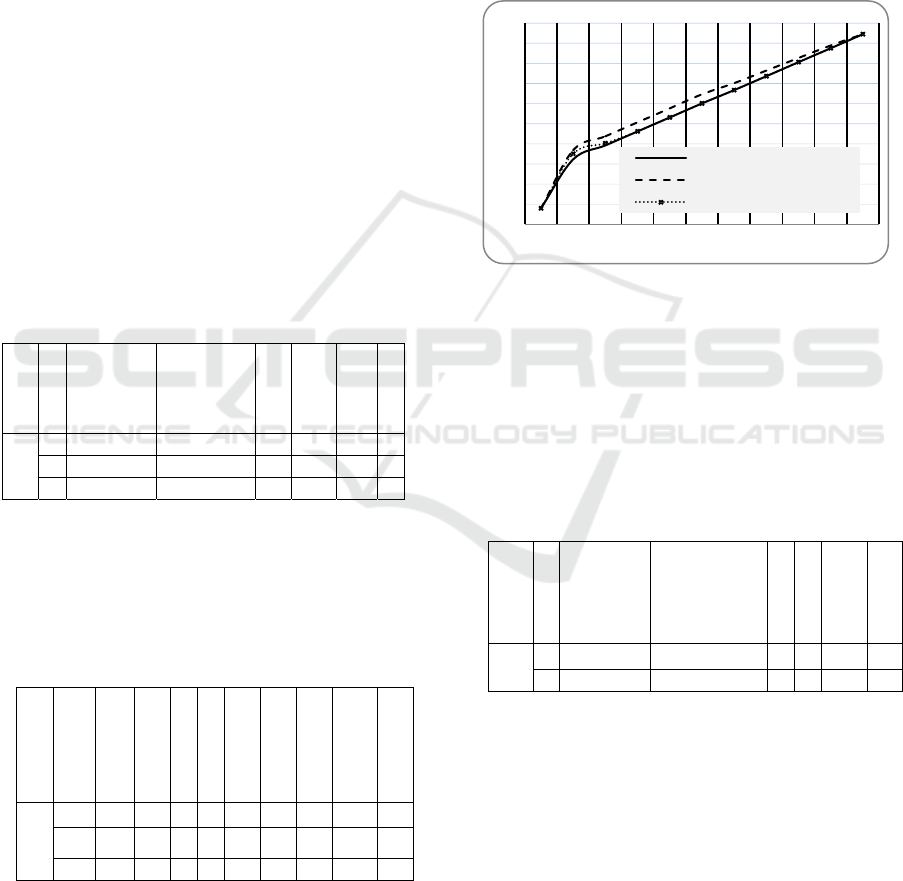
after 10 bus passages at 10h:27 min. We diagram the

regulation process for the bus of line 008 in figure 5.

It presents the three passage times of the bus at Al

Bateen station. This diagram shows that the passage

time curve after the regulation is closer to the

theoretical (scheduled) time passages curve (Bus 08 –

before perturbation) than the passage time curve

without the use of our regulation (Bus 08 – after

perturbation). The same results are obtained for the

other lines (009 and 010) of this scenario.

Figure 5: Time of passages for line 08 bus.

5.3 Scenario 2

Scenario 2 shows perturbation that was detected after

a delay for lines 032 and 052 on Zayed Sports City

station. This delay is due to an accident in the

embassy area (see Figure 4). Buses information and

distributed weights are given in table 3:

Table 3: Buses Information at Zayed Sport City.

Line

Fre

uenc

Theoretical

time at

Station

Detecting

perturbation

time



032 20 05h:42 pm 05h:47 pm 22 0.4 0.4 0.2

052 20 05h:38 p

05h:43 p

17 0.3 0.3 0.4

In this case, the two lines have at station four

correspondences buses for lines 040, 044, 052 and

054. We cite in table 4 all factor values f

correspondence buses. We note that when buses have

the same direction in the transfer station, the

correspondence factor value is zero (see table 4).

06:00

06:28

06:57

07:26

07:55

08:24

08:52

09:21

09:50

10:19

10:48

1234567891011

PassagenumberatAlBateenstation

Bus08‐Beforeperturbation

Bus08‐Afterperturbation

Bus08‐Afterregulation

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

424

Table 4: Distribution of Factor Values.

Factor Values

for lines

Line 032 034 040 044 052 054

032 0.40 0.20 0.00 0.4 0.00

052 0.25 0.00 0.20 0.30 0.25

After simulation of the different feasible

regulation actions, the regulator of each coming bus

executes its optimization phase and recommends that

the better action is short-turning. Moreover, in order

to transport passengers witing in Zayed station to the

next one a Short-cut operation is recommended(see

table 5 and 6).

Table 5: Decision after Optimization Phase.

Line

Detect.

Vr Opt.

Detect.

Opt.

Detect.

Opt.

before

start

opt

032 25 39 5 24 13 23 4.61 2.61 17.77 14.21

052 25 31 5 11 16.3 22.5 8.03 2.52 17.13 12.23

Table 6: Result Values in Regulation Process - Scenario 2.

Line U-turn at station Save

032 06h: 03 pm 6 mn

052 06h: 00 pm 11 mn

The diagram of figure 6 proves the efficiency of

our system. The after regulation curve becomes

closer to the before perturbation one (scheduled time

passages).

Figure 6: Time of passages for bus of line 32.

The results of the two scenarios show that F

opt

, on

which the decision is based improves the service

performance of the passenger by minimizing the

travel time of disturbed busses.

6 CONCLUSION AND

PERSPECTIVES

This paper shows that the assessment of the quality of

the solution produced by traffic regulation systems

should be based on public transport key performance

indicators.

The first contribution of this paper has been to

provide an overview of the key performance

indicators measurement and how to compute these

KPIs to regulate perturbation. The second

contribution consists in introducing our Support

System of Public Transport (RSSPT). This system

ensures two phases of regulation: detection of

perturbation and optimization resolution to regulate

the disturbance. To detect perturbation, the system

distinguishes the degradation of the passenger quality

service in terms of waiting time at the station for the

coming busses. The optimization resolution is based

on the performance measures that describe the Key

Performance Indicators (KPIs) of the public

transportation traffic. Our system is based on a multi-

agent approach. It relies on the principle of

coordination between different autonomous agents in

a dynamic, open and complex environment.

To validate our model, we conducted tests by

simulating two perturbation scenarios in a real traffic

network. The obtained results show an improvement

of the performance of the passenger quality service in

perturbation cases.

In perspective, to minimize the development

eﬀort in the optimization phase and avoid the

knowledge bottleneck of network traffic, we have to

improve the system behavior by adding a learning

module that would be used in case of new situations

like unfamiliar perturbations, new traffic parameter,

etc. Therefore, the regulator agent has to use the

outcomes and update its knowledge base to deal with

future situations.

REFERENCES

Newell, G.F. , Potts, R.B. , 1964. Maintaining a bus

schedule. In: Australian Road Research Board (ARRB)

Conference, 2nd, 1964, Melbourne, 2.

Moreira-Matias, L. , Ferreira, C. , Gama, J.A. , Mendes-

Moreira, J.a. , de Sousa, J.F. , 2012. Bus bunching

detection by mining sequences of headway deviations.

In: Advances in Data Mining. Applications and

Theoretical Aspects. Springer, pp. 77–91.

Verbich, D. , Diab, E. , El-Geneidy, A. , 2016. Have they

bunched yet? An exploratory study of the impacts of

15:36

16:48

18:00

19:12

20:24

1234567

PassagenumberatZayedSportsCitystation

Bus32‐beforeperturbation

Bus32‐afterperturbation

Bus32‐afterregulation

Intelligent Regulation System to Optimize the Service Performance of the Public Transport

425

bus bunching on dwell and 1 running times 2. running

times 2, 3 .

Newell, G. , 1977. Unstable Brownian motion of a bus trip.

In: Statistical Mechanics and Statistical Methods in

Theory and Application. Springer, pp. 645–667.

Zhao, J. , Dessouky, M. , Bukkapatnam, S. , 2006. Optimal

slack time for schedule-based transit operations.

Transp. Sci. 40 (4), 529–539.

Feng, W. , Figliozzi, M. , 2011. Empirical findings of bus

bunching distributions and attributes using archived

avl/apc bus data. In: Proc., 11th Int. Conf. of Chinese

Transportation Professionals (ICCTP). ASCE Reston,

Gershenson, C. , Pineda, L.A. , 2009. Why does public

transport not arrive on time? the pervasiveness of equal

headway instability. PloS One 4 (10), e7292.

Newell, G.F. , Potts, R.B. , 1964. Maintaining a bus

schedule. In: Australian Road Research Board (ARRB)

Conference, 2nd, 1964, Melbourne, 2.

Zolfaghari, S. , Azizi, N. , Jaber, M.Y. , 2004. A model for

holding strategy in public transit systems with real-time

information. Int. J. Transp. Manage. 2 (2), 99–110.

Bartholdi, J.J. , Eisenstein, D.D. , 2012. A self-coördinating

bus route to resist bus bunching. Transp. Res. Part B 46

(4), 4 81–4 91.

Xuan, Y. , Argote, J. , Daganzo, C.F. ,2011. Dynamic bus

holding strategies for schedule reliability: optimal

linear control and performance analysis. Transp. Res.

Part B 45 (10), 1831–1845

Pilachowski, J.M. , 2009. An Approach to Reducing Bus

Bunching. University of California Transportation

Center.

Daganzo, C.F. , Pilachowski, J. , 2011. Reducing bunching

with bus-to-bus cooperation. Transp. Res. Part B 45 (1),

267–277.

He, S.-X. , 2015. An anti-bunching strategy to improve bus

schedule and headway reliability by making use of the

available accurate information. Comput. Ind. Eng. 85,

17–32.

Albright, E. , Figliozzi, M.A. , 2012. Analysis of the

impacts of transit signal priority on bus bunching and

performance. In: Proceedings of the Conference on

Advanced Systems for Public Transport (CASPT),

Santiago, Chile.

Bhouri, Balbo, Pinson and Tlig, 2011, Web Intelligence and

Intelligent Agent Technology, IEEE/WIC/ACM

International Conference on (2011) Lyon, France, Aug.

22, 2011 to Aug. 27, 2011, ISBN: 978-0-7695-4513-4

pp: 7-13

M. Napiah,, I. Kamaruddin and Suwardo, “Punctuality

index and expected average waiting time of stage buses

in mixed traffic”, WIT Transactions on The Built

3509 (on-line), 2015

Meead Saberi and Ali Zockaie K., 2013. “Definition and

Properties of Alternative Bus Service Reliability

Measures at the Stop Level”. Journal of Public

Transportation, 16 (1): 97-122

Kenneth J Dueker, Thomas J Kimpel, James G Strathman,

“Determinants of Bus Dwell Time”, Journal of Public

Transportation, March 2004, DOI: 10.5038/2375-

0901.7.1.2

"Dwell time - Transportation Research Thesaurus (TRT)".

trt.trb.org. Retrieved 2017-06-30.

Levinson, Herbert (1983). Analyzing transit travel time

performance, Transportation Research Record 915,

Vu The Tran, Peter Eklund, Chris Cook. 2012, “Toward

real-time decision making for bus service reliability”,

International Symposium on Communications and

Information Technologies (ISCIT), DOI:

10.1109/ISCIT.2012.6380856

Cats, Nabavi, Koutsopoulos and Burghout, 2011, “Impacts

of holding control strategies on transit performance: A

bus simulation model analysis”, Transportation

Research Record Journal of the Transportation

Research Board, Pages 51-58.

Theuns Henning, Mohammed Dalil Essakali et Jung Eun

Oh, 2011, Transport Research Support: A Framework

for urban transport benchmatking, The International

Bank for Reconstruction and Development / The World

Bank.

Linstone HA and Turrof M. The Delphi method -

Techniques and applications, Addison-Wesley

Publishing Company.

Todd Litman, “Public Transit’s Impact on Rural and Small

Towns, A Vital Mobility Link”, PUBLISHED BY

American Public Transportation Association. February.

Hugh M. Clark, Karen Basinger, Katie Maloney and Callie

Whiteman. “Who Rides Public Transportation”,

PUBLISHED BY American Public Transportation

Association. January

John Neff and Matthew Dickens, “Public Transportation

Fact PUBLISHED BY American Public Transportation

Association, ”, 67th Edition,.

Mark Tromp, Xiang Liu and Daniel J. Graham,

“Development of Key Performance Indicator to

Compare Regularity of Service Between Urban Bus

Operators”, Transportation Research Record Journal of

the Transportation Research Board 2216(-1), 2011

Mark Trompet.”The Development of a Performance

Indicator to Compare Regularity of Service between

Urban Bus Operators”, Skempton (Civil Eng.) Bldg,

Imperial College London, December 2010.

Oded Cats Oded Cats, Wilco Burghout, Tomer Toledo, and

Haris N. Koutsopoulos, “Mesoscopic Modeling of Bus

Public Transportation”, No. 2188, Transportation

Research Board of the National Academies,

Washington, D.C., 2010, pp. 9–18, 2010

Neila Bhouri, Maurice Aron and Gérard Scemama, “Gini

Index for Evaluating Bus Reliability Performances for

Operators and Riders”, Transportation Research Board,

Washington, United States. Transportation Research

Board, 13p, June 2016.

Gary Henderson, Philip Kwong and Heba Adkins,

“Regularity Indices for Evaluating Transit

Performance”, TRANSPORTATION RESEARCH

RECORD 1297, 1991.

Noorfakhriah Yaakub and Madzlan Napiah, “Public

Transport: Punctuality Index for Bus Operation”,

World Academy of Science, Engineering and

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

426

Technology, International Journal of Civil and

Environmental Engineering, Vol:5, No:12, 2011

Xumei Chen, Lei Yu, Yushi Zhang, and Jifu Guo,

“Analyzing Urban Bus Service Reliability At The Stop,

Route, and Network Levels”, Transportation Research

Part A 43, pp. 722–734, 2009

Vaniyapurackal Jilu Joseph, “Punctuality Index for the City

Bus Service”, International Journal of Engineering

Research Volume No.4, Issue No.4, pp : 206-208,

ISSN:2319-6890, April 2015.

S. Carosi a,, S. Gualandi b, F. Malucelli c and E. Tresoldi,

“Delay management in public transportation: service

regularity issues and crew re-scheduling”, 18th Euro

Working Group on Transportation, EWGT, Delft, The

Netherlands., July 2015.

Ceder, A. A., “Public Transit Planning and

Operation:Theory, modelling and practice”: Elsevier

Ltd, 2007.

E. Foloff, M. RIZI and A. Sapiroto, “Bases et pratiques de

regulation”, RATP Direction du reseau

routier,RC/MSE,

Zhenliang Ma, Luis Ferreira and Mahmoud Mesbah, “A

Framework for the Development of Bus Service

Reliability Measures”, Australasian Transport

Research Forum, Brisbane, Australia, October 2013

Hartani, Thesis, “Modélisation des systèmes fous :

Contributions théoriques et applications”.Univetsité de

Paris 6, Jun 95.

European Commission, “White paper – Roadmap to a

single European Transport Area” - Towards a

competitive and resource efficient transport system.

2011.

Intelligent Regulation System to Optimize the Service Performance of the Public Transport

427