
Towards a Tailored Hybrid Recommendation-based System for
Computerized Adaptive Testing through Clustering and IRT
Wesley Silva
1 a
, Marcos Spalenza
1 b
, Jean-R
´
emi Bourguet
2 c
and Elias de Oliveira
1 d
1
Postgraduate Program of Informatics (PPGI), Federal University of Esp
´
ırito Santo, Vit
´
oria, Brazil
2
Department of Computer Science, Vila Velha University, Vila Velha, Brazil
Keywords:
Technology-enhanced Learning, Computerized Adaptive Testing, Intelligent Tutoring Systems, Item Re-
sponse Theory, Clustering, Recommendation-based System, Collaborative Filtering, Content-based Filtering.
Abstract:
Creating a student individualized evaluation path composed by a sequence of activities is a hard task and
requires efforts and time for teachers. In such cases, the activities have to be well adjusted to the latent
knowledge of specific students groups. In this paper, we propose a hybrid system that automatically selects and
recommends activities based on a historical evolution of past students during the teaching-learning process.
Our system is supported by the hybrid usage of Item Response Theory and techniques of clustering to output
different kinds of recommendations as filters to select activities and build the tailored evaluation path.
1 INTRODUCTION
Nowadays we can easily encounter a large set of in-
formation from various sources such as Facebook,
Twitter, LinkedIn, and so forth. But, this huge
bunch of data can be confusing for users who want
to select particular items and discard others. A
recommendation-based system is a well known solu-
tion to solve this issue. For example, if users explic-
itly indicate a preference for a style of music called
MPB (Brazilian Popular Music), the recommendation
system may recommend some Tom Jobim’s songs.
Such an approach is founded on content-based fil-
tering (see Pazzani and Billsus, 2007). On the other
hand, it exists a collaborative filtering approach (see
Herlocker et al., 2004) in which the system generates
a group of similar users in terms of interests produc-
ing a recommendation based on the analysis of their
characteristics. For example, in the case of a musical
platform, the user profiles would be defined in terms
of the songs already consumed or liked through the
service. With this a priori knowledge, the system can
generate a group of similar users in terms of interest
and perform a set of recommendations based on the
analysis of the singular characteristics in the group.
a
https://orcid.org/0000-0001-9103-0536
b
https://orcid.org/0000-0002-3826-1500
c
https://orcid.org/0000-0003-3686-1104
d
https://orcid.org/0000-0003-2066-7980
In the field of educational data, some similar sit-
uations exist, especially when teachers have to select
assessment items according to some expected perfor-
mances of their students. Considering the ongoing
grades in a discipline, it is possible to group current
and past students by the similarity of their perfor-
mances in different moments of the teaching-learning
process. For example in the seminal works of Oliveira
et al. (2013), a recommendation-based system can se-
lect assessment items that are expected to be compat-
ible with coherent educational objectives.
In this paper, we propose a new implementation
of this system by clustering students in accordance
with their similar past performances and recommend-
ing an evaluation path that should maximize their fu-
ture performances based on the data collected by sim-
ilar past students. The characterization of the assess-
ment items is supported by the Item Response The-
ory (IRT) that generates descriptors based on proba-
bilities of success in function of presupposed student
latent traits. IRT allows both qualitative and quan-
titative items analysis to support the construction of
an evaluation path (Baker, 2001). Therefore, our hy-
brid recommendation-based system deals with both
the students characteristics and the probabilities of
success. With our data processing, we can select a
neat sequence of items to build a tailored evaluation
path individualized for each student. If a student has
a certain ongoing latent trait, our system can progres-
sively route this student through a steady and coherent
260
Silva, W., Spalenza, M., Bourguet, J. and de Oliveira, E.
Towards a Tailored Hybrid Recommendation-based System for Computerized Adaptive Testing through Clustering and IRT.
DOI: 10.5220/0009419902600268
In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 1, pages 260-268
ISBN: 978-989-758-417-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

evaluation path. By identifying their weaknesses and
strengths, the system recommends the most suitable
activities to improve students performances. There-
fore, our system try to soften the exams recommend-
ing questions guided by the detections of students
learning gaps as advocated by Perrenoud (1998).
The organization of this paper is structured as fol-
lows. In Section 2, we briefly detail some works
which have similarities with our approach in this pa-
per. In Section 3, we introduce the theories and tech-
niques that support our system. The description of our
tailored hybrid recommendation-based system and its
particular filtering approaches is presented in Section
4. Finally, we conclude the paper with some consid-
erations and perspectives in Section 5.
2 RELATED WORKS
The taxonomy of educational data mining applica-
tions proposed by Bakhshinategh et al. (2018) des-
ignates student modeling as an essential task to per-
form behavior predictions. Student models can be
separate into two broad categories: expert-centric or
data-centric (Mayo and Mitrovic, 2001). While the
expert-centric approach relies on experts to identify
the skills required to solve a problem by providing
the structure of the model, the data-centric approach
relies on using the evaluation data to uncover the stu-
dent abilities (Johns et al., 2006).
Consequently, the trails left by the past students
assessments represent strategic data about the ef-
fectiveness of the teaching-learning process. By
observing the students on their multidimensional
characteristics during the teaching-learning process,
the lecturer can isolate key performance indicators
which could hinder students progress (Lieberman,
1990). Since the learning evaluations aim to mea-
sure variables not directly observed, it is relevant to
use standardized and certified assessment processes
to understand in detail what is measured (Baker,
2001). Following such approaches, it is now rec-
ognized that assessments can provide new inputs
for possible recommendation-based systems in terms
of next learning steps guided by detected learning
gaps (Bakhshinategh et al., 2018). Since information
retrieval is a pivotal activity in technology-enhanced
learning (TEL), Manouselis et al. (2011) emphasize
that deployments of recommender systems has at-
tracted a lot of interest.
In the literature, the large part of the
recommendation-based systems during the teaching-
learning process mainly suggests learning resources
sets. For example, in the work of Romero et al.
(2007), the system uses web mining techniques
for recommending links to visit to students. Lee
et al. (2010) propose an architecture to recommend
contents that can reinforce areas in which a par-
ticular student needs improvements. In the paper
of Shishehchi et al. (2010), a semantic recommender
system for e-learning is released by means of which,
learners are able to find and choose the right learning
materials suitable to their field of interest. The system
described by Timms (2007) provides error feedbacks
and hints to support the students confronted to a
series of problems. The aforementioned system is
able to determine the level of hints that students need
during a problem solving.
Lastly, the acronym CAT (standing for Comput-
erized Adaptive Testing) has been conceptualized as
the set of the methods for administering tests that are
adapted to the examinee’s ability level (Lee et al.,
2010). On the other hand, derived from Psychometry,
the Item Response Theory (IRT) represents a possible
support for CAT, as it can better explain the results of
a given evaluation (van der Linden and Hambleton,
2013). As stated by Roijers et al. (2012), IRT can
be used to inform students about their competence
and learning, and teachers about students progresses.
According to Sinharay et al. (2006), model checking
in IRT is an underdeveloped area. This last work
examines the performance of a number of discrep-
ancy measures for assessing different aspects of fit
of common IRT models and the creation of specific
recommendations. Unlike the usual IRT models,
MixIRT models do not assume a single homogeneous
population. Rather, these models assume that there
exist latent subpopulations in the data (Sen and Co-
hen, 2019). In their work, Johns et al. (2006) propose
to train IRT models to predict how the student should
fare on the next problem based on past students
performances on previous problems. The prediction
reaches an accuracy of 72% whether a student would
answer a multiple choice problem correctly. In their
paper, Wauters et al. (2010) explore the possibility of
designing an adaptive item sequencing by matching
the difficulty of the items to the learner’s knowledge
level in intelligent tutoring systems. Lee and Cho
(2015) propose a method to select items and create a
customized assessment sheet for adaptive testing con-
sidering both the learner’s ability and characteristics.
Farida et al. (2011) propose a method to generate
exercises from the learner’s progression observed
through the information collected. Lee et al. (2010)
developed an intelligent tutoring system for English
learning that provides content suitable for specific
levels of ability supported by an IRT-based approach.
Finally, in the approach of Yeung (2019), IRT was
Towards a Tailored Hybrid Recommendation-based System for Computerized Adaptive Testing through Clustering and IRT
261
coupled with Knowledge Tracing Modeling (i.e.
modeling students’ knowledge to determine when a
skill has been learned).
As we argued in introduction, establishing assess-
ment criteria suitable to measure learning variations
encountered is a well known challenge (Perrenoud,
1998). This challenge increases in proportion to the
volume of students in the class. Nevertheless sup-
ported by virtual learning environments, the appli-
cations of activities and assessments are facilitated,
enabling more efficient uses of the information (see
Spalenza et al., 2018). In their works, Oliveira et al.
(2013) used clustering and classification-based tech-
niques to tackle the individual learning gaps through
word processing of the students answers. In this pa-
per, we extend this approach by using IRT to a new
tailored hybrid recommendation-based system.
3 PRELIMINARIES
Nowadays, it is common to generate artificial datasets
to support new prototypes (see Bourguet, 2017). We
assigned to the students a set of pseudo activities to
simulate assessments. Such datasets were generated
for three different types of distributions.
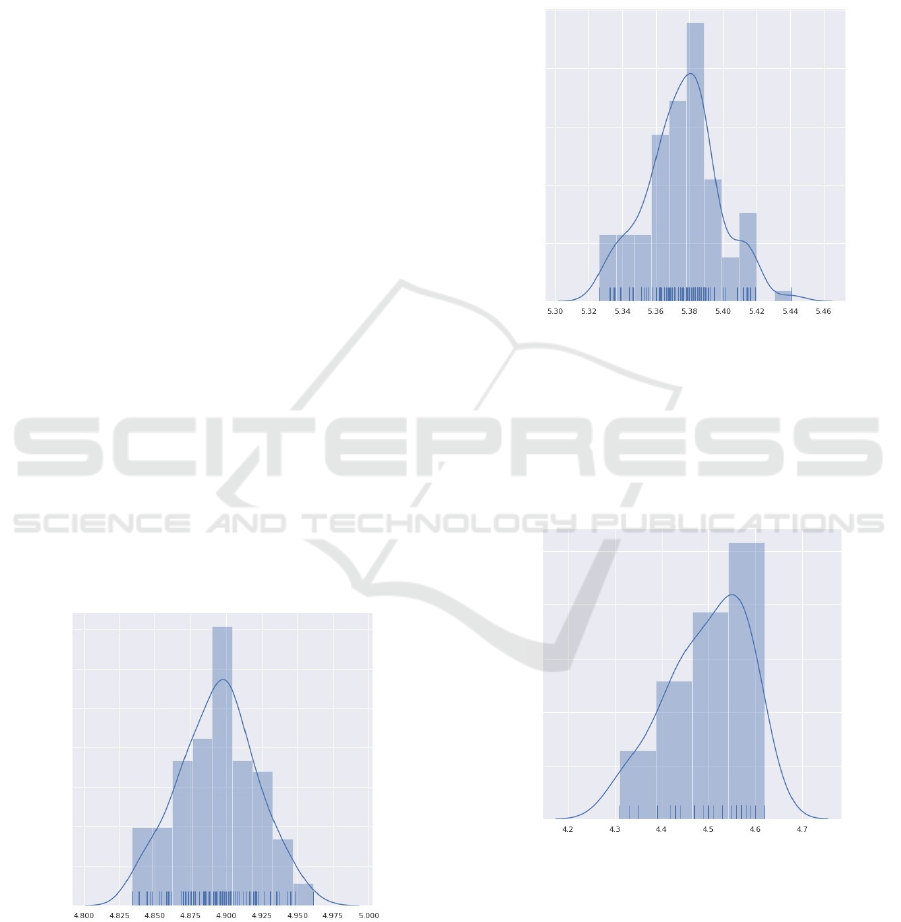
Normal Distribution
The composition of our normal law-based distribu-
tion is supported by different proportions parameters:
70% of N p5, 3q, 15% of N 2, 1q and 15% of N p8, 1q.
Figure 1 presents the histogram of the grades means.
Figure 1: Normal Distribution.
Uniform Distributions
The composition of our first uniform law-based dis-
tribution is supported by different proportions param-
eters: 25% of Up1, 3q, 25% of Up4, 6q, 25% Up7, 9q
and 25% of Up0, 10q and 25%. Figure 2 presents the
histogram of the grades means.
Figure 2: Uniform Distribution with Floats.
The previous distribution deals with float numbers
while the second uniform law-based distribution (set
with the same parameters as above) generates only in-
teger numbers.
Figure 3 presents the histogram of the grades
means for the second uniform law-based distribution.
Figure 3: Uniform Distribution with Integers.
Here, our intention is to generate different datasets
representing as close as possible real-world cases
about students evaluations.
CSEDU 2020 - 12th International Conference on Computer Supported Education
262

The Clustering Process
The clustering process aims to identify students who
are similar to others according to their performances.
Clustering by the k-means technique establishes cen-
troids according to a specified number k. In our case,
we assume three groups of performances in a class-
room: a high, medium and low performing group.
Similarity by cosine distance was used to classify stu-
dents in the clusters. The evaluation of the clusters
was performed by checking the distribution density
of the grades in each cluster.
Figure 4 shows some metrics (intra-cluster grades
densities on the left side and intra-cluster density of
euclidean distances on the right side) after the clus-
tering of the normal distribution.
Figure 4: Clustering Metrics (Normal Distribution).
Figure 5 shows the same metrics after the cluster-
ing of the first uniform distribution.
Figure 5: Clustering Metrics (First Uniform Distribution).
Figure 6 shows the same metrics after the cluster-
ing of the second uniform distribution.
The Item Response Theory
IRT (Baker, 2001) has been considered by many ex-
perts as a milestone for the modern Psychometrics
and an extension of the Classical Test Theory (CTT).
While CTT is founded on the proposition that mea-
surement error, a random latent variable, is a compo-
nent of the evaluation score (Traub, 1997), IRT con-
siders the probability of getting particular items right
or wrong given the ability of the examinees. Each
Figure 6: Clustering Metrics (Second Uniform Distribu-
tion).
examinee possesses some amount of the underlying
ability (also called latent trait) materialized as an abil-
ity score (i.e. a numerical value denoted θ) on a rating
scale. IRT advocates that depending of a certain abil-
ity level, there will naturally be a probability denoted
Ppθq with which an examinee will answer correctly to
the item. The S-shaped curve of this function is called
item characteristic curve, and each item have its own.
The relation between this probability and the ability
score is modeled by a logistic (i.e. sigmoid) function.
Such functions relate the natural assumption that the
probability will be low for examinees with weak abil-
ities and high for examinees with great abilities, the
probability tends to zero at the lowest levels of ability
and tends to 1 at the highest. The function depends on
parameters describing some properties of each item.
The Difficulty. Whatever the number of parameters
used to define the characteristic curve of an item, the
parameter difficulty is always present. The difficulty
of an item i denoted δpiq is the ability score which
corresponds to a probability of success equal to 0.5.
The Discrimination. A second important feature of
the item is its discriminative power, i.e. its capacity
to differentiate examinees (i.e. distinguish those who
succeed from those who fail the item) in relation to
their underlying ability score. The discrimination of
an item i denoted αpiq is the maximum slope of the
characteristic curve of the item (i.e. the slope of the
geometric tangent passing through the inflection point
of the curve). Therefore, the slope can be more or
less inclined: the more the slope is steep, the more
the item is discriminative and inversely.
The Pseudo-guessing. Even if, the examinee
doesn’t have any skill in the scope being evaluated,
he or she may have a non-null probability of correctly
answering the item. This is particularly the case
for evaluations based on multiple-choices. The
pseudo-guessing of an item i denoted γpiq is the
probability of success in the item corresponding to
Towards a Tailored Hybrid Recommendation-based System for Computerized Adaptive Testing through Clustering and IRT
263
the minimal underlying ability score.
There are different possible models (with one,
two or three parameters aforementioned) to build the
functions representing the characteristic curves of
the itens. Equation 1 presents the model with three
parameters.
Let an item i and δpiq (resp. αpiq, γpiq) its dif-
ficulty (resp. discrimination, pseudo-guessing), the
probability of success in the item i for an examinee
with an ability score of θ is defined as follow:
Ppθq “ γpiq `
1 ´ γpiq
1 ` e
´1.7αpiqpθ´δpiqq
(1)
The notion of precision (or information), defined
in Equation 2 assumes an essential role since it indi-
cates in particular on which portion of the underlying
ability scale (i.e. for which category(s) of examinees)
the precision of the item is the highest. An hard item
will give very few information about the examinees
with the weakest skills and in the contrary an easy
item will not be an accurate test for the examinees
with the strongest skills.
Let an item i, αpiq (resp. γpiq) its discrimination
(resp. pseudo-guessing),Ppθq the probability of suc-
cess for an examinee with an ability score in of θ, the
precision of such ability score is defined as follow:
Ipθq “ 2.89 αpiq
2
ˆ
1 ´ Ppθq
Ppθq
˙ ˆ
Ppθq ´ γpiq
1 ´ γpiq
˙
2
(2)
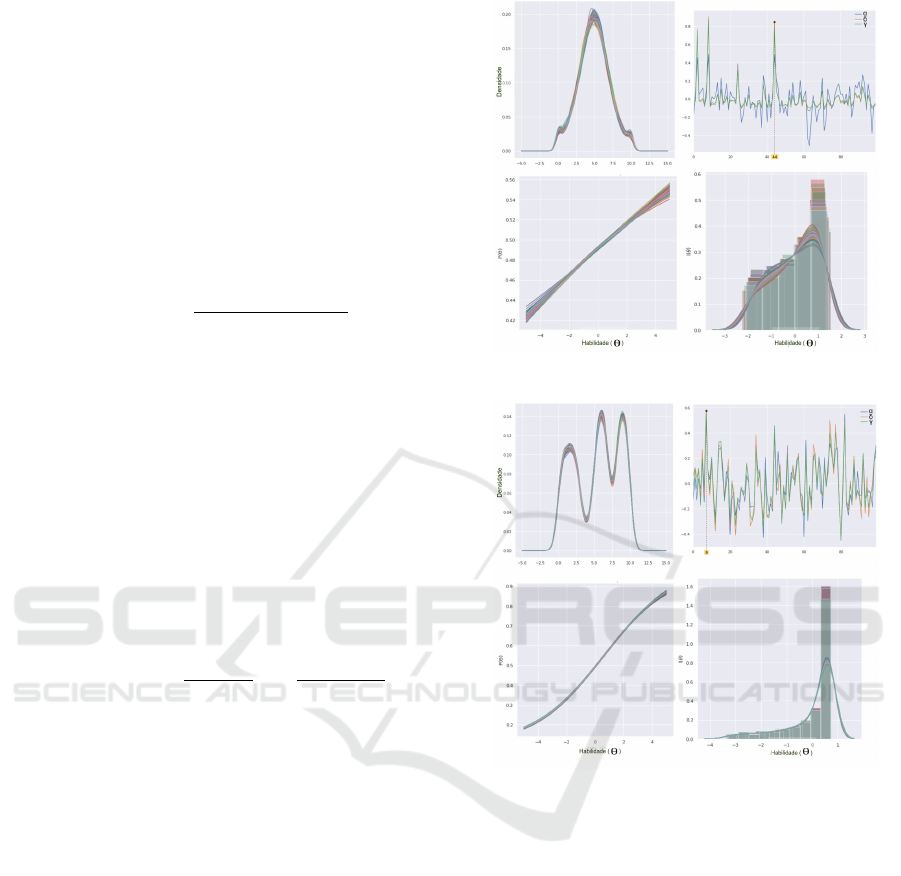
Figure 7 shows in the top left corner the density
distribution; in the top right the parameters estimated
by the model IRT, normalized to mean 0 and standard
deviation 1; in the bottom left the few discriminative
characteristic curves; and finally in the bottom right
the information curves.
Figure 8 shows the same kind of plots as the
ones shown in Figure 7. The notable differences are
that the characteristic curves are more discriminative
forming sigmoid curves. The information curves are
concentrated on the right of 0 representing the ability
of the items to be descriptive in such levels of latent
trait.
Figure 9 shows the same kind of plots as the ones
shown in Figure 7 and Figure 8. The notable differ-
ences are that the characteristic curves are very dis-
criminative and describe easy items. Due to the ge-
ometry of the data, it was not possible to calculate the
covariance that is an information required to build in-
formation curves.
Figure 7: IRT Analysis for Normal Distribution.
Figure 8: IRT Analysis for Uniform Distribution.
4 SYSTEM DESCRIPTION
We argue that successful past actions may be applied
to similar students to stimulate their developments.
Therefore, we propose to select items with a con-
trolled probability of success that match with the esti-
mated capacity of a given student. Our tailored hy-
brid recommendation-based system deals with both
the students characteristics and the probabilities of
performances.
System Workflow
Our system manages the students in models of per-
formances by gathering together similar students and
recommend initiatives to solve the learning gaps. The
adoption of data mining and machine learning tech-
CSEDU 2020 - 12th International Conference on Computer Supported Education
264

Figure 9: IRT Analysis for Uniform Distribution.
niques helps to better understand the performances
behaviors of the students. Figure 10 represents the
global work flow of our approach.
Figure 10: Recommendation-based System Workflow.
In the processing step, student grades represented
by a spreadsheet file icon are used as predictor param-
eters. To implement the recommendation system with
a collaborative filtering approach, we used the clus-
tering technique, in order to group similar students
grades vectors. Treating each student’s list of grades
as a vector, a clustering algorithm is able to group
the most similar vectors related to a centroid. On the
other hand, to discriminate the evaluation items, sup-
ported by IRT, our system can generate for each item
the values of the so-called parameter of difficulty, dis-
crimination and pseudo-guessing. Therefore, the sys-
tem can cluster students and activities. A desirable
situation is illustrated on the left side highlighting a
fair variation of students and activities. On the other
hand, on the right side occurs an undesirable situa-
tion in which it was not possible to separate groups
of activities and students. By combining the infor-
mation generated by these two techniques, the system
is able to compose personalized assessments path for
each student.
Historical Data
Our Historical Data module represents a foundation
for our system in the sense that it represents an his-
torical dataset supporting the process to compute the
recommendations. First, our approach is based on a
cartesian approach, then we presuppose that our pool
of activities P is stratified and sequentially organized
such that P “ A
0
Y ¨¨ ¨ Y A
n
with A
i
a set of activity
corresponding to the i-th scope of a given discipline.
A
0
represents a set of initial activities aiming to pre-
liminarily evaluate the students. The evaluation path
of a student is a function such that for a student s
i
we have Eps
i
q “ pA
0
i
, . . . , A
n
i
q and @ j P v1, nw we have
A
j
i
Ď A
j
and |A
j
i
| “ N. Note that apk, A
t
i
q returns the
k-th activity from the set of the activities realized by
the student s
i
in the level (or strate) t. The function
g : S, P Ñ r0, 10s will return a grade in function of a
given student performing a given activity. When the
activities were not assigned to the student, the func-
tion can return a value NA (i.e. Not Available).
In the case of our simulation, we artificially gener-
ate 1000 students that are confronted to 100 activities,
the first activity is always the same after what we ran-
domly pick up one activity among three possible ac-
tivities and repeat this process consecutively until the
end. At the end, all the students will have start their
evaluations path in the same way before to proceed
on singular roads (sometimes similar) until a certain
point.
Our recommendation process is performed using
both cluster and IRT analysis as explained thereafter.
Recommendation Process
When a student will perform a new activity at a cer-
tain level t (1 ď t ď n), the system considers that his
latent trait is actually the pondered (by item difficulty
δ) mean of all the grades he obtained until to pass the
new activity as described in Equation 3.
θ
t
ps
i
q “
1
t
t
ÿ
j“1
ř
N
k“1
δpapk, A
j
i
qq.gps
i
, apk, A
j
i
qq
ř
N
k“1
δpapk, A
j
i
qq
(3)
The set of past activities of a student at a given
level t is outputted through the function A
p
: S Ñ P.
Each time a student performed a given set of activ-
ities, the vector of his past activities is upgraded by
adding a new position at the end of the vector with
the aforementioned activities. The function g
p
: S Ñ
r0, 10s
tˆN
will associate a student with his current
vector of grades at the level t.
Towards a Tailored Hybrid Recommendation-based System for Computerized Adaptive Testing through Clustering and IRT
265

Recommendation Guided by Difficulty
The first option to guide the recommendation is to use
the parameter of difficulty and the clustering. After to
have upgraded the vector of past activities, the system
selects the set of students Sps
i
q who performed the
same past activities as those of the student s
i
such
that Sps
i
q “ ts
j
|A
p
ps
j
q “ A
p
ps
i
qu. Thus, the system
proceeds to a clustering task using the vector g
p
ps
i
q
and the vectors of the set
Ť
s
j
PSps
i
q
g
p
ps
j
q. Note that a
cluster is built in relation to the internal similarity ρ
of its members.
Let C
ρ
ps
i
q the set of students currently present in
the same cluster as s
i
, the set of the κ activities rec-
ommended for the student s
i
is denoted R
κ
1
ps
i
q and is
described in the Equation 4. Note that κargmax will
select the arguments from the κ maximum scores.
R
κ
1
ps
i
q “ κargmax
a P A
t`1
j
s.t. s
j
P C
ρ
ps
i
q
n
ÿ
l“t`1
ř
N
k“1
δpapk, A
l
j
qqgps
i
, apk, A
l
j
qq
pn ´ tq
ř
N
k“1
δpapk, A
l
j
qq
(4)
Recommendation Guided by Discrimination
The second option to guide the recommendation is to
use the parameter of discrimination. As explained in
Section 3, the discrimination is the capacity to differ-
entiate examinees (i.e. distinguish those who succeed
from those who fail the item) in relation to their un-
derlying ability score. The higher the value of the
parameter α, the more the item is considered dis-
criminating. To guide the interpretation of the pa-
rameter α, Baker (2001) offers an evaluation grid:
null if α “ 0, very weak if α P r0, 01;0, 34s, weak if
α P r0, 35; 0, 64s, moderate if α P r0, 65;1, 34s, strong
if α P r1, 35; 1, 69s, very strong if α ą 1, 70 and perfect
if α tends to `8. In the case of our recommendation-
based system, the student will be challenged by rec-
ommending an evaluation in a certain level of knowl-
edge that corresponds to the student’s latent trait. In-
stead of using the κargmax operator as previously, the
system selects a set of items that correspond to the
level of the student by applying a threshold parame-
ter. Once selected, these items are ranked using their
own parameters of discrimination. Let a student s
i
at a
level t, and his latent trait θ
t
ps
i
q as described in Equa-
tion 3, the system builds a partial preorder on the set
activities such that @pa
j
, a
k
q P A
t`1
we have:
pa
j
, a
k
q Pĺô |θ
t
ps
i
q ´ δpa
j
q| ď |θ
t
ps
i
q ´ δpa
k
q| (5)
Let d a threshold s.t. d P vN, Mw with M the total
number of available activities, the system selects the
d-th closest difficulties in relation to the latent trait of
the student by applying a function D : S, A
k
, N Ñ A
k
.
After what, as described in Equation 6, a κargmax
operator is applied to the set in order to select the κ
items that will challenge the most the student.
R
κ
2
ps
i
q “ κargmax
a P Dps
i
,A
t`1
,dq
αpaq (6)
Recommendation Guided by Pseudo-guessing
Note that the two last recommendations can be used
as filters, applying one after another. The system gets
a last filter considering the pseudo-guessing parame-
ter. With this filter, the chance can be minimized by
selecting the activities with minimal pseudo-guessing
as described in Equation 7.
R
κ
3
ps
i
q “ κargmin
a P Dps
i
,A
t`1
,dq
γpaq (7)
Applying all the filters together, the system can
allocate weights to the filters by setting different
values for κ.
Let κ
1
, κ
2
, κ
3
the weights for the different filters of
recommendations R
κ
1
1
, R
κ
2
2
and R
κ
3
3
, a recommended
set of activities for a given student is described in
Equation 8.
W ps
i
q “
č
j P v1,3w
R
κ
j
j
ps
i
q (8)
Simulation of an Evaluation Path
An evaluation path is represented in Figure 11 for
each of the three distributions. As you can observe on
the plots situated on the left side, a given student be-
longs to different clusters along his evolution through
the evaluation path. The best score for the student
grades vector in relation to its cluster is informed on
the vertical axis. The left side of the figure shows the
cosine similarities distribution inside the student clus-
ter at some levels of the path.
The clusters performed on the scaled values of
the IRT parameters (difficulty, discrimination and
pseudo-guessing) are represented on the right side
of Figure 12 through the characteristic curves of the
items. In this figure, three different clusters (C0, C1
and C2) were represented and the densities of the
scaled values of the IRT parameters are represented
on the left side.
CSEDU 2020 - 12th International Conference on Computer Supported Education
266

Figure 11: Evaluation Path for a given Student.
Figure 12: Clustering the Item through the IRT Parameters.
5 CONCLUSION
Everyone who teaches has to spend a lot of time cre-
ating exams, inspecting and evaluating students ac-
tivities to discover their learning gaps (Mangaroska
et al., 2019). The trails left by the past students assess-
ments represent strategic data about the effectiveness
of the teaching-learning process. Some existent sys-
tems (see for example Oliveira et al., 2013) can rec-
ommend activities indicated for similar profiles that
already received recommendations. However, build-
ing an appropriate evaluation path in which the levels
of knowledge of each student are frequently refreshed
and contextualized across the set of available items
remained an opened issue.
This article proposes a strategy for selecting the
appropriate activities through a tailored evaluation
path for each student. We use historical data, i.e.
assessments of previous students to build a statisti-
cal model in order to predict the future student suc-
cess. Our system is supported by the common usage
of IRT and techniques of clustering to output differ-
ent kinds of recommendations as filters to select ac-
tivities. IRT guarantees the employment of a content-
based filtering related to the extrinsic qualities of the
recommended items while clustering techniques sup-
port the collaborative-based filtering related to the in-
trinsic profiles of the students. As future proposals,
we intend to provide an interface for our system to
support the selection of the items either by using the
clustering techniques or by applying the different fil-
ters presented in this work.
REFERENCES
Baker, F. B. (2001). The basics of item response theory.
Education Resources Information Center.
Bakhshinategh, B., Zaiane, O. R., Elatia, S., and Ipperciel,
D. (2018). Educational Data Mining Applications and
Tasks: A Survey of the Last 10 Years. Education and
Information Technologies, 23(1):537–553.
Bourguet, J. (2017). Purely synthetic and domain indepen-
dent consistency-guaranteed populations in SHIQ(D).
In Lossio-Ventura, J. A. and Alatrista-Salas, H., ed-
itors, 4th Annual International Symposium, SIMBig
2017, Lima, Peru, September 4-6, 2017, volume 795
of Communications in Computer and Information Sci-
ence, pages 76–89. Springer.
Farida, B., Malik, S., Catherine, C., and Jean, C. P. (2011).
Adaptive exercises generation using an automated
evaluation and a domain ontology: the odala+ ap-
proach. International Journal of Emerging Technolo-
gies in Learning (iJET), 6(2):4–10.
Herlocker, J. L., Konstan, J. A., Terveen, L. G., and Riedl,
J. T. (2004). Evaluating collaborative filtering recom-
Towards a Tailored Hybrid Recommendation-based System for Computerized Adaptive Testing through Clustering and IRT
267

mender systems. ACM Transactions on Information
Systems (TOIS), 22(1):5–53.
Johns, J., Mahadevan, S., and Woolf, B. P. (2006). Estimat-
ing student proficiency using an item response theory
model. In Ikeda, M., Ashley, K. D., and Chan, T., ed-
itors, Intelligent Tutoring Systems, 8th International
Conference, ITS 2006, Jhongli, Taiwan, June 26-30,
2006, Proceedings, volume 4053 of Lecture Notes in
Computer Science, pages 473–480. Springer.
Lee, Y. and Cho, J. (2015). Personalized item genera-
tion method for adaptive testing systems. Multimedia
Tools Appl., 74(19):8571–8591.
Lee, Y., Cho, J., Han, S., and Choi, B. (2010). A person-
alized assessment system based on item response the-
ory. In Luo, X., Spaniol, M., Wang, L., Li, Q., Nejdl,
W., and Zhang, W., editors, Advances in Web-Based
Learning - ICWL 2010 - 9th International Conference,
Shanghai, China, December 8-10, 2010. Proceedings,
volume 6483 of Lecture Notes in Computer Science,
pages 381–386. Springer.
Lieberman, D. A. (1990). Learning: Behavior and Cogni-
tion. International Student Edition. Wadsworth Pub-
lishing Company, Belmont, CA.
Mangaroska, K., Vesin, B., and Giannakos, M. N. (2019).
Cross-platform analytics: A step towards personaliza-
tion and adaptation in education. In Proceedings of
the 9th International Conference on Learning Analyt-
ics & Knowledge, LAK 2019, Tempe, AZ, USA, March
4-8, 2019, pages 71–75. ACM.
Manouselis, N., Drachsler, H., Vuorikari, R., Hummel, H.,
and Koper, R. (2011). Recommender systems in tech-
nology enhanced learning. In Recommender systems
handbook, pages 387–415. Springer.
Mayo, M. and Mitrovic, A. (2001). Optimising its be-
haviour with bayesian networks and decision theory.
International Artificial Intelligence Education Soci-
ety, 12:124–153.
Oliveira, M. G., Marques Ciarelli, P., and Oliveira, E.
(2013). Recommendation of programming activities
by multi-label classification for a formative assess-
ment of students. Expert Systems with Applications,
40(16):6641–6651.
Pazzani, M. J. and Billsus, D. (2007). Content-based rec-
ommendation systems. In Brusilovsky, P., Kobsa, A.,
and Nejdl, W., editors, The Adaptive Web, Methods
and Strategies of Web Personalization, volume 4321
of Lecture Notes in Computer Science, pages 325–
341. Springer.
Perrenoud, P. (1998). From formative evaluation to a
controlled regulation of learning processes. towards
a wider conceptual field. Assessment in Education:
Principles, Policy & Practice, 5(1):85–102.
Roijers, D. M., Jeuring, J., and Feelders, A. (2012). Prob-
ability estimation and a competence model for rule
based e-tutoring systems. In Proceedings of the 2nd
International Conference on Learning Analytics and
Knowledge, LAK ’12, page 255–258, New York, NY,
USA. Association for Computing Machinery.
Romero, C., Ventura, S., Delgado, J. A., and Bra, P. D.
(2007). Personalized links recommendation based on
data mining in adaptive educational hypermedia sys-
tems. In Duval, E., Klamma, R., and Wolpers, M., edi-
tors, Creating New Learning Experiences on a Global
Scale, Second European Conference on Technology
Enhanced Learning, EC-TEL 2007, Crete, Greece,
September 17-20, 2007, Proceedings, volume 4753 of
Lecture Notes in Computer Science, pages 292–306.
Springer.
Sen, S. and Cohen, A. S. (2019). Applications of mixture irt
models: A literature review. Measurement: Interdis-
ciplinary Research and Perspectives, 17(4):177–191.
Shishehchi, S., Banihashem, S. Y., and Zin, N. A. M.
(2010). A proposed semantic recommendation system
for e-learning: A rule and ontology based e-learning
recommendation system. In 2010 International Sym-
posium on Information Technology, volume 1, pages
1–5.
Sinharay, S., Johnson, M. S., and Stern, H. S. (2006).
Posterior predictive assessment of item response the-
ory models. Applied Psychological Measurement,
30(4):298–321.
Spalenza, M. A., Nogueira, M. A., de Andrade,
L. B., and Oliveira, E. (2018). Uma Fer-
ramenta para Minerac¸
˜
ao de Dados Educacionais:
Extrac¸
˜
ao de Informac¸
˜
ao em Ambientes Virtuais
de Aprendizagem. In Anais do Computer on
the Beach, pages 741–750, Florian
´
opolis, Brazil.
https://computeronthebeach.com.br/.
Timms, M. J. (2007). Using item response theory (IRT)
to select hints in an ITS. In Luckin, R., Koedinger,
K. R., and Greer, J. E., editors, Artificial Intelli-
gence in Education, Building Technology Rich Learn-
ing Contexts That Work, Proceedings of the 13th Inter-
national Conference on Artificial Intelligence in Ed-
ucation, AIED 2007, July 9-13, 2007, Los Angeles,
California, USA, volume 158 of Frontiers in Artificial
Intelligence and Applications, pages 213–221. IOS
Press.
Traub, R. E. (1997). Classical test theory in historical per-
spective. Educational Measurement, 16:8–13.
van der Linden, W. J. and Hambleton, R. K. (2013). Hand-
book of modern item response theory. Springer Sci-
ence & Business Media.
Wauters, K., Desmet, P., and Van Den Noortgate, W. (2010).
Adaptive item-based learning environments based on
the item response theory: possibilities and challenges.
Journal of Computer Assisted Learning, 26(6):549–
562.
Yeung, C. (2019). Deep-irt: Make deep learning based
knowledge tracing explainable using item response
theory. In Desmarais, M. C., Lynch, C. F., Merceron,
A., and Nkambou, R., editors, Proceedings of the 12th
International Conference on Educational Data Min-
ing, EDM’19, Montr
´
eal, Canada, July 2-5, 2019. In-
ternational Educational Data Mining Society.
CSEDU 2020 - 12th International Conference on Computer Supported Education
268
