
Map Attribute Validation using Historic Floating Car Data and
Anomaly Detection Techniques
Carl Esselborn
1
, Leo Misera
1
, Michael Eckert
1
, Marc Holzäpfel
1
and Eric Sax
2
1
Dr. Ing. h.c. F. Porsche AG, Weissach, Germany
2
Department of Electrical Engineering, Karlsruhe Institute of Technology, Karlsruhe, Germany
Keywords: Map Data, Validation, Floating Car Data, Anomaly Detection, Autoencoder, Yield Signs.
Abstract: Map data is commonly used as input for Advanced Driver Assistance Systems (ADAS) and Automated
Driving (AD) functions. While most hardware and software components are not changed after releasing the
system to the customer, map data are often updated on a regular basis. Since the map information can have a
significant influence on the function’s behavior, we identified the need to be able to evaluate the function’s
performance with updated map data. In this work, we propose a novel approach for map data regression tests
in order to evaluate specific map features using a database of historic floating car data (FCD) as a reference.
We use anomaly detection methods to identify situations in which floating car data and map data do not fit
together. As proof of concept, we applied this approach to a specific use case finding yield signs in the map,
which are currently not present in the real world. For this anomaly detection task, the autoencoder shows a
high precision of 90% while maintaining an estimated recall of 45%.
1 INTRODUCTION
Map data is a common input for automated driving
(AD) functions and Advanced Driver Assistance
Systems (ADAS), complementing the vehicle’s on-
board sensors as an additional, virtual sensor. The
map information, provided as electronic horizon
(Ress, Etermad, Kuck, & Boerger, 2006), enables
anticipatory driving by extending the sight distance of
the vehicle’s on-board sensors. Especially
longitudinal control functions benefit from
knowledge about the upcoming road section and
allow for a very comfortable and smooth driving
style. An example is the predictive deceleration on an
upcoming yield or stop sign or a speed limit which is
substantially lower than the current driving speed of
the vehicle. In that case, the driving function can start
to reduce the vehicle’s speed even before the driver
or the conventional sensors recognize the respective
traffic sign (Albrecht & Holzäpfel, 2018). Thus, the
driving function can approximate the driving style of
a very experienced driver, who already knows the
route, without having to drive too carefully.
However, map data present only a snapshot of the
road network from the moment the map was created.
Therefore, regular updates have to be provided to
keep the map up-to-date. From the perspective of an
Original Equipment Manufacturer (OEM), these map
updates bring new challenges. Currently, driving
functions for longitudinal and lateral control are
extensively tested as an overall system prior to market
release. Each change of one part of the overall system
after the function’s release requires considering
possible negative effects on other components of the
system. Updated map data present a new sensor input,
which has to be validated. Using methods of
functional decomposition, the testing activities can be
reduced substantially (Amersbach & Winner, 2017),
if the respective software component allows for a
direct validation.
Most of the map attributes are not directly safety
relevant, due to the redundancy given by the on-board
sensors. Additionally, the systems currently on the
market (SAE International level < 3) rely on the
responsibility of the driver, who has to interfere in case
of a malfunction. However, to increase the usability
and thus the driver’s satisfaction, the accuracy of map
data is still a topic of high priority for OEMs.
In this contribution, we focus on predictive
longitudinal control functions that plan and adjust the
vehicle’s speed. We propose a scalable method to
evaluate map attributes based on speed information
from floating car data. With this approach, we enable
504
Esselborn, C., Misera, L., Eckert, M., Holzäpfel, M. and Sax, E.
Map Attribute Validation using Historic Floating Car Data and Anomaly Detection Techniques.
DOI: 10.5220/0009425905040514
In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2020), pages 504-514
ISBN: 978-989-758-419-0
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

regression tests for map data and we are able to keep
up with high frequency map updates.
The remainder of this paper is organized as
follows. In the related work (section 2), existing
approaches to map inference and update are
structured depending on the applied data source and
the addressed map attributes. Based on our map
evaluation concept using floating car data with speed
information, presented in section 3, an exemplary
implementation of an anomaly detection technique
follows in section 4. This work is concluded with an
evaluation (section 5) and the conclusion (section 6).
2 RELATED WORK
Map data can be divided into SD and HD maps. While
SD maps originate from navigation systems, HD
maps have been developed specifically for the
application in automated driving. However, SD maps
can contain most of the information relevant for a
longitudinal control, without knowledge about the
lane individual road layout. Therefore, we do not
restrict our approach to HD maps only.
The maps, currently employed in production
systems, are captured by map providers, for example
HERE
1
or Ushr
2
, with a fleet of reference vehicles
equipped with precise sensors for environment
representation (Rogers, 2000). After the initial map
creation, the fleet is used to update the map
incrementally. This approach ensures a high quality
of the recorded map data. However, the limited
number of mapping vehicles and the great extent of
the road network results in low update rates.
An alternative is to combine crowd-sourced
ground and aerial images and extract the road
characteristic. While the aerial images provide an
absolute location, the ground images offer detailed
information about road attributes (Máttyus, Wang,
Fidler, & Urtasun, 2016). However, the accuracy of
the inferred map strongly depends on the quality of
the available images.
Since longitudinal control functions use map data
to derive a velocity, it seems obvious to examine
crowd-sourced speed data in order to evaluate the
respective map data. While a lot of research already
makes use of floating car data for map inference, most
of the approaches aim at deriving road and lane
geometries (section 2.1). Relating to the map layer
model presented by PEGASUS
3
, the road geometry
information can be associated with the street level
1
https://www.here.com/products/automotive/hd-maps
2
https://www.ushrauto.com/our-story-1
(level 1). For longitudinal control, many map
attributes are located on level 2, including road signs
like speed limits and other signs representing the
traffic rules. In the following, we will give an
overview about existing approaches for the use of
floating car data for map inference and update. Based
on that, we show how the speed component from
floating car data is currently used for traffic analytics.
2.1 Map Inference from Floating Car
Data
In order to create lane accurate maps of the road
geometry without the expensive and resourceful use
of dedicated mapping vehicles, research has focused
on approaches based on floating car data. These
approaches make use of GNSS data in combination
with different other data sources, like for example
odometry data to achieve a sufficiently accurate
position information (Biagioni & Eriksson, 2012).
Concepts, which use traces of position data, can
benefit from the knowledge that consecutive data
samples belong together. In that case, even sparse
GPS traces with a sampling rate of 1 minute can still
be useful to infer road geometry (Liu, et al., 2012).
With increasing number of connected vehicles, an
infrastructure supporting the probe data management
is necessary in order to derive road geometry for HD
maps (Massow, et al., 2016).
When calling in objects detected by the probe
vehicles a simultaneous location and mapping
approach enables the crowdsourced generation of HD
map patches (Liebner, Jain, Schauseil, Pannen, &
Hackelöer, 2019). Focusing on high frequency GPS
traces and applying deep learning classification
techniques, an accurate speed information can be
derived and makes it possible to infer further map
attributes like traffic lights, street crossings and urban
roundabouts (Munoz-Organero, Ruiz-Blaquez, &
Sánchez-Fernández, 2018).
Continuous traces of floating car data also allow
for the detection and localization of traffic signals
based on the spatial distribution of vehicle stop
points, when applying map inference techniques like
a random forest classificator (Méneroux, et al., 2018).
2.2 Map Update and Validation
The introduced work on map inference is basis for also
using floating car data in order to update and validate
already existing map data. Starting from GPS traces,
3
https://www.pegasusprojekt.de/files/tmpl/PDF-
Symposium/04_Scenario-Description.pdf
Map Attribute Validation using Historic Floating Car Data and Anomaly Detection Techniques
505

which are matched to the existing road network in the
map data, semantic relationships can help to find road
sections that need an update with respect to the road
geometry (Li, Qin, Xie, & Zhao, 2012). For the high
accuracy of the road geometry in HD maps, research
shows that a change detection can be realized using a
SLAM approach combined with a set of weak
classifiers (Pannen, Liebner, & Burgard, 2019).
Apart from the road geometry, further map
attributes including the directionality, speed limit,
number of lanes, and access can be automatically
updated by means of full GPS trajectories (Van
Winden, Biljecki, & Van der Spek, 2016). However,
the accuracy of that approach, especially for the speed
limit, is not high enough to be directly used in an
automotive application. For a higher accuracy when
inferring map attributes, floating car data can be
useful in combination with a manual update based on
the recorded video stream from probe vehicles
(Ammoun, Nashashibi, & Brageton, 2010). The
disadvantage of that approach is the reduced
scalability due to the necessary human effort.
For slope and elevation information in digital map
data, existing validation methods still rely on a fleet
of vehicles equipped with reference sensors (Kock,
Weller, Ordys, & Collier, 2014), which is not easily
scalable, if the whole road network is to be covered.
Besides the algorithms for inferring map
information, research also provides concepts for a
map update protocol (Jomrich, Sharma, Rückelt,
Burgstahler, & Böhnstedt, 2017).
2.3 Further Research on Traffic Data
In recent years, floating car data (FCD) has gained
attention in traffic research as an alternative to
stationary loop collectors for analyzing traffic speed.
While the information value of the data varies
substantially, a broad range of different use cases has
emerged. One part of the traffic data is spatial
information, e.g. a GNSS position, which is common
to all approaches in literature. Additionally, traffic
data can contain speed information associated with
the position reference.
This setup is often used for travel time estimation
and prediction. The floating car data can be obtained
from mobile devices, which are carried while
travelling (Herrera, et al., 2010). In addition to a
GNSS position, the speed information can also be
referenced to a link of the road network (De Fabritiis,
Ragona, & Valenti, 2008). In this context, a link is the
map-representation of a defined road segment. Since
not every vehicle participating in traffic is providing
its speed information, the traffic conditions often
have to be estimated based on sparse probe data using
probabilistic modelling frameworks, such as Coupled
Hidden Markov Models (Herring, Hofleitner, Abbeel,
& Bayen, 2010).
Other approaches try to learn the travel dynamics
from sparse probe data by applying probabilistic
models in combination with a hydrodynamic traffic
theory model (Hofleitner, Herring, Abbeel, & Bayen,
2012). As an alternative to calculating a link-based
travel time, other methods suggest a route-based
travel time estimating based on low frequency speed
data (Rahmani, Jenelius, & Koutsopoulos, 2015). In
order to expand the often-sparse database, research on
multi-sourced data showed how to use a combination
of sparse GPS and speed data as well as social media
event data to give a traffic estimation.
Apart from routing implementations and traffic
predictions, speed data can also be used to analyze
road traffic networks supporting the development of
smart traffic management systems and giving route
recommendations to commuters (Anwar, Liu, Vu,
Islam, & Sellis, 2018). Other applications include the
analysis of the driving behavior by means of
observational smartphone data (Lipkowitz &
Sokolov, 2017) or the derivation of traffic scenarios
in the context of the development of driver assistance
systems (Zofka, et al., 2015).
2.4 Anomaly Detection
Finally, we give a rough overview of current anomaly
detection techniques as a basis for the selection of a
suitable approach to be applied to our dataset in this
work. An extensive summary of different approaches
to detect anomalies is provided by Chandola et al.
(Chandola, Banerjee, & Kumar, 2009). They divided
approaches for anomaly detection into different
categories. For each category, possible algorithms are
indicated.
Classification-based algorithms can be trained
certain characteristics of normal or abnormal data. In
the testing phase, new data can be classified given the
trained model. In multi-class classification there are
multiple normal classes opposed to just a single normal
class in one-class classification. Implementations of
classification-based anomaly detectors can leverage,
for example, neural networks (Williams, Baxter, He,
Hawkins, & Gu, 2002), Bayesian networks (Barbara,
Wu, & Jajodia, 2001), support vector machines
(Rätsch, Mika, Schölkopf, & Müller, 2002), or rule-
based techniques (Mahoney & Chan, 2003).
Anomaly detection techniques based on nearest
neighbor algorithms make use of a measure of
distance or density of neighboring data points.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
506

Anomalies are expected to lie in an area far away
from their neighbors. K-th
nearest neighbor is a
popular implementation taking into account the
distance of each data sample to its k-th nearest
neighbor (Guttormsson, Marks, El-Sharkawi, &
Kerszenbaum, 1999).
Clustering-based approaches can find anomalies in
different ways. For example, anomalous data instances
can be revealed when they belong to no cluster. (Guha,
Rastogi, & Shim, 2000) and (Ester, Kriegel, Sander,
Xu, & others, 1996) presented clustering algorithms
suitable for this particular case, because data samples
are not forced to belong to any cluster.
In statistical anomaly detectors, a statistical model
is created. When a data point lies in a region of low
probability according to the statistical model, it is
considered an anomaly (Eskin, 2000).
In techniques based on information theory,
anomalies are assumed to have an effect on the
information content and complexity of the data set.
Possible measures are entropy (He, Deng, Xu, &
Huang, 2006) or Kolmogorov Complexity (Keogh,
Lonardi, & Ratanamahatana, 2004).
The last category of anomaly detectors presented
by (Chandola, Banerjee, & Kumar, 2009) is spectral
anomaly detection. It is tried to find subspaces in
which anomalies can be identified more clearly.
Principal component analysis (PCA) is commonly
used for anomaly detection (Dutta, Giannella, Borne,
& Kargupta, 2007).
3 MAP EVALUATION CONCEPT
USING FLOATING CAR DATA
The existing approaches presented in section 2 cannot
be applied to the validation of the attribute layer (map
level 2) of maps for automated driving. Focusing on
map features that influence the longitudinal control of
a vehicle, relevant map attributes include speed
limits, yield and stop signs as well as road curvatures.
We seek for a scalable approach that can be
applied to the map data of a whole country as easily
as of a city without requiring considerably more
resources. Thus, concepts that need manual tagging
by humans beyond limited training data are not
scalable in this sense. So far, only the process of road
geometry inference exists in a scalable kind.
3.1 Map Inference Concept
In order to avoid the resourceful and time-consuming
manual evaluation of those map attributes we propose
a novel and scalable approach using processed and
aggregated speed information from floating car data
as a reference source. The schematic diagram in
Figure 1 shows the main idea for using floating car
data for map validation. The upper half of the scheme
describes how the floating car data is created. Drivers
choose their vehicle’s speed depending on the
environment, which can be described as a scenario.
From that scenario, we are interested in one attribute,
which is also represented in the map data and object
of our validation. The rest of the environmental
impacts are collected in the scenario context. An
exemplary map attribute could be the speed limit,
which influences the driver’s speed choice. The same
speed limit in different environments can lead to
different vehicle speeds. Those influences are
represented in the scenario context. From the driving
behavior of one driver, it is difficult to derive
meaningful information. However, if the floating car
data of multiple traffic participants is aggregated over
a longer time period, regularities become visible. This
is substance of the lower half of the scheme. Taking
into account the same context information during
FCD-generation, we try to derive the looked for map
attributes from the aggregated and processed speed
information.
Figure 1: Concept scheme for using floating car data for to
derive speed related map features.
This indirect approach requires many data pre-
processing due to the numerous influencing factors
during formation of the FCD. However, it comes with
a variety of advantages. No continuous traces of FCD
are necessary, which increases the usable database
data and therefore allows for a high coverage of the
road network with speed data. Another advantage is
the interpretation of the respective scenario by the
Longitudinal
driver behavior
Map
attribute
(reality)
Vehicle speed
Inverse
longitudinal
driver model
processed speed
information
Spatio-temporal
aggregation
Scenario context
information
Map
attribute
(inferred)
FLOATING CAR DATA GENERATION (REAL WORLD)
DATA PROCESSING AND INFERENCE
Map Attribute Validation using Historic Floating Car Data and Anomaly Detection Techniques
507

driver and therefore a human being. While computer
vision based sensors are proficient in detecting and
reading traffic signs, they often still lack ability to
interpret which sign really applies.
The scenario context information depicted in
Figure 1 is a critical factor when interpreting the
FCD. Many of those elements of the context
information can be gained from other map attributes,
which are not being evaluated. Other, mostly dynamic
elements like the influence of weather remain as
uncertainty in the data driven model.
Before proving the feasibility of this concept on a
practical example, the characteristics of the FCD are
introduced.
3.2 Characteristics of the Used Floating
Car Data
The floating car data used for this concept has already
been preprocessed in order to reduce the data volume
and therefore enabling an extensive storing of
historical speed data. The preprocessing consists of
several steps. Starting point is the raw probe data
consisting of the current speed of the vehicle together
with the current absolute position. These probes are
matched on a road segment using map-matching
methods. If a vehicle transmits more than one speed
measurement for the same road segment, these speeds
are averaged. In the second step, the mean segment
speeds from every vehicle that transmits at least one
piece of speed information in a period of one hour are
used to generate a frequency distribution of the
velocity. The distribution is represented by every 5th
percentile, ranging from 0 to 100% and additionally
the absolute number of vehicles that contributed to
this distribution.
This approach comes with the advantage of low
memory requirements that are also independent of the
number of vehicles that transmit probe data for a
specific road segment in a specific period. However,
there is also a disadvantage in terms of a reduced
precision depending on the road segment’s length.
Since the individual speed measurements, which are
matched to one road segment, are averaged, the
information about the spatial progression of the speed
on a road segment is lost. Therefore, the length of the
road segments limits the applicability of these data for
further analysis. For an exemplary road segment on a
freeway with speed limit 100 km/h, Figure 2 shows
the influence of the considered period and therefore
the absolute number of vehicles that contribute to the
velocity distribution. Since only a fraction of all
vehicles sends information to the speed data service
used for this work the regarded period has to be long
enough to encompass a sufficient number of vehicles.
Figure 2: Influence of the number of vehicles contributing
to the speed distributing for an exemplary link
4 EXAMPLARY
IMPLEMENTATION
In order to proof our concept we apply the method on
yield signs, which are represented as attribute in the
map data. This attribute enables an automated driving
function to decelerate anticipatorily even if the on-
board camera of the vehicle has not recognized the
traffic sign yet. Therefore, the yield sign feature can
increase the comfort for the passengers significantly,
but also poses the risk of an unnecessary deceleration,
if there is a yield sign in the map, but not in reality.
The other case, where there is a sign in reality, which
is not incorporated in the map data, can be better
covered by the redundancy given by the camera.
Therefore, we want to identify all yield signs in
the map data that have no equivalent in reality. This
proof of concept is only one example of several
applications, where FCD can be used as a source for
validation. Yield signs represent only short, distinct
events during a drive, which makes it easier to deploy
the developed methods. However, the same approach
can be applied to other above mentioned map
attributes that influence the longitudinal control of a
vehicle, for example the speed limit information.
In the following, we give a short description of the
used data set and the necessary preprocessing of the
floating car data. This is followed by an anomaly
detection method to identify wrong yield signs in the
map data.
rel. Frequency
r
el. F
r
e
q
uency
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
508
4.1 Dataset Preparation and
Characteristics
The present map data consist of a graph-like structure
of nodes and links. Two links are connected by one
node. The road geometry is represented by the
absolute position of the nodes as coordinates relating
to the World Geodetic System (WGS84). An event
where the vehicle has to yield to other traffic is always
located at a point where several links connect to each
other. Therefore, the yield sign is clearly defined by a
node and the link, on which the vehicle is
approaching the node.
For this proof of concept, we created a dataset
containing all intersections in Germany that have at
least one yield sign with no traffic light present. Links
with traffic lights are excluded, because the traffic
light overrules the effect of the yield sign. From these
chosen intersection-nodes, we identified all links that
connect to the nodes.
From that set, we remove all intersections that
connect a ramp to a controlled access road. These
cases are excluded since vehicles normally accelerate
in order to merge into the traffic on the controlled
access road rather than slowing down for yielding.
Thereby the dataset is reduced by 4.9%.
For all remaining links, we aggregate the historic
FCD for the four months period from May to August
2019. Links on smaller roads, where fewer vehicles
operate on, are filtered out, if equal or less than 50
cars have transmitted speed data. This measure
reduces the dataset by another 25.1%, but makes sure
that the data basis is sufficient to infer meaningful
decisions.
Besides the speed data distribution for each link
in the dataset, also some context information is given
by the map data, including the possible travel
direction on the link, the speed limit for the link and
the length of the road segment, which the link
represents. Based on the context information, the
dataset is further cleaned. Edges with one-way traffic
leaving the node are filtered out, since from this edge
no vehicle is supposed to enter the intersection. In
addition, links with rare speed limits of 5, 10, 20, 25,
90, 110, 120, and 130 km/h are filtered out, leading to
a reduction of 1.8%. The resulting speed limit
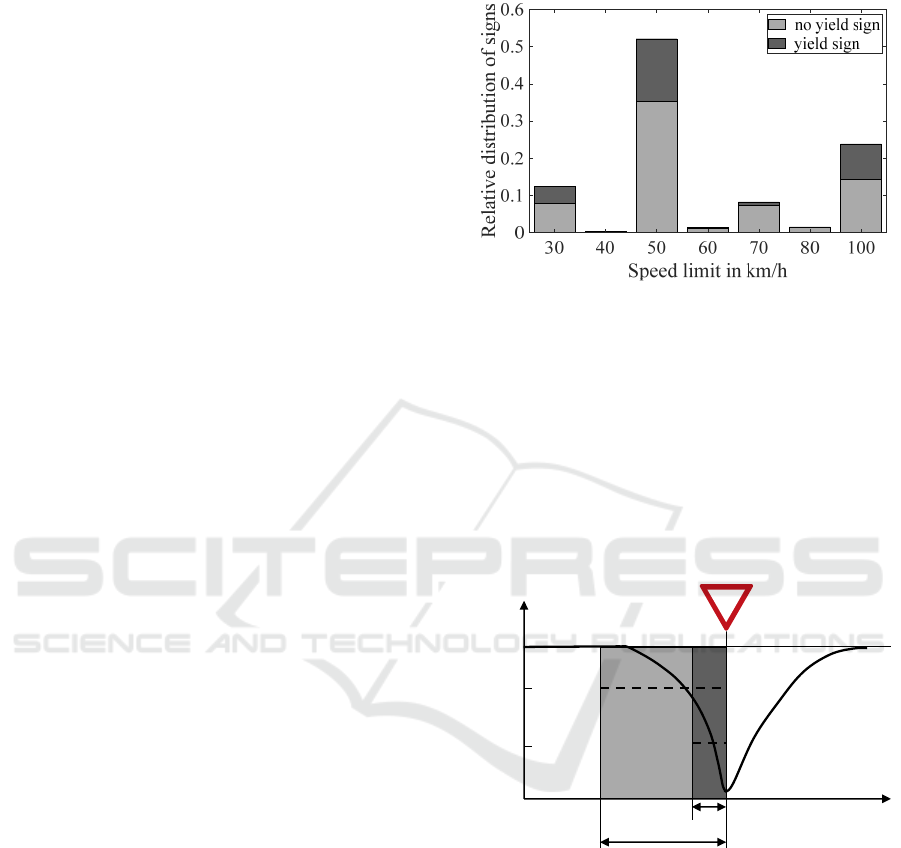
distribution is shown in Figure 3.
Since the reaction on an upcoming yield sign leads
to a deceleration, the velocity course on the road
section in front of the yield sign is not constant.
However, the FCD only provide a mean velocity of
the vehicle along the edge. Therefore, the given mean
velocity heavily depends on the length of the link,
which is illustrated in Figure 4. A short link with
length l
1
has a much lower mean speed ̅
than a
longer link with mean speed ̅
.
Figure 3: Link speed limit distribution in dataset.
The link length
is defined within the map data
and it varies depending on the road structure as well
as the road attributes. A road section is split into
several links if at least one road attribute changes, e.g.
the speed limit, since the attributes have to be
constant along one link. For very long links, the
deceleration process at the end of the link, just before
the yield sign, has almost no weight in the resulting
mean link speed. Thus, links with a length
> 500 m
are filtered out, resulting in a reduction of 3.1%.
Figure 4: Schematic speed course at an intersection with a
yield sign.
Besides the link length
, the speed limit
,
,
which is valid on the edge i, has an important
influence on the resulting average link velocity ̅
,
which can be seen from Figure 4. The higher the
speed limit the higher is the velocity from which
vehicles are expected to slow down for a yield sign.
Therefore, the deceleration phase is expected to be
longer for higher speed limits. The final dataset
covers 76.8% of all yield signs, which are registered
in the map data in Germany.
Speed
Distance
l
l
̅
1
2
̅
Map Attribute Validation using Historic Floating Car Data and Anomaly Detection Techniques
509
4.2 Annotation of Samples
In order to give an estimate of the recall of the
anomaly detector and to provide a basis for the
hyperparameter tuning in the following anomaly
detection approach using an autoencoder (AE), we
created a validation set with annotated samples. For
every sample in the validation set, we investigate the
true label indicating the presence of a yield sign in
reality.
Satellite images provide the necessary
information. Especially the type of lane markings on
each of the road segments leading to the intersection
is a good indicator to determine the true yield sign
label. Since satellite images are only a snapshot of the
respective situation, we made sure to only use up-to-
date images. A proportion of 3.6% of the annotation
set cannot be annotated unambiguously. In these
cases the quality of the image is insufficient or it is
not possible to detect lane markings clearly, e.g.
caused by occlusion by trees. The validation data set
contains 1,951 samples.
4.3 Selection of Anomaly Detection
Algorithms
The challenge is to select an algorithm that can
distinguish between links with a yield sign and links
without a yield sign, based on a given set of features.
In section 2.5 we presented various categories of
anomaly detection algorithms. Many different
approaches can lead to good results.
A supervised anomaly detector requires a
sufficient number of normal and abnormal samples
with annotations, preferably in a balanced data set. In
a semi-supervised approach, a data set with only
normal or only abnormal data has to be available. In
the unsupervised case, the model is trained with data
that contains much more normal than abnormal data
(Chandola, Banerjee, & Kumar, 2009). From
annotating the validation set (section 4.2) we know
that this property holds true for our annotated
validation data set. We assume the same property for
the full data set, since the validation set is a randomly
selected subset of the complete data set. This means
that most yield sign labels are correct. Consequently,
we can use an unsupervised approach and we do not
have to annotate a large data set.
Based on this dataset, we implemented two
anomaly detection algorithms. The approach
leveraging AEs outperformed our rule-based
statistical approach. For the sake of conciseness, we
only present the AE-based anomaly detector to show
a proof of concept.
4.4 Anomaly Detection using
Autoencoders (AEs)
The AE-based approach is straightforward, fast to
implement and effective. Bottleneck AEs are a
powerful tool capable of learning compact non-linear
representations of the data without needing annotated
training data. AEs are replicator neural networks
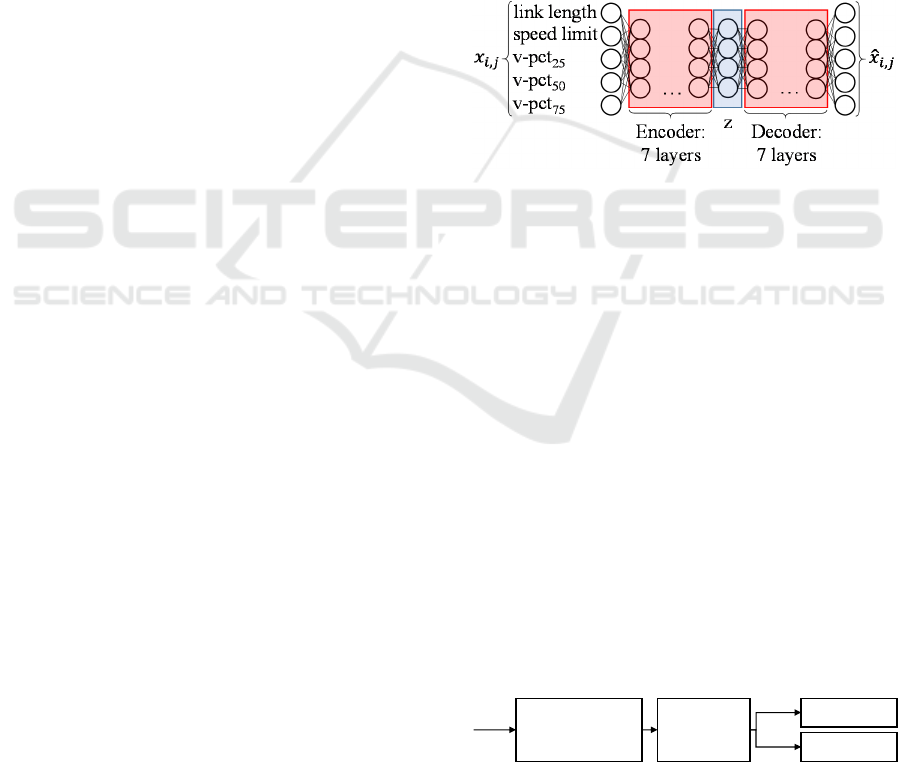
(NNs). The encoder NN compresses the data to a
compact vector z as shown in Figure
5
. The decoder
NN then reconstructs the sample given the latent
vector z (Goodfellow, Bengio, & Courville, 2016).
Data points that are similar to the training data are
expected to be reconstructed with a low error. In
contrast, anomalous data is assumed to be
reconstructed with a high error. The reconstruction
error can therefore be seen as a score for abnormality.
Figure 5: Architecture of the AE.
Feature selection is crucial for data-based
decision-making. For each link, the respective length
and speed limit are provided. On top of that,
information about the distribution of the average
velocity is included in the data set. We find that the
25th, the 50th and the 75th percentiles provide
sufficient information about the distribution to reveal
anomalies.
4.4.1 Training of the AEs
The training pipeline is shown schematically in
Figure 6. Before feeding the training data to the
networks, it is normalized column-wise to values
between 0 and 1 to improve the training behavior of
both AEs. The anomaly detection network consists of
two bottleneck AEs. At first, the data is split into two
separate data sets based on their label that is provided
in the map data. It is worth emphasizing that the map
data contains anomalies that we seek to detect.
Figure 6: Training pipeline of the AEs.
Column-wise
normalization
Data split
Train AE
0
Train AE
1
yield
1
yield
0
Data
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
510
The first fraction only contains the data with yield
sign label = 1. In the following sections, we call this
data set yield
1
. The first AE is only trained with data
set yield
1
and is therefore called AE
1
.
The second fraction only contains the data with
yield sign label = 0. This data set is called yield
0
.
Consequently, the AE trained with data set yield
0
is
called AE
0
.
Given the analysis of the annotated validation set,
we can assume the amount of normal instances to be
a lot larger than the amount of anomalies in our data
set. Therefore, both AEs are expected to reconstruct
abnormal data samples with a major error than normal
samples.
4.4.2 Anomaly Detection Step
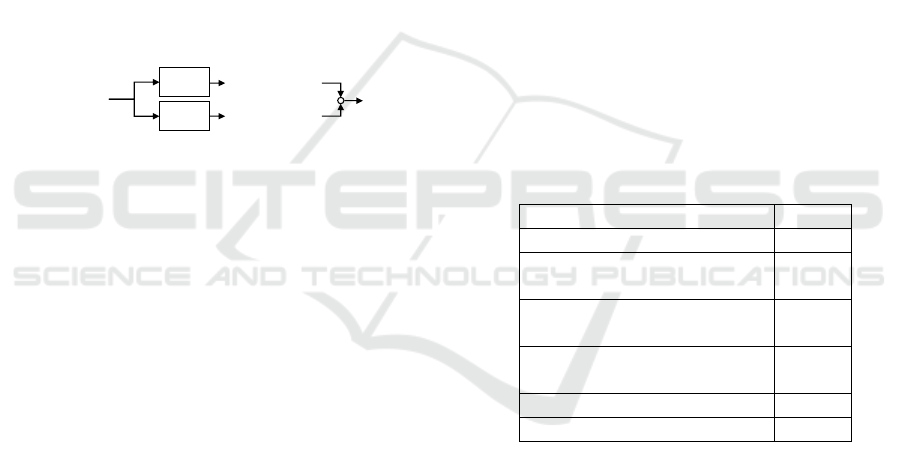
The evaluation procedure is illustrated in Figure 7.
The objective of the proposed AE approach is to
detect samples in the yield
1
set that in fact belong to
yield
0
meaning that their true yield sign label = 0.
Figure 7: Evaluation procedure of the AE.
We denote them as false positive samples. These
are expected to have a high reconstruction error in
AE
1
. Consequently, the reconstruction error of AE
0
is
assumed minor.
,
,
,
,,
(1)
,
,
,
,,
(2)
,
,
,
,
,
(3)
Each sample in the yield
1
set is passed to both
AEs. In each AE the total reconstruction error of
sample i is calculated by taking the sum over the
absolute reconstruction errors of each column j
following equations (1) and (2). Calculating the
column-wise absolute reconstruction error resulted in
higher precision in anomaly detection than the
column-wise squared reconstruction error. The total
reconstruction error of sample i in AE
1
is then
subtracted by the reconstruction error in AE
0
as
shown in equation (3). A high error difference
indicates a false positive.
4.4.3 Hyperparameter Tuning
The training of the two AEs is performed in an
unsupervised manner, since we do not know which
samples are anomalies. However, the performance of
the models has to be evaluated to determine a good
set of hyperparameters. For this purpose, we use the
annotated validation set, described in chapter 4.2.
The best set of hyperparameters is determined
empirically. These define the architecture of the AEs
and the learning parameters. For the sake of
simplicity, AE
0
and AE
1
are assigned the same set of
hyperparameters. Encoder and decoder always have
the same shape.
Table 1 shows the hyperparameters we optimize
and the resulting values. We use ADAM as an
optimizer and mean squared error as loss function. An
exponential linear unit (ELU) activation function is
used in all but the last layer and sigmoid activation in
the last layer to limit the output to values between 0
and 1. In Figure
5, the architecture is illustrated. The
hyperparameters are optimized by observing how
many false positive samples in the annotated dataset
are detected by each of the different configurations
with a precision of more than 0.9.
Table 1: Optimized hyperparameters.
Parameter Value
Number of epochs 20
Number of neurons
(intermediate layer z)
4
Number of neurons
(encoder/decoder layers)
4
Number of
encoder/decoder layers
7
Batch size 32
Learning rate 0.0001
The AEs with the best performing
hyperparameters are then used to predict false
positive samples in the whole yield
1
data set. The
outputted list contains all samples sorted by their
reconstruction error difference defined in equation
(3). The performance is evaluated in section 5.
5 EVALUATION
For the evaluation of the presented anomaly detection
approach on map data and FCD, we are interested in
two metrics, namely precision and recall. Precision
describes which percentage of the found anomalies
are true anomalies. Recall is a measure for the
∈
AE
0
AE
1
,
,
,
,
‐
,
Map Attribute Validation using Historic Floating Car Data and Anomaly Detection Techniques
511
percentage of revealed true anomalies compared to all
anomalies in the given dataset.
In order to define recall one has to annotate the
whole dataset. We estimate recall by using the
annotated validation dataset which was initially used
to define the hyperparameters. Since that dataset has
been selected randomly, we assume the percentage of
false positives in the validation data set to be roughly
the same as in the complete dataset. Therefore, we can
extrapolate the number of expected anomalies to the
whole dataset.
In order to evaluate precision, we carry out a
second annotation round on the samples that the
anomaly detection methods declared as anomalous.
Since the output is ranked according to an anomaly
score, a decreasing precision is expected with
declining anomaly score. Thus, we are interested in
the course of the precision over the ranked output of
the anomaly detector.
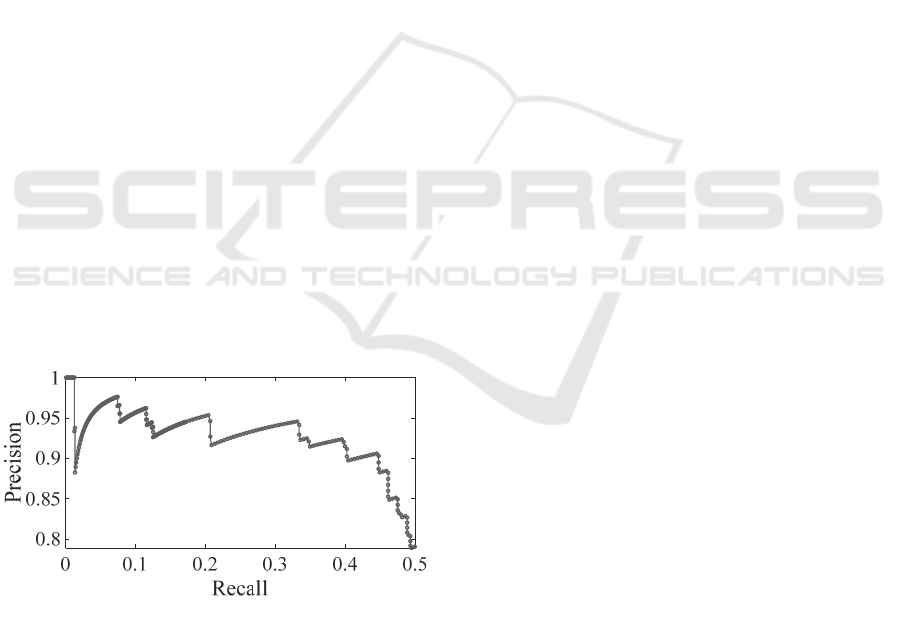
To accelerate the annotation process, while still
capturing the course of the precision, the first 200
samples and afterwards every fifth sample are
annotated manually. That way we get a precision
estimate for the first 700 instances of the list, which
is shown in Figure 8. For the calculation of the
precision, the annotations for the samples 201 to 700
are weighted with the factor 5 in order to take into
account the different sampling.
Figure 8 shows that the AE approach can keep its
high precision of around 90% still at a recall of 45%.
For the use case of map evaluation, a high precision
is of much higher importance than a high recall.
Therefore, we did not analyze the further course of
the precision with increasing recall.
Figure 8: Precision over recall for the AE approach.
It is worth mentioning that many wrongly
detected anomalies lead to a few intersection types,
where our approach does not work. For intersection
that are well observable even from distance and with
only little traffic, our assumption that drivers have to
slow down in order to yield, does not hold. In this
case, drivers can cross an intersection without
slowing down considerably, which is reflected in the
FCD. Another example where drivers do not tend to
decelerate is on ramp-like roads that run almost
parallel to the road with right of way, but which are
not freeway ramps. The freeway ramps have been
filtered out in the dataset preparation step.
6 CONCLUSION AND FUTURE
WORK
In this work, we presented a new approach to evaluate
map features that are relevant for evaluation of map
features for longitudinal control of automated driving
function based on FCD. An extensive analysis of
existing related work on map evaluation, inference,
and applications of FCD was conducted. While most
of the literature focusses on road geometry inference,
for specific map attributes, including traffic signs, no
scalable methods exist. We introduced our new
concept of deriving map attributes from aggregated,
spatio-temporal FCD and demonstrated the feasibility
with a proof of concept.
We showed that we could find an estimate of 45%
of all wrong yield signs with a precision of 90% in a
set of outdated map data by using processed FCD as
a reference. It should be noted that this performance
is reached with relatively simple techniques.
This method can help map providers and OEMs
to improve the digital map data for automated driving.
This is relevant even for higher levels of automation,
since information from an electronic horizon
provided by a map mainly serves comfort related
tasks. A driving function can respond to an upcoming
event anticipatorily and increase the comfort for the
passengers. However, if the map information is
faulty, the redundant on-board sensors interfere.
Therefore, our method can be applied to both assisted
and automated driving functions.
Although many true anomalies have been found
with relatively low effort, the approach has its
limitations. The biggest one is that it is only
applicable to speed related map features.
Additionally, the method can only be as good as the
underlying database of FCD.
Having shown the general feasibility, future
research can focus on three main topics. Building on
the first implemented anomaly detection approaches,
more sophisticated techniques could be evaluated.
While the feature selection was mainly based on
logical reasoning, a more data driven strategy could
bring further improvements.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
512

While the FCD as major reference source for the
anomaly detection are just aggregated for each link, a
thorough data preprocessing can potentially help to
improve the precision even with a higher recall.
Influences from heavy traffic and weather could be
filtered out in a data preparation step.
The third and biggest open research topic is the
application of the map validation concept to other,
more complex map features. The speed limit as a map
attribute was already mentioned. While yield signs
are single events with a relatively low occurrence, the
speed limit is a map attribute available on every link
in the road network and subject to relatively high
change frequencies.
REFERENCES
Albrecht, M., & Holzäpfel, M. (2018). Vorausschauend
effizient fahren mit dem elektronischen Co-Piloten.
ATZextra, 23, 34-37.
Amersbach, C., & Winner, H. (2017). Functional
decomposition: An approach to reduce the approval
effort for highly automated driving. 8. Tagung
Fahrerassistenz.
Ammoun, S., Nashashibi, F., & Brageton, A. (2010).
Design of a new GIS for ADAS oriented applications.
2010 IEEE Intelligent Vehicles Symposium, (S. 712-
716).
Anwar, T., Liu, C., Vu, H. L., Islam, M. S., & Sellis, T.
(2018). Capturing the spatiotemporal evolution in road
traffic networks. IEEE Transactions on Knowledge and
Data Engineering, 30, 1426-1439.
Barbara, D., Wu, N., & Jajodia, S. (2001). Detecting novel
network intrusions using bayes estimators. Proceedings
of the 2001 SIAM International Conference on Data
Mining, (S. 1-17).
Biagioni, J., & Eriksson, J. (2012). Inferring road maps
from global positioning system traces: Survey and
comparative evaluation. Transportation research
record, 2291, 61-71.
Chandola, V., Banerjee, A., & Kumar, V. (2009). Anomaly
detection: A survey. ACM computing surveys (CSUR),
41, 15.
De Fabritiis, C., Ragona, R., & Valenti, G. (2008). Traffic
estimation and prediction based on real time floating car
data. Intelligent Transportation Systems, 2008. ITSC
2008. 11th International IEEE Conference on, (S. 197-
203).
Dutta, H., Giannella, C., Borne, K., & Kargupta, H. (2007).
Distributed top-k outlier detection from astronomy
catalogs using the demac system. Proceedings of the
2007 SIAM International Conference on Data Mining,
(S. 473-478).
Eskin, E. (2000). Anomaly detection over noisy data using
learned probability distributions.
Ester, M., Kriegel, H.-P., Sander, J., Xu, X., & others.
(1996). A density-based algorithm for discovering
clusters in large spatial databases with noise. Kdd, 96,
S. 226-231.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep
learning. MIT press.
Guha, S., Rastogi, R., & Shim, K. (2000). ROCK: A robust
clustering algorithm for categorical attributes.
Information systems, 25, 345-366.
Guttormsson, S. E., Marks, R. J., El-Sharkawi, M. A., &
Kerszenbaum, I. (1999). Elliptical novelty grouping for
on-line short-turn detection of excited running rotors.
IEEE Transactions on Energy Conversion, 14, 16-22.
He, Z., Deng, S., Xu, X., & Huang, J. Z. (2006). A fast
greedy algorithm for outlier mining. Pacific-Asia
Conference on Knowledge Discovery and Data Mining,
(S. 567-576).
Herrera, J. C., Work, D. B., Herring, R., Ban, X. J.,
Jacobson, Q., & Bayen, A. M. (2010). Evaluation of
traffic data obtained via GPS-enabled mobile phones:
The Mobile Century field experiment. Transportation
Research Part C: Emerging Technologies, 18
, 568-583.
Herring, R., Hofleitner, A., Abbeel, P., & Bayen, A. (2010).
Estimating arterial traffic conditions using sparse probe
data. Intelligent Transportation Systems (ITSC), 2010
13th International IEEE Conference on, (S. 929-936).
Hofleitner, A., Herring, R., Abbeel, P., & Bayen, A. (2012).
Learning the dynamics of arterial traffic from probe
data using a dynamic Bayesian network. IEEE
Transactions on Intelligent Transportation Systems, 13,
1679-1693.
Jomrich, F., Sharma, A., Rückelt, T., Burgstahler, D., &
Böhnstedt, D. (2017). Dynamic Map Update Protocol
for Highly Automated Driving Vehicles. VEHITS, (S.
68-78).
Keogh, E., Lonardi, S., & Ratanamahatana, C. A. (2004).
Towards parameter-free data mining. Proceedings of
the tenth ACM SIGKDD international conference on
Knowledge discovery and data mining, (S. 206-215).
Kock, P., Weller, R., Ordys, A. W., & Collier, G. (2014).
Validation methods for digital road maps in predictive
control. IEEE Transactions on Intelligent
Transportation Systems, 16, 339-351.
Li, J., Qin, Q., Xie, C., & Zhao, Y. (2012). Integrated use
of spatial and semantic relationships for extracting road
networks from floating car data. International Journal
of Applied Earth Observation and Geoinformation, 19,
238-247.
Liebner, M., Jain, D., Schauseil, J., Pannen, D., &
Hackelöer, A. (2019). Crowdsourced HD Map Patches
Based on Road Model Inference and Graph-Based
SLAM. 2019 IEEE Intelligent Vehicles Symposium
(IV), (S. 1211-1218).
Lipkowitz, J. W., & Sokolov, V. (2017). Clusters of Driving
Behavior from Observational Smartphone Data. arXiv
preprint arXiv:1710.04502.
Liu, X., Biagioni, J., Eriksson, J., Wang, Y., Forman, G., &
Zhu, Y. (2012). Mining large-scale, sparse GPS traces
for map inference: comparison of approaches.
Proceedings of the 18th ACM SIGKDD international
conference on Knowledge discovery and data mining,
(S. 669-677).
Map Attribute Validation using Historic Floating Car Data and Anomaly Detection Techniques
513

Mahoney, M. V., & Chan, P. K. (2003). Learning rules for
anomaly detection of hostile network traffic. Tech. rep.,
Third IEEE International Conference on Data Mining.
Massow, K., Kwella, B., Pfeifer, N., Häusler, F., Pontow,
J., Radusch, I., . . . Haueis, M. (2016). Deriving HD
maps for highly automated driving from vehicular
probe data. 2016 IEEE 19th International Conference
on Intelligent Transportation Systems (ITSC), (S. 1745-
1752).
Máttyus, G., Wang, S., Fidler, S., & Urtasun, R. (2016). Hd
maps: Fine-grained road segmentation by parsing
ground and aerial images. Proceedings of the IEEE
Conference on Computer Vision and Pattern
Recognition, (S. 3611-3619).
Méneroux, Y., Kanasugi, H., Saint Pierre, G., Le Guilcher,
A., Mustière, S., Shibasaki, R., & Kato, Y. (2018).
Detection and Localization of Traffic Signals with GPS
Floating Car Data and Random Forest. 10th
International Conference on Geographic Information
Science (GIScience 2018).
Munoz-Organero, M., Ruiz-Blaquez, R., & Sánchez-
Fernández, L. (2018). Automatic detection of traffic
lights, street crossings and urban roundabouts
combining outlier detection and deep learning
classification techniques based on GPS traces while
driving. Computers, Environment and Urban Systems,
68, 1-8.
Pannen, D., Liebner, M., & Burgard, W. (2019). HD map
change detection with a boosted particle filter. 2019
International Conference on Robotics and Automation
(ICRA), (S. 2561-2567).
Rahmani, M., Jenelius, E., & Koutsopoulos, H. N. (2015).
Non-parametric estimation of route travel time
distributions from low-frequency floating car data.
Transportation Research Part C: Emerging
Technologies, 58, 343-362.
Rätsch, G., Mika, S., Schölkopf, B., & Müller, K.-R.
(2002). Constructing boosting algorithms from SVMs:
An application to one-class classification. IEEE
Transactions on Pattern Analysis & Machine
Intelligence, 1184-1199.
Ress, C., Etermad, A., Kuck, D., & Boerger, M. (2006).
Electronic Horizon-Supporting ADAS applications
with predictive map data. PROCEEDINGS OF THE
13th ITS WORLD CONGRESS, LONDON, 8-12
OCTOBER 2006.
Rogers, S. (2000). Creating and evaluating highly accurate
maps with probe vehicles. ITSC2000. 2000 IEEE
Intelligent Transportation Systems. Proceedings (Cat.
No. 00TH8493), (S. 125-130).
Van Winden, K., Biljecki, F., & Van der Spek, S. (2016).
Automatic update of road attributes by mining GPS
tracks. Transactions in GIS, 20, 664-683.
Williams, G., Baxter, R., He, H., Hawkins, S., & Gu, L.
(2002). A comparative study of RNN for outlier
detection in data mining. 2002 IEEE International
Conference on Data Mining, 2002. Proceedings., (S.
709-712).
Zofka, M. R., Kuhnt, F., Kohlhaas, R., Rist, C., Schamm,
T., & Zöllner, J. M. (2015). Data-driven simulation and
parametrization of traffic scenarios for the development
of advanced driver assistance systems.
Information
Fusion (Fusion), 2015 18th International Conference
on, (S. 1422-1428).
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
514
