Comparing Supervised Classiﬁcation Methods for Financial Domain

Problems

Victor Ulisses Pugliese

, Celso Massaki Hirata

and Renato Duarte Costa

Instituto Tecnol

ogico de Aeron

autica, Prac¸a Marechal Eduardo Gomes, 50, S

ao Jos

e dos Campos, Brazil

Keywords:

Ranking, Machine Learning, XGBoost, Nonparametric Statistic, Optimization Hyperparameter.

Abstract:

Classiﬁcation is key to the success of the ﬁnancial business. Classiﬁcation is used to analyze risk, the oc-

currence of fraud, and credit-granting problems. The supervised classiﬁcation methods help the analyzes by

’learning’ patterns in data to predict an associated class. The most common methods include Naive Bayes,

Logistic Regression, K-Nearest Neighbors, Decision Tree, Random Forest, Gradient Boosting, XGBoost, and

Multilayer Perceptron. We conduct a comparative study to identify which methods perform best on prob-

lems of analyzing risk, the occurrence of fraud, and credit-granting. Our motivation is to identify if there

is a method that outperforms systematically others for the aforementioned problems. We also consider the

application of Optuna, which is a next-generation Hyperparameter optimization framework on methods to

achieve better results. We applied the non-parametric Friedman test to infer hypotheses and we performed

Nemeyni as a posthoc test to validate the results obtained on ﬁve datasets in Finance Domain. We adopted the

performance metrics F1 Score and AUROC. We achieved better results in applying Optuna in most of the eval-

uations, and XGBoost was the best method. We conclude that XGBoost is the recommended machine learning

classiﬁcation method to overcome when proposing new methods for problems of analyzing risk, fraud, and

credit.

1 INTRODUCTION

Business success and failure have been extensively

studied. Most of the studies try to identify the var-

ious determinants that can affect business existence

(Yu et al., 2014). Businesses operations are con-

ducted based on how companies make ﬁnancial de-

cisions and depend on models to support the deci-

sions. Inadequate models can lead to business failure

(Damodaran, 1996).

In most of the studies, decisions are based on

the prediction of classiﬁcation about problems such

as granting credit, credit card fraud detection, and

bankruptcy risk and are commonly treated as binary

classiﬁcation problems (Yu et al., 2014)(Lin et al.,

2011).

In this paper, we conduct a comparative study to

identify which supervised classiﬁcation methods per-

form best on problems of analyzing risk, the occur-

rence of fraud, and credit granting. The motivation is

to identify a winning method that has the best perfor-

https://orcid.org/0000-0001-8033-6679

https://orcid.org/0000-0002-9746-7605

https://orcid.org/0000-0002-8378-5485

mance for all the aforementioned problems.

In order to achieve the goal, we selected nine pre-

dictive methods. To contextualize our work, we made

a survey of the related work. Then, we conducted an

evaluation comparing the methods using two groups

of datasets. The ﬁrst group is associated to ﬁnance

domain. The other is related to health care and iono-

sphere. Finally, we present the main ﬁndigs and con-

clude the paper.

2 BACKGROUND

This section brieﬂy describes the nine methods for

ﬁnancial prediction. They are Naive Bayes, Logis-

tic Regression, Support Vector Classiﬁer, k-Nearest

Neighbors, Decision Tree, Random Forest, Gradient

Boosting, XGBoost, and Multilayer Perceptron.

ıve Bayes (NB) classiﬁer is based on applying

Bayes’s theorem with strong (na

ıve) independence as-

sumptions (Rish et al., 2001):

p(X|Y ) =

∏

i=1

p(X

|Y ) (1)

440

Pugliese, V., Hirata, C. and Costa, R.

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems.

DOI: 10.5220/0009426204400451

In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 440-451

ISBN: 978-989-758-423-7

where p is a probability, X(X

, . . . , X

) is a feature

vector and Y is a class. The theorem establishes that

the class Y given the feature X, the posterior prob-

ability, p(Y |X), can be calculated by the class prior

probability, p(Y ), multiplied by the observed feature

probability, p(X|Y ), or likelihood, divided by the to-

tal feature probabilit, p(X), which is constant for all

classes (Pearl et al., 2016).

p(Y |X) =

p(Y ) ∗ p(X|Y )

p(X)

(2)

Although the independence between features is a con-

dition not fully sustained in most cases, the Na

ıve

Bayes has proved its strength in practical situations

with comparable performance to Neural Network and

Decision Tree classiﬁers (Islam et al., 2007).

Logistic Regression (LR) is a classiﬁcation

method used to predict the probability of a categori-

cal dependent variable assigning observations to a dis-

crete set of classes (yes or no, success or failure). Un-

like linear regression which outputs continuous num-

ber values, logistic regression transforms its output

using the logistic sigmoid function (Equation 3) to re-

turn a probability value, which can then be mapped to

discrete classes. The logistic sigmoid function maps

any real value into another value between 0 and 1. A

decision threshold classiﬁes values into classes 0 or 1.

S(z) =

1 + e

−z

(3)

The Logistic Regression is binary if the dependent

variable is a binary variable (pass or fail), multino-

mial if the dependent variable is categorical as type

of animal or ﬂower, and ordinal for ordered classes

like Low, Medium or High. Ng and Jordan (Ng and

Jordan, 2002) present a comparison between Na

ıve

Bayes and Logistic Regression classiﬁer algorithms.

K-Nearest Neighbor (kNN) is a non-parametric

method for classiﬁcation and regression tasks. It is

one of the most fundamental and simplest methods,

being the ﬁrst choice method for classiﬁcation when

there is little or no prior knowledge about the distribu-

tion of the data (Peterson, 2009). Examples are clas-

siﬁed based on the class of their nearest neighbors.

It is usually used to identify more than one neighbor,

where k is a referee for determining classes number.

This method uses metrics that must conform to the

following four criteria (where d(x, y) refers to the dis-

tance between two objects x and y) (Cunningham and

Delany, 2007):

• d(x, y) is greater or equal to zero; non-negativity

• d(x, y) is equal to zero only if x=y; identity

• d(x, y) is equal to d(y, x); symmetry

• d(x, z) is less or equal to d(x, y) + d(y, z); triangle

inequality

Support Vector Classiﬁer (SVC) is a statistical learn-

ing method that is suitable for binary classiﬁcation

(Zareapoor and Shamsolmoali, 2015). The objective

of the Support Vector Classiﬁer is to ﬁnd a hyper-

plane in n-dimensional space, where n is the number

of features, that distinctly classiﬁes the data (Suykens

and Vandewalle, 1999).

Decision Tree (DT) is a ﬂow chart like tree struc-

ture, where each internal node denotes a test on an

attribute, each branch represents an outcome of the

test, and each leaf node holds a class label (Lavanya

and Rani, 2011). Decision tree classiﬁers are com-

monly used in credit card, automobile insurance, and

corporate fraud problems.

Random Forest (RandFC) is proposed as an ad-

ditional layer of randomness bagging tree (Breiman,

2001) (Liaw et al., 2002). The Random Forest col-

lects data and searches a random selection of features

for the best division on each node, regardless of pre-

vious trees. In the end, a simple majority vote is made

for prediction. Random Forest performs very well

compared to many other classiﬁers, including dis-

criminant analysis, support vector classiﬁer and neu-

ral networks, being robust against overﬁtting (Liaw

et al., 2002).

Gradient Boosting (GradB) is based on a differ-

ent constructive strategy of ensemble set like Random

Forest. The Boosting’s main idea is to add new mod-

els to the ensemble sequentially (Natekin and Knoll,

2013). Boosting ﬁts the “weak” tree classiﬁers to

different observation weights in a dataset (Ridgeway,

1999). In the end, a weighted vote is made for predic-

tion (Liaw et al., 2002).

XGBoost (XGB) is a scalable machine learning

system for optimized tree boosting. The method

is available as an open source package. Its im-

pact has been widely recognized in a number of ma-

chine learning and data mining challenges (Chen and

Guestrin, 2016). XGBoost became known after win-

ning the Higgs Challenge, available at https://www.

kaggle.com/c/higgs-boson/overview. XGBoost has

several features such as parallel computation with

OpenMP. It is generally over 10 times faster than Gra-

dient Boosting. XGBoost takes several types of input

data. It supports customized objective function and

evaluation function. It has better performance on sev-

eral different datasets.

Multilayer Perceptron (NN) is a feed-forward ar-

tiﬁcial neural network model for supervised learn-

ing, composed by a series of layers of nodes or neu-

rons with full interconnection between adjacent layer

nodes. The feature vector X is presented to the in-

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems

441

put layer. Its nodes output values are fully connected

to the next layer neurons through weighted synapses.

The connections repeat until the output layer, respon-

sible to present the results of the network. The learn-

ing of NN is made by the back-propagation algo-

rithm. The training is done layer by layer, adjusting

the synaptic weights from the last to the ﬁrst layer, to

minimize the error. Accuracy metrics such as mini-

mum square error is used. The algorithm repeats the

training process several times. Each iteration is called

epoch. On each epoch, the conﬁguration that presents

the best results is used as the seed for the next inter-

action, until some criterion as accuracy or number of

iterations is reached.

To measure the performance of the predictive

methods employed in this study, we use the metrics:

F1 Score, Precision, Recall and AUROC.

F1 Score is the harmonic mean of Precision and

Recall. Precision is the number of correct positive

results divided by the number of positive results pre-

dicted. Recall is the number of correct positive results

divided by the number of all samples that should have

been identiﬁed as positive. F1 score reaches its best

value at 1 (perfect precision and recall) and worst at 0

(Equation 4).

F1Score = 2 ∗

Precision ∗ Recall

Precision + Recall

(4)

AUROC (Area under the Receiver Operating Charac-

teristic) is a usual metrics for the goodness of a pre-

dictor in a binary classiﬁcation task.

To evaluate the methods with the datasets, we em-

ploy some tests. The Friedman Test is a nonparamet-

ric equivalent of repeated measures analysis of vari-

ance (ANOVA) (Dem

sar, 2006). The purpose of the

test is to determine if one can conclude from a sample

of results that there is a difference between the treat-

ment effect (Garc

ıa et al., 2010).

The Nemenyi Test is a post-hoc test of Friedman

applied when all possible pairwise comparisons need

to be performed. It assumes that the value of the sig-

niﬁcance level α is adjusted in a single step by di-

viding it merely by the number of comparisons per-

formed.

Hyperparameter optimization is one of the essen-

tial steps in training Machine Learning models. With

many parameters to optimize, long training time and

multiple folds to limit information leak, it is a cum-

bersome endeavor. There are a few methods of deal-

ing with the issue: grid search, random search, and

Bayesian methods. Optuna is an implementation of

the latter one

Optuna is a next-generation Hyperparameter Op-

timization Framework (Akiba et al., 2019). It has

the following features: deﬁne-by-run API that allows

users to construct the parameter search space dynam-

ically; efﬁcient implementation of both searching and

pruning strategies; and easy-to-setup, versatile archi-

tecture

3 RELATED WORK

There are two systematic literature reviews (Bouazza

et al., 2018) (Sinayobye et al., 2018) that describe the

works on data mining techniques applied in ﬁnancial

frauds, healthcare insurance frauds, and automobile

insurance frauds.

Moro et al. (Moro et al., 2014) propose a data

mining technique approach for the selection of bank

marketing clients. They compare four models: Logis-

tic Regression, Decision Tree, Neural Networks, Sup-

port Vector Machines, using the performance metrics

AUROC and LIFT. For both metrics, the best results

were obtained by Neural Network. Moro et al. do not

use bagging or boosting tree.

Zareapoor and Shamsolmoali (Zareapoor and

Shamsolmoali, 2015) apply ﬁve predictive methods:

Naive Bayes, k-Nearest Neighbors, Support Vector

Classiﬁer, Decision Tree, and Bagging Tree to credit

card’s dataset. They report that Bagging Tree shows

better results than others. Zareapoor and Shamsol-

moali do not use Boosting Tree, Neural Network and

Logistic Regression as we do. Their survey does not

have a nonparametric test.

Wang et al. (Wang et al., 2011) explore credit

scoring with three bank credit datasets: Australian,

German, and Chinese. They made a comparative as-

sessment of performance of three ensemble methods,

Bagging, Boosting, and Stacking based on four base

learners, Logistic Regression, Decision Tree, Neural

Network and Support Vector Machine. They found

that Bagging performs better than Boosting across

all credit datasets. Wang et al do not use k-Nearest

Neighbors and XGBoost.

4 EVALUATION OF THE

METHODS WITH DATASETS

OF THE FINANCIAL AREA

We used ﬁve datasets of the ﬁnancial domain in the

evaluations. They are brieﬂy described as follows.

The Bank Marketing dataset is about direct mar-

keting campaigns (phone calls) of a Portuguese bank-

ing institution. It contains personal information and

banking transaction data of clients. The classiﬁca-

tion goal is to predict if a client will subscribe to a

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

442

term deposit. The dataset is multivariate with 41188

instances (4640 subscription), 21 attributes (5 real,

5 integer and 11 object), no missing values and it

is available at https://archive.ics.uci.edu/ml/datasets/

Bank+Marketing (Moro et al., 2014).

The Default of Credit Card Clients dataset con-

tains information of default payments, demographic

factors, credit data, history of payment, and bill

statements of credit card clients in Taiwan from

April to September 2005. The classiﬁcation goal

is to predict if the clients is credible. The dataset

is multivariate with 30000 instances (6636 credita-

tion), 24 integer attributes, no missing values, and it

is available at https://archive.ics.uci.edu/ml/datasets/

default+of+credit+card+clients (Bache and Lichman,

2013).

The Kaggle Credit Card dataset is a modiﬁed

version of Default of Credit Card Clients, with data

in the same period. Both datasets have the same

classiﬁcation goal: predict if the client is credible.

However, Kaggle Credit Card has more features, al-

most 31 only numerical attributes. and a lower num-

ber of positive credible client instances. The dataset

has 284807 instances (492 positive credible client in-

stances). The dataset is highly unbalanced and the

positive class accounts for 0.172% of all instances.

It is available at https://www.kaggle.com/uciml/

default-of-credit-card-clients-Dataset (Dal Pozzolo

et al., 2015)

The Statlog German Credit dataset contains cat-

egorical and symbolic attributes. It contains credit

history, purpose, personal client data, nationality, and

other information. The goal is to classify clients using

a set of attributes as good or bad for credit risk. We

used an alternative dataset provided by Strathclyde

University. The ﬁle was edited and several indica-

tor variables were added to make it suitable for al-

gorithms that cannot cope with categorical variables.

Several attributes that are ordered categorically (such

as attribute 17) were coded as integer. The dataset is

multivariate with 1,000 instances (300 instances are

classiﬁed as Bad), 24 integer attributes, no missing

values and it is available at https://archive.ics.uci.edu/

ml/datasets/statlog+(german+credit+data) (Hofmann,

1994).

The Statlog Australian Credit Approval dataset is

used for analysis of credit card operations. All at-

tribute names and values were anonymized to pro-

tect data privacy. The dataset is multivariate with

690 instances (307 instances are labeled as 1), 14

attributes (3 real and 11 integer), no missing val-

ues and it is available at http://archive.ics.uci.edu/ml/

datasets/statlog+(australian+credit+approval) (Quin-

lan, 1987).

For each dataset, we preprocessed the attributes, sam-

pled the data, and divided the data into 90% for train-

ing and 10% for testing. After splitting the dataset,

we employed cross-validation with ten Stratiﬁed k-

folds, ﬁfteen seeds (55, 67, 200, 245, 256, 302, 327,

336, 385, 407, 423, 456, 489, 515, 537), and nine pre-

dictive methods. Firstly, the methods used the scikit-

learn default hyperparameters. The F1 Score and AU-

ROC metrics were measured. Tests were performed

on the measured metrics to rank statistic differences

over methods. Finally, we employed Optuna to opti-

mize the hyperparameters and used the classiﬁcation

methods again.

The main scikit-learn default hyperparameters

used to test the different methods are::

• GaussianNB: priors=’None’, and

var smoothing=’1e-09’.

• Logistic Regression: C=1.0, ﬁt intercept=True,

intercept scaling=1, max iter=100, penalty=’l2’,

random state=None, solver=’warn’, and

tol=0.0001.

• kNN: algorithm=’auto’, leaf size=30, met-

ric=’minkowski’, n neighbors=5, p=2, and

weights=’uniform’.

• SVC: C=1.0, cache size=200, deci-

sion function shape=’ovr’, degree=3, ker-

nel=’rbf’, shrinking=True, and tol=0.001.

• Decision Tree: criterion=’gini’,

min samples split=2, and splitter=’best’.

• Random Forest: bootstrap=True, criterion=’gini’,

min samples leaf=1, min samples split=2, and

n estimators=’warn’.

• Gradient Boosting: criterion=’friedman mse’,

learning rate=0.1, loss=’deviance’, max depth=3,

min samples leaf=1, min samples split=2,

n estimators=100, subsample=1.0, tol=0.0001,

and validation fraction=0.1.

• XGBoost: base score=0.5, booster=’gbtree’,

learning rate=0.1, max depth=3, and

n estimators=100.

• Multilayer Perceptron: activation=’relu’, hid-

den layer sizes=(100,), learning rate=’constant’,

max iter=200, solver=’adam’, and tol=0.0001.

We have used Optuna to optimize the hyperparame-

ters in the methods, running one study with 100 itera-

tions, using the following ranges:

• GaussianNB: none.

• Logistic Regression: C range: 1e-10 to 1e10.

• kNN: N neighbors range: 1 to 100; Distances

range: 1 to 10.

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems

443

• SVC: C range: 1e-10 to 1e10; Kernel options: lin-

ear, rbf, poly; Gamma range: 0.1 to 100; Degree

range: 1 to 6.

• Decision Tree: Max

depth range: 2 to

32; Min samples split range: 2 to 100;

Min samples leaf range: 1 to 100.

• Random Forest: Same hyperparameters used in

Decision Tree; N estimators range: 100 to 1000.

• Gradient Boosting: Same hyperparameters used

in Random Forest; Learning rate range: 0.01 to 1.

• XGBoost: Booster options: gbtree, gblinear, dart;

Lambda range: 1e-8 to 1.0; Alpha range: 1e-8

to 1.0. Testing booster as gbtree or dart, than

Max depth range: 1 to 9; eta range: 1e-8 to 1.0;

Gamma range: 1e-8 to 1.0; Grow policy options:

depthwise or lossguide. As Dart Booster, we

could test too, Sample type options: uniform or

weighted; Normalize type options: tree or forest;

Rate drop range: 1e-8 to 1.0; Skip drop range:

1e-8 to 1.0.

• Multilayer Perceptron: Hidden Layer Sizes op-

tions: (100,), (50,50,50), (50,100,50); Activation

options: identity, logistic, tanh, relu; Solver op-

tions: sgd or adam; Alpha range: 0.0001 to 5;

Learning rate options: constant or adaptive.

5 RESULTS WITH THE

DATASETS OF THE FINANCE

DOMAIN

In this section, we present the results of the classi-

ﬁcation methods for the ﬁve datasets in the ﬁnance

domain.

For the Bank Marketing dataset, we transformed

categorical data with One-Hot-Encoding. Afterwards,

we applied undersampling to balance the dataset.

Undersampling is an algorithm to deal with class-

imbalance problems. It uses only a subset of the ma-

jority class for efﬁciency (Liu et al., 2008), and we

employed the methods. The results are shown in Ta-

ble 1.

As it can be observed, the lowest values of F1

Score and AUROC were obtained by Naive Bayes

with 65.47% and 71.59%, respectively. The best

results were achieved with GradientBoosting with

88.87% of F1 Score and 88.41% of AUROC, followed

by XGBoost (88.76% of F1 and 88.23% of AUROC).

With respect to standard deviations for F1 Score and

AUROC, Gradient Boosting resulted in 0.08% and

0% respectively and XGBoost resulted in 0% for both.

Table 1: Cross-validation for Bank Marketing Dataset.

Classiﬁers F1 std AUROC std

DT 83.19 0.18 83.19 0.11

RandFC 86.43 0.20 86.47 0.21

GradB 88.87 0.08 88.41 0.00

XGB 88.76 0.00 88.23 0.00

LR 87.01 0.00 86.85 0.00

SVC 85.62 0.00 84.76 0.00

kNN 85.48 0.00 85.20 0.00

NN 81.97 2.26 80.95 1.83

NB 65.47 0.00 71.59 0.00

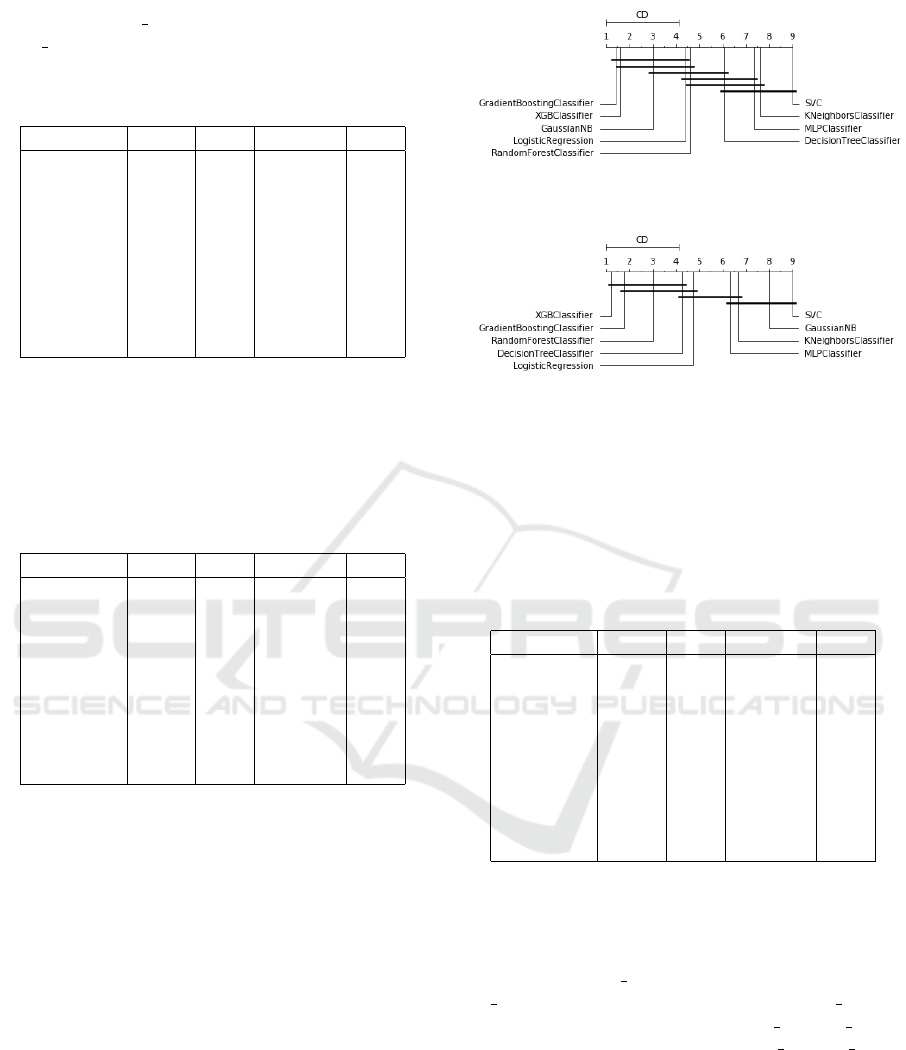
Figures 1 and 2 illustrate the Critical Difference Di-

agram constructed using Nemenyi Test for F1 Score

and AUROC in the Bank Marketing dataset.

Figure 1: Critical difference diagram over F1 measure of

Bank Marketing Dataset.

Figure 2: Critical difference diagram over AUROC measure

of Bank Marketing Dataset.

As it can be seen in Bank Marketing dataset, Gradient

Boosting, XGBoost, Logistic Regression, and Ran-

dom Forest are the best, but no statistically signiﬁcant

difference could be observed among them. Thus, the

methods can be used, with similar efﬁciency, to clas-

sify clients for a term deposit.

We employed Optuna over the methods in the

Bank Marketing dataset (Table 2). The best result was

achieved with XGBoost with 89.56% of F1 Score and

89.11% of AUROC.

We obtained the best results using XGBoost

with Optuna for the Bank Marketing dataset,

with the following setting parameters: ’booster’

= ’dart’, ’lambda’ = 4.763778055855053e-06, ’al-

pha’ = 0.0056726686023193555, ’max

depth’ =

5, ’eta’ = 1.9313322604903697e-07, ’gamma’ =

1.567431491678084e-08, ’grow policy’ = ’loss-

guide’, ’sample type’ = ’uniform’, ’normalize type’

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

444

= ’forest’, ’rate drop’ = 0.003875800179107411,

’skip drop’ = 1.4617070871276763e-08.

Table 2: Cross-validation with Optuna in Bank Marketing

Dataset.

Classiﬁers F1 std AUROC std

DT 84.54 0.00 84.31 0.00

RandFC 84.62 0.20 84.07 0.11

GradB 88.60 0.00 88.11 0.00

XGB 89.56 0.00 89.11 0.00

LR 87.02 0.00 86.85 0.00

SVC 87.08 0.00 86.88 0.00

kNN 85.80 0.00 85.45 0.00

NN 87.25 0.00 86.59 0.00

NB 65.47 0.00 71.59 0.00

For the Default of Credit Card Clients dataset, we

applied undersampling to balance the dataset. Af-

terwards, we employed the methods. The results are

shown in Table 3

Table 3: Cross-validation for Default of Credit Card Clients

Dataset.

Classiﬁers F1 std AUROC std

DT 62.77 0.19 62.64 0.17

RandFC 65.15 0.35 67.99 0.26

GradB 68.43 0.09 70.84 0.07

XGB 68.43 0.00 70.85 0.00

LR 65.19 0.00 62.54 0.00

SVC 8.49 0.00 51.51 0.00

kNN 59.23 0.00 58.87 0.00

NN 59.14 3.12 58.85 1.19

NB 67.38 0.00 54.16 0.00

As it can be observed, the lowest values of F1 Score

and AUROC were obtained by Support Vector Clas-

siﬁer with 8.49% and 51.51%, respectively. The best

results were achieved with XGBoost with 68.43% of

F1 Score and 70.85% of AUROC, followed by Gra-

dient Boosting with 68.43% of F1 and 70.84% of

AUROC. With respect to standard deviations for F1

Score and AUROC, Gradient Boosting and XGBoost

resulted in almost 0%.

Figures 3 and 4 show the Critical Difference Dia-

gram constructed using Nemenyi Test for F1 Score

and AUROC in the Default of Credit Card Clients

dataset.

As it can be seen, Gradient Boosting, XGBoost,

and Naive Bayes are the best, but no statistically sig-

niﬁcant difference could be observed among them.

Thus, the above methods can be used with similar ef-

ﬁciency for classifying a credible client.

We employed Optuna over the methods in the De-

Figure 3: Critical difference diagram over F1 measure of

Default of Credit Card Clients Dataset.

Figure 4: Critical difference diagram over AUROC measure

of Default of Credit Card Clients Dataset.

fault of Credit Card Clients dataset (Table 4). The

best results were achieved by GradB with 68.88% of

F1 Score and 70.91% of AUROC, with standard de-

viation of 0.00%. XGBoost obtained very similar re-

sults.

Table 4: Cross-validation with Optuna for Default of Credit

Card Clients Dataset.

Classiﬁers F1 std AUROC std

DT 61.81 0.00 68.31 0.00

RandFC 66.19 0.17 69.50 0.13

GradB 68.88 0.00 70.91 0.00

XGB 68.61 0.00 70.52 0.00

LR 65.26 0.00 61.75 0.00

SVC 61.01 0.00 60.56 0.00

kNN 64.70 0.00 61.28 0.00

NN 58.01 5.37 58.74 0.67

NB 67.38 0.00 54.21 0.00

We obtained the best results using GradB with

Optuna for the Default of Credit Card Clients

dataset, with the following setting parame-

ters: ’learning rate’: 0.06551574044228455,

’n estimators’: 355.41370517846616, ’max depth’:

4.935444994782639, ’min samples split’:

12.868275268442062, ’min samples leaf’:

5.444818807968713.

For the Kaggle Credit Card dataset, we applied

undersampling to balance the dataset. Afterwards, we

employed the methods. The results are shown in Ta-

ble 5.

As it can be observed, the lowest values of F1

Score and AUROC were obtained by Naive Bayes

(89.88% and 90.68%), and Decision Tree (90.18%

and 90.31%). The best results were achieved by XG-

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems

445

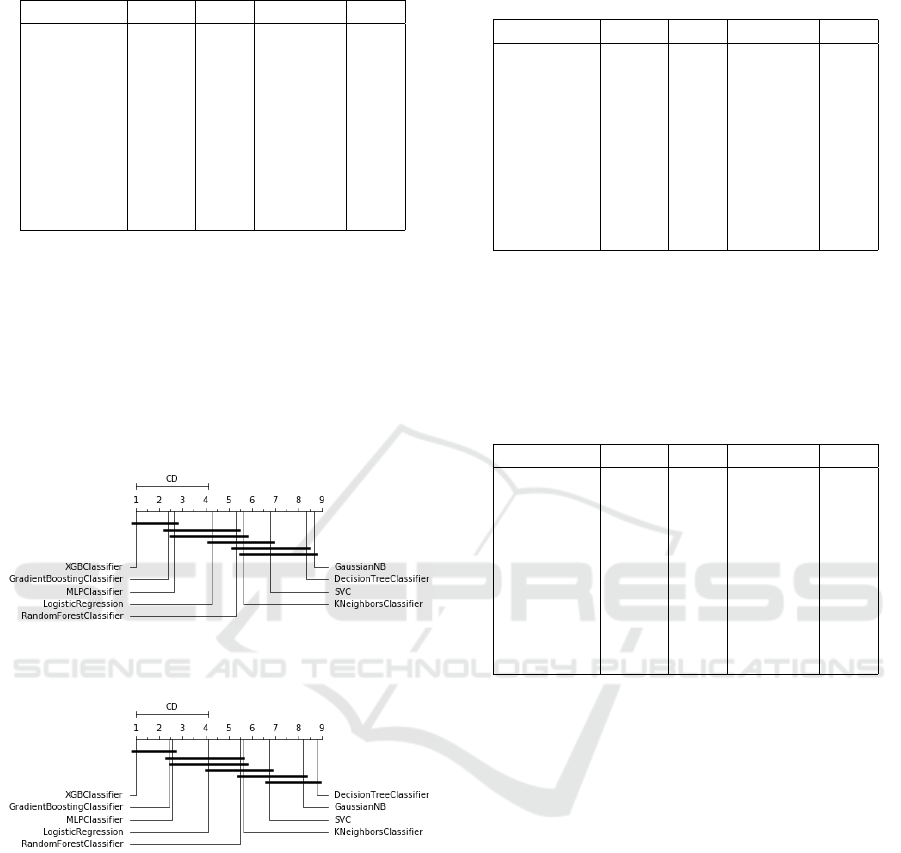
Table 5: Cross-validation for Kaggle Credit Card Dataset.

Classiﬁers F1 std AUROC std

DT 90.18 0.60 90.31 0.36

RandFC 92.62 0.47 92.94 0.37

GradB 93.50 0.07 93.76 0.06

XGB 94.07 0.00 94.29 0.00

LR 92.98 0.00 93.26 0.00

SVC 92.28 0.00 92.59 0.00

kNN 92.51 0.00 92.89 0.00

NN 93.40 0.25 93.68 0.20

NB 89.88 0.00 90.68 0.00

Boost with 94.07% of F1 Score and 94.29% of AU-

ROC, and Gradient Boosting (93.50% and 93.76%).

When it comes to standard deviation for F1 Score and

AUROC, Gradient Boosting and XGBoost resulted in

0%.

Figures 5 and 6 bring the Critical Difference Di-

agram constructed using Nemenyi Test for F1 Score

and AUROC in the Kaggle Credit Card dataset.

Figure 5: Critical difference diagram over F1 measure of

Kaggle Credit Card Dataset.

Figure 6: Critical difference diagram over AUROC measure

of Kaggle Credit Card Dataset.

As it can be seen in Kaggle Credit Card dataset, XG-

Boost, Gradient Boosting, Multilayer Perceptron, and

Logistic Regression obtained the best results, but no

statistically signiﬁcant difference could be observed

among them. Thus, the above methods can be used

with similar efﬁciency for classifying who is a cred-

itable client or not.

We employed Optuna over the methods in the

Kaggle Credit Card dataset (Table 6). XGBoost keeps

the best results after applying Optuna as well for this

dataset.

For Statlog German Credit dataset, we applied

SMOTE algorithm to balance the dataset. In SMOTE,

Table 6: Cross-validation with Optuna in Kaggle Credit

Card Dataset.

Classiﬁers F1 std AUROC std

DT 91.03 0.00 91.36 0.00

RandFC 91.57 0.00 93.88 0.00

GradB 93.66 0.00 92.13 0.00

XGB 94.05 0.00 94.28 0.00

LR 92.39 0.00 92.70 0.00

SVC 92.28 0.00 92.59 0.00

kNN 92.96 0.00 93.26 0.00

NN 93.37 0.00 93.56 0.00

NB 89.88 0.00 90.68 0.00

the minority class is oversampled by duplicating sam-

ples. Depending on the oversampling required, num-

bers of nearest neighbors are randomly chosen (Bha-

gat and Patil, 2015). Afterwards, we employed the

predictive methods. The results are shown in Table 7.

Table 7: Cross-validation for Statlog German Credit.

Classiﬁers F1 std AUROC std

DT 72.57 0.00 72.17 1.41

RandFC 77.23 0.25 78.17 1.33

GradB 81.39 0.00 81.31 0.52

XGB 82.06 0.00 82.03 0.00

LR 79.46 0.00 79.33 0.00

SVC 80.95 0.00 48.57 0.00

kNN 78.92 0.00 81.31 0.00

NN 81.83 1.43 67.90 1.32

NB 72.06 0.00 74.24 0.00

As it can be observed, the lowest values of F1 Score

and AUROC were obtained by Naive Bayes with

72.06% and 74.24%, respectively. The best results

were achieved by XGBoost with 82.06% of F1 Score

and 82.03% of AUROC. When it comes to standard

deviation for F1 Score and AUROC, XGBoost re-

sulted in 0% .

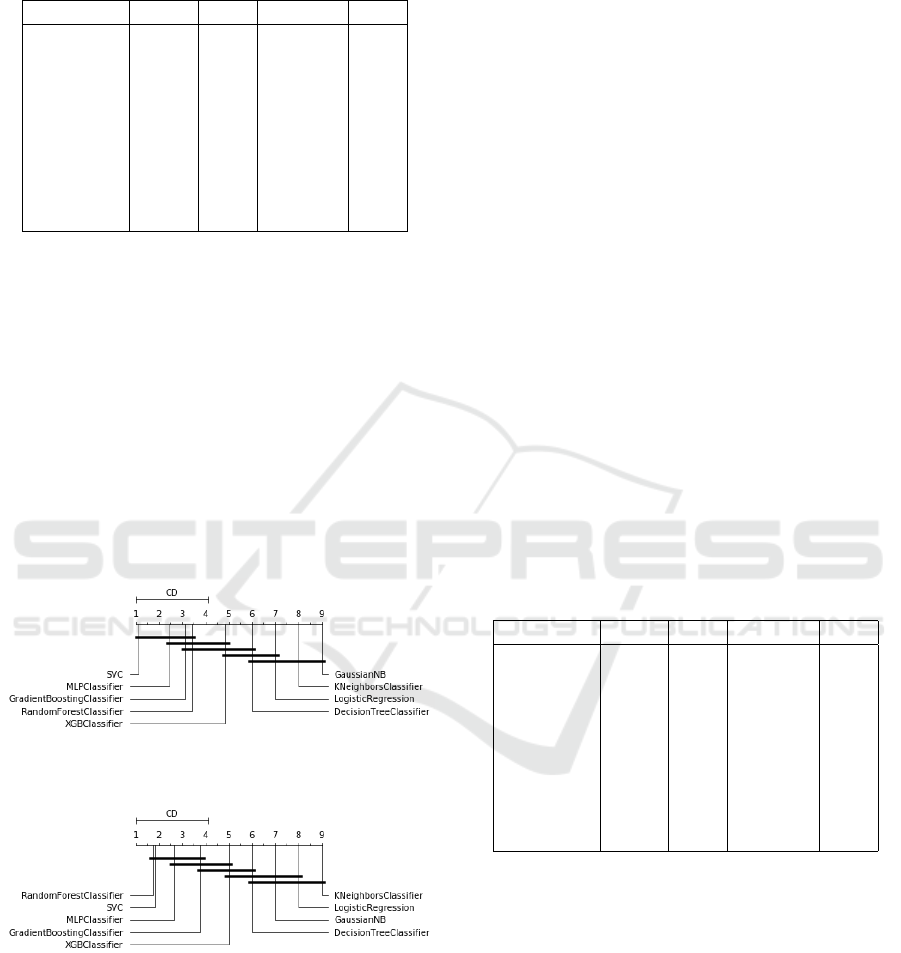
Figures 7 and 8 show the Critical Difference Di-

agram constructed using Nemenyi Test for F1 Score

and AUROC in the Statlog German Credit dataset.

As it can be seen in the ﬁgures, Support Vector

Classiﬁer, Multilayer Perceptron, Gradient Boosting,

and XGBoost obtained the best results, but no statisti-

cally signiﬁcant difference could be observed among

them. Thus, the aforementioned methods can be em-

ployed with similar efﬁciency for classifying who is

credible client.

We employed Optuna over the methods in the

Statlog German Credit dataset (Table 8). The best re-

sults were achieved by XGBoost with 84.93% of F1

Score and 70.95% of AUROC.

We obtained the best results using XGBoost with

Optuna for the Statlog German Credit dataset,

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

446

Figure 7: Critical difference diagram over F1 measure of

Statlog German Credit Dataset.

Figure 8: Critical difference diagram over AUROC measure

of Statlog German Credit Dataset.

Table 8: Cross Validation with Optuna for Statlog German

Credit.

Classiﬁers F1 std AUROC std

DT 81.37 0.00 60.42 0.00

RandFC 85.31 0.57 64.01 1.32

GradB 80.55 0.00 64.76 0.00

XGB 84.93 0.00 70.95 0.00

LR 81.42 0.00 69.04 0.00

SVC 75.55 0.00 63.09 0.00

kNN 65.00 0.00 59.52 0.00

NN 83.00 1.05 61.57 1.87

NB 72.06 0.00 74.24 0.00

with the following setting parameters: ’booster’

= ’gbtree’, ’lambda’ = 0.0005393794046856518,

’alpha’ = 4.896353471497812e-07, ’max depth’

= 6, ’eta’ = 3.48108440454574e-07, ’gamma’

= 0.004501584677856371, ’grow policy’ = ’loss-

guide’.

For the Statlog Australian Credit Approval

dataset, we just employed the methods without pre-

processing the data. The results are shown in Table

As it can be observed, the worst values of F1 Score

and AUROC were obtained by Support Vector Classi-

ﬁer with 6.04% and 50.01%, respectively. The best

results were achieved by XGBoost with 84.78% of

F1 Score and 86.23% of AUROC, followed by Gra-

dient Boosting (84.53% and 85.97%). When it comes

to standard deviation for F1 Score and AUROC, XG-

Boost resulted in 0%.

Figures 9 and 10 show the Critical Difference

Diagram constructed using Nemenyi Test among F1

Scores and AUROCs of Statlog Australian Credit

dataset.

Table 9: Cross-validation for Statlog Australian Credit

Dataset.

Classiﬁers F1 std AUROC std

DT 79.09 0.50 80.62 0.31

RandFC 83.63 0.96 85.54 0.78

GradB 84.53 0.00 85.97 0.00

XGB 84.78 0.00 86.23 0.00

LR 84.15 0.00 85.52 0.00

SVC 6.04 0.00 50.01 0.00

kNN 59.79 0.00 66.53 0.00

NN 72.20 2.41 73.42 2.32

NB 74.89 0.00 78.74 0.00

Figure 9: Critical difference diagram over F1 measure of

Statlog Australian Credit Dataset.

Figure 10: Critical difference diagram over AUROC mea-

sure of Statlog Australian Credit Dataset.

As it can be seen in the ﬁgures, XGBoost, Gra-

dient Boosting, Logistic Regression, and Random

Forest were considered the best, but no statistically

signiﬁcant difference can be observed among them.

Thus, the methods can be used with similar efﬁciency

for classifying who is a credible client.

We employed Optuna over the methods in the

Statlog Australian Credit dataset (Table 10). The

best result was achieved by Gradient Boosting with

85.34% of F1 Score and 86.75% of AUROC. Again,

XGBoost obtained similar results.

We obtained the best results using Gradient

Boosting with Optuna for the Statlog Australian

Credit dataset, with the following setting param-

eters: ’learning rate’: 0.19027288485989355,

’n estimators’: 214.4696898054894, ’max depth’:

5.367595574055688, ’min samples split’:

70.98506021007175, ’min samples leaf’:

1.4109947261432878.

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems

447

Table 10: Cross-validation with Optuna for Statlog Aus-

tralian Credit Dataset.

Classiﬁers F1 std AUROC std

DT 84.67 0.00 85.69 0.00

RandFC 84.26 0.32 85.94 0.27

GradB 85.34 0.36 86.75 0.20

XGB 84.78 0.00 86.23 0.00

LR 84.26 0.00 85.59 0.00

SVC 78.57 0.00 81.68 0.00

kNN 59.80 0.00 65.07 0.00

NN 79.53 0.97 81.96 0.72

NB 74.89 0.00 78.74 0.00

6 EVALUATIONS OF THE

METHODS IN OTHER

DOMAINS

In this section, we show the results of the methods

in domains other than Finance. We employed three

other datasets to verify the performance of XGBoost

in healthcare and ionosphere domains.

The Heart Disease dataset contains information

on patient’s heart exams, and the complete dataset

has 76 attributes. Typically, published experiences re-

fer to the use of a subset with no missing values and

14 numerical attributes, such as client personal data

and cardiac test results. We used the dataset from

Cleveland database because it is the only one that has

been used by Machine Learning researchers. The pur-

pose of using the dataset is to classify who has or

does not have a heart disease. It is available at https:

//archive.ics.uci.edu/ml/datasets/Heart+Disease (Dua

and Graff, 2017).

For the Heart Disease dataset, we just employed

the predictive methods without preprocessing the

data. The results are shown in Table 11.

Table 11: Cross-validation for Heart Disease Dataset.

Classiﬁers F1 std AUROC std

DT 78.20 0.81 74.79 1.02

RandFC 83.00 1.74 80.47 1.36

GradB 80.24 0.19 76.52 0.21

XGB 81.57 0.00 79.07 0.00

LR 84.27 0.00 80.73 0.00

SVC 71.39 0.00 50.00 0.00

kNN 65.38 0.00 59.39 0.00

NN 83.09 1.55 79.47 1.72

NB 84.03 0.00 81.55 0.00

As it can be observed, the worst value of F1 Score

was obtained by kNN with 65.38%. With SVC, we

obtained the worst value of AUROC with 50.00%.

The best results were achieved by Logistic Regression

with 84.27% for F1 Score and 80.73% for AUROC,

followed by Naive Bayes (84.03% and 81.55%).

When it comes to standard deviation for F1 Score and

AUROC, both methods resulted in 0%.

Figures 11 and 12 show the Critical Difference Di-

agram constructed using Nemenyi Test between F1

Score and AUROC of Heart Disease dataset.

Figure 11: Critical difference diagram over F1 measure of

Heart Disease Dataset.

Figure 12: Critical difference diagram over AUROC mea-

sure of Heart Disease Dataset.

As it can be seen in Heart Disease dataset, Logis-

tic Regression, Naive Bayes, Multilayer Perceptron,

and Random Forest were considered the best, but no

statistically signiﬁcant difference is observed among

them. Thus, the above methods can be used with sim-

ilar efﬁciency for classifying who has heart disease.

We employed Optuna over the methods in the

Heart Disease dataset. With Random Forest, we ob-

tained 86.14% for F1 Score and 82.56% for AUROC.

These results are better than those obtained without

Optuna.

The Ionosphere dataset consists of a phased array

of 16 high-frequency antennas with a total transmit-

ted power in the order of 6.4 kilowatts. The targets

were free electrons in the ionosphere. ”Good” radar

returns are those showing evidence of some type of

structure in the ionosphere. ”Bad” returns are those

pass through the ionosphere. The purpose of using

the dataset is to classify what is returned from radar.

The dataset is multivariate with 351 instances (224

instances are ”Good”), 34 attributes (32 real and 2 in-

teger), no missing values and it is available at https:

//archive.ics.uci.edu/ml/datasets/ionosphere (Dua and

Graff, 2017).

For the Ionosphere dataset, we just employed the

predictive methods without preprocessing the data.

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

448

The results are shown in Table 12.

Table 12: Cross-validation for Ionosphere Dataset.

Classiﬁers F1 std AUROC std

DT 90.96 0.60 86.27 1.18

RandFC 93.77 0.63 91.11 1.13

GradB 93.80 0.27 89.32 0.36

XGB 93.14 0.00 88.50 0.00

LR 89.14 0.00 79.86 0.00

SVC 94.83 0.00 90.63 0.00

kNN 88.49 0.00 77.41 0.00

NN 94.16 0.37 89.95 0.57

NB 85.19 0.00 82.72 0.00

As it can be observed, the lowest value of F1 Score

was obtained by Naive Bayes with 85.19%. With

kNN, we obtained the lowest value of AUROC with

77.41%. The best results were achieved by Sup-

port Vector Classiﬁer with 94.83% of F1 Score and

90.63% of AUROC, followed by Multilayer Per-

ceptron (94.48% and 89.95%). When it comes to

standard deviation for F1 Score and AUROC, SVC

method resulted in 0% for both metrics, and Multi-

layer resulted in 0.37% and 0.57% respectively.

Figures 13 and 14 bring the Critical Difference Di-

agram constructed using Nemenyi Test between F1

Scores and AUROCs of Ionosphere dataset.

Figure 13: Critical difference diagram over F1 measure of

Ionosphere Dataset.

Figure 14: Critical difference diagram over AUROC mea-

sure of Ionosphere Dataset.

As it can be seen for Ionosphere dataset, Support Vec-

tor Classiﬁer, Random Forest, Multilayer Perceptron,

and Gradient Boosting methods are considered the

best, but no statistically signiﬁcant difference can be

observed among them. Thus, the above methods can

be used with similar efﬁciency to classify what is re-

turned from radar.

We employed Optuna over methods in the Iono-

sphere dataset. XGBoost obtained 95.01% of F1

Score and 91.50% of AUROC. These results are bet-

ter than those obtained with Support Vector Classiﬁer

without Optuna.

The Blood Transfusion Service Center dataset is

intended to evaluate the RFMTC marketing model.

To build the model, 748 donors were selected from

the donor database. The donor dataset includes the

following information: months since last donation,

total number of donations, volume of blood donated,

months since ﬁrst donation (Yeh et al., 2009). The

purpose of using the dataset is to classify who can do-

nate blood.

For the Transfusion dataset, we applied the

SMOTE algorithm, and employed the methods. The

results are shown in Table 13.

As it can be observed, the worst values of F1 Score

and AUROC were obtained by Multilayer Perceptron

with 69.24% and 69.26% respectively. The best re-

sults were achieved with kNN with 75.89% of F1

Score and 74.23% of AUROC, followed by Random

Forest (75.16% and 75.99%). When it comes to stan-

dard deviations for F1 Score and AUROC, kNN re-

sulted in 0% for F1 Score and 0% for AUROC, and

Random Forest resulted in 0.97% and 0.57% respec-

tively.

Table 13: Cross-validation for Blood Transfusion Service

Center Dataset.

Classiﬁers F1 std AUROC std

DT 72.93 0.24 74.08 0.40

RandFC 75.16 0.97 75.99 0.57

GradB 73.06 0.10 72.76 0.08

XGB 74.00 0.00 74.32 0.00

LR 71.11 0.00 69.23 0.00

SVC 71.18 0.00 69.71 0.00

kNN 75.89 0.00 74.23 0.00

NN 69.24 0.46 69.26 0.33

NB 71.23 0.00 67.69 0.00

Figures 15 and 16 show the Critical Difference Di-

agram constructed using Nemenyi Test between F1

Scores and AUROCs of Transfusion Blood dataset.

As it can be seen, kNN, Random Forest, XG-

Boost, and Gradient Boosting obtained the best re-

sults, but no statistically signiﬁcant difference could

be observed among them. Therefore the aforemen-

tioned methods can be used with similar efﬁciency for

classifying if a person can donate blood.

kNN with Optuna obtained 76.82% of F1 Score

and 76.15% of AUROC, followed by XGBoost

(75.86% and 75.96%), these results are better results

than obtained with default hyperparameters.

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems

449

Figure 15: Critical difference diagram over F1 measure of

Transfusion Blood Dataset.

Figure 16: Critical difference diagram over AUROC mea-

sure of Transfusion Blood Dataset.

7 CONCLUDING REMARKS

This study has investigated supervised classiﬁcation

methods for ﬁnance problems with focus on risk,

fraud and credit analysis. Nine supervised predictive

methods were employed in ﬁve ﬁnancial datasets. All

of them are public. The methods were evaluated using

the classiﬁcation performance metrics F1 Score and

AUROC. The nonparametric Friedman Test was used

to infer hypotheses and the Nemeyni Test to validate

it with Critical Difference Diagram. In the ﬁnance

domain, we obtained the best results with the deci-

sion tree family of classiﬁcation methods. XGBoost

regularly showed good results in the evaluations.

We experimented the methods in other problem

domains such as health care and ionosphere, where

XGBoost also obtained good results, but not system-

atically better than Logistic Regression, Naive Bayes,

Multilayer Perceptron, Random Forest, Support Vec-

tor Classiﬁer, and Gradient Boosting.

When we applied Optuna in both domains, we

achieve better results in all evaluations, and XGBoost

was the best method again for the ﬁnance domain. So,

we believe that one of the reasons is the setting of hy-

perparameters required in the dataset. However, this

overﬁtting can be misleading, perhaps in production

systems, we have to consider the concept drift for re-

training the method.

Nielsen (Nielsen, 2016) explains that there are

some reasons for the good performance of XGBoost.

XGBoost can be seen as a Newton’s method of nu-

merical optimization, using a higher-order approxi-

mation at each iteration, being capable of learning

“better” tree structures. Second, XGBoost provides

clever penalization of individual trees, turning it to

be more adaptive than other Boosting methods, be-

cause it determines the appropriate number of termi-

nal nodes, which might vary among trees. Finally,

XGBoost is a highly adaptive method, which care-

fully takes the bias-variance trade-off into account in

nearly every aspect of the learning process.

Other non-tree methods, such as Naive Bayes,

Support Vector Classiﬁer and k-Nearest Neighbors al-

gorithms have shown performance worse than the de-

cision tree classiﬁcation methods. The analysis in-

dicates that the non-tree methods are not the recom-

mended ones for the ﬁnance problems we investi-

gated.

Based on the conducted evaluations, we conclude

that XBGoost is the recommended machine learning

classiﬁcation method to be overcome when proposing

new methods for problems of analyzing risk, fraud,

and credit.

REFERENCES

Akiba, T., Sano, S., Yanase, T., Ohta, T., and Koyama, M.

(2019). Optuna: A next-generation hyperparameter

optimization framework. In Proceedings of the 25th

ACM SIGKDD International Conference on Knowl-

edge Discovery & Data Mining, pages 2623–2631.

ACM.

Bache, K. and Lichman, M. (2013). Uci machine learning

repository [http://archive. ics. uci. edu/ml]. irvine, ca:

University of california. School of information and

computer science, 28.

Bhagat, R. C. and Patil, S. S. (2015). Enhanced smote

algorithm for classiﬁcation of imbalanced big-data

using random forest. In 2015 IEEE International

Advance Computing Conference (IACC), pages 403–

408. IEEE.

Bouazza, I., Ameur, F., et al. (2018). Datamining for fraud

detecting, state of the art. In International Conference

on Advanced Intelligent Systems for Sustainable De-

velopment, pages 205–219. Springer.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Chen, T. and Guestrin, C. (2016). Xgboost: A scalable

tree boosting system. In Proceedings of the 22nd acm

sigkdd international conference on knowledge discov-

ery and data mining, pages 785–794. ACM.

Cunningham, P. and Delany, S. J. (2007). k-nearest neigh-

bour classiﬁers. Multiple Classiﬁer Systems, 34(8):1–

17.

Dal Pozzolo, A., Caelen, O., Johnson, R. A., and Bontempi,

G. (2015). Calibrating probability with undersampling

for unbalanced classiﬁcation. In 2015 IEEE Sym-

posium Series on Computational Intelligence, pages

159–166. IEEE.

Damodaran, A. (1996). Corporate ﬁnance. Wiley.

ICEIS 2020 - 22nd International Conference on Enterprise Information Systems

450

Dem

sar, J. (2006). Statistical comparisons of classiﬁers

over multiple data sets. Journal of Machine learning

research, 7(Jan):1–30.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory.

Garc

ıa, S., Fern

andez, A., Luengo, J., and Herrera, F.

(2010). Advanced nonparametric tests for multi-

ple comparisons in the design of experiments in

computational intelligence and data mining: Exper-

imental analysis of power. Information Sciences,

180(10):2044–2064.

Hofmann, H. (1994). Statlog (german credit data) data set.

UCI Repository of Machine Learning Databases.

Islam, M. J., Wu, Q. J., Ahmadi, M., and Sid-Ahmed,

M. A. (2007). Investigating the performance of naive-

bayes classiﬁers and k-nearest neighbor classiﬁers. In

2007 International Conference on Convergence Infor-

mation Technology (ICCIT 2007), pages 1541–1546.

IEEE.

Lavanya, D. and Rani, K. U. (2011). Performance

evaluation of decision tree classiﬁers on medical

datasets. International Journal of Computer Applica-

tions, 26(4):1–4.

Liaw, A., Wiener, M., et al. (2002). Classiﬁcation and re-

gression by randomforest. R news, 2(3):18–22.

Lin, W.-Y., Hu, Y.-H., and Tsai, C.-F. (2011). Machine

learning in ﬁnancial crisis prediction: a survey. IEEE

Transactions on Systems, Man, and Cybernetics, Part

C (Applications and Reviews), 42(4):421–436.

Liu, X.-Y., Wu, J., and Zhou, Z.-H. (2008). Exploratory

undersampling for class-imbalance learning. IEEE

Transactions on Systems, Man, and Cybernetics, Part

B (Cybernetics), 39(2):539–550.

Moro, S., Cortez, P., and Rita, P. (2014). A data-driven

approach to predict the success of bank telemarketing.

Decision Support Systems, 62:22–31.

Natekin, A. and Knoll, A. (2013). Gradient boosting ma-

chines, a tutorial. Frontiers in neurorobotics, 7:21.

Ng, A. Y. and Jordan, M. I. (2002). On discriminative vs.

generative classiﬁers: A comparison of logistic re-

gression and naive bayes. In Advances in neural in-

formation processing systems, pages 841–848.

Nielsen, D. (2016). Tree boosting with xgboost-why does

xgboost win ”every” machine learning competition?

Master’s thesis, NTNU.

Pearl, J., Glymour, M., and Jewell, N. P. (2016). Causal

inference in statistics: A primer. John Wiley & Sons.

Peterson, L. E. (2009). K-nearest neighbor. Scholarpedia,

4(2):1883.

Quinlan, J. R. (1987). Simplifying decision trees. Inter-

national journal of man-machine studies, 27(3):221–

234.

Ridgeway, G. (1999). The state of boosting. Computing

Science and Statistics, pages 172–181.

Rish, I. et al. (2001). An empirical study of the naive bayes

classiﬁer. In IJCAI 2001 workshop on empirical meth-

ods in artiﬁcial intelligence, volume 3, pages 41–46.

Sinayobye, J. O., Kiwanuka, F., and Kyanda, S. K.

(2018). A state-of-the-art review of machine learn-

ing techniques for fraud detection research. In 2018

IEEE/ACM Symposium on Software Engineering in

Africa (SEiA), pages 11–19. IEEE.

Suykens, J. A. and Vandewalle, J. (1999). Least squares

support vector machine classiﬁers. Neural processing

letters, 9(3):293–300.

Wang, G., Hao, J., Ma, J., and Jiang, H. (2011). A compar-

ative assessment of ensemble learning for credit scor-

ing. Expert systems with applications, 38(1):223–230.

Yeh, I.-C., Yang, K.-J., and Ting, T.-M. (2009). Knowledge

discovery on rfm model using bernoulli sequence. Ex-

pert Systems with Applications, 36(3):5866–5871.

Yu, Q., Miche, Y., S

everin, E., and Lendasse, A. (2014).

Bankruptcy prediction using extreme learning ma-

chine and ﬁnancial expertise. Neurocomputing,

128:296–302.

Zareapoor, M. and Shamsolmoali, P. (2015). Applica-

tion of credit card fraud detection: Based on bag-

ging ensemble classiﬁer. Procedia computer science,

48(2015):679–685.

Comparing Supervised Classiﬁcation Methods for Financial Domain Problems

451