Introducing Conics in 9

Grade: An Experimental Teaching

Borislav Yordanov Lazarov

and Dimitar Georgiev Dimitrov

Institute of Mathematics and Informatics, Bulgarian Academy of Sciences, Blok 8 Georgi Bonchev Str., Sofia, Bulgaria

125

Secondary School, Sofia, Bulgaria

Keywords: Conics, Loci, Envelopes, Integrated Approach, Synthetic Competence.

Abstract: Under consideration is an experimental teaching focused on presenting the conics in a dual manner: as loci

and envelopes. A bunch of computer technologies is drawn to explore and investigate this duality of the

conics. An example of how it is done for a particular conic is given. The target group includes secondary

school students who are advanced in math and information technologies. The theoretical base is an original

didactical model for designing individual educational trajectories that is adapted for the team-working mode.

The educational goal includes developing synthetic competence of an entire team. The individual

characteristics of the team members complement one another for resolving complex problems from the local

behavioral environment, which were specifically formed for the purposes of the experimental teaching.

1 INTRODUCTION

The new Bulgarian educational legislation allows a

type of schools (so-called innovative schools) to vary

the syllabus including integrated subjects into the

school plan. Such status quo provides the opportunity

for creative teaching. However, there are no

textbooks neither educational plans nor guidelines for

the new subjects. Therefore, any good practice is

welcome in this slippery twilight zone. Below we are

going to share our experience in teaching conics in 9

grade, hoping it is a kind of good practice.

The approach we applied integrates areas of

several types.

1) Organizational: it is an example of integrating

school and academic staff.

2) Technological: it integrates classical geometry

with computer technologies.

3) Didactical: we combine the deductive with

algorithmic method in math.

4) Mathematical: we synthesized the concepts of

locus and envelope by a common algorithm for any

of the conics.

The experimental teaching took part in 2018/2019

scholastic year with a team of three ninthgraders, who

are advanced both in math and ICT. Further we refer

to this team as the Team. The small numbers of the

students in the Team allowed to apply individual

approach on one hand, and to take advantages of the

team work on the other hand. The didactical model

we applied is a modification of DMT (Lazarov, 2013)

for indiviual educational trajectory of small team.

Some details of the model are given in (Lazarov,

2019).

2 CHOOSING THE TOPIC

We carefully selected the topic for our experimental

teaching to satisfy two controversial requirements:

the matter to be in the zone of proximal development

and to be beyond the curriculum. Our previous

practice in teaching conics is presented in (Lazarov

and Todorova, 2014), where parabola was introduced

in an inquiry based mode of classroom activity. The

modest results of this experiment was related with the

attempt to organize Socratic style teaching in a large

group of students. Nevertheless, some of them made

considerable progress, which gave us reasons to

reconsider the topic, this time applying individual

approach.

The concept of locus used to be a part of the 8

grade Bulgarian curriculum until 2016. Nowadays it

remains just a trace of this concept in the 7

grade

curriculum. The loci are included implicitly in the

properties of the segment bisector and the angle

bisector. Fortunately, these two loci was just we need

as a base for developing the topic. The concept of

envelope of one parametric family of lines was

436

Lazarov, B. and Dimitrov, D.

Introducing Conics in 9th Grade: An Experimental Teaching.

DOI: 10.5220/0009430204360441

In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020) - Volume 1, pages 436-441

ISBN: 978-989-758-417-6

completely new matter for the Team (it is rather far

from the secondary school mathematics). The modern

dynamic geometry software (DGS) provides some

opportunities to elaborate the envelope in pure

geometrical mode, which is acceptable for the

advanced school students (Lazarov, 2011). However,

some concepts, which are routine for the calculus,

should be reconsidered from the secondary school

viewpoint.

3 ABOUT THE DEFINITIONS

The proper selection of definitions is another

challenge we met. A variety of didactical approaches

could be used for introducing a math concept: by

examples and counterexamples, constructively,

deductively etc. Our key reason was to stay as close

to the curriculum as possible.

3.1 Basic Concepts

In our opinion, the closest to the 9

grade math

curriculum are the following definitions:

 Parabola is the locus of points in the plane that are

equidistant from a given point (focus) and a given

line (directrix).

 Ellipse is the locus of points for which the sum of

the distances to two given points (foci) is constant.

 Hyperbola is the locus of points for which the

absolute value of the difference of the distances to

two given points (foci) is constant.

The ‘is constant’ in the last two bullets means ‘equals

a given segment’. These definitions also match the

GeoGebra operators for drawing the conics

(GeoGebra, 2019). In fact, the GeoGebra operators

require a third point for constructing the ellipse and

hyperbola (as say the operator icons). The ‘given

segment’ appears as a sum or difference of the

distances from this third point to the foci.

3.2 Calculus-circumventing

The calculus definition of tangent line to a curve is

inapplicable in 9

grade. We defined the tangency in

a specific manner for any particular conic. A line is

tangent to:

 parabola, iff it has exactly one common point with

it and is not perpendicular to its directrix;

 ellipse, iff it has exactly one common point with

it;

 hyperbola, iff it has exactly one common point

with it and is not parallel to any of its asymptotes.

These definitions extended the familiar concept of

tangent line to a circle.

Further, we need to elaborate into geometry the

concept of parameter that is common for algebra. The

parameter was introduced as:

 point at a straight line when consider parabola;

 point at a circle when consider ellipse;

 point at two circle arcs when consider hyperbola.

We considered only one-parameter families of

straight lines, which allowed us to restrict the notion

of envelope of a one-parametric family of lines. It is

a conic, which touches each line from the family in a

single point and any line from the family is tangent to

this conic.

So, we managed to avoid the concepts from the

calculus and to stay inside the secondary school

mathematics. Let us note that a similar approach is

adopted in (Lazarov, 2011) (but due to the larger

generality of considerations in that work, a need to

introduce the concept of tangent curves appears).

4 THE CONSTRUCTIONS

Three algorithms for constructing conics were the

core of the experimental teaching. Geometrical

constructions are included in 7

and 8

grade of the

Bulgarian curriculum. Among the conics, only

parabola is studied but just as the graph of quadratic

function and with no properties of the curve itself.

We decide to develop a constructive method to

unify in one algorithm the dual nature of a conic: as

locus on one hand and as envelope on the other hand.

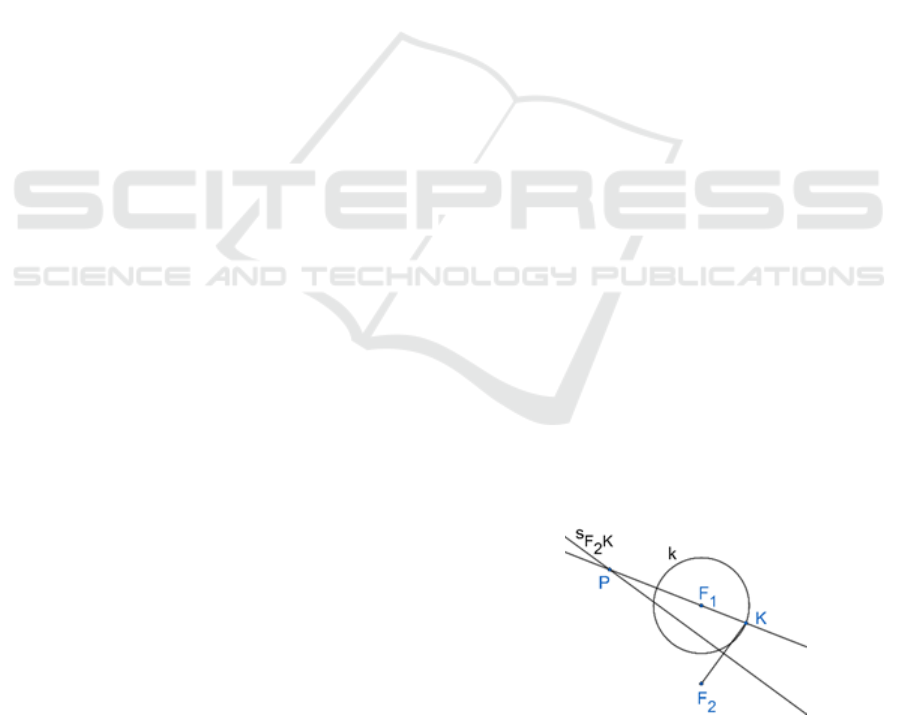
Here it is the algorithm for the hyperbola H having

foci 𝐹

,

and passing through a given point 𝑇:

1) Denote 𝑐|𝐹



𝑇𝐹



𝑇| and draw the circle

𝑘 with radius 𝑐 centred at 𝐹



2) Take an arbitrary point 𝐾∈𝑘.

3) Draw the segment bisector 𝑠







of 𝐹



𝐾 (Figure 1).

Figure 1: Thе hyperbola construction algorithm.

Lemma 1. When it exists, the intersection point 𝑃

of 𝐹



𝐾 and 𝑠







is at H.

Introducing Conics in 9th Grade: An Experimental Teaching

437

(The proofs of this lemma and the statements that

follow are given in the Appendix.)

Lemma 2. If 𝑃 exists then 𝑠







is the tangent to H

at 𝑃.

Parametrizing the algorithm by 𝐾, we can obtain

both objects: points at the hyperbola H (according to

Lemma 1) and tangents to it (according to Lemma 2).

Let us note that 𝑃 exists iff 𝐹



𝐾 is not a tangent to 𝑘.

The tangency of 𝐹



𝐾 and 𝑘 happens in two points

𝐾

,

that split 𝑘 into two arcs 𝑘

,

. So, we can take

these two arcs as the domain of 𝐾. In the case, when

𝐾 runs along 𝑘



∪𝑘



, we obtain a one-parametric-

family of lines 𝓗



𝑠







:𝐾 ∈𝑘



∪𝑘



. (The lines

𝑠







,

are the asymptotes of H.)

Theorem 1. H is the envelope of 𝓗

Figure 2: The hyperbola as the envelope of 𝓗 .

Thus, the hyperbola H occurs in the same time

the locus of 𝑃 and the envelope of 𝑠







. Similar

constructions were done for parabola and ellipse. In

fact, the construction algorithm for the parabola

(Lazarov, 2011) serves as a template for the ellipse

and hyperbola algorithms, which were done by the

Team. It is clear that the algorithms are device-

independent: any one could be realized either as a

DGS applet or as a traditional ruler-and-compass

construction.

5 DIVIDENDS

The unified algorithmic introduction of the conics

allows an easy explanation of the reflective properties

of these curves. Let us note that according to the laws

of the geometric optics a smooth curve reflects an

incoming ray as it does the tangent line at the

reflection point. Having a conic as locus of points,

one operate with a ‘real object’. The envelope

configures the conic as a phantom, but this phantom

performs the reflection of a beam: any ray is reflected

by the corresponding tangent line. Combining the

dual nature of the conic, one gets the big picture of

the reflection. We will illustrate this again with the

hyperbola.

Theorem 2. A ray coming from inside of one of

the branches of H and directed to the focus inside the

other branch, after reflection by H, passes through the

focus inside the first branch (Figure 3).

Figure 3: Thе reflective property of the hyperbola.

Scholium. The reflective property of the hyperbola

could work in the reverse manner of the one that is

described in Theorem 3: in Figure 3 the sound coming

from 𝐹



, after reflection by 𝐻 , is uniformly

distributed inside the branch, which contains 𝐹



. In

our opinion, Netrebko and Garanca (2007) use this

property when they sing facing the wall. It is also

applied to improve the acoustics of the cathedral La

Sagrada Familia in Barcelona (Burry et al., 2011).

Connecting mathematical results with high

achievements in arts significantly lifts the students’

attitude to math (Lazarov, 2019).

6 TEAM EDUCATIONAL

TRAJECTORY

We followed the general structure of the model DMT

(Lazarov, 2013, 2019) for the experimental teaching,

which consists of iterative steps (climbing floors).

However, the design of the individual educational

trajectory (IET) needed slight modification taking

into account the students’ interaction inside the Team.

In our general educational plan, the proximal

educational goals were stated to the Team but any

student was in charge for some details. Nevertheless,

the elaboration of the details happened in

collaboration of the team members and as result a

team product appears when the particular educational

goal was reached.

CSEDU 2020 - 12th International Conference on Computer Supported Education

438

6.1 On the First Floor of the IET

We started the experimental teaching during the

summer holyday. The students were proposed to

examine closely GeoGebra by themselves and to get

an idea about TeX.

During the first term of the scholastic year, we had

lectures once weekly. The introductory part of the

teaching we devoted to the basic facts about the conic

sections. Initially their properties were examined

experimentally but then were rigorously proven.

Meanwhile, students mastered their skills in

GeoGebra and TeX.

6.2 On the Second Floor of the IET

The proximal educational goal after introductory part

was to apply the knowledge about conics and the

DGS skills for modifying the parabola module to

similar modules about ellipse and hyperbola. These

activities were directed to prepare a paper for the

Bulgarian national math journal for school students

Matematika.

The Team was motivated and the students did

their best to polish all details. E.g., 39 GeoGebra

applets were made and there were done several

interim variants for the most of them. The paper also

needed several redactions. These efforts paid

themselves: the paper was published (Dimitrov et al.,

2019). Let us note that students’ papers were not

published in the journal for a rather long time before.

This paper resurrected the column Students’ works (in

Bulgarian „Ученическо творчество“ – Figure 4).

Figure 4: Thе first page of the Team’s paper.

6.3 On the Third Floor of the IET

The final educational goal of the experimental

teaching was to foster a kind of synthetic competence.

This means to examine the students’ knowledge-

skills-attitude (KSA) package for multifunktionality

and transferability. The didactical innovation was in

the team-competence we developed. The stimulus of

the Team to continue studying the conics was the

presentation of the project at a school symposium and

then at an international conference for school

students.

6.3.1 Implementation of Old-tech

The pre-computer technology for visualization of

envelopes require ingenuity and deep understanding

of the matter. The Team prepared a short movie about

paper-and-pencil drawing of a parabolic envelope

(Figure 5).

Figure 5: An old-tech method performed and filmed by the

Team.

The theoretical base for this drawing relates to

another parametrization of the tangents to a parabola:

the right-angled vertex of the wooden triangle moves

along the line, which is located in the middle between

the focus and the directrix. The Team proved the

corresponding theorem relying on the parabola

construction algorithm.

6.3.2 Explanation of the Terminology

The definitions for conics we adopted do not explain

the terminology ‘conic sections’, but we did not need

other definitions for the project. However, it was

good manner for the Team to show their classmates

the origin of the concept.

Figure 6: Thе Team’s illustration of conic sections.

For us, it was another opportunity to check the

transferability and multifunktionality of the Team’s

Introducing Conics in 9th Grade: An Experimental Teaching

439

KSA-package. Therefore, we urge the Team to make

the images on Figure 6 and to argue that the three

curves, which appears on the wall, are sections of

conic shape by plane.

6.3.3 Searching for Applications

Our role on the final stage of the experimental

teaching was to state some guidelines for informal

learning in accordance with the findings of Petrovic

(2018). The didactical goal we stated to the Team was

to find appropriate implementations of the reflective

properties of the conics. We adopted a kind of

tutoring style to force the multifunktionality of the

Team’s KSA-package beyond the context of its

development. The testing area for the transferability

of the students’ knowledge and skills was real-life

applications of conic surfaces.

We already discussed some potential applications

of hyperbolic surfaces in the Scholium above. The

implementation of the reflective property of parabolic

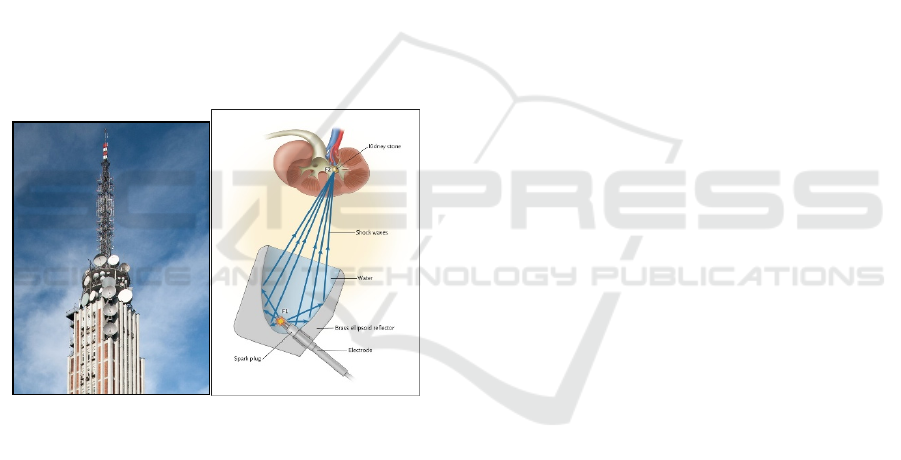
surface in modern communications could be observed

just walking around the city (Figure 7, left).

Figure 7: Applications of conic sections surfaces.

More sophisticated was the case with the ellipse.

To find some proper applications, the Team was

urged to investigate different areas including

professional medical sources. The image in the Figure

7 (right) illustrates how an elliptic surface focuses

shockwaves for pulverizing renal and ureteric stones

(Pearl, 2012). The Team prepared an explanation of

the theoretical background of how the lithotripter

works.

7 CONCLUSIONS

On the top floor of the IET, the Team demonstrates a

large arsenal of multifunctional knowledge and skills

cemented by a positive attitude toward mathematics

and ICT. The collaboration between the students

allowed reaching the stated educational goals via a

synergetic effect, which was a kind of revelation for

us.

The team synthetic competence developed on this

final stage of the experimental teaching encouraged

us to continue our individual experimental teaching

with the same students for the upcoming school term.

The complex way we introduced conics created a

solid fundament for consideration more advanced

mathematical topics. We plan to enlarge students’

synthetic competence entering higher mathematics

via computer algebra system.

ACKNOWLEDGEMENTS

The authors are grateful to Mrs. S. Petrova who is the

vice-principle of 125

Secondary School, Sofia, for

upholding the experimental teaching. The study is

partially supported by the Chernorizec Hrabar

Educational and Research Program of the Institute of

Mathematics and Informatics, Sofia. All figures in the

text are done by the Team.

Authors’ contributions: D. Dimitrov –

management and didactical support; B. Lazarov –

conceptual frame, tutoring and the paper text.

REFERENCES

Burry, J., Davis, D., Peters, B., Ayres, P., Klein, J., Pena de

Leon, A., & Burry, M. (2011). Modelling Hyperboloid

Sound Scattering: The Challenge of Simulating,

Fabricating and Measuring. In C. Gengnagel, A. Kilian,

N. Palz, & F. Scheurer (Eds.), Computational Design

Modelling: Proceedings of the Design Modelling

Symposium Berlin 2011 (pp. 89-96). Berlin: Springer

Dimitrov, M., Peeva, G., and Stoyanov, B. (2019) Conics

as loci and envelopes. Matematika, Vol. LIX, No 1, pp

46-57 (in Bulgarian)

GeoGebra (2019). https://www.geogebra.org (last visited in

Nov 2019)

Lazarov, B., (2011). Teaching envelopes in secondary

school. The Teaching of Mathematics, vol. XIV, 1, pp

45-55

Lazarov, B. (2013). Application of some cybernetic models

in building individual educational trajectory.

Information Models and Analyses. Vol. 2, No1, 2013,

pp. 90-99.

Lazarov, B. (2019). Improving the Attitude towards

Mathematics via an ICT Rearrangement of the 8

Grade Math Curriculum. In Proceedings of the 11

International Conference on Computer Supported

Education. Volume 1, Heraklion, Crete – Greece, May

2 - 4, SCITEPRESS, pp 391-397

CSEDU 2020 - 12th International Conference on Computer Supported Education

440

Lazarov, B., Todorova. M., (2014). DGS Enhanced

Socratic Style Teaching. In Nicolescu, V. et al. (Edts)

15th International BASOPED Conference, Lumina

Publishing, Bucharest, pp 504-510

Netrebko, A., Garanca, E. (2007). Duo des fleurs by Leo

Delibe. Baden-Baden Opera Gala https://

www.youtube.com/watch?v=Vf42IP__ipw (6:00-6:25)

Pearle, M. (2012) https://images.app.goo.gl/8NkueDj6c

XKL9Bnk8 (last visited in Nov 2019). This link refers

to DOI: 10.1056/NEJMct1103074 Shock-Wave

Lithotripsy for Renal Calculi. N Engl J Med 2012;

367:50-57,

Petrovic O. (2018). Digital Media’s Alteration Mechanism

for Informal Learning. In Proceedings of the 10th

International Conference on Computer Supported

Education - Volume 2: CSEDU, ISBN 978-989-758-

291-2, p. 321-330. DOI: 10.5220/0006772303210330.

APPENDIX

We follow the notations from section 4.

Proof of Lemma 1. Consider the configuration

on Figure 8. We have 𝑃∈𝑠







⟹ 𝐹



𝑃𝐾𝑃. Now

𝐹



𝑃 𝐹



𝑃



𝐹



𝐾𝐾𝑃



 𝐹



𝑃



𝐹



𝐾𝐾𝑃



𝐾𝑃 𝐹



𝐾  𝑐 ⟹ 𝑃 ∈ H. □

Figure 8: Configuration of Lemma 1.

Proof of Lemma 2. Suppose the contrary: 𝑠







has a second common point 𝑄 with H, i.e. there exists

△𝑄𝐹



𝐾. Let 𝑍  𝐹



𝑄∩𝑘 (Figure 9). Now:

𝑄∈ H ⟹ 𝑄𝐹



𝑄𝐹



𝑐⟹



𝑄𝑍  𝑍𝐹





𝑄𝐹



𝑐⟹



𝑄𝑍  𝑐



𝑄𝐹



𝑐⟹𝑄𝑍𝑄𝐹



𝑄∈𝑠







⟹ 𝑄𝐹



𝑄𝐾⟹𝑄𝑍𝑄𝐾.

Applying the triangle inequality for △𝑄𝐹



𝐾, we

get

𝑄𝐾  𝐾𝐹



𝑄𝐹



𝑄𝑍𝑍𝐹



⟹𝐾𝐹



𝑍𝐹



which is a contradiction. □

Proof of Theorem 1. According to Lemma 2,

𝑠







is tangent to H for every 𝐾∈𝑘



∪𝑘



. Now let

𝑃 be an arbitrary point at H such that 𝑃𝐹



𝑃𝐹



𝑐.

Let 𝐾  𝐹



𝑃∩𝑘. Hence 𝑃𝐾  𝑃𝐹



𝑐𝑃𝐹



, i.e.

𝑃∈𝑠







, which is tangent to H. □

Figure 9: Configuration of Lemma 2.

Proof of Theorem 2. Consider the configuration

in Figure 10 where 𝐴 is an arbitrary point inside the

hyperbola branch containing 𝐹



. Let 𝐴𝐹



meets this

branch at 𝑃 and 𝐴𝐹



∩𝑘𝐾. Denote by 𝑀 the

midpoint of 𝐾𝐹



. We have to prove that the rays 𝐴𝑃

→

and 𝑃𝐹



→

conclude equal angles with the tangent to

H at 𝑃. According to Lemma 2, this tangent is 𝑠







Following the notations in Figure 10, we have to

prove that 𝛼𝛽.

Figure 10: Configuration of Theorem 2.

Since 𝑃∈𝑠







, then 𝐾𝑃  𝑃𝐹



. In the isosceles

triangle 𝐾𝑃𝐹



, the segment bisector of 𝐾𝐹



is angle

bisector of ∠𝐾𝑃𝐹



. Hence, 𝛽∠𝐾𝑃𝑀 .

Furthermore, 𝛼∠𝐾𝑃𝑀 as vertical angles. Thus

𝛼𝛽. □

Introducing Conics in 9th Grade: An Experimental Teaching

441