The Construction of a Network for Indoor Navigation

Eliseo Clementini

and Andrea Pagliaro

Dept. of Industrial and Information Engineering and Economics, University of L’Aquila, L’Aquila, Italy

Keywords:

Indoor Navigation, Network Construction, Straight Skeleton, Visibility Graph.

Abstract:

Navigation systems provide help to moving agents by enabling them to reach a desired destination. The

development of the Global Positioning System (GPS) has enabled the development of outdoor navigation

systems, which are based on the knowledge of a map and the user’s location and provide guidance indications.

The reality of indoor navigation systems is much different: difﬁculties stem from the fact that the movement

of users is not constrained to belong to a well-established network such as the road network in the case of cars,

but it is generally freer and less codiﬁable. This paper focuses on the automatic construction of a navigation

graph superimposed on the map of a building that describes the possibilities of movement of a user within the

building itself. The construction of the graph tries to replicate the spontaneous movement of users.

1 INTRODUCTION

In many situations of real life, it is often necessary

to know the path to be performed within a large

and complex structure. Navigation systems such as

Google Maps or TomTom have from long time ad-

dressed such a goal, allowing us to obtain the best

route to be followed on foot, by bike or car, based

on our GPS position. At the moment, however, nav-

igation systems are limited to exterior use. A current

research trend is to expand the navigation technology

to inside space, where the GPS signal is not available

or its resolution for common handheld devices is not

enough. Indoor navigation introduces a methodology

that, through the availability of the plans of a building,

manages to build a navigation path (Zlatanova et al.,

2020; Yang and Worboys, 2015). Navigation implies

guidance along the best path to a destination avoiding

that the user gets lost (Fallah et al., 2013). Indoor nav-

igation systems have been studied also in reference

to building models such as CityGML or IFC (Kolbe

et al., 2005).

The focus of this paper is the construction of a net-

work to be overlaid to the building plan for helping

navigation. The rationale behind this network is that

it should simulate the most natural path of a pedes-

trian walking inside the building, therefore, avoiding

narrow angles, walking not too close to walls and ob-

stacles, taking advantage of visibility of landmarks,

https://orcid.org/0000-0002-3057-7105

and so on. Much work has already been done for

network construction, but the resulting networks al-

ways have some critical parts. Taking the medial axis

of indoor space, such as in (Yao and Rokne, 1991)

and (Lee, 2004), is generally acceptable for long cor-

ridors, but it is less natural for large spaces such as

halls, where the medial axis looses its signiﬁcance.

In the literature of navigation meshes in simulation

and gaming, e.g., (van Toll et al., 2018), medial axis

are modiﬁed with various techniques to improve path

planning. Further, the medial axis of a non-convex

shape contains parabolic arcs: those arcs increase the

difﬁculty of computing the medial axis and represen-

tations are more complex; further, parabolic arcs do

not work well in map-matching algorithms (Taneja

et al., 2016). Algorithms based on straight skeletons

have been suggested to overcome this limitation (Fu

et al., 2020).

Taking the visibility graph between vertices of

the shape (Taneja et al., 2011) allows us to consider

shorter paths to cross a large area such as a hall, but

it leads to unnatural path segments too much close

to walls and obstacles. An interesting data structure

that modiﬁes a visibility graph with Voronoi diagrams

to obtain more natural-looking paths was proposed in

(Wein et al., 2007). Hybrid approaches to the deter-

mination of navigation networks have been devised to

mediate between the above approaches. For example,

in (Mortari et al., 2019), a constrained Delaunay tri-

angulation combined with inward offset polygons is

able to produce a navigation network that solves the

254

Clementini, E. and Pagliaro, A.

The Construction of a Network for Indoor Navigation.

DOI: 10.5220/0009488902540261

In Proceedings of the 6th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2020), pages 254-261

ISBN: 978-989-758-425-1

disadvantage of medial axis, but it is critical for doors

near vertices of the room, where serpentine routes

with too many intermediate points are generated.

In this paper, we conceive a new technique for the

network construction, which starts from the straight

skeleton of an indoor space. The straight skeleton has

no curved segments contrary to the medial axis but

it may lead to unnatural narrow turns. Therefore, we

smooth the narrow angles of the straight skeleton by

avoiding turns bigger than 90

◦

. Then, other points

of interest, such as doors, are added to the network.

Hence, nodes of the obtained network are shortcut by

computing the visibility between nodes, thus suggest-

ing shorter paths. Further simpliﬁcations regard the

deletion of paths that are too close to walls by inter-

secting the network with an inner buffer of the indoor

space.

In the remainder of this paper, we introduce ba-

sic data structures and the straight skeleton algorithm

(Section 2). In Section 3, we modify the network to

include semantic information such as the doors. In

Section 4, we make the network smoother to avoid

sharp turns. In Section 5, we add shortcuts between

visible points. In Section 6, we remove paths too

much closer to the walls. Short conclusions end the

paper (Section 7).

2 DATA STRUCTURES AND

ALGORITHMS

From a cognitive perspective (Montello, 1993), in-

door navigation is a problem that can be placed at

the environment space, that is, a space that can be

perceived by moving and sight, contrary to outdoor

navigation, which is placed at geographic scale. Inde-

pendently of scale, indoor navigation involves the use

of methods and algorithms of geographic information

science.

An indoor map can be schematized as an irregular

tiling, where each polygon models a room or another

identiﬁable portion of space. Even if the rooms are

not actually closed, we will consider them as poly-

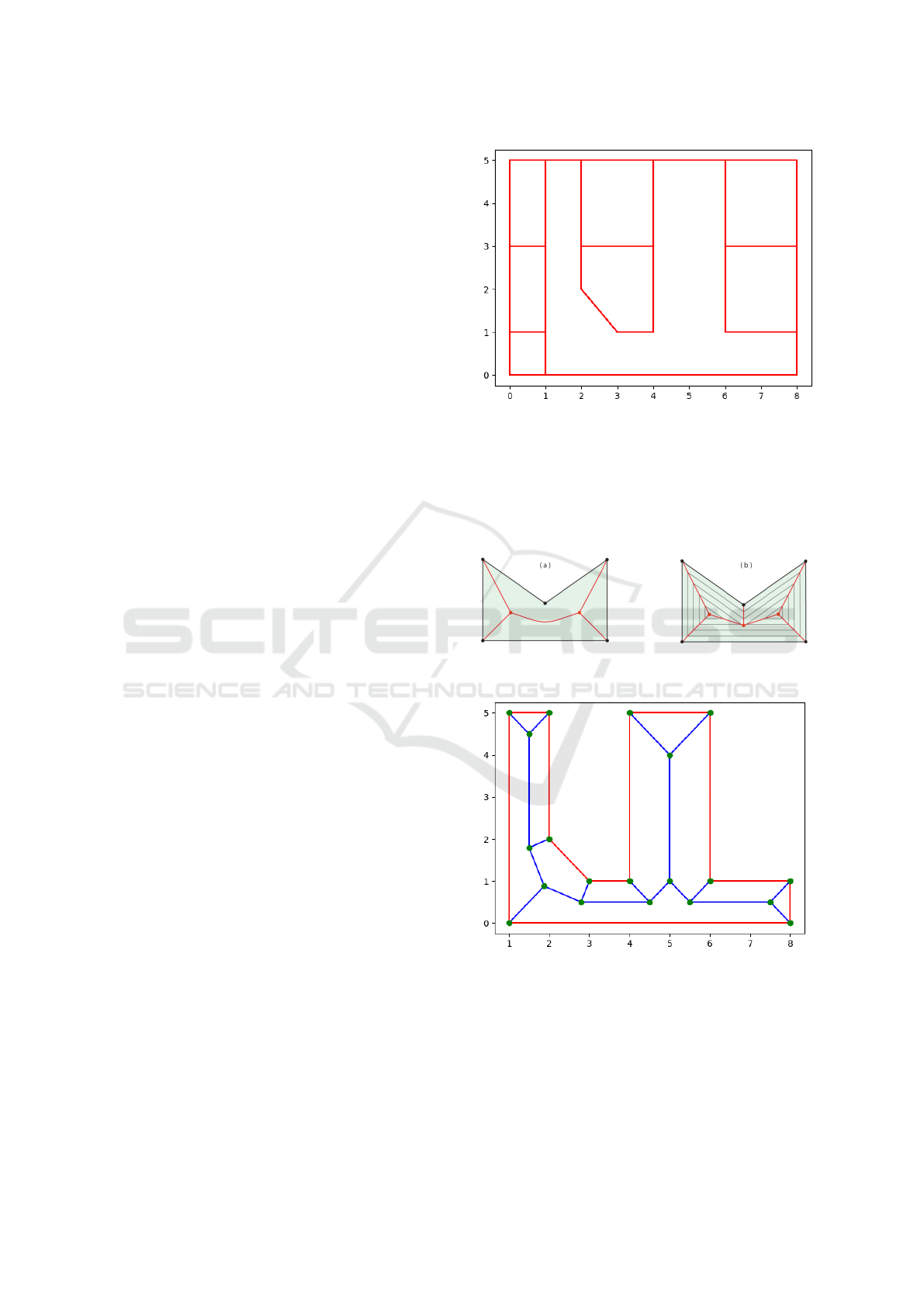
gons, like the indoor map of Figure 1.

Let us consider the difference between the medial

axis and the straight skeleton. Both are algorithms

that allow us to extract a representative linear object

from a planar shape. The medial axis of a polygon

is deﬁned as the place of the points within the poly-

gon which have equal distance from more than one

point of the boundary. If a polygon is non-convex,

the medial axis has curved parts in correspondence

of non-convex vertices of the polygon. To avoid this

difﬁculty, it is possible to consider the straight skele-

Figure 1: Case study.

ton. The latter is deﬁned as the trace of vertices when

a progressive shrinking of the polygon is performed.

The two deﬁnitions coincide for convex polygons and

mark a difference for non-convex polygons, as shown

in Figure 2.

Figure 2: Differences between medial axis (a) and straight

skeleton (b).

Figure 3: Skeletonized non-convex polygon.

Straight skeletons can be more easily implemented

both from the algorithmic point of view and from the

necessary data structures. Figure 3 clearly shows the

effect after applying the algorithm on a non-convex

polygon of our case study map. Storing the results

derived from the application of the straight skeleton

algorithm requires a suitable data structure, which we

The Construction of a Network for Indoor Navigation

255

identify as an undirected graph weighed on the Eu-

clidean distance between the nodes, for which we

used a Python3 library called “networkx”.

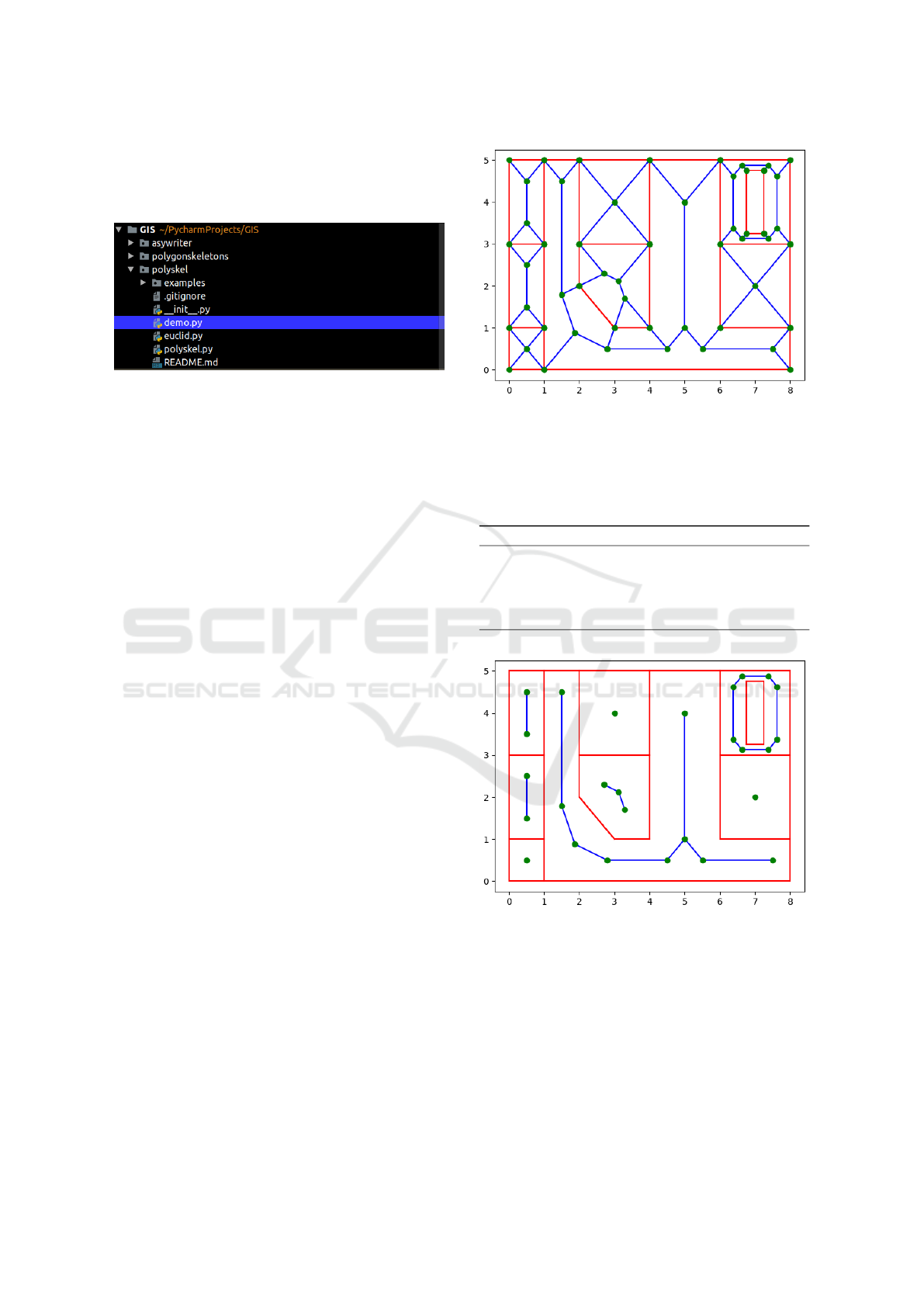
Figure 4: Straight skeleton package organization.

We used an open-source solution of the straight

skeleton (github project: https://github.com/Botffy/

polyskel.git), which represents a Python3 implemen-

tation of the algorithm by (Felkel and Obdr

alek,

1998). Such a package (Figure 4) is organized as fol-

lows:

• demo.py is a main program that imports the

points to describe a polygon and its internal holes.

This information is enclosed in an external ﬁle and

imported when it is run.

• skeleton.py is the class that contains all the func-

tions that describe the straight skeleton algorithm.

• euclid.py is a basic Euclidean geometry library

that is used to instantiate objects such as points

and segments and perform intersection and con-

nection operations between them.

We applied the algorithm to the scenario of Figure 1,

after having inserted some holes to simulate the pres-

ence of objects inside the rooms and understand how

the algorithm behaved in this situation. The algorithm

was applied separately to each polygon, obtaining a

set of graphs that represent the skeletonized rooms

(see Figure 5).

3 INSERTING POINTS OF

INTEREST

In this section, we describe two aspects: the elimina-

tion from the graphs of uninteresting points for navi-

gation, such as the room vertices, and the insertion of

semantically rich points, such as the doors.

3.1 Graph Simpliﬁcation

For navigability, it is not necessary to reach the cor-

ners of rooms. So we can eliminate the unnecessary

vertices from the graphs by eliminating from each

Figure 5: Straight skeletons of all rooms.

graph the nodes with only one incoming arc, that is,

the leaves of the graph (Algorithm 1). The result of

the simpliﬁcation is shown in Figure 6, where each

room has its simpliﬁed graph.

Algorithm 1: Reduce graph of straight skeleton.

1: for node in graph.nodes do

2: if node.degree is < 2 then

3: delete node from the graph

4: end if

5: end for

Figure 6: Simpliﬁed graphs.

3.2 Inserting Access Points

To this point, we have a set of separate graphs for each

room deriving from the straight skeleton. To allow

the transition from one room to another, we need to

add a connection between the two graphs of adjacent

rooms. We build each connection with a central node

(deﬁned from now on as a door node) connected to the

graphs by means of two arcs. Connecting the rooms

GISTAM 2020 - 6th International Conference on Geographical Information Systems Theory, Applications and Management

256

is important to apply a search algorithm for the short-

est paths between a source and a destination node be-

longing to different rooms. To facilitate and improve

the management of information that allows us to un-

derstand which rooms are connected via that door, we

deﬁne a matrix called the room-door connection ma-

trix. This matrix is composed by a door node for each

row by and a room for each column.

Algorithm 2: Construction of room-door connection matrix.

1: matrix=[]

2: for door node in door nodes do

3: row=[]

4: for polygon room in polygon rooms do

5: if room intersects door then

6: add true in row

7: else

8: add False in row

9: end if

10: end for

11: add row to matrix

12: end for

Starting from a list of door nodes, we calculate if a

door intersects a given room and populate the matrix

row by row (Algorithm 2). Therefore, in each row

of the matrix, there will no more than two matches,

since the only cases that can occur are those in which

a door belongs to a single room (external door) or two

rooms (internal door). On the other hand, in each col-

umn, we can observe the number of doors connecting

a room.

Algorithm 3: Construction of the door paths.

1: door paths=[ ]

2: for graph room that matches adjacency matrix do

3: conn distance edges vector

4: for edge in graph do

5: ﬁnd the minimum distance from the door and

the edge and add to conn

6: end for

7: take the edge with minimum distance from conn

and build a new edge that connects this one with the

door

8: if vertex u or v of edge are not in graph then split

edge

9: end if

10: the result is added to door paths

11: end for

Algorithm 3 allows us to obtain the door paths, that

is, the pairs of arcs that have doors as the central node

and that connect graphs of two different rooms. This

algorithm creates the arcs that connect a door node to

graph rooms. For each door, the algorithm looks for

the closest point between all the arcs of the matching

graph. If the closest point is a node of the graph, the

connection is simpler. If the closest point falls inside

an arc, then it is necessary to split the arc into two

shorter arcs. The results of the application of the op-

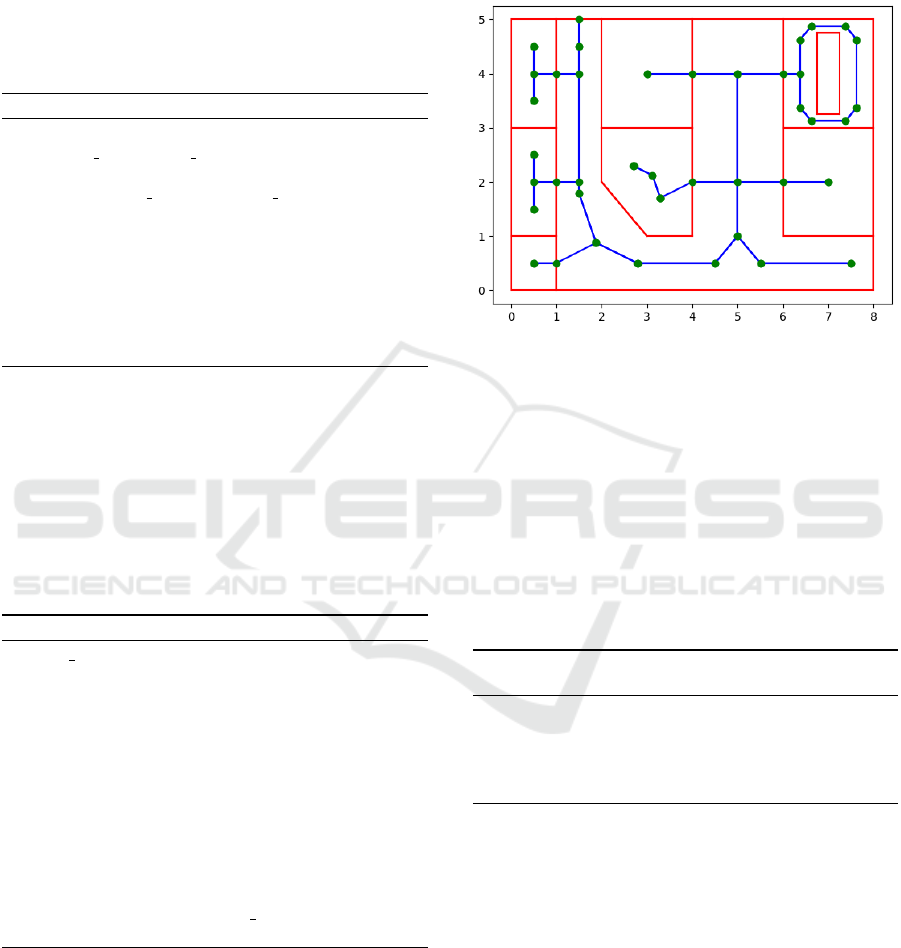
erations just mentioned are visible in Figure 7.

Figure 7: Graph with door paths.

3.3 Association of Nodes to Rooms

When joining all the single graphs with the paths on

the newly calculated door nodes, it is necessary to

keep trace of the room every node belongs to. The

door nodes are already represented in the previously

mentioned matrix, where they belong to two rooms.

For the nodes inside the rooms, Algorithm 4 iterates

over each graph and check the nodes by attributing to

each of them the identiﬁcation number of its room.

Algorithm 4: Function to add information about node mem-

bership.

1: for graph in graphs do

2: for node in graph.nodes do

3: add in node info about the membership room

4: end for

5: end for

4 SMOOTHING SHARP ANGLES

The straight skeleton algorithm for polygons with in-

ternal angles greater than 270

◦

leads to linear shapes

with sharp turning angles, like in the case of Figure 8.

It is for this kind of situations that the straight skeleton

algorithm deviates from the medial axis. In this sec-

tion, we adopt a strategy of “cutting” the vertices in

correspondence of internal angles greater than 270

◦

Algorithm 5 identiﬁes the vertices to be cut. Each

identiﬁed vertex is substituted in the room boundary

by two vertices at a small distance. In Figure 8 and

The Construction of a Network for Indoor Navigation

257

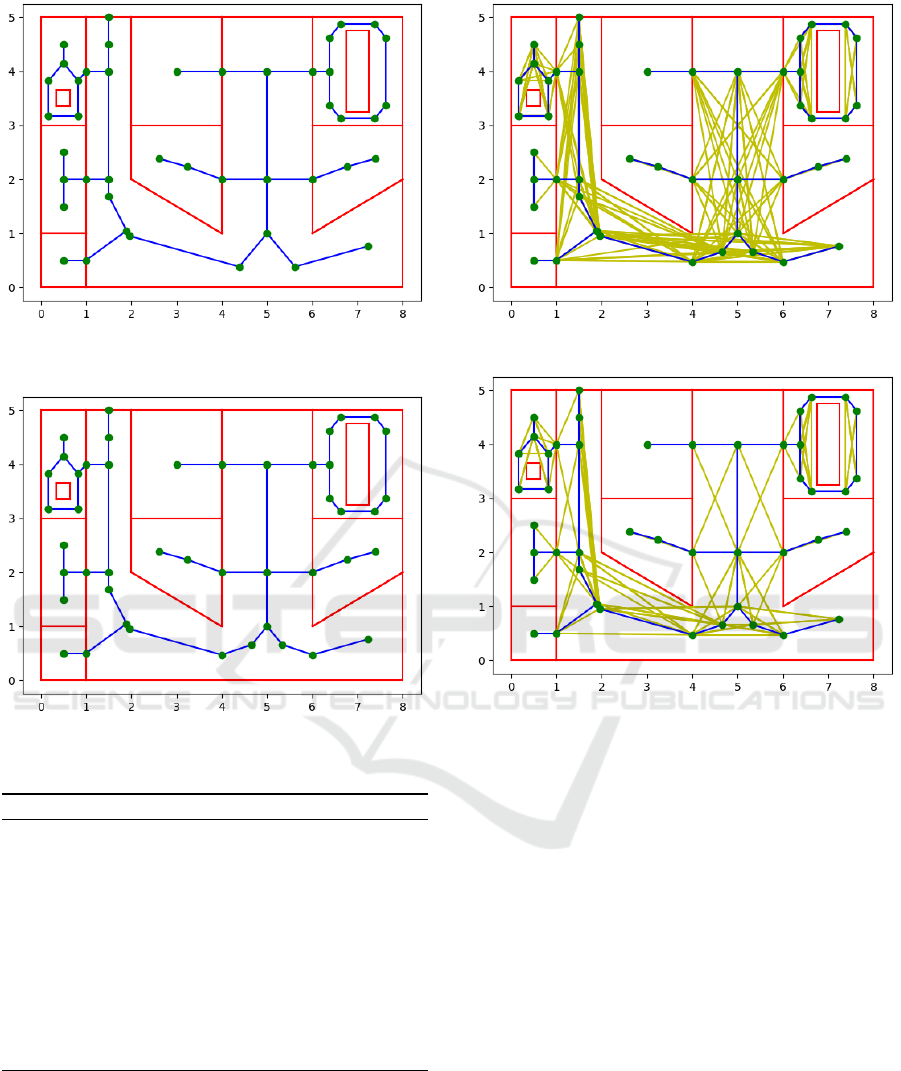
Figure 8: The network before the application of function to

smooth sharp vertices.

Figure 9: The network after the application of function to

smooth sharp vertices.

Algorithm 5: Function to smooth angle.

1: procedure AnglePolygonSmooth(rooms,c)

2: for room in rooms do

3: for poly in room do

4: for incremental triple of vertex do

5: compute the angle between them

6: if internal angle is > 270 degrees then

needs to be cut

7: end if

8: end for

9: end for

10: end for

11: end procedure

Figure 9, it is possible to compare the map before and

after the application of this algorithm, with the choice

of a very small factor for cutting the sharp vertex. In

such a ﬁgure, it is difﬁcult to notice the removal of

the vertex and its substitution with two extra vertices,

but the change in the straight skeleton is evident and

qualitatively more appealing for navigation.

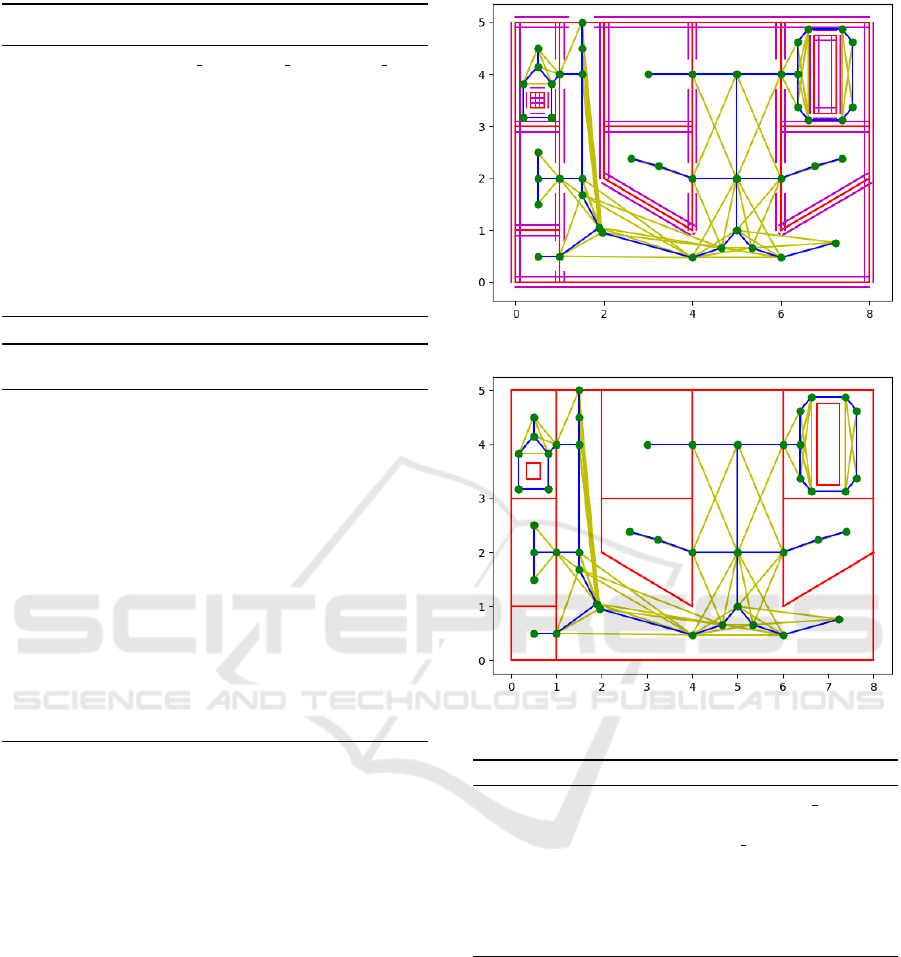
Figure 10: Overlay with visibility graph.

Figure 11: Visibility graph after removal of intersections.

5 ADDING VISIBILITY GRAPH

As explained in the introduction, in our strategy we

combine straight skeletons with visibility graphs. By

connecting nodes that are in clear visibility, we obtain

shorter paths that mimic the behaviour of other cat-

egories of navigation algorithms. Therefore, we use

the network nodes already found in previous section

and we compute the visibility graph based on these

nodes. Algorithm 6 allows the creation of the visibil-

ity graph (see Figure 10).

After the visibility graph is obtained, we reduce

the number of arcs by eliminating the arcs that in-

tersect with existing arcs of the initial network (see

Figure 11). The intersection between a point and a

line necessary in Algorithm 6 was obtained with Al-

gorithm 7. The latter calculates the collinearity be-

tween a point and a segment via a cross product.

GISTAM 2020 - 6th International Conference on Geographical Information Systems Theory, Applications and Management

258

Algorithm 6: Function that checks the visibility between

two nodes.

1: procedure visibility check( first node,second node,

room)

2: intersection = False

3: for wall in room do

4: if wall intersects segment composed by ﬁrst

node and second node then

5: intersection = True

6: end if

7: end for

8: if intersection is False then append edge to the vis-

ibility graph

9: end if

10: end procedure

Algorithm 7: Function to compute intersection between

Point and Segment.

1: function IntersectionBetweenPointandSegment(P,S)

2: M =





S.p1.x S.p1.y 1

S.p2.x S.p2.y 1

P.x P.y 1





3: if det(M) = 0 then  collinearity test

4: D(S.p1, S. p2)  distance between S.p1 and

S.p2

5: if D(S.p1, P) < D(S.p1, S. p2) and D(S.p2, P) <

D(S.p1, S. p2) then

6: return True

7: else

8: return False

9: end if

10: else

11: return False

12: end if

13: end function

6 NETWORK BUFFERIZATION

A problem of a navigation network based on visibility

is that produces links that are too much close to walls.

As a ﬁnal phase of the network construction, we avoid

such a problem by applying an inward buffer to the

polygons that make up the building plan and then re-

moving the links that intersect the buffer.

The width of the buffer can be chosen depending

on the extension of the room: therefore, we make it

dependent from the apothem of each polygon. The

implementation of the buffer for our study case has

been made by translating each segment representing

a wall by the chosen width and connecting them by

circular arcs centered on segment endpoints. Then, a

method has been added to verify the intersection with

navigation network. The doors between rooms have

not been bufferized. The application of the method

just discussed on the visibility graph is visualized in

Figure 12.

Figure 12: Bufferization of the rooms.

Figure 13: Final graph.

Algorithm 8: Function to ﬁlter not connected elements.

1: procedure FilterNotConnected(principal node)

2: for node in graph.nodes do

3: if Dijkstra from principal node to node outputs

not achievable then

4: delete node

5: end if

6: end for

7: end procedure

It can be seen seen that in this graph there are several

eliminations of previous arcs. During this process, it

can happen that the elimination of some arcs caused

the disconnection of graph components making the

graph no longer connected. To verify the reachability

of all the nodes of the graph, we choose a main node

(which could be for example the entrance of the build-

ing) and apply Dijkstra from the main node to other

nodes. If reachability is not veriﬁed, those nodes will

be eliminated making the graph connected again. This

function is represented in Algorithm 8. Normally,

choosing a thin buffer does not provoke the interrup-

The Construction of a Network for Indoor Navigation

259

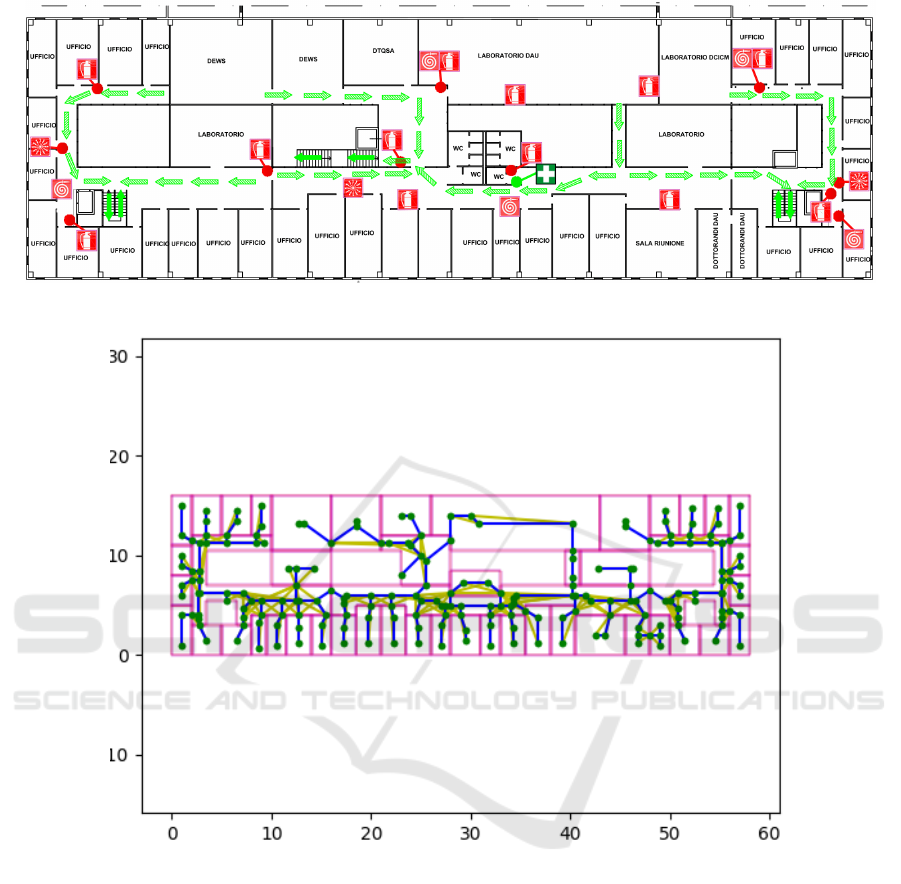
Figure 14: Emergency plan of university ﬂoor.

Figure 15: Navigation network for university ﬂoor.

tion of the navigation graph. Therefore, this action

can be useful if from the main entrance the navigating

agent has a considerable size and we want to discard

the parts of the map where the agent does not ﬁt. In

Figure 13, there is the ﬁnal navigation network for the

case study.

7 CONCLUSIONS

In this paper, we proposed the automatic construction

of a navigation network for the map of a typical build-

ing ﬂoor. While there are several proposals in the lit-

erature (e.g., (Lee, 2004; Taneja et al., 2011; Mortari

et al., 2019)), there are recognized drawbacks in each

proposal. In our contribution, we try to overcome all

the drawbacks. We start from computing the straight

skeleton of the map and combine it with a visibility

graph over the straight skeleton nodes. We believe

that this approach interprets a good qualitative model-

ing of the movement of people inside an indoor envi-

ronment, obtaining a smooth path at the center of cor-

ridors and around vertices and ﬁnding shorter paths

on larger halls based on visibility. Semantic aspects

have been introduced to keep trace of rooms and doors

connecting them. An inward bufferization can also

avoid movements too close to walls and solve naviga-

tion planning for sizeable agents (e.g., for people with

reduced mobility).

GISTAM 2020 - 6th International Conference on Geographical Information Systems Theory, Applications and Management

260

At the time of writing, we started an evaluation of

the algorithm for some real building ﬂoors. In Fig-

ure 14, we took into consideration an emergency map

of a ﬂoor in our university and we applied the algo-

rithm to ﬁnd the navigation network for this map: the

result is shown in Figure 15. Further work will follow

in several research directions. To validate the shape

of the network, we plan to collect various trajecto-

ries of moving people inside a building instructing

them to walk from the entrance to a given target and

compare their trajectories with the proposed naviga-

tion network to assess if it could be considered as the

representation of the average trajectory. Another de-

velopment is to ﬁnd an automatic way of extracting

qualitative directions for moving inside the building

ﬂoor, similarly to the work of (Russo et al., 2014).

Directions should not be expressed in terms of angles

and metric distances, but in qualitative terms, making

use of various models for qualitative spatial reason-

ing (e.g., (Clementini, 2013; Fogliaroni and Clemen-

tini, 2015; Bartie et al., 2013; Clementini and Cohn,

2014; Tarquini and Clementini, 2008)). An extension

of the proposed network is necessary as well to con-

nect building ﬂoors among them via stairs or elevators

and with outdoor space.

REFERENCES

Bartie, P., Clementini, E., and Reitsma, F. (2013). A quali-

tative model for describing the arrangement of visible

cityscape objects from an egocentric viewpoint. Com-

puters, Environment and Urban Systems, 38(1):21–

34.

Clementini, E. (2013). Directional relations and frames of

reference. GeoInformatica, 17(2):235–255.

Clementini, E. and Cohn, A. (2014). RCC*-9 and CBM*.

In Duckham, M., Pebesma, E., Stewart, K., and Frank,

A., editors, GIScience 2014: Geographic Information

Science, volume 8728 of Lecture Notes in Computer

Science, pages 349–365, Cham. Springer.

Fallah, N., Apostolopoulos, I., Bekris, K., and Folmer, E.

(2013). Indoor human navigation systems: A survey.

Interacting with Computers, 25(1):21–33.

Felkel, P. and Obdr

alek, S. (1998). Straight skeleton imple-

mentation. In Szirmay-Kalos, L., editor, Proceedings

of Spring Conference on Computer Graphics, pages

210–218, Budmerice, Slovakia.

Fogliaroni, P. and Clementini, E. (2015). Modeling visi-

bility in 3D space: A qualitative frame of reference.

In Breunig, M., Al-Doori, M., Butwilowski, E., Ku-

per, P., Benner, J., and Haefele, K., editors, 9th Inter-

national 3DGeoInfo Conference, 2014, Lecture Notes

in Geoinformation and Cartography, pages 243–258,

Cham. Springer.

Fu, M., Liu, R., Qi, B., and Issa, R. R. (2020). Generating

straight skeleton-based navigation networks with in-

dustry foundation classes for indoor way-ﬁnding. Au-

tomation in Construction, 112:103057.

Kolbe, T., Gr

oger, G., and Pl

umer, L. (2005). CityGML:

Interoperable access to 3D city models. In van Oost-

erom, P., Zlatanova, S., and Fendel, E., editors, Geo-

information for Disaster Management, pages 883–

898, Berlin, Heidelberg. Springer.

Lee, J. (2004). A spatial access-oriented implementation of

a 3D GIS topological data model for urban entities.

GeoInformatica, 8(3):237–264.

Montello, D. R. (1993). Scale and multiple psychologies of

space. In Frank, A. U. and Campari, I., editors, Spa-

tial Information Theory A Theoretical Basis for GIS,

pages 312–321, Berlin, Heidelberg. Springer.

Mortari, F., Clementini, E., Zlatanova, S., and Liu, L.

(2019). An indoor navigation model and its network

extraction. Applied Geomatics, 11(4):413–427.

Russo, D., Zlatanova, S., and Clementini, E. (2014). Route

directions generation using visible landmarks. In 6th

ACM SIGSPATIAL International Workshop on Indoor

Spatial Awareness, ISA 2014, pages 1–8, New York,

NY, USA. Association for Computing Machinery.

Taneja, S., Akinci, B., Garrett, J. H., and Soibelman, L.

(2016). Algorithms for automated generation of nav-

igation models from building information models to

support indoor map-matching. Automation in Con-

struction, 61:24 – 41.

Taneja, S., Akinci, B., Garrett, J. H., Soibelman, L., and

East, B. (2011). Transforming IFC-based building

layout information into a geometric topology network

for indoor navigation assistance. In International

Workshop on Computing in Civil Engineering 2011,

pages 315–322. American Society of Civil Engineers

(ASCE).

Tarquini, F. and Clementini, E. (2008). Spatial relations

between classes as integrity constraints. Transactions

in GIS, 12(SUPPL. 1):45–57.

van Toll, W., Cook Iv, A. F., van Kreveld, M. J., and Ger-

aerts, R. (2018). The medial axis of a multi-layered

environment and its application as a navigation mesh.

ACM Transactions on Spatial Algorithms and Sys-

tems, 4(1):1–21.

Wein, R., van den Berg, J. P., and Halperin, D. (2007).

The visibility–Voronoi complex and its applications.

Computational Geometry, 36(1):66 – 87.

Yang, L. and Worboys, M. (2015). Generation of naviga-

tion graphs for indoor space. International Journal of

Geographical Information Science, 29(10):210–218.

Yao, C. and Rokne, J. (1991). A straightforward algorithm

for computing the medial axis of a simple polygon. In-

ternational Journal of Computer Mathematics, 39(1-

2):51–60.

Zlatanova, S., Yan, J., Wang, Y., Diakit

e, A., Isikdag,

U., Sithole, G., and Barton, J. (2020). Spaces in

spatial science and urban applications—state of the

art review. ISPRS International Journal of Geo-

Information, 9(1):58.

The Construction of a Network for Indoor Navigation

261