Scalable Logistic Cell RFID Witness Model

Bernhard Heiden

1,3 a

, Volodymyr Alieksieiev

1,2 b

and Bianca Tonino-Heiden

3 c

Industrial Engineering and Management Studiengang, University of Applied Sciences, Europastrasse 4, Villach, Austria

Institute for Mechanical Engineering and Transport, National Technical University, ’Kharkiv Polytechnic Institute’,

Kyrpychova 2, Kharkiv, Ukraine

Philosophy Institute, University of Graz, Heinrichstrasse 26, Graz, Austria

Keywords:

Logistics, Witness, RFID, Logistics-simulation.

Abstract:

This paper describes a scalable logistic cell Radio Frequency IDentiﬁcation (RFID) Witness Model. First, a

scalable logistic cell analysis is done which can be applied to the logistics of any size-scale and application.

This model is then implemented into Witness and simulated, for different cases. To show practicability, the

model is mirrored in a physical Internet of Things (IoT) device in form of an Arduino micro-controller board

which is attached to an RFID-Reader, together with a model-warehouse / forklift truck unit. The speciﬁc

challenge of this work is to design a universal logistic model, for demonstration of all possible logistic appli-

cations with one simple cell, together with a single step IoT connection, and that can be easily built as well as

a physical, as a computer simulation model.

1 INTRODUCTION

Nowadays production, logistics, and general process

simulation is increasingly important in industry and is

applied to different ﬁelds like e.g. Business Process

Management (Garc

ıa-Garc

ıa et al., 2020). There is a

trend in the last years of using distributed Software,

which may be important for collaboration, as well as

cloud-based solutions, increasing simulation velocity

(Lunesu et al., 2018). This can also be subsumed to

the efforts to decrease the effects of the nowadays

increasing endangerment of actual pandemic devel-

opments, making remote collaboration more feasible

and even necessary. Furthermore, there can be seen a

trend in process simulation towards agent-based sim-

ulations (Ali et al., 2014), which shows the neces-

sity of increasing Artiﬁcial Intelligence (AI) models,

for simulation of decision processes, that depict in-

creasing complexity and needed ﬂexibility in indus-

trial production as well as logistic processes. There

exists now also a wide variety of process simulation

software (Leporis and Kr

alov

a, 2010), which is im-

portant to implement a virtual twin of industrial pro-

duction, logistics, and many other processes.

The goal of this work is to implement a simple and

https://orcid.org/0000-0001-8324-6505

https://orcid.org/0000-0003-0792-3740

https://orcid.org/0000-0001-7648-2833

powerful scalable model for a universal logistic pro-

cess, that is hence useful in a wide variety of logistic

applications. To give an immediate insight together

with a process simulation a simpliﬁed logistic process

is implemented as an educational demonstration tool

with a micro-controller application. For this the Ar-

duino Platform is used, where an excellent summary

for the Arduino can be found with the ”Arduino in

A Nutshell Book” which is quite practically useful,

as there is also given a description of the electronics

needed for the periphery of this Microcontroller Plat-

form (Borchers, 2013). The challenge of this work is

to implement a simple model for an educational pur-

pose, that depicts some essential universal and scal-

able aspects of an IoT-system in the context of an

industrial applicable logistic network, as a physical-

IoT-model and as a digital twin simulation. In this

work, ﬁrst in section two, the position of this paper is

given. In section three a scalable logistic cell is de-

veloped, which has the property of being scalable and

widely applicable. Section four gives then a practical

application of a virtual twin of this model. Section

ﬁve shows then the results of an IoT application of

this simulation model in a real-world model, imple-

mented with the Arduino platform in connection with

a Radio Frequency IDentiﬁcation (RFID)-Reader. Fi-

nally in section six the summary and a short outlook

are given.

420

Heiden, B., Alieksieiev, V. and Tonino-Heiden, B.

Scalable Logistic Cell RFID Witness Model.

DOI: 10.5220/0009490204200427

In Proceedings of the 5th International Conference on Internet of Things, Big Data and Security (IoTBDS 2020), pages 420-427

ISBN: 978-989-758-426-8

2 POSITION

The position of this paper is, that a simple logistic cell

model with one exemplary IoT-sensor application, is

adequate for implementing a scalable logistic process

and that this process can be hence demonstrated by a

simple physical model as well as a simulation model.

It is further suggested, that such a model can be eas-

ily scaled up and interconnected to depict an indus-

trial real-world logistic process. This process is ad-

missable because it can be interpreted as an orgiton

(Heiden et al., 2019) or a fractal program (Mandel-

brot, 1991) that is based on a core element (cell, orgi-

ton, fractal generator) that is multiplied and intercon-

nected.

3 A SCALABLE LOGISTIC CELL

The term ”logistic cell” can be derived from cyber-

netics and namely from the concept of cybernetic

systems, which are informational open and func-

tional closed (compare also (Weber, 2010), (Luh-

mann, 1997)). The system is deﬁned as open if it has

an energetic and matter exchange with the external

world. The term ”external world” is taken in this con-

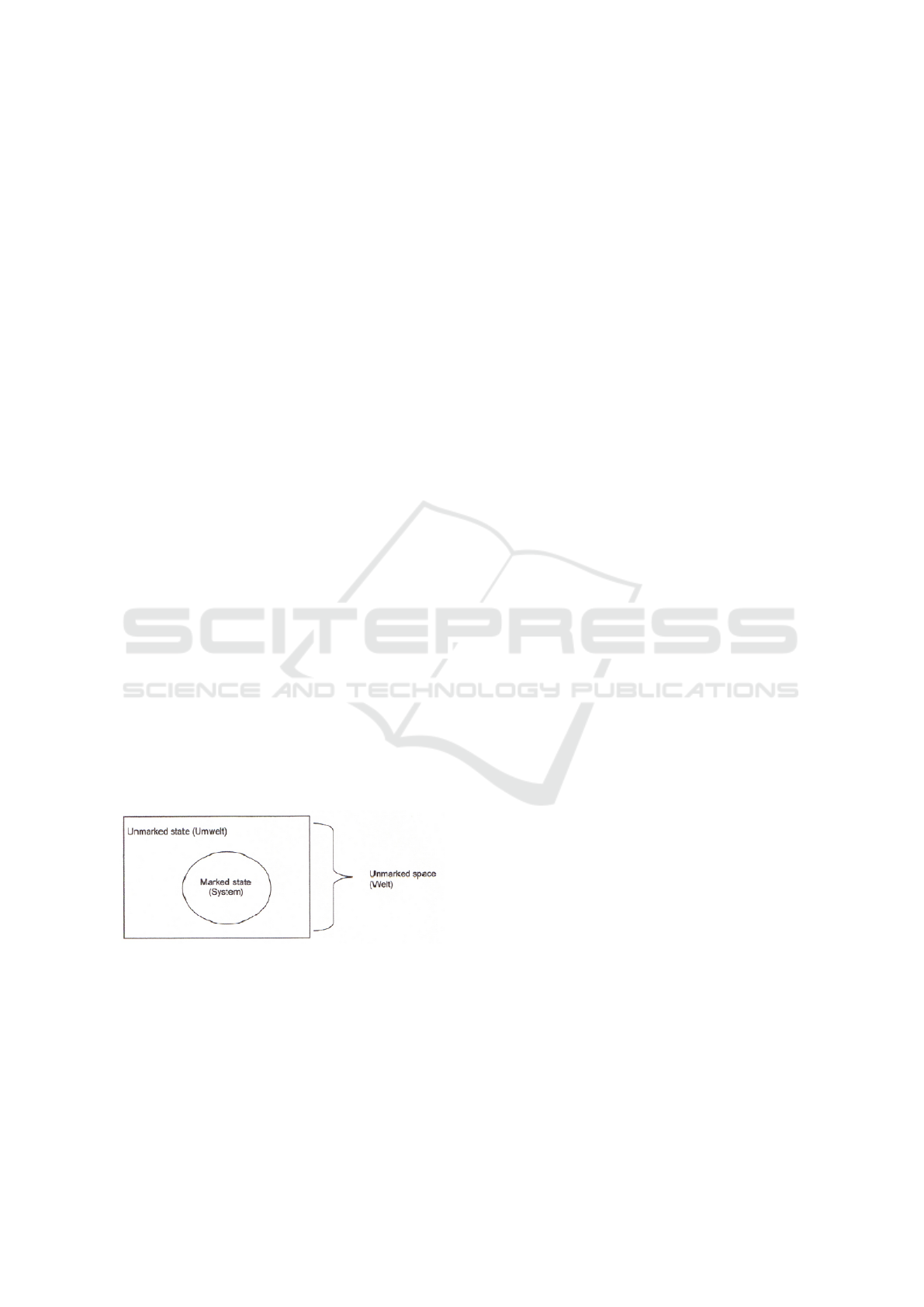
text from the theory of systems of George Spencer-

Brown, where the system appears from the separation

as a marked state (system) from the unmarked state

(external world) (Spencer-Brown, 2008) (q.v. Figure

1). An informational open system means that the ex-

change of information between this system and the

external world also exists. Functional closed means,

on the other hand, that the system can deﬁne a method

of communication with the external world indepen-

dently, using its functional organization.

Figure 1: Appearance of a system in the theory of George

Spencer-Brown (Spencer-Brown, 2008).

This term of a cybernetic system can be also applied

in the logistical context. For the deﬁnition of a lo-

gistic cell, the cybernetic system has to be modiﬁed

in that way, that it is deﬁned as open for matter and

information because it always has an exchange in the

matter (material, transport and people ﬂow) and in-

formation (external communication) levels. For that

these ﬂows are ﬂowing, they have to be powered by

energy. The unity of these natural components can be

determined through the Orgiton-Theory of Bernhard

Heiden et al. (Heiden et al., 2019), where it is called

“Orgiton”. If a system is deﬁned as matter-open it

has also to be answered, which can be designated as a

border of this system. Concerning the logistic cell, the

boarders have to be so deﬁned that they are pulled or

pushed by the observer. So, the system has to be con-

sidered by an observer, where a concrete object has to

be marked (marked state) as a cell. To specify it as

a technical model, functional interaction of the ”cell”

has to be considered. The main feature of this inter-

action is functional autonomy, which means that it is

operationally closed. It means, that the system can

work without external input requirements because it

has sufﬁcient own functionality. On the other hand,

this system is determined as matter open, because it

e.g. pulls the information from the external world and

can communicate with other cells through matter, en-

ergy and information exchange. From that two main

features for the determination of logistic cell can be

taken:

(1) The autonomous self-sufﬁciency and the

(2) potential interaction with similar cells in their re-

spective matter, energy and information levels.

This second property of the here deﬁned logistic cell

can be denoted as scalability. Scalability can be un-

derstood as the property of a logistic cell that allows

for applying volume and / or size changes in the sys-

tem. At the same time it has to be noticed, that the

borders of logistic cells are strongly connected with

the borders of ﬂows, respectively, the bigger is the

Material-Energy-Information (MEI)-ﬂow, the bigger

is the ”input surface” and with it tendentiously the cell

(q.v. Figure 2). Mathematically this can be described

by Equation (1), where G

and G

are respectively the

borders of ﬂow and cell systems.

= f (G

) (1)

This means that the size of the connection of the

cells changes with the material ﬂow e.g. Imagine a

pipeline, that has to be bigger when more material is

passing between two cells. This has a manifold of ap-

plications in nature, es e.g. in trees, blood vessels,

or lung branches (compare e.g. (Mandelbrot, 1991)).

The scalability of a cell is hence closely connected

to these to borders, border of the border in the pro-

jection, and the border of the cell. This is then a

self-referential structure, an orgiton of a higher or-

der, or according to Beno

ıt Mandelbrot a fractal self-

referential structure.

To sum up the deﬁnition of the scalable logistic

cell: The scalable logistic cell is a material and func-

Scalable Logistic Cell RFID Witness Model

421

Figure 2: Dependence Between Borders of Flow System

and Cell System.

tional open system, which on the one hand is auto-

nomic and has, on the other hand, potential interac-

tion with other logistic cells on material, informa-

tional and energetic levels.

4 WITNESS-MODEL

This simple logistic cell model has then been sim-

ulated in the simulation software Witness 2014 to-

gether with a storage option. The choice of this sim-

ulation software was based on many of Witness, ad-

vantages, which sets it apart from other process sim-

ulation software in the industrial environment. These

advantages are:

• Powerful construction principle

• Unlimited number of intelligent objects, modular

structure

• Seamless integration with ERP, BDE, MES, etc.

• Automated mass experiments with the integrated

WITNESS Experimenter

• Automatic 3D visualization with WITNESS

Quick 3D (LannerGroupLimited, 2020)

The whole logistic cell simulation model is shown in

Figure 3.

Figure 3: Logistic Cell with a Storage Option in the Witness

Model.

The model consists of the considered logistic cell with

a storage option (cell 2) and schematically depicts cell

1 and cell 2, which play the role of e.g. the supplier

and the customer respectively. The main idea of this

model is to show the speciﬁc functions of a logistic

cell with a storage option as well as the interaction be-

tween different cells on the matter, information, and

energetic levels. As an application, this can be e.g. a

production facility, that gets material from other com-

panies and delivers products to customers by truck.

So the logstic cell in Witness depicts the internal and

the external logistic process in the model. The exten-

sion to a network can then be done easily by copying

and connecting the cells accordingly.

4.1 RFID as IoT Application

To demonstrate an industrial logistics identiﬁcation

procedure, of incoming goods the technology of

Radio-Frequency Identiﬁcation (RFID) was used as

an application example in the model explained in the

next section, where the Witness model is the digital

twin. Compared to the second most popular identi-

ﬁcation technology – the barcode technology, whose

work is based on optical (laser) contact, the working

principle of the RFID-technology is based on radio

waves transmission between RFID-Reader and chip

and has many advantages. The most important ad-

vantages are

• an opportunity to scan up to 1000 items per sec-

ond,

• to overcome distances up to 100 meters (in special

cases) between RFID-Reader and chip,

• that sight contact is not needed and

• the possibility to store up to 64 Kb as information

in a chip in comparison to 3000 bytes as informa-

tion with barcode technology.

That is why the RFID-technology was chosen for the

model used here.

4.2 Logistic Process

A simulation process of the logistic model looks as

follows:

Step 1: Cell 1 obtains pallets (PT) and boxes

(Box1), assembles them to the one unit and sends

them to the cell 2 by truck (Truck1). Cell 1 plays

in such a model the role of the supplier, whose

main task is to provide a considered element with

necessary sub-elements. Through the movement

of goods, there arises a ﬂow (material ﬂow).

Step 2: The goods arrive at the unload point and

are unloaded and separated by labor (Lab2) to

boxes and pallets. The boxes are transported in

the direction of the interim storage (Boxes in), the

empty pallets are transported to the pallets storage

(PALLWAR) and are waiting for the boxes for as-

sembly.

IoTBDS 2020 - 5th International Conference on Internet of Things, Big Data and Security

422

Step 3: The boxes are transported in the direc-

tion of the main storage (Warehouse) by a fork-

lift truck (G

) through the RFID-system (G

f (G

), compare Figure 1, ”RFID in” in Figure

3). This is one of the key elements of this cell,

which shows the most important advantage of

RFID namely:

• The possibility to identify many goods per sec-

ond, and that there is

• no necessity to direct sight contact and that the

• distance between the RFID-Reader and good

can be much larger, than with the barcode tech-

nology.

For the demonstration of the identiﬁcation pro-

cedure a variable was added in the ”output ac-

tions” of the RFID-system and shows in the model

the number of boxes, which have already gone

through the RFID-system.

Step 4: After the RFID-identiﬁcation process the

goods are coming to the storage part. Here they

are stored in the main storage (Warehouse), as-

sembled in pallets on the assemble station (As-

sembly) by labor (Lab1) and are going to the in-

terim storage (Pallets sort) to be prepared for the

departure.

Step 5: After assembling the pallets are com-

ing to the interim storage, where they are sent to

the last interim storage (Pallets Togo) by a fork-

lift truck (G

) through the outgoing RFID-system

= f (G

)). This system has the same func-

tions as an incoming system, as well as a similar

variable, to show, how many pallets are going out.

Step 6: Load procedure. When goods are coming

to the last interim storage, they have to be assem-

bled in the shipment by labor (Lab3) and prepared

for the departure.

Step 7: In the last steps, the shipment has to be

taken away by the truck and sent to the cell 3. This

step shows, where the ﬂow is leaving a cell 2 and

going to the next cell, which plays in this model

a role of a potential customer or the next member

of the logistic chain.

4.3 Bottleneck Analysis

The simulation can help the companies and parties in

the logistics supply chain to identify, understand and

prevent a potential inconvenience already in the step

of planning and modeling, as the Witness model can

be regarded as a virtual twin. An important possibil-

ity is the identiﬁcation of a bottleneck in the factory

through simulation. The term ”bottleneck” is used

Figure 4: Statistics of Active Elements of Cell 2.

to describe a point of congestion in any system from

computer networks to a factory assembly line. In such

a system, there is always some process, task, machine,

etc. that is the limiting factor preventing a greater

throughput and thus determines the capacity of the

entire system. Knowing the bottleneck allows us to

increase the ﬂow by improving just one process in the

system rather than all its remaining parts. Vice versa,

if there is a bottleneck, nothing done elsewhere in the

value stream can improve the throughput (Leporis and

alov

a, 2010). With the statistical instrument in Wit-

ness, it is possible to show, how the work progress is

going in the different steps. Figure 4 shows a dia-

gram, which compares the different ”active” points of

logistic cell 2. Under ”active” points in Witness those

points are understood, where there is active work done

on or with the goods. In this diagram the pink color

designates a time when an element is blocked, the

yellow color means, that the element is inactive, the

green color means that the element (machine) is pro-

ductive. The dark blue color means that the element is

waiting for labor and the light blue means that there is

a preparing time slot. From this, it can be concluded,

that the Assembly point and the Unload point are po-

tential bottlenecks because in these points the biggest

processing time is calculated for the simulation case.

5 RFID-ARDUINO-APPLICATION

To show the practicability of such a logistic cell, the

model is mirrored in a physical Internet of Things

(IoT) device in form of an Arduino micro-controller

board which is attached to an RFID-Reader, together

with a model-warehouse / forklift truck unit. Arduino

is an open-source electronics platform based on easy-

to-use hardware and software. Arduino boards can

”read” inputs and turn it into an output (Arduino,

2020) as they consist of an Input / Output (IO) system

together with a calculation unit, which can be also re-

garded as a basic cybernetics system.

Scalable Logistic Cell RFID Witness Model

423

5.1 Model

For the demonstration and for educational purposes

a practical model has been implemented. The model

of the here described logistic cell consists of a board,

made from a plywood sheet, a forklift truck, an Ar-

duino microcontroller board, an end-stop-switch, and

an RFID-Reader (q.v. Figure 5).

Figure 5: Set Up of the Model; The End-Stop-Switch is Sit-

uated Under the Plywood Plate, on the Left Side of the En-

trance. The Entrance Ramp is not Mounted in this Picture

yet as in Figure 6.

Figure 6: Model of the Logistic Cell.

The plywood board has the function of a cell, where

goods are coming in or going out. It consists of a

few plywood sheets, which were cut out by a laser

cutter and connected. A forklift truck is a trans-

porter, which delivers goods in and out of the cell.

For this model, a toy forklift truck was used (q.v.

Figures 8 and 9). For this model, it was chosen an

Arduino-Uno as the most popular, cheap, and easy-to-

use micro-controller-board, the RFID-Reader model

MAKEVMA405 and a (simple) mechanical end-stop

switch to register, together with the Arduino-Uno,

whether a forklift truck is coming in or going out.

5.2 Arduino-hardware Set-up

The scheme, how the RFID-Reader was connected to

the Arduino-board is shown in Figure 7.

The Light Emitting Diode (LED) was connected

to the Arduino-board using a breadboard. To deter-

mine, whether the forklift is going in or out of the

Figure 7: Scheme of the Connection of the RFID-Reader

MakeVMA405 to the Arduino Uno.

cell, a ramp was separated into two equal parts, one

of them can move up and down and the second is

strongly connected. Under the ﬁrst part the end-stop

switch was installed (q.v. Figures 5 and 6).

The forklift is loaded with a pallet and a package

of goods, which have an RFID-chip inside. When it is

entering a warehouse, it is pushing an end-stop switch

and going near the RFID-Reader. It reads then infor-

mation from the chip and shows it on the computer-

screen, as well as the message ”Incoming” in the Ar-

duino IDE monitor port, which means, that the fork-

lift is going in. When a forklift is going out, it is go-

ing near the backside of the RFID-Reader and through

the strongly connected part of the ramp. In this case,

the end-stop switch will not be pushed, so, the mes-

sage on the screen will be ”outgoing”. The process

of ”ingoing” and ”outgoing” of a forklift as well as

screen-shots from the monitor screen are shown in

Figure 8 and Figure 9. For a demonstration of ware-

house work, the LED was added. According to the

program code, given in the APPENDIX, it is on dur-

ing the forklift is in the warehouse and is out, when it

leaves.

6 CONCLUSIONS, SUMMARY,

AND OUTLOOK

This work tries to bridge the gap of modeling a com-

plex industrial large scale logistic process, with a ba-

sic cell, that can be combined to simulate this net-

work. Additionally, an essential upgrade to yield a ba-

sic IoT-system is done, as this is an inner closing from

material logistic processes to informational computer

systems. In this work, only a basic logistic cell is

shown with a basic IoT-system.

First, a general logistic cell was developed, that

is applicable for a variety of applications. It shows

the properties of being autonomous and scalable. The

simulation was done with Witness, and the ﬁrst results

IoTBDS 2020 - 5th International Conference on Internet of Things, Big Data and Security

424

were shown, for this basic process, as well as for the

model, that can be used in educational environments,

for immediately showing the functionality of the lo-

gistic cell, and its IoT application connected with the

RFID-Reading process, associated with the material,

energetic and informational transport process.

Figure 8: Incoming of a Forklift: Model (a) and Arduino

Monitor Screenshot (b).

Future work has also to investigate, what does it mean

to scale up the model in times of computation time,

and also overall realistic predictions of the logistic

process. Another point is that the model shall be used

in an educational context to make sensible for the in-

creasing necessity of IoT-applications as well as inter-

connected computer simulations. This offers a wide

variety of possibilities in the educational as well as

the industrial context.

Future research applications shall also implement

decision processes, that shall be done e.g. by the Ar-

tiﬁcial Intelligence (AI) - language PROLOG (q.v.

(Sterling and Shapiro, 1994)), in combination with

Witness. Utilizing this approach real-time decision

models shall be simulated conveniently. This would

account for the increasing necessity of agent-based

decisions (Garc

ıa-Garc

ıa et al., 2020) that could be

implemented with this method. Another branch of

investigations is aiming at large scale networks, and

their applicability concerning modeling accuracy, op-

timization, and program performance. Finally, the

Figure 9: Outgoing of a Forklift: Model (a) and Arduino

Monitor Screenshot (b).

research question is open, in which IoT-systems can

enhance the systems adequately to yield higher order

systems, leading e.g. to better performance, reliability

and prediction accuracy.

INDEX

Symbol / Name Description

AI . . . Artiﬁcial Intelligence

Arduino . . . Micro-Controller

BDE . . . Operational Data Retrieval

ERP . . . Enterprise Resource Planning

IO . . . Input / Output System

IoT . . . Internet of Things

LED . . . Light Emitting Diode

MEI . . . Material, Energy, Information

MES . . . Management Execution

Systems

PROLOG . . . AI Computer Language

RFID . . . Radio Frequency

Identiﬁcation

Witness . . . Production Process

Simulation Software

Scalable Logistic Cell RFID Witness Model

425

REFERENCES

Ali, N. B., Petersen, K., and Wohlin, C. (2014). A system-

atic literature review on the industrial use of software

process simulation. Journal of Systems and Software,

97:65–85. https://doi.org/10.1016/j.jss.2014.06.059.

Arduino (2020). Homepage: http://www.arduino.cc. ac-

cessed 01/27/2020.

Borchers, J. (2013). Arduino in a Nutshell. accessed

01/29/2020, http://hci.rwth-aachen.de/arduino.

Garc

ıa-Garc

ıa, J. A., Enr

ıquez, J. G., M. Ruiz, C. A.,

and Jim

enez-Ram

ırez, A. (2020). Software pro-

cess simulation modeling: Systematic literature re-

view. Computer Standards & Interfaces, 70.

https://doi.org/10.1016/j.csi.2020.103425.

Heiden, B., Heiden, B. T., Wissounig, W., Nicolay, P.,

Roth, M., Walder, S. W., Mingxing, X., and Maat, W.

(2019). Orgiton theory. unpublished.

LannerGroupLimited (2020). Homepage:

http://www.lanner.com. accessed 01/27/2020.

Leporis, M. and Kr

alov

a, Z. (2010). A simulation approach

to production line bottleneck analysis. In Interna-

tional Conference February 10 - 13, 2010, CYBER-

NETICS AND INFORMATICS.

Luhmann, N. (1997). Die Gesellschaft der Gesellschaft.

Suhrkamp Verlag, Frankfurt/Main.

Lunesu, M. I., M

unch, J., Marchesi, M., and Kuhrmann,

M. (2018). Using simulation for understand-

ing and reproducing distributed software de-

velopment processes in the cloud. Informa-

tion and Software Technology, 103:226–238.

https://doi.org/10.1016/j.infsof.2018.07.004.

Mandelbrot, B. B. (1991). Die fraktale Geometrie der

Natur. Birkh

auser Verlag, Basel Boston Berlin.

Spencer-Brown, G. (2008). Laws of Form. Bohmeier, Joh.

Sterling, L. and Shapiro, E. (1994). The Art of Prolog. MIT

Press.

Weber, S. (2010). Systemtheorie der Medien. Anwendung

der Systemtheorie (Luhmann) auf die Modellierung

von Massenmedien und Publizistik (Marcinkowski

u.a.), pages 189–206. UVK Verlagsgesellschaft, Kon-

stanz.

APPENDIX - ARDUINO PROGRAM

CODE

1 # in clu de < SPI .h >

2 # in clu de < MF RC5 22 . h>

3 # de fin e SS_P IN 10

4 # de fin e R S T_ P IN 9

5 int e nds t op_x = 4;

6 int led = 8;

7 M F RC5 22 m f rc 5 22 ( SS_PIN , R S T_P IN

);

8 void s et up ()

9 {

10 Serial. b eg in (9 600 ) ;

11 SPI . beg in () ;

12 mf rc5 2 2 . PC D_I n it () ;

13 Serial. p r int ln ( " Ap p rox i m a te

your card to the rea der

... " ) ;

14 Serial. p r int ln () ;

15 pi nMo d e ( led , O UT PUT );

16 }

17 void loop ()

18 {

19 if ( ! m frc 522 .

PICC_ I s N e w C a r d P r e s e n t

() )

20 {

21 ret urn ;

22 }

23 if ( ! m frc 522 .

PICC _ R e a d C a r d S e rial ()

)

24 {

25 ret urn ;

26 }

27 Serial. p ri nt ( " UID tag : " ) ;

// " UID T eT a : "

28 St ri n g c o nt e nt = "";

29 byt e let ter ;

30 for ( byte i = 0; i <

mf rc5 2 2 . uid . size ; i ++)

31 {

32 Serial. print ( mf rc5 2 2 .

uid . u i dBy te [ i ] < 0

x10 ? " 0 " : " " );

33 Serial. print ( mf rc5 2 2 .

uid . u i dBy te [ i ] , HEX

);

IoTBDS 2020 - 5th International Conference on Internet of Things, Big Data and Security

426

1 co nte n t . c onc at ( S tr i ng (

mf rc5 2 2 . uid . uid Byt e

[i ] < 0 x10 ? " 0" :

" ") ) ;

2 co nte n t . c onc at ( S tr i ng (

mf rc5 2 2 . uid . uid Byt e

[i ] , HEX ) ) ;

3 }

4 Serial. p r int ln () ;

5 Serial. p ri nt ( " M ess age : "

);

6 co nte n t . to U pper C a s e () ;

7 if ( c ont ent . sub s trin g (1)

== " 79 45 0 A 64 " )

8 {

9 Serial. p r int ln ( "

Ga b e l s tapl e r 1" ) ;

10 Serial. p r int ln () ;

11 delay ( 300 0) ;

12 }

13 else {

14 Serial. p r int ln ( " Acce ss

de nie d " ) ;

15 delay ( 300 0) ;

16 }

17 if ( d i gita l R e ad ( e n d sto p _x )

==0) {

18 Serial. print ( " Inc o min g

") ;

19 dig i t a l Writ e ( led , HIGH

);

20 // d el ay ( 10 ) ;

21 }

22 els e {

23 Serial. p ri nt ( "

Ou t goi n g " ) ;

24 di g i t a lWri t e (led , LOW

);

25 // dela y (10) ;

26 }

27 }

Scalable Logistic Cell RFID Witness Model

427