
Termination of Ethereum’s Smart Contracts
∗
Thomas Genet, Thomas Jensen and Justine Sauvage
Univ. Rennes, Inria, CNRS, IRISA, France
Keywords:
Formal Methods for Security, Ethereum, Smart Contracts, Security in Distributed Systems.
Abstract:
Ethereum is a decentralized blockchain technology equipped with so-called Smart Contracts. A contract is a
program whose code is public, which can be triggered by any user, and whose actual execution is performed by
miners participating in Ethereum. Miners execute the contract on the Ethereum Virtual Machine (EVM) and
apply its effect by adding new blocks to the blockchain. A contract that takes too much time to be processed
by the miners of the network may result into delays or a denial of service in the Ethereum system. To prevent
this scenario, termination of Ethereum’s Smart Contracts is ensured using a gas mechanism. Roughly, the
EVM consumes gas to process each instruction of a contract and the gas provided to run a contract is limited.
This technique could make termination of contracts easy to prove but the way the official definition of the
EVM specifies gas usage makes the proof of this property non-trivial. EVM implementations and formal
analysis techniques of EVM’s Smart Contracts use termination of contracts as an assumption, so having a
formal proof of termination of contracts is crucial. This paper presents a mechanized, formal, and general
proof of termination of Smart Contracts based on a measure of EVM call stacks.
1 INTRODUCTION
A blockchain is a decentralized ledger, shared over a
network, on which all users agree. Users can submit
new elements to be added to this ledger. To add new
elements in the ledger, one needs to add a new block
(containing the new elements) to the blockchain. A
block will be added to the blockchain if most of the
participants agree on it. In Bitcoin, to add a new
block to the chain, one has to solve a cryptographic
puzzle on this new block in a limited amount of time
(around 10 minutes in Bitcoin). This is called mining
a block. Since the puzzle is computationally difficult
it requires that most users participate in its resolution.
Users contributing to the resolution are called miners.
The fact that most miners try to solve the same puzzle
entails that they all agree on the block itself and on
all the added elements.
Bitcoin is equipped with a programming lan-
guage, called Script (script, 2014), that is used to de-
fine programs reading inputs in the blockchain and
proposing outputs (new elements) to be added to
the blockchain. It is the role of the miners to exe-
cute the Script programs and to build the new blocks
containing the outputs of those programs. If one
∗
This work was partially supported by Laboratoire
d’excellence CominLabs.
Script program is non-terminating, this prevents min-
ers from building new blocks and adding them to
the blockchain within the 10 minutes time limit. If
many Script programs are non terminating, this could
cause a denial of service in the Bitcoin system. This
is the reason why the Script language is not Turing-
complete, in particular it has no loops.
Ethereum extends Bitcoin’s blockchain with a
Turing-complete programming language and the abil-
ity to store those programs (called contracts) in the
blockchain itself. Contracts are programmed into
dedicated high-level languages like Solidity (solid-
ity, 2014) or Vyper (vyper, 2017) and compiled to a
bytecode format executed by the so-called Ethereum
Virtual Machine (EVM). Since the programming lan-
guage is Turing-complete, Ethereum needs to prevent
looping contracts. In addition, Ethereum also targets
to accelerate the pace of block additions w.r.t. Bit-
coin. Thus, a terminating contract that takes too long
to complete is another source of denial of service for
Ethereum. Ethereum protects its system from non ter-
minating programs and too complex programs with
a single mechanism: the gas (Buterin, 2013). Intu-
itively, the EVM consumes gas to process each in-
struction of a contract and the gas provided to run a
contract is limited.
Though this mechanism looks simple and robust,
the protection it offers against denial of service is
Genet, T., Jensen, T. and Sauvage, J.
Termination of Ethereum’s Smart Contracts.
DOI: 10.5220/0009564100390051
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 39-51
ISBN: 978-989-758-446-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
39

fragile. For instance, in 2016, badly chosen gas val-
ues for some EVM instructions resulted into several
denial of service of Ethereum. This had to be fixed
by two consecutive hard forks of the system (Hudson,
2016a; Hudson, 2016b). Independently of choosing
for the best gas cost for each instruction, a general
question to ask is whether the gas mechanism is suf-
ficient to prove termination of any contract? Surpris-
ingly, proving formally that this is true is not trivial
because of the complexity of the EVM semantics (see
Section 5).
The goal of this paper is twofold: to prove that no
program can execute indefinitely without consuming
gas in the EVM execution model, and to prove it in
a way that can be used in a mechanized proof. More
precisely, we present two termination proofs on two
slightly different EVM semantics. The first model is
the formal semantics of the (foundational) Ethereum
Yellow Paper (Gavin, 2014), the Isabelle/HOL EVM
semantics (Hirai, 2017; Amani et al., 2018) and the
small-step formal semantics of (Grishchenko et al.,
2018b). The second model is the semantics of the
reference implementations of EVM such as (pevm,
2017; gevm, 2014). Noteworthy, the implementations
and the Yellow Paper disagree on the gas consumption
when calling a contract from another contract. In the
Yellow Paper, when a contract c
1
calls another con-
tract c
2
with, say, g units of gas, the gas associated
to c
1
is not charged immediately. In implementations,
this gas is immediately consumed. This little differ-
ence in the semantics makes a big difference when
we are interested in proving the termination of con-
tracts. Indeed, with the Yellow Paper semantics, a
contract c
1
calling itself can loop without consuming
gas, until it exhausts the call stack. This paper pro-
vides a termination proof of contracts for the two se-
mantics. Proving termination of contracts when gas is
charged immediately is natural and will be briefly dis-
cussed in Section 7. Proving termination of the con-
tracts for the Yellow Paper semantics is more difficult
and requires a complex termination measure on call
stacks. Though the Yellow Paper semantics differs
from the reference implementations, having a termi-
nation proof for this semantics is important. First, this
termination proof contributes evidence that the Yel-
low Paper semantic model is indeed coherent. Sec-
ond, this semantics serves as a base for formal verifi-
cation tools, such as (Grishchenko et al., 2018b; Gr-
ishchenko et al., 2018a), or for formal semantics such
as (Hirai, 2017; Amani et al., 2018). In those tools
and semantics, the termination of contracts is used as
an assumption. In particular, in the Isabelle/HOL for-
malization of (Hirai, 2017; Amani et al., 2018) the
termination of the contract evaluation is proven using
an internal step counter, which is not related to the
gas, and simplifies the proofs.
1
Our proof comple-
ment their work by showing how the gas itself ensures
termination of contracts, and thus assuming termina-
tion of contracts in the Yellow Paper semantics was
indeed correct.
Contributions. This paper gives the first formal and
mechanized proof of termination of EVM contracts,
written in EVM bytecode. The central part is a mea-
sure that can be used for the proof of termination in a
proof assistant (in our case Isabelle/HOL). We prove
termination for:
• the two variants of the semantics of the contract
call described above;
• a formal model where contracts can add and run
arbitrary new contracts;
• a formal model that safely over-approximates the
EVM semantics with minimal assumptions. In
particular, for non-zero cost byte code operations
(i.e. all operations except STOP, RETURN, RE-
VERT), we only require that they have any strictly
positive cost. Similarly, we only require the call
stack size is upper-bounded by any natural num-
ber greater than 0.
Note that having minimal assumptions on the con-
crete gas costs for each operation is valuable because
the gas cost has already changed several times dur-
ing the EVM’s lifetime
2
and is likely to evolve again
since gas pricing of operations is still not fully satis-
factory (Yang et al., 2019).
2 RELATED WORK
The Ethereum system has been formalized in the so-
called Yellow Paper (Gavin, 2014) which has been
updated recently (Gavin, 2019). This update does not
impact gas consumption but provides some new in-
structions which are taken into account in our formal
proof. A nice complementary reading is the White Pa-
per (Buterin, 2013) which provides useful intuitions
about the system. There are several available refer-
ence implementations of EVM such as (pevm, 2017;
gevm, 2014).
1
In the comments of the lem/evm.lem specification file,
it becomes evident that the termination proof uses an artifi-
cial step counter and not the gas mechanism. This choice
was made to simplify the proof as stated line 1859 of
lem/evm.lem (FEL, 2018).
2
There was a cost increase for 8 EVM instructions on
2016/10/18 (Hudson, 2016a) and a cost increase for one
EVM instruction on 2016/11/18 (Hudson, 2016b)
SECRYPT 2020 - 17th International Conference on Security and Cryptography
40
Grishchenko et al. have proposed
EtherTrust (ethertrust, 2017) a verification framework
for the static analysis of contracts code (Grishchenko
et al., 2018a). The static analysis tools focus on
proving some security properties on contracts, such
as single-entrancy (Grishchenko et al., 2018b).
EtherTrust comes with a complete small-step seman-
tics for EVM (Grishchenko et al., 2018b) that uses
the Yellow Paper semantics for the contract call.
There are several attempts to define a mechanized
and formal semantics of EVM. The first one was de-
fined in Lem by Yoichi Hirai (Hirai, 2017). This se-
mantics was defined to prove safety and security prop-
erties on specific contracts. It is partially executable
and can be used to export Isabelle/HOL theories. The
objective here was to compile EVM bytecode to Is-
abelle/HOL theories so that properties on those spe-
cific contracts can be proved in Isabelle/HOL. This
semantics is very precise w.r.t. specification of low
level operations of EVM but it does not precisely fol-
low the gas consumption during calls (see Section 6.2
of (Hirai, 2017)). Thus, this mechanized semantics
is not usable, as is, for the proof we want to carry
out. Another mechanized semantics is the one by Ev-
erett Hildenbrandt et al. (Hildenbrandt et al., 2018)
in the K framework. This semantics is fully exe-
cutable and passes official test suite of EVM (ETS,
2015). This semantics consumes gas at the call
point (see rule <k> callWithCode in https://github.
com/kframework/evm-semantics/blob/master/evm.md). In
Section 7, we will discuss termination of contracts in
this specific setting.
A contract running out of gas stops without com-
pleting its task and becomes useless. Thus estimat-
ing gas consumption of contracts is an active research
subject. For instance, (Grech et al., 2018) proposes a
static analysis of contract’s code to detect resumable
loops, loops bounded by inputs, etc. that can lead to
an execution running out of gas. Our objective here
is different since we aim at proving that whatever the
contract code, it cannot loop forever while not spend-
ing gas.
3 ETHEREUM
The blockchain of Ethereum describes the global state
of the system, noted σ. In Ethereum a global state
σ contains accounts. An account is a structure com-
posed of 4 elements: a nonce, a balance (an amount
of money in the virtual currency called Ether), a data
storage and a code. In Ethereum, there exists two
types of accounts: external accounts with an empty
code and contracts with a non-empty code.
Calling a Contract. External accounts are used to
store information and Ether. Like in Bitcoin, it is
possible to transfer Ether from an account to another
through a transaction. When a transaction is sent
to an account having a code, i.e. a contract, a part
of the money is used to pay for the execution of the
code
3
. This is called calling a contract. When call-
ing a contract, the sent money is not collected by the
contract itself but by the miner who accepts to exe-
cute contract’s code and to add the updated accounts
and blocks to the blockchain. In other words, from
a given global state σ, the miners produce the new
global state σ
0
resulting of the transactions (and con-
tracts) application on σ. Since adding blocks to the
blockchain costs computation power, the miner needs
a way to estimate if the reward (money sent to the
contract) is competitive with its own computational
effort. In Ethereum, this estimation is made possible
through the gas mechanism. Every basic instruction
of contract’s code has a fixed cost in gas and every
contract claims an (estimated) maximal cost in gas to
run its code. Besides, when an account calls a con-
tract it also fixes a gas price in Ether. This is used to
motivate miners to execute one particular transaction
by increasing the gas price and thus their reward.
Ethereum
Account a
i
Balance 130
Storage
Code i++
Balance
Storage
Code
Account a
j
20
/
/
Transaction T
a
j
a
i
g
Account a
i
Balance 130
Storage
Code i++
Balance
Storage
Code
Account a
j
/
/
[i : 5][i : 4]
20-g+g
0
Account m ( miner of T)
Balance += g-g'
State σ State σ
0
(1)
(2)
(3)
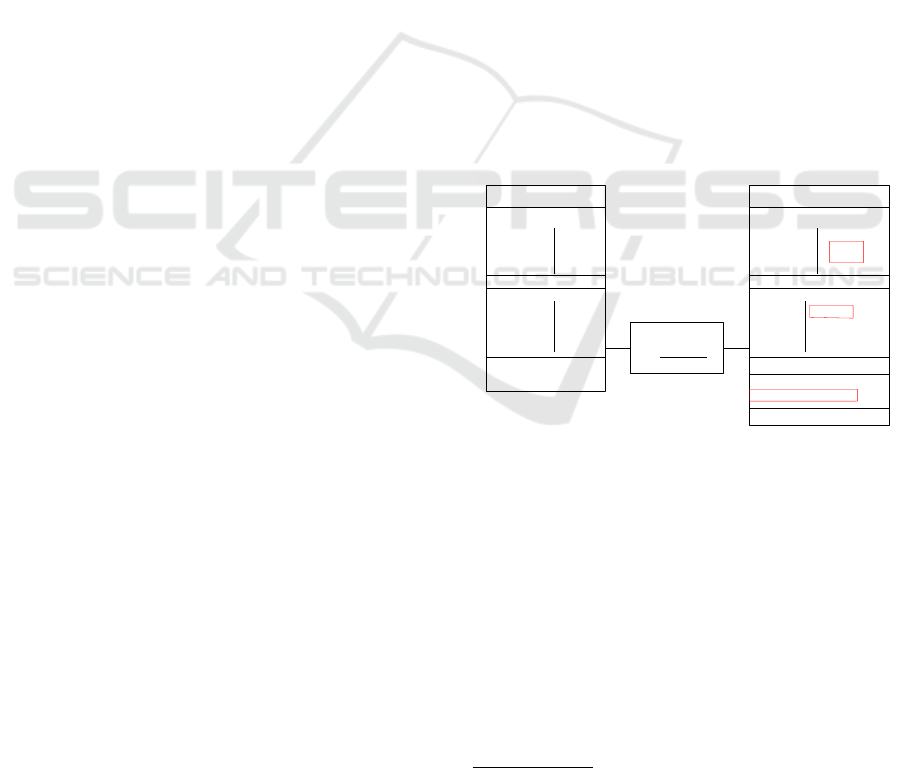
Figure 1: Account a
j
calls contract a
i
and miner m process
the transaction.
Example 1. On the left-hand side of Figure 1, in the
state σ, there are two accounts a
i
and a
j
with a re-
spective balance 130 and 20. Account a
i
is a contract
and a
j
is an external account. Account a
i
has a stor-
age called i whose value is 4. The code of a
i
is simply
i++, i.e., it increments i. Assume that the estimated
maximal cost of contract a
i
is g. Assume that account
a
j
builds a transaction T towards a
i
, where a
j
calls
a
i
with g gas. To simplify the presentation, we do not
consider gas price and assume that one gas costs one
Ether. Assume that a miner m processes the transac-
3
In addition, it is possible to transfer money to a con-
tract, but this part is not important for our termination proof
and will not be modeled here.
Termination of Ethereum’s Smart Contracts
41

tion T and then adds the new blocks encoding the new
values of accounts a
i
and a
j
in the new blockchain
global state σ
0
. In σ
0
, in the account a
i
, i is now 5 (1).
Note that balance of a
i
has not evolved. Balance of a
j
has been decreased of g gas unit and increased by g
0
which is a (possible) gas refund (2). Indeed, contract
a
i
claims to need g gas units to run its code but less
gas may actually be needed. Here we assume that
there were g
0
gas left after the execution of a
i
. This
gas is refunded to a
j
. Finally, the miner m who adds
the blocks in σ
0
is rewarded by g −g
0
gas (3). An-
other possibility would have been that execution of a
i
needs more than g gas. In this case, the execution of
a
i
runs out of gas, an exception is thrown, the value
of i in a
i
does not change, the g gas are lost by a
j
,
and the miner m wins g gas. Precise estimation of
gas consumption for contracts is, in itself, a research
subject (Grech et al., 2018).
Creating a Contract. Any contract c
1
can create a
(new) contract c
2
with any arbitrary code, provided
that c
1
is given enough gas to store all the instruc-
tions of the bytecode of c
2
in the new global state σ
0
.
If contract creation succeeds, this makes contract c
2
publicly available in σ
0
.
4 ETHEREUM VIRTUAL
MACHINE: EVM
Contract code is run on the Ethereum Virtual Machine
(EVM). Contracts are written in high-level languages
such as Solidity (solidity, 2014) or Vyper (vyper,
2017) and compiled to a bytecode format specific to
EVM. A bytecode program is a list of instructions
and during the execution a program counter (pc) gives
the index of the next instruction to execute. EVM is
a stack machine and the effect of arithmetic instruc-
tions, test instructions, storage instructions is to read
and/or modify this stack, called the execution stack.
There are more than 60 different instructions in
EVM. We can split them in 5 families:
• Execution Stack Operations. This family en-
compasses all arithmetic, logic and test instruc-
tions like ADD, SUB, AND, OR, EQ, LT, etc.
This family also contains instructions that push,
pop, swap or duplicate the elements on the execu-
tion stack.
• Memory Access. This family contains instruc-
tions whose effect is to transfer data between the
execution stack and either the temporary local
memory (MLOAD, MSTORE) or into the perma-
nent memory (SLOAD, SSTORE). The temporary
local memory is a memory where a contract can
read and write during its execution and which is
erased after contract’s completion. The perma-
nent memory is in accounts’ storage (thus in the
blockchain) and will survive after contract’s com-
pletion, like variable i in contract a
i
of Example 1.
• Environment Operations. These are the opera-
tions that gather information on the current trans-
action and contract (who called this contract, how
many gas unit are left, etc.).
• Control Flow Operations. Those operations
modify the control flow inside the same contract:
JUMP, JUMPI (conditional jump), JUMPDEST
(marks a jump destination), ...
• System Operations. This family gathers all the
operations that permit to create and destroy a con-
tract (CREATE, SUICIDE in (Gavin, 2014), or
SELFDESTRUCT in (Gavin, 2019)) and the call
and exit operations on contracts (CALL, CALL-
CODE, DELEGATECALL, RETURN) and ad-
ditional (REVERT, CALLSTATIC) in (Gavin,
2019).
The differences between the four types of call
(CALL, CALLCODE, DELEGATECALL, CALL-
STATIC) are subtle. The differences essentially lies in
the way the global state is affected by calling the con-
tract and not about the way gas is consumed. The con-
tract called by CALL changes the state of the callee,
like in Example 1. The contract called by CALL-
CODE changes the state of the caller, like when call-
ing a library code. In Example 1, assume that state
of account a
j
has a field i, then a CALLCODE on
a
i
, would have incremented the value of this field in
the state of account a
j
. The DELEGATECALL acts
as a CALLCODE except that the identity of the con-
tract caller is different. In a contract c
1
, if contract
c
2
is called with DELEGATECALL, the call to con-
tract c
2
happens like with a CALLCODE except that
identity of the caller is not c
1
but the identity of the
caller of c
1
. See (Grishchenko et al., 2018a) for de-
tails. Finally, CALLSTATIC is similar to CALL ex-
cept that no modification of the state is permitted. It
can be considered as a “pure” function call without
side-effects. Since there is no difference between the
4 call instructions w.r.t. to gas consumption, we will
abstract them in the same way in Section 6.2.
As explained above, to implement the gas mecha-
nism, EVM’s designers have chosen to associate each
operation with a cost in gas. All operations, ex-
cept zero-cost operations (STOP, REVERT and RE-
TURN), have a cost strictly greater than zero. Some
instructions, like SELFDESTRUCT or SSTORE may
result into a gas refund. SELFDESTRUCT destroys
SECRYPT 2020 - 17th International Conference on Security and Cryptography
42

the current executed contract and the Ether which
may be present in the account is refunded. SSTORE
writes information in the permanent storage of the
account and, thus, in the blockchain. Refund with
SSTORE happens when it replaces a non-zero value
by a zero. This kind of erasure permits to save space
in the blockchain and is, thus, rewarded. Refunds ob-
tained using SELFDESTRUCT or SSTORE are ac-
cumulated during the execution in a separate counter
and given back after the completion of the whole con-
tract. As a result, during the contract execution, the
available gas is not increased by those specific re-
funds.
Now, to give some intuition about EVM’s be-
havior, we describe more precisely the semantics of
some particular instructions. We present all those in-
structions through their EtherTrust (ethertrust, 2017)
small-step semantic rules. Some examples of Yellow
Paper semantics and their EtherTrust counterpart can
be found here (Genet et al., 2020). The interest of
EtherTrust rules w.r.t to the Yellow Paper is that they
describe in the same place the effect of the instruction
on the state of the system and the gas consumption.
4.1 The ADD Instruction
The rules for the ADD instruction are given Figure 2-
1. In these rules, µ is the local state of the stack ma-
chine where µ.s denotes the execution stack, µ.pc the
program counter, µ.gas the available gas. The other
record ι represents the parameters of the transaction
where ι.code denotes the program under execution.
Thus ι.code[µ.pc] is the current instruction to execute.
Below the line of the semantic rules, (µ, ι,σ,η) :: S is
the current call stack. An element of the call stack
is called a frame, e.g., (µ,ι,σ, η) is the top frame of
the current call stack. The field η is a transaction ef-
fect where the only information that could be relevant
for us w.r.t. gas consumption would be the refund
counter. However, as explained in Section 4, this re-
fund counter is separate from the gas available for op-
eration execution. Finally, σ is the current state of the
global state. Since, there are no side effects, every up-
date on this global state is propagated by the semantic
rules. In the first rule, for ADD, there is enough gas to
execute ADD and an execution stack with at least two
elements. Thus, the call stack becomes (µ
0
,ι, σ,η) :: S
where µ
0
is µ with an updated execution stack, an in-
creased program counter µ.pc, and a µ.gas decreased
of 3 gas units. The second rule defines the execution
of ADD when there are not enough elements on the
execution stack or not enough gas to execute ADD.
This results into stacking an exception frame (EXC)
on top of the call stack.
4.2 The CALL Instruction
The rule for the CALL (Figure 2-2) defines the CALL
execution when everything is OK: the execution stack
contains enough arguments to perform the call (µ.s
has at least 7 elements), there is enough gas to per-
form the call µ.gas ≥ c, and there is room in the call
stack to add a new frame (|A|+ 1 < 1024). The cost c
is the sum of the costs for calling the CALL instruc-
tion itself (700 gas units) plus a variable cost depend-
ing on the size of the input and output of the con-
tract: this gas is paid when reading contract param-
eters and outputting its future result. On the lower
part of this rule, the call stack (µ,ι, σ,η) :: S becomes
(µ
0
,ι
0
,σ
0
,η
0
) :: (µ,ι,σ, η) :: S where (µ
0
,ι
0
,σ
0
,η
0
) is a
new frame stack which has been added on top of the
call stack, where µ
0
is a new record, where µ
0
.gas =
c
call
is the gas transferred to the new frame stack by
the old one and µ
0
.pc is set to 0. The code to exe-
cute in this new frame is ι
0
.code = σ(to).code where
σ(to) is the account receiving the call. Note that, like
it was stated in the above sections, the new call stack
is (µ
0
,ι
0
,σ
0
,η
0
) :: (µ, ι,σ, η) :: S where the gas sent to
the new frame (µ
0
.gas) has not been subtracted from
the frame (µ,ι,σ, η) (µ is the same, thus so is µ.gas).
The gas is retracted when the contracts returns. Note
also that this is compatible with the Yellow Paper se-
mantics where, to update the gas w.r.t. the execution
of the CALL, one has to know how much gas g
0
will
be refunded after the execution of the called contract,
see (Genet et al., 2020).
4.3 The RETURN Instruction
Contract returning is performed by two rules (Fig-
ure 2-3). The first rule processes the RETURN
operation, where the current instruction to execute
ι.code[µ.pc] is abbreviated by ω
µ,ι
. The effect of this
rule is to replace the frame by an HALT frame with
the information that should be provided to the caller,
i.e., the possible updates on the global state σ, the re-
maining gas g, a result d and transaction effects η.
Finally, the HALT frame is popped by the second rule
of (Figure 2-3). We only present the rule for the stan-
dard case, i.e., in the frame below the HALT frame,
the current instruction is a CALL and the execution
stack contains all the information that were necessary
to perform the call. Then, we retract the gas units
necessary to perform the call (noted c) and refund gas
units of gas coming from the HALT frame. The global
store σ
0
coming from the HALT frame replaces σ in
the current frame. For the semantics of the CREATE
instruction, see (Genet et al., 2020).
Termination of Ethereum’s Smart Contracts
43

1
A Semantic Framework for the Security Analysis 251
– gas ∈ N
256
is the current amount of gas still available for execution;
– pc ∈ N
256
is the current program counter;
– m ∈ B
256
→ B
8
is a mapping from 256-bit words to bytes that represents the
local memory;
– i ∈ N
256
is the current number of active words in memory;
– s ∈ L(B
256
)isthelocal256-bitwordstackofthestackmachine.
The execution of each internal transaction starts in a fresh machine state, with
an empty stack, memory initialized to all zeros, and program counter and active
words in memory set to zero. Only the gas is instantiated with the gas value
available for the execution.
3.4 Small-Step Rules
In the following, we will present a selection of interesting small-step rules in
order to illustrate the most important features of the semantics.
For demonstrating the overall design of the semantics, we start with the
example of the arithmetic expression ADD performing addition of two values on
the machine stack. Note that as the word size of the stack machine is 256, all
arithmetic operations are performed modulo 2
256
.
ι.code [µ.pc]=ADD
µ.s = a :: b :: sµ.gas ≥ 3 µ
′
= µ[s → (a + b)::s][pc += 1][gas −= 3]
Γ ! (µ, ι, σ, η)::S → (µ
′
, ι, σ, η)::S
ι.code [µ.pc]=ADD (|µ.s| < 2 ∨ µ.gas < 3)
Γ ! (µ, ι, σ, η)::S → EXC :: S
We use a dot notation, in order to access components of the different state
parameters. We name the components with the variable names introduced for
these components in the last section written in sans-serif-style. In addition, we
use the usual notation for updating components: t[c → v]denotesthatthe
component c of tuple t is updated with value v.Forexpressingincremental
updates in a simpler way, we additionally use the notation t[c += v] to denote
that the (numerical) component of c is incremented by v and similarly t[c −= v]
for decrementing a component c of t.
The execution of the arithmetic instruction ADD only p erforms local changes
in the machine state affecting the local stack, the program counter, and the
gas budget. For deciding upon the correct instruction to execute, the currently
executed code (that is part of the execution environment) is accessed at the
position of the current program counter. The cost of an ADD instruction is
constantly three units of gas that get subtracted from the gas budget in the
machine state. As every other instruction, ADD can fail due to lacking gas or due
to underflows on the machine stack. In this case, the exception state is entered
and the execution of the current internal transaction is terminated. For better
readability, we use here the slightly sloppy ∨ notation for combining the two
error cases in one inference rule.
A Semantic Framework for the Security Analysis 251
– gas ∈ N
256
is the current amount of gas still available for execution;
– pc ∈ N
256
is the current program counter;
– m ∈ B
256
→ B
8
is a mapping from 256-bit words to bytes that represents the
local memory;
– i ∈ N
256
is the current number of active words in memory;
– s ∈ L(B
256
)isthelocal256-bitwordstackofthestackmachine.
The execution of each internal transaction starts in a fresh machine state, with
an empty stack, memory initialized to all zeros, and program counter and active
words in memory set to zero. Only the gas is instantiated with the gas value
available for the execution.
3.4 Small-Step Rules
In the following, we will present a selection of interesting small-step rules in
order to illustrate the most important features of the semantics.
For demonstrating the overall design of the semantics, we start with the
example of the arithmetic expression ADD performing addition of two values on
the machine stack. Note that as the word size of the stack machine is 256, all
arithmetic operations are performed modulo 2
256
.
ι.code [µ.pc]=ADD
µ.s = a :: b :: sµ.gas ≥ 3 µ
′
= µ[s → (a + b)::s][pc += 1][gas −= 3]
Γ ! (µ, ι, σ, η)::S → (µ
′
, ι, σ, η)::S
ι.code [µ.pc]=ADD (|µ.s| < 2 ∨ µ.gas < 3)
Γ ! (µ, ι, σ, η)::S → EXC :: S
We use a dot notation, in order to access components of the different state
parameters. We name the components with the variable names introduced for
these components in the last section written in sans-serif-style. In addition, we
use the usual notation for updating components: t[c → v]denotesthatthe
component c of tuple t is updated with value v.Forexpressingincremental
updates in a simpler way, we additionally use the notation t[c += v] to denote
that the (numerical) component of c is incremented by v and similarly t[c −= v]
for decrementing a component c of t.
The execution of the arithmetic instruction ADD only p erforms local changes
in the machine state affecting the local stack, the program counter, and the
gas budget. For deciding upon the correct instruction to execute, the currently
executed code (that is part of the execution environment) is accessed at the
position of the current program counter. The cost of an ADD instruction is
constantly three units of gas that get subtracted from the gas budget in the
machine state. As every other instruction, ADD can fail due to lacking gas or due
to underflows on the machine stack. In this case, the exception state is entered
and the execution of the current internal transaction is terminated. For better
readability, we use here the slightly sloppy ∨ notation for combining the two
error cases in one inference rule.
2
252 I. Grishchenko et al.
A more interesting example of a semantic rule is the one of the CALL instruc-
tion that initiates an internal call transaction. In the case of calling, several
corner cases need to be treated which results in several inference rules for this
case. Here, we only present one rule for illustrating the main functionality. More
precisely, we present the case in that the account that should be called exists,
the call stack limit of 1024 is not reached yet, and the account initiating the
transaction has a sufficiently large balance for sending the s pecified amount of
wei to the called account.
ι.code [µ.pc]=CALL µ.s = g :: to :: va :: io :: is :: oo :: os :: s
σ(to) ̸= ⊥|A|+1< 1024 σ(ι.actor).b ≥ va aw = M (M (µ.i, io, is), oo, os)
c
cal l
= C
gascap
(va, 1,g,µ.gas) c = C
base
(va, 1) + C
mem
(µ.i, aw)+c
cal l
µ.gas ≥ cσ
′
= σ
!
to → σ(to)[b += va]
"!
ι.actor → σ(ι.actor)[b −= va]
"
d = µ.m [io, io + is −1] µ
′
=(c
cal l
, 0,λx.0, 0,ϵ)
ι
′
= ι[sender → ι.actor][actor → to][value → va][input → d][code → σ(to).code]
Γ ! (µ, ι, σ, η)::S → (µ
′
,ι
′
,σ
′
,η)::(µ, ι, σ, η)::S
For performing a call, the parameters to this call need to be specified on the
machine stack. These are the amount of gas g that should be given as budget to
the call, the recipient to of the call and the amount va of wei to be transferred
with the call. In addition, the caller needs to specify the input data that should
be given to the transaction and the place in memory where the return data of
the call should be written after successful execution. To this end, the remaining
arguments specify the offset and size of the memory fragment that input data
should be read from (determined by io and is)andreturndatashouldbewritten
to (determined by oo and os).
Calculating the cost in terms of gas for the execution is quite complicated in
the case of CALL as it is influenced by several factors including the arguments
given to the call and the current machine state. First of all, the gas that should
be given to the call (here denoted by c
call
)needstobedetermined.Thisvalueis
not necessarily equal to the value g specified on the stack, but also depends on
the value va transferred by the call and the currently available gas. In addition,
as the memory needs to be accessed for reading the input value and writing the
return value, the number of active words in memory might be increased. This
effect is captured by the memory extension function M.Asaccessingadditional
words in memory costs gas, this cost needs to be taken into account in the
overall cost. The costs resulting from an increase in the number of active words
is calculated by the function C
mem
. Finally, there is also a base cost charged for
the call that depends on the value va.Asthecostalsodependsonthespecificcase
for calling that is considered, the cost calculation functions receive a flag (here
1) as arguments. These technical details are spelled out in the full version [22].
The call itself then has several effects: First, it transfers the balance from
the executing state (actor in the execution environment) to the recipient (to).
To this end, the global state is updated. Here we use a special notation for the
functional update on the global state using ⟨⟩ instead of []. Second, for initializing
the execution of the initiated internal transaction, a new regular execution state
3
Logging instructions The logging operation allows to append a new log entry to the log
series. The log series keeps track of archived and indexable checkpoints in the execution
of Ethereum byte code. The motivation of the log series is to allow external observers
to track the program execution. A log entry consists of the address of the currently
executing account, up to for ’topics’ (specified on stack) and a fraction of the memory.
There are four logging instructions, but as seen before we describe their effects using
common rules parameterising the instruction by the amount of log information read
from the stack.
!
µ,◆
= LOGnµ.s = pos
m
:: size :: (s
1
++s
2
) |s
1
| = n
aw = M (µ.i, pos
m
, size) c = C
mem
(µ.i, aw) + 375 + 8 · size + n · 375
valid (µ.gas, c, |µ.s|) µ
0
= µ[s ! s][pc += 1][gas = c][i ! aw]
d = µ.m[pos
m
, pos
m
+ size 1] ⌘
0
= ⌘[L ! ⌘.L ++[(◆.actor,s
1
,d)]]
✏ (µ, ◆, , ⌘)::S ! (µ
0
,◆,,⌘
0
)::S
!
µ,◆
= LOGn
µ.s = pos
m
:: size :: (s
1
++s
2
) |s
1
| = n aw = M (µ.i, pos
m
, size)
c = C
mem
(µ.i, aw) + 375 + 8 · size + n · 375 ¬valid (µ.gas, c, |µ.s|)
✏ (µ, ◆, , ⌘)::S ! EXC :: S
!
µ,◆
= LOGn |µ.s| <n+2
✏ (µ, ◆, , ⌘)::S ! EXC :: S
Halting instructions The execution of a RETURN command requires to read data from
the local memory. Consequently the cost for memory consumption is charged. Addi-
tionally the read data is recorded in the halting state in order to potentially propagate it
to the caller.
!
µ,◆
= RETURN
µ.s = io :: is :: s aw = M (µ.i,io,is) c = C
mem
(µ.i,aw)
valid (µ.gas,c,|s|) d = µ.m[io, io + is + 1] g = µ.gas c
✏ (µ, ◆, , ⌘)::S ! HALT(, g, d, ⌘)::S
!
µ,◆
= RETURN µ.s = io :: is :: s
aw = M (µ.i,io,is) c = C
mem
(µ.i,aw) ¬valid (µ.gas,c,|s|)
✏ (µ, ◆, , ⌘)::S ! EXC :: S
!
µ,◆
= RETURN |µ.s| < 2
✏ (µ, ◆, , ⌘)::S ! EXC :: S
The execution of a STOP command halts execution without propagating any data
to the caller.
3. The execution of the called code ends with an exception. In this case the remaining
arguments are removed from the caller’s stack and instead 0 is written to the caller’s
stack. The caller does not get the remaining gas refunded
As the first two cases can be treated analogously, we just need two rules for returning
from a call.
!
µ,◆
= CALL
µ.s = g :: to :: va :: io :: is :: oo :: os :: s to
a
= to mod 2
160
flag = .to
a
= ??0 : 1 aw = M (M (µ.i, io, is), oo, os)
c
call
= C
gascap
(va, flag,g,µ.gas) c = C
base
(va, flag)+C
mem
(µ.i, aw)+c
call
µ
0
= µ[i ! aw][s ! 1::s][pc += 1][gas += gas c][m ! µ.m[[oo, oo + s 1] ! d]]
✏ HALT(
0
,⌘
0
, gas,d)::(µ, ◆, , ⌘)::S ! (µ
0
,◆,
0
,⌘
0
)::S
!
µ,◆
= CALL
µ.s = g :: to :: va :: io :: is :: oo :: os :: s to
a
= to mod 2
160
flag = (to
a
)=??0 : 1 aw = M (M (µ.i, io, is), oo, os)
c
call
= C
gascap
(va, flag,g,µ.gas) c = C
base
(va, flag)+C
mem
(µ.i, aw)+c
call
µ
0
= µ[i ! aw][s ! 0::s][pc += 1][gas = c]
✏ EXC :: (µ, ◆, , ⌘)::S ! (µ
0
,◆,,⌘)::S
The two other instructions for calling (CALLCODE and DELEGATECALL) are
similar to CALL.
The CALLCODE instruction only differs in the fact that the control flow is not
handed over to the called contract, but only its code is executed in the environment of
the calling account. This means in particular that the amount of money transferred is
only relevant as a guard for the call, but does not need to be actually transferred. In
addition, in case that the account whose code should be executed does not exists, this
account is not created, but only the empty code is run. However, still the amount of
Ether specified on the stack influences the execution cost.
!
µ,◆
= CALLCODE
µ.s = g :: to :: va :: io :: is :: oo :: os :: s to
a
= to mod 2
160
(to
a
) 6= ?
|A| +1 1024 (◆.actor).b va aw = M (M (µ.i, io, is), oo, os)
c
call
= C
gascap
(va, 1,g,µ.gas) c = C
base
(va, 1) + C
mem
(µ.i, aw)+c
call
valid (µ.gas,c,|s| + 1) d = µ.m [io, io + is 1] µ
0
=(c
call
, 0,x.0, 0,✏)
◆
0
= ◆[sender ! ◆.actor][value ! va][input ! d][code ! (to
a
).code]
✏ (µ, ◆, , ⌘)::S ! (µ
0
,◆
0
,,⌘)::(µ, ◆, , ⌘)::S
Figure 2: The EtherTrust definitions for ADD, CALL and RETURN.
5 AN EVM MODEL
SPECIALIZED FOR GAS
ANALYSIS
The gas mechanism ensures that a contract can only
run a finite number of “local” instructions, i.e., in-
structions whose effect is local to the current contract
(no call, return, etc.). As mentioned above, when a
contract c
1
calls another contract c
2
with, say, g units
of gas, the gas associated to c
1
is not charged immedi-
ately. Thus, using Yellow Paper semantics, a contract
c
1
calling itself is indefinitely looping. The Yellow
Paper prevents this by fixing a call stack size limit.
If a contract exhausts the stack limit then its execu-
tion ends by an exception. However, unlike other vir-
tual machines, EVM has no exception catching mech-
anism. When an exception is raised in a contract c, the
execution of c stops, the information of the contract c
is popped from the stack and the control flow goes
back to the previous contract in the stack if it exists,
otherwise the execution stops.
To sum up, termination of contracts in the formal
semantics of the Yellow Paper is enforced by the gas
mechanism and the fact that the call stack is finite.
In the following, to formally prove termination we
prove that, whatever the contracts may be, the call
stacks decrease w.r.t. a well founded-ordering. First,
we define the call stacks and the frames composing
the call stacks based on the formal small-step seman-
tics of (Gavin, 2014; Gavin, 2019) and (Grishchenko
et al., 2018b; Grishchenko et al., 2018a).
The Maximal Call Stack Size. The maximal call
stack size is denoted by stack lim. We assume that
stack lim is a natural number strictly greater to 0.
Abstraction of the Frames. For running a contract
c
1
, the EVM stores information in the call stack. In
the following, we call this information a frame. Fol-
lowing (Grishchenko et al., 2018b), our frames can
denote standard program execution frames, HALT
frames and EXC frames. In our EVM model spe-
cialized for gas analysis, we can abstract frames by
three different frame forms: either Ok(g, pc, p,e),
Halt(g,e) or Exception, where g is a gas value, pc
is a program counter, p is a program code, and e is
an environment. Like in (Grishchenko et al., 2018b),
this environment is an abstraction of the global state
of the system σ. In our model, this environment
maps contract names to the associated codes. An
Ok(g, pc, p,e) frame represents a standard execution
frame (µ,ι, σ,η), where we abstract away η and most
parts of µ (including the execution stack and the lo-
cal memory). In µ, we only keep track of µ.pc the
program counter and µ.gas the available gas. Simi-
larly, we forget everything about ι except ι.code the
current program to execute. In σ, we only follow the
contract names associated to code and forget about all
other type of information. A Halt(g,e) frame repre-
sents a contract that successfully reaches a RETURN
instruction, where g is the gas remaining after the ex-
ecution of the contract (the refund) and e is the (possi-
bly) modified environment. In particular, e may con-
tain new contract names and their associated code.
On the opposite, the result value d and the effect η
are not stored in our abstract version of the seman-
tics, because they have no impact on the control flow
nor on gas consumption. In particular, if a conditional
jump depends on the result d then this will be mod-
eled in our abstract semantics by the fact that the ab-
stract Jump instruction can jump to any valid position
in the current contract. Finally an Exception frame
represents a contract whose execution has failed be-
cause it exhausted the available gas, overflowed the
SECRYPT 2020 - 17th International Conference on Security and Cryptography
44

call stack, jumped to an invalid pc or tried to execute
an undefined instruction.
The Call Stacks. Call stacks will be represented by
lists of frames, where the top of the stack is the left-
most element of the list.
Example 2. (1) Assume that we are running a
unique contract c
1
having 18 gas units left, a pro-
gram counter pc, a program p and an environ-
ment e. The corresponding call stack will thus
be [Ok(18, pc, p,e)]. (2) Assume that the instruc-
tion at position pc in p is a CALL to contract c
2
with a calling gas value of 10, then the call stack
becomes [Ok(10,0, p2,e2), Ok(18, pc, p, e)], where
p2 and e2 are the program and environment as-
sociated to c
2
. (3) Now assume that the instruc-
tion at position 0 in p2 consumes 2 gas units, the
call stack is now [Ok(8,1, p2,e3), Ok(18, pc, p, e)]
where e2 may have been transformed into e3.
(4) Then, assume that contract c
2
reaches program
point pc2 with 4 gas units left and the environ-
ment e4: [Ok(4, pc2, p2, e4),Ok(18, pc, p,e)]. (5) At
pc2 in p2 there is a RETURN instruction so that
c
2
halts on a valid state. The call stack becomes:
[Halt(4,e4), Ok(18, pc, p, e)]. (6) Then, the frame of
contract c
2
is popped and control is returned back to
c
1
that called c
2
. When returning back to c
1
, we have
to consume all the gas used for the call: the cost of
the call instruction itself with the cost of calling c
2
.
Assume that the call instruction costs 3 gas. Thus, we
need to consume 3 gas plus the gas that was planned
at step (2) for calling contract c
2
: 10. Besides, we
refund the 4 gas returned by Halt and place the en-
vironment e4 into c
1
frame. Thus, the call stack be-
comes [Ok(9, pc+ 1, p,e4)]. (7) Now we assume that,
the execution of contract c
1
ends with an exceptional
state. The resulting stack is thus [Exception].
6 TERMINATION PROOF FOR
THE YELLOW PAPER
SEMANTICS IN
ISABELLE/HOL
6.1 The Termination Measure
A usual technique to prove termination of a recur-
sive function f mapping values of type A to values
of type B is to define a well-founded strict ordering
on elements of type A. This ordering has to be
defined such that for all x ∈ A if f(x) evaluates to
f(y), noted f (x) f(y), then we have x y. If
such a well-founded ordering exists then it proves
termination of f . Indeed, for any infinite deriva-
tion f(t
1
) f(t
2
) ..., we have an infinite chain
t
1
t
2
..., which contradicts the fact that is well-
founded.
To prove termination of the EVM semantics, we
need to show that when executing one EVM byte-
code on a stack s
1
we obtain a stack s
2
which is
strictly smaller to s
1
w.r.t. a well-founded order-
ing . Finding such an order is not straightfor-
ward as we show on the following example. For in-
stance, to prove termination on the execution of Ex-
ample 2, we need a well-founded ordering such that
(1) [Ok(18, pc, p,e)]
(2) [Ok(10, 0, p2,e2),Ok(18, pc, p,e)]
(3) [Ok(8, 1, p2,e3),Ok(18, pc, p,e)]
(4) [Ok(4, pc2, p2,e4), Ok(18, pc, p,e)]
(5) [Halt(4, e4),Ok(18, pc, p, e)]
(6) [Ok(9, pc+ 1, p, e4)]
(7) [Exception]
Since we may have loops in a frame, we may have
two consecutive frames with the same pc or ascend-
ing pc. Thus, the program counter is not relevant for
the ordering. In the same way, since environments
e,e2,e3,e4 and programs p, p2 may not evolve be-
tween two frames, they are hardly usable for a strict
ordering. Hence, the ordering can only depend on the
gas value of the frames. If we abstract away anything
but gas from the previous example, we obtain:
[Ok(18)]
[Ok(10),Ok(18)]
[Ok(8),Ok(18)]
[Ok(4),Ok(18)]
[Halt(4), Ok(18)]
[Ok(9)]
[Exception]
Note that, using a simple ordering for does not sat-
isfy the above ordering chain. For instance, the fol-
lowing orderings fail:
• comparing the size of the list:
[Ok(18)] 6 [Ok(10),Ok(18)]
• comparing the gas value of the topmost frame:
[Halt(4),Ok(18)] 6 [Ok(9)]
• comparing the gas value of frames from bottom to
top:
[Ok(18)] 6 [Ok(10),Ok(18)]
• comparing the sum of the gas values:
[Ok(18)] 6 [Ok(10),Ok(18)]
• or, lexicographic combinations of them starting
from the leftmost part of the list:
[Halt(4),Ok(18)] 6 [Ok(9)]
Termination of Ethereum’s Smart Contracts
45

• or, lexicographic combinations of them starting
from the rightmost part of the list:
[Ok(18)] 6 [Ok(10),Ok(18)]
The order we define to prove termination of EVM se-
mantics is based on measure functions, i.e., functions
mapping frames to natural numbers. Thus, stacks can
be evaluated into lists of natural numbers and lists of
natural numbers are compared using a lexicographic
combination of the order > on natural numbers. Be-
fore defining our measure functions, we complete the
call stacks by dummy frames up to the frame stack’s
maximal size stack lim. These dummy frames (noted
D) have a gas value depending on the type of the top-
most frame and on its gas value if there is one (for
Ok and Halt) and 0 otherwise (for Exception). If the
topmost frame is Ok(i) then the dummy frames will
be D(i + 3), if the topmost frame is Halt(i) then the
dummy frames will be D(i+ 2). If the topmost frame
is Exception then the dummy frames will be D(0).
Assuming that the maximal stack size is 4, the frame
stacks of our previous example will be completed up
to size 4 in the following way:
[ D(21), D(21), D(21), Ok(18) ]
[ D(13), D(13), Ok(10), Ok(18) ]
[ D(11), D(11), Ok(8), Ok(18) ]
[ D(7), D(7), Ok(4), Ok(18) ]
[ D(6), D(6), Halt(4), Ok(18) ]
[ D(12), D(12), D(12), Ok(9) ]
[ D(0), D(0), D(0), Exception ]
Using this completion of call stacks, the order
becomes straightforward: we compare frame’s
measures lexicographically, starting from the
rightmost part of the list, i.e., from the bottom
of the stack. We use the following measure
function for frames: measure(Ok(i)) = i + 3,
measure(Halt(i)) = i + 2, measure(D(i)) = i and
measure(Exception) = 1. Thus, on the above
example, we have [D(21),D(21),D(21),Ok(18)]
[D(13),D(13),Ok(10), Ok(18)] because the 4
th
ele-
ment of the two stacks are equal (Ok(18)) but the 3
rd
element of the first stack has a measure of 21 where
the 3
rd
element of the second stack has a measure of
13. Similarly, we have [D(21),D(21),Ok(4),Ok(18)]
[D(13),D(13),Halt(4),Ok(18)] because
measure(Ok(4)) = 7 and measure(Halt(4)) = 6.
The values for the measure of frames,
measure(Ok(i)) = i + 3, measure(Halt(i)) = i + 2,
measure(D(i)) = i and measure(Exception) = 1,
have been chosen so that an Ok frame halting (cor-
rectly) with a gas i and moving to a Halt with the
same gas value i can be ordered. With this measure,
we have [Ok(i), f
1
,..., f
n
] [Halt(i), f
1
,..., f
n
], for
all i ≥ 0 and all frames f
1
,. .. , f
n
. This is crucial
since this sequence of frame stacks is possible with
the EVM semantics.
Definition 1 (Stack Measure). Let Es be the maximal
height of the EVM call stack. Let s be an EVM call
stack represented by a list of frames of the form Ok(i),
Halt( j), or Exception where i, j are strictly positive
natural numbers. Let s(k) be the k-th element of the
stack s for 0 ≤ k < |s|, thus s(0) is the topmost frame.
For 0 ≤ k < |s|, let
m
k
=
i+ 3 if s(k) = Ok(i)
i+ 2 if s(k) = Halt(i)
1 if s(k) = Exception
d =
i+ 3 if s(0) = Ok(i)
i+ 2 if s(0) = Halt(i)
0 if s(0) = Exception
The stack measure of s is a list of natural numbers, of
length Es, defined by:
measure(s) = [d,.. ., d]
| {z }
Es−|s|
@[m
0
,. .. ,m
|s|−1
]
where @ denotes list concatenation.
With this measure, we can prove the following termi-
nation theorem.
Theorem 1. The execution of any contract on the
EVM terminates.
The proof amounts to showing that each EVM exe-
cution step results in a decrease of the measure on
call stacks defined in Definition 1. To prove this for-
mally, we need to define an abstract version of the
EVM semantics specialized for gas analysis. This will
be done in the next section where we propose an Is-
abelle/HOL formalization of this specialized seman-
tics.
6.2 Implementation in Isabelle/HOL
The Isabelle datatype for instructions and the type for
programs are the following:
type_synonym datatype instr = Nil
gas = nat | Local "gas"
| Jump "gas"
type_synonym | Call "gas*gas*contractName"
pc= nat | Stop
type_synonym program = "instr list"
The abstraction of frames defined in Section 6.1 only
keeps track of the gas, the current program to ex-
ecute, the program counter, and the environment.
With this abstraction, many EVM instructions have
a similar behavior and can be abstracted by a gen-
eral Local instruction whose only parameter is its
SECRYPT 2020 - 17th International Conference on Security and Cryptography
46

gas cost. The Local(g) instruction represents any
instruction whose effect is local to the current frame,
does not affect the control flow, and whose cost in
gas is the natural number g. This instruction repre-
sents all instructions of the families Execution Stack
Operations, Memory Access and Environment Op-
erations of Section 4, i.e., instructions such as ADD,
SSTORE, MSTORE, LT, AND, PUSHi, POP, DUPi,
SWAPi, . . . The Nil instruction stands for undefined
instruction (an undefined opcode) that may appear in
a program or the INVALID instruction. The Jump(g)
instruction represents the JUMP and JUMPI instruc-
tions where g is the cost of executing the jump. There
is no destination associated with the Jump instruction
because the abstract semantics will arbitrarily chose
the destination when executing the Jump. This is
an over-approximation of all the possible JUMP and
JUMPI behaviors with any position in the contract
tagged by a JUMPDEST instruction. Thus, we cover
all the instructions of the Control Flow Operations
family of Section 4. The family of System Opera-
tions is represented by two different abstract instruc-
tions. The (Call gcall ccall cname) instruction
represent EVM’s CREATE, CALL, CALLCODE,
DELEGATECALL, and CALLSTATIC where gcall
is the cost in gas of executing the call instruction it-
self, ccall is the gas transferred to the called con-
tract, and cname is the contract name to be called.
Having CREATE and CALL abstracted by the same
Call instruction is coherent with EVM semantics,
where the difference between the two is small. In
the case of a CALL, the contract name exists in the
environment and is associated to a program. In the
case of a CREATE the contract name does not exist
and the association is added in the environment of the
new frame, see (Genet et al., 2020) for details. The
last abstract instruction for the family System opera-
tions is the Stop instruction which represents STOP,
RETURN, REVERT and SELFDESTRUCT EVM’s
instructions. Finally, a program p is a list of such in-
structions and a program counter pc of p is a position
between 0 and length(p) −1 in this list.
Note that, in EVM, all instructions (except STOP,
REVERT and RETURN) have a gas cost which is
strictly greater than zero. However, the above Is-
abelle/HOL datatype only imposes that gas costs are
of type nat, i.e., that they are greater or equal to
zero. Thus, we complement this datatype with a
valid_prog(p) predicate stating that, in a program
p, every instruction with a cost g is such that g > 0.
The function defining the EVM semantics
is smallstep and its Isabelle/HOL type is
call_stack ⇒ call_stack. Starting from a
call stack, whose top frame is Ok(g, pc, p,e) this
function executes the instruction at position pc in
p with environment e and returns the resulting call
stack. Recall that there are three kinds of frames:
Ok, Halt or Exception. The Isabelle/HOL type
call_stack is simply a list of frames. Thus, this
type includes invalid call stacks, i.e., stacks that
contain frames whose program is invalid, and stacks
that cannot be produced by a correct execution of the
EVM semantics (such as [Exception, Exception]).
Since functions in Isabelle/HOL have to be total,
we need to define the smallstep function for all
stacks including the invalid ones. To ensure totality
of smallstep, while preserving its soundness w.r.t.
EVM, we map any invalid call stacks to the result
stack [Invalid f rame], where Invalid f rame is an
additional kind of frame. Here is the corresponding
Isabelle/HOL datatype.
datatype
frame =
Ok "gas*pc*program*env"
| Exception
| Halt "gas*env"
| Invalid_frame
type_synonym
call_stack = "frame list"
We define a predicate valid_stack checking that a
call stack is valid: it contains only valid programs,
valid environments and valid sequence of frames.
A valid sequence does not contain Invalid f rame,
and Exception or Halt cannot be below other
frames. We now present the smallstep function of
type smallstep::"call_stack ⇒ call_stack" and
whose role is to execute the abstract instructions on
a call stack. The complete Isabelle/HOL code can be
found here (EFSyellow, 2020). Note that this seman-
tics is executable and some examples can be found
and run at the end of the theory file. We here only
give some excerpts of the smallstep function.
6.3 Semantics for Stop, Nil and Local
Instructions
The first one illustrates the execution of Stop, Nil
and Local instructions. Recall that the Local in-
struction covers the Execution stack, Memory ac-
cess and Environment families of operations of Sec-
tion 4. This code has to be compared with the seman-
tic rules of Section 4.1.
"smallstep ((Ok (g,pc,p,e))#l) =
(case p.(pc) of
Stop ⇒ ((Halt (g,e))#l) |
Nil ⇒ (Exception#l)|
Local(n) ⇒(if (n>0) then (
if (n≤g) then
((Ok ((g-n),pc+1,p,e))#l)
Termination of Ethereum’s Smart Contracts
47

else (Exception#l))
else [Invalid_frame] )|
[...]
In the case of a Local(n) instruction, if n = 0 this re-
sults into a [Invalid f rame]. Otherwise if n is lesser
or equal to the available gas g then instruction is ex-
ecuted, gas is updated and pc is incremented. Other-
wise, an exception is stacked on the call stack.
6.4 Semantics for the Jump Instuction
Now, we present the semantics of the Jump instruc-
tion which covers the operations of the Control Flow
family of Section 4.
"smallstep ((Ok (g,pc,p,e))#l) =
(case p.(pc) of
[...]
Jump(n) ⇒
if (n>0) then
(let pj= (any_jump 0) in
if (n≤g) then
(if (pj<(length p)) then
((Ok(g-n,pj,p,e))#l)
else (Exception#l))
else (Exception#l))
else [Invalid_frame] )
[...]
Like above, for Local(n) if n = 0 this results into a
[Invalid f rame]. Otherwise we compute an arbitrary
value for the destination of the jump, named pj, using
the function any_jump. This function is left unspec-
ified, we only known its type any_jump::’a ⇒ nat.
Thus, pj= (any_jump 0) associates any natural
number to pj. This models the fact that the jump
can be conditional and JUMPDEST labels can be at-
tached to any part of the current contract. Then,
if there is enough gas to execute the jump (n≤g)
and the jump destination is in the range of the cur-
rent contract (pj<(length p)) then the program
counter is updated with pj and the top frame be-
comes (Ok(g-n,pj,p,e). Otherwise, an exception
is stacked on the call stack.
6.5 Semantics for the CALL Return
The semantics of the contract call is straightforward,
see (EFSyellow, 2020). Thus, the third excerpt, il-
lustrates the return of a contract call. This has to be
compared with the second rule of Section 4.3.
[...]
"smallstep ((Halt(gend,ef))#(Ok(g,pc,p,e))#l) =
(case p.(pc) of
Call(gcall,ccall,name) ⇒
if ((gcall+ccall)>g) then [Invalid_frame]
else if (gcall≤0) then [Invalid_frame]
else if (ccall≤0) then [Invalid_frame]
else
if (ccall<gend) then
(Exception#(Ok (g,pc,p,e))#l)
else
((Ok((g+gend-gcall-ccall),
(pc+1),p,ef))#l)
|_ ⇒ [Invalid_frame] )"|
[...]
When a contract halts correctly (frame
(Halt (gend,ef)) on top of the stack, with
gas refund gend and environment ef) then if the
frame below is a frame (Ok (g,pc,p,e)) such that
the instruction at position pc in p is a call, and such
that all calling conditions were satisfied before the
call, then we pop the Halt frame and continue in
the Ok frame, with gas (g+gend-gcall-ccall),
at position pc+1 and with (possibly) modified en-
vironment ef. Any other behavior results into an
[Invalid f rame].
6.6 Soundness and Termination Proof
Since we completed the EVM semantics with a new
type of frames (Invalid f rame) to have a total func-
tion smallstep, we first need to verify that this mod-
ification does not break the EVM semantics encoded
in the smallstep function. This can be checked us-
ing the following Isabelle/HOL theorem stating that
validity of stacks is preserved by smallstep.
lemma validstack_smallstep:
"(valid_stack l)−→
(valid_stack (smallstep l))"
In other words, when running smallstep on a valid
stack, then Invalid f rame will never show up. The
(complete) execution of a contract starts from a call
stack, applies the smallstep function until a Halt,
Exception or Invalid_frame is reached. The result
of a complete execution is a single frame. It is defined
in Isabelle/HOL in the execute function as follows:
function (sequential)
execute :: "call_stack ⇒ frame"
where
"execute ([]) = Invalid_frame"|
"execute ([Halt (g,e)]) = (Halt (g,e))"|
"execute ([Exception]) = (Exception)"|
"execute ([Invalid_frame]) = Invalid_frame"|
"execute l = (if (length l > stack_lim) then
Invalid_frame
else execute (smallstep l))"
Again, we can lift the previous theorem to prove
that adding Invalid f rame does not break the seman-
tics, i.e. executing a valid stack always result into a
valid stack, where stack lim is an arbitrary constant
(greater than 0) which defines the maximal stack size.
lemma finalSoundnessTheorem:
"(valid_stack l ∧ (length l ≤ stack_lim))
−→ (valid_stack [(execute l)])"
SECRYPT 2020 - 17th International Conference on Security and Cryptography
48

Now, we can state and prove in Isabelle/HOL the
termination theorem (Theorem 1) which corresponds
to the termination proof of the execute function.
The proof of this property relies on the measure
technique described in section 6.1 extended with
measure(Invalid_frame) = 1 and encoded into Is-
abelle/HOL. Note that this final termination theorem
is valid for any stack size (stack lim), where the ter-
mination measure is the one defined in Section 6.1
and formalized by the list order Isabelle/HOL
function.
termination execute
apply (relation
"measures (list_order stack_lim)")
The Isabelle/HOL development is around 1200 lines.
Excluding definitions, the proof of soundness is com-
posed of 18 intermediate lemmas and of 300 lines of
Isabelle/HOL. The proof of termination is composed
of 57 intermediate lemmas and of 400 lines of Is-
abelle/HOL.
7 TERMINATION PROOF FOR
THE EVM REFERENCE
IMPLEMENTATIONS
SEMANTICS
As explained in the introduction, implementa-
tions generally use a slightly different seman-
tics for the call: g is retracted to c
1
at the
calling point for c
2
and g
ref und
is added when
the control flow returns from c
2
. This is the
case for (pevm, 2017) (see class BaseCall and
class Call(BaseCall) in https://github.com/ethereum/
py-evm/blob/master/eth/vm/logic/call.py). Executing Ex-
ample 2 with this other semantics yields the following
sequence of call stacks.
Example 3. (1) Assume that we are running a
unique contract c
1
having 18 gas units left, a pro-
gram counter pc, a program p and an environ-
ment e. The corresponding call stack will thus be
[Ok(18, pc, p,e)]. (2) Assume that the instruction at
position pc in p is a CALL to contract c
2
with a call-
ing gas value of 10, and the cost of a CALL is 3. Then
the call stack becomes
[Ok(10, 0, p2,e2), Ok(5, pc, p, e)],
where p2 and e2 are the program and environment
associated to c
2
. (3) Now assume that the instruction
at position 0 in p2 consumes 2 gas units, the call stack
is now
[Ok(8, 1, p2,e3), Ok(5, pc, p, e)]
where e2 may have been transformed into e3.
(4) Then, assume that contract c
2
reaches program
point pc2 with 4 gas units left and the environment
e4:
[Ok(4, pc2, p2,e4),Ok(5, pc, p,e)].
(5) At pc2 in p2 there is a RETURN instruction so
that c
2
halts on a valid state. The call stack becomes:
[Halt(4,e4), Ok(5, pc, p, e)].
(6) Then, the frame of contract c
2
is popped and con-
trol is returned back to c
1
that called c
2
, the 4 gas are
refunded to c
1
and we place the environment e4 into
c
1
frame. Thus, the call stack becomes
[Ok(9, pc + 1, p, e4)].
(7) Now we assume that, the execution of contract c
1
ends with an exceptional state. The resulting stack is
thus [Exception].
To prove termination we now need a well-founded
strict ordering that satisfy the following ordering con-
straints:
(1) [Ok(18, pc, p,e)]
(2) [Ok(10, 0, p2,e2),Ok(5, pc, p,e)]
(3) [Ok(8, 1, p2,e3),Ok(5, pc, p,e)]
(4) [Ok(4, pc2, p2,e4), Ok(5, pc, p,e)]
(5) [Halt(4, e4),Ok(5, pc, p, e)]
(6) [Ok(9, pc+ 1, p, e4)]
(7) [Exception]
Note that the ordering used for the previous semantics
does not satisfy those constraints. If we complete our
stacks up to size 4, we obtain:
[ D(21), D(21), D(21), Ok(18) ]
[ D(13), D(13), Ok(10), Ok(5) ]
[ D(11), D(11), Ok(8), Ok(5) ]
[ D(7), D(7), Ok(4), Ok(5) ]
[ D(6), D(6), Halt(4), Ok(5) ] 6
[ D(12), D(12), D(12), Ok(9) ]
[ D(0), D(0), D(0), Exception ]
However, with this second semantics, finding a sat-
isfying termination order is easier. The termination
ordering is a lexicographic combination of an order
comparing the sum of all gas in the frames, an or-
der comparing the size of the call stack, and finally
an order comparing the type of the frame (where
Ok > Halt > Exception). See (EFSimplem, 2020) for
the complete formalization and Isabelle/HOL proof.
The Isabelle/HOL development is around 900 lines.
The proof of soundness is very similar to the previ-
ous one. The proof of termination is composed of 14
intermediate lemmas and is around 130 lines.
Termination of Ethereum’s Smart Contracts
49

8 CONCLUSION
Termination is an important property of any smart
contract. To this end, the Ethereum platform (EVM)
has introduced a mechanism based on gas which gets
consumed as the execution progresses. This paper
presents an abstract model of EVM execution that fo-
cuses on gas consumption. On this model, we prove
that for any EVM execution, gas is used in such a way
that it is impossible to construct an infinite loop that
does not consume any gas. This property is not im-
mediate to establish for the specification in the EVM
Yellow Paper, because of the decidedly nontrivial se-
mantics of contract calls and the fact that cashing-in
of the cost of the call is delayed until after the return
(whether regular or exceptional).
The proof relies on a non-trivial measure on con-
tract call stacks and has the salient feature that it is
independent of the specific costing of instructions, as
long as they are greater than 0. This latter point is im-
portant as the costs of certain instructions of the EVM
has evolved over its rather short life.
The mechanized proof is based on an abstract
model of the EVM and fills a gap in current formal
developments on verification of contracts with proof
assistants (Hirai, 2017; Amani et al., 2018). There
are a number of steps for further work related to this
mechanization. First, it would be worthwhile formal-
izing the relation to the complete semantic formal-
ization by Grishchenko (Grishchenko et al., 2018a)
or even the Isabelle/HOL formalization (Hirai, 2017;
Amani et al., 2018). This can likely be done by set-
ting up a simulation relation between the concrete and
the abstract semantics. Second, it would be useful to
show that the gas consumption in the two semantics
are similar or, at least, that the consumption of one is
bounded by a polynomial function of the consumption
of the other. Another possible extension stems from
the fact that this proof is only for one transaction. It
does not take into account several transaction rounds.
ACKNOWLEDGEMENTS
Many thanks to Emmanuelle Anceaume, Vincent La-
porte, Romaric Ludinard, and Clara Schneidewind for
valuable discusions about Ethereum and SmartCon-
tracts.
REFERENCES
Amani, S., B
´
egel, M., Bortin, M., and Staples, M. (2018).
Towards verifying ethereum smart contract bytecode
in isabelle/hol. In CPP’18, pages 66–77. ACM.
Buterin, V. (2013). Ethereum: A Next-Generation Smart-
Contract and Decentralized Application Platform.
https://github.com/ethereum/wiki/wiki/White-Paper.
EFSimplem (2020). Ethereum Formal Semantics for
Gas Consumption Analysis - Implementations seman-
tics. https://github.com/thomas-genet/abstEVM/blob/
master/abstEvm2.thy.
EFSyellow (2020). Ethereum Formal Semantics for
Gas Consumption Analysis - Yellow paper seman-
tics. https://github.com/thomas-genet/abstEVM/blob/
master/abstEvm.thy.
ethertrust (2017). Ethertrust - Trustworthy smart contracts.
https://www.netidee.at/ethertrust.
ETS (2015). Official ethereum test suite. https://github.
com/ethereum/tests.
FEL (2018). Formalization of Ethereum Virtual Machine in
Lem. https://github.com/pirapira/eth-isabelle.
Gavin, W. (2014). Ethereum: A secure decentralised gen-
eralised transaction ledger. Ethereum project yellow
paper 151, EIP-150 Revision, http://gavwood.com/
Paper.pdf.
Gavin, W. (2019). Ethereum: A secure decentralised gen-
eralised transaction ledger. Ethereum project yel-
low paper, BYZANTIUM VERSION e7515a3, https:
//ethereum.github.io/yellowpaper/paper.pdf.
Genet, T., Jensen, T., and Sauvage, J. (2020). Termina-
tion of Ethereum’s Smart Contracts. Technical report,
Univ Rennes, Inria, CNRS, IRISA. https://hal.inria.fr/
hal-02555738.
gevm (2014). Official Go implementation of the Ethereum
protocol. https://github.com/ethereum/go-ethereum.
Grech, N., Kong, M., Jurisevic, A., Brent, L., Scholz,
B., and Smaragdakis, Y. (2018). Madmax: surviv-
ing out-of-gas conditions in Ethereum smart contracts.
PACMPL, 2(OOPSLA):116:1–116:27.
Grishchenko, I., Maffei, M., and Schneidewind, C. (2018a).
Foundations and Tools for the Static Analysis of
Ethereum Smart Contracts. In CAV’18, volume 10981
of LNCS, pages 51–78. Springer.
Grishchenko, I., Maffei, M., and Schneidewind, C. (2018b).
A Semantic Framework for the Security Analysis of
Ethereum Smart Contracts. In POST’18, volume
10804 of LNCS, pages 243–269. Springer.
Hildenbrandt, E., Saxena, M., Rodrigues, N., Zhu, X., Da-
ian, P., Guth, D., Moore, B.-M., Park, D., Zhang, Y.,
Stefanescu, A., and Rosu, G. (2018). KEVM: A Com-
plete Formal Semantics of the Ethereum Virtual Ma-
chine. In CSF’18, pages 204–217. IEEE Computer
Society.
Hirai, Y. (2017). Defining the Ethereum Virtual Machine
for Interactive Theorem Provers. In FC’17, volume
10323 of LNCS, pages 520–535. Springer.
Hudson, J. (2016a). Upcoming Ethereum Hard Fork.
2016/10/18, https://blog.ethereum.org/2016/10/18/
faq-upcoming-ethereum-hard-fork/.
Hudson, J. (2016b). Upcoming Ethereum Hard
Fork. 2016/11/22, https://blog.ethereum.org/2016/11/
18/hard-fork-no-4-spurious-dragon/.
SECRYPT 2020 - 17th International Conference on Security and Cryptography
50

pevm (2017). A Python implementation of the
Ethereum Virtual Machine. https://github.com/
ethereum/py-evm.
script (2014). The script Bitcoin Programming Language.
https://en.bitcoin.it/wiki/Script.
solidity (2014). The Solidity Language. https://solidity.
readthedocs.io/.
vyper (2017). Pythonic Smart Contract Language for the
evm. https://vyper.readthedocs.io/.
Yang, R., Murray, T., Rimba, P., and Parampalli, U. (2019).
Empirically Analyzing Ethereum’s Gas Mechanism.
In 2019 IEEE European Symposium on Security and
Privacy Workshops, pages 310–319. IEEE.
Termination of Ethereum’s Smart Contracts
51
