
Tournament Selection Algorithm for the Multiple Travelling Salesman
Problem
Giorgos Polychronis and Spyros Lalis
University of Thessaly, Volos, Greece
Keywords:
Multiple Travelling Salesman Problem, Tournament Selection, Large Neighbourhood Search,
Quality/Execution Time Trade-off.
Abstract:
The multiple Travelling Salesman Problem (mTSP) is a generalization of the classic TSP problem, where the
cities in question are visited using a team of salesmen, each one following a different, complementary route.
Several algorithms have been proposed to address this problem, based on different heuristics. In this paper, we
propose a new algorithm that employs the generic tournament selection heuristic principle, hybridized with a
large neighbourhood search method to iteratively evolve new solutions. We describe the proposed algorithm
in detail, and compare it with a state-of-the-art algorithm for a wide range of public benchmarks. Our results
show that the proposed heuristic manages to produce solutions of the same or better quality at a significantly
lower runtime overhead. These improvements hold for Euclidean as well as for general topologies.
1 INTRODUCTION
The Travelling Salesman Problem (TSP) is a well
studied combinatorial problem, which is NP-hard.
The mTSP is a more general variant where multiple
salesmen visit the cities of interest in parallel. A com-
mon objective is to minimize the total cost, which is
the sum of the cost of the different routes that are fol-
lowed by the salesmen. This version is also known as
the min-sum problem. A different objective is to min-
imize the travel cost of the most costly (worst) route,
referred to as the min-max or min-makespan problem.
In practical terms, this is equivalent to load-balancing
the task of city visits among the available salesmen.
The min-max mTSP is directly relevant to appli-
cation scenarios where a given task should be com-
pleted with the smallest possible delay. Besides tra-
ditional logistics and transport applications, this is a
key concern in several modern applications that in-
volve unmanned vehicles, such as drones. For exam-
ple, in smart agriculture, multiple drones can be used
to scan large crop fields and plantations in order to
spot areas that need more irrigation or a stronger dose
of pesticide. Similarly, in a search and rescue opera-
tion, multiple drones can be employed to scan a large
territory in order to detect missing persons. In both
cases it is obviously important to minimize the mis-
sion completion time, so that one avoids production
losses and manages to save human lives, respectively.
In this paper we propose a hybrid algorithm for
the min-max mTSP, which combines a tournament se-
lection heuristic with a large neighbourhood search
method. The algorithm supports two different meth-
ods for the mutation of solutions, one designed for
general problems and one for problems where the
edge costs reflect the Euclidean distance between the
points of travel. We compare the proposed algorithm
with a state-of-the-art algorithm for a range of pub-
lic benchmarks, showing that it achieves solutions of
equal or slightly better quality while being signifi-
cantly faster.
To the best of our knowledge, this is the first time
tournament selection is used as the top-level heuristic
to tackle the mTSP. Unlike other approaches, instead
of keeping or even increasing the size of the initial
population in order to explore more neighbourhoods,
the proposed method starts with a large random initial
population and iteratively decreases its size by keep-
ing the best solutions, thereby focusing the search ef-
fort on the most promising ones.
The rest of the paper is structured as follows. Sec-
tion 2 gives an overview of related work. Section 3
provides a formal description of the min-max mTSP.
Section 4 presents our algorithm in detail. Section 5
discusses the performance of the proposed algorithm.
Finally, Section 6 concludes the paper.
Polychronis, G. and Lalis, S.
Tournament Selection Algorithm for the Multiple Travelling Salesman Problem.
DOI: 10.5220/0009564905850594
In Proceedings of the 6th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2020), pages 585-594
ISBN: 978-989-758-419-0
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved
585

2 RELATED WORK
The mTSP has been studied extensively and there is
a wide literature on different solutions for it. Indica-
tive surveys can be found in (Anbuudayasankar et al.,
2014),(Gutin and Punnen, 2006), (Davendra, 2010).
In this paper, we focus on the single depot min-max
variant of the problem, where all salesmen start from
and have to return back to the same city, and where
the objective is to minimize the longest / most costly
path. Next, we give an overview of the various algo-
rithms that have been proposed for this problem.
A popular method for tackling the mTSP are ge-
netic algorithms. A genetic algorithm is basically a
metaheuristic that is inspired by the principle of nat-
ural selection. Genetic algorithms start with an ini-
tial population, where each individual (chromosomes)
represent a different solution to the problem. New so-
lutions can be created either as the result of crossover
operations between two different solutions or by per-
forming mutation operations on an individual solu-
tion. Given that the population is not allowed to ex-
ceed a maximum number of solutions, only the fittest
ones are typically selected to remain in the popula-
tion while the rest are dropped. In (Carter and Rags-
dale, 2006), the two-part chromosome representation
is proposed for the mTSP, where a solution is encoded
using a n-length part that is the order of cities to-
gether with a m-length part that corresponds to the as-
signment of cities to the different salesmen. This en-
coding reduces the search space of the problem com-
pared to other representations. This representation
is also used by (Yuan et al., 2013) to devise a new
operator that generates a new solution by removing
and reinserting genes (cities) at each salesman sepa-
rately while modifying the second part of the repre-
sentation in a random way. This approach improves
the search component of the algorithm. The group-
based genetic algorithmic principle was first intro-
duced in (Falkenauer, 1992) in combination with a
two-part chromosome, where the first part encodes
a solution of the problem and the second part in-
cludes the groups of the main part. The mutation
and crossover operators are applied in the second part.
Based on this approach, (Brown et al., 2007) proposed
a grouping generic algorithm for the mTSP with a
suitably adapted solution structure. Finally, (Singh
and Baghel, 2009) propose a grouping genetic algo-
rithm with a different solution representation, where
the solutions are represented as m different routes
without any ordering or mapping to a specific sales-
man. This makes it possible to reduce the redundant
individuals in a population.
Several researchers have proposed nature-inspired
methods. In (Venkatesh and Singh, 2015), the authors
propose two metaheuristic solutions for the min-max
mTSP, an artificial bee colony algorithm and an in-
vasive weed optimization algorithm (IWO). The for-
mer is an optimization technique that simulates the
foraging behaviour of honey bees. On the other hand,
IWO is a technique inspired by the weed colonization
and distribution in the ecosystem. The IWO algorithm
starts from an initial population of weeds, each repre-
senting a solution. Based on the fitness of the weeds
they produce a number of seeds, which in their turn
join the previous population. However, the number
of weeds in the population must remain lower than
an upper bound, so there is strong similarity to the
genetic algorithms where the fittest individuals stay
in the population. (Liu et al., 2009) and (Vallivaara,
2008) approach the problem using an ant colony op-
timization algorithm. This is a probabilistic tech-
nique, simulating an ant colony and the pheromone
used by ants to communicate with each other in order
to find good paths toward a food source. Simulated
ants move to a customer/city/node randomly, but with
a higher chance to pick nodes with high pheromone
trails. An approach based on neural networks is pro-
posed in (Somhom et al., 1999). In (Lupoaie et al.,
2019), the authors hybridize the neural network ap-
proach with different metaheuristic techniques such
as evolutionary algorithms and ant colony systems.
In (Wang et al., 2017) a memetic algorithm is
proposed, based on variable neighbourhood descend.
A memetic algorithm is a hybridization of a genetic
algorithm with a local search procedure. Variable
neighbourhood descend is a local search where mul-
tiple neighbourhoods of a solution are checked un-
til a local minimum is reached. Each neighbour-
hood corresponds to a different mutation operator.
(Soylu, 2015) propose a general variable neighbour-
hood search. The general variable neighbourhood
search is a metaheuristic that starts from an initial
feasible solution (which at first is also the current
solution), improves the current solution with a local
search procedure (it usually uses multiple operators)
and escapes local minimums with a shaking function.
(Franc¸a et al., 1995) and (Golden et al., 1997)
propose a tabu search, which is a metaheuristic tech-
nique to escape local minimums. The solution moves
to the best neighbour solution and avoids cycling by
keeping a list of forbidden moves, the so called tabu
list. The authors in (Franc¸a et al., 1995), also propose
two exact algorithms to tackle the min-max problem.
(Vandermeulen et al., 2019) propose a task allocation
strategy to solve the mTSP. They present an algorithm
that first partitions the graph to m subgraphs, and then
solve the 1-TSP for each subgraph.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
586

In (Bertazzi et al., 2015), a comparison is made
between the min-sum and min-max mTSP. It is shown
that the length of the longest tour in the min-sum
problem is at most m times longer than the length of
the longest tour in the min-max problem with m vehi-
cles, whereas the total cost is at most m times higher
in the min-max than in the min-sum problem. The
fact that min-sum mTSP solutions can be highly sub-
optimal for the min-max mTSP justifies the design
of heuristic and metaheuristic algorithms specifically
for the latter. But one should also keep in mind that
a min-max solution may result to higher aggregated
cost compared to a min-sum solution.
Finally, there are approaches for finding exact so-
lutions to the mTSP, such as (Franc¸a et al., 1995).
However, given the complexity of the problem, these
are not practically applicable when the number of
cities is large and there are many alternative paths that
can be followed by the salesmen to visit them.
3 PROBLEM FORMULATION
The topology for the multiple Travelling Salesman
Problem (mTSP) can be abstracted as a directed graph
G = (N ,E), where N is the set of nodes and E is the
set of edges in G. A node n
i
∈ N ,i 6= 0 represents a
customer/city that needs to be visited. We assume a
single depot node n
0
, which is the starting point for
all salesmen. An edge e
i, j
∈ E represents the ability
to move directly from node n
i
to node n
j
.
Each edge e
i, j
is associated with a cost c
i, j
> 0,
which is the time it takes to move from n
i
to n
j
. The
edge costs can be defined based on the Euclidean dis-
tance between the locations of the nodes (Euclidean
problem), or they may not be directly related to the
node’s location (general problem). In the latter case, it
is possible to capture in a flexible way additional fac-
tors that may affect travel time, like the quality, wide-
ness, curviness, steepness of a road, which can have
significant impact in travel time. Note that edge costs
can be symmetrical, where c
i, j
= c
j,i
,∀n
i
,n
j
∈ N , or
asymmetrical, where ∃n
i
,n
j
∈ N : c
i, j
6= c
j,i
.
Assuming a team of several salesmen who can
travel in parallel to each other, the goal is to find a
route for each salesman, such that each node is vis-
ited only once and all the nodes are visited by some
salesman. The min-max optimization objective is to
minimize the cost of the longest route.
More formally, let the route r
m
of the m
th
sales-
man, 1 ≤ m ≤ M, where M is the number of sales-
men. It can be encoded as a sequence of nodes, where
r
m
[k] is the k
th
node in r
m
, where 1 ≤ k ≤ len(r
m
)
and len(r
m
) is the length of the route. Equivalently,
we say that e
i, j
∈ r
m
if r
m
[k] = n
i
and r
m
[k + 1] = n
j
for 1 ≤ k ≤ len(r
m
) − 1. The cost of route r
m
is
cost(r
m
) =
∑
∀e
i, j
∈r
m
c
i, j
. We say that route r
m
is prop-
erly formed if it starts from the depot node and ends
at the depot node, so r
m
[1] = n
0
and r
m
[len(r
m
)] = n
0
,
and if it does not overlap with the route r
m
0
of another
salesman, so r
m
∩r
m
0
= ∅,1 ≤ m,m
0
≤ M. Then, the
objective is to find M properly formed routes, so that
max
1≤m≤M
cost(r
m
) is minimized.
4 TS-LNS ALGORITHM
This section describes the proposed algorithm. It is
a heuristic based on the principle of tournament se-
lection (TS), combined with the large neighbourhood
search (LNS) method, originally proposed by (Shaw,
1998). Each solution is a list of M routes, one for
each salesman. The representation of the routes is
similar to the one used in (Singh and Baghel, 2009),
(Venkatesh and Singh, 2015) and (Wang et al., 2017).
As a fitness function for a given solution, we use
the inverse of the cost of the most expensive (worst)
route. When comparing between two solutions, we
prefer the one for which the fitness function returns
the larger value.
In the sequel, we present the algorithm in a top-
down fashion. We start with the main logic and then
proceed to discuss the different functional compo-
nents of the algorithm in more detail.
4.1 Top-level Iteration Function
The starting point of the algorithm is the TS-LNS()
function, described in Algorithm 1. It builds an ini-
tial population consisting of MaxPopSize random so-
lutions, and subsequently evolves this population in
an iterative fashion.
In each iteration, the fittest solutions from the pre-
vious population are kept, decreasing the size of the
population by a factor f . For each solution in the
remaining population, a large neighbourhood search
(LNS) is performed.
The iterations are repeated until the size of the
population drops to/below a pre-specified threshold
MinPopSize. The fittest of the remaining solutions
is returned as the end result.
4.2 Large Neighbourhood Search
The large neighbourhood search procedure is de-
scribed as a separate function LNS() in Algorithm 2.
It takes a solution as input and returns as a result an-
other solution, which is produced by trying out a num-
Tournament Selection Algorithm for the Multiple Travelling Salesman Problem
587

Algorithm 1 : TS-LNS algorithm for M salesmen (option
rmvopt sets the node removal method).
function TS-LNS(N ,M,rmvopt)
nullsol ← ∅
pop ←{}
repeat M times
nullsol = nullsol + {[n
0
,n
0
]}
end repeat
repeat MaxPopSize times
pop ← pop + INSERT(nullsol,N )
end repeat
sort(pop)
mut ← initLNSMutations()
repeat
pop ← getFittest(pop,size(pop)/ f )
for each sol ∈ pop do
sol ← LNS(sol,mut,rmvopt)
end for
sort(pop)
mut ← adjustLNSMutations(mut)
until size(pop) ≤ MinPopSize
return getFittest(pop, 1)
end function
ber of so-called mutations. The number of mutations
to be performed is a parameter, provided by the top-
level TS-LNS() function.
Each mutation generates a new solution based on
the best solution found up to that point, first by de-
stroying it and then by repairing it. The destruction
operation involves the removal of some nodes from
their assigned routes, and the repair operation rein-
serts those nodes to some (other) routes. If the new
solution is fitter than the current one, it is adopted as
the best solution, which, in turn, will be used as a ba-
sis for the remaining mutations.
The node insertion and removal methods used
to implement the mutations are discussed separately.
Note that LNS() is designed to work using two dif-
ferent node removal methods. The selection is done
via the rvmopt parameter, which is set by the user
when invoking the top-level TS-LNS() function. In
any case, the number of nodes to be removed and
then reinserted in every mutation is decided randomly.
However, the interval for this random pick is defined
as a function of either |N | or
p
|N |, depending on
the node removal method used.
4.3 Node Insertion
The node insertion logic is given as a separate func-
tion INSERT() in Algorithm 3. This seems to be sim-
Algorithm 2 : LNS method (option rmvopt sets the node
removal method).
function LNS(sol,no f mutations, rmvopt)
if rmvopt = RAND then
lower,upper ← α ∗|N |,β ∗|N |
else if rmvopt = PROXIMITY then
lower,upper ← α ∗
p
|N |,β ∗
p
|N |
end if
best ← sol
repeat no f mutations times
rmv ← random(lower,upper)
if rmvopt = RAND then
tmp, f ree ← RMVR(best, rmv)
else if rmvopt = PROXIMITY then
seeds ← random(1, upper/10)
tmp, f ree ← RMVP(best, rmv,seeds)
end if
new ← INSERT(tmp, f ree)
if f itness(new) > f itness(best) then
best ← new
end if
end repeat
return best
end function
ilar to the approach used in (Venkatesh and Singh,
2015), however the authors only give a very informal
(verbal) description for it.
Briefly, a node is picked randomly from the set
of nodes to be incorporated in the solution, and an
exhaustive search is performed to find the best route
and the best position within that route for the node in
question. The objective for the insertion is to min-
imize the cost of the worst (most costly) route in
the solution. The current solution is updated accord-
ingly. The process is repeated until all nodes have
been added, and the resulting solution is returned.
The routes are considered in such an order so that
the worst route with the largest cost will be checked
last. This way, the worst route will be checked only
if the node’s insertion at any other route makes that
route even more costly than the currently worst route.
Also, if several insertion options result to the same
worst-case cost, as a tie-break we pick the one that
minimizes the cost increase for the route where the
node is added. These optimizations are not shown in
Algorithm 3, for brevity.
Figure 1 gives an indicative example for the inser-
tion of a node in a solution that includes two routes
(for two salesmen). In this case, the node is added to
the blue route (on the right) because this does not in-
crease the cost of the worst (most costly) orange route
(on the left). Also, the node is added in the blue route
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
588

Algorithm 3: Node insertion method.
function INSERT(sol, nodes)
cur ← sol
while nodes 6= ∅ do
minwcost ← ∞ min cost of worst route
n
j
←rmvNodeRandom(nodes)
for each r ∈ cur (increasing cost order) do
for each n
i
∈ r do
r
0
← addNode(r,n
i
,n
j
)
wc ← worstCost(cur −r + r
0
)
if wc < minwcost then
bestr,bestr
0
← r,r
0
minwcost ← wc
end if
end for
end for
cur ← cur −bestr + bestr
0
end while
return cur
end function
in a position that minimizes the cost increase.
The node insertion function is invoked in two
places. On the one hand, it is used in the top-level
TS-LNS() function to construct the initial popula-
tion. In this case, different random solutions are gen-
erated by inserting each time the full set of nodes to
an empty solution, thereby building a solution from
scratch. On the other hand, it is used in the LNS()
function in order to repair a solution, by adding-back
the nodes that have been previously removed from it
in the destruction process.
4.4 Node Removal (Route Destruction)
For the destruction of a given solution, we support
two different node removal methods, which are de-
scribed in Algorithm 4.
The first method, shown in function RMVR(), re-
moves a number of nodes from the given solution in a
random way. Figure 2 gives an example of such ran-
dom node removal, followed by the node insertion.
This method is suitable for the general form of the
problem, where edge costs do not necessarily reflect
the Euclidean distance between the nodes.
The second method, in function RMVP(), removes
nodes in a more targeted way, assuming that the edge
costs reflect the Euclidean distance between nodes.
The rationale is to remove nodes that are in the prox-
imity of so-called seed nodes (the number of seeds
is an additional parameter of this method). The seed
nodes are picked randomly, but the rest of the nodes
to be removed are picked with reference to the seed
nodes. More specifically, for each seed the method
Algorithm 4: Node removal methods.
function RMVR(sol,no f nodes)
cur ← sol
nodes ← pickRandom(N , no f nodes)
f ree ← ∅
for each n ∈ nodes do
r ← routeOf(cur,n)
r ← rmvNode(r,n)
f ree ← f ree + n
end for
return cur, f ree
end function
function RMVP(sol,no f nodes, no f seeds)
cur ← sol
no f nodes
0
← no f nodes/no f seeds
seeds ← pickRandom(N , no f seeds)
f ree ← ∅
for each s ∈ seeds do
repeat no f nodes
0
times
n ← nearestNode(s) incl. s itself
r ← routeOf(cur,n)
r ← rmvNode(r,n)
f ree ← f ree + n
end repeat
end for
return cur, f ree
end function
removes the nodes that are closer to it, based on the
costs of the edges that connect the seed to other nodes.
As a form of balancing, the total number of nodes
to be removed is evenly distributed among the seed
nodes. We refer to this method as the proximity-based
method, as opposed to the fully random node removal
method. Figure 3 gives an example of the proximity-
based node removal, followed by node insertion.
The node removal functions are invoked from the
LNS() function, for a randomly chosen number of
nodes. When using the proximity-based node removal
method, the number of seed nodes is also chosen in
random but from a smaller interval so that the num-
ber of seeds is guaranteed to be smaller than the total
number of nodes to be removed. Note that RMVR()
is always invoked for a number of nodes that is in
the order of |N |, whereas RMVP() is invoked for a
number of nodes in the order of
p
|N |. The rationale
for removing (and then reinserting) fewer nodes when
using the proximity-based method is that since in this
case removal is more targeted, around relatively few
seed nodes, removing a large number of nodes in the
same neighbourhood would lead to an overly aggres-
sive destruction of the current solution, which actually
reduces the chances of finding a better one.
Tournament Selection Algorithm for the Multiple Travelling Salesman Problem
589

Figure 1: Sequence of node insertion for a solution with two routes (from left to right). The algorithm first checks all possible
insertion points in both routes (to avoid clutter, only the best option for each route is shown). The algorithm chooses to insert
the node in the blue route. This is because the orange route has a total cost of 12 which would further increase to 14 if the
node would be added there, whereas by adding the node to the blue route its cost increases to 12, without increasing the cost
of the worst / most expensive route, which remains 12 as before.
Figure 2: Sequence of random destruction with a following repair for a solution with two routes (from left to right). Destruc-
tion is performed by removing a total of six nodes. The nodes are all chosen randomly, and then they are reinserted in the
solution using the node insertion method (insertion details not shown).
Figure 3: Sequence of proximity-based destruction with a following repair for a solution with two routes (from left to right).
Destruction is performed based on two randomly selected seed nodes, which happen to belong to different routes. For each
seed, another two nodes are removed, chosen based on their proximity to the respective seed node. Note that the nodes are
chosen based on their physical proximity to the seed, and may be part of a different route. In total, six nodes are removed, and
are reinserted in the the solution using the node insertion method (insertion details not shown).
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
590

4.5 Complexity
We discuss the complexity of the algorithm in a
bottom-up fashion, starting from the node insertion
and removal functions, then for the large neighbour-
hood search and finally for the entire algorithm. For
convenience, we let N = |N |.
The INSERT() function checks for every node to
be added every possible insertion point in the routes of
the current solution. Given that an exhaustive search
is performed for each node, this procedure has com-
plexity of O(k ×N), where k is the number of nodes
that need to be added.
The random node removal function RMVR() has
O(k) complexity, where k is the number of nodes to
remove. The same holds for the proximity-based re-
moval function RMVP(), where k is the total number
of nodes to be removed (the seeds plus the nodes in
proximity).
In each mutation that is performed within LNS(),
the number k of nodes to be removed from and then
reinserted into the solution is chosen randomly. How-
ever, recall that when using RMVR() then k is in
the order of N, but when using RMVP() then k is
in the order of
√
N (see Algorithm 2). As a conse-
quence, in the first case, the combined complexity of
every mutation is O(N) + O(N ×N) which translates
to O(N
2
), whereas in the second case the complexity
is O(
√
N) +O(N ×
√
N) or equivalently O(N ×
√
N).
Finally, we focus on the top-level TS-LNS()
function (Algorithm 1). Note that the number of
LNS() invocations decrease in each iteration as the
size of the population becomes smaller, but the num-
ber of mutations that are performed in each invocation
of LNS() is also adjusted. Assuming an average of K
total LNS mutations in each top-level iteration, and a
total number of I iterations, the overall complexity of
the algorithm is O(I ×K ×N
2
) when using the ran-
dom node removal method and O(I ×K ×
√
N ×N)
when using the proximity-based method. Note that,
in turn, I depends on the size of the initial population
MaxPopSize, the lower threshold for the population
size MinPopSize and the rate f at which the size of
population is decreased in each iteration.
5 EVALUATION
We compare the proposed TS-LNS algorithm with a
state of the art algorithm, the IWO algorithm pro-
posed in (Venkatesh and Singh, 2015). A recent com-
parison that is presented in (Wang et al., 2017) shows
that IWO is dominant in various benchmark prob-
lems. Next, we describe the experimental setup and
configurations of the two algorithms, and then we dis-
cuss the results obtained through experiments on both
Euclidean and general problems/graphs.
5.1 Setup/Configuration
We implement the IWO algorithm and the TS-LNS
algorithm in Python 3.5.2, and run them on a Ubuntu
16.04 distribution in a VM using Vmware on top of
Windows 10. The machine we use to run the experi-
ments has an Intel i7-8550u CPU at 1.8GHz-4.0GHz
and 8GB of RAM. The CPU has 4 physical cores with
hyperthreading support for a total of 8 threads. The
VM is configured to have 6 virtual cores (mapped to
6 threads) and 4GB of RAM.
We configure the IWO algorithm to perform 100
top-level iterations. Each such iteration leads to 300
node removal/insertion operations, yielding a total of
30000 operations.
The TS-LNS algorithm is configured to run for
MaxPopSize = 100 and MinPopSize = 6. The rate
of population reduction is set to f = 2, so in every it-
eration we keep only half of the population, the fittest
50% of the solutions. In this configuration, TS-LNS
performs four top-level iterations.
Regarding the number of LNS mutations that are
performed on each solution of the current population,
we initially start with 200 LNS mutations, increasing
this number by 200 in each iteration. The rationale is
for the search effort to be smaller when the number of
solutions is large, and increase as the number of so-
lutions gets smaller. More specifically, 200 mutations
are performed for each of the fittest 50 random solu-
tions in the first iteration, 400 LNS mutations are per-
formed for each of the fittest 25 solutions in the sec-
ond iteration, and 600 LNS mutations are performed
for each of the fittest 12 solutions in the third iteration.
For the remaining 6 solutions, as an exception, only
467 LNS mutations are performed in order to have a
total of 30002 node removal/insertion operations, on
par with the IWO algorithm.
We refer to TS-LNS with the random node re-
moval method as TS-LNS-g given that this configu-
ration is more suitable for the general form of mTSP.
In this case, we set α = 0.2 and β = 0.4, so that the
interval that is used to randomly pick the number of
nodes to be removed is [0.2 ∗N..0.4 ∗N]. TS-LNS
with the proximity-based node removal method is re-
ferred to as TS-LNS-e as this is more suitable for the
Euclidean form of mTSP. When using this configura-
tion, we set α = 1.0 and β = 4.0, so the respective
interval is [
√
N..4 ∗
√
N].
Tournament Selection Algorithm for the Multiple Travelling Salesman Problem
591

Table 1: Results of IWO.
Benchmark M Cost Avg Cost StD Exec (s)
eil51
3 159.56 0 16.58
5 118.13 0 18.71
10 112.08 0 22.86
kroB100
3 8503.41 22.73 56.69
5 7008.01 15.06 63.61
10 6700.04 0 75.57
ch150
3 2455.21 20.66 124.20
5 1768.66 8.86 135.26
10 1554.64 0 162.98
lin318
3 17138.27 161.83 593.22
5 12379.09 68.36 651.16
10 9816.99 20.62 751.88
Table 2: Results of TS-LNS-g.
Benchmark M Cost Avg Cost StD Exec (s)
eil51
3 159.56 0 13.39
5 118.13 0 15.03
10 112.08 0 18.13
kroB100
3 8497.79 19.69 43.98
5 6982.58 17.05 48.02
10 6700.04 0 59.40
ch150
3 2446.41 15.03 97.41
5 1764.80 8.68 107.05
10 1554.64 0 128.31
lin318
3 16556.07 109.40 451.50
5 11701.93 53.67 486.72
10 9731.16 0 581.72
5.2 TS-LNS-g vs. IWO for Euclidean
Problems
In a first set of experiments, we compare
TS-LNS-g against IWO. As input graphs, we
use the eil51, kroB100, ch150 and lin318 bench-
marks from the TSPLIB suite (Reinelt, 1991). These
correspond to Euclidean problems for graphs with
51,100, 150 and 318 nodes, respectively. For each
benchmark, we run the algorithms for a team of 3, 5
and 10 salesmen. The results for IWO are given in
Table 1 and for TS-LNS-g in Table 2. We report the
averages over 20 runs.
As fas as the quality of the solutions is concerned,
TS-LNS-g produces the same solutions as IWO for
the small problem with 51 nodes, and equal or better
solutions for the larger problems. More specifically,
the solutions of TS-LNS-g are on average marginally
better, by 0.1% and 0.2%, than those of IWO for
100 and 150 nodes, respectively. For the problem
with 318 nodes, the solution of TS-LNS-g is on av-
erage 3.2% better than IWO. The standard deviation
is small in all cases, with TS-LNS-g having an even
smaller deviation than IWO.
Figure 4: Speed-Up of TS-LNS-g vs. IWO.
We note that both algorithms manage to find the
optimal solution in the problems with 51, 100 and 150
nodes with 10 salesmen. In all these cases, the cost of
the solution is indeed equal to twice the cost of the
edge that connects the depot node and the node that
is farthest away from it (it is impossible for the worst
route to have a lower cost). Moreover, TS-LNS-g also
finds optimal solution for the problem with 318 nodes
and 10 salesmen.
At the same time, TS-LNS-g is considerably faster
than IWO, as shown in Figure 4. The average speed-
up is equal to 1.25x, 1.30x, 1.27x and 1.31x for the
benchmarks with 51, 100, 150 and 318 nodes, respec-
tively, at an overall average of 1.28x. Note that both
algorithms perform the same number of mutations,
with each mutation (node removal and reinsertion op-
eration) having O(N
2
) complexity. However, the mu-
tations of TS-LNS-g involve fewer nodes, on average
0.3 ×N vs. 0.5 ×N in IWO, leading to a smaller total
number of node removal/reinsertions. This reduction
in the search space does not seem to have any impact
on the solution quality of TS-LNS-g.
5.3 TS-LNS-g vs. TS-LNS-e for
Euclidean Problems
In a second series of experiments, we run TS-LNS-e
for the same same set of benchmarks as above. Recall
that TS-LNS-e is designed to work well specifically
for Euclidean problems. Table 3 shows the results.
Again, the averages over 20 runs are reported.
We observe that TS-LNS-e produces the same re-
sults as TS-LNS-g and IWO for the problems with 51
nodes, and finds better solutions for all larger prob-
lems. Namely, for the problems with 100, 150 and
318 nodes, the solutions of TS-LNS-e are on av-
erage 0.1%, 0.7% and 1.5% better than TS-LNS-g,
and roughly 0.3%, 0.9% and 4.6% than the solutions
found by IWO.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
592
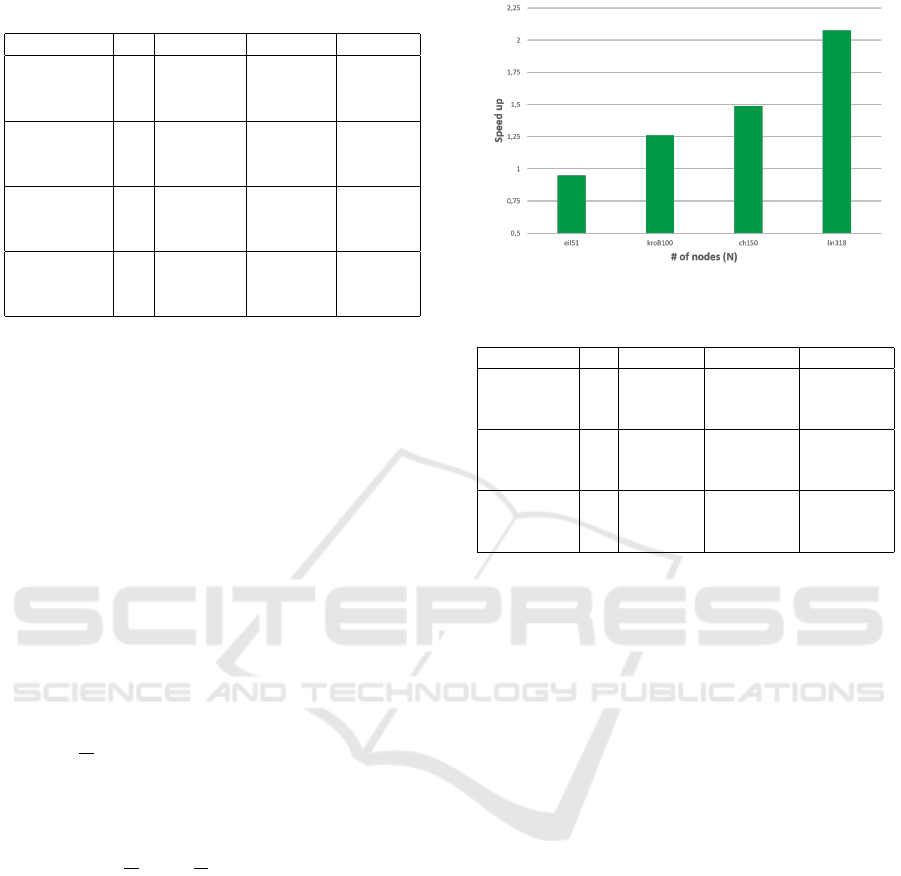
Table 3: Results of TS-LNS-e.
Benchmark M Cost Avg Cost StD Exec (s)
eil51
3 159.56 0 13.98
5 118.13 0 15.87
10 112.08 0 19.41
kroB100
3 8482.50 5.88 34.43
5 6965.85 17.56 38.81
10 6700.04 0 46.98
ch150
3 2416.55 13.47 65.09
5 1747.36 5.66 72.32
10 1554.64 0 86.62
lin318
3 16113.78 46.12 215.62
5 11500.98 43.78 236.42
10 9731.16 0 281.31
The standard deviation of TS-LNS-e is less or
equal to that of TS-LNS-g in most of the problems.
As an exception, for 100 nodes and 5 salesmen the de-
viation of TS-LNS-e is slightly larger than TS-LNS-g
for the same problem, but it is also higher than that
of TS-LNS-e itself for the problem with 100 nodes
and 3 salesmen. This could be an indication that it
might be beneficial to take into account the number
of salesmen when deciding the number of nodes to be
removed/reinserted in each mutation.
Importantly, TS-LNS-e is also much faster than
TS-LNS-g for bigger problem sizes, as shown in Fig-
ure 5. The average speed-up is 1.26x, 1.49x and
2.07x, for the benchmarks with 100, 150 and 318
nodes, respectively. This performance is even more
impressive if compared with IWO, yielding a speed-
up of 1.64x, 1.89x and 2.71x, for these benchmarks.
This significant improvement is due to the lower
O(N ×
√
N) complexity of TS-LNS-e compared to
O(N
2
) for TS-LNS-g and IWO.
Note, however, that TS-LNS-e is somewhat
slower than TS-LNS-g for the smallest problem with
51 nodes. The reason is that, in this particular case,
the interval [
√
N..4 ∗
√
N] used in TS-LNS-e to de-
cide the number of nodes to be removed/reinserted in
each mutation, becomes [7..29] and has a much larger
upper bound than the interval [0.2 ∗N..0.4 ∗N] used
in TS-LNS-g, which is [10..20]. As a result, in each
mutation, TS-LNS-e removes/reinserts on average a
larger number of nodes than TS-LNS-g.
5.4 TS-LNS-g/e vs. IWO for General
Problems
In a last series of experiments, we evaluate the al-
gorithms using as input more general graphs. For
this purpose we use three different benchmarks of the
TSPLIB suite (Reinelt, 1991), kro124p, gr120 and
f tv170 with 100, 120 and 171 nodes, respectively.
Figure 5: Speed-Up of TS-LNS-e vs. TS-LNS-g.
Table 4: Solution cost of the algorithms for general graphs.
Benchmark M IWO TS-LNS-g TS-LNS-e
kro124p
3 13470.05 13539.90 13313.2
5 9137.3 9157.15 8990.55
10 6419.4 6343.45 6322.45
gr120
3 2614.15 2604.95 2580.50
5 1834.25 1823.0 1812.30
10 1558.0 1554.40 1555.35
f tv170
3 1026.75 1026.1 986.65
5 688.85 673.63 654.15
10 447.70 432.37 427.53
In all cases, the edge costs are non-Euclidean. In
gr120 the edge/travel costs are symmetrical, whereas
in kro124p and f tv170 they are asymmetrical. In or-
der for TS-LNS-e to work on graphs with asymmetri-
cal costs, the nodes to be removed around a seed are
chosen based on the two-way trip cost between them.
Table 4 reports the cost of the solutions that are
generated by each algorithm, averaged over 20 runs.
As in the previous experiments, the standard deviation
is small. Also, the previous observations regarding
the execution speed of the algorithm still hold. This
information is not reported here, for brevity.
It can be seen that both TS-LNS variants once
again produce solutions that are close and most of
the times even better than those of IWO, yielding an
improvement of up to 3.4% for TS-LNS-g or even
5.0% for TS-LNS-e. In fact, TS-LNS-e always gen-
erates better solutions than IWO. We attribute this
(somewhat surprisingly) good performance to the fact
that these general benchmark graphs are non-random
and specifically in the case of gr120 and ftv170 they
are based on real-world routes and travel costs. So,
even though the costs are not a direct function of the
straight-line Euclidean distances, the most significant
costs can still have a strong affinity to them.
Tournament Selection Algorithm for the Multiple Travelling Salesman Problem
593

6 CONCLUSION
We propose TS-LNS, a hybrid heuristic that combines
the capabilities of large neighbourhood search with
the filtering principle of tournament selection. The
results of the proposed algorithm on various bench-
mark problems is promising, showing that it achieves
good results with a lower overhead than IWO, which
is already considered to be a good algorithm for the
mTSP. Furthermore, the TS-LNS version that specifi-
cally targets the Euclidean problem, produces slightly
better results while reducing the execution time very
significantly for larger problem sizes.
As part of future work, we wish to test the algo-
rithm with more sophisticated removal/insertion func-
tions, using a more educated selection of the nodes to
be removed. We also plan to extend the algorithm in
order to tackle more complex problem versions, for
topologies with multiple depot nodes and for scenar-
ios where the salesmen have capacity limitations that
reduce their operational autonomy.
ACKNOWLEDGEMENTS
This research has been co-financed by the Euro-
pean Union and Greek national funds through the
Operational Program Competitiveness, Entrepreneur-
ship and Innovation, under the call RESEARCH -
CREATE - INNOVATE, project PV-Auto-Scout, code
T1EDK-02435.
REFERENCES
Anbuudayasankar, S., Ganesh, K., and Mohapatra, S.
(2014). Survey of methodologies for tsp and vrp. In
Models for Practical Routing Problems in Logistics,
pages 11–42. Springer.
Bertazzi, L., Golden, B., and Wang, X. (2015). Min–
max vs. min–sum vehicle routing: A worst-case anal-
ysis. European Journal of Operational Research,
240(2):372–381.
Brown, E. C., Ragsdale, C. T., and Carter, A. E. (2007). A
grouping genetic algorithm for the multiple traveling
salesperson problem. International Journal of Infor-
mation Technology & Decision Making, 6(02):333–
347.
Carter, A. E. and Ragsdale, C. T. (2006). A new approach
to solving the multiple traveling salesperson problem
using genetic algorithms. European journal of opera-
tional research, 175(1):246–257.
Davendra, D. (2010). Traveling Salesman Problem: Theory
and Applications. BoD–Books on Demand.
Falkenauer, E. (1992). The grouping genetic algorithms-
widening the scope of the gas. Belgian Journal of Op-
erations Research, Statistics and Computer Science,
33(1):2.
Franc¸a, P. M., Gendreau, M., Laporte, G., and M
¨
uller, F. M.
(1995). The m-traveling salesman problem with min-
max objective. Transportation Science, 29(3):267–
275.
Golden, B. L., Laporte, G., and Taillard,
´
E. D. (1997). An
adaptive memory heuristic for a class of vehicle rout-
ing problems with minmax objective. Computers &
Operations Research, 24(5):445–452.
Gutin, G. and Punnen, A. P. (2006). The traveling sales-
man problem and its variations, volume 12. Springer
Science & Business Media.
Liu, W., Li, S., Zhao, F., and Zheng, A. (2009). An ant
colony optimization algorithm for the multiple trav-
eling salesmen problem. In 2009 4th IEEE confer-
ence on industrial electronics and applications, pages
1533–1537. IEEE.
Lupoaie, V.-I., Chili, I.-A., Breaban, M. E., and Raschip, M.
(2019). Som-guided evolutionary search for solving
minmax multiple-tsp. In 2019 IEEE Congress on Evo-
lutionary Computation (CEC), pages 73–80. IEEE.
Reinelt, G. (1991). Tsplib—a traveling salesman problem
library. ORSA journal on computing, 3(4):376–384.
Shaw, P. (1998). Using constraint programming and local
search methods to solve vehicle routing problems. In
International conference on principles and practice of
constraint programming, pages 417–431. Springer.
Singh, A. and Baghel, A. S. (2009). A new grouping genetic
algorithm approach to the multiple traveling salesper-
son problem. Soft Computing, 13(1):95–101.
Somhom, S., Modares, A., and Enkawa, T. (1999).
Competition-based neural network for the multiple
travelling salesmen problem with minmax objective.
Computers & Operations Research, 26(4):395–407.
Soylu, B. (2015). A general variable neighborhood search
heuristic for multiple traveling salesmen problem.
Computers & Industrial Engineering, 90:390–401.
Vallivaara, I. (2008). A team ant colony optimization al-
gorithm for the multiple travelling salesmen prob-
lem with minmax objective. In Proceedings of the
27th IASTED International Conference on Modelling,
Identification and Control, pages 387–392. ACTA
Press.
Vandermeulen, I., Groß, R., and Kolling, A. (2019). Bal-
anced task allocation by partitioning the multiple trav-
eling salesperson problem. In Proceedings of the 18th
International Conference on Autonomous Agents and
MultiAgent Systems, pages 1479–1487. International
Foundation for Autonomous Agents and Multiagent
Systems.
Venkatesh, P. and Singh, A. (2015). Two metaheuristic ap-
proaches for the multiple traveling salesperson prob-
lem. Applied Soft Computing, 26:74–89.
Wang, Y., Chen, Y., and Lin, Y. (2017). Memetic algorithm
based on sequential variable neighborhood descent
for the minmax multiple traveling salesman problem.
Computers & Industrial Engineering, 106:105–122.
Yuan, S., Skinner, B., Huang, S., and Liu, D. (2013). A new
crossover approach for solving the multiple travelling
salesmen problem using genetic algorithms. European
Journal of Operational Research, 228(1):72–82.
VEHITS 2020 - 6th International Conference on Vehicle Technology and Intelligent Transport Systems
594
