
Combining Semi-formal and Formal Methods for Safety Control in
Autonomous Mobility-on-Demand Systems
Mohamed Naija, Rihab Khemiri and Ernesto Exposito
Univ. Pau & Pays Adour, E2S UPPA, LIUPPA, Anglet, France
Keywords: AMoD, Adaptability, Safety, Net Condition/Event Systems (NCESs), Simulation.
Abstract: Ensuring the safety control of Autonomous Mobility-on-Demand systems is one of the biggest challenges
facing designers to successful deployment. The addition of adaptability to such systems further hardens and
delays modelling and validating phase, especially due to the current lack of design models and tools. The
formal methods have proven to be useful for making the development process reliable at early design stages.
Based on this approach, this paper proposes a mixed process to specify, design and verify safety requirements
in adaptive AMoD Systems. This process provides analytical proofs of safety requirements during the design
stage of a system when changes are cheap. This contribution deals with combining the UML MARTE profile
for modelling the workload behaviour of the system and the formalism Net Condition Event System for
consistency validation of safety properties. To verify the effectiveness of our proposal, several formal analyses
are carried out using the model checker SESA. The evaluation of the proposed architecture, simulated by the
Sumo software, proves the impact of the number of autonomous vehicles on the global performance and the
intended quality of service (QoS) in the framework of the TORNADO project.
1 INTRODUCTION
Autonomous Mobility-on-Demand (AMoD) appears
as a complementary solution to intelligent transport
system. Specifically, an AMoD system is a fleet of
driverless cars that can be accessed at specific
locations in a city providing public transport. Such
systems are considered as high-assurance systems
since run-time errors could result in fatal accidents
(Chao et al., 2019). Consequently, a stronger form of
verification is likely to be needed to ensure the
correctness of the system and provide sufficient
evidence for safety certification.
In AMoD systems, each autonomous vehicle
(AV) clearly needs to communicate with the fleet
operator in order to control and manage change in
their operating environment (i.e., location change,
new trip request, and undesirable event). This global
control requires reliable V-2-I (Vehicle-to-
Infrastructure) communication. When
communication faults occur, the autonomous vehicle
must be able to operate without the fleet's instructions
while remaining secure and controllable. This
property called adaptability allows the vehicle to
continue its intended mission, possibly at a reduced
level, rather than failing completely. When adapting
to new operational mode, the autonomous vehicle
may have to switch from a source mode to a target
mode and modify the software configuration
according to predefined rules and conditions. Hence,
the specification of the dynamic behaviour by
enumerating all the system's operational modes
constitutes a first step in the definition of a structure
able to fulfil the requirements of the system.
After building a Workload model, it is necessary
to verify and validate the safety requirements (i.e.
efficiency, reliability, robustness, stability, and
vivacity) of the adaptive AMoD system before its
implementation. Thus, an analysis carried out earlier
makes it possible to ensure that the system functions
in a safe state during and after adaptation. In such
systems, we need an approach that provides analytical
proofs of safety, rather than checking traffic
situations using simulation (Schwarting, 2018).
To address this need, it is recommended to use
model checking formalism to automatically
analyzing models for compliance to formal
proprieties (Zhang et al., 2009)(Li et al., 2013).
Formal safety proofs can be obtained using a variety
of methods. In particular, the Net Condition Event
System (NCES) (Rausch and Hanisch, 1995) offers a
promising solution for this kind of analysis, its
514
Naija, M., Khemiri, R. and Exposito, E.
Combining Semi-formal and Formal Methods for Safety Control in Autonomous Mobility-on-Demand Systems.
DOI: 10.5220/0009570005140521
In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2020), pages 514-521
ISBN: 978-989-758-421-3
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

hierarchical composition allows a considerable
reduction of the size and complexity of the nets
(Zhang et al., 2009)(Li et al., 2013). In addition, it
provides one useful and robust model checker called
SESA (Vyatkin, 2007) that allows performing
analysis of typical properties and computing sets of
reachable states exactly and effectively.
In this paper, we present a novel approach to
safety control in AMoD that relies on combining
semi-formal and formal method in order to modeling
and providing formal guarantees that runtime physics
matches the model of the system. We focus on
analyzing all possible modes and configurations of
the system by (i) representing modes, (ii) specifying
adaptation conditions and (iii) verifying which of the
architecture characteristics are valid or not in a given
mode. Our contribution adopts model-driven
engineering and model checking for modeling and
verifying safety properties at early design stages to
achieve design-time assurance guarantees. Indeed,
the workload behavior of the AMoD system that is in
response to external stimuli is annotated with
MARTE (OMG, 2008) profile stereotypes. This input
model is then mapped into NCES formalism to
generate a well-formed analyzable model. Finally, we
call the model checker SESA to check functional
properties and verify safety requirements. Since
unpredictability of the dynamic environment delay
the complete understanding of the system at design
time and is resolved only when the system will face
to concrete and specific pre-defined configurations,
we extend the process of safety verification to
runtime phase using well-defined simulations tests.
The outline of this paper is as follows. First, we
provide an overview of the formalisms NCES and
CTL in section 2. Next, section 3 outlines the
proposed methodology as well as the formal
verification results. In section 4, we present
experimental validation. In section 5 state of the art
is discussed. Finally, section 6 concludes the paper.
2 BACKGROUND
We present in this section enough information about
NCES formalism that will be useful for presenting the
paper’s contribution.
2.1 Definition
The Net Condition/Event Systems (NCES) is a
special extended class of Petri net. It consist of
modules whose dynamic behaviour is modelled by
means of Petri nets. According to definition reported
in (Rausch and Hanisch, 1995), NCES is described by
the following tuple:
NCES = {P, T, F, M
O
, , CN, EN}
(1)
where:
P : is an ordered set of n places p;
T : is an ordered set of m transitions t;
F : is the incidence matrix;
M
O
: is the initial marking;
: is the input/output structure;
CN ⊆ (P × T) is a set of condition signals;
EN:⊆(T×T) is a set of event signals.
The semantics of NCES are defined by the firing rules
of transitions (Vyatkin, 2007). A transition t has three
degrees of enabling (Li et al., 2013). First, as it is in
ordinary Petri nets, a transition t
i
ϵ T is marking
enabled if min (M - Fm(., i))> 0. That means that all
pre-places have to be marked with at least one token
before firing. Furthermore, a transition t
i
ϵ T may
have incoming condition arcs from places and event
arcs from other transitions. A transition t
i
ϵ T is a
condition enabled if min (M - CN(.,j))> 0. The third
possibility on the firing can be described by event
signals EN which allows connecting two or more
transitions. A transition is said to be event enabled if
max (EN (.,i)) = 0. Transitions are spontaneous if
there are no incoming event arcs to the transition,
otherwise they are considered as forced. A transition
can fire spontaneously if it is marking enabled and
condition enabled and if max (E
N
(t
i
)) = 0. A forced
transition is enabled if it has token concession and it
is enabled by condition and event signals.
2.2 Computational Tree Logic
The Computational tree logic (CTL) and its
extensions extended CTL (eCTL) or Timed CTL
(TCTL) are well used for the definition of non-
functional properties of complex systems that must be
checked. In this paper, CTL and eCTL are used to
describe the safety properties of an AMoD system,
and TCTL is used to specify temporal constraints.
The CTL queries are formed of pairs of path
quantifiers A (Always) or E (Exists) and a path
operators G (Globally) or F (Finally) and are denoted
by the satisfaction relation |=. For example, the query
EF p (respectively AF p) means that there exists at
least one state satisfying the property p on at least one
path (respectively on all paths) starting from the
initial state (Arcile et al., 2019). In TCTL clock
constraints allows specifying of the delay time that
must elapse before certain transitions can be enabled
to fir.
Combining Semi-formal and Formal Methods for Safety Control in Autonomous Mobility-on-Demand Systems
515

3 METHODOLOGY
The proposed methodology addresses the safety
control at the early design stage of adaptive AMoD
systems. The methodology defines a flow depicted on
Figure 1: (i) the first activity consists in building the
workload model able to fulfil requirements of the
system. This high-level model specifies end-to-end
scenarios of the system annotated with MARTE
profile, (ii) this model is then mapped into NCES
formalism in order to generate a well-formed
analyzable model and finally, (iii) the safety analysis
results of the evaluated model is given as an artefact.
Figure 1: Proposed Methodology flow.
The main idea of starting from a MARTE model to
ensure safety analysis assumes that all the required
information for verification of adaptive behaviour is
already part of the MARTE model (Naija el al.,
2015). The MARTE model allows modelling of inter-
behaviour information (e.g. events, tasks, shared
resources, execution time, etc.) and intra-behaviour
information (e.g. transitional modes and adaptation
condition). In the followings subsections, we present
more details of the intermediate models generated by
our methodology.
3.1 Workload Model
In high-level design, software components are used to
manage complexity. This functional model is in
providing whole system functions, which are sharply
enlarging (
Niang et al., 2017).
Once the gathering of components structure is
realized, it is necessary to build the workload
behaviour of the system. The latter describes end-to-
end flow of the executed actions during a certain
system mode (Naija el al., 2015). When the system is
in a given mode, it provides a subset of system
features (Naija el al., 2016) (Mansour el al., 2019). In
this work, we study the behaviour of autonomous
vehicle in normal mode (NM) and degraded mode
(DM) as shown in Figure 2.
Figure 2: Workload Behavior of the AMoD system.
The end-to-end scenarios, stereotyped
«saEndtoEndFlow», are activated by external event.
However, the event Localization_act actives the GPS
component every 30 milliseconds and is annotated
with MARTE «GaWorkloadEvent» stereotype. The
property «arrivalPattern» allows defining its period.
In both modes, multiple operations must be
performed to achieve system computations. Each
operation is extended with «saStep» stereotype and
has an execution time (execTime property). In NM,
the step positioning_act sends the current position of
the vehicle to the fleet manager. The latter sends the
guidance instructions to the vehicle through the
input_acquisition activity. After that, the vehicle
plans the necessary maneuvers
(navigation_planning) to complete its mission by
sending instructions to be executed to the control
system via the compute_dir step. In DM, the
autonomous vehicle plans the maneuvers
(motion_planning) without waiting for the fleet
ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering
516
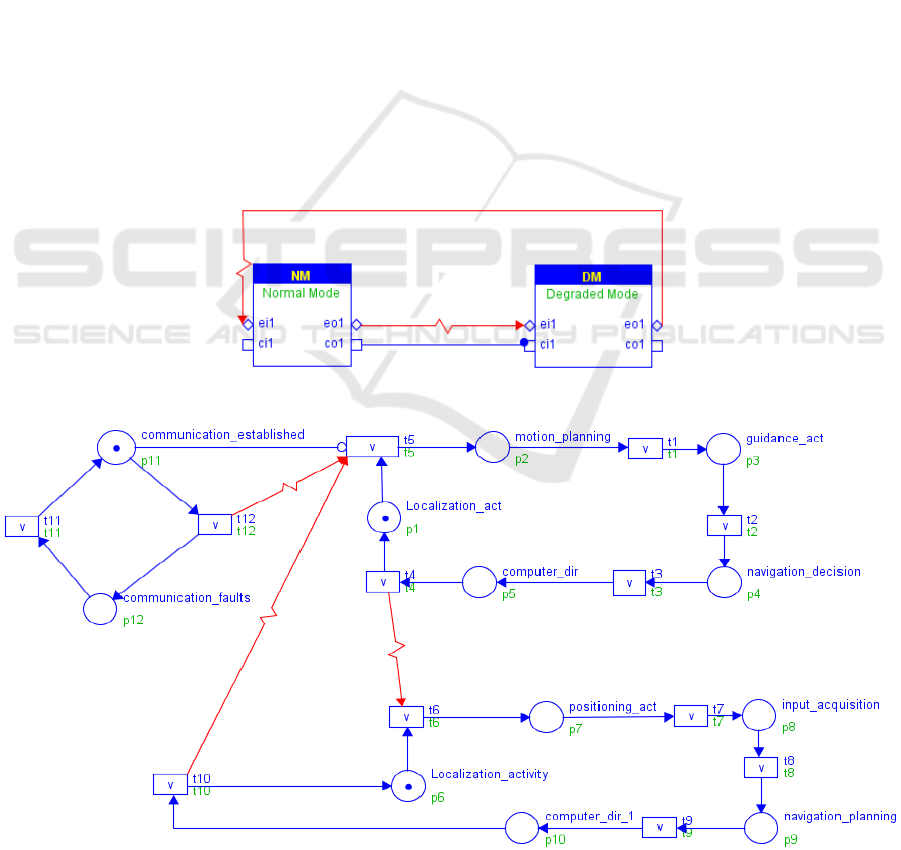
manager. The steering commands are calculated from
the speed of the vehicle (guidance_act) and sent to
the control system (compute_dir). The behaviour of
each mode should not include information about each
other. The switching mode is specified with an
Exception Handlers from the interruptible activity
(input_acquisition) to the destination process.
3.2 Mapping Workload Behaviour to
NCES
At this level, a preliminary transformation of the
workload model to NCES formalism is required to
enhance formal analysis. In this paper, the mapping
of end-to-end flow into formal models is inspired
from previously published works (Kacem et al., 2012)
(Yang et al., 2010). Therefore, each end-to-end
scenario is represented with an oriented graph of
places and transitions. After mapping each scenario
to an NCES component (Figure 3), it is necessary to
specify the intra-behaviour of each component and
adaptation rules.
These are conditions that should be respected
before and after adaptation scenario. In this work, each
condition C is modelled in the normal form C and
negative form ¬C and should be linked to the source
and/or target configuration to fulfil adaptation
requirements. Thus, we model the adaptation
condition of the AMoD system in its normal form
(communication_established) and in its negative form
(communication_faults). In addition, we transform the
exception handlers of the activity diagram to an event
signal to specify transitional modes.
The use of event signal arcs makes it possible to
model the possible links between the configurations.
In our case, initially the vehicle is in the normal mode.
It can switch as soon as it detects a communication
problem to the degraded mode (DM). Likewise, if the
vehicle turn in a degraded mode, it can return to the
normal mode if communication with the fleet
management station is re-established. The complete
transformation is illustrated in Figure 4.
3.3 Safety Analysis
Once the mapping process is realized, the final stage
consists of analyzing the NCES model in order to
verify
and validate safety properties of finite-state
Figure 3: NCES Components Model of the AMoD System with switching modes.
Figure 4: Dynamic Behaviour of the NCES Based-Components Model.
Combining Semi-formal and Formal Methods for Safety Control in Autonomous Mobility-on-Demand Systems
517

systems. As already mentioned, the advantage with
NCES-based models is that offers an effective
solution based on their reachability graph to reduce the
verification cost. The safety of an AMoD system
requires the correctness of each configuration and of
the reconfiguration scenarios. The verification process
is to check the reconfiguration scenarios (inter-
verification) and the internal behaviour of each
configuration (intra-verification). As part of
verification, we start by checking the vivacity of the
net, dead transitions or states and boundedness in
order to prove correctness, stability, and consistency
of the AMoD system. If these behavioural properties
are well verified, other safety requirements are
specified by the computation tree logic (CTL) as well
as its extensions (eCTL and TCTL) and are verified
using the model-checker SESA.
In the next paragraphs, three examples illustrate
the checking properties using CTL formulas will be
presented. The three important checked properties are
(1) verify when an adaptation signal is received, the
system can respond and select a proper configuration
(2) verify that all modes are achievable and no
deadlock will occur and (3) verify that after
adaptation scenario timing constraint are respected.
Example 1: The following CTL formula is proposed
to control adaptation scenario in Figure 4:
z
0
|= AGA t
12
XAFE t
1
X p
3
(2)
This formula is checked true by SESA. Firing t
12
means that if an adaptation signal is received at run-
time, the Degraded Mode must be executed.
Example 2: The eCTL formula below is applied to
control behaviour of the AMoD system:
z
0
|= AGA t
4
XAFE t
5
AND t
6
X TRUE (3)
This formula is proven false. When t
4
fires, either
t
5
or t6 will eventually fire. The system cannot be in
Normal Mode and Degraded Mode at the same time.
Example 3: The TCTL formula below is applied to
check timing constraint before switching between
modes behaviour:
z
0
|= EF [19, 25] p
8
= 1 (4)
This formula has been proven true by SESA. The
communication faults can be detected before or after
running the input_acquisition step. Thus, the
Degraded Mode can be activated (i.e, M (p
2
) = 1) in at
least 19 time units after the system starts.
The evaluation of the AMoD system requirements
is provided as an output of our methodology in the
form of a Safety Analysis Results. This artefact
provides a guideline for designer to detect errors in
adaptive logic before implementation and
deployment. The safety concept presented in this
paper consists in verifying if the controlled system
can be or not exposed to dangerous states leading to
human and equipment damage (
Jharko, 2019).
4 EXPERIMENTAL VALIDATION
In this section, we fulfil the goal of extending safety
verification to the level of simulation to provide
evidence that the system goals are satisfied during
operation (Makartetskiy, 2019). We are interested in
exploring the impact of the adaptability on the
Quality of Service (QoS) with a large number of
vehicles.
4.1 Experimental Design
We use the SUMO (Behrischet al., 2011) simulator to
validate the adaptive behaviour of the AMoD. It is an
open-source simulator including a realistic simulation
of road dynamics. The simulator is able to represent
unlimited network size and vehicles number with
different configurations.
In this study, we focus on the transportation
network of Paris city with an exact customer request.
This scenario is representative of the challenges
targeted by our research project (Tornado, 2020). For
each depart time, autonomous vehicles become
available for servicing passengers. The vehicle drives
a distance of 5181 meters from pickup to drop-off for
one trip. We assumed that each vehicle can transport
up to four passengers at the same time. The vehicles
are identical in the fleet and are modelled with
realistic physics properties. The vehicle's speed and
safety distance varies according to the operating
mode and configurations. In order to demonstrate the
advantage of our proposal, we have performed several
simulations for both normal and degraded mode. First,
we have followed realistic scenarios to estimate the
trip time with different fleet size. Second, we have
interested in calculating the number of messages
exchanged between the fleet manager and vehicles for
each trip.
4.2 Results
The obtained results are interesting and subject of
several interpretations.
In normal mode, the communication quality
between the fleet management and vehicles is stable
and no disturbances occur. The safety distance (inter-
vehicle distance) is predefined to 10 m and the average
ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering
518
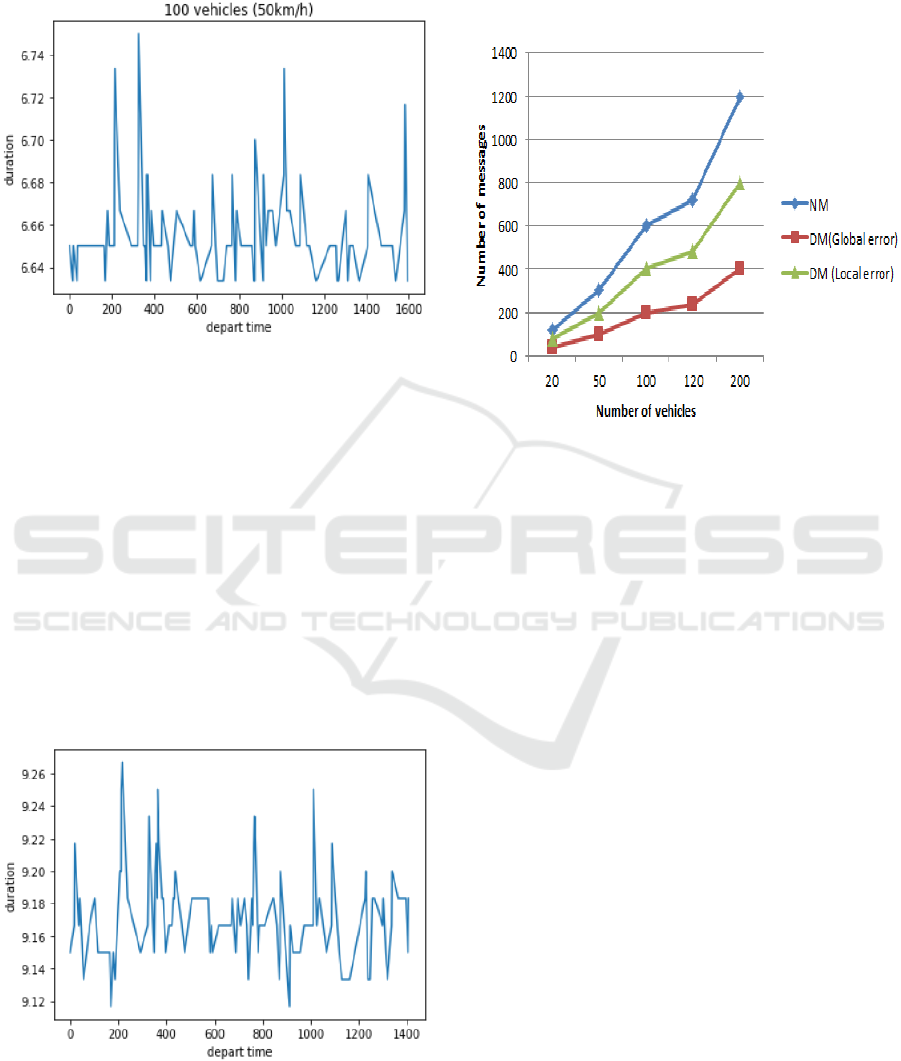
speed is up to 50Km/h for the entire trip (5181 m). The
simulations are shown that the average trip time is
equal to 6.66 minutes (Figure 5).
Figure 5: Estimated trip time in normal mode with 100
Vehicles in a straight two-lanes road.
In the degraded mode, the behaviour of the vehicles
can be affected regarding communication degradation.
We simulate this malfunction using the Bernoulli
distribution (Marshal and Olkin, 1985). Since we
study the worst case, we apply a strong probability of
packet loss equal to 50% (implying only 50% of
vehicles can communicate correctly with the fleet
operator) and all the vehicles are switching from the
normal mode to degraded mode at the same time.
When vehicle changes to DM, the speed has to be
reduced to 30Km/h and the safety distance is
predefined to 8m. The simulation are shown that the
average trip time is equal to 9.17 minutes. These
metrics are plotted for 100 vehicles in Figure 6.
Figure 6: Estimated trip time in degraded mode with 100
Vehicles in a straight two-lanes road.
We have also conducted other simulation tests to
quantify the number of messages exchanged between
the fleet manager and the vehicles for each trip
(Figure 7). The simulations are assessed for both
normal and degraded modes.
Figure 7: Tracking results of exchanging data between
vehicles and fleet. The Tracking curve is color-coded blue
for NM, red for DM with a global error and green for DM
with a local error.
In normal mode, each vehicle exchanges 6 messages
with the fleet during one trip. This exchange starts
from the parking lot, where the autonomous vehicle
is parked waiting for its next mission, to the drop-off.
The simulations are carried out with different number
of vehicles (20, 50, 100, 120, and 200 vehicles) in
order to have relevant results.
In the degraded mode, we studied the worst case
for both local and global communications failure. In
local error, communication with the fleet is possible
for some autonomous vehicles but not for others. This
failure is due to the hardware crash or the entry of
some vehicles in a non-covered network area. We
conducted these simulations with the probability of
only 50% of the vehicles that can communicate with
the fleet, which is considered as a worst-case in the
Tornado mobility project, that we are working on. In
global error, the fleet manager is out of order and no
AV can send/receive notifications and alerts with the
control center after receiving his mission.
From these results, we conclude that ideally the
trip between the pickup to drop-off takes 6.66 minutes.
If a disturbance problem has occurred, the estimated
trip time can reach up to 9.17 minutes for 50% of the
passengers in the worst case. This is tolerable in our
project where the safety of passengers comes first.
Compared to classical AMoD approaches, only 50%
Combining Semi-formal and Formal Methods for Safety Control in Autonomous Mobility-on-Demand Systems
519

of passengers will reach their destination and 50% of
passengers will be blocked or in danger. Thereby, the
adaptive architecture allows the vehicle to continue its
intended mission, when abrupt threats appear, at a
reduced level of QoS, rather than failing completely.
This contribution facilitates complex autonomous
vehicles modelling and checking, reduces the
development time, cost, and improves software
process quality.
5 STATE OF THE ART
In the past decades, the robotics community has
extensively studied verification of safety requirements
in intelligent transport. We will discuss in the
following the methodologies that particularly use
formal verification.
In (Althoff and Dolan, 2014) the authors propose
an online verification approach using reachability
analysis in order to capture all future possible
scenarios. Safety is guaranteed with respect to the
modelled uncertainties and behaviours if the
occupancy of the autonomous vehicle does not
intersect that of other traffic participants for all times.
To allow a faster verification in an emergency
situation, specific maneuvers can be stored in a
database. Nevertheless, online verification cannot
predict safety for infinitely many states such as offline
verification (Bohrer, 2019).
Instead of safety online verification, (Liebenwein
et al., 2017) propose an alternative framework based
on building a library of local and verified road models
that are composed together to certify safety for entire
road networks. Since the number of configurations can
be very large, this combinatorial explosion makes the
autonomous behaviour difficult to analyze or
inapplicable.
In (Iftikhar and Weyns, 2014), the authors propose
a formal approach for self-adaptation in robotic
transport systems. The system is presented as a
collection of Timed Automaton (TA) models, which
are executed by a virtual machine to realize
adaptation. The model checking verification assures
that the adaptation goals that are verified offline are
guaranteed at runtime. Unfortunately, safety
verification is not considered.
In (Arcile et al., 2019) a framework called
VerifiCar is detailed. It is designed to allow modelling
and checking of safety properties in communicating
autonomous vehicles (CAVs) against their decision
policy using UPPALL model checker. Although, the
uses of UPPAAL based-model in this work limit the
exposition of the state space, but is not always suitable
for complex situations and can carry to inaccurate
checking.
Other efforts have been specifically tailored to
platoon system (enabling vehicles to travel as a group
on the roads), in which vehicle-to-vehicle
communication is permitted.
In (Kamali et al., 2017), a mixed strategy is
devoted to ensure that the autonomous behaviour
never violates the safety requirements but only for
one-mode system.
In (Karoui et al., 2017) authors adopt a switching
approach between two platoon modes to solve
disturbance problems. This closest work allows
reconfiguration to manage communication quality
degradation with clear safety assumptions. Although
this contribution supports safety inter-behaviour
verification, stronger intra-behaviour verification is
mandatory in order to check the entire system before
and after adaptation.
6 CONCLUSION
Automotive systems are playing an increasingly
crucial role in smart cities while becoming more
complex and dangerous. This highlights the need for
considering the safety of such systems as a core
requirement in the design stage. In this paper, a new
methodology for safety control in AMoD system is
proposed. We use the UML MARTE profile for
modelling all configuration of the system as an end-
end flow. This high-level requirement model is then
mapped into NCES formalism, which allows an
efficient checking of safety properties, expressed in
CTL formulas. The main advantage of this
contribution is the ability to verify entire system
behaviour at early design stages.
As a main line of future work, we will investigate
in proposing an agent-based architecture to better
control V-2-I communication and manage the system
reconfiguration according to the fleet operator
requirements. Another open line is to automate as
much as possible the generation of a formal model
from a semi-formal model, which extends this
methodology to become a perfect framework for
safety modelling and checking.
ACKNOWLEDGEMENTS
This work is financed by national funds FUI 23 under
the French TORNADO project focused on the
interactions between autonomous vehicles and
infrastructures for mobility services in low-density
ENASE 2020 - 15th International Conference on Evaluation of Novel Approaches to Software Engineering
520

areas. Further details of the project are available at
https://www.tornado-mobility.com/.
REFERENCES
Althoff, M., & Dolan, J. M., 2014. Online verification of
automated road vehicles using reachability analysis.
IEEE Transactions on Robotics, 30(4), 903-918.
Arcile, J., Devillers, R., & Klaudel, H., 2019. VerifCar: a
framework for modeling and model checking
communicating autonomous vehicles. Autonomous
agents and multi-agent systems, 33(3), 353-381.
Behrisch, M., Bieker, L., Erdmann, J., & Krajzewicz, D. ,
2011. SUMO–simulation of urban mobility: an
overview. In Proceedings of SIMUL 2011, The Third
International Conference on Advances in System
Simulation. ThinkMind.
Ben Mansour, A., Naija, M., & Ben Ahmed, S., 2019. A
MARTE-Based Design Pattern for Adaptive Real-Time
Embedded Systems. In Proceedings of the 14th
International Conference on Evaluation of Novel
Approaches to Software Engineering (pp. 242-248).
SCITEPRESS-Science and Technology Publications,
Lda.
Bohrer, B., Tan, Y. K., Mitsch, S., Sogokon, A., & Platzer,
A., 2019. A Formal Safety Net for Waypoint-Following
in Ground Robots. IEEE Robotics and Automation
Letters, 4(3), 2910-2917.
Chao, Q., Jin, X., Huang, H. W., Foong, S., Yu, L. F., &
Yeung, S. K., 2019. Force-based heterogeneous traffic
simulation for autonomous vehicle testing. In 2019
International Conference on Robotics and Automation
(ICRA). pp. 8298-8304. IEEE.
Iftikhar, M. U., & Weyns, D., 2014. Activforms: Active
formal models for self-adaptation. In Proceedings of the
9th International Symposium on Software Engineering
for Adaptive and Self-Managing Systems (pp. 125-134).
Jharko E. (2019). Formalizing the Safety Functions to
Assure the Software Quality of NPP Safety Important
Systems.In Proceedings of the 16th International
Conference on Informatics in Control, Automation and
Robotics - Volume 2: ICINCO, ISBN 978-989-758-380-
3, pages 637-644. DOI: 10.5220/ 0007922506370644
Kacem, Y. H., Mahfoudhi, A., Magdich, A., Mraidha, C., &
Karamti, W., 2012. Using mde and priority time petri
nets for the schedulability analysis of embedded systems
modeled by uml activity diagrams. In 19
th
International
Conference and Workshops on Engineering of
Computer-Based Systems (pp. 316-323). IEEE.
Kamali, M., Dennis, L. A., McAree, O., Fisher, M., & Veres,
S. M., 2017. Formal verification of autonomous vehicle
platooning. Science of computer programming, 148, 88-
106.
Karoui, O., Khalgui, M., Koubâa, A., Guerfala, E., Li, Z., &
Tovar, E., 2017. Dual mode for vehicular platoon safety:
Simulation and formal verification. Information
Sciences, 402, 216-232.
Liebenwein, L., Schwarting, W., Vasile, C. I., DeCastro, J.,
Alonso-Mora, J., Karaman, S., & Rus, D., 2020.
Compositional and contract-based verification for
autonomous driving on road networks. In Robotics
Research (pp. 163-181). Springer, Cham.
Makartetskiy, D., Marchetto, G., Sisto, R., Valenza, et al.
2019. (User-friendly) formal requirements verification
in the context of ISO26262. Engineering Science and
Technology, an International Journal.
Marshall, A. W., & Olkin, I., 1985. A family of bivariate
distributions generated by the bivariate Bernoulli
distribution. Journal of the American Statistical
Association, 80(390), 332-338.
Naija, M., & Ahmed, S. B., 2016. A New MARTE
Extension to Address Adaptation Mechanisms in
Scheduling View. In International Conference on
Evaluation of Novel Approaches to Software
Engineering (pp. 27-43). Springer, Cham.
Naija, M., Ahmed, S. B., & Bruel, J. M., 2015. New
schedulability analysis for real-time systems based on
MDE and petri nets model at early design stages. In 2015
10th International Joint Conference on Software
Technologies (ICSOFT) (Vol. 1, pp. 1-9). IEEE.
Niang M., Philippot A., Gellot F., Coupat R., Riera B. and
Lefebvre S. (2017). Formal Verification for Validation
of PSEEL’s PLC Program.In Proceedings of the 14th
International Conference on Informatics in Control,
Automation and Robotics - Volume 1: ICINCO, ISBN
978-989-758-304-9, pages 567-574. DOI: 10.5220/
0006418705670574.
OMG Object Management Group, 2008. A UML Profile for
MARTE: Modeling and Analysis of Real-Time
Embedded systems, Beta 2.
Rausch, M., & Hanisch, H. M., 1995. Net condition/event
systems with multiple condition outputs. In Proceedings
1995 INRIA/IEEE Symposium on Emerging
Technologies and Factory Automation. ETFA'95 (Vol.
1, pp. 592-600). IEEE.
Schwarting, W., Alonso-Mora, J., & Rus, D., 2018. Planning
and decision-making for autonomous vehicles. Annual
Review of Control, Robotics, and Autonomous Systems.
Tornado Mobility FUI Project. [online]. [Accessed
10/01/2020]. Available from: https://www.tornado-
mobility.com/
Vyatkin. V., 2007. “Modeling and verification of discrete
control systems”.
Yang, N., Yu, H., Sun, H., & Qian, Z., 2010. Mapping uml
activity diagrams to analyzable petri net models. In 10th
International Conference on Quality Software (pp. 369-
372). IEEE.
Zhang, J., Goldsby, H. J., & Cheng, B. H., 2009. Modular
verification of dynamically adaptive systems. In
Proceedings of the 8th ACM international conference on
Aspect-oriented software development pp. 161-172.
Zhang, J., Khalgui, M., Li, Z., Mosbahi, O., & Al-Ahmari,
A. M., 2013. R-TNCES: A novel formalism for
reconfigurable discrete event control systems. IEEE
Transactions on Systems, Man, and Cybernetics:
Systems, 43(4), 757-772.
Combining Semi-formal and Formal Methods for Safety Control in Autonomous Mobility-on-Demand Systems
521
