
Learning to Close the Gap: Combining Task Frame Formalism and
Reinforcement Learning for Compliant Vegetable Cutting
Abhishek Padalkar
1,2
, Matthias Nieuwenhuisen
1
, Sven Schneider
2
and Dirk Schulz
1
1
Cognitive Mobile Systems Group, Fraunhofer Institute for Communication,
Information Processing and Ergonomics FKIE, Wachtberg, Germany
2
Department of Computer Science, Bonn-Rhein-Sieg University of Applied Sciences, St. Augustin, Germany
Keywords:
Compliant Manipulation, Reinforcement Learning, Task Frame Formalism.
Abstract:
Compliant manipulation is a crucial skill for robots when they are supposed to act as helping hands in ev-
eryday household tasks. Still, nowadays, those skills are hand-crafted by experts which frequently requires
labor-intensive, manual parameter tuning. Moreover, some tasks are too complex to be specified fully using a
task specification. Learning these skills, by contrast, requires a high number of costly and potentially unsafe
interactions with the environment. We present a compliant manipulation approach using reinforcement learn-
ing guided by the Task Frame Formalism, a task specification method. This allows us to specify the easy to
model knowledge about a task while the robot learns the unmodeled components by reinforcement learning.
We evaluate the approach by performing a compliant manipulation task with a KUKA LWR 4+ manipulator.
The robot was able to learn force control policies directly on the robot without using any simulation.
1 INTRODUCTION
The demand for service robots has grown signifi-
cantly in recent years. Nowadays, mainly simple
household chores are performed by robots, e.g., vac-
uum cleaning. Nevertheless, the demand for robots
that can aid, e.g., elderly or handicapped persons, in
many more tasks is high. This requires systems that
are simple to adapt to new applications without the
need for complex handcrafting of each individual be-
havior by experts. We aim at providing a solution
that allows a user to specify a task in a high-level
task description, augmented with learned parameter-
ized policies that close the gap between simple task
specifications and complex task dynamics.
Many robotic manipulation tasks require compli-
ant manipulation, where the robot needs to respond to
the contact forces while executing a task. Tasks like
cutting vegetables (depicted in Figure 1), opening
doors, or cleaning surfaces, involve deliberate contact
of the robot with the environment. Classical planning
and control approaches fail to perform satisfactorily,
here, due to the lack of precise models of contact
forces and a high computational complexity (Kalakr-
ishnan et al., 2011). Simplistic models for control,
e.g., linear approximations and stiffness controllers,
Figure 1: Tasks like vegetable cutting require compliant ma-
nipulation. A combination of a task description and learning
of the free variables allows a robot to quickly adapt to new
situations.
have been proposed for such cases, but they
still need manual tuning (Duan et al., 2018).
Task specification approaches allow to specify a
task by defining constraints for a motion without ex-
plicitly planning a trajectory (Mason, 1981). This in-
cludes constraining the movement in some directions
while allowing or enforcing the motion into other di-
rections. Such approaches simplify the definition of
contact-rich tasks, because not all parameters of the
problem instance have to be known beforehand. Still,
many of the parameters used in a task specification
need to be tuned manually, which is a tedious task
Padalkar, A., Nieuwenhuisen, M., Schneider, S. and Schulz, D.
Learning to Close the Gap: Combining Task Frame Formalism and Reinforcement Learning for Compliant Vegetable Cutting.
DOI: 10.5220/0009590602210231
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 221-231
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
221

and requires a number of human interventions. More-
over, sometimes the task is too complex to be fully-
specified.
Reinforcement learning (RL), on the other hand,
has the advantage that skills to solve a problem can
be learned without a handcrafted set of motions. An
agent learns skills by exploring the environment and
adopting the parameters which govern its behavior.
Learning all parameters of a policy can be compu-
tationally very expensive and might require a large
number of interactions with the environment. If exe-
cuted with a real robot those are costly and potentially
dangerous. Sometimes it is possible to learn the skills
in a simulated environment, but this requires to model
the problem accurately in simulation which might be
even more complex as solving the initial task. The
application of reinforcement learning is, thus, limited
by the above reason.
For humans, learning a new task is often a combi-
nation of explanation and demonstration, followed by
an improvement of the skill by experience. We pro-
pose to combine task specification methods and re-
inforcement learning to create a solution for a com-
pliant manipulation task. By employing task-specific
information using a formal task specification frame-
work helps to reduce the number of interactions with
the environment required by a reinforcement learn-
ing algorithm. Moreover, hard safety limits set by the
task specification framework make the learning pro-
cess safe.
Our main contribution in this paper is a working
system that learns how to cut vegetables based on
a specification of the known parameters of the task
without simulation. As free parameter the cutting
force is learned for different vegetables. This com-
bination allows the robot to learn the cutting parame-
ters for a new vegetable with only a few environment
interactions.
2 RELATED WORK
The manipulation of only partially known objects is a
challenging problem. It has been tackled with a vari-
ety of hand-crafted and automatically derived strate-
gies so far. Furthermore, many manipulation tasks re-
quire compliant manipulation, where the robot needs
to respond to the contact forces while executing a
task (Kalakrishnan et al., 2011; Leidner et al., 2015).
Task Specification Methods. A task specification
framework allows a programmer to specify the task
in terms of a high-level description. The low-level
motion commands are automatically derived from this
specification. This framework simplifies the integra-
tion of robots into daily tasks where programming
explicit motions is not a viable option (Bruyninckx
and De Schutter, 1996). It can be seen as an inter-
face layer between the robot control architecture and
a high-level task planning framework.
Leidner (2017) presents a representation in the
form of action templates that describe robot actions
using symbolic representations and a geometric pro-
cess model. The symbolic representation of the
task—specified in the planning domain definition lan-
guage (PDDL)—allows planners to consider actions
in the high-level, abstract task plan The geomet-
ric representation of the task specifies the sequence
of low-level movement sequences needed to execute
these actions.
The instantaneous task specification and control
framework (iTaSC) synthesizes control inputs based
on provided task space constraints (De Schutter et al.,
2007; Decr
´
e et al., 2009, 2013). This approach is
very powerful in terms of obtaining an optimal con-
troller, but requires the modeling of a large number of
constraints and geometric uncertainties. Smits et al.
(2008) present an systematic approach for modeling
the instantaneous constraints and geometric uncer-
tainties.
Mason (1981) present the idea behind the Task
Frame Formalism (TFF) for specifying compliant
tasks. Different control modes—position, velocity,
or force control—are assigned to the individual axes
of the task frame (N
¨
agele et al., 2018). Bruyninckx
and De Schutter (1996) use TFF to open doors. This
framework doesn’t consider the specification of task
quality or motion quality related parameters like ve-
locity damping or instantaneous sensory inputs.
Reinforcement Learning. Reinforcement learning
in general requires many interactions of an agent with
the environment to learn a reasonable policy. For
robotic applications this is often prohibitively expen-
sive, especially when trying to learn the complete
value function for all possible state-action pairs.
Policy-search methods have the advantage that
they learn the policy for taking actions directly based
on the observable state of the robot. This mitigates
the burden to learn a value function (Deisenroth et al.,
2013; Polydoros and Nalpantidis, 2017). This reduces
the required interactions with the environment. Fur-
thermore, policy-search methods are computationally
less expensive. Given these advantages, we focus on
policy-search methods to solve the problem of com-
pliant manipulation.
The REINFORCE algorithm is based on the
maximum-likelihood approach, which uses the policy
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
222
gradient theorem for the estimation of the gradient of
a policy (Deisenroth et al., 2013; Sutton and Barto,
2018). Actions are drawn from a Gaussian distribu-
tions and then executed by the robot for exploration.
It has been successfully applied to problems with dis-
crete state and action space as well as robotic control
problems (Peters and Schaal, 2006; Sutton and Barto,
2018). It is a very generic algorithm suited for a vari-
ety of problem formulations, but the exploration noise
added at every time step can render learning a policy
on a real robot infeasible.
The path integral policy improvement (PI
2
) al-
gorithm (Theodorou et al., 2010a) is a widely used
policy-search algorithm for trajectory optimization.
Theodorou et al. (2010b) use it for teaching a robot
to jump over a gap, Chebotar et al. (2017) for open-
ing a door and grasping an object. In many examples,
trajectories were learned by demonstration with dy-
namic motion primitives (DMP) and then further op-
timized for a particular task using the path integral ap-
proach. Nevertheless, PI
2
has limited applications in
reinforcement learning to the trajectory optimization
problems. Therefore, it is hard adopt it for learning
compliant control policies for contact situations.
Nemec et al. (2017) propose a control algorithm
by combining reinforcement learning with intelligent
control to learn a force policy to open a door. They
take into account the constraints of the door motion
and the closed kinematic chain resulting from a firm
grasp of the robot hand on the door handle. While
opening the door in such configuration, high internal
forces are generated in the directions where the mo-
tion is not possible. This knowledge is employed to
learn a compliant force-control policy.
Policy learning by weighting exploration with the
returns (PoWER) from Kober and Peters (2014) is an
expectation-maximization-based learning algorithm.
By adding the exploration noise for batches of ex-
ploration trials, it is well-suited for learning a force
control policy on a real-robot system.
Our approach combines the features of model-
based manipulation solutions and reinforcement
learning. We formalize constraints in terms of al-
ready existing task specification methods, which can
be generalized to a number of compliant manipulation
tasks.
Vegetable Cutting. Lioutikov et al. (2016) solve
the task of vegetable cutting by learning dynamic mo-
tion primitives (DMPs). Their approach does not con-
sider vegetable cutting as a compliant manipulation
problem. Thus, the contact forces are not taken into
account during execution. As a result, multiple cut-
ting motions are required to cut the vegetable com-
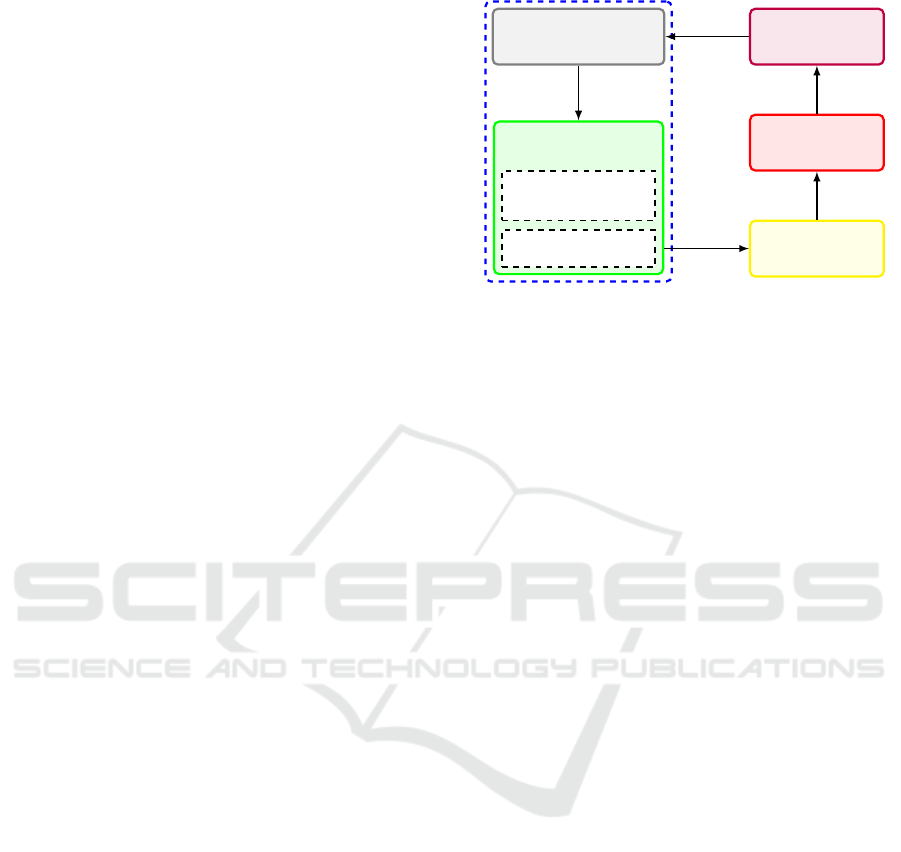
Task Specification
Task Model and
Policy Parameters
Policy
Policy Updates
Robot
Controller
Dynamics
Solver
Robot and
Environment
Reinforcement Learning
Joint
Torques
Control
Commands
Reward
Updated
Parameters
Actions
Figure 2: Outline of our architecture. The task specification
contains defined twist and wrench setpoints, as well as the
learned policy for the unmodeled parameters.
pletely. By contrast, we aim at cutting the vegetable
in one swipe.
Lenz et al. (2015) approach the problem of cut-
ting food by using a deep recurrent neural network
with model predictive control. This neural network is
trained offline with the collected cutting data to mimic
the object dynamics. A controller generates control
inputs, i.e., the force to be applied by the robot, by
optimizing the control law for predicted states given
a cost function. Furthermore, their task model is up-
dated during the cutting process by observing the pre-
dicted and actual state of the system. The major draw-
back of this approach is the requirement of a large cut-
ting dataset to learn the forward and backward models
of the food to cut.
Mitsioni et al. (2019) extends this approach for
a velocity and position controlled robot employing a
force torque sensor.
3 APPROACH
We solve the compliant vegetable cutting task by pro-
viding an incomplete task specification in combina-
tion with reinforcement learning to learn the unmod-
eled components. As mentioned before, this has the
advantage that the provided task specification will
greatly reduce the number of dimensions of the rein-
forcement learning problem while keeping the neces-
sary flexibility. Figure 2 outlines our proposed frame-
work.
Our task specification contains the manually de-
fined twist and wrench setpoints of the constrained
endeffector dimensions in the defined task frame.
Furthermore, it contains a learned policy for the un-
modeled parameters. The policy is updated according
Learning to Close the Gap: Combining Task Frame Formalism and Reinforcement Learning for Compliant Vegetable Cutting
223

to the rewards after execution of the task. We em-
ploy an impedance controller that executes the mo-
tions synthesized by the task specification framework.
Task Specification. To facilitate the easy addition
of new tasks to the system, their definition should
be possible as abstract task description with task-
oriented concepts. For the robot controller, never-
theless, this formulation has to be concrete enough
to devise the robot motion commands (Bruyninckx
and De Schutter, 1996). To achieve this goal, we em-
ploy the TFF framework (Mason, 1981), because it is
well-suited to model contact situations during com-
pliant manipulation. Sensor feedback is implicitly in-
tegrated when satisfying the modeled constraints, the
motion specification can be updated online, and an
appropriate task frame can be specified.
The TFF is based on the following assumptions:
I) the robot and the manipulated object are rigid bod-
ies, II) the constraint model of the manipulation task
is simple, i.e., no non-linearities, like deformations
and contact frictions, are modeled, III) the required
force controller is simple and easy to implement on
the robot, and IV) only kinetostatic concepts are used
to implement the control, i.e., twists (linear and angu-
lar velocities), wrenches (forces and torques), and the
reciprocity relationship between both.
TFF allows a programmer to specify a task by
means of twist and wrench constraints in the task
frame, extended by a stopping condition. For the pro-
posed vegetable cutting task the above assumptions
are partially satisfied as vegetables are not rigid bod-
ies and cutting inherently implies the deformation of
the body. We relax this assumption by defining con-
straints by a learned policy.
The basis of the TFF lies in the kinetostatic reci-
procity of the manipulated object. The manipulated
rigid object must execute an instantaneous rigid body
motion t = [ω
T
v
T
]
T
that is reciprocal to all ideal, i.e.,
friction-less, reaction forces w = [ f
T
m
T
]
T
that the ac-
tual contact situation can possibly generate:
ω
T
m + v
T
f = 0, (1)
with angular velocity ω, linear velocity v, force f , and
moment m. The moment is the sum of the applied ex-
ternal moment and the moment generated by the ap-
plied force. Equation (1) is the physical property that
no power is generated against the reaction forces by
the twist t. The twist and wrench spaces are always re-
ciprocal in these type of contact situations. Adhering
to this condition, a task can be fully specified in a suit-
able orthogonal reference frame by modeling all con-
tact twist and force constraints. Such an orthogonal
reference frame—the task frame—decouples twists
and wrenches.
move c o m p l i a n t l y {
w it h t a s k f ra me d i r e c t i o n s
x t : v e l o c i t y 0
y t : v e l o c i t y v ( t )
z t : f o r c e f ( en v ir on m en t , r o b o t ,
t a s k )
a x t : v e l o c i t y 0
a y t : v e l o c i t y 0
a z t : v e l o c i t y 0
} u n t i l d i s t a n c e y > d
Figure 3: Task specification for cutting vegetables.
A three-dimensional task frame has six pro-
grammable task frame directions: one linear velocity
or force and one angular velocity or torque per axis.
By the selection of a suitable task frame, a task can be
fully specified by the definition of task constraints for
all directions. These are satisfied by the application
of twists and wrenches in the correct task frame direc-
tions and compliance in the other directions. Bruyn-
inckx and De Schutter (1996) provide a detailed anal-
ysis for the selection of suitable task frames for a va-
riety of tasks. The selection of a task frame starts with
modeling natural constraints of the body, i.e., identi-
fying the force controlled directions and the velocity
or position controlled directions (Mason, 1981). This
condition is called geometric compatibility of the task
frame. The actions required for the completion of the
task are then specified on top of these natural con-
straints in the same task frame. A chosen task frame
should always remain compatible over time, i.e., the
force controlled, and velocity or position controlled
directions should not vary over time.
For vegetable cutting the task is represented in the
chopping board frame, such that the Z-axis is perpen-
dicular to the chopping board and the Y-axis is along
the cutting direction. We refer to the movement in
Y -direction as sawing motion and in downward Z-
direction as cutting motion. These motions cannot
be modeled or parameterized by constants, they are
represented by parameterized policies. The advan-
tage of the approach is that only the remaining free
parameters need to be learned. This reduces the learn-
ing problem from six to one or, if the sawing mo-
tion should also be learned, two dimensions. Figure 3
shows our task description for vegetable cutting. v(t)
is the time-dependent sawing velocity and f is the cut-
ting force in Z-direction, a function of the environ-
ment, the robot, and the task.
Reinforcement Learning. For choosing an appro-
priate reinforcement learning algorithm, the limita-
tions of the robotic system and the applicability to
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
224

the task to solve have to be taken into account. The
most important requirement is a fast convergence of
the learned policy, as robot interactions with environ-
ment are costly and learning in simulation would be
required, otherwise. Other challenges include I) a po-
tentially high-dimensional continuous state and action
space for compliant manipulation tasks, resulting in
bad performance of value iteration-based approaches,
II) complex transition dynamics of the robotic sys-
tem, making the creation of a model hard, III) robot
hardware, robot controllers, and contact-rich compli-
ant tasks have damping properties by design, thus, all
these components act as low pass filter, IV) close to
real-time control requirements of robotic systems re-
quire a fast command update rate, requiring low com-
putational cost algorithms. Furthermore, safe opera-
tion of the robot is crucial at all times during learning
in order avoid damage to the robot and environment.
In addition, the algorithm should be generic enough
to optimize any arbitrary policy for a given cost func-
tion.
A model-free policy search algorithm for solving
the learning problem matches these properties and re-
quirements particularly well. We have selected the
policy learning by weighting exploration with the re-
turns (PoWER) algorithm, which is based on expec-
tation maximization (Kober and Peters, 2014).
In the following, we will denote important defi-
nitions for the reinforcement learning algorithm. π
θ
denotes the probabilistic policy for taking action a,
given the current state s, parameterized by the policy
parameters θ. It is differentiable with respect to θ.
The probability of taking an action is governed by a
Gaussian distribution, such that
a ∼ π(θ,s) ∼N (µ,σ), (2)
where µ = f (θ, s) is a function of the policy param-
eters θ and state s and is differentiable with respect
to θ (Sutton and Barto, 2018). f can be any function
approximator, e.g., splines, neural networks, or a lin-
ear combination of inputs. σ is the exploration noise
added to each mean action µ.
The quality of the solution provided by executing
policy π
θ
is evaluated over a complete episode of T
time steps. It is defined as performance measure
J(θ) = E[
T −1
∑
t=0
r
t+1
], (3)
where r
t+1
is the immediate reward received by per-
forming action a
t
in state s
t
, specified by the reward
function R(a, s) (Sutton and Barto, 2018). The ob-
jective of the reinforcement learning process is to find
the policy parameters that maximize this performance
measure, also referred to as return.
This can be achieved by updating the policy pa-
rameters employing gradient ascent with the update
rule
θ
i+1
= θ
i
+
∂
∂θ
J(θ
i
). (4)
J(θ) depends on reward r
t+1
, which itself depends
on action a
t
taken in state s
t
and resulting in state s
t+1
.
It means that J(θ) depends not only on action selec-
tions, but also on the state distribution (transition dy-
namics). In a given state s, it is straightforward to
calculate the effect of the policy parameters on the re-
ward r and, thus, on J(θ) from the knowledge of the
effect of the policy parameters on the action a. Never-
theless, the effect of a policy on the state distribution
is a function of the environment which is unknown.
The problem is to find the gradient of J(θ) with
respect to θ, with the unknown transition dynamics
of the environment. Employing the policy gradient
theorem (Sutton and Barto, 2018) lets us rewrite the
formulation to
∇
θ
J(θ) =
T −1
∑
t=0
∇
θ
log(π
θ
(a
i
,s
i
))
T −1
∑
t=0
r
t+1
. (5)
Since J(θ) is a function of θ as well as of the tran-
sition dynamics of the environment, the gradient is
calculated by extracting information from trials con-
ducted in the environment.
Expectation Maximization. Policy gradient meth-
ods show major drawbacks because of the state-
independent unstructured exploration in the action
space (Kober and Peters, 2009). The added Gaus-
sian noise in the actions increases the variance of
the parameter updates for longer episodes. Exploring
the action space at each time step adds high-frequent
noise to the robotic system which itself acts as a low-
pass filter. As a result, the exploration signal vanishes.
Furthermore, the unstructured exploration can dam-
age the robotic system.
The expectation maximization-based method pol-
icy learning by weighting exploration with the returns
(PoWER) from Kober and Peters (2014) uses state-
dependent low-frequency noise for exploration It adds
noise to the parameters at the beginning of a roll-out
consisting of several trials instead of each action at
every time step. Hence, the actions are constructed
according to
a = f (θ + ε,s
t
), (6)
where ε ∼ N (0,Σ). To calculate the parameter up-
date, the left hand side of Equation (5) can be set to
zero in the case where π
θ
belongs to the exponential
Learning to Close the Gap: Combining Task Frame Formalism and Reinforcement Learning for Compliant Vegetable Cutting
225
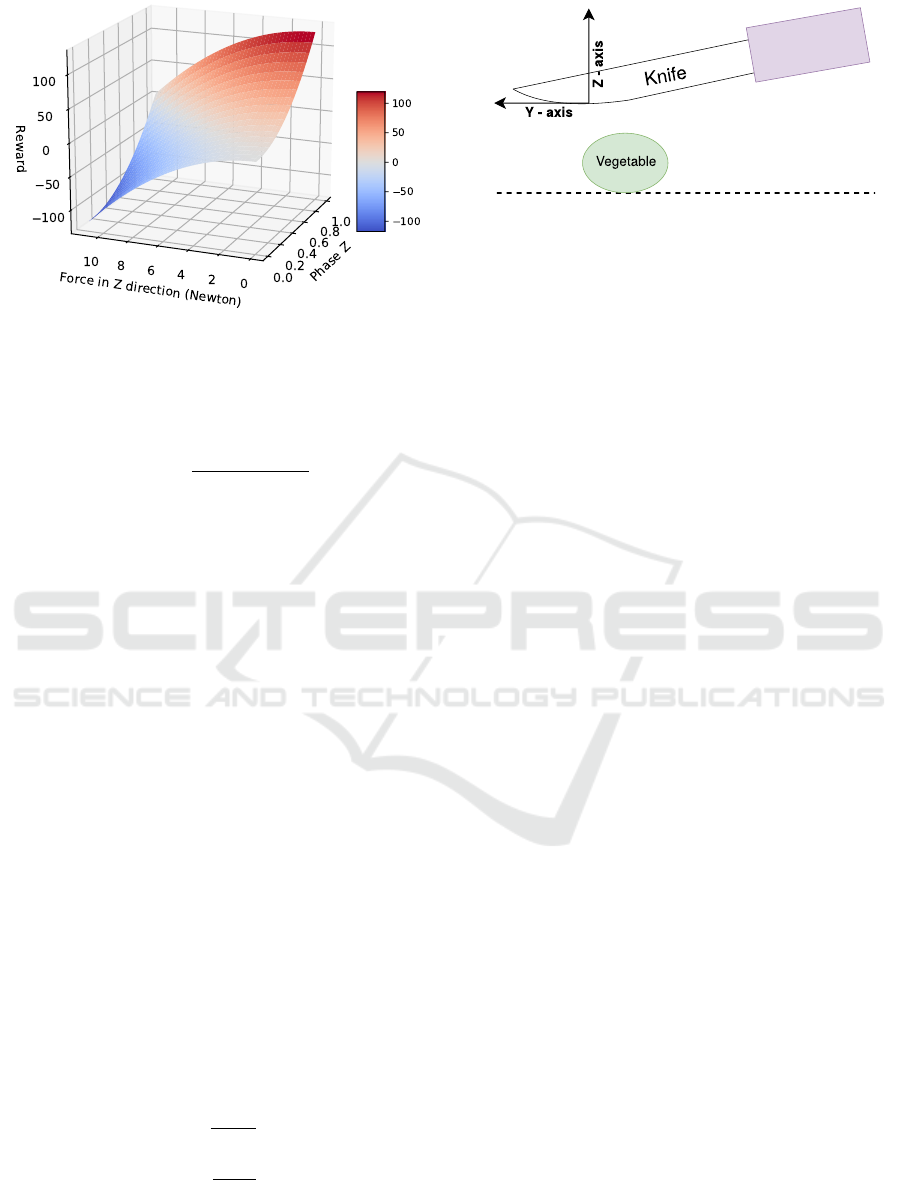
Figure 4: Example reward function surface for the vegetable
cutting task.
family (Kober and Peters, 2014). As a result, we get
the update rule
θ
0
i
= θ
i
+
E[
∑
T =1
t=0
ε
i
r
t+1
]
E[
∑
T −1
t=0
r
t+1
]
. (7)
Reward Function. The employed reward function
for learning the policy penalizes the applied force at
each time step and gives a positive reward for pro-
gressing the cut in downward direction. It is given by
r = C
1
∗φ
2
z
−C
2
∗ f
2
z
, (8)
where φ
z
is the downward progress normalized with
the vegetable diameter and f
z
is the applied force. C
1
and C
2
are positive constants that affect the behavior
learned by the policy. Figure 4 shows the surface plot
of the reward function with C
1
= 100 and C
2
= 1. At
the end of the of each successful trial a positive termi-
nal reward is awarded to the robot.
Reinforcement Learning for Cutting Vegetables
with the TFF. As discussed earlier, the vegetable
cutting task can be modeled with the TFF, but specify-
ing the force required for cutting is not trivial. Hence,
we propose to learn the downward cutting force em-
ploying reinforcement learning. The task frame for
this task is depicted in Figure 5. We define the cut-
ting progress by sawing phase φ
y
—the motion paral-
lel to the chopping board—and cutting phase φ
z
—the
downward motion—in Y and Z direction respectively
as follows:
φ
y
=
y
s
−y
y
d
, (9)
φ
z
=
z
s
−z
z
d
. (10)
y and z are the partial position of the tool center point
(TCP), y
s
and z
s
are the respective starting positions.
Figure 5: Task frame for the vegetable cutting task.
y
d
is the desired sawing distance and z
d
is the height,
or circumference, of the vegetable. y
d
can be specified
as parameter in the task specification and the height
of the vegetable z
d
is measured online. The measure-
ment is detailed in the evaluation section. φ
y
and φ
z
are dimensionless quantities and take values between
0 and 1.
Force Policy for Cutting Vegetables. We compare
two force policy functions, a linear policy and a more
expressive policy based on weighted Gaussian distri-
butions. The linear policy is given by
f = −(A ˙y + B(0.5
2
−(0.5 −φ
y
)
2
) +C(1 −φ
z
)),
(11)
where A,B,C are the policy parameters to be learned,
collectively referred to as θ. If we interpret the phys-
ical meaning of this policy, A ˙y can be seen as me-
chanical admittance, where A becomes the recipro-
cal of the admittance in Ns/m. The second term,
B(0.5
2
−(0.5 −φ
y
)
2
), resembles that the applied cut-
ting force should be higher in the middle of the sawing
motion. With positive values of B, the second term
becomes zero at the beginning (when φ
y
= 0) and end
of the motion (when φ
y
= 1). It takes its maximum
value at the middle of the sawing phase (φ
y
= 0.5)
and it rises and falls exponentially. As φ
y
is dimen-
sionless, B is a force in Newton. The third term in the
policy can be seen as an impedance provided by the
vegetable to the motion of the knife during cutting.
As φ
z
is also dimensionless, C is a force in Newton,
again. While designing the task, we tried to bring in
the observed knowledge of general cutting tasks. Due
to the limitations on observability, the policy may not
completely capture the correct underlying dynamics
of the task. Nevertheless, the task is modeled suffi-
ciently well to learn a behavior that shows reasonable
performance on the task.
To model more complex task dynamics, we em-
ploy a second more generic policy consisting of a
weighted sum of equally-spaced Gaussian functions
with centers lying in the interval [0,1]. This Gaussian
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
226
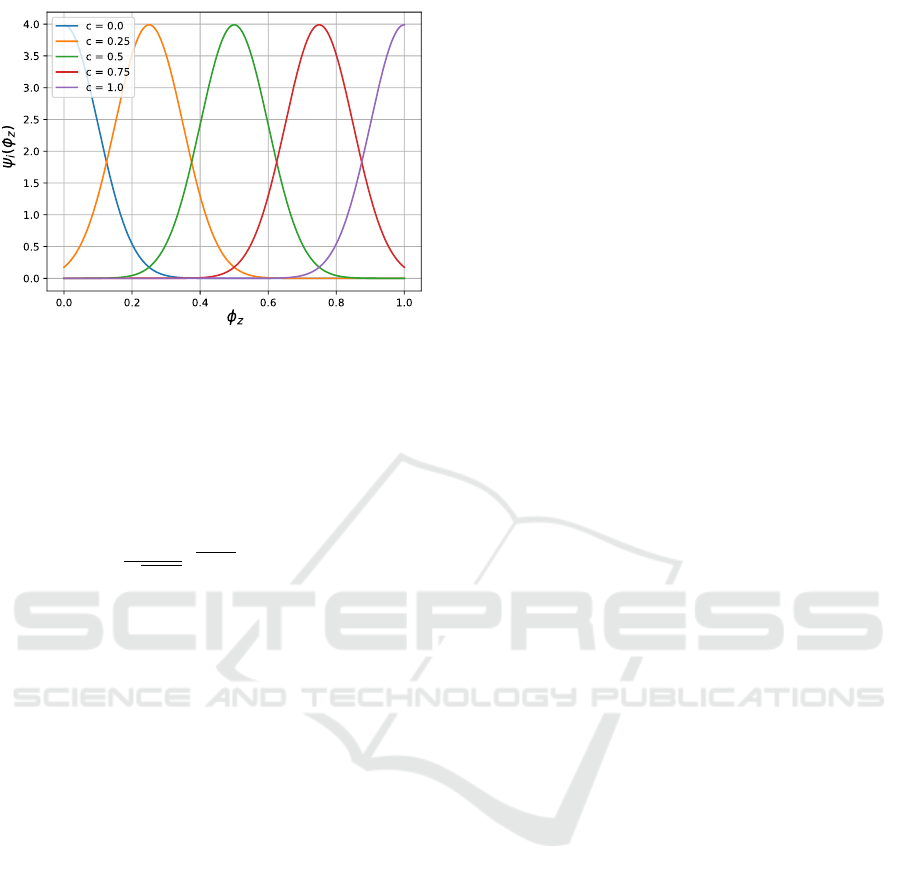
Figure 6: Five Gaussian functions with centers c placed
equidistant on φ
z
axis.
policy is given by
f = −(A ˙y + B(0.5
2
−(0.5 −φ
2
y
)) (12)
+
N−1
∑
i=0
W ψ
i
(φ
z
)), (13)
ψ
i
(φ
z
) =
1
√
2πσ
2
e
(c
i
−φ
z
)
2σ
2
, (14)
where W is the weight vector, N is the number of
Gaussian functions, c
i
is the center of the i
th
Gaus-
sian, and σ is the width of each Gaussian function.
This policy is more generic than the previously used
policy as any arbitrary non-linear function can be ap-
proximated by a weighted sum of Gaussian functions.
Here, we project the phase φ
z
to a high dimensional
non-linear space to capture the force distribution re-
quired at different phases of the cutting task. Figure 6
shows the Gaussian functions placed equidistantly on
the phase axis.
The sawing motion can either be learned or it can
be engineered. To keep the overall learning problem
simple, we specify it as a continuous function of time
in the task description. We have chosen a Gaussian
function for the velocity profile as it has a smooth first
order derivative, which represents acceleration in this
particular case. This profile resembles human behav-
ior, it can be fully parameterized by the distance to be
traveled and the maximum velocity.
Robot Controller. For the realization of the above-
mentioned high-level task specification framework, a
motion controller is necessary to execute the task on
the manipulator. If an accurate model of the environ-
ment is available then it is possible to calculate pre-
cise motion commands analytically to keep all con-
tact forces within specified bounds while executing
the task. For our application this would include an
exact model of the soft vegetable, which is difficult
to obtain. Thus, we employ a compliant controller
that is able to respond to the contact forces to prevent
damage to the robot and the environment.
Compliance in the motion can be achieved in two
different ways: by impedance and by admittance con-
trol. Both approaches achieve the same goal of estab-
lishing a relationship between an external force and
the resulting position error of the manipulator. We
employ impedance control, where the robot hardware
acts like a mechanical admittance (Ott et al., 2010).
Here, the controller is designed to be a mechanical
impedance. This resembles a loaded mass-spring sys-
tem.
A torque-controlled manipulator with gravity
compensation acts as a free-floating body constrained
by its kinematic chain (Ott et al., 2010, 2015). To
minimize a measured position error of the endeffec-
tor the controller increases the commanded forces on
the endeffector. The applied force is directly propor-
tional to the error. The impedance control scheme is
defined by
F
F
F = k
k
k
c
e
e
e + D
D
D(
˙
e
e
e), (15)
e
e
e = x
x
x
dsr
−x
x
x
msr
, (16)
where F
F
F is the force generated at the endeffector by
the manipulator, k
k
k
c
is the stiffness of the manipulator,
D
D
D(
˙
e
e
e) is a damping term, e
e
e is the error in the desired
position x
x
x
dsr
, and x
x
x
msr
is the measured position of
the endeffector. By using this control strategy along
with the inverse dynamics equation of the manipula-
tor, joint torque setpoints τ
τ
τ
cmd
can be calculated by
τ
τ
τ
cmd
= J
J
J
T
(
(
(k
k
k
c
e
e
e +
+
+ D
D
D(
(
(
˙
e
e
e)
)
))
)
) + f
dynamics
(
¨
q
q
q,
,
,
˙
q
q
q,
,
,q
q
q), (17)
where f
dynamics
(
¨
q
q
q,
,
,
˙
q
q
q,
,
,q
q
q) is the joint torque vector re-
quired for the compensation of natural forces, domi-
nated by gravity and friction. It is calculated by the
dynamics solver of the manipulator.
4 EVALUATION
We evaluate our proposed solution with a KUKA
LWR 4+ manipulator learning to cut cucumbers and
bananas. For the cutting experiments, we mount an
ordinary kitchen knife with a modified handle at the
robot endeffector. The vegetable to cut is fixated us-
ing an adjustable clamp on top of a fixed chopping
board such that it cannot move throughout the exper-
iments. We place the vegetable such that its long axis
is approximately perpendicular to the cutting motion,
i.e., the x-axis of the specified task frame depicted
in Figure 5. The knife is manually steered to a pose
Learning to Close the Gap: Combining Task Frame Formalism and Reinforcement Learning for Compliant Vegetable Cutting
227
above the first cut, we assume that this pose can be de-
termined by an external perception system later. Fig-
ure 1 shows the setup.
At the beginning of the experiment the manipu-
lator measures the height of the chopping board sur-
face by approaching it with a downward motion until
contact. The measured height is used throughout the
entire experiment.
While learning the policy, the individual cutting
trials start at one end of the vegetable. The manipula-
tor moves along the x-axis after each cutting trial. The
movement distance moves determines the size of the
slices and can be configured by the user. Before per-
forming a cut, the manipulator measures the diameter
of the vegetable employing the same method as for
measuring the height of the chopping board surface.
With Equation (10) the normalized phase of the cut
in the z-direction can be determined from the current
position of the manipulator.
REINFORCE. After first promising simulation re-
sults, we tested the REINFORCE algorithm to learn
the linear force policy for the cucumber cutting task
given by Equation (11). The return is expected to in-
crease over the training period, but the tests showed
an opposite behavior, meaning that the algorithm was
not able to learn the intended behavior. A probable
explanation is that adding exploration noise at every
time step is a high-frequency signal that is filtered by
the low-pass dynamics of the system. First, the robot
hardware acts as low-pass filter to this noise due to the
inertia of the links, mechanical friction, and damping.
Second, the Cartesian impedance controller resem-
bles the behavior of a damped mass spring system.
And third, the vegetable acts as a viscous medium and
damps any movements through it. This impedes the
exploration in the state-action space. Furthermore,
the robot endeffector is vibrating as a result of the
noise. The learning algorithm is unaware of these as-
pects and expects the force commands to be executed
perfectly. As a result, the REINFORCE algorithm di-
verges during learning. This failure in learning the
task shows that compliant manipulation tasks differ
from trajectory optimization tasks. For the latter it
is possible to execute motion commands with explo-
ration noise at every time step and learn the policy
effectively, according to the discussed literature.
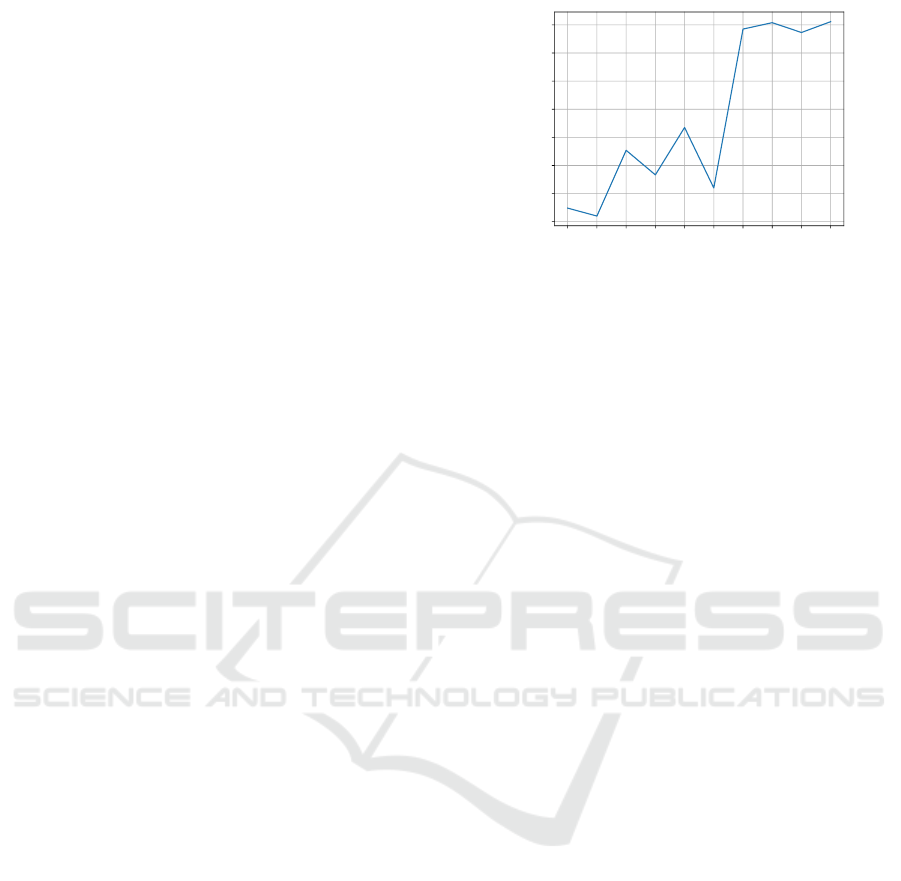
PoWER with Linear Policy. Because of the above
mentioned limitations on adding exploration noise at
every time step, we employed the PoWER algorithm
for subsequent experiments. PoWER adds explo-
ration noise directly to the policy parameters at the
beginning of each trial. The policy parameters to be
0 1 2 3 4 5 6 7 8 9
Number of episodes
0
2
4
6
8
10
12
14
Return (x1000)
Figure 7: Learning progress of PoWER with linear policy.
Depicted is the average return after each episode.
learned are θ = (A,B,C) from Equation (11). The re-
ward function (Equation (8)) is used with C
1
= 100
and C
2
= 1. A terminal reward of 1000 is given if the
cucumber is completely cut through during the trial.
The sawing motion is specified in the task description
with a sawing distance of 10 cm and a maximum ve-
locity of 5 cm/s.
Each training episode consists of ten trials. The
initial values of θ are A = B = C = 0.5. At the begin-
ning of an episode, we sample new policy parameters
[θ
1
... θ
10
] from the Gaussian distribution N (θ, Σ),
with Σ = [1.5,1.5,1.5]. The mean policy parameter
vector θ is updated at the end of each episode.
Figure 7 shows the average return of all tri-
als in each episode. The algorithm converges after
six episodes with a policy that can successfully cut
through the cucumber in one swipe. Before the sixth
episode, the return is largely affected by the depth of
the previous cut. The finally-learned policy param-
eters are A = −0.63, B = 1.56, and C = 6.15. It
can be observed that C contributes most to the gener-
ated force. According to our physical interpretation,
this means that the policy has learned the impedance
caused by the vegetable to the motion of the knife.
The applied force and evolution of cutting phase are
depicted in Figures 8a and 8b, respectively.
PoWER with Gaussian Policy. To evaluate our ap-
proach employing the more expressive Gaussian pol-
icy (Equation (14)), we let the robot learn to cut cu-
cumbers and, in addition, bananas. Here, the policy
parameters to be learned are θ = (A,B,W ). We use
five Gaussian functions with σ = 0.15.
For learning to cut cucumbers, we use the same
reward function as before with C
1
= 140 and C
2
= 1.
The terminal reward is 1500. We increased the value
of C
1
to encourage a more aggressive application of
force to cut through the vegetable. In this experiment,
each episode contains 15 trials. The new parameter
vectors [θ
1
... θ
15
] are sampled from a Gaussian dis-
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
228
0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5
Time (s)
0
1
2
3
4
5
6
Force (N)
Run 1
Run 2
Run 3
Run 4
Run 5
(a) Force applied at TCP.
(b) Cutting phase φ
z
.
Figure 8: Cutting motion of the knife in Z-direction with
linear policy.
tribution with Σ = (10, 1, [0.9,...,0.9]
T
). The initial
values of the parameters are A = 15, B = 0.6, and
W = [2,. . . ,2]
T
.
Figure 9 shows the average return for learning the
cucumber cutting task. The task could be learned
within 20 episodes. To evaluate the learned policy,
we ran multiple tests, in which the robot was able to
cut through the cucumber completely every time. The
learned parameter values are A = 40.02, B = 2.08, and
W = [1.84,1.89, 1.79, 2.16,3.56]
T
.
A better initialization and a high variance of the
exploration noise helped in learning a suitable value
of A, which represents the mechanical admittance.
The robot learns a cutting motion with varying force
depending on the cutting phase φ
z
, represented by the
different weights in W .
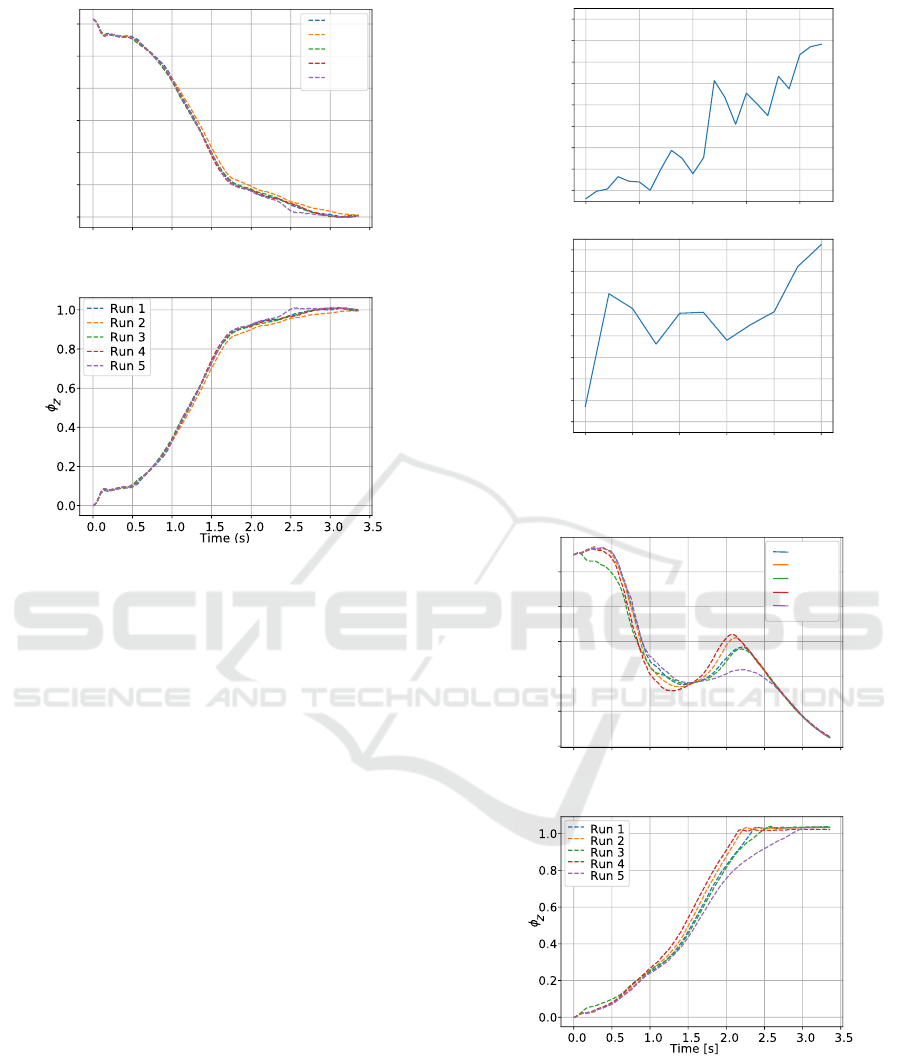
Figure 10a shows the applied cutting force for five
test runs. The evolution of the cutting phase over
time is depicted in Figure 10b for the same runs. It
can be seen that the robot was able to reach the value
φ
z
= 1 earlier than in the previous experiment. This
means that the resulting cutting speed achieved with
the Gaussian policy is higher than with the linear pol-
icy.
Values of φ
t
that are slightly greater than one are
explained by the slightly uneven surface of the chop-
0 5 10 15 20
Number of Episodes
4
6
8
10
12
14
16
18
20
Return (x1000)
0 2 4 6 8 10
Number of Episodes
4
6
8
10
12
14
16
18
20
Return (x1000)
Figure 9: Learning progress of PoWER with Gaussian pol-
icy for cucumber (left) and banana (right) cutting.
0.0 0.5 1.0 1.5 2.0 2.5 3.0
3.5
Time [s]
1.0
1.5
2.0
2.5
3.0
3.5
Force [N]
Run 1
Run 2
Run 3
Run 4
Run 5
(a) Force applied at TCP.
(b) Cutting phase φ
z
.
Figure 10: Cutting motion of the knife in Z-direction with
Gaussian policy.
ping board caused by deformations from the clamp
arrangement.
In addition to cutting cucumbers, we evaluated the
approach by learning to cut bananas. Bananas are a
Learning to Close the Gap: Combining Task Frame Formalism and Reinforcement Learning for Compliant Vegetable Cutting
229

0.0 0.5 1.0 1.5 2.0 2.5 3.0
Time [s]
0.4
0.8
0.6
1.0
1.2
1.4
Force [N]
Run 1
Run 2
Run 3
Run 4
Run 5
(a) 1 day old.
0
.
0 0
.
5 1
.
0 1
.
5 2
.
0 2
.
5 3
.
0
Time [s]
0
.
4
0
.
6
0
.
8
1
.
0
1
.
2
1
.
4
Force [N]
Run 1
Run 2
Run 3
Run 4
Run 5
(b) 2 days old.
0
.
0 0
.
5 1
.
0 1
.
5 2
.
0 2
.
5 3
.
0
Time [s]
0
.
4
0
.
6
0
.
8
1
.
0
1
.
2
1
.
4
Force [N]
Run 1
Run 2
Run 3
Run 4
Run 5
(c) 3 days old.
Figure 11: Force applied at TCP in Z-direction for cutting bananas with different ripeness.
0
.
0 0
.
5 1
.
0 1
.
5 2
.
0 2
.
5 3
.
0
Time [s]
0
.
0
0
.
2
0
.
4
0
.
6
0
.
8
1
.
0
φ
z
Run 1
Run 2
Run 3
Run 4
Run 5
(a) 1 day old.
0
.
0 0
.
5 1
.
0 1
.
5 2
.
0 2
.
5 3
.
0
Time [s]
0
.
0
0
.
2
0
.
4
0
.
6
0
.
8
1
.
0
φ
z
Run 1
Run 2
Run 3
Run 4
Run 5
(b) 2 days old.
0
.
0 0
.
5 1
.
0 1
.
5 2
.
0 2
.
5 3
.
0
Time [s]
0
.
0
0
.
2
0
.
4
0
.
6
0
.
8
1
.
0
φ
z
Run 1
Run 2
Run 3
Run 4
Run 5
(c) 3 days old.
Figure 12: Phase φ
z
evolution of the cutting motion in Z-direction for cutting bananas with different ripeness.
different class of vegetables with a harder skin and a
soft core. As the slices of the banana tend to stick to-
gether after cutting, we make sure that they are com-
pletely cut and removed by a cleaning motion after
each trial. This is necessary to ensure similar starting
conditions in each cutting attempt. Due to the result-
ing reduced variance the task could be learned in 9
trials, less that half of the trials required to learn to
cut cucumbers. Figure 11 shows the force required
for cutting bananas with different ripeness and Fig-
ure 12 shows the corresponding cutting progress. The
learning progress is depicted in Figure 9.
5 CONCLUSIONS
We implemented and evaluated the ability of the TFF
aided by reinforcement learning for the task of cut-
ting vegetables. The introduction of reinforcement
learning generalizes the TFF for tasks with hard to
model parameters. On the other hand, employing
the the Task Frame Formalism simplified the rein-
forcement learning problem to learn a one dimen-
sional force policy. Experiments with a KUKA LWR
4+ manipulator demonstrated that the robot was able
to learn a linear policy for cutting vegetables within
six episodes and a Gaussian policy within twenty
episodes. With careful modeling of the task, even
complicated tasks with complex contact force dynam-
ics can be learned directly with the robot without us-
ing any simulation. All learned policies were able to
cut the vegetables completely in one swipe. In addi-
tion, the use of the the Fask Frame Formalism facil-
itated safe operation of the robot by a deterministic
motion specification in the remaining five direction,
including the sawing motion.
REFERENCES
Bruyninckx, H. and De Schutter, J. (1996). Specifica-
tion of force-controlled actions in the ”task frame
formalism”-a synthesis. IEEE Trans. on Robotics and
Automation, 12(4):581–589.
Chebotar, Y., Kalakrishnan, M., Yahya, A., Li, A., Schaal,
S., and Levine, S. (2017). Path integral guided policy
search. In Proc. of IEEE Int. Conf. on Robotics and
Automation (ICRA).
De Schutter, J., De Laet, T., Rutgeerts, J., Decr
´
e, W., Smits,
R., Aertbeli
¨
en, E., Claes, K., and Bruyninckx, H.
(2007). Constraint-based task specification and esti-
mation for sensor-based robot systems in the presence
of geometric uncertainty. The Int. Journal of Robotics
Research (IJRR), 26(5):433–455.
Decr
´
e, W., Bruyninckx, H., and De Schutter, J. (2013). Ex-
tending the iTaSC constraint-based robot task specifi-
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
230

cation framework to time-independent trajectories and
user-configurable task horizons. In Proc. of IEEE Int.
Conf. on Robotics and Automation (ICRA).
Decr
´
e, W., Smits, R., Bruyninckx, H., and De Schutter, J.
(2009). Extending iTaSC to support inequality con-
straints and non-instantaneous task specification. In
Proc. of IEEE Int. Conf. on Robotics and Automation
(ICRA).
Deisenroth, M. P., Neumann, G., and Peters, J. (2013). A
survey on policy search for robotics. Foundations and
Trends in Robotics, 2:1–142.
Duan, J., Ou, Y., Xu, S., Wang, Z., Peng, A., Wu, X., and
Feng, W. (2018). Learning compliant manipulation
tasks from force demonstrations. In IEEE Int. Conf.
on Cyborg and Bionic Systems (CBS).
Kalakrishnan, M., Righetti, L., Pastor, P., and Schaal, S.
(2011). Learning force control policies for compliant
manipulation. In Proc. of IEEE/RSJ Int. Conf. on In-
telligent Robots and Systems (IROS).
Kober, J. and Peters, J. (2014). Policy search for motor
primitives in robotics. In Learning Motor Skills, pages
83–117. Springer.
Kober, J. and Peters, J. R. (2009). Policy search for motor
primitives in robotics. In Advances in Neural Infor-
mation Processing Systems (NIPS).
Leidner, D., Borst, C., Dietrich, A., Beetz, M., and Albu-
Sch
¨
affer, A. (2015). Classifying compliant manipula-
tion tasks for automated planning in robotics. In Proc.
of IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-
tems (IROS).
Leidner, D. S. (2017). Cognitive reasoning for compliant
robot manipulation. PhD thesis, Universit
¨
at Bremen.
Lenz, I., Knepper, R. A., and Saxena, A. (2015). DeepMPC:
Learning deep latent features for model predictive
control. In Proc. of Robotics: Science and Systems
(RSS).
Lioutikov, R., Kroemer, O., Maeda, G., and Peters, J.
(2016). Learning manipulation by sequencing motor
primitives with a two-armed robot. In Intelligent Au-
tonomous Systems 13. Springer.
Mason, M. T. (1981). Compliance and force control for
computer controlled manipulators. IEEE Trans. on
Systems, Man, and Cybernetics, 11(6).
Mitsioni, I., Karayiannidis, Y., Stork, J. A., and Kragic, D.
(2019). Data-driven model predictive control for the
contact-rich task of food cutting. In Proc. of Int. Conf.
on Humanoid Robots (HUMANOIDS).
N
¨
agele, F., Halt, L., Tenbrock, P., and Pott, A. (2018). A
prototype-based skill model for specifying robotic as-
sembly tasks. In Proc. of IEEE Int. Conf. on Robotics
and Automation (ICRA).
Nemec, B.,
ˇ
Zlajpah, L., and Ude, A. (2017). Door open-
ing by joining reinforcement learning and intelligent
control. In Proc. of Int. Conf. on Advanced Robotics
(ICAR).
Ott, C., Mukherjee, R., and Nakamura, Y. (2010). Unified
impedance and admittance control. In Proc. of IEEE
Int. Conf. on Robotics and Automation (ICRA).
Ott, C., Mukherjee, R., and Nakamura, Y. (2015). A hybrid
system framework for unified impedance and admit-
tance control. Journal of Intelligent & Robotic Sys-
tems (JINT), 78(3-4):359–375.
Peters, J. and Schaal, S. (2006). Policy gradient methods for
robotics. In Proc. of IEEE/RSJ Int. Conf. on Intelligent
Robots and Systems (IROS).
Polydoros, A. S. and Nalpantidis, L. (2017). Survey of
model-based reinforcement learning: Applications on
robotics. Journal of Intelligent & Robotic Systems
(JINT), 86(2):153–173.
Smits, R., De Laet, T., Claes, K., Bruyninckx, H., and
De Schutter, J. (2008). itasc: A tool for multi-sensor
integration in robot manipulation. In Proc. of IEEE
Int. Conf. on Multisensor Fusion and Integration for
Intelligent Systems (MFI).
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Theodorou, E., Buchli, J., and Schaal, S. (2010a). Learning
policy improvements with path integrals. In Proc. of
Int. Conf. on Artificial Intelligence and Statistics.
Theodorou, E., Buchli, J., and Schaal, S. (2010b). Rein-
forcement learning of motor skills in high dimensions:
A path integral approach. In Proc. of IEEE Int. Conf.
on Robotics and Automation (ICRA).
Learning to Close the Gap: Combining Task Frame Formalism and Reinforcement Learning for Compliant Vegetable Cutting
231
