
Convexification of Semi-activity Constraints Applied to Minimum-time
Optimal Control for Vehicles with Semi-active Limited-slip Differential
Tadeas Sedlacek
1,2 a
, Dirk Odenthal
1 b
and Dirk Wollherr
2 c
1
BMW M GmbH, Daimlerstr. 19, 85748 Garching near Munich, Germany
2
Chair of Automatic Control Engineering, Department of Electrical and Computer Engineering, Technical University of
Munich, Theresienstr. 90, 80333 Munich, Germany
Keywords:
Minimum Lap Time, Semi-active Limited-slip Differential, Convexification, Time Optimal Control,
Hermite-Simpson Collocation, Vehicle System Dynamics.
Abstract:
Semi-active actuators provide a good compromise between low energy consumption and high performance.
Thus, they are deployed in many engineering applications, often combined with other actuators into complex
systems requiring an integrated control concept for optimal performance. Optimal control can be used to
objectively evaluate the performance of such systems as well as to deduce optimal control input trajectories
and optimal passive system designs. We present a novel approach which enables considering a broad class
of semi-active actuators in optimal control problems via convex sets. This procedure is exemplarily depicted
for semi-active limited-slip differentials which are used in automotive applications for lateral torque distribu-
tion. The performance benefit gained by installing a semi-active limited-slip differential at the rear axle of
a vehicle is objectively quantified by numerically computing time-optimal trajectories on a racetrack via di-
rect optimal control with Hermite-Simpson collocation. Although the overall problem remains nonconvex for
this particular application, this procedure is a first step towards a fully convex implementation. By iteratively
increasing the upper boundary for the differential torque in multiple optimisations, we identify the smallest
upper differential torque boundary for optimal laps and determine the lap time sensitivity regarding this limit.
1 INTRODUCTION
Semi-active actuators are used in many engineer-
ing applications since they provide a good com-
promise between low energy consumption and high
performance (Savaresi et al., 2010). For instance,
semi-active dampers are deployed in automotive sus-
pension systems (Savaresi et al., 2010), in landing
gears for aircrafts (Kr
¨
uger, 2000), in robotics to im-
prove running (Kim et al., 2018), in architectural and
bio-mechanical structures and many more (Poussot-
Vassal et al., 2010). Further examples for semi-active
actuators in the field of automotive engineering are
semi-active limited-slip differentials (SLDs) for lat-
eral torque distribution, semi-active transfer cases for
longitudinal torque allocation and airsprings for an
adjustable stiffness (Cheli et al., 2006; Savaresi et al.,
2010). This paper focusses on SLDs which enable
transferring torque from the faster spinning wheel to
a
https://orcid.org/0000-0002-6191-6173
b
https://orcid.org/0000-0002-6651-8369
c
https://orcid.org/0000-0003-2810-6790
the slower one. Since only the amount of torque trans-
ferred by the differential can be controlled, whereas
the direction of the torque transfer is dictated by
the wheel speed difference, these actuators represent
semi-active components. SLDs improve the corner-
ing performance of vehicles by enhancing accelera-
tion potential and yaw agility (Cheli et al., 2006). Lap
times on racetracks can be used as a metric to objec-
tively evaluate these benefits in vehicle performance.
The time-optimal input trajectories for the multiple
actuators of a vehicle under consideration of actuator
limitations and track boundaries can be deduced by
optimal control methods.
Optimal control has been successfully applied to
compute input trajectories for limited-slip differen-
tials (LDs) aiming at minimum lap times on race-
tracks. Passive LDs have been analysed via opti-
mal control methods in (Kelly, 2008; Perantoni and
Limebeer, 2014; Limebeer et al., 2014; Limebeer
and Perantoni, 2015; Tremlett et al., 2015), whereas
optimal trajectories for SLDs have been identified
in (Tremlett and Limebeer, 2016). All approaches
Sedlacek, T., Odenthal, D. and Wollherr, D.
Convexification of Semi-activity Constraints Applied to Minimum-time Optimal Control for Vehicles with Semi-active Limited-slip Differential.
DOI: 10.5220/0009593600150025
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 15-25
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

have in common that the torque transmitted by the dif-
ferential is depicted as a function of the wheel speed
difference. In the simplest form, the wheel speed dif-
ference is scaled by a factor which is either fixed for
passive LDs or represents a system input when SLDs
are considered. The computed differential torque has
been either inserted into the differential equations of
the system (Kelly, 2008) or has been considered by
equality constraints (Perantoni and Limebeer, 2014;
Limebeer et al., 2014; Limebeer and Perantoni, 2015;
Tremlett et al., 2015; Tremlett and Limebeer, 2016).
Except for (Kelly, 2008; Tremlett et al., 2015), only
quasi steady-state wheel dynamics have been consid-
ered for the wheel speed to simplify the optimisation
problem.
In this paper, we revisit the optimal control prob-
lem (OCP) introduced in (Sedlacek et al., 2020b) and
augment the baseline vehicle model by a SLD at the
rear axle. Since the rotational wheel speeds are deci-
sive variables for LDs, the corresponding differential
equations are included into the system dynamics. Fur-
thermore, we consider maximum differential torque
boundaries for the SLD. Formulating the contem-
plated OCP via the methods used in previous papers
would result in either quadratic equality constraints or
nonconvex sets, both prohibiting a fully convex OCP
beforehand (Boyd and Vandenberghe, 2004). Using
the SLD as an example, we present a novel OCP-
modelling approach for semi-active components with
convex subsets in the two quadrants dictated by the
passivity constraint (Savaresi et al., 2010). The non-
convex set is transformed into two convex ones by
separate consideration of positive and negative con-
trol inputs. The downside of this method is the re-
quirement of an extra input and a generally higher
number of constraints. However, this convexification
procedure is a first step towards a fully convex OCP
for such vehicles. The correctness of the approach is
confirmed by analysing the resulting optimal trajec-
tories. Finally, we identify the smallest upper differ-
ential torque boundary for optimal laps on a speci-
fied racetrack and determine the lap time sensitivity
regarding this limit.
The remainder of this paper is organised as fol-
lows. The considered track model and vehicle model
are presented in section 2. The OCP aiming at com-
puting trajectories for minimum lap time is formu-
lated in section 3 and its solution is discussed in sec-
tion 4. Section 5 concludes the paper and gives an
outlook for future work. The appendix contains fur-
ther modelling details and parameter values.
2 VEHICLE MODEL
A nonlinear two-track vehicle model in combination
with a flat track model is used to investigate opti-
mal lap trajectories for the Nuerburg-ring Grand-Prix
course. The topview of the vehicle model with re-
spect to the racetrack is illustrated in figure 1. We in-
troduce the index k ∈ K
:
= {1, 2,3,4} to distinguish
the individual wheels and make use of several co-
ordinate frames. Vectors given in the body coordi-
nate frame, which is coupled with the centre of grav-
ity (COG) of the vehicle and rotated by the yaw angle
ψ around the z-axis of the inertial frame, are marked
with the superscript b. Analogously, the wheel coor-
dinate frame w is the result of a rotation by the front
steering angle δ
f
. Calligraphic symbols denote vector
components given in the corresponding wheel coordi-
nate frame.
Drive torque generated by a combustion engine
is transmitted via a gear box and a SLD to the rear
wheels. The wheel-based engine torque T
e
considers
gear ratios and constant efficiencies of transmission
and SLD. The drive torque transferred laterally by
the SLD is denoted with T
d
. The front wheels are
mounted on individual axles and are thus decoupled.
Wheel-independent brake torques T
br,k
facilitate a lon-
gitudinal and lateral brake torque allocation. We as-
sume that the differential only transfers drive torque
and brake torque is solely allocated via the braking
system. This yields the individual wheel torques
T
1
T
2
T
3
T
4
=
−T
br,1
−T
br,2
1
2
(T
e
+ T
d
) − T
br,3
1
2
(T
e
− T
d
) − T
br,4
. (1)
As will be shown in section 3.2.3, it is beneficial to
split the differential torque into a positive and negative
d
hw
d
R
δ
f
ψ
β
Θ
v
tot
v
y
v
x
Θ
R
R
B
1/κ
R
s
R
x
y
z
F
x,3
F
y,3
F
x,4
F
y,4
F
x,1
F
y,1
F
x,2
F
y,2
a
x
a
y
0
1
2
3
4
Figure 1: Top view of vehicle model on a racetrack with
centre line R and track border B (Sedlacek 2020a).
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
16

part according to
T
d
:
= T
+
d
+ T
−
d
. (2)
The total torque and total brake torque are computed
by
T
tot
=
4
∑
k=1
T
k
and T
br,tot
=
4
∑
k=1
T
br,k
, (3)
respectively. Furthermore, we assume δ
1
= δ
f
= δ
2
and δ
3
≡ 0 ≡ δ
4
. The n
u
= 8 system inputs are accu-
mulated in the input vector
u
T
=
T
e
T
+
d
T
−
d
T
T
br
δ
f
∈ R
n
u
(4a)
with T
T
br
=
T
br,1
T
br,2
T
br,3
T
br,4
. (4b)
The longitudinal and lateral vehicle speed at the
COG in the body reference frame are denoted with
v
x
and v
y
, respectively. The yaw rate of the vehi-
cle and the rotational wheel speeds are represented
by
˙
ψ and ω
k
, respectively. The vehicle motion is
described using wheel forces which are represented
by F
b
k
=
F
x,k
F
y,k
T
and F
w
k
=
F
x,k
F
y,k
T
in the
body and the corresponding wheel coordinate frame,
respectively. The wheel forces depend on the wheel
loads and wheel slips, as specified in the appendix.
The longitudinal drag force F
air,x
and the rolling resis-
tance torque T
roll,y,k
are given by (36) and (37), respec-
tively. In the subsequent equations, we use following
parameters: vehicle mass m, vehicle inertia J
zz
, dis-
tance from COG to front axle l
f
or to rear axle l
r
, track
width of front axle b
f
or rear axle b
r
, dynamic rolling
radius of the corresponding tire r
k
and inertia of the
corresponding wheel-unit J
k
. Applying Newton’s sec-
ond law (Schramm et al., 2014) provides equations for
the translational motion
˙v
x
˙v
y
=
1
m
∑
4
k=1
F
x,k
+ F
air,x
∑
4
k=1
F
y,k
| {z }
:
=
h
F
x
F
y
i
T
+
˙
ψv
y
−
˙
ψv
x
(5a)
and the yaw movement of the vehicle
¨
ψ =
Σ
f
l
f
− Σ
r
l
r
+ ∆
f
b
f
2
+ ∆
r
b
r
2
J
zz
(5b)
Σ
f
:
= F
y,1
+ F
y,2
and Σ
r
:
= F
y,3
+ F
y,4
(5c)
∆
f
:
= F
x,2
− F
x,1
and ∆
r
:
= F
x,4
− F
x,3
(5d)
as well as for the rotational wheel motion
˙
ω
k
=
1
J
k
T
k
− F
x,k
r
k
+ T
roll,y,k
∀k ∈ K. (5e)
For the modelling of the SLD, we define the wheel
speed difference of the rear axle and the correspond-
ing differential equation as
ω
d
= ω
4
− ω
3
and
˙
ω
d
=
˙
ω
4
−
˙
ω
3
, (5f)
respectively. In order to avoid an algebraic loop when
computing the wheel loads via (38a), delayed accel-
erations, given in the body reference frame, are in-
troduced using first-order lag elements with time con-
stant τ
acc
˙a
j
=
1
τ
acc
1
m
F
j
− a
j
∀ j ∈ {x, y}. (5g)
These low-pass filters can be motivated by neglected
chassis dynamics (Bianco et al., 2019) and the dy-
namic tire force generation (Sedlacek et al., 2020b).
The centre line of the racetrack is denoted with R
and characterised by its curvature κ
R
over the arc
length s
R
. The track boundary B is described using
the arc length-dependent track half-width d
hw
. The
connection between vehicle model and track is estab-
lished via curvilinear coordinates using (Sharp et al.,
2000)
˙s
R
=
v
x
cos(Θ) − v
y
sin(Θ)
1 − d
R
κ
R
, (6a)
˙
d
R
= v
x
sin(Θ) + v
y
cos(Θ) and (6b)
˙
Θ =
˙
ψ − κ
R
˙s
R
. (6c)
The difference between vehicle orientation and tan-
gent angle of the reference line Θ
R
is given by the
tangent error angle Θ = ψ − Θ
R
. The lateral devia-
tion d
R
describes the normal distance of the tangent
to the COG of the vehicle.
Using (5) and (6), the system behaviour is char-
acterised by a continuous, input nonaffine, nonlinear
differential equation system
˙
x = f(x,u,p) ∈ R
12
(7)
with the state vector
x =
x
veh
x
ref
with x
T
ref
=
s
R
d
R
Θ
, (8a)
x
T
veh
=
v
x
v
y
˙
ψ ω
T
a
x
a
y
(8b)
and ω
T
=
ω
1
ω
2
ω
3
ω
d
. (8c)
Furthermore, the values of the model parameters p are
given in table 2.
3 OPTIMAL CONTROL
PROBLEM
In this section, we present the nonconvex OCP for
completing a lap in minimum time using the model
introduced in section 2. Before formulating the con-
straints and cost function of the OCP in sections 3.2
and 3.3, several preliminaries are outlined in sec-
tion 3.1. Model approximations are introduced to pro-
vide smooth system behaviour and avoid singularities,
Convexification of Semi-activity Constraints Applied to Minimum-time Optimal Control for Vehicles with Semi-active Limited-slip
Differential
17

the free final time OCP is transformed into an OCP
with fixed final arc length and the OCP is scaled to
enhance convergence rate.
The OCP is transcribed via Hermite-Simpson col-
location and posed using the domain-specific mod-
elling language JuMP (Dunning et al., 2017) for
mathematical optimisation embedded in the program-
ming language Julia. The resulting nonlinear pro-
gram is solved with IPOPT which uses a primal-dual
interior-point strategy with a filter line-search and fur-
ther features for performance enhancement (W
¨
achter
and Biegler, 2006). Forward Mode Automatic Differ-
entiation is embedded in the JuMP-framework yield-
ing the necessary gradients and Hessians in advance
in machine precision.
3.1 Preliminaries
We adopt the smooth approximations introduced
in (Sedlacek et al., 2020a) to provide a differentiable
system for the computation of the derivatives. On the
one hand, we smooth the longitudinal slips (42a) via
λ
x,k
≈
∆
v,k
1
2
Σ
v,k
+
q
∆
2
v,k
+ ε
λ,x
(9a)
with ∆
v,k
= ω
k
r
k
− v
x,k
and (9b)
Σ
v,k
= ω
k
r
k
+ v
x,k
∀k ∈ K. (9c)
On the other hand, the total slips in (43c) are replaced
by
λ
k
≈
q
λ
2
n,x,k
+ λ
2
n,y,k
+ ε
λ,tot
∀k ∈ K (9d)
which also eliminates the singularity in (43d).
Minimum-time OCPs have a free final time. To
generate a fixed final arc length problem, we change
the independent variable to the arc length of the ref-
erence line associating all inputs and states explicitly
to the position on the racetrack (Perantoni and Lime-
beer, 2014). This transformation requires a scaling of
the differential equation system according to
x
0
(s
R
) =
∂x
∂s
R
=
˙
x
1
˙s
R
=
1
˙s
R
f =
:
˜
f. (10)
After the transformation, the elapsed time is retrieved
by the differential equation
t
0
(s
R
) =
∂t
∂s
R
=
1
˙s
R
with t(s
R,0
) = 0. (11)
With transformation (10) in mind, we exchange the
independent variables in the state vector (8) resulting
in
˜
x
T
=
x
T
veh
t d
R
Θ
. (12)
The corresponding differential equation in (7) is re-
placed with (11) and the right-hand side of the differ-
ential equation system is adapted according to (10).
The OCP is scaled according to (Sedlacek et al.,
2020a) to improve convergence speed. This includes
adapting the states and inputs, which represent deci-
sion variables when collocation is used, to lie within
the the range [−1,1]. Furthermore, constraints are
normalised to the domain [−1, 0]. The interrelations
between the scaled and non-scaled variables are given
by
ˆ
x = S
˜x
˜
x + k
˜x
⇔
˜
x = S
−1
˜x
(
ˆ
x − k
˜x
) (13a)
ˆ
u = S
u
u + k
u
⇔ u = S
−1
u
(
ˆ
u − k
u
) (13b)
ˆ
f(
ˆ
x,
ˆ
u) = S
˜x
˜
f(
ˆ
x,
ˆ
u). (13c)
Adequate values for the scaling matrices S
˜x
and S
u
as well as the shifting vectors k
˜x
and k
u
are given
in (Sedlacek et al., 2020a).
3.2 Constraints
This section presents the constraints for the contem-
plated optimisation problem which are used to con-
sider the system dynamics, set initial values, capture
non-modelled physical effects and avoid numerical
problems.
3.2.1 Collocation Constraints
We use Hermite-Simpson collocation to consider the
continuous system dynamics (13c) in the OCP. Thus,
the system inputs and the right-hand sides of the
differential equations are approximated by piecewise
quadratic polynomials. The integration interval s
R
∈
[s
R,0
,s
R, f
] is divided into n
seg
segments with n
coll
=
n
seg
+1 collocation points. Simpson quadrature is ap-
plied on each segment i = 0,. . .,n
seg
− 1 yielding the
collocation constraints
ˆ
x
i+1
−
ˆ
x
i
=
h
i
6
(
ˆ
f
i
+ 4
ˆ
f
i+
1
2
+
ˆ
f
i+1
) (14a)
ˆ
x
i+
1
2
=
1
2
(
ˆ
x
i
+
ˆ
x
i+1
) +
h
i
8
(
ˆ
f
i
−
ˆ
f
i+1
) (14b)
with the segment width h
i
= s
R,i+1
−s
R,i
(Betts, 2010;
Kelly, 2017). The margins of each segment repre-
sent collocation points with the corresponding values
(·)
i
and (·)
i+1
. Values at the midpoint are marked as
(·)
i+
1
2
. All following constraints, except for the initial
conditions, are set at each collocation point and mid-
point but we omit the index for readability. Once the
optimal values at the collocation points and midpoints
are computed, the intermediate values for the inputs
and states are determined by piecewise quadratic and
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
18
piecewise cubic polynomials, respectively. The cor-
responding formulas can be found in (Sedlacek et al.,
2020a).
3.2.2 Initial Values
The vehicle starts at the centre of the racetrack in
alignment with the reference line yielding d
R
= Θ =
ψ = 0. The first track section is straight, thus lateral
speed, yaw rate and initial steering angles are set to
zero. By setting the initial longitudinal speed to a
small value v
x
= v
x,k
= 1
m
s
, we avoid the singularity
of the tire slip angles (42b) at vanishing speed. We
presume that the vehicle is initially in steady-state, no
brake torque is applied, the SLD is open and aerody-
namic forces are compensated by the rear tire forces.
Thus, accelerations are zero resulting in only static
wheel loads. Then, (5a) and (5e) enable the compu-
tation of the front and rear tire forces as well as the
engine torque according to (Sedlacek et al., 2020b)
F
x,1
=
1
r
1
T
roll,y,1
= F
x,2
, (15a)
F
x,3
=
1
2
(−F
air,x
− F
x,1
− F
x,2
) = F
x,4
, (15b)
T
e
= F
x,3
r
3
+ F
x,4
r
4
− T
roll,y,3
− T
roll,y,4
. (15c)
Using the tire forces (15a)-(15b), the longitudinal slip
can be computed from (43f) and the initial rotational
wheel speeds can be identified via (42a).
3.2.3 Input Constraints
Due to actuator limitations, box constraints are set for
the brake torques
0 ≤ T
br,k
≤ T
br,k
∀k ∈ K (16)
as well as for the front steering angle
− δ
f
≤ δ
k
≤ δ
f
∀k ∈ {1,2}. (17)
The wheel-based engine torque depends on the en-
gine characteristic as well as the gear ratios and effi-
ciencies of transmission and SLD. Since we assume
a rigid connection between engine and rear axle, the
torque constraint is formulated utilising the rotational
speed of the rear axle
ω
r
≈
1
2
(ω
3
+ ω
4
). (18)
Assuming constant mechanical efficiencies and an au-
tomatic selection of the optimal gear, the admissible
set for the wheel-based engine torque T
e
is approxi-
mated by the constraints
0 ≤ T
e
≤ T
e
and T
e
≤
P
e
ω
r
=
:
T
e,pow
(19a)
using the maximum engine torque T
e
and maximum
engine power P
e
(Sedlacek et al., 2020b; Gillespie,
1992). We presume that the vehicle has a launch
control functionality which immediately provides the
maximum torque T
e
at the race start. Thus, the com-
bined constraint
T
e,con
:
= min(T
e
,T
e,pow
) (20)
represents the upper boundary for the engine torque.
3.2.4 Semi-activity Constraint
Semi-active components do not introduce energy
into systems and thus fulfill the passivity con-
straint (Savaresi et al., 2010). In this section, we
present a novel convexification procedure for semi-
active components which have a convex subset in
each of the two quadrants dictated by the passivity
premise. The approach is depicted using the SLD as
an example, whereas we compare our method with
previous approaches.
The SLD enables a lateral distribution of torque,
however the direction of the torque transfer depends
on the rotational speed difference ω
d
within the SLD.
As mentioned in section 1, previous approaches have
modelled the differential torque via
T
d
= ξ
d
ω
d
(21)
or a more complicated version with trigonometric
functions. If T
d
and ξ
d
are chosen as system inputs,
the SLD can be included into the OCP using the con-
straints
T
d
= ξ
d
ω
d
(22a)
−T
d
≤ T
d
≤ T
d
(22b)
−T
e
≤ T
d
≤ T
e
(22c)
with T
d
denoting the maximum differential torque of
the SLD. With ξ
d
and ω
d
being an input and state,
ω
d
ω
−ω
T
d
T
d
−T
d
S
+
T
S
−
T
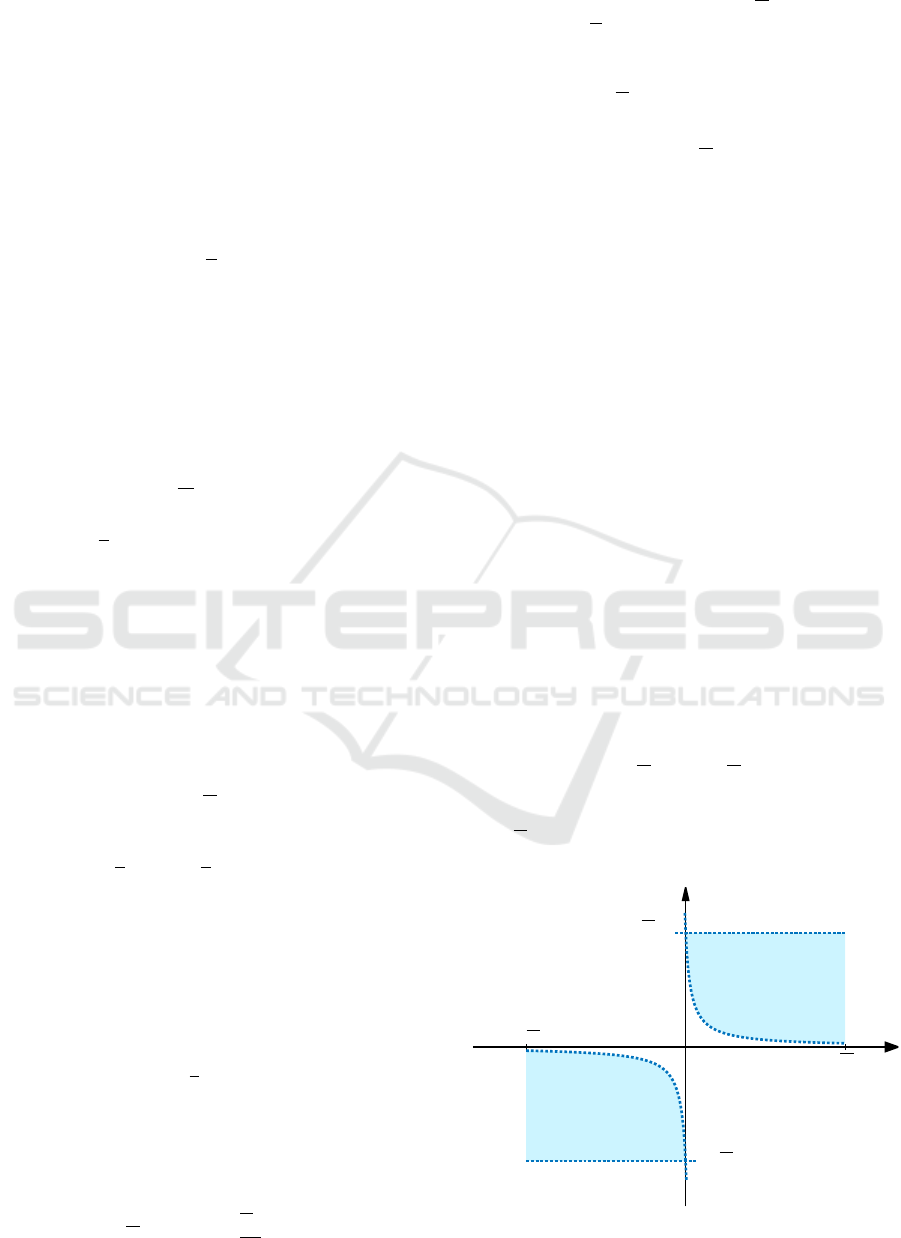
Figure 2: Convexified set for SLD (exaggerated).
Convexification of Semi-activity Constraints Applied to Minimum-time Optimal Control for Vehicles with Semi-active Limited-slip
Differential
19

both represent optimisation variables. Thus, equal-
ity constraint (22a) is quadratic in the optimisation
parameters and would prevent a convex OCP before-
hand (Boyd and Vandenberghe, 2004).
Alternatively, (21) can be inserted into the differ-
ential equations with ξ
d
being a system input. How-
ever, this would result in the nonconvex sets
−T
d
≤ ξ
d
ω
d
≤ T
d
(23a)
−T
e
≤ ξ
d
ω
d
≤ T
e
. (23b)
In this paper, we suggest splitting the differential
torque T
d
into a positive part T
+
d
and a negative
one T
−
d
which enables the formulation of the convex
sets
−T
e
≤ T
+
d
+ T
−
d
≤ T
e
(24a)
S
+
T
:
= {(T
+
d
,ω
d
)|T
+
d
∈
0,T
d
∧ g
+
T
≤ 0} (24b)
with g
+
T
:
= −T
+
d
ω
d
+
ε
T
T
d
+ ε
T
(24c)
S
−
T
:
= {(T
−
d
,ω
d
)|T
−
d
∈
−T
d
,0
∧ g
−
T
≤ 0} (24d)
with g
−
T
:
= −T
−
d
ω
d
−
ε
T
T
d
+ ε
T
. (24e)
Figure 2 depicts sets (24b) and (24d). Being confined
to the first and third quadrant, the passivity constraint
is satisfied. By selecting a sufficiently small parame-
ter ε
T
= 10
−10
, the excluded area for simultaneously
small wheel speed differences ω
d
and small differen-
tial torques T
d
is negligible. Notice that with (24b)-
(24e) from ω
d
= 0 follows T
+
d
= T
d
= −T
−
d
which
results in T
d
= 0. However, we point out that this con-
vexification comes at the price of a larger OCP due to
one extra input and additional constraints.
Theorem 1. The set given by (24) is convex.
Proof. Convexity of set (24) is proven using theorems
from (Boyd and Vandenberghe, 2004). Set (24a) rep-
resents a half-space which is convex. We denote the
graph associated with the epigraph (24c) by
f (T
+
d
)
:
=
ε
T
T
+
d
−
ε
T
T
d
. (25a)
The second derivative of (25a)
f
00
(T
+
d
) =
2ε
T
T
+
d
3
> 0 ∀T
+
d
> 0 (25b)
is positive for the parameter range T
+
d
∈ T
+
:
=
0,T
d
given in (24b). Thus, the graph is convex in this
region and consequently (24c) represents a convex
set for T
+
d
∈ T
+
. Furthermore, the box constraint
T
+
d
∈ T
+
in (24b) defines a polyhedron which is also
convex. The intersection of convex sets results in a
convex set. Thus, set (24b) is convex. The convexity
proof of (24d) is equivalent, since sets (24b) and (24d)
are established analogously. Finally, the intersection
of the convex sets (24a), (24b) and (24d) yields a con-
vex set.
Remark 1. It is tempting to choose the set
S
+
T
:
= {(T
+
d
,ω
d
)|T
+
d
∈
0,T
d
∧ T
+
d
ω
d
≥ 0}.
However, this set is nonconvex since it includes ar-
bitrary ω
d
, such as ω
d
= −c < 0, if T
+
d
= 0. If we
exclude T
+
d
= 0 by choosing the convex set
S
+
T
:
= {(T
+
d
,ω
d
)|T
+
d
∈
0,T
d
∧ T
+
d
ω
d
≥ 0},
we still cannot guarantee that T
d
= 0 ∀ω
d
= 0.
Remark 2. The presented approach is applicable to
other semi-active actuators with convex subsets in
the first and third quadrant. Considering semi-active
dampers with damper speed v
d
, a possible convex set
can be approximated by splitting the damper force ac-
cording to F
d
= F
+
d
+ F
−
d
and using the constraints
k
d
v
d
≤ F
+
d
≤ k
d
v
d
and F
+
d
≤
ˆ
k
d,0
+
ˆ
k
d,1
v
d
with analogous constraints for F
−
d
. Therein we use
coefficients k
d
and k
d
to restrict the admissible area
yielding F
+
d
(v
d
= 0) = 0 and employ an upper bound-
ary using a linear constraint with parameters
ˆ
k
d,0
and
ˆ
k
d,1
. Note that by using different constraint parame-
ters for F
+
d
and F
−
d
, differing characteristics for com-
pression and rebound can be implemented without
discarding smoothness of the OCP. Other convex sub-
sets for semi-active dampers are depicted in (Savaresi
et al., 2010).
3.2.5 State Constraints
Since driving backwards is not expedient on race-
tracks, positive longitudinal speeds and wheel speeds
are enforced by the box constraints
0 < v
x
≤ v
x
≤ v
x
and 0 ≤ ω
k
≤ ω ∀k ∈ K. (26)
The yaw rate and steering angles are generally small
enough, especially on racetracks, that (26) results
in v
x,k
,v
x,k
> 0 (Sedlacek et al., 2020b). This enables
the simplification made in (42a) and avoids the singu-
larity in (42b).
In order to keep the vehicle on the racetrack, the path
constraints
− d
hw
+
b
veh
2
≤ d
R
≤ d
hw
−
b
veh
2
(27)
limit the lateral deviation of the vehicle employing the
arc length-dependent track half-width d
hw
and chassis
width b
veh
.
For an efficient tire usage, we restrict the tire
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
20

forces (43) to stay within the region of adhesion
which excludes sliding and thus decreases tire wear.
Since tire wear reduces the tire force potential, this
constraint is eligible. This is accomplished by the
load-dependent friction ellipse constraints for the tire
slips
λ
x,k
λ
?
x,k
!
2
+
λ
y,k
λ
?
y,k
!
2
− 1 ≤ 0 ∀k ∈ K (28)
using (42a), (42b) and (44b) (Sedlacek et al., 2020b).
When wheels lift off, no tire force can be gener-
ated. To avoid introducing additional discontinuities
as in (Perantoni and Limebeer, 2014) and since the
lift-off of wheels is undesired for industrial sports
cars, we enforce positive wheel loads (38a) with
F
z,k
> 0 ∀k ∈ K. (29)
Furthermore, the additional constraint
˙s
R
≥ ε
˙s
> 0 (30)
is employed to avoid dividing by zero when using the
transformation (10). Since we exclude driving back-
wards, this assumption is legitimate.
3.3 Objective
The cost function is comprised of three objectives ac-
cording to
J = J
t
+ J
˙u
+ J
η
. (31)
The main goal is minimising the required lap time
which is accomplished with
J
t
=
Z
t
f
t
0
1dt =
Z
s
R, f
s
R,0
1
˙s
R
ds
R
= t(s
R, f
). (32)
To avoid non-unique solutions and therefore improve
convergence, a small regularisation term which is
quadratic in the inputs can be added to the objective
function (Kelly, 2017). Using Simpson quadrature
and the input derivative vector
ˆ
u
0
(s
R
), we include the
regularisation term
J
˙u
= ε
˙u
n
u
∑
j=1
n
seg−1
∑
i=0
h
i
6
j
˙u,ji
(33a)
j
˙u,ji
= ˆu
0
j
(s
R,i
)
2
+ 4 ˆu
0
j
s
R,i
+
h
i
2
2
+
ˆu
0
j
(s
R,i
+ h
i
)
2
(33b)
which generates a preference for smooth input solu-
tions. Smooth inputs are generally desirable for hu-
man drivers which justifies the penalty term (33a).
The computation of the input derivatives is shown
in (Sedlacek et al., 2020a).
To enhance efficiency and durability, simultaneous
drive and brake torques are avoided by adding the ob-
jective (Sedlacek et al., 2020b)
J
η
=
ε
η
T
norm
n
seg
−1
∑
i=0
h
i
6
j
η,i
(34a)
j
η,i
= T
η
(s
R,i
) + 4 T
η
s
R,i
+
h
i
2
+
T
η
(s
R,i
+ h
i
)
(34b)
T
η
(s
R,i
) = T
e
(s
R,i
)T
br,tot
(s
R,i
) (34c)
T
norm
= T
e
+ T
br,r
. (34d)
The unscaled torques are used in (34c), since they are
limited to positive values. Scaling factors ε
˙u
and ε
η
are chosen sufficiently small so that the modified ob-
jective (31) is nearly time-optimal.
4 RESULTS
The OCP presented in section 3 is solved using a dis-
cretisation mesh of 1000 equally spaced collocation
points yielding a mesh interval of about 2.5 metres.
The optimal trajectories for the vehicle with an open
differential at the rear axle instead of the SLD, which
we name setup C0, have been computed in (Sedlacek
et al., 2020b). Configuration C1 represents a vehicle
with SLD at the rear axle and T
d
= 1250Nm. Us-
ing (38b), we define the torque shift variable as
k
d
:
= −
T
d
F
z,0,r
with F
z,0,r
= ρ
1
l
f
gr
3
. (35)
It represents the lateral torque shift of the SLD nor-
malised by the static rear axle load. The torque shift
variable (35) is displayed in figure 3 together with
the acceleration and braking points which are char-
acterised by sign changes in T
tot
. The first subplot of
figure 4 illustrates the track curvature and the lap time
advantage progression ∆t of C1. The wheel speed
difference and differential torque for C1 are shown
in the second subplot. The third subplot considers
setup C1 and depicts the individual wheel torques,
the total torque and the upper boundary for the engine
torque (20).
As expected, acceleration starts at the corner
apexes and high speed corners like
1
and
3
are
passed without braking. The lateral wheel load
shift during cornering results in different optimal
slips (44b) between the left and right wheel of an
axle. Thus, the SLD enhances traction conditions dur-
ing cornering by applying a higher drive torque to the
outer wheel at the expense of a lower drive torque at
the inner wheel. Only small torques are transmitted
Convexification of Semi-activity Constraints Applied to Minimum-time Optimal Control for Vehicles with Semi-active Limited-slip
Differential
21
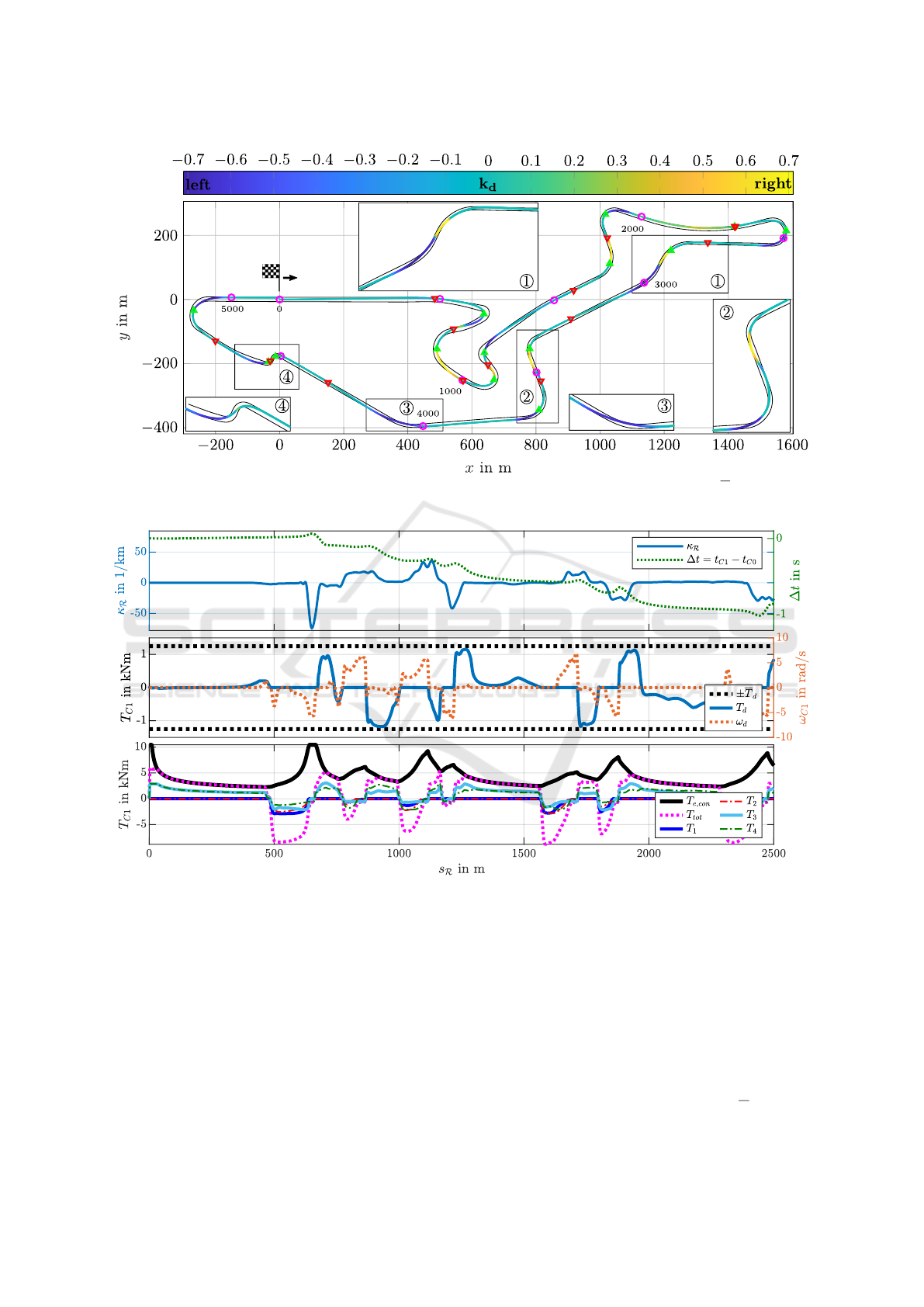
Figure 3: Normalised torque shift variable for lateral drive torque distribution via SLD at the rear axle with T
d
= 1250 Nm.
Symbols: ◦ 500m marks, M start acceleration, O start braking.
Figure 4: Track curvature, progression of lap time benefit, wheel speed difference and torques.
by the SLD when driving on paths with small curva-
ture and no differential torque is applied during brak-
ing due to (24a) and (34a). The lateral torque distribu-
tion, either by the SLD or the braking system, affects
the yaw motion of the vehicle: An additional yaw mo-
mentum is generated by the difference in longitudinal
tire forces between the left and right side. When ac-
celerating after corner apexes, the lateral drive torque
allocation by the SLD increases agility, whereas a
stabilising momentum is induced by the braking sys-
tem before corners. The lateral drive torque distribu-
tion by the SLD is primarily performed after corner
apexes to enhance acceleration and agility. With a lap
time of 146.68 seconds, an overall improvement of
2.37 seconds or 1.59% is achieved, whereas lap time
benefits due to the SLD occur primarily when exiting
corners.
The lap time sensitivity regarding the maximum
torque of the SLD is depicted in figure 5. The sensi-
tivity curve is constructed via cubic spline interpola-
tion of computed sampling points which are generated
by solving the OCP for several values of T
d
. Gener-
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
22
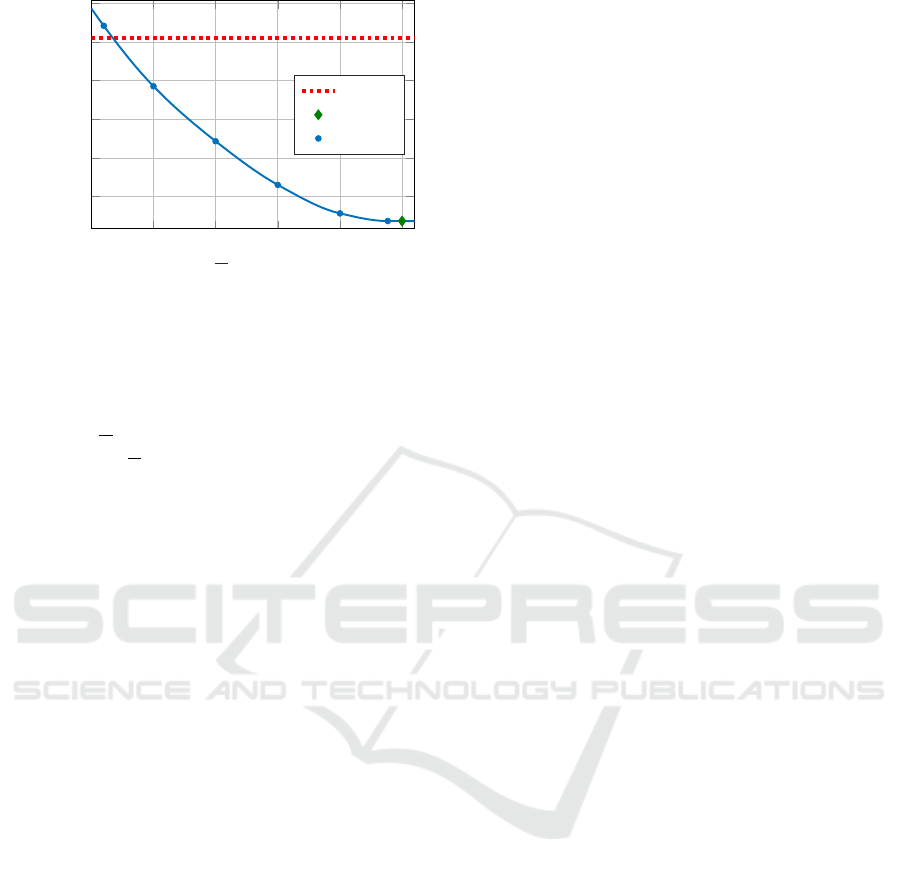
0
250 500 750
1000
1250
147
147.5
148
148.5
149
149.5
T
d
in Nm
t
f
in s
C0
C1
sample
Figure 5: Lap time over maximum torque of SLD.
ally, the increased vehicle weight and inertia due to
the SLD, implemented according to (Sedlacek et al.,
2020b), is detrimental for cornering. The benefit of
lateral drive torque allocation outweighs this disad-
vantage for T
d
> 87.3Nm, whereas lap time reduces
with increasing T
d
. Since for the current track and ve-
hicle setup |T
d
| ≤ 1193Nm holds, lap time reductions
due to the SLD only occur up this threshold value.
However, this result strongly depends on the consid-
ered track and vehicle setup.
5 CONCLUDING REMARKS
A novel OCP-modelling approach for a broad class
of semi-active actuators has been presented. The pro-
cedure transforms the originally nonconvex set dic-
tated by the passivity constraint into multiple con-
vex sets. However, this convexification requires an
extra input and generally a higher number of con-
straints. The method has been applied to compute
minimum-lap-time trajectories for a vehicle with rear-
wheel drive and SLD at the rear axle. The OCP
has been solved using Hermite-Simpson collocation
implemented in an open-source framework. Com-
pared to a vehicle with open differential instead of
the SLD, lap time is greatly reduced by 2.37 seconds
or 1.59% with lap time benefits primarily occurring
when exiting corners. Although the overall OCP re-
mains nonconvex for the considered application, the
presented convexification measure is a first step to-
wards a fully convex OCP for such vehicles which
we will address in the future. Considering our pre-
vious work (Sedlacek et al., 2020b; Sedlacek et al.,
2020a), the proposed method will be used to com-
pare different powertrain topologies for vehicles with
combustion engine or electric machines while simul-
taneously identifying the respective optimal passive
vehicle setups. A detailed experimental comparison
of the proposed modelling-method with the existing
methods presented in section 3.2.4 is subject of future
work.
REFERENCES
Betts, J. T. (2010). Practical Methods for Optimal Control
and Estimation Using Nonlinear Programming. So-
ciety for Industrial and Applied Mathematics, second
edition.
Bianco, N. D., Bertolazzi, E., Biral, F., and Massaro, M.
(2019). Comparison of direct and indirect methods for
minimum lap time optimal control problems. Vehicle
System Dynamics, 57(5):665–696.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press, Cambridge, sev-
enth edition.
Cheli, F., Pedrinelli, M., Resta, F., Travaglio, G., Zanchetta,
M., and Zorzutti, A. (2006). Development of a new
control strategy for a semi-active differential for a
high-performance vehicle. Vehicle System Dynamics,
44(sup1):202–215.
Dunning, I., Huchette, J., and Lubin, M. (2017). Jump:
A modeling language for mathematical optimization.
SIAM Review, 59(2):295–320.
Gillespie, T. (1992). Fundamentals of Vehicle Dynamics.
SAE International.
Kelly, D. (2008). Lap time simulation with transient vehicle
and tyre dynamics. PhD thesis, Cranfield University.
Kelly, M. (2017). An introduction to trajectory optimiza-
tion: How to do your own direct collocation. SIAM
Review, 59(4):849–904.
Kim, Y., Kwon, C., Moon, H., Kim, K., Cho, J., and Kong,
K. (2018). Optimization of semi-active pneumatic ac-
tuators for an exoskeleton robot for running. 2018
15th International Conference on Ubiquitous Robots
(UR), pages 119–124.
Kr
¨
uger, W. (2000). Integrated design process for the de-
velopment of semi-active landing gears for transport
aircraft. PhD thesis, University of Stuttgart.
Limebeer, D., Perantoni, G., and Rao, A. (2014). Optimal
control of formula one car energy recovery systems.
International Journal of Control, 87(10):2065–2080.
Limebeer, D. J. N. and Perantoni, G. (2015). Optimal con-
trol of a formula one car on a three-dimensional track-
part 2: Optimal control. Journal of Dynamic Systems,
Measurement, and Control, 137(5).
Perantoni, G. and Limebeer, D. J. (2014). Optimal control
for a formula one car with variable parameters. Vehi-
cle System Dynamics, 52(5):653–678.
Poussot-Vassal, C., Savaresi, S. M., Spelta, C., Sename, O.,
and Dugard, L. (2010). A methodology for optimal
semi-active suspension systems performance evalua-
tion. In 49th IEEE Conference on Decision and Con-
trol (CDC), pages 2892–2897.
Savaresi, S. M., Poussot-Vassal, C., Spelta, C., Sename, O.,
and Dugard, L. (2010). Semi-Active Suspension Con-
trol Design for Vehicles. Elsevier, first edition.
Convexification of Semi-activity Constraints Applied to Minimum-time Optimal Control for Vehicles with Semi-active Limited-slip
Differential
23

Schramm, D., Hiller, M., and Bardini, R. (2014). Vehi-
cle Dynamics - Modeling and Simulation. Springer,
Berlin, Heidelberg.
Sedlacek, T., Odenthal, D., and Wollherr, D. (2020a).
Minimum-time optimal control for battery electric ve-
hicles with four wheel-independent drives considering
electrical overloading. Vehicle System Dynamics, Sub-
mitted for publication.
Sedlacek, T., Odenthal, D., and Wollherr, D. (2020b).
Minimum-time optimal control for vehicles with ac-
tive rear-axle steering, transfer case and variable pa-
rameters. Vehicle System Dynamics, pages 1–29.
Sharp, R., Casanova, D., and Symonds, P. (2000). A mathe-
matical model for driver steering control, with design,
tuning and performance results. Vehicle System Dy-
namics, 33(5):289–326.
Tremlett, A., Massaro, M., Purdy, D., Velenis, E., Assadian,
F., Moore, A., and Halley, M. (2015). Optimal control
of motorsport differentials. Vehicle System Dynamics,
53(12):1772–1794.
Tremlett, A. J. and Limebeer, D. J. N. (2016). Optimal tyre
usage for a formula one car. Vehicle System Dynamics,
54(10):1448–1473.
W
¨
achter, A. and Biegler, L. T. (2006). On the implementa-
tion of an interior-point filter line-search algorithm for
large-scale nonlinear programming. Math. Program.,
106(1):25–57.
APPENDIX
Subsequently, further modelling details are addressed.
We assume windless conditions and consider the lon-
gitudinal drag force (Schramm et al., 2014)
F
air,x
= −
1
2
ρ
air
c
air,x
A
air
v
x
q
v
2
x
+ v
2
y
. (36)
The parameters are air density ρ
air
, drag coeffi-
cient c
air,x
and vehicle crossspan area A
air
. Due to
rolling resistance forces, the tires are subject to load-
dependent torques opposed to the rolling direction
T
roll,y,k
= − f
roll,0
F
z,k
r
k
(37)
with the rolling resistance coefficient f
roll,0
.
For simplicity, quasi steady-state conditions are pre-
sumed for the wheel load computation. Assuming
that the roll momentum is allocated via the roll mo-
ment distribution factor ξ
roll
, the wheel loads are com-
puted via (Sedlacek et al., 2020b)
F
z,1
F
z,2
F
z,3
F
z,4
= ρ
1
l
r
g − h a
x
l
r
g − h a
x
l
f
g + h a
x
l
f
g + h a
x
+ ρ
2
−ξ
roll
b
f
ξ
roll
b
f
ξ
roll
−1
b
r
1−ξ
roll
b
r
(38a)
with ρ
1
=
m
2(l
f
+ l
r
)
and ρ
2
= m h a
y
. (38b)
The velocity of the wheel centre points in the
body coordinate frame is denoted with v
b
k
=
v
x,k
v
y,k
T
∀k ∈ K and computed by
v
b
1
=
v
x
−
˙
ψ
b
f
2
v
y
+
˙
ψl
f
, v
b
2
=
v
x
+
˙
ψ
b
f
2
v
y
+
˙
ψl
f
, (39a)
v
b
3
=
v
x
−
˙
ψ
b
r
2
v
y
−
˙
ψl
r
and v
b
4
=
v
x
+
˙
ψ
b
r
2
v
y
−
˙
ψl
r
. (39b)
These speeds are transformed into the corresponding
wheel coordinate frame via
v
w
k
=
v
x,k
v
y,k
= R
z
(δ
k
)
v
x,k
v
y,k
∀k ∈ K. (40)
Therein the two-dimensional rotation matrix
R
z
(γ)
:
=
cos(γ) sin(γ)
−sin(γ) cos(γ)
(41)
performs a mathematical rotation by the angle γ
around the z-axis of the inertial frame. Assuming
ω
k
,v
x,k
≥ 0 ∀k ∈ K, the longitudinal wheel slips are
defined as
λ
x,k
=
ω
k
r
k
− v
x,k
max
ω
k
r
k
,v
x,k
. (42a)
The wheel slip angles are given by
λ
y,k
= δ
k
− arctan
v
y,k
v
x,k
!
. (42b)
We employ the tire model presented in (Sedlacek
et al., 2020b) which is based on (Kelly, 2008). For
readability, we only list the basic equations for the
longitudinal tire forces and omit the index k. Equa-
tions for the lateral tire forces are constructed analo-
gously. The tire parameters differ in the longitudinal
and lateral direction as well as for the front and rear
wheels. The linear equations
λ
max,x
=
¯
λ
b,x
−
¯
λ
a,x
¯
F
b
−
¯
F
a
F
z
−
¯
F
a
+
¯
λ
a,x
(43a)
D
x
=
¯
D
b,x
−
¯
D
a,x
¯
F
b
−
¯
F
a
F
z
−
¯
F
a
+
¯
D
a,x
(43b)
approximate the load-dependent tire slip optimum
and the nonlinear wheel load degressivity, respec-
tively. The variables in (43a) and (43b) marked as
¯
(·)
represent fixed tire parameters. The normalised slips
and the combined slip coefficient are defined as
λ
n,x
=
λ
x
λ
max,x
and λ =
q
λ
2
n,x
+ λ
2
n,y
, (43c)
respectively. Using the tire shape parameter C
x
, the
tire force shape curve is characterised by
F
shape,x
=
λ
n,x
λ
sin
C
x
arctan(B
x
λ)
(43d)
with B
x
=
π
2 arctan(C
x
)
. (43e)
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
24

With (38a), (43b), (43d) and the road friction coeffi-
cient µ, the longitudinal component of the tire force is
given by
F
x
= µ F
z
D
x
F
shape,x
. (43f)
The total tire force F
w
=
F
x
F
y
reaches its peak
values at the friction limit which can be represented
by the ellipse equation
λ
x
λ
?
x
2
+
λ
y
λ
?
y
2
= 1. (44a)
The positive optimum slip values are given by
λ
?
x
=
tan
π
2C
x
(F
z
−
¯
F
a
)
¯
λ
b,x
− (F
z
−
¯
F
b
)
¯
λ
a,x
B
x
(
¯
F
b
−
¯
F
a
)
.
(44b)
With F
w
k
∀k ∈ K denoting the tire force vector in the
corresponding wheel coordinate frame, the tire force
components in the body reference frame are given by
F
b
k
= R
z
(−δ
k
)F
w
k
∀k ∈ K. (45)
Parameter values for the considered OCP and the ve-
hicle model are listed in table 1 and 2, respectively.
Table 1: Parameter values for OCP.
variable value
optimisation
T
br,1/2
/T
br,3/4
7024 Nm/4032 Nm
T
e
/P
e
10.5 kNm/390.6 kW
δ
f
0.6981 rad
v
x
/v
x
0.9 ms
−1
/83.3 ms
−1
ω 277.8 rad/s
ε
˙u
/ε
η
2 · 10
−2
/2 · 10
−4
ε
˙s
1.0 ms
−1
ε
λ,x
/ε
λ,tot
10
−6
/10
−8
Table 2: Parameter values for model.
variable value
env.
g 9.81 ms
−2
µ 1.0
ρ
air
1.2041 kgm
−3
tires
¯
F
a
/
¯
F
b
2000 N/6000 N
¯
λ
a,x,1/2
/
¯
λ
b,x,1/2
0.124/0.108
¯
λ
a,y,1/2
/
¯
λ
b,y,1/2
0.144/0.133
¯
D
a,x,1/2
/
¯
D
b,x,1/2
1.560/1.396
¯
D
a,y,1/2
/
¯
D
b,y,1/2
1.603/1.258
C
x,1/2
/C
y,1/2
1.949/1.941
¯
λ
a,x,3/4
/
¯
λ
b,x,3/4
0.111/0.099
¯
λ
a,y,3/4
/
¯
λ
b,y,3/4
0.109/0.099
¯
D
a,x,3/4
/
¯
D
b,x,3/4
1.898/1.597
¯
D
a,y,3/4
/
¯
D
b,y,3/4
1.945/1.515
C
x,3/4
/C
y,3/4
1.949/1.858
vehicle
r
1/2
/r
3/4
0.3429 m/0.3474 m
b
f
/b
r
/b
veh
1.626 m/1.594 m/1.90 m
l
f
/l
r
/h 1.479 m/1.503 m/0.540 m
m/J
zz
1988 kg/3485 kgm
2
J
1/2
/J
3/4
2.20 kgm
2
/6.95 kgm
2
A
air
2.44 m
2
c
air,x
/ f
roll,0
0.31/0.0031
τ
acc
0.03 s
Convexification of Semi-activity Constraints Applied to Minimum-time Optimal Control for Vehicles with Semi-active Limited-slip
Differential
25
