A Function Dependency based Approach for Fault Localization with D

∗

Arpita Dutta

and Rajib Mall

Indian Institute of Technology Kharagpur, India

Keywords:

Function Dependency Graph, Fault Localization, Comprehensibility, Program Analysis, Debugging.

Abstract:

We present a scheme for hierarchically localizing software faults. First the functions are prioritized based on

their suspiciousness of containing a fault. Further, the bug is localized within the suspected functions at the

speciﬁc statement level. In our approach, a new function dependency graph is proposed, and based on that

function prioritization is performed. In order to differentiate between the functions with equal suspiciousness

value, function complexity metrics are considered. We proposed two different dependency edge weighting

techniques, viz., Distribution Speciﬁed Normalization (DSN) method, and Highest Weight Normalization

(HWN) method. These techniques help to measure the relevance of an edge in propagating a fault. We use

spectrum-based fault localization (SBFL) technique DStar(D

∗

) to localize the bugs at the statement level.

We also extended our approach to localize multiple fault programs. Based on our experimental results, it is

observed that using DSN and HWN scoring schemes, there is a reduction of 43.65% and 38.88% of statements

examined compared to the well-accepted SBFL technique DStar(D

∗

) respectively.

1 INTRODUCTION

With the increasing size and complexity of software

systems, bugs are inevitable. Advancements in soft-

ware development techniques and testing practices

help to detect most of the faults in early stages of soft-

ware life cycle (Mall, 2018). However though few

remain, and numerically these are substantial consid-

ering the size of the program. Debugging is a time-

consuming and effort-intensive activity. Bug local-

ization is the most vital task during debugging. Tech-

niques that can minimize the effort and time required

to localize the bugs can help to reduce the overall cost

of development and also enhance the quality of the

software (Wong et al., 2016). In the past two-to-three

decades, various fault localization (FL) techniques are

reported in the literature (Liu et al., 2005; Abreu et al.,

2009; Ascari et al., 2009; Feng and Gupta, 2010;

Wong et al., 2013; Wong et al., 2016; Yu et al., 2017;

Spinellis, 2018; Ardimento et al., 2019; Dutta et al.,

2019; Thaller et al., 2020).

Weiser (Weiser, 1984) proposed the concept of

program slicing. A program slice contains list of

statements that effects the value of a variable at a

speciﬁc location of program. Later, Agrawal et al.

(Agrawal and Horgan, 1990) extended their approach

https://orcid.org/0000-0001-7887-3264

https://orcid.org/0000-0002-2070-1854

by adding the execution-time information of test in-

puts and named their approach as dynamic slicing.

Dynamic slicing helps to minimize the search space

as compared to the static slicing. Program spectrum-

based fault localization (SBFL) techniques are re-

ported as both effective and efﬁcient (Wong et al.,

2013; Liu et al., 2005; Wong et al., 2016). Initially,

SBFL approaches considered only failed test case in-

formation (Korel, 1988), but they were shown to be

ineffective (Agrawal et al., 1995). Later, Jones et

al. (Jones and Harrold, 2005) proposed an executable

statement hit spectrum based FL approach to increase

the effectiveness of the SBFL schemes. Wong and

colleagues (Wong and Qi, 2009; Wong et al., 2010)

and Dutta et al. (Dutta et al., 2019) reported neural

network models for the same.

Several fault localization techniques have become

popular, but these techniques are time-consuming and

ineffective for large-size programs. Even for small

programs, these techniques require to examine 40%-

45% of program code. Our objective is to develop an

FL technique which requires fewer number of state-

ment examination as compared with the contempo-

rary fault localization methods.

For a given source program, we ﬁrstly deﬁne

a Function Dependency Graph (FDG). This graph

is generated by obtaining data, control, and inter-

procedural dependencies from an equivalent control

Dutta, A. and Mall, R.

A Function Dependency based Approach for Fault Localization with D*.

DOI: 10.5220/0009769402730283

In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 273-283

ISBN: 978-989-758-443-5

273

ﬂow graph (CFG) of the same program. We further

assign weights to the dependency edges of the FDG

based on their contribution in propagating a fault.

The value of assigned weights to the dependencies

are computed using the coverage information of the

failed and passed test cases. We reported two dif-

ferent schemes Distribution Speciﬁed Normalization

(DSN) and Highest Weight Normalization (HWN) to

calculate the weights of the dependency edges. Sub-

sequently, the nodes of the FDG are prioritized based

on their suspiciousness values and function compre-

hensibility measure. The hierarchical procedure helps

to reduce the search space to the top most suspicious

functions only. Then, existing spectrum-based FL

technique DStar(D

∗

) is used to prioritize the state-

ments of obtained set the most suspicious functions.

The remaining sections of the paper are written as

follows: ﬁrst, we present the basic concepts in Section

2. Subsequently, the proposed approach is explained

in Section 3. The experimental setup and obtained

results are discussed in Section 4. Section 5, presents

the extension of our proposed approach to handle pro-

grams with multiple faults. Threats to the validity of

experimental results are discussed in Section 6. We

present a comparison with related works in Section 7.

Lastly, we conclude our work in Section 8.

2 BASIC CONCEPTS

This section presents few important deﬁnitions which

are essential to understand our work.

• Program Dependency Graph (PDG). For a pro-

gram P, PDG is represented as G

=(V, E), where

V is the set of nodes representing statements of P

and E is the set of control and data dependency

edges (Mund G. B., 2007).

• System Dependency Graph (SDG). The SDG

for a program P is represented as G

=(V, E),

where V is the set of nodes representing state-

ments of P and E is the set of edges represent

the control, data, and inter-procedure dependen-

cies among the statements (Mund G. B., 2007).

• Weighted System Dependency Graph

(WSDG). A WSDG is primarily a system

dependency graph in which all the dependency

edges ( Data, Control, and Inter-procedure) have

weights linked with them (Deng and Jones,

2012).

• Comprehensibility. The facileness with which a

code segment can be understood is called its com-

prehensibility (Miara et al., 1983). It is inversely

proportional to the code block complexity. If a

code segment is complex and challenging to un-

derstand, then it has a higher possibility of bug

containment.

• DStar(D

∗

). It is a executable hit spectrum based

based FL technique reported by (Wong et al.,

2013). DStar uses a modiﬁed form of Kulczynski

coefﬁcient (Choi et al., 2010). In this method, the

suspiciousness score of statement s is calculated

using Equation 1.

susp(s) =

e f

)

∗

+ s

n f

(1)

where, susp(s) shows the suspiciousness score of

statement s; s

e f

and s

represents the number

of failed and passed test cases that have exer-

cised statement s. s

n f

shows the number of failed

test inputs that have not invoked the statement s.

DStar performs best for

∗

= 2, i.e., D

, in most of

the programs. The ‘

∗

’ is a numerical variable, and

it varies for different programs.

3 PROPOSED APPROACH: FDBD

∗

We named our proposed approach as FDBD

∗

. It is an

abbreviation for Function Dependency Based FL with

∗

In this work, a hierarchical method is used to re-

duce the search space and the time required to local-

ize a fault. We have assumed that a fault is propagated

by exercising various dependencies present in a pro-

gram, from an incorrect statement to the output. Each

time a test case executes, the bug present in a function

gets carried towards the called function by executing

some of the dependencies that exist between them.

The statements present in the functions invoked by the

failed test cases are called as Potential Contributors

for propagating a fault. On the other hand, the de-

pendencies executed by a successful test case are less

potential for propagating a fault. A PDG can model

a program with single function. However, in prac-

tice, a program contains multiple functions. An SDG

is used to represent a program with more than one

functions. But, it represents each instruction as a sin-

gle node. This results to a complex and huge graph,

even for a medium-size program. The space complex-

ity of an SDG is O(s + d) where, s and d represent

the statements presents in the program and dependen-

cies among the statements respectively. Therefore, it

becomes quite expensive to traverse the graph to lo-

calize the faulty instruction for large-size programs.

To solve this problem, we propose a Function Depen-

dency Graph (FDG). It presents a function level ab-

straction of SDG. FDG contains only the dependency

ICSOFT 2020 - 15th International Conference on Software Technologies

274

entry: main

entry: foo1

entry: foo

call: foo

call: foo1

1 2

actual-in and actual-

out arguments

formal-in and formal-

out arguments

calling node

for function

entry node

for function

edges available

in FDG

edges not

available in FDG

Figure 1: Function Dependency Graph.

information among functions and yields an efﬁcient

way to localize the faults.

3.1 Function Dependency Graph (FDG)

Deﬁnition 1. An FDG for a program P is represented

as G = (N, E). It is a directed graph. The nodes in set

N represent the functions, and the edges in set E show

the dependencies exist among the nodes in set N.

Structure of an FDG. Every ordinary C-program

contains the main function and different other func-

tions. We represent each function with a speciﬁc en-

try node called FEN (Function Entry Node). FEN is

connected with three types of nodes (vertices). These

nodes are argument-in, argument-out, and call ver-

tices. Call vertex represents the call site of the func-

tion. Argument-in and -out vertices show the propa-

gation of data from the actual to formal parameters

and from formal to actual parameters, respectively.

These two vertices are control dependent on the con-

nected FEN. Values from the calling function are

copied to the argument-in parameters, and the func-

tion return values are copied back to the argument-out

parameters. Figure 1 represents the generated FDG

for the C-program shown in Figure 2.

3.2 Fault Localization with FDBD

∗

A fault is transmitted from the buggy function to-

wards the output by exercising different dependency

edges. We attach weights to the dependency edges

based on their probability of propagating a bug. The

weight attached to a dependency edge is computed by

the frequency that the edge is being exercised during

the propagation of fault towards the output of the pro-

gram. The weights of the dependency edges exercised

void main(){

int var_a, var_b;

var_a=0;

var_b=1;

var_c=foo(var_a, var_b);

var_d=foo1(var_a);

}

int foo(int var_a,int var_b){

var_a = var_a+var_b;

return var_a;

}

int foo1(int var_c){

return var_c+10;

}

Figure 2: Example C-program with three functions.

by failed test cases are multiplied by a factor that lies

in between 0 to 1. On the other hand, edges used by

passed test cases are multiplied with another factor

that is higher than 1. The dependency edges weights

are inversely proportional to their likelihood of prop-

agating a bug. Speciﬁcally, an edge with a higher

weight has less probability of participating in the fault

propagation.

3.2.1 Weighting Schemes for Dependencies

We ﬁrst present some notations which we use in the

deﬁnition of two different dependency edge scoring

methods:

• P = Number of passed test cases present.

• F = Number of failed test cases present.

• P(i) = Total passed test cases that have invoked

the i

dependency edge (1 ≤ i ≤ n) and n is the

number of dependency edges in FDG.

• F(i) = Total failed test cases that have invoked the

dependency edge (1 ≤ i ≤ n) and n is the num-

ber of dependency edges in FDG.

1. Highest Weight Normalization Method(HWN): In

this method, two heuristic constants, w

pass

> 1)

and w

f ail

(0 < w

f ail

< 1) are used. With these two

constants, we calculate the weight that will be as-

signed to any dependency edge. At the very begin-

ning, weights of all dependency edges are initialized

with 1. For every pass test case, weight of all the in-

voked dependency edges are increased by multiplying

them with a factor w

pass

. In contrary, for the failed

test case, weights of the edges are reduced by multi-

plying them with factor w

f ail

. After the execution of

all test cases, the weight of a dependency edge can be

computed using Equation 2.

W (i) = (w

pass

)

P(i)

∗ (w

f ail

)

F(i)

(2)

A Function Dependency based Approach for Fault Localization with D*

275

where, W (i) presents the weight obtained by the i

dependency edge. Further, weights of the dependen-

cies are normalized with respect to the highest weight

value obtained by the considered set of dependency

edges using Equation 3.

NW (i) =

(W(i))

max(W(1), ...,W (n))

(3)

where, NW (i) and n represents the normalized weight

of dependency edge i and number of dependency

edges present in FDG, respectively.

2. Distribution Speciﬁed Normalization Method

(DSN): It is usually noticed that during the execu-

tion of a test suite, some of the dependency edges

are invoked in every execution. These edges are in-

voked by all the pass and the failed test cases. Assume

that there are 80% of fail and 20% of pass test cases

present in a test suite. Then, even if the edges are not

involved in propagating any fault, but they are com-

puted as suspicious for 80% of test cases. Here, the

weight attained by a dependency edge is dominated

by the factor w

f ail

over w

pass

To overcome the above-stated problem, we pro-

pose another dependency edge scoring scheme called

DSN. Our scheme considers the distribution of the

failed as well as the passed test cases for an exercised

dependency to assign the weight. In this method,

we use the previously determined factor w

f ail

(0 <

f ail

< 1) as it is. Whereas, we compute the value

of w

pass

based on the distribution of both failed and

passed test cases. The dependency edges that are in-

voked by every test input are known as unbiased de-

pendencies. We deﬁne some notations related to an

unbiased dependency:

1. PU(i): Number of pass test inputs which have ex-

ercised the i

unbiased dependency edge.

2. FU(i): Number of fail test inputs which have ex-

ercised the i

unbiased dependency edge.

With the above two notations, we compute the value

of factor w

pass

using Equation 4.

pass

)

PU(i)

∗ (w

f ail

)

FU(i)

= 1

pass

= [

f ail

)

FU(i)

]

PU(i)

(4)

By using these values for w

pass

and w

f ail

, we cal-

culate the weight of the rest dependencies using Equa-

tion 5:

W (i) = (w

pass

)

P(i)

∗ (w

f ail

)

F(i)

(5)

In the proposed DSN scheme, value of heuristic pa-

rameter w

pass

is required to be computed separately

for each program, unlike the HWN scheme. Further,

we normalize weights of all dependency edges with

Equation 3, and they have values in range of 0 to 1.

3.2.2 Prioritization of Functions

After the weight assigned to all the dependency edges,

the next step is to discover the potential contributors.

For this, we calculate the Fault Propagation score (FP-

score) of each FEN. FEN represents a function in

FDG. Hence, FP-score shows the suspiciousness of

a function for containing a fault. Dependencies enter-

ing and leaving into the function are liable for prop-

agating a fault. We take average of all the dependen-

cies connected with a FEN to calculate the FP-score,

as shown in Equation 6.

FP-score =

∑

i=m

i=1

NW (i) +

∑

j=n

j=1

NW ( j)

m + n

(6)

Where, m and n represents the number of incoming

and outgoing dependencies to an FEN. After assign-

ing weights to all the FENs, the resultant graph is

termed as a weighted dependency graph (WFDG).

3.2.3 Comprehensibility

Given a large-size program and a test suite, it is very

likely that many dependency edges end up with the

same weight. It results in a tie among multiple func-

tions. We considered the fact that complex function

has more chances of containing a fault, to break the

tie among different functions. We calculate the com-

plexity of each function. Because, it is widely ac-

cepted fact that complexity measure directly propor-

tional with the expected number of latent faults (Mc-

Cabe, 1976).

Let CF(i) be the complexity of i

function . We

use the following six metrics to calculate function

complexity: cyclomatic complexity, executable lines

of code (ELOC), count of parameters passed in func-

tion, total number of variables used, number of paths,

and maximum depth of nesting (if structure/ loops).

Each attribute is normalized using min-max normal-

ization using Equation 7 and their resultant values are

in between 0 to 1.

i j

− X

min

max

− X

min

(7)

where, X

max

and X

min

are respective maximum and

minimum values for attribute j among all the func-

tions. X

i j

and X

i j

are the normalized and original

value of j

attribute of i

function. Further, we com-

pute comprehensibility of function i using Equation 8

with normalized attribute values.

CF(i) =

∑

j=1

i j

∑

i=1

∑

j=1

i j

(8)

where, k shows the count of attributes considered.

ICSOFT 2020 - 15th International Conference on Software Technologies

276

void print(int a, int b,int c){

printf("%d %d %d",a,b,c);

}

int add(int a, int b){

a = a + b;

return a;

}

int sub(int a, int b){

a = a * b;

return a;

}

void main(int argc, char **argv){

int a, b,c;

a = 0;

b = 0;

scanf("%d",&a);

if(a>=0){

b=2*a;

c=add(a, b);

print(a,b,c);}

else{

b=-1;

c=sub(a, b);

print(a,b,c);}

}

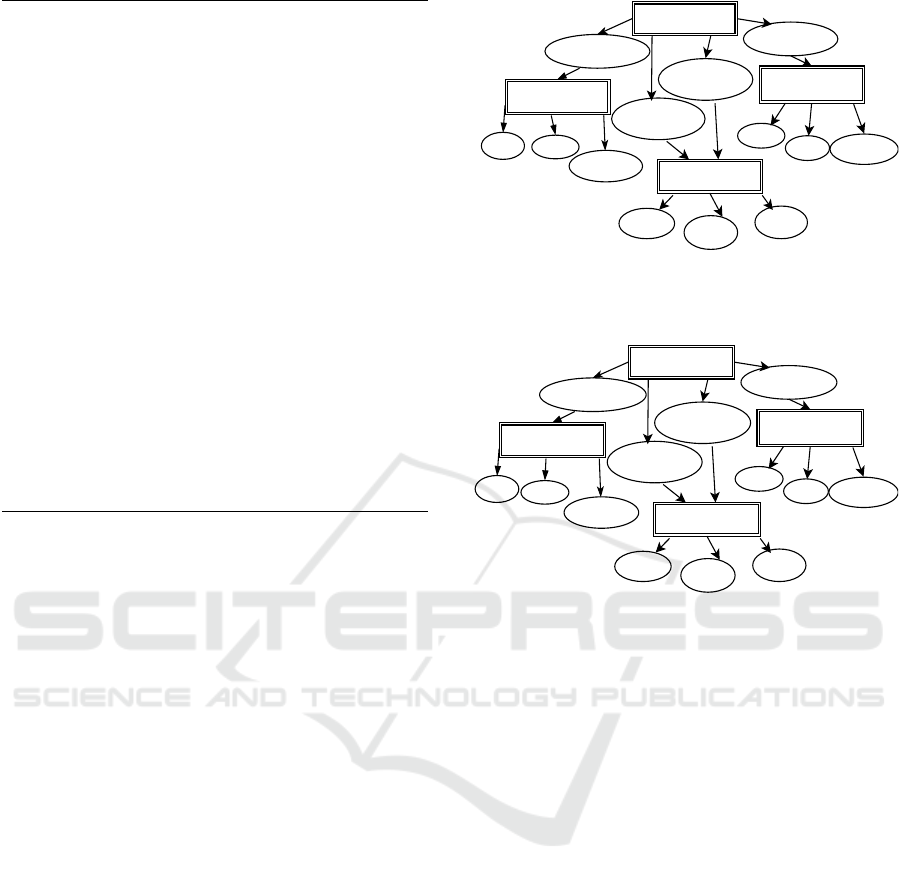
Figure 3: An example C-program.

3.2.4 Localization of Faulty Statements

After prioritizing the functions based on FP-Score and

comprehensibility, we examined the statements of the

functions in the top one-third of the suspected func-

tions list. To rank the statements of suspicious func-

tions, we adopted the SBFL technique DStar (Wong

et al., 2013). In the worst case, if the bug is not lo-

cated in the former set of functions, we search the bug

in the next one-third of the ranked list. The reason

behind choosing DStar is that it is state-of-the-SBFL

techniques (Wong et al., 2013).

3.3 Example

In this section, we explain our proposed approach us-

ing an example C-program shown in Figure 3. As it

can be seen that the program contains four functions,

namely main(), add(), sub(), and print(). The

add() and sub() functions present add and subtract

operation respectively. The print() function prints

the values of parameters passed to it. The subtraction

function contain a bug i.e., in place of subtraction op-

erator, multiplication operator has been used.

Figure 4 shows the resultant Functional Depen-

dency Graph (FDG) for the example C-program

shown in Figure 3. Each dependency edge is marked

with its edge number and weight, separated with a

slash symbol. We use HWN (Highest Weight Nor-

malization) scoring scheme in this example. The

entry: main

entry: add

entry: print

entry: sub

call: add(a, b)

call:

print(a, b, c)

call:

print(a, b, c)

call: sub(a, b)

a=a_in b=b_in

c_out=a+b

a=a_in

b=b_in c_out=a*b

a=a_in

b=b_in

c=c_in

1/1 3/1

5/1

7/1

9/1

16/1

17/1

10/1

11/1

12/1

13/1

14/1

15/1

2/1

4/1

6/1

8/1

Figure 4: Function Dependency Graph(FDG) for the C-

program of Figure 3 with initial weights of all dependency

edges initialized to 1.

entry: main

entry: add

entry: print

entry: sub

call: add(a, b)

call:

print(a, b, c)

call:

print(a, b, c)

call: sub(a, b)

a=a_in

b=b_in

c_out=a+b

a=a_in

b=b_in c_out=a*b

a=a_in

b=b_in

c=c_in

1/1.5 3/1

5/1.5

7/1

9/1.5

16/1

17/1

10/1.5

11/1.5

12/1.5

13/1.5

14/1.5

15/1

2/1.5

4/1

6/1.5

8/1

Figure 5: Modiﬁed weights of dependency edges after exe-

cution of the ﬁrst test case.

heuristic parameters w

pass

and w

f ail

have been initial-

ized with weights 1.5 and 0.5 respectively. In the be-

ginning, all dependency edges have been initialized

with weight 1.

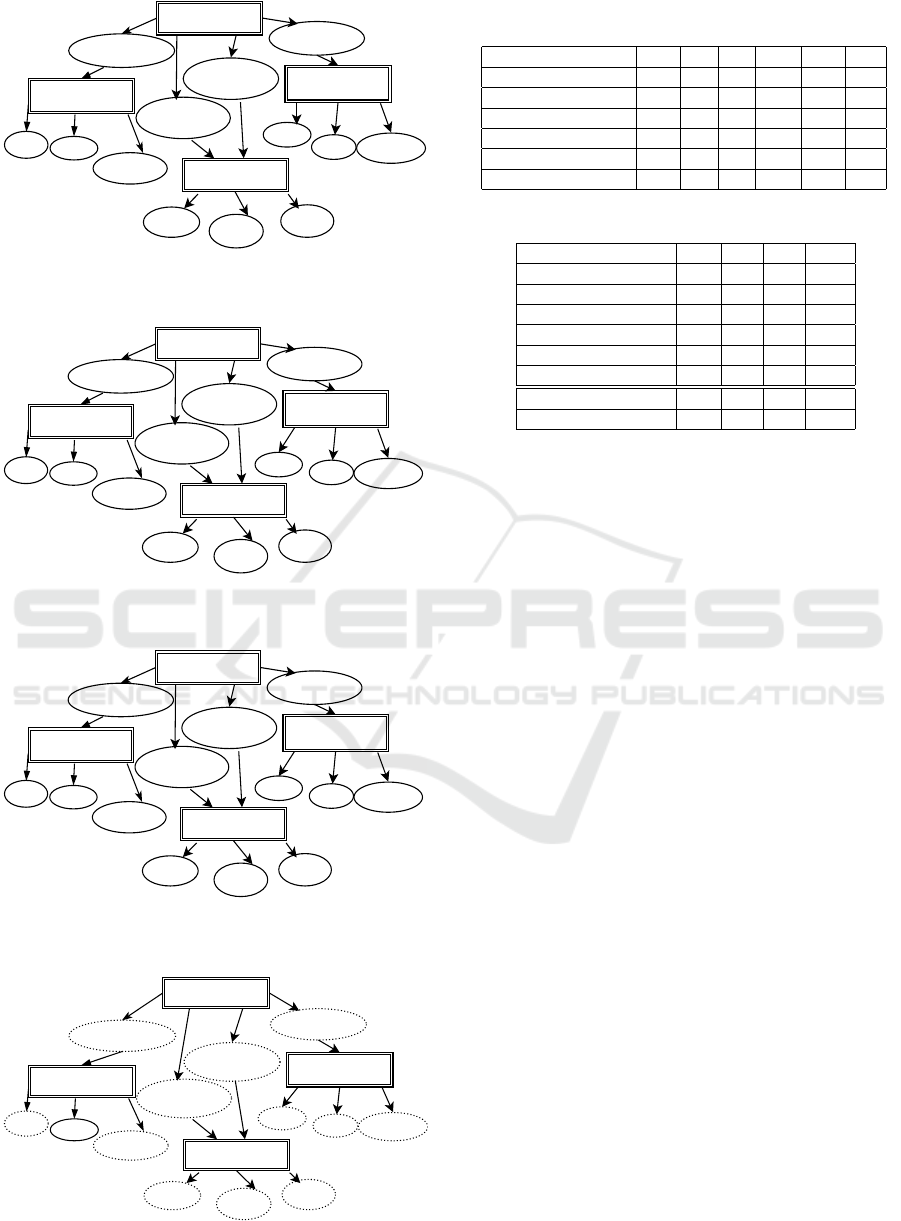
For the ﬁrst pass test case, the weight of each ex-

ercised dependency edge is multiplied with the factor

pass

. Figure 5 shows the weights of the dependency

edges after the execution of the ﬁrst test case. The

second test case is a failed one. For this test input, the

weights of each exercised dependency edge is multi-

plied by the factor w

f ail

. Figure 6 shows the modiﬁed

weights of the dependency edges after execution of

second test case. Figure 7 shows the resultant weights

of the dependency edges after all the seven test cases

are executed in which 5 test cases are pass and 2 are

failed. Figure 8 shows the normalized weights of the

dependency edges.

Figure 9 shows the weights of each function at

their function entry node (FEN). It is calculated by

taking the average weights of all the dependency

edges entering and leaving the node using Equation

6. Further, the function nodes are arranged based

upon their suspiciousness scores. It is observed that

the probability of the bug containment of the func-

tions is as: sub(a,b) > print(a,b,c) > main() >

add(a,b) It implies that the probability of presence

A Function Dependency based Approach for Fault Localization with D*

277

entry: main

entry: add

entry: print

entry: sub

call: add(a, b)

call:

print(a, b, c)

call:

print(a, b, c)

call: sub(a, b)

a=a_in

b=b_in

c_out=a+b

a=a_in

b=b_in c_out=a*b

a=a_in

b=b_in

c=c_in

1/1.5 3/0.5

5/1.5

7/0.5

9/1.5

16/0.5

17/0.5

10/1.5

11/1.5

12/.75

13/.75

14/.75

15/0.5

2/1.5

4/0.5

6/1.5

8/0.5

Figure 6: Modiﬁed weights of dependency edges after exe-

cution of the second test case.

entry: main

entry: add

entry: print

entry: sub

call: add(a, b)

call:

print(a, b, c)

call:

print(a, b, c)

call: sub(a, b)

a=a_in

b=b_in

c_out=a+b

a=a_in

b=b_in c_out=a*b

a=a_in

b=b_in

c=c_in

1/7.59

3/0.25

5/7.59

7/0.25

9/7.59

16/0.25

17/0.25

10/7.59

11/7.59

12/1.89

13/1.89

14/1.89

15/0.25

2/7.59

4/0.25

6/7.59

8/0.25

Figure 7: Modiﬁed weights of dependency edges after exe-

cution of seven test cases (5-Pass and 2-Fail).

entry: main

entry: add

entry: print

entry: sub

call: add(a, b)

call:

print(a, b, c)

call:

print(a, b, c)

call: sub(a, b)

a=a_in

b=b_in

c_out=a+b

a=a_in

b=b_in c_out=a*b

a=a_in

b=b_in

c=c_in

1/1

3/0.03

5/1

7/0.03

9/1

16/0.03

17/0.03

10/1

11/1

12/0.24

13/0.24

14/0.24

15/0.03

2/1

4/0.03

6/1

8/0.03

Figure 8: Normalize edge weights (by considering the high-

est weight as 7.59).

entry: main

entry: add

entry: print

entry: sub

call: add(a, b)

call:

print(a, b, c)

call:

print(a, b, c)

call: sub(a, b)

a=a_in

b=b_in

c_out=a+b

a=a_in

b=b_in c_out=a*b

a=a_in

b=b_in

c=c_in

0.515

0.03

0.35

Figure 9: Suspicious score of function at FEN by averaging.

Table 1: Values of various static metrics of functions present

in Figure 3.

Metrics print add sub main Max Min

Executable code line 1 2 2 10 10 1

Cyclomatic Complexity 1 1 1 2 2 1

No. of variables 3 2 2 3 3 2

Function Parameter 3 2 2 2 3 2

Max Nesting 0 0 0 1 1 0

Count Path 0 0 0 1 1 1

Table 2: Comprehensibility score of functions in Figure 3.

Metrics print add sub main

Executable code line 0 0.11 0.11 1

Cyclomatic Complexity 0 0 0 1

Number of variables 1 0 0 1

Function Parameter 1 0.66 0.66 0

Max Nesting 0 0 0 1

Count Path 0 0 0 1

Sum 2 0.77 0.77 5

Comprehensibility Score 0.23 0.09 0.09 0.585

of fault in sub() function is highest. Also, the fault

present in the sub() function. The statements of

sub(a,b) function is ranked according to a SBFL

technique.

Table 1 shows the values of different com-

plexity metrics for every function in the program.

These values were obtained through a static analy-

sis tool Understand-C(SCI-Tools, 2010). The last

two columns represent the highest and lowest value

for each metric, respectively. In Table 2, ﬁrst six

rows represent the normalized value for every metric

through min-max normalization. Row 7 shows the ad-

dition of normalized values of complexity metrics for

each function. Row 8 presents the comprehensibility

score for each function computed using Equation 8.

4 EXPERIMENTAL STUDIES

We ﬁrst discuss the setup used for experimental eval-

uation. Further, we present the subject programs and

estimation of heuristic parameters for the proposed

FDBD

∗

technique. Subsequently, we analyze the ob-

tained results.

4.1 Setup

We developed a prototype tool for our FL technique

and named it as FDBD

∗

tool. It was developed on

64-bit ubuntu 16.04 machine with 3.8 GB RAM. The

input is requested to be in ANSI-C format. Python

is used as a scripting language for developing all the

modules. The open-source tools used are Gcov (Gcov,

2005), MILU (Milu, 2008), and Understand-C (SCI-

Tools, 2010). We have used Gcov (Gcov, 2005) for

ICSOFT 2020 - 15th International Conference on Software Technologies

278

collecting test case execution results and coverage in-

formation. For creating mutants, MILU (Milu, 2008)

was used. Understand-for-C (SCI-Tools, 2010), a

static analysis tool, was used to measure various func-

tion complexity metrics.

4.2 Subject Programs

To evaluate the performance of FDBD

∗

, we used

the Siemens suite (SIR, 2005). It is considered as

a benchmark for comparing different FL techniques

(Jones et al., 2001; Wong et al., 2013; Dutta et al.,

2019). Table 3 presents the characteristics of all the

seven subjects present in the suite. The table con-

tains program name, total faulty versions, lines of

code (LOC), functions, executable LOC, and test suite

size for the respective programs in Columns 2, 3, 4,

5, and 6, respectively. Programs Print Tokens2 and

Print Tokens are used as a token identiﬁer in the com-

piler. Schedule2 and Schedule are priority schedulers.

Replace, Tot info, and Tcas are used for text replace-

ment, information measurement, and trafﬁc collision

avoidance system respectively.

Table 3: Program characteristics.

Program No. of LOC No. of No. of No. of

Name Faulty Func. Exec. Test

Versions LOC Cases

Print Tokens 7 565 18 195 4130

Print Tokens2 10 510 19 200 4115

Replace 32 521 20 244 5542

Tot info 23 406 7 122 1052

Tcas 41 173 9 65 1608

Schedule 9 412 18 152 2650

Schedule2 10 307 16 128 2710

4.3 Estimation of Heuristic Parameters

Potential values for heuristic parameters w

f ail

and

pass

for dependency scoring method (HWN) and

f ail

for another dependency scoring scheme (DSN)

are determined experimentally. For HWN scoring

scheme, we experimented with the values of w

pass

and w

f ail

within the range of [1.01 to 2.0] and [0.01

to 0.90] respectively with an interval of 0.01. Simi-

larly, for the DSN scoring scheme, we experimented

with changing the value of w

f ail

in the range of [0.01

to 0.90] and the same interval of 0.01. We observed

from the experimental results that HWN prioritize the

functions most effectively with the values of w

pass

and

f ail

in range of [1.01 to 1.50] and [0.01, 0.20] re-

spectively. Similarly, DSN performs best when the

value of w

f ail

lies in the range of [0.50, 0.90].

4.4 Evaluation Metric

To determine the effectiveness of our FDBD

∗

method,

we used the EXAM score metric (Renieres and Reiss,

2003). EXAM score for a program P is calculated

using Equation 9.

EXAM score =

examined

| ∗ 100%

|V |

(9)

where, set V contains all the statements of program

P and set V

examined

consists of the statements exam-

ined during the bug localization. A technique with

lower EXAM Score is more effective in localizing the

faults.

Table 4: Function prioritization result.

S. Program HWN DSN

No. Name 1/3

2/3

1/3

2/3

1 Print Tokens 100.00% 100.00% 100.00% 100.00%

2 Print Tokens2 100.00% 100.00% 100.00% 100.00%

3 Replace 81.48% 100.00% 88.88% 100.00%

4 Tot Info 84.21% 100.00% 89.47% 100.00%

5 Tcas 81.08% 100.00% 91.89% 100.00%

6 Schdeule 100.00% 100.00% 100.00% 100.00%

7 Schdeule2 87.50% 100.00% 62.50% 100.00%

4.5 Results

This section discusses the result obtained for single-

fault localization.

4.5.1 Function Prioritization Result

Table 4 presents the function prioritization results

using our two reported dependency edge scoring

schemes: HWN and DSN for the Function Depen-

dency Graph. The table shows the percentage of ver-

sions for which the buggy function is ranked within

the top 1/3

or 2/3

of the prioritized functions

list. The obtained results for HWN and DSN scor-

ing schemes are shown in Columns 3, 4, and 5, 6,

respectively. It can be observed that for all the buggy

programs, the incorrect statement is present within the

top 2/3

of the ranked functions. The HWN and DSN

schemes are effectively localized the faulty function

in the top 1/3

of the prioritized functions list for an

average, 90.61% and 90.39% of buggy program ver-

sions.

4.5.2 Statement Localization Result

In this section, we compare the effectiveness of our

proposed FDBD

∗

approach with an established SBFL

A Function Dependency based Approach for Fault Localization with D*

279

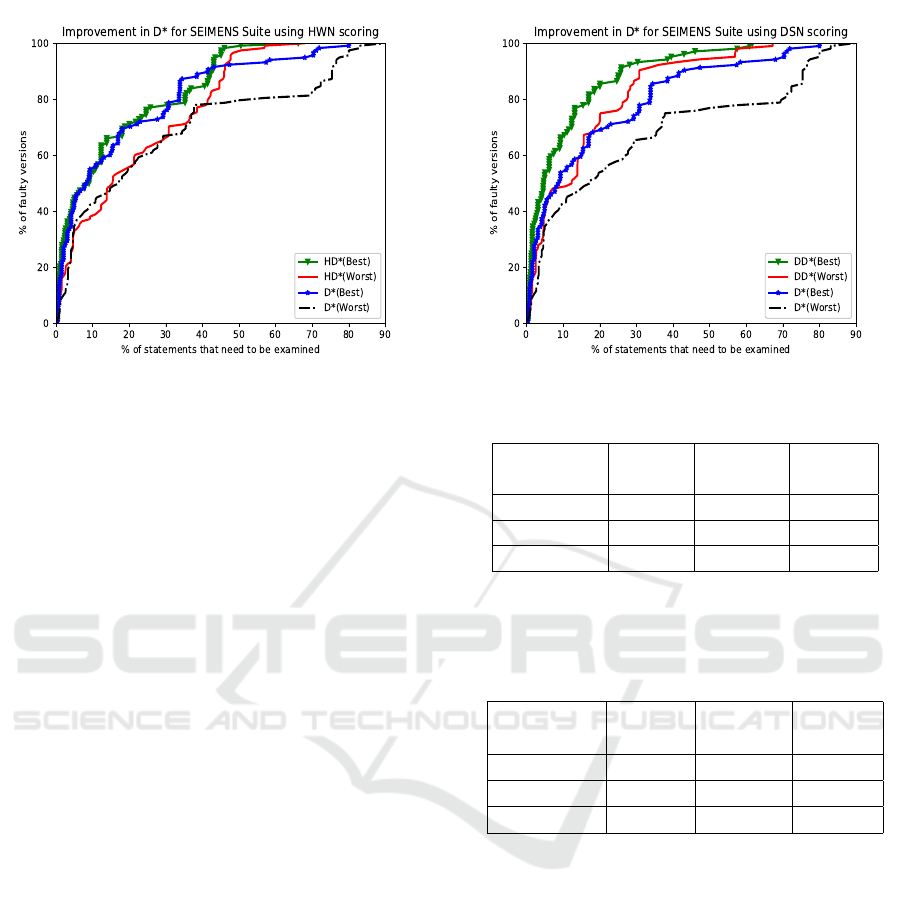
Figure 10: Effectiveness comparison of HD

∗

against D

∗

technique: DStar (Wong et al., 2013). SBFL tech-

niques assign two different types of effectiveness: the

best and the worst. For more details please refer

(Jones et al., 2001; Wong et al., 2016). Proposed

two different scoring techniques are combined with

∗

and referred to as DD

∗

and HD

∗

for DSN and

HWN scoring, respectively.

Figure 10 presents the effectiveness comparison

of HD

∗

against D

∗

using the Siemens suite. In the

line graphs, the x-axis and y-axis show the percent-

age of executable statements analyzed and the per-

centage of faulty program versions localized, respec-

tively. HD

∗

(Best) localizes bugs in 24.10% faulty ver-

sions by analyzing less than 1% of program code. On

the other hand, D

∗

(Best) localizes faults in 16.96%

of faulty versions only by checking the same percent-

age of program code. Likewise, HD

∗

(Worst) localizes

bugs in 42.85% of faulty programs by examining 5%

of program code whereas D

∗

(Worst) determine bugs

in 36.60% of faulty versions with the same percentage

of code examination. An interesting, as well as im-

portant observation, is that for many of the x values,

∗

(Worst) is also performing better than D

∗

(Best).

There is an improvement of 32.31% in the worst-

case effectiveness of D

∗

by adding the FDG(HWN)

scheme, and this change is signiﬁcant. A careful com-

parison shows that (i) HD

∗

(Best) is more adequate as

compared to D

∗

(Best) (ii) HD

∗

(Worst) is more ade-

quate than both D

∗

(Worst) and D

∗

(Best) with many

exam score points when all the faulty versions are

considered.

Table 5 presents the pairwise comparison between

the effectiveness of HD

∗

with D

∗

from three differ-

ent perspectives. It can be observed from the ta-

ble that HD

∗

(Best) is more effective than D

∗

(Best) in

58.03% of faulty program versions, equally effective

in 33.03% faulty versions and less effective in 8.92%

Figure 11: Effectiveness comparison of DD

∗

against D

∗

Table 5: Pairwise comparison between HD

∗

and D

∗

(Best) HD

∗

(Worst) HD

∗

(Worst)

vs D

∗

(Best) vs D

∗

(Worst) vs D

∗

(Best)

More effective 58.03% 62.50% 33.92%

Equally effective 33.03% 27.67% 12.50%

Less effective 8.92% 9.825% 53.57%

of versions. Similarly, HD

∗

Worst is either equal or

more effective as D

∗

(Worst) for 90.17% of faulty ver-

sions and least effective for only 9.73% of versions.

Table 6: Pairwise comparison between DD

∗

and D

∗

(Best) DD

∗

(Worst) DD

∗

(Worst)

vs D

∗

(Best) vs D

∗

(Worst) vs D

∗

(Best)

More effective 63.39% 68.75% 34.82%

Equally effective 31.25% 27.67% 16.07%

Less effective 5.35% 3.57% 49.10%

Figure 11 shows the effectiveness comparison of

∗

with D

∗

over the Siemens suite. It can be ob-

served from the ﬁgure that DD

∗

(Best) is more effec-

tive than D

∗

(Best), DD

∗

(Worst) localizes bugs by ex-

amining less code than both D

∗

(Best) and D

∗

(Worst)

in many faulty programs. D

∗

(worst) requires to ex-

amine the complete program to localize the faults for

some programs. Whereas, DD

∗

(Worst) examines at-

most 67.18% of program code to localize faults in any

of the considered set of programs versions.

Table 6 presents a pairwise effectiveness compar-

ison between DD

∗

and D

∗

techniques. It can be ob-

served from the table that DD

∗

(Best) is at least as ef-

fective or more effective than D

∗

(Best) for 94.64%

of faulty programs. Only for the 5.35% of sub-

ject programs, DD

∗

(Best) performs less effectively

than D

∗

(Best). Similarly, only for 3.57% of versions

∗

(Worst) is performing less code examination than

ICSOFT 2020 - 15th International Conference on Software Technologies

280

∗

(Worst). Also, DD

∗

(Worst) is at least as effective

as D

∗

(Best) in 50.89% of faulty versions. On aver-

age, our proposed DD

∗

performs 43.65%, and HD

∗

performs 38.88% more effectively than existing D

∗

5 MULTIPLE FAULTS

Till now, we have discussed the localization in single

fault programs. But, usually, a program contains more

than one fault. We discuss an extension of FDBD

∗

localize programs with more than one bug. It is a two-

step procedure. In the ﬁrst step, we cluster the failed

test cases into fault-focusing clusters. Such that all

the tests present in a cluster are failed on account of

the same fault. Many techniques are available in the

literature to create fault-focused clusters (Jones et al.,

2007; Cellier et al., 2011). In the second step, each of

the failed test cases is merged with all the successful

test cases for localizing the targeted fault. We have

used the same approach as described in (Jones et al.,

2007) to generate the clusters of failed test cases. The

only difference is that instead of using SBFL tech-

niques (Tarantula or D

∗

) scores on all the statements,

we use our proposed method of selective function’s

statements scores to generate the fault focused clus-

ters. This way, we have extended our FDBD

∗

tech-

nique for localizing programs with multiple-faults.

We have injected two to four faults in different

programs. For comparison with existing approaches,

we have created fault focused clusters with their re-

spective scoring techniques. We have debugged the

program faults in parallel and reported the cumula-

tive EXAM score to localize all the bugs in that pro-

gram. Table 7 shows the comparison of the EXAM

score required by D

∗

, HD

∗

, and DD

∗

fault local-

ization techniques. Column 2 of the table is in

the format of ‘PName VNum’. Here PName de-

notes the program name, and VNum shows the cre-

ated faulty version number. Column 3 shows the to-

tal faults injected in the respective program version.

Columns 4-9 present the best and worst-case EXAM

scores of different techniques. On average, the ef-

fectiveness of HD

∗

(Best) is 4.31%, and HD

∗

(Worst)

is 2.90% better than D

∗

(Best) and D

∗

(Worst) respec-

tively. DD

∗

(Best) is 7.26% more competent than

∗

(Best), and DD

∗

(Worst) is 4.88% more effective

than D

∗

(Worst).

6 THREATS TO VALIDITY

We discuss the threats to the validity of our proposed

approach and obtained results:

1. The effectiveness of FDBD

∗

for FL relies on both

the number of pass and failed test inputs. If all

the test inputs are either completely pass or failed,

then, our approach may not localize the bug cor-

rectly.

2. In the paper, we experimented over a limited set of

programs. It is possible that our approach might

not work for speciﬁc types of programs. However,

to mitigate this risk, we have considered programs

with different functionality, size, faulty versions,

test inputs used, etc.

3. We have adopted EXAM

Score metric to check

the performance of our FDBD

∗

approach. But,

EXAM Score does not quantify the amount of

time spend by a developer to analyze a single

statement. So, we can not estimate the total

amount of effort spends by a developer to local-

ize the bugs.

4. The behavior of the program analyzer and test

case executor varies in different platforms (OS/

compiler). To mitigate this threat, we re-

implemented the existing FL technique and pro-

posed approach in the same machine.

7 COMPARISON WITH

RELATED WORK

Cleve et al. (Cleve and Zeller, 2005) reported a state-

model based FL technique and named it as cause tran-

sition. They identiﬁed the program points where the

root cause of failure is transferred from one variable

to the other variable. Cause transition is an exten-

sion of authors’ earlier work called delta debugging

(Zeller and Hildebrandt, 2002). Jones et al. (Jones

et al., 2001) showed that the FL technique Tarantula

is more effective than set union, set intersection, and

cause-transition approaches in terms of code exami-

nation. Based on our experimental results, it is ob-

served that our proposed FDBD

∗

approach is more

effective than Tarantula.

Renieris et al. (Renieres and Reiss, 2003) pro-

posed the nearest-neighbor approach for FL. They tar-

geted to ﬁnd the most similar trace generated from the

successful test cases with a failed test case trace. Fur-

ther, they applied a set difference to eliminate the ir-

relevant statements from the failed test case trace and

returns a list of suspicious statements. The effective-

ness of their approach is completely dependent on the

used test suite. Also, in some cases, it returns a null

set of suspected statements. Whereas, FDBD

∗

uses

the test suite ﬁrst to prioritize the function and then,

localized the bug at the statement level.

A Function Dependency based Approach for Fault Localization with D*

281

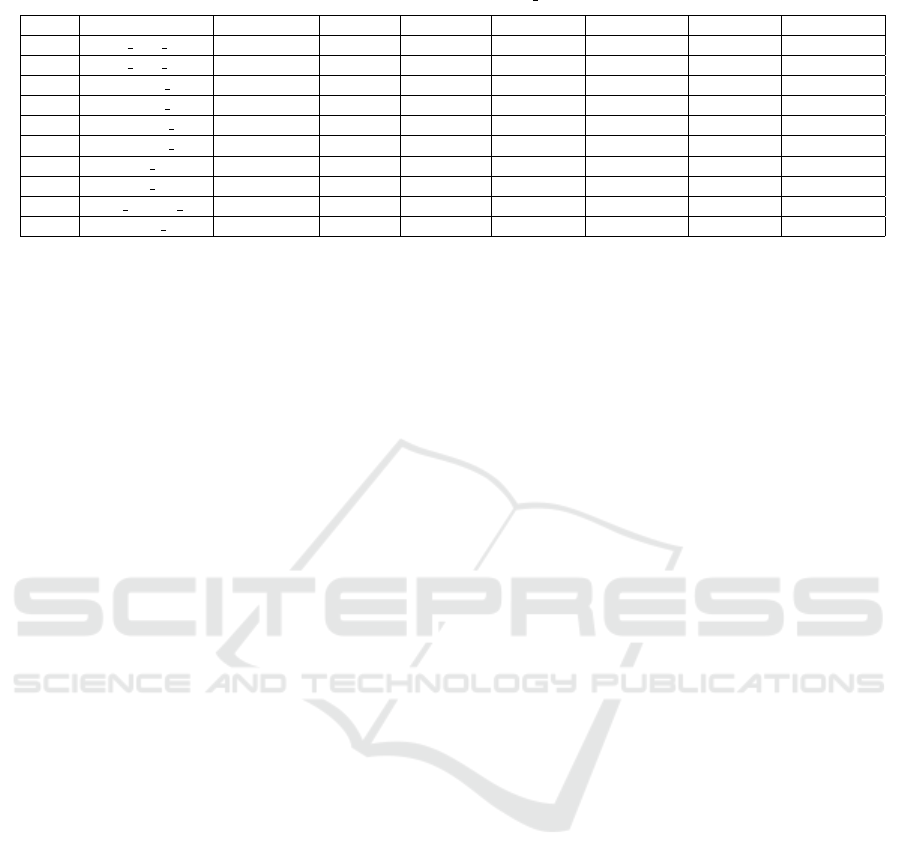
Table 7: Comparison of D

∗

with HD

∗

and DD

∗

based on the Exam Score metric for multiple fault localization.

S.No. Program No. of faults D

∗

(Best) D

∗

(Worst) HD

∗

(Best) HD

∗

(Worst) DD

∗

(Best) DD

∗

(Worst)

1 Tot Info V1 2 36.88% 45.90% 34.42% 43.44% 31.14% 40.16%

2 Tot Info V2 4 52.45% 68.85% 49.18% 65.57% 49.18% 65.57%

3 Schedule V1 3 35.52% 43.42% 28.94% 36.84% 28.94% 36.84%

4 Schedule V2 3 21.71% 35.52% 16.44% 30.26% 15.13% 28.94%

5 Schedule2 V1 4 37.50% 49.21% 45.31% 57.03% 43.75% 55.46%

6 Schedule2 V2 3 28.12% 46.87% 26.56% 45.31% 26.56% 45.31%

7 Tcas V1 3 55.38% 92.30% 52.30% 89.23% 52.30% 89.23%

8 Tcas V2 4 43.07% 89.23% 43.07% 89.23% 43.07% 89.23%

9 Print Tokens V1 2 22.56% 29.74% 24.61% 31.79% 23.58% 30.76%

10 Replace V2 4 49.18% 65.57% 45.08% 61.47% 40.98% 57.37%

In the literature, various slicing based FL tech-

niques are reported (Weiser, 1984; Agrawal and Hor-

gan, 1990). Slicing focused techniques return a list

of suspicious instructions, but these techniques do not

assign ranks to the instructions. Also, it is possible

that a slice may contain all the program instructions,

and this nulliﬁes the performance of slicing. On the

other hand, our FDBD

∗

approach returns a ranked

list of statements present in the most suspicious func-

tions.

Wong et al. (Wong and Qi, 2009) was the ﬁrst

to introduce neural networks (NN) for FL. Wong et

al. (Wong et al., 2010) also used RBF (radial basis

function) NN for the same. Dutta et al. (Dutta et al.,

2019) reported a hierarchical approach for FL using

deep neural networks (DNN). They have used DNNs

for both function and statement prioritization. NNs

easily map complex functions with the help of the

training set. However, NNs require a large amount

of time for parameter estimation and model training.

Whereas, the time required in each step of the pro-

posed FDBD

∗

is reasonable and deterministic. Hence,

our proposed approach will work efﬁciently for large-

size programs.

8 CONCLUSION

We have presented a hierarchical FL technique using

Weighted Function Dependency Graph (WFDG) and

existing SBFL technique D

∗

. The WFDG models the

function dependency information, and the weights as-

signed in the dependency edges indicate the relevance

of an edge in propagating a fault. With the help of

the weighted dependency edges, the functions are pri-

oritized. To differentiate between the functions with

equal suspiciousness value, we have incorporated the

information computed using static analysis. From our

experimental evaluation, it is observed that the pro-

posed FDBD

∗

technique is, on average, 41.27% more

effective than the existing SBFL technique D

∗

We extend our technique to handle object-oriented

programs. We also intend to investigate learning-

oriented methods to estimate the heuristic parameters.

REFERENCES

Abreu, R., Zoeteweij, P., and Van Gemund, A. J. (2009).

Localizing software faults simultaneously. In 2009

Ninth International Conference on Quality Software,

pages 367–376. IEEE.

Agrawal, H. and Horgan, J. R. (1990). Dynamic program

slicing. ACM SIGPlan Notices, 25(6):246–256.

Agrawal, H., Horgan, J. R., London, S., and Wong, W. E.

(1995). Fault localization using execution slices and

dataﬂow tests. In Proceedings of Sixth International

Symposium on Software Reliability Engineering. IS-

SRE’95, pages 143–151. IEEE.

Ardimento, P., Bernardi, M. L., Cimitile, M., and Ruvo,

G. D. (2019). Reusing bugged source code to support

novice programmers in debugging tasks. ACM Trans-

actions on Computing Education (TOCE), 20(1):1–

24.

Ascari, L. C., Araki, L. Y., Pozo, A. R., and Vergilio, S. R.

(2009). Exploring machine learning techniques for

fault localization. In 2009 10th Latin American Test

Workshop, pages 1–6. IEEE.

Cellier, P., Ducass

e, M., Ferr

e, S., and Ridoux, O. (2011).

Multiple fault localization with data mining. In SEKE,

pages 238–243.

Choi, S.-S., Cha, S.-H., and Tappert, C. C. (2010). A survey

of binary similarity and distance measures. Journal of

Systemics, Cybernetics and Informatics, 8(1):43–48.

Cleve, H. and Zeller, A. (2005). Locating causes of program

failures. In Proceedings. 27th International Con-

ference on Software Engineering, 2005. ICSE 2005.,

pages 342–351. IEEE.

Deng, F. and Jones, J. A. (2012). Weighted system depen-

dence graph. In 2012 IEEE Fifth International Con-

ference on Software Testing, Veriﬁcation and Valida-

tion, pages 380–389. IEEE.

Dutta, A., Jain, R., Gupta, S., and Mall, R. (2019). Fault

localization using a weighted function dependency

graph. In 2019 International Conference on Quality,

Reliability, Risk, Maintenance, and Safety Engineer-

ing (QR2MSE), pages 839–846. IEEE.

ICSOFT 2020 - 15th International Conference on Software Technologies

282

Feng, M. and Gupta, R. (2010). Learning universal prob-

abilistic models for fault localization. In Proceed-

ings of the 9th ACM SIGPLAN-SIGSOFT workshop

on Program analysis for software tools and engineer-

ing, pages 81–88.

Gcov (2005). http://ltp.sourceforge.net/coverage/gcov.php.

Jones, J. A., Bowring, J. F., and Harrold, M. J. (2007). De-

bugging in parallel. In Proceedings of the 2007 inter-

national symposium on Software testing and analysis,

pages 16–26.

Jones, J. A. and Harrold, M. J. (2005). Empirical evalua-

tion of the tarantula automatic fault-localization tech-

nique. In Proceedings of the 20th IEEE/ACM inter-

national Conference on Automated software engineer-

ing, pages 273–282.

Jones, J. A., Harrold, M. J., and Stasko, J. T. (2001). Vi-

sualization for fault localization. In in Proceedings of

ICSE 2001 Workshop on Software Visualization. Cite-

seer.

Korel, B. (1988). Pelas-program error-locating assistant

system. IEEE Transactions on Software Engineering,

14(9):1253–1260.

Liu, C., Yan, X., Fei, L., Han, J., and Midkiff, S. P.

(2005). Sober: statistical model-based bug localiza-

tion. ACM SIGSOFT Software Engineering Notes,

30(5):286–295.

Mall, R. (2018). Fundamentals of software engineering.

PHI Learning Pvt. Ltd.

McCabe, T. J. (1976). A complexity measure. IEEE Trans-

actions on software Engineering, (4):308–320.

Miara, R. J., Musselman, J. A., Navarro, J. A., and Shnei-

derman, B. (1983). Program indentation and compre-

hensibility. Communications of the ACM, 26(11):861–

867.

Milu (2008). https://github.com/yuejia/milu.

Mund G. B., Goswami D, M. R. (2007). Program Slicing:

The compiler design handbook. CRC Press.

Renieres, M. and Reiss, S. P. (2003). Fault localization

with nearest neighbor queries. In 18th IEEE Interna-

tional Conference on Automated Software Engineer-

ing, 2003. Proceedings., pages 30–39. IEEE.

SCI-Tools (2010). https://scitools.com/.

SIR (2005). http://sir.unl.edu/portal/index.php.

Spinellis, D. (2018). Modern debugging: the art of ﬁnding

a needle in a haystack. Communications of the ACM,

61(11):124–134.

Thaller, H., Linsbauer, L., Egyed, A., and Fischer, S.

(2020). Towards fault localization via probabilis-

tic software modeling. In 2020 IEEE Workshop on

Validation, Analysis and Evolution of Software Tests

(VST), pages 24–27. IEEE.

Weiser, M. (1984). Program slicing. IEEE Transactions on

software engineering, (4):352–357.

Wong, W. E., Debroy, V., and Choi, B. (2010). A fam-

ily of code coverage-based heuristics for effective

fault localization. Journal of Systems and Software,

83(2):188–208.

Wong, W. E., Debroy, V., Gao, R., and Li, Y. (2013). The

dstar method for effective software fault localization.

IEEE Transactions on Reliability, 63(1):290–308.

Wong, W. E., Gao, R., Li, Y., Abreu, R., and Wotawa, F.

(2016). A survey on software fault localization. IEEE

Transactions on Software Engineering, 42(8):707–

740.

Wong, W. E. and Qi, Y. (2009). Bp neural network-based

effective fault localization. International Journal of

Software Engineering and Knowledge Engineering,

19(04):573–597.

Yu, X., Liu, J., Yang, Z., and Liu, X. (2017). The bayesian

network based program dependence graph and its ap-

plication to fault localization. Journal of Systems and

Software, 134:44–53.

Zeller, A. and Hildebrandt, R. (2002). Simplifying and iso-

lating failure-inducing input. IEEE Transactions on

Software Engineering, 28(2):183–200.

A Function Dependency based Approach for Fault Localization with D*

283