Method for Improving Multi-stage Compressor Parameters using the

IOSO Optimizer

Evgenii Goriachkin, Grigorii Popov

, Oleg Baturin, Valery Matveev

and Andrei Volkov

Samara National Research University, Samara, Russia

Keywords: Parametric Model, Optimization, Efficiency, CFD Simulation, Numerical Model Settings, Multistage

Compressor, Profiling.

Abstract: In the presented work, an algorithm was developed for finding the optimal configuration of the blades of

multi-stage axial compressors using 3D CFD modeling as the main tool and using commercial optimization

programs. When developing the algorithm, special attention was paid to the development of a method for

parameterizing the shape of the blade and a program based on it, which allow you to automatically change

the shape of the blade of the axial compressor. They were used by the authors during optimization as a tool

that converts variable parameters into the “new” blade geometry. The created algorithm can be used to

improve the basic parameters of the compressor (efficiency, pressure ratio, mass flow rate, etc.) due to the

correction of the shape of the blade profiles and their position relative to each other. In this case, the algorithm

considers the possible presence of various constraints.

NOMENCLATURE

GTE - gas turbine engine

MAC - multistage axial compressor

FV - finite volume

RB - rotor blade

RW - rotor wheel

GV - guide vane

𝜋



∗

- pressure ratio

𝜂



∗

- compressor efficiency

Ks - stability margins

n - rotational speed

G - mass flow rate of the working fluid

 - flow angle in absolute motion

1 INTRODUCTION

One of the most important tasks in gas turbine engine

building is to increase the energy efficiency of the

engines (to reduce fuel consumption). It is determined

by many multidirectional influencing parameters

characterizing all components and the entire engine.

One of the most significant is the compressor

efficiency. The shortfall in the efficiency of each

https://orcid.org/0000-0003-4491-1845

https://orcid.org/0000-0001-8111-0612

compressor by 1.0% can increase the specific fuel

consumption of a gas turbine engine by up to 0.5%

(Kulagin, 2002).

The compressor efficiency is laid at the design

stage. Therefore, increasing the efficiency of the

design process and the design tools can significantly

help to achieve high compressor efficiency.

Recently, compressor design methods have

evolved significantly due to the numerical

simulations based on the Navier-Stokes equations and

the exponential growth of computer capabilities.

These factors made it possible to conduct not only a

detailed 3D simulation of the working processes of

multistage axial compressors, but also to optimize the

spatial shape of the blades using mathematical

optimization methods.

The latter circumstance allows to create the design

variants of the compressor in an automated mode that

best satisfy all the design requirements, considering

the existing constraints of various kinds. At the same

time, the blade that best suits the task can have

complex spatial shape (offsets of the sections in axial

and circumferential directions, the complex law of

changing the chords along the blade height etc.).

There may be an opinion that optimization is a

magic tool that allows the engineer to get the best

Goriachkin, E., Popov, G., Baturin, O., Matveev, V. and Volkov, A.

Method for Improving Multi-stage Compressor Parameters using the IOSO Optimizer.

DOI: 10.5220/0009769601630170

In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2020), pages 163-170

ISBN: 978-989-758-444-2

163

compressor variant for each case, with minimal user

involvement, which reduces the requirement for the

qualification of the designer and the likelihood of

errors. However, the use of mathematical

optimization in the design and development of the

MACs has not yet become widespread. Today, only a

small number of successful applications of this

method are known, and most of them relate only to

individual blade rows and stages.

Among the main difficulties hindering the

widespread use of optimization are the following.

Firstly, for successful optimization, a 3D numerical

model of the MAC workflow is required, which can

adequately predict the effect of changes in the design

parameters of the compressor on its workflow.

Secondly, the mathematical model of the compressor

must have an acceptable calculation time, since often

at least 1000-3000 iterations with the computational

model are necessary for solving the optimization

problem. Thirdly, stable parametric models of

compressor blades are required coupled with the

geometry of the computational domain, which can

automatically rebuild the 3D model of the blades. To

describe the three-dimensional shape of a compressor

blade in a parametric form, many variables are

required, and their maximum available number is

limited when solving the optimization problem. All

the components of the optimization system must be

combined within a single automated software that

works stably in the entire possible variation range of

the parameters with minimal user involvement.

The contradictory nature of the requirements and

the absence of stable working parameterization tools

are the main reasons why multicriteria optimization

techniques are currently used to a limited extent when

modernizing multistage compressors.

In the presented work, the authors set as the goal

the development and practical testing of methods and

tools for multicriteria optimization of the MAC

flowpath elements using numerical parametric three-

dimensional models of their working process.

Hereinafter, the MAC efficiency criteria are

understood as: efficiency 𝜂



∗

, pressure ratio 𝜋



∗

and

gas-dynamic stability margin Ks.

2 REVIEW OF THE

OPTIMIZATION METHODS

AND TOOLS FOR THE

COMPRESSOR

At the first stage, an analysis of the MAC

optimization experience was carried out based on the

available scientific and technical publications.

Summary of the information showed that the usage of

optimization methods is one of the most promising

ways for improving the design methods and gas-

dynamic modernization of the MAC.

In the works (Safari et al., 2013; Ning et al., 2016;

Yan et al., 2017), there are examples of optimizing

compressor stages using genetic optimization

algorithms (genetic algorithm). A genetic algorithm

is a search algorithm used for the optimization and

simulation problems by randomly selecting,

combining, and varying the desired parameters using

mechanisms like natural selection.

In papers (Yang et al., 2016; Zamboni et al., 2016;

Vasilopoulos et al., 2017), the adjoint methods are

used to find the optimal shape of the axial compressor

blades. With this approach, the objective function, as

well as the gradient function are calculated after the

creating the vector of independent variables. Then,

the necessary changes in the vector of independent

variables are calculated based on the gradient

function, and the cycle is repeated until the desired

result is achieved. An important advantage of this

method is that the rate of convergence of the

optimization problem is practically independent of

the number of variable parameters.

In (Barsi et al., 2014), the examples of optimizing

the shape of the axial compressor blades using neural

networks (artificial neuron network) are shown.

The papers (Sonoda et al., 2014; Zhaoyun et al.,

2016) show the examples of the optimization problem

using the particle swarm optimization method. This is

a computational method that optimizes a problem

iteratively trying to improve a candidate’s solution

with respect to a given quality score. During

optimization with the swarm method, an initial set of

solutions is formed, called particles, which move

around the project space based on the simple

formulas. The movement of particles obeys the

principle of the best position found in this space,

which constantly changes when particles find more

favorable positions.

Also, commercial optimization packages are used

in several studies. In (Ling et al., 2014) the iSight

package was used. The examples of using the IOSO

optimization program (IOSO, 2020) are shown in

(Marchukov et al., 2019; Vinogradov et al., 2018). In

several works, researchers use in-house codes

(Kuzmenko et al., 2007; Kröger et al., 2012; Aulich

et al., 2013; Komarov et al., 2014).

Summary of the analysis results showed that

today there is no unequivocal opinion on which

method is best suited for optimizing the MACs. The

choice of the method is often based on the traditions

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

164

of the research team and affordable software.

Moreover, the following general elements can be

distinguished in all optimization algorithms found

during the review:

 a parameterization component used to create a

geometric model of the blades and blade rows

based on a set of variable parameters;

 a component intended for the automated

creation of a FV model of the MAC flowpath

with a modified geometry;

 component of the mathematical model of the

MAC workflow, which is used to determine the

parameters of interest for the investigated

object.

In all studies, it is noted that for successful

optimization, all these components must be combined

into a single computational algorithm.

It was also noted that only one or two blade rows

are considered in most works on the optimization of

axial compressors, which indicates the difficulties

encountered in the application of optimization

methods for the entire flowpath of the MAC and

confirms the relevance of the work.

3 PARAMETRIZATION OF

COMPRESSOR BLADE

PROFILES

One of the key technologies of the multicriteria

optimization method for the MAC flowpath elements

is parameterization of the blade shape. Hereinafter,

parameterization refers to a set of independent

variables that fully describe the shape of the blade

profile of in conjunction with the algorithm for its

construction.

The authors of the article developed and

implemented their own method of parameterizing

compressor blades. It is carried out in 2 stages (Figure

1, Table 1).

At the first stage, a description of the shape of the

planar control sections (cylindrical or conical

sections, the rotational axis of which coincides with

the rotational axis of the turbomachine) is performed

in the Profiler program (Dmitrieva ana Shabliy,

2014). It was developed at the Department of Aircraft

Engine Theory of Samara National Research

University (Samara University, 2020). This program

can convert the coordinate table, which in the design

drawing describes the shape of the blade, into text

files of the initial data for constructing design models

of turbomachines in the NUMECA and TurboGrid

programs. The Profiler also can change the shape of

the midline, the stagger angle of the profile, and

several other important characteristics of the shape of

the blade profile (Dmitrieva ana Shabliy, 2014). The

appearance of the Profiler interface is shown in

Figure 2.

The second stage of parameterization is carried

out in the Profiler 3D program developed by the

authors of the article (Popov, et al., 2017). It can

perform the followings:

 change the relative position (shifts in axial,

radial and circumferential directions) of the

control sections of the blade based on the

selected stacking law of the sections along the

blade height;

 scale the thickness and chords of the cross

sections of the blade by correcting the laws of

change in scaling factors along the height of the

blade.

Figure 1: Schematic diagram of the created parameterization scheme.

Method for Improving Multi-stage Compressor Parameters using the IOSO Optimizer

165

Table 1: Parameterization stages and their characteristics.

Stage 1 2

Implemented

in the program

Profiler Profiler 3D

What changes

at the stage?

‒ Stagger angle

of the middle

line

‒ Position of

the control

points on the

middle line

‒ Shift of individual

sections in the axial

and circumferential

direction

‒ Scaling of the

profile chord

‒ Scaling of the

profile thickness

How is the

pattern of

shape change

set?

The coordinates

or parameters

of each

corrected

section and the

midline points

are directly

changed

The dependence of the

change of the adjusted

parameter along the

blade height is set and

the parameters of the

control points of the

dependence are

modified

The algorithm underlying the Profiler 3D was

built considering the characteristics of the compressor

workflow. It is well known that the flow in the blade

row has a complex spatial nature, and depends on the

loading of the blade rows, which can be different for

different stages. Therefore, the parameterization

scheme was chosen based on physical ideas about the

flow structure in blade rows, so as to be able to

purposefully influence the shape of the blades in the

characteristic areas of the blade passages: in the flow

core, near the endwall regions of hub and shroud.

The second feature is that the number of blade

rows in the MAC can be large and exceed the value

of 30. Considering that the number of variable

parameters during the optimization process is usually

limited, the selected parameterization scheme for the

MAC blades provides the user with the opportunity to

change the number of variable parameters per one

row depending on the dimension of the task.

Figure 2: Profiler software.

The main idea of a parametric description of the

relative position of the sections along the blade

height, implemented in the Profiler 3D, is to use the

dependence of the variable parameter distribution

along the radius x

=f(r) (for example, the

displacement of the section along the coordinate axes)

(Figure 3). The linkage changes by correcting the

value of the variable in the control points of the

dependence x

=f(r).

In the developed program, the user can

fundamentally change the law of distribution of

parameters along the radius by choosing the number

of control points on the dependence x

=f(r). In

principle, the following laws can be implemented

(Figure 3):

 linear – by two control points (shroud and hub);

 dependence of degree 2 – by three control

points (shroud, hub and intermediate);

 dependence of degree 3 – by four control points

(shroud, hub and two intermediate);

 dependence of an arbitrary degree (with an

arbitrary number of control points).

Figure 3: Different ways of describing parameter changes along the radius in Profiler 3D.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

166

The values of variables in arbitrary points of the

dependence x

=f(r) are calculated by the equation of

a polynomial of the corresponding degree (Flanders,

1973). The patterns of parameter changes along the

radius can be different for different rows of the same

MAC.

The fundamental choice of parameter changing

law (the number of control sections) along the height

of the blade gives the user an effective tool to reduce

the number of variables describing the shape of the

profile. As the law becomes more complicated, the

user gets more flexibility during optimization, which

will help to achieve a better result, but the required

number of variables for describing the profile

increases significantly. The impact on the radial

position of the control points can adjust the degree of

deformation along the blade and change the blade to

a greater extent where it is really needed (differently

in the core and near the endwall regions).

The law of scaling the chords and thicknesses of

the blade profiles is set similarly to how the sections

are aligned along the blade height.

A coupling of Profiler and Profiler 3D programs

(Figure 1) receives the value of independent variables

as the input describing the shape of the blades in

accordance with the accepted parameterization

schemes. As a result, files are generated for each row

that describe the geometry of the blades in the

.geomturbo format adopted in the NUMECA

AutoGrid 5 (Numeca AutoGrid, 2020). There, a mesh

of finite volumes for the new flowpath is generated.

The same program can adjust the axial position of the

rows relative to each other, as well as to set, if

necessary, a circumferentially variable pitch of the

blades. In the process of optimization, the required

values of the displacement of the blades in the blade

rows are automatically calculated by a special macro

and recorded in a script executed during the

optimization process.

4 MULTI-STAGE COMPRESSOR

OPTIMASATION ALGORITHM

Based on the literature review and practical

experience, an algorithm for multicriteria

optimization of the shape and relative position of the

MAC blades using commercial optimizer and

numerical parametric 3D model of its workflow was

developed. The algorithm was implemented based on

the Numeca software system (Numeca FineTurbo,

2020) and the IOSO optimizer program (IOSO, 2020)

using in-house programs described above (Dmitrieva

ana Shabliy, 2014; Popov et al., 2017).

Any mathematical optimization algorithm or

commercial program can be used for the

optimization. The developed algorithm is universal

and the choice of the best mathematical method for

finding the optimum function is not the goal of this

study. The authors of the article tested their

algorithms using the IOSO program available on the

market. Its choice is due to the large number of results

of its successful application in the tasks of aircraft

engine building, including by the team of authors of

the article (Marchukov et al., 2019; Vinogradov et al.,

2018; Popov et al., 2018; Popov et al., 2016; Popov

et al., 2019; Baturin et al., 2017). The specified

program was used as a finished commercial product.

No upgrades were made to the optimization

algorithms. A description of the algorithms used in

the program can be found on the website and

publications of the program developer (IOSO, 2020).

The flow chart of the algorithm is shown in Figure

4. The task of optimizing the MAC is solved

iteratively. Before the optimization, variable

parameters are set (usually this is the blade geometry

using the parameters specified in Section 2), their

ranges, criteria (usually the pressure ratio, efficiency,

working fluid flow rate or the stability margins) and

constraints (strength, structural or technological). The

adopted set of variable parameters ensure complete

change of the shape of the blade (angles, thicknesses,

the shape stacking line of profiles in the radial

direction).

The optimization cycle is implemented in the

following sequence. Initially, the optimization

program (for example, IOSO), based on a list of

variable data and a special mathematical algorithm,

generates a vector of variable parameters 𝑥



𝑥



,…,𝑥





, which represents the values of the

variables of the blades’ parametric model and their

relative position for the formed variant of the MAC.

The values of the vector of variable parameters are

automatically written to text files, which are used as

initial data for the programs for parametric

construction of blade rows Profiler and Profiler 3D

(see section 2). These programs generate files with

the geometry of the blades in the .geomturbo format,

which are then transferred to the NUMECA AutoGrid

5, where the FV grid is created (in accordance with

the recommendations of Section 3).

Then, the MAC workflow is calculated for one or

more operating modes in the CFD software

NUMECA FINE/Turbo. It should be noted that the

compressor workflow is calculated using a joint

model that considers all stages at the same time and

Method for Improving Multi-stage Compressor Parameters using the IOSO Optimizer

167

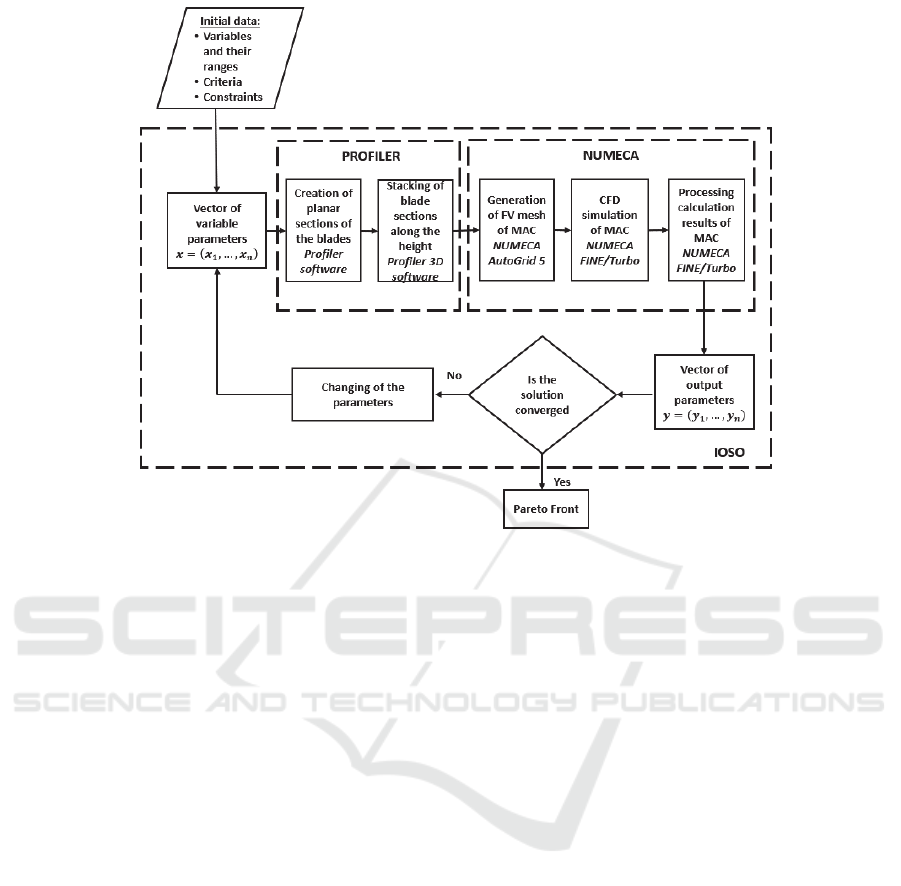
Figure 4: Flow chart of the developed optimization algorithm.

their mutual influence. If the configuration proposed

by the optimizer does not work stably for some

reason, the CFD solution does not converge at this

point and this was considered when the optimizer is

working.

At the end of the calculation, a text file is formed

with the values of the relevant compressor operation

parameters. The values of these parameters determine

the vector of output parameters 𝑦



𝑦



,…,𝑦





which is automatically transferred to IOSO. The

vector of output parameters may contain the values of

the integral parameters of the flow, for example, the

flow rate, the values of pressures and temperatures in

the cross sections of the MAC flowpath, as well as

complex parameters determined by mathematical

expressions based on the integral parameters of the

flow, for example, the margin of gas-dynamic

stability, the efficiency of the MAC. In IOSO, an

analysis of the obtained compressor variant and its

saving in the search history of the problem are

performed based on a distinctive mathematical

algorithm. As a result of the analysis, a front of

Pareto-compromise solutions is formed (particular

solutions in which an improvement of one of the

criteria cannot be achieved without deterioration of

the others) among the best MAC variants that satisfy

the given constraints, and also a vector of variable

parameters for a new iteration is created.

The developed optimization algorithm has been

repeatedly tested by the authors in solving various

industrial problems. A brief description of some

tasks, as well as links to publications that describe

them in detail, are given in Table 2.

5 CONCLUSION

The paper describes an algorithm developed by the

authors for finding the optimal configuration of the

blades of multistage axial compressors using 3D CFD

modeling as the main tool and using commercial

optimization programs. An important element of the

algorithm is the original way of parameterizing the

shape of the blades and the program based on it,

which allow to automatically change the shape of the

axial compressor blades. They were used as an

important part of the optimization algorithm as a tool

that converts variable parameters into the “new”

blade geometry. The created algorithm for searching

for the optimal shape of the compressor blades can be

used to improve the basic parameters of its operation

(efficiency, pressure ratio, flow rate, etc.) by

correcting the shape of the profiles of the blades and

their position relative to each other. In this case, the

method takes into account the possible presence of

various constraints.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

168

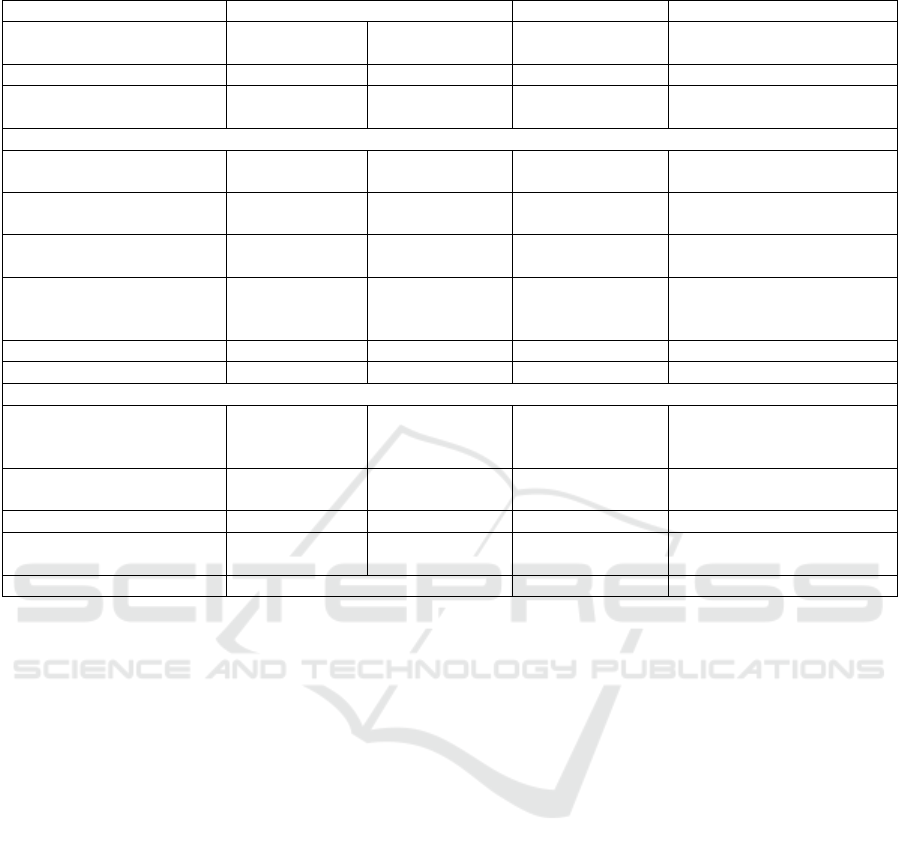
Table 2: The results of some optimization tasks solved using the developed algorithm.

Example 1 (HPC) 2 (LPC) 3 (Three-spool compressor)

Number of optimized

parameters

1 2 2

Number of optimized

parameters

Number of constraints no 4 3 Number of constraints

Number of variable

parameters

3 15 61

Number of variable

parameters

Variable parameters

Stagger angle of the entire

blade

+ + -

Stagger angle of the entire

blade

Stagger angles of individual

profiles

- - +

Stagger angles of individual

profiles

Position of the points of the

profile middle line

- - +

Position of the points of the

profile middle line

Shift of individual section

relative to the initial

position

- - +

Shift of individual section

relative to the initial position

Chord scaling - - - Chord scaling

Blade thickness scaling - - - Blade thickness scaling

Results

Efficiency increase

0.3% at 100%

mode

1.2% at 95%

mode and 0.5 at

100% mode

1.3 at 100% mode Efficiency increase

Change in the pressure ratio - no

+4% (according to

the task)

Change in the pressure ratio

Change in stability margins no no no Change in stability margins

Change in mass flow rate -3% no

- 8 % (according

to the task)

Change in mass flow rate

Reference Marchukov, 2017 Goryachkin, 2015 Popov, 2019

The developed optimization algorithm can solve a

problem with an unlimited number of variable

parameters, constraints and optimization criteria.

However, it is obvious that their increase will

significantly complicate the search for the optimum

and increase (up to the unacceptable) time to search

for a solution. However, in practice, the authors did

not solve problems in which the number of

optimization criteria was more than two (due to the

complexity of analyzing the results with a larger

number of variables), and the number of variable

parameters was not more than 99 (due to limitations

of the available license for the IOSO optimizer

program).

REFERENCES

Kulagin, V. V. 2002. Teoria, raschet i proektirovanie

Safari, A., Lemu H.G. and Assadi, M. 2013. A Novel

Combination of Adaptive Tools for Turbomachinery

Airfoil Shape Optimization Using a Real-Coded

Genetic Algorithm. In Proceedings of the ASME Turbo

Expo 2013: Turbine Technical Conference and

Exposition.

Ning, Tao, Gu, Chun-wei, Li, Xiao-tang and Liu, Tai-qiu.

2016. Three-Dimensional Aerodynamic Optimization

of a Multi-Stage Axial Compressor. In Proceedings of

the ASME Turbo Expo 2016: Turbomachinery

Technical Conference and Exposition

Yan, Cheng, Yin, Zeyong, Guo, Fushui, Shen, Xiuli, Fan,

Jun and Luo, Ju. 2017. A Newly Improved

Collaborative Optimization Strategy: Application to

Conceptual Multidisciplinary Design Optimization of a

Civil Aero-Engine. In Proceedings of the ASME Turbo

Expo 2017: Turbomachinery Technical Conference and

Exposition.

Yang, Jing, Luo, Jiaqi, Xiong, Juntao and Liu, Feng. 2016.

Aerodynamic Design Optimization of the Last Stage of

a Multi-Stage Compressor by Using an Adjoint

Method. In Proceedings of the ASME Turbo Expo 2016:

Turbomachinery Technical Conference and Exposition.

Zamboni, Giulio, Banks, Gabriel and Bather, Simon. 2016.

Gradient-Based Adjoint and Design of Experiment

CFD Methodologies to Improve the Manufacturability

of High Pressure Turbine Blades. In Proceedings of the

ASME Turbo Expo 2016: Turbomachinery Technical

Conference and Exposition.

Vasilopoulos, Ilias, Flassig, Peter and Meyer, Marcus.

2017. CAD-Based Aerodynamic Optimization of a

Compressor Stator Using Conventional and Adjoint-

Driven Approaches. In Proceedings of the ASME Turbo

Method for Improving Multi-stage Compressor Parameters using the IOSO Optimizer

169

Expo 2017: Turbomachinery Technical Conference and

Exposition.

Barsi, Dario, Costa, Carlo, Cravero, Carlo and Ricci,

Gianluca. 2014. Aerodynamic Design of a Centrifugal

Compressor Stage Using an Automatic Optimization

Strategy. In Proceedings of the ASME Turbo Expo

2014: Turbine Technical Conference and Exposition.

Sonoda, Toyotaka, Endicott, Giles, Arima, Toshiyuki and

Olhofer, Markus. 2014. A Novel Transonic Fan Swept

Outlet Guide Vane Using 3D Design Optimization. In

Proceedings of the ASME Turbo Expo 2014: Turbine

Technical Conference and Exposition.

Zhaoyun, Song, Liu, Bo, Xiaochen, Mao and Xiaofeng, Lu.

2016. Optimization of Tandem Blade Based on

Improved Particle Swarm Algorithm. In Proceedings of

the ASME Turbo Expo 2016: Turbomachinery

Technical Conference and Exposition. GT2016-56901.

DOI:10.1115/GT2016-56901.

Ling, Jing, Du, Xin, Wang, Songtao and Wang, Zhongqi.

2014. Relationship Between Optimum Curved Blade

Generate Line and Cascade Parameters in Subsonic

Axial Compressor. In Proceedings of the ASME Turbo

Expo 2014: Turbine Technical Conference and

Exposition.

IOSO Optimization Technology. Access mode:

http://www.iosotech.com.

Marchukov, E., Egorov, I., Kretinin, G., Karonic, B. and

Fedechkin, K. 2019. Optimization of geometry blade

for modern high pressure compressor. In IOP

Conference Series: Materials Science and Engineering.

Vinogradov, K. A., Kretinin, G. V., Leshenko, I. A.,

Otriakhina, K. V., Fedechkin, K. S., Vinogradova,

O.V., Bushmanov, V. V. and Khramin, R. V. 2018.

Robust multiphysics optimization for fan blade

aerodynamic efficiency, structural properties and flutter

sensitivity. In Proceedings of the ASME Turbo Expo

2018: Turbine Technical Conference and Exposition.

Kuzmenko, M.L., Egorov, I.N., Shmotin, Yu. N. and

Fedechkin K.S. 2007. Optimization of the gas turbine

engine parts using methods of numerical simulation. In

Proceedings of the ASME Turbo Expo 2007: Turbine

Technical Conference and Exposition.

Kröger, Georg, Schnell, Rainer and Humphreys, Nicholas

D. 2012. Optimised aerodynamic design of an OGV

with reduced blade count for low noise aircraft engines.

In Proceedings of the ASME Turbo Expo 2012: Turbine

Technical Conference and Exposition.

Aulich, Anne-Laure, Goerke, Daniel, Blocher, Michael,

Nicke, Eberhard and Kocian, Frank. 2013.

Multidisciplinary automated optimization strategy on a

counter rotating fan. In Proceedings of the ASME Turbo

Expo 2013: Turbine Technical Conference and

Exposition.

Komarov, Oleg V., Sedunin, Viacheslav A. and Blinov,

Vitaly L. 2014. Application of optimisation techniques

for new high-turning axial compressor profile topology

design. In Proceedings of the ASME Turbo Expo 2014:

Turbine Technical Conference and Exposition.

Shabliy, L.S. 2013. Software tool for creating and

modifying computer models of turbomachine blades

Profiler. Certificate of state registration of a computer

program No. 2013617453.

Samara University. Access mode: https://ssau.ru/english/.

Dmitrieva, I. B. and Shabliy, L. S. 2014. Programma

PROFILER dlya sozdania i modifikacii lopatok

turbomoshin v ramkah zadach optimizacii. In Problemy

i perspectivy razvitia dvigatelestroenia: materialy

dokladov megdunarodnoy nauchno-tehnicheskoy

konferencii: pp. 201 – 203.

Popov, G., Matveev, V., Baturin, O., Novikova, Y.,

Kolmakova, D. and Zubanov, V. 2018. Estimation of

the Effect of 3D Grid Parameters on the Simulation of

the Working Process of Axial Turbines. In Proceedings

of 8th International Conference on Simulation and

Modeling Methodologies, Technologies and

Applications.

Popov, G. M., Gorjachkin, Baturin, O. V. Novikova, Ju. D.

and Volkov, A.A. 2017. Program for parametric

change of 3D shape of axial turbomachine blades

Profiler 3D. Certificate of state registration of a

computer program No.2017613128.

Flanders, Harley. 1973. Elementary Functions and Analytic

Geometry. Elsevier.

Numeca AutoGrid, Access mode: https://www.numeca.

com/product/autogrid5

Numeca FineTurbo, Access mode: https://www.numeca.

com/product/fineturbo

Popov, Grigorii, Goriachkin, Evgenii, Kolmakova, Daria

and Novikova, Yulia. 2016. Multicriteria Optimization

of Axial Low Pressure Compressor of Gas Turbine

Power Plant. In Proceedings of the ASME Turbo Expo

2016: Turbine Technical Conference and Exposition.

Popov, G. M., Egorov, I. N., Dmitriev, D. N., Goriachkin,

E. S. and Volkov, A. A. 2019. Complex gas dynamic

optimization of a three spool axial compressor of an

industrial gas turbine engine. In Proceedings of SME

Gas Turbine India Conference.

Baturin, Oleg, Tkachenko, Andrei, Krupenich, Ilia, Popov,

Grigorii and Goryachkin, Eugene. 2017. Identifying the

Approach to Significantly Improve the Performance of

NK-36ST Gas Turbine Power Plant. In Proceedings of

the ASME Turbo Expo 2017: Turbine Technical

Conference and Exposition.

Marchukov, E., Egorov, I., Popov, G., Baturin, O.,

Goriachkin, E., Novikova, Y. and Kolmakova, D. 2017.

Improving of the working process of axial compressors

of gas turbine engines by using an optimization method,

In IOP Conference Series: Materials Science and

Engineering.

Goryahkin, E., Popov, G., Baturin, O. and Kolmakova, D.

2015. Three-stage low pressure compressor

modernization by means of optimization methods. In

Proceedings of the ASME Turbo Expo 2015: Turbine

Technical Conference and Exposition.

SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

170