
Auxiliary Decision-making for Controlled Experiments based on
Mid-term Treatment Effect Prediction: Applications in Ant Financial’s
Offline-payment Business
Gang Li
1
and Huizhi Xie
2
1
Ant Financial Services Group, Internet Financial Center, Haidian, Beijing, China
2
Ant Financial Services Group, Huanglong International Building, Hangzhou, Zhejiang, China
Keywords:
Controlled Experiments, A/B Testing, Mid-term Treatment Effect Prediction, BG/NBD Model, Counting
Metrics.
Abstract:
Controlled experiments are commonly used in technology companies for product development, algorithm
improvement, marketing strategy evaluation, etc. These experiments are usually run for a short period of
time to enable fast business/product iteration. Due to the relatively short lifecycle of these experiments, key
business metrics that span a longer window cannot be calculated and compared among different variations of
these experiments. This is essentially a treatment effect prediction issue. Research in this paper focuses on
experiments in the offline-payment business at Ant Financial. Experiments in this area are usually run for one
or two weeks, sometimes even shorter, yet the accumulating window of key business metrics such as payment
days, payment counts is one month. In this paper, we apply the classic BG/NBD model(Fader et al., 2005) in
marketing to predict users payment behavior based on data collected from the relatively short experimentation
periods. The predictions are then used to evaluate the impact on the key business metrics. We compare
this method with supervised learning methods and direct modelling of treatment effect as a time series. We
show the advantage of the proposed method using data collected from plenty of controlled experiments in
Ant Financial. The proposed technique has been integrated into Ant Financial experimentation reporting
platform, where metrics based on the predictions are one of the auxiliary evaluation criteria in offline-payment
experiments.
1 INTRODUCTION
Controlled experimentation has become a hot topic in
the last ten years. Major internet companies, includ-
ing Microsoft (Kohavi et al., 2007), Google (Tang
et al., 2010), Facebook (Bakshy et al., 2014), Net-
flix (Gomez-Uribe and Hunt, 2016), Airbnb (Lee and
Shen, 2018) etc. rely heavily on controlled exper-
iments for product improvement and marketing de-
sign. Controlled experiments enable agile and fast it-
eration and thus are indispensable to innovation. Pro-
fessor Stefan Thomke from Harvard business school
once said "If you want to be good at innovation,
you have to be good at business experimentation"
(Thomke, 2003).
Ant Financial Group provides comprehensive fi-
nancial services to hundreds of millions of people in
China and all over the world. Its flagship mobile ap-
plication Alipay is one of the most used applications
in China. Data-driven decisions are crucial for the
success of Ant’s business due to its huge scale and the
diversity of its businesses. A few years ago, the exec-
utive team at Ant Financial realized the importance
of experimentation as a key data-driven tool. They
started the initiative to build a company-wide experi-
mentation platform in 2016. This initiative has been
proven to be a success. Tens of thousands of experi-
ments were run on this platform since its birth. One
of the business areas that rely heavily on experimenta-
tion is offline-payment. Offline-payment refers to mo-
bile payment in offline scenarios, such as restaurants,
supermarkets, malls, etc. In the offline-payment area,
we use experimentation heavily for marketing design,
offline-payment product improvement, marketing al-
gorithm iteration, and so on.
Metrics are a key element in experimentation. If
you cannot measure the performance of your busi-
ness, you cannot experiment on it. Metric develop-
ment for experimentation is a non-trivial process and
has been discussed in quite a few papers(Kohavi et al.,
Li, G. and Xie, H.
Auxiliary Decision-making for Controlled Experiments based on Mid-term Treatment Effect Prediction: Applications in Ant Financial’s Offline-payment Business.
DOI: 10.5220/0009770500190030
In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 19-30
ISBN: 978-989-758-440-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
19

2007; Roy, 2001). Kohavi and coauthors (Kohavi
et al., 2007) introduced the so-called overall evalua-
tion criterion (OEC) in their 2007 KDD paper. In ad-
dition to the challenges of finding OEC with good di-
rectionality and sensitivity, another challenge is to in-
clude metrics that reflect an improvement in the long
term. Experiments with good short-term performance
do not necessarily enjoy good long-term performance
(Kohavi et al., 2012). The difficulty of measuring
long-term effect comes from the nature of experimen-
tation. Controlled experiments are typically designed
to run for a relatively short period of time to enable
fast business/product iteration. From the perspective
of statistical modelling, correlating short-term effect
with long-term effect is essentially a prediction prob-
lem. As important for businesses as it is to measure
long-term effect, there is relatively little literature on
this topic, which reflects the difficulty of this prob-
lem. Hohnhold et al. (Hohnhold et al., 2015) de-
veloped an experiment methodology for quantifying
long-term user learning. They applied the method-
ology to ads shown on Google search and created a
model that uses metrics measurable in the short-term
to predict the long-term performance. Dmitriev et al.
(Dmitriev et al., 2016) shared pitfalls of long-term
online controlled experiments, including cookie in-
stability, survivorship bias, selection bias, perceived
trends, side effects, seasonality etc. They also sug-
gested some methodologies to partially address some
of these pitfalls. In the area of offline-payment at Ant
Finacial, we also suffer from the issue of only observ-
ing short-term effect in the experiments. However,
our challenge is slightly lower in the sense that we do
not need to predict long-term effect but rather mid-
term effect. Using the same terminology as in (Hohn-
hold et al., 2015), long-term effect is what would hap-
pen if the experiment launches and users receive the
experiment treatment in perpetuity. Mid-term effect
refers to impact in the range of a few weeks to a
few months. The business argument for focusing on
mid-term effect in offline-payment is that it is a rel-
atively new (compared to areas such as search) area
and things change much faster.
In this paper, we focus on the prediction of two
OEC metrics in offline-payment: payment days and
payment counts. Both are counting metrics. Their
definition is given in Section 2.1 and also Section
4. We propose to use stochastic process models for
counting metrics to tackle the prediction problem.
The main advantage of these stochastic process mod-
els are that we do not need to train the models based
on pre-experiment data. The models are trained us-
ing data collected in the experimentation period, sep-
arately for control and treatment, and thus potentially
have higher prediction accuracy. We first review a few
well-known stochastic process models in the market-
ing area, including Pareto/NBD, BG/NBD, and their
extensions. Although these models were developed
in the marketing area, they can potentially be used
to model any counting metric. We then apply these
models in the context of experimentation. We define
three levels of accuracy in model evaluation. They
are metric prediction accuracy, treatment effect pre-
diction accuracy, and decision-making prediction ac-
curacy. We explicitly call out these three levels of ac-
curacy and show that high decision-making prediction
accuracy is much easier to achieve than the other two.
Hence it is meaningful to invest in prediction in the
context of experimentation. We demonstrate the ef-
fectiveness of this methodology using experiments in
the area of offline-payment at Ant Financial. The pro-
posed methodology has been integrated into Ant Fi-
nancial’s experimentation reporting platform, where
metrics based on the predictions are one of the key
evaluation criteria in offline-payment experiments.
The contributions of this paper are summarized
as follows. i) To the best of our knowledge, we
are the first to apply stochastic process models for
treatment effect prediction in controlled experiments.
These stochastic process models are built separately
for control and treatment versions in each experiment
on the fly. Hence they enjoy higher prediction ac-
curacy for both control and treatment versions, and
finally treatment effect. ii) We propose three levels
of prediction accuracy: metric level, treatment ef-
fect level, and decision-making level. We show that
decision-making level accuracy is most attainable and
also most meaningful from the decision-making point
of view. iii) We provide numerous case studies based
on real data from Ant Financial and show the effec-
tiveness of the proposed solution in this paper.
The remainder of this paper is organized as fol-
lows. We give a brief overview of controlled exper-
iments in the offline-payment business at Ant Finan-
cial in Section 2.1. A few well-known stochastic pro-
cess models for counting metrics are reviewed in Sec-
tion 2.2. The application of stochastic process mod-
els to predict mid-term treatment effect is discussed
in Section 3. In Section 4, we share case studies at
Ant Financial to demonstrate the effectiveness of the
idea in this paper. We conclude the paper in Section
5, where we summarize the work in this paper as well
as a few future research directions.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
20

2 BACKGROUND AND
OVERVIEW OF STOCHASTIC
PROCESS MODELS FOR
COUNTING METRICS
2.1 Brief Overview of Controlled
Experiments in Offline-payment at
Ant Financial
As mentioned in the introduction section, most
changes in the offline-payment business at Ant Finan-
cial are evaluated via controlled experiments prior to
launch. These changes include marketing algorithm
iteration, marketing strategy development, payment
product improvement, and so on. Due to the page
limit, we do not review the basic concepts of con-
trolled experiments in this paper. Readers can refer
to (Kohavi et al., 2007) for details. The two key busi-
ness metrics in offline-payment are payment days and
payment counts in the window of a few months. Pay-
ment days is calculated as follows. Given a time pe-
riod, number of days with at least one payment for
each user is calculated, then a sum is taken across all
users as the payment days metric. Similarly for pay-
ment counts, we first calculate number of payments
for each user and then take a sum. Payment days
and payment counts are essentially counting metrics.
They are first calculated at user level and then the sta-
tistical summary sum is calculated. In controlled ex-
periments, since the traffic percentage between con-
trol and treatment are not necessarily the same, we
typically use average instead of sum as the statisti-
cal summary. Statistical inference for the compari-
son between control and treatment is conducted using
standard two-sample t-test thanks to the large sample
sizes.
2.2 Stochastic Process Models for
Counting Metrics
Stochastic process models for counting metrics in
marketing can be classified into two categories: non-
contractual scenarios and contractual scenarios. Typ-
ical examples of contractual scenarios include cell
phone services, bank services, etc (Fader and Hardie,
2007). Customer’s relationship with Ant Financial
in offline payment is noncontractual. We therefore
review a few well-known stochastic process models
in the noncontractual scenario and their recent appli-
cations (Dahana et al., 2019; Dechant et al., 2019;
Venkatesan et al., 2019).
2.2.1 The Pareto/NBD Model
The Pareto/NBD model was proposed by Schmittlein
et al. in (Schmittlein et al., 1987) to model repetitive
purchase behavior. Under the model, customers drop
out with a certain probability at any given time. The
dropout is unobservable due to the noncontractual na-
ture. For customer i, define the following notations.
• x
i
is the number of purchases made by this cus-
tomer in (0, T
i
], where (0, T
i
] is the observation
window for this customer. Note that customers
come into observation at different times and thus
the observation window varies across customers.
The starting point "0" is the time of the first pur-
chase. The calculation x
i
excludes the first pur-
chase.
• t
x
i
is the time of the last purchase in the observa-
tion window.
• T
i
is the observation length of customer i. T
i
also
varies across customers.
The main assumptions of the Pareto/NBD model
are as follows.
1. For a given active customer, the repetitive pur-
chase behavior of this customer follows a Poisson
process with transaction rate λ
i
. Active customers
refer to those that have not dropped out.
2. For any given customer, let τ
i
denote the life time
of this customer. Note that τ
i
is not observable in
the noncontractual scenario. τ
i
follows an expo-
nential distribution with dropout rate µ
i
.
3. λ
i
varies across customers and follows a gamma
distribution with parameters (r, α).
4. µ
i
varies across customers and follows a gamma
distribution with parameters (s,β).
5. λ
i
and µ
i
are independent from each other.
The Poisson process repetitive purchase behavior and
exponential life time imply the lack of memory prop-
erty. These assumptions have been proven to hold in
many marketing scenarios (Ehrenberg, 1972; Karlin,
2014). We will discuss the validation of these as-
sumptions in the case study section.
For a fixed observation window, the input of the
Pareto/NBD model are the tuples (x
i
,t
x
i
, T
i
) of cus-
tomers. The parameters (r, α, s, β) are estimated using
the maximum likelihood estimation technique. For
any given customer i, the two important output of the
Pareto/NBD model are as follows.
• E(Y
i
(t)|X
i
= x
i
,t
x
i
, T
i
, r, α, s, β): the conditional
expectation of number of purchases in a future pe-
riod (T
i
, T
i
+t]
Auxiliary Decision-making for Controlled Experiments based on Mid-term Treatment Effect Prediction: Applications in Ant Financial’s
Offline-payment Business
21

• P(τ
i
> T
i
|X
i
= x
i
,t
x
i
, T
i
, r, α, s, β): the conditional
probability of dropping out after T
i
or the condi-
tional probability of being active after time T
i
These two outputs can be used to calculate most of
the common managerial questions such as:
• How many (active) retail customers does the firm
now have?
• Which individuals on this list most likely repre-
sent active customers? Inactive customers?
• What level of transactions (for example offline-
payment counts) should be expected next month
by those on the list, both individually and collec-
tively?
2.2.2 The BG/NBD Model
Despite the solid theoretical foundation of the
Pareto/NBD model, people have found it hard to use
because of the efforts needed to estimate the pa-
rameters. Recall one of the key assumptions of the
Pareto/NBD model is that customers can drop out at
any given time, independent of their purchase behav-
ior. This assumption implies that the dropout process
is continuous, which makes the optimization of the
likelihood function difficult. To solve this issue, Fader
et al. developed the beta-geometric/NBD (BG/NBD)
model in 2005 ((Fader et al., 2005)). The key dif-
ference of the BG/NBD model from the Pareto/NBD
model is that it assumes the dropout of a customer can
only occur immediately after a purchase. This slight
variation makes the BG/NBD model much easier to
implement. Interested readers can refer to (Fader
et al., 2005) for more details. The BG/NBD model
has been proven to have similar performance as the
Pareto/NBD model in terms of prediction accuracy in
many applications (Trinh, 2013; Dziurzynski et al.,
2014).
The input of the BG/NBD model is exactly the
same as that of the Pareto/NBD model. The assump-
tions for BG/NBD model is listed as follows:
1. For a given active customer, the repetitive pur-
chase behavior of this customer follows a Poisson
process with transaction rate λ
i
.
2. An active customer drops out with probability
p
i
after a purchase. Therefore, the total num-
ber of purchases J
i
of a customer before dropout
follows a geometric distribution P(J
i
= j|p
i
) =
p
i
(1 − p
i
)
j−1
.
3. λ
i
varies across customers and follows a gamma
distribution with parameters (r, α)
4. p
i
varies across customers and follows a beta dis-
tribution with parameters (a,b).
5. λ
i
and p
i
are independent from each other.
Parameter estimation of BG/NBD is much easier
than Pareto/NBD model, and outputs of the BG/NBD
model is similar to that of the Pareto/NBD model. For
any given customer i, the two main output are as fol-
lows.
• E(Y
i
(t)|X
i
= x
i
,t
x
i
, T
i
, r, α, a, b) (Fader et al., 2005)
• P(τ
i
> T
i
|X
i
= x
i
,t
x
i
, T
i
, r, α, a, b) (Fader et al.,
2008)
Both Pareto/NBD and BG/NBD model purchases in
continuous time, i.e., purchases can happen at any
time. However, some businesses track repeat pur-
chases on a discrete-time basis. To model purchases
on a discrete-time basis, Fader et al. proposed the
discrete-time analog of the BG/NBD model, the beta-
geometric/beta-Bernoulli (BG/BB) model. The de-
tails of this model can be found in the original pa-
per(Fader et al., 2010) and omitted here due to page
limit.
2.2.3 A Hierarchical Bayes Extension to the
Pareto/NBD Model
In the Pareto/NBD and BG/NBD models, the hetero-
geneity of transaction rate and dropout rate across
customers are modelled using a single distribution
separately. Individual-level rates cannot be esti-
mated. Also, the independence assumption of these
two random variables is hard if not impossible to
verify. In order to address these issues, Abe ex-
tended the Pareto/NBD model using a hierarchical
Bayesian framework in (Abe, 2009). The hierarchical
Bayesian extension allows incorporation of customer
characteristics as covariates, which can potentially in-
crease prediction accuracy and also relax the indepen-
dence assumption. The Hierarchical Bayes Extension
(HBE) model is based on the following assumptions.
1. A customer’s relationship with the merchant has
two phases: alive and dead. This customer’s life-
time τ
i
is unobserved and follows an exponential
distribution with dropout rate µ
i
, i.e. f (τ
i
|µ
i
) =
µ
i
e
−µ
i
τ
i
2. While alive, this customer purchase behavior fol-
lows a Poisson process with transaction rate λ
i
,
i.e. P(x
i
|λ
i
,t
x
i
) =
(λ
i
t
x
i
)
x
i
x
i
!
e
−λ
i
t
x
i
,t
x
i
≤ T
i
3. λ and µ follow a bivariate lognormal distribution,
i.e.
log(λ
i
)
log(µ
i
)
∼ BVN(θ
0
=
θ
λ
θ
µ
, Γ
0
=
σ
2
λ
σ
λµ
σ
λµ
σ
2
µ
) where BVN denotes the bi-
variate normal distribution.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
22

4. λ and µ are correlated with some covariates such
as customer characteristics through a linear re-
gression model, i.e.
log(λ
i
)
log(µ
i
)
= β
T
d
i
+ e
i
where β ∈ R
k×2
is the regression coefficients vec-
tor, d
i
∈ R
k
is the covariate vector and e
i
∼
BVN(0, Γ
0
) is random error.
The first two assumptions of the HBE model are ex-
actly the same as those of the Pareto/NBD model. The
lognormal and linear model assumptions are mainly
for mathematical convenience. The input to the HBE
model includes customer’s transaction information
and covariate information. The model parameters are
estimated using the MCMC procedure. For more de-
tails, please refer to (Abe, 2009). Since covariate in-
formation is included, the HBE model can produce
individual-level transaction rate and dropout rate es-
timates. The prediction outputs are the same as the
aforementioned models and thus not repeated.
3 PREDICTING MID-TERM
TREATMENT EFFECT IN
CONTROLLED EXPERIMENTS
In this section, we discuss the application of the afore-
mentioned stochastic process models in controlled ex-
periments. For a given metric, treatment effect is de-
fined as the expected difference of this metric between
control and treatment. In the offline-payment busi-
ness, the two OEC metrics are payment counts and
payment days over one month. The detailed calcu-
lation was presented in the background section and
thus not repeated here. The observation window of
metrics in controlled experiments is the experimen-
tation period. Customers enter an experiment at dif-
ferent times. Hence the observation length of each
customer is different. The dashboard of experiment
results showing treatment effects is typically updated
on a daily basis. After an experiment starts, on a given
day, the observation window is from the beginning of
the experiment to the given day. For customer i, the
time of the first purchase during this observation pe-
riod is set as "0", and T
i
is the duration between time
"0" and the given day (for continuous time, we use the
last second of the given day). we collect the following
transaction statistics in (0, T
i
].
• number of repeated payments or number of re-
peated days with payment, denoted as x
i
. Note
that the number of payment is for the metric pay-
ment counts and the number of days with payment
is for the metric payment days. Note that the first
purchase is not included.
• the latest payment time (day) t
x
i
: if x
i
> 0 then
t
x
i
> 0 else t
x
i
= 0
• observation length T
i
: the time difference between
the first purchase and the given day (ending point
of observation period)
Since the dashboard of experiment results is updated
on a daily basis, these models are also retrained on
a daily basis using the above collected information
as input, separately for control and treatment. With
the trained models, we can then predict individual-
level number of payments and number of days with
payment in a future period. These predictions are
treated as user-level predictions, and we predict the
OEC metrics by averaging these predictions across
customers. The prediction of treatment effect refers to
the calculation of treatment effect based on the metric
predictions. Specifically, we define the prediction of
treatment effect as the difference of metrics between
control and treatment. Statistical inference of these
predictions is done similarly as for metrics observed
in the experimentation period.
The accuracy of the predictions in the context of
controlled experiments is evaluated at three levels,
from the most difficult to the easiest.
• The first level is metric level prediction accuracy.
It is defined as the difference in the average of the
actual metric value and the predictions for a co-
hort of users, e.g. users in control.
• The second level is treatment effect level predic-
tion accuracy. It is defined as the difference in the
observed treatment effect and the predicted treat-
ment effect.
• The third level is decision-making level prediction
accuracy. At the stage of decision-making, there
are three possible outcomes: control is statisti-
cally significantly better than treatment; control
is statistically significantly worse than treatment;
control and treatment are not statistically signifi-
cantly different. Decision-making level prediction
accuracy is defined as the proportion of decisions
where statistical inference based on observed met-
rics agree with that based on predicted metrics.
In general, it may be easier to achieve high prediction
accuracy at treatment effect level than metric level.
This is because prediction error for control and treat-
ment can be biased toward the same direction and thus
cancel each other. Decision-making level prediction
is easier than treatment effect level because it essen-
tially looks at the sign, not the actual value.
There are two things worth noting here. First, for
a given observation period, users without purchases
Auxiliary Decision-making for Controlled Experiments based on Mid-term Treatment Effect Prediction: Applications in Ant Financial’s
Offline-payment Business
23
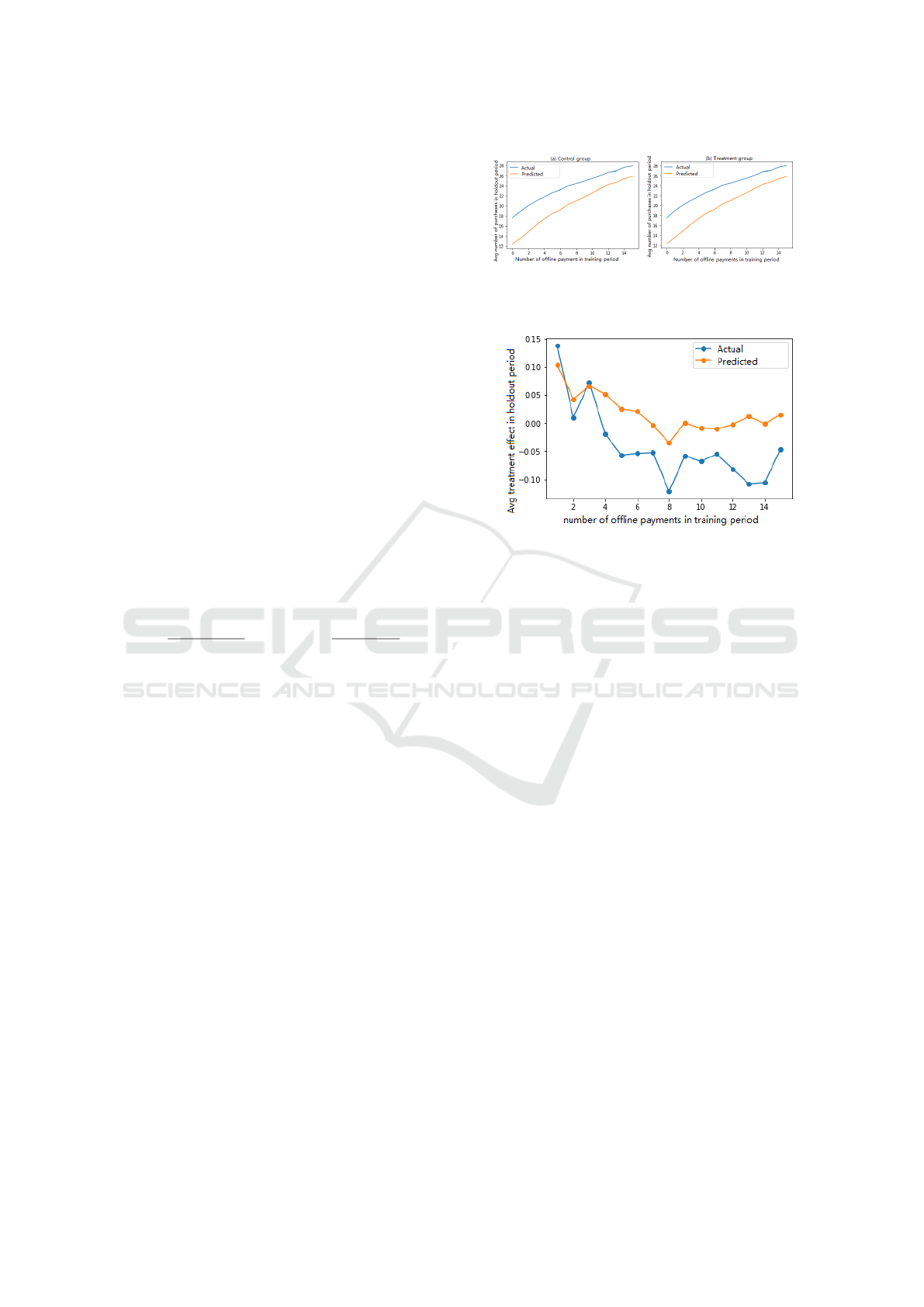
do not participate in model training. The predictions
for them in a given future period are 0. Note this is
by design and can be a future improvement direction.
Secondly, as will be seen in the case study section,
variance of the predicted metrics is usually lower than
the observed metrics. The possible explanation is as
follows. Let M and
ˆ
M denote the actual metric and the
predicted metric respectively. We have M =
ˆ
M + e,
where e is the variation in M that is not accounted for
by
ˆ
M. If we can assume the independence between e
and M (in linear models we can show that this is true),
then it is trivial to show that Var(M) > Var(
ˆ
M).
4 CASE STUDIES AT ANT
FINANCIAL
In this section, we show some numerical results of
the application of the aforementioned models to con-
trolled experiments in the offline-payment business
at Ant Financial. Again, the two metrics of inter-
est are payment counts and payment days. Real
values are masked for the purpose of data security.
Throughout this section, APC and APD refer to the
average payment counts and the average payment
days across customers respectively. More precisely,
APC =
∑
i
∑
j
paycount
i j
∑
i
and APD =
∑
i
∑
j
payday
i j
∑
i
where
paycount
i j
refers to the paycounts for customer i in
day j and payday
i j
= 1 if paycount
i j
> 0 else 0. There
are several remarks regarding the data used in the pa-
per as follows:
1. The data used in this research does not involve any
Personal Identifiable Information (PII)
2. The data used in this research were all processed
by data abstraction and data encryption, and the
researchers were unable to restore the original
data.
3. Sufficient data protection was carried out during
the process of experiments to prevent the data
leakage and the data was destroyed after the ex-
periments were finished.
4. The data is only used for academic research and
sampled from the original data, therefore it does
not represent any real business situation in Ant Fi-
nancial Services Group.
4.1 Results of the BG/NBD Model
We start with the BG/NBD model since it is easier to
implement and has been shown to have similar perfor-
mance as the Pareto/NBD model. The first example is
based on an algorithm experiment. Number of users
Figure 1: Metric Level Prediction Accuracy of APC by User
Cohort in the Holdout Period for (a) Control and (b) Treat-
ment in Example 1.
Figure 2: Treatment Effect Level Prediction Accuracy of
APC by User Cohort in the Holdout Period in Example 1.
in control and treatment are both at the level of tens of
thousands. The training period is the first two weeks
of the experiment period. The holdout or prediction
period is the 30-day window right after the first two
weeks. We present metric level prediction accuracy
with respect to number of purchases in the training
period. The results are in Figure 1 for control and
treatment separately. There is significant bias in met-
ric level prediction accuracy. The bias can be due
to either internal operational activities such as new
promotions or external changes such as promotions
from competitors. This proves the difficulty of metric
level prediction. The bias seems to decrease for heavy
users. This is probably due to their higher contribu-
tion in terms of data volume in the training period.
Treatment effect level prediction is presented in Fig-
ure 2. The absolute bias is much smaller because bias
in control and treatment to some extent cancels each
other. Decision-making level results are presented in
Table 1. The prediction result agrees with the actual
outcome.
To be more convincing, we share results of a few
more examples. The setting of these examples and
prediction results are presented in Table 2 and Table
3 respectively. We have the following observations
from Table 3.
• It is very difficult to achieve high metric level
prediction accuracy. This is expected. Payment
counts and payment days can both be affected
by many factors, within or outside Ant Financial.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
24

Table 1: Prediction Accuracy in the Holdout Period for Ex-
ample 1.
Observed
APC
Predicted
APC
Observed
APD
Predicted
APD
Treatment 33.55 28.95 10.8 8.6
Control 33.45 28.75 10.75 8.5
Treatment
Effects
(std)
0.1
(0.02)
0.2
(0.02)
0.05
(0.007)
0.1
(0.005)
Inference
Results
Sig.
higher
Sig.
higher
Sig.
higher
Sig.
higher
’Sig. higher’ means ’statistically significantly higher’. ’std’ refers
to ’standard deviation’.
Table 2: Application Setting of Examples 2-5.
Number
of Users
Training
Duration
Holdout
Duration
Example 2 Tens of
thousands
6 days 8 days
Example 3 Millions 8 days 29 days
Example 4 Millions 6 days 11 days
Example 5 Millions 30 days 30 days
For example, a promotion event or a holiday can
change the distribution of these metrics signifi-
cantly. We will provide a more specific example
shortly.
• The standard deviation of predicted treatment ef-
fect is indeed lower than that of the observed treat-
ment effect. The intuition was briefly discussed in
Section 3. The results here empirically confirmed
the intuition.
• The absolute difference between predicted treat-
ment effect and observed treatment effect is usu-
ally much smaller than that between predicted
metric value and observed metric value. How-
ever, the relative difference in treatment effect is
not necessarily smaller.
• Decision-making level prediction accuracy is sig-
nificantly higher than the other two. In Section
4.4, we will show more results of decision-making
level prediction accuracy.
In Figure 3, we show the temporal trend of the pre-
diction accuracy in the holdout period of Example 3.
The x-axis is the number of days since the beginning
of the holdout period. Note the sudden drop of pre-
diction accuracy on day 15, which turns out to be the
Lunar Spring Festival. Although the holiday causes
significant bias in the prediction in both control and
treatment (can be seen as the seasonality of predic-
tion task), the treatment effect prediction accuracy as
shown in Figure 4 seems to be much less affected.
This is another typical example where the prediction
bias in control and treatment cancel each other.
Table 3: Prediction Accuracy in the Holdout Period for Ex-
amples 2-5.
Obs
APC
Pred
APC
Obs
APD
Pred
APD
Treatment2 6.26 7.09 2.34 1.91
Control 2 6.36 7.25 2.37 1.95
TE 2 (std) -0.1
(0.054)
-0.16
(0.05)
-0.028
(0.012)
-0.03
(0.005)
IR 2 Not
sig.
Sig.
lower
Sig.
lower
Sig.
lower
Treatment3 4.93 6.72 3.01 3.81
Control 3 4.90 6.69 2.98 3.79
TE 3 (std) 0.032
(0.008)
0.035
(0.008)
0.035
(0.0034)
0.02
(0.0025)
IR 3 Sig.
higher
Sig.
higher
Sig.
higher
Sig.
higher
Treatment4 1.71 1.78 0.86 0.805
Control 4 1.72 1.78 0.86 0.805
TE 4 (std) -0.009
(0.005)
-0.004
(0.004)
-0.001
(0.0016)
-
0.0014
(0.0010)
IR 4 Not
sig.
Not
sig.
Not
sig.
Not
sig.
Treatment5 4.63 3.09 2.73 2.02
Control 5 4.59 3.07 2.71 2.01
TE 5 (std) 0.039
(0.02)
0.026
(0.009)
0.028
(0.006)
0.017
(0.004)
IR 5 Sig.
higher
Sig.
higher
Sig.
higher
Sig.
higher
’Sig. higher’ means ’statistically significantly higher’.’Sig. lower’
means ’statistically significantly lower’. ’Not sig’ means ’Not sta-
tistically significantly different’. ’std’ refers to ’standard deviation’.
’TE’ is ’Treatment Effect’, ’IR’ is ’Inference Results’, ’Obs’ means
’observed’, ’Pred’ means ’Predicted’
4.2 Comparison between the BG/NBD
Model and Other Models
In this section, we compare the BG/NBD model with
other models. We first compared the BG/NBD model
with the BG/BB model on metric APD. We expect the
BG/BB model to perform better than the BG/NBD
model on APD since APD is discrete-time based.
However, we did not find any gain in the BG/BB
model after numerous example evaluations. The re-
sults are not included here due to page limit. We
suspect the reason may be the number of transaction
opportunities in controlled experiments is not high
enough to fully explore the strength of the BG/BB
model.
We then compared the BG/NBD model with the
hierarchical Bayesian extension of the Pareto/NBD
model (called HBE for short in discussion that fol-
lows). 40+ user characteristic features that are se-
Auxiliary Decision-making for Controlled Experiments based on Mid-term Treatment Effect Prediction: Applications in Ant Financial’s
Offline-payment Business
25
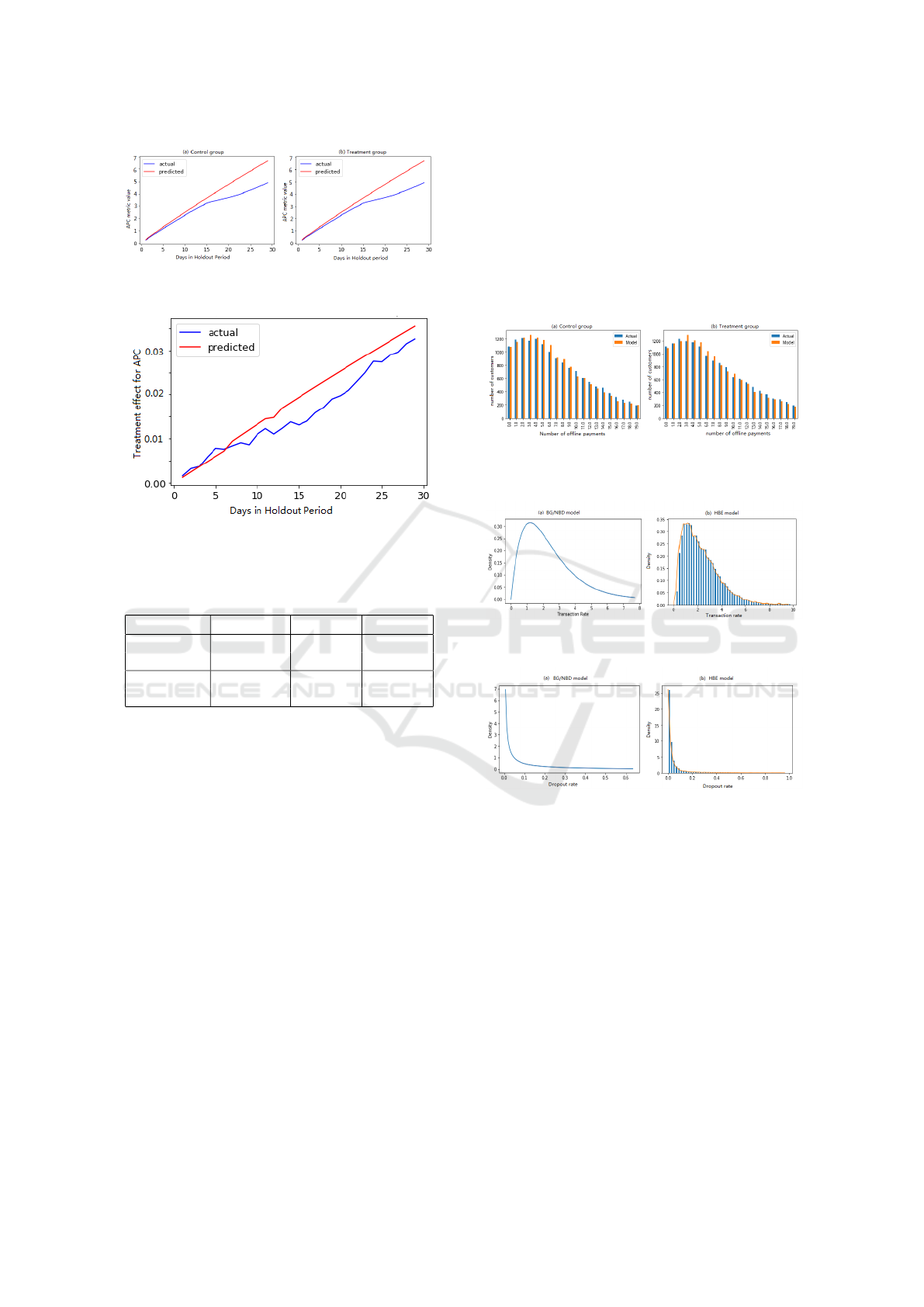
Figure 3: Temporal Trend of APC Prediction for (a) Control
Group and (b) Treatment Group in Example 3.
Figure 4: Temporal Trend of APC Treatment Effect Predic-
tion in Example 3.
Table 4: Comparison of BG/NBD and HBE on Prediction
Accuracy.
Model R
2
MSE
Example 6 BG/NBD 0.438 18
HBE 0.441 17.93
Example 7 BG/NBD 0.46 59
HBE 0.41 65
lected from a tree based feature importance proce-
dure are included in the HBE model. The two eval-
uation criterion are R
2
and mean squared error (MSE)
in the holdout period. Since the two criterion are well-
known in the literature, we do not repeat the definition
of them here. The implementation of the HBE model
is quite complicated. The R package "BTYDPlus" is
very slow. We had to implement the HBE model in
python with some modifications. The key modifica-
tions include replacement of the Bayesian regression
model with the elastic net model, removing the cap-
ping restriction of dropout rate, modification of the
sampling window, etc. The implementation details
are not included due to page limitation. Results of two
out of numerous examples we tried are shown in Table
4. Based on the examples in table 4 and more exam-
ples not listed, the performance of the HBE model is
not stably outperformed. We could not conclude uni-
formly better prediction accuracy of the HBE model.
In fact, in a non-trivial number of trials, the HBE
model performs worse than the BG/NBD model, even
after a fine tuning of the hyper-parameters. This may
have something to do with the relatively short period
of training data or that the user characteristic infor-
mation is already fully captured in the user purchase
behavior. The instability and the high latency of the
HBE model make it unsuitable for reporting purpose
in controlled experiments.
4.3 Validation for Model Assumptions
Figure 5: Distribution of Number of Purchases in the Train-
ing Period for (a) Control Group and (b)Treatment Group
in Example 2.
Figure 6: Distribution of Transaction Rate from (a)
BG/NBD Model and (b) HBE Model in Example 6.
Figure 7: Distribution of Dropout Rate from (a) BG/NBD
Model and (b) HBE Model in Example 6.
We discuss the validation for the assumptions of
the BG/NBD model in this section. Although it has
been proven to work in the past, it is worth checking
with our data. The set of assumptions can be decom-
posed into two parts: (1) Poisson repetitive purchase
and exponential life; (2) the Gamma distribution of
transaction rate and Beta distribution of dropout rate
as well as their independence. For the first part, we
compare fitted histogram of number of purchases with
the actual and use their closeness as an indirect way
to verify the assumption. Note that this comparison
is done in the training period and a good fit in the
training period does not necessarily lead to a high
metric level prediction accuracy in the holdout pe-
riod. We were able to empirically confirm the va-
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
26
lidity of part (1) based on quite a few experiments.
We share one such example in Figure 5, where the
Kullback - Leibler (KL) distance from actual distri-
bution to predicted distribution are 0.0014 and 0.0021
for control and treatment group respectively. KL dis-
tance, defined as D
KL
(P|Q) =
∑
i
P(i)log
P(i)
Q(i)
where
P, Q are two discrete distributions, also called relative
entropy , is often used to measure the closeness of
two distribution. KL distance has two properties, i)
D
KL
∈ [0, ∞), and D
KL
= 0 only when two distribu-
tions totally match, ii) the lower KL is , the closeness
is higher between two distributions. The above results
of KL distance are considerably lower which implies
the good fitness of the used model.
For part (2), we rely on results from the HBE
model since it can produce user level transaction rate
and dropout rate. In the experiment we analyzed, we
were also able to confirm this part of the model as-
sumptions. We share one such example in this paper.
The distributions of transaction rate and dropout rate
based on the BG/NBD model and the HBE model are
presented in Figures 6 and 7 respectively. KL dis-
tance from Gamma distribution (Fig6a) to estimated
transaction rate distribution (Fig6b) is calculated as
0.053, and KL distance from Beta distribution (Fig7a)
to estimated dropout rate distribution (Fig7b) is 0.167.
The KL distances are small, which indicates a good
match for both transaction rate and drop rate. Also,
the empirical correlation coefficient between user-
level transaction rate and dropout rate is 0.051, which
shows the independence assumption is reasonable.
An important thing to note is that the purpose of
model assumption verification is really to discover
improvement opportunities and future research direc-
tion. At the end of the day, what we care about is the
decision-making level prediction accuracy.
4.4 Production Results
4.4.1 Baseline Models
Besides stochastic process models, there are other
ways to model and predict treatment effect in con-
trolled experiments. We introduce a few such models
in this section. The first is to model treatment effect
as a time series. Commonly used time series mod-
els include ARMA, AR, MA models etc. The main
difficulty of using time series models is the lack of
data points since controlled experiments are run for
only weeks if not days. The second is to model treat-
ment effect as a function of time point t. Let y
t
de-
note the treatment effect at time t. The model can
be written as y
t
= f (t) + ε
t
, where ε
t
is random er-
ror. Again, due to the lack of data points, f (t) has
to be simple. Two such functions are linear function
f (t) = at + b and exponential function f (t) = be
at
.
Based on the empirical results, the linear function
seems to be more robust than the exponential func-
tion. Hence we share two examples of the comparison
between the BG/NBD model and the linear model. In
the two examples, the first seven days is the training
period and the BG/NBD model is trained based on
data in this period. For the linear model, we treat
users in the training period as the cohort of interest
and use data from the training period and the first five
days of the holdout period to train the linear function.
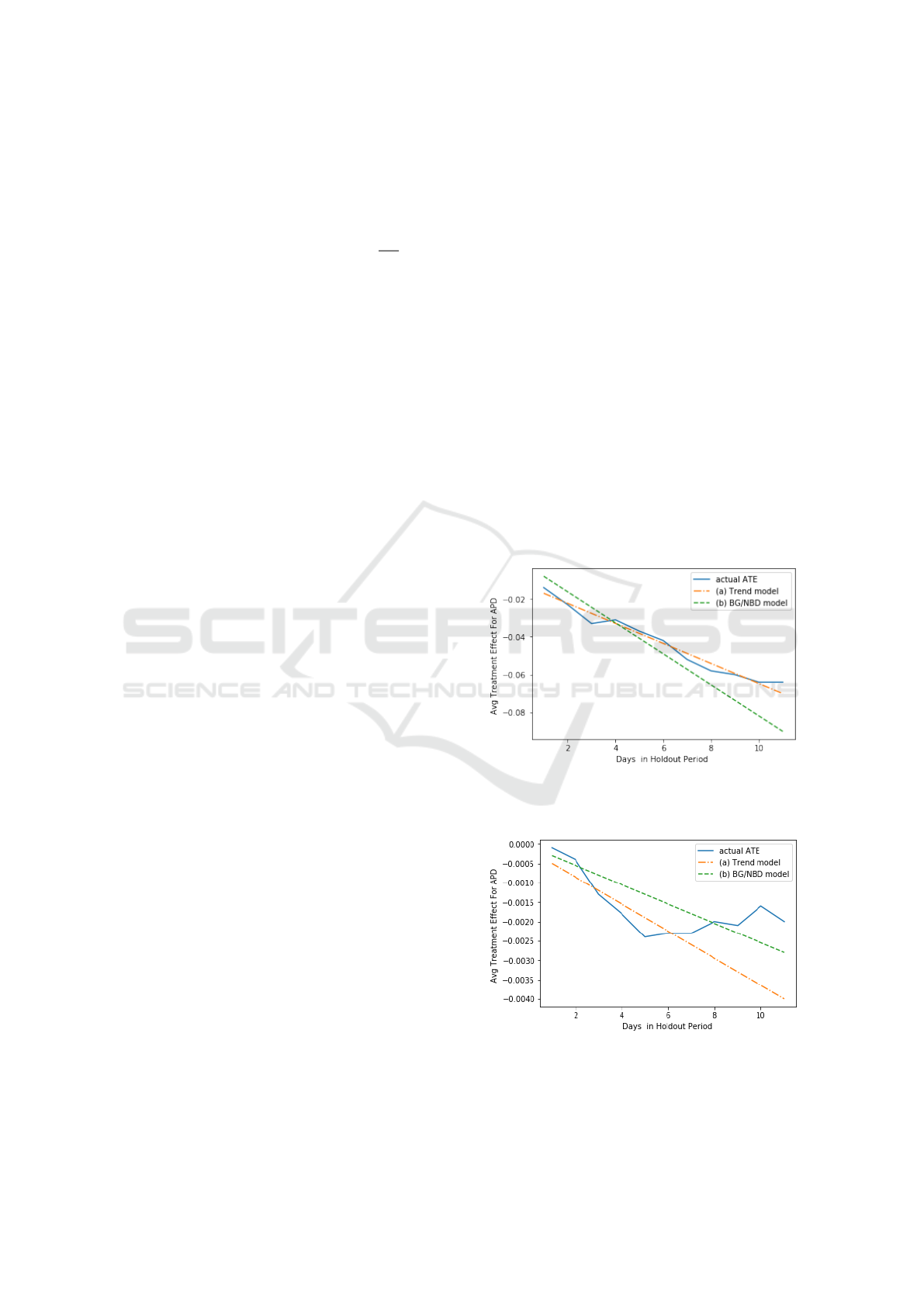
The results are presented in Figures 8 and 9, which
clear indicates the linear trend model heavily relies
on the fitted trend of early training points. If the trend
of training points is consistent with test points, the
model works well as shown in Fig.8. If the trend of
training points happens to have a large disturbance,
the predicted trend deviates from actual trend a lot
as shown in Fig. 9. This should be due to the fact
that BG/NBD models user-level data while the linear
model is trained on summarized data where signifi-
cant amount of information can be lost.
Figure 8: Temporal Trend Prediction of treatment effect in
APD with (a) Trend model (b) BG/NBD model in Example
2.
Figure 9: Temporal Trend Prediction of treatment effect in
APD with (a) Trend model (b) BG/NBD model in Example
3.
Auxiliary Decision-making for Controlled Experiments based on Mid-term Treatment Effect Prediction: Applications in Ant Financial’s
Offline-payment Business
27

Another baseline model is a supervised learning
model. In the supervised learning model, we model
user-level data. At a given time, for each user, the tar-
get variable is the number of days with payment and
number of payments in the next 30 days. Features in-
clude user’s demographics and behavior data up to the
given time. The algorithm we pick is xgboost based
on its superior empirical performance compared to
other supervised learning models. As mentioned be-
fore, for a given experiment, we cannot train the su-
pervised learning model based on data collected in the
experiment. This is because there is no label for the
target variable. Instead we have to train the model be-
fore the experiment based on historical data and then
predict for the experiment. Intuitively, change in the
distribution of users in the experiment, especially in
the treatment variation, can potentially lead to low
decision-making level prediction accuracy. We will
compare the xgboost model with the BG/NBD model
in production.
4.4.2 Comparison Results
Based on the empirical results, we concluded that the
BG/NBD model is the most suitable to be produc-
tionized for both OEC metrics. We implemented the
model using in-house tools and integrated with the ex-
perimentation reporting pipeline. As mentioned be-
fore, the predictions are treated as metrics and sta-
tistical inference is done on them. We show results
of thirty-day prediction based on both the BG/NBD
model and the aforementioned xgboost model in this
section. Decision-making accuracy for thirty-day pre-
diction is presented in Table 5 , which contains 35 ex-
periments or 796 records (experiment version * days)
in total. Since the results are based on a limited num-
ber of experiments, we also report the 95% confidence
interval of the accuracy to incorporate uncertainty of
the results with bootstrap method. Note that there
are three possible inference outcomes: treatment sig-
nificantly higher than control; treatment significantly
lower than control; treatment not significantly differ-
ent from control. Hence a random guess of the infer-
ence result in a future period would give an accuracy
of 33%. We have the following observations from Ta-
ble 5.
• Prediction accuracy based on the BG/NBD model
is much higher than random guess and the xg-
boost model, which shows the effectiveness of the
proposed approach. Even with a 0.78 R
2
in the
training data, the prediction accuracy of the xg-
boost model is very low and even lower than ran-
dom guess for APD, which is most probably be-
cause the model is not trained based on data in
the current experiments. Many things can change
between the experiments and historical data, e.g.
distribution of user characteristics, the relation-
ship between the features and the target variable,
etc.
• Prediction accuracy for APC is higher than that
for APD, especially when the training duration
is short. This is because APD is discrete-time
based. The same training duration yield much
less information for APD (measured by number
of days) than for APC (measured by continuous
time). A related observation is that as the dura-
tion increases, the gain in prediction accuracy for
APD is much more significant than that for APC.
In fact, from the 95% confidence intervals, we can
see that the prediction accuracy for APC is not
significantly different at 5% significance level be-
tween the "training duration < 15 days" scenario
and the "training duration ≥ 15 days" scenario
(break-point 15days is set in means of the predic-
tion accuracy for BG/NBD).
Since there is a gap between predicted value and
real value for the mid-term OEC metric, and the pre-
dicted metric usually has smaller variance than real
metric, we suggest to use these predicted mid-term
metrics as auxiliary metrics, which tends to reflect the
developing trend from the behavior data during the
experiment period.
5 CONCLUSIONS
In this paper, we tackle the problem of prediction for
counting metrics, with applications in controlled ex-
periments in the offline-payment business at Ant Fi-
nancial. We propose to use stochastic process mod-
els for the prediction purpose. The main advantage
of these stochastic process models is that they can
be (re)trained on data collected from users in live
experiments. Since the training and prediction are
done for the same users for different experiment varia-
tions separately, the prediction accuracy is potentially
higher. The relationship between users and Ant Fi-
nancial is noncontractual. We thus review and apply
well-known stochastic process models in the noncon-
tractual scenario in marketing. With these stochastic
process models from the noncontractual scenario, we
also do not run into the difficulty of labelling (we do
not observe when a user drops out) as in supervised
learning models. We empirically compare the models
based on data from real experiments in Ant Financial.
Based on the empirical results, we conclude that the
BG/NBD model is the most suitable for the purpose
of mid-term treatment effect prediction in controlled
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
28

Table 5: Thirty-day Decision-making Prediction Accuracy in Production.
Model Stochastic Process model Regression Model with Xgboost
APC APD APC APD
Overall 78.1% 58.4% 39.5% 23.7%
[75.1%, 80.8%] [54.9%, 61.8%] [36.1%, 42.9%] [20.1%, 25.9%]
duration < 15 days 79.2% 40.2% 40% 20%
[75.1%, 83.2%] [35.3%, 45.0%] [35.1%, 44.8%] [16.0%, 23.9%]
duration ≥ 15 days 77.1% 75.8% 39.1% 27%
[73.0%, 81.1%] [71.6%, 79.9%] [34.2%, 43.7%] [22.6%, 31.3%]
experiments in the offline-payment business at Ant
Financial. Possible explanation of the results is also
given. The BG/NBD model has been productionized.
Production results show the effectiveness of the pro-
posed methodology. Analysis of the effect of train-
ing duration on prediction accuracy is also conducted.
This analysis is very useful to guide the operation of
controlled experiments, e.g., decide the run time of
experiments. Two possible future directions are as
follows. First, although the stochastic process mod-
els are from the marketing area, they can be used to
model any counting metric. Hence extension to other
counting metrics in Ant Financial is desired. The sec-
ond direction is to extend the stochastic process mod-
els to achieve higher prediction accuracy, e.g., relax
the lack of memory assumption, add nonstationarity,
etc.
REFERENCES
Abe, M. (2009). “counting your customers” one by one: A
hierarchical bayes extension to the pareto/nbd model.
Marketing Science, 28(3):541–553.
Bakshy, E., Eckles, D., and Bernstein, M. S. (2014). De-
signing and deploying online field experiments. In
Proceedings of the 23rd international conference on
World wide web, pages 283–292. ACM.
Dahana, W. D., Miwa, Y., and Morisada, M. (2019).
Linking lifestyle to customer lifetime value: An ex-
ploratory study in an online fashion retail market.
Journal of Business Research, 99:319–331.
Dechant, A., Spann, M., and Becker, J. U. (2019). Posi-
tive customer churn: An application to online dating.
Journal of Service Research, 22(1):90–100.
Dmitriev, P., Frasca, B., Gupta, S., Kohavi, R., and Vaz, G.
(2016). Pitfalls of long-term online controlled exper-
iments. In Big Data (Big Data), 2016 IEEE Interna-
tional Conference on, pages 1367–1376. IEEE.
Dziurzynski, L., Wadsworth, E., and McCarthy, D. (2014).
BTYD: Implementing Buy ’Til You Die Models. URL
http://CRAN.R-project.org/package=BTYD. R pack-
age version, 2.
Ehrenberg, A. S. C. (1972). Repeat-buying; theory and ap-
plications. North-Holland Pub. Co.
Fader, P. S. and Hardie, B. G. (2007). How to project
customer retention. Journal of Interactive Marketing,
21(1):76–90.
Fader, P. S., Hardie, B. G., and Lee, K. L. (2005). “counting
your customers” the easy way: An alternative to the
pareto/nbd model. Marketing science, 24(2):275–284.
Fader, P. S., Hardie, B. G., and Lee, K. L. (2008). Comput-
ing p(alive) using the bg/nbd model.
Fader, P. S., Hardie, B. G., and Shang, J. (2010). Customer-
base analysis in a discrete-time noncontractual setting.
Marketing Science, 29(6):1086–1108.
Gomez-Uribe, C. A. and Hunt, N. (2016). The netflix rec-
ommender system: Algorithms, business value, and
innovation. ACM Transactions on Management Infor-
mation Systems (TMIS), 6(4):13.
Hohnhold, H., O’Brien, D., and Tang, D. (2015). Focusing
on the long-term: It’s good for users and business. In
Proceedings of the 21th ACM SIGKDD International
Conference on Knowledge Discovery and Data Min-
ing, pages 1849–1858. ACM.
Karlin, S. (2014). A first course in stochastic processes.
Academic press.
Kohavi, R., Deng, A., Frasca, B., Longbotham, R., Walker,
T., and Xu, Y. (2012). Trustworthy online controlled
experiments: Five puzzling outcomes explained. In
Proceedings of the 18th ACM SIGKDD international
conference on Knowledge discovery and data mining,
pages 786–794. ACM.
Kohavi, R., Henne, R. M., and Sommerfield, D. (2007).
Practical guide to controlled experiments on the web:
listen to your customers not to the hippo. In Proceed-
ings of the 13th ACM SIGKDD international confer-
ence on Knowledge discovery and data mining, pages
959–967. ACM.
Lee, M. R. and Shen, M. (2018). Winner’s curse: Bias
estimation for total effects of features in online con-
trolled experiments. In Proceedings of the 24th
ACM SIGKDD International Conference on Knowl-
edge Discovery & Data Mining, pages 491–499.
ACM.
Roy, R. K. (2001). Design of experiments using the Taguchi
approach: 16 steps to product and process improve-
ment. John Wiley & Sons.
Schmittlein, D. C., Morrison, D. G., and Colombo, R.
(1987). Counting your customers: Who-are they
and what will they do next? Management science,
33(1):1–24.
Auxiliary Decision-making for Controlled Experiments based on Mid-term Treatment Effect Prediction: Applications in Ant Financial’s
Offline-payment Business
29

Tang, D., Agarwal, A., O’Brien, D., and Meyer, M. (2010).
Overlapping experiment infrastructure: More, better,
faster experimentation. In Proceedings of the 16th
ACM SIGKDD international conference on Knowl-
edge discovery and data mining, pages 17–26. ACM.
Thomke, S. H. (2003). Experimentation matters: unlock-
ing the potential of new technologies for innovation.
Harvard Business Press.
Trinh, G. (2013). Modelling changes in buyer purchasing
behaviour. PhD thesis, University of South Australia.
Venkatesan, R., Bleier, A., Reinartz, W., and Ravishanker,
N. (2019). Improving customer profit predictions with
customer mindset metrics through multiple overimpu-
tation. Journal of the Academy of Marketing Science,
47(5):771–794.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
30
