
PHRI Safety Control using a Virtual Flexible Joint Approach
J. Diab, A. Fonte, G. Poisson and C. Novales
Laboratoire PRISMES, Université d'Orléans, 8 rue Léonard de Vinci-45072, Orléans, France
Keywords: Physical Human-Robot Interaction, Virtual Adjustable Stiffness, Articulation Flexibility Control.
Abstract: Physical Human-Robot Interaction (PHRI) emphasize on human safety. In literature, two techniques were
presented to improving this critical factor concerning moving devices; the first solution is purely mechanical,
while the second one is based on the control. In this paper, we describe a new approach combining the two
previous solutions. Our proposed paper explores a control scheme involving the use of a virtual component
with an adjustable stiffness supposed to be placed between the motor shaft and the robot link. This scheme
proposes a Variable Impedance Actuator (VIA) robot control methodology based on the integration of a
virtual component, reflecting the behaviour of a real intrinsic Series Elastic Actuator (SEA). This novel
method is potentially beneficial in reducing injuries in human/robot interaction by combining a mechanical
operating principle and a control approach in order to reduce the collision forces in collaborative applications.
This proposed approach was simulated and validated using a UR3 robot model, showing great capacities in
reducing collision’s peak forces. This paper begins with particular attention to the robot dynamics, then the
articulation flexibility and force estimation have been tackled and finally ending the control architecture.
1 INTRODUCTION
The presence of unknown obstacles and
unpredictable human presence in the modern robotic
application implies the usages of more sophisticated
control strategies not based only on position control,
but a control strategy which allows some degree of
flexibility to avoid physical collisions. The nature of
those proximate physical interactions is classified
into five classes (République Francaise 2017). Those
classes can have an unconstraint or constraint impact
as a primary source of collision with detailed injury
severity description found in ISO/TS 15066 (Sami
Haddadin 2008). Reducing personal injuries leads to
the spread of flexible articulated robots with SEA or
VIA as the primary type of actuator. What separates
the SEA and VIA is impedance adjustability. SEA
uses active control strategies, like force control,
admittance or impedance control, while conserving
the joint mechanical properties (Navarro et al.
2018),(Ansarieshlaghi and Eberhard 2019),(Schüthe,
Wenk, and Frese 2016), (Zeng and Hemami 1997),
(Pratt and Williamson 1995), opposing to the VIA,
which changes its behavioural properties like
stiffness and damping to ensure expected joint
flexibility (Vanderborght et al. 2013), (Tonietti,
Schiavi, and Bicchi 2005), (Lenzi et al. 2011),(Forget
et al. 2018), (Spong 1987).
Furthermore, typical collision detection strategies
use visual feedback and global interpretation of the
working environment to predict the possibility of the
probable unwanted interaction (Morikawa et al.
2007), (Kagami et al. 2003), (Ebert and Henrich
2002). In order to achieve a complete knowledge of
the environment in robotics applications, a new data
type is added to the visual feedback representing the
external forces and torques. These forces and torques
could be estimated from the movement and the
dynamics of the robot, or, for better accuracy, they
could be measured by a force sensor located on the
end effector.
By acquiring both data feedback, modern robotic
has accomplished more advanced tasks and lead to
human-robot collaboration in the industry without the
need for separation bars.
The novel structure of data highlighted the
necessity of force control. Force control in robotics
date back to 60th (Whitney 1985), (Maples and
Becker 1986); hence it is well defined. This control
strategy incorporates the assumption of rigid-body
mechanics and assumes a rigid robot with rigid links
and joints, even if the current trend is towards soft
robots or robots with flexible articulations or links.
262
Diab, J., Fonte, A., Poisson, G. and Novales, C.
PHRI Safety Control using a Virtual Flexible Joint Approach.
DOI: 10.5220/0009777702620271
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 262-271
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The compliance, in this case, could be achieved by
one of these following control strategies: Impedance
Control, Admittance Control, or Flexible Joints
(Bruno and Khatib 2013), (Bissell 2009).
This work focuses on the compliance by the third
type control strategies. There are two approaches in
order to introduce the flexibility in robot joint: the
first one uses the intrinsic mechanical approach with
passive safety built in the joint mechanics (Tonietti,
Schiavi, and Bicchi 2005), (Sebastián Arévalo et al.
2019), and the second one based fundamentally on the
control (De Luca et al. 2006), (Navarro et al. 2016).
In literature, joint flexibility was modelled as spring
(often linear one) connecting the motor shaft and the
following link (Spong 1987), and only a few papers
relating to Force/Torque control for this model. Our
approach is to keep the usage of the real robot’s
mechanics but to bring virtual joint flexibility in the
control loop in order to mimic the behaviour of a real
flexible joint, providing the rigid robot with some
degrees of flexibility. This introduced component is
here a nonlinear torsional spring located between the
geared motor and robot links. The virtual aspect of
this coupling can make it possible to modify the
mechanical characteristics of the component as
required, while it is impossible to modify the
mechanical characteristics of a real joint. The control
by virtual joint provides then a nonlinear stiffness,
and a variable stiffness trajectory representation,
given it more adaptability, not like a fixed mechanical
device that retains the same stiffness response.
2 ROBOT MODEL
In our study, we used a 6 degrees of freedom (DOF)
collaborative robot, the UR3 from Universal Robots.
Those DOF refer to the number of rotational joints,
modelled using modified Denavit–Hartenberg (DH)
representation or known as Khalil representation
(Khalil and Kleinfinger n.d.) “Table 1”.
From “Table 1,” the kinematic model of the rigid
robot is extracted. The transition from the kinematic
model to the dynamic one needs multiple parameters
as the link masses and centre of inertia positions;
those criteria are located in the robot
datasheet(Universal-Robots 2012). Once all
parameters are located, the dynamic robot model was
obtained through the Lagrange derivation method.
We used this one in favour of its practicality in the
extraction of robot dynamic symbolic equations
(simple derivation of system kinetic and potential
energy), comparing it to the recursive Newton-Euler
approach. The above method provided the
mathematical representation of the UR3’s articulated
mechanism(Kufieta 2014). This model has completed
afterwards with the UR3 motors modelling.
Table 1: UR3 modified DH table (RAD and MM).
joints
Table Column Head (rad and mm)
𝝈
𝒊
𝜶
𝒊𝟏
𝒂
𝒊𝟏
𝜽
𝒊
𝒓
𝒊
1
0 0 0
𝜃
-248.1
2 0
/2
0
θ
0
3 0 0 243.65
θ
0
4 0 0 213.25
θ
112.35
5 0
/2
0
θ
85.35
6 0
/2
0
θ
81.9
The used UR3 was developed for light assembly
tasks and direct physical cooperation with humans
with a payload not exceeding 30N. This robot has
±360° of rotational wrists and an infinite end-effector
rotational joint. Its maximum extended arm reaches
500 mm.
Since the workspace is a joint space, the canonical
equation of the robot dynamics is formulated by the
following:
𝑀
𝑞
𝑞𝐶
𝑞,𝑞
𝑞𝑔
𝑞
𝜏𝜏
(1)
Where M(q), C(q,q ̇ ), g(q), τ, and τ_ext represent
robot inertia matrix, Coriolis force matrix, robot links
gravitational force vector, joint actuation torques, and
the external joint torques.
Figure 1: Rigid UR3 complete joint model.
“Equation_1” does not take in consideration the
effects of the motor on the robot dynamics; the
enhanced formulation of this equation could be
presented by the following:
𝐻
𝑞
𝑞
𝜃
Γ
𝑞,𝑞
𝑞𝑔
𝑞
𝜏𝜏
𝜏
(2)
Where 𝐻
𝑞
, Γ
𝑞,𝑞
and 𝜏
represent the global
inertia matrix, global Coriolis force matrix, and the
motor torques.
“Equation_2” assumes that the robot link is
directly connected to the motor shaft, as shown in
“Figure 1”.
PHRI Safety Control using a Virtual Flexible Joint Approach
263

The extracted model presented in “Equation_1”
and “Equation_2” is rigid and do not allow any
compliance or any movement between the motor
shaft and robot link, to ensure a compliance behaviour
in such system joint flexibility must be integrated into
the model to vary joints rigidities.
3 JOINT FLEXIBILITY
Without taking into account the mechanical
reversibility introduced in the mechanical field as
variable-stiffness transmission (Nelson, Nouaille, and
Poisson 2019). “Figure 1” and “Equation_2” presents
a rigid model without any flexible part between the
rotor shaft and the robot link. This model does not
allow any compliance in case of a collision or human
interaction. To solve this problem, “Equation_2”
could integrate a new term to allow such motion.
The joint flexibility in this context is provided by
a virtual flexible joint, with a nonlinear spring
supposed to be located between the rotor and the link
similar to “Figure 2”. The virtual spring, once
provided with the motor and robot joint angular
position, produces the correspondent torque needed
by the robot.
In order to adapt “Equation_2”, Spong’s
assumption must be respected: 1. The kinetic energy
of the rotor is due mainly to its rotation, 2. The
rotor/gear inertia is symmetric about the rotor rotation
axis (Spong 1987). Motor electrical dynamic (i.e.,
feedback current in the control loop) was neglected,
with the assumption that the electric system time
constant is much smaller than the mechanical one.
The newly implemented spring introduces a new
term in system potential energy. Therefore, the
potential energy is divided into two parts:
• The old gravity potential of “Equation_2”.
• The stiffness potential V
k
(Radomirovic and
Kovacic 2013)
.
𝑉
𝑞,𝜃
𝑉
,
𝑞
,𝜃
(3
)
𝑉
,
𝑞
,𝜃
𝑓
𝜃
,𝑞
𝑑
𝜃
𝑞
(4
)
Where f(i, qi), is a nonlinear function expressing
the spring torque in the function of spring deflection
(i-qi).
The derivation of “Equation_3” respectively to
and q and its reintroduction in the “Equation_2”
gives:
𝐻
𝑞
𝑞
𝜃
Γ
𝑞,𝑞
𝑞
𝑔
𝑞
F,q
F,q
𝜏
𝜏
(5)
Where F(, q) is nonlinear spring torque vector
with:
F,q
𝑓
𝜃
,𝑞
…
𝑓
𝜃
,𝑞
(6)
While colliding into an obstacle, the deflection
angle (-q) becomes increasingly significant. The
gape introduced between rotors and links angular
positions, as shown in “Figure 2”, requests the
stiffness coefficient of f(i, qi) to be adjusted.
Figure 2: Flexible joint.
The stiffness of nonlinear spring is given by:
𝐾
,
(7)
The reduced form of the “Equation_5” can be
written according to (De Luca et al. 2006), (Martinoli
et al. 2012) by the following:
𝑀
𝑞
𝑞𝐶
𝑞,𝑞
𝑔
𝑞
F
,q
𝜏
(8)
𝐵𝜃
F
,q
𝜏
(9)
Where B is the rotors inertia matrix.
f(i, qi) could be a constant, decreasing, or
increasing, linear, or nonlinear function. This wide
variety of choices is not applicable in the flexible
mechanical joint due to the limitation in the
adjustability of the mechanical component. As a
result, the function f(i, qi) has to provide a suitable
torque to the links in all cases (colliding or not).
Following Spong's definition (Spong 1987) and
(Haddadin et al. 2008), f(i, qi) is given by an
equation which respects Hook’s Law:
𝑓
𝜃
,𝑞
𝐾∗𝜃
𝑞
(10)
Where K, is a fixed spring stiffness coefficient.
With a small sampling time, the local zone of
nonlinear spring has similar behaviour to Hook’s law
presented in the “Equation_10”. Consequently, the
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
264

simulated nonlinear spring could be defined as linear
spring with variable stiffness K.
In this paper, K is ranged between two values:
Kmin and Kmax, representing respectively the
minimum and maximum spring’s stiffness. In the
absence of collision, K equals Kmax, but while
colliding, K degenerates rapidly until Kmin. To be
able to distinguish one case from another, a trigger
should be integrated into the selection of K. The
deflection angle (i-qi) is used for this purpose. The
value of (i-qi) < ~0.0873 rad is used as a threshold
to activate K, as shown in “Figure 3”. Kmax is
different for each articulation because it depends on
the maximal torque of each UR3’s motors varying
between 12 Nm and 56 Nm.
“Figure 3” is used to illustrate a trajectory of K,
with Kmax=100 Nm/rad
K is defined as the following:
𝐾
K
; i
f
q
~0.0873rad
K
∗sin4
q
K
∗cos3
q
K
; i
f
q
~0.5236rad
(11)
“Equation_11” uses a combination of sin and cos
to insure a fast degeneration of K when 5°< -q <30°.
Figure 3: Spring stiffness K, with Kmin=0.001 Nm/rad,
Kmax=100 Nm/rad.
In order to control the new flexible robot, external
torques should be introduced into the robot dynamics
“Equation_8”. The simplest way to introduce those
requirements is to estimate those parameters.
4 FORCE ESTIMATION
The transmitted torques between the simulated robot
and the trajectory generation subsystem shown in
“Figure 4” are easily measured on UR3. Those
measurements are possible because of UR3 associates
torque sensors in its articulation. Those torques were
taken into account using the robot model
“Equation_1”.
Figure 4: The control architecture.
The external joint torques 𝜏
according to (De
Luca and Mattone 2005), is coupled to the
generalized contact force Fext by:
𝜏
𝐽
∗𝐹
(12)
“Equation_12” adopt the knowledge of external
forces applied on the end-effector in the contact point
with the object, those external contact forces were
obtained in our case by a linear spring-damper model
to estimate or simulate 𝐹
. Those reaction forces
are then calculated afterwards according to the end
effector penetration depth and velocity. For this
purpose, the object position could be extracted from
image processing algorithms (Collet et al. 2009), but
in this study, it was supposed located in a fixed,
known Cartesian frame [x,y,z].
The calculated reaction forces are based on linear
spring-damper contact mechanism model given by:
𝐹
𝐾
∗𝑋
∗ 𝑠𝑖𝑔𝑛𝑋
∗𝐷∗𝑉
(13)
Where Ks is the spring stiffness, Xpen is the
difference between the robot end-effector Cartesian
position and the object position, D and
Vpen=∆Xpen/∆t, are respectively, the spring
damping coefficient and the speed of end-effector
penetration.
“Equation_12” and “Equation_13” construct the
first external force/torque estimator. This torque is
added subsequently to the joint torques calculated
using the dynamic robot model. The combined
torques provide the complete joint torque, used as an
input to the trajectory generation subsystem, where
the second torque estimator is located.
The 6
th
order polynomial trajectory generator
“Figure 5” ensures a smooth trajectory, with a smooth
high order derivative, resulting in consideration of the
equality in the desired and the real articulation
position. This assumption leads to a newer
description of robot dynamics using the desired
positions and their derivatives.
From all the above, a second torque observer can
be derived from the desired positions. This torque
observer represents the expected joint torques in a
collision-free environment regarding the desired
PHRI Safety Control using a Virtual Flexible Joint Approach
265

trajectory. Introducing those assumptions in
“Equation_1” gives:
𝜏̂𝑀
𝑞
𝑞
𝐶
𝑞
,𝑞
𝑔
𝑞
(14)
In the absence of collision, “Equation_1” is
identical to “Equation_14”. This equality promotes
the extraction of the estimated external torque
presented in “Equation_15”.
𝜏
𝜏
𝑒𝑥𝑡
𝜏𝜏
(15
)
The first estimator provides the simulation with
the external forces and torques undergo by the end
effector, while the output of the second estimator can
alter the robot trajectory.
Figure 5: Trajectory generation subsystem.
The estimated external torques are crucial factors
in the control architecture and the trajectory
generation because they indicate the variation of joint
torques before and upon a collision. This identified
variation can be a trigger to change robot motion in
control architecture.
5 CONTROL ARCHITECTURE
The architecture of the complete system is divided
into four subsystems: (1) Trajectory generation, (2)
Control Unit, (3) Motor and Flexible joint, (4) Robot
and Environment see “Figure 4”.
Trajectory generation subsystem takes a
destination in the articulation space with a starting
and ending time, and generate a smooth trajectory
from the reference to the desired position.
The primary role of the Control Unit subsystem is
to compensate for system errors. Those errors contain
gravitation, Coriolis/centrifugal forces, and position.
We used a feedforward combined with a PD
controller to generate a torque command U for the
motor model (De Luca 2000).
The robot and environment subsystem combine
the simulated robot and its interaction effects on the
simulated body (i.e., fixe object).
Referring to “Equation_8”, our dynamic model is
a nonlinear system, and therefore in order to control
such a mechanism, a nonlinear control approach must
be used.
To preserve robot articulation and to ensure a
displacement without stepping, robot trajectory must
be smooth without any discontinuities in its
movement, velocity, or acceleration. In addition to
previous constraints, the robot displacement must
obey a finale delay to accomplish a predefined task.
Those above conditions render the trajectory
generation a time-dependent problem. Thus, an
interpolation method needed in order to link space
and time.
The trajectory generation subsystem in “Figure
5”, relays on time scaling to generate the appropriate
desired trajectory using sixth-order polynomial
interpolation.
Discrete-time 𝑡
, is written as 𝑡
𝑡
𝑡,
regarding t, the discrete sampling time. To combine
space and time vector, we need to redefine our
interpolation time in order to change the trajectory
upon an undesired collision. This task is provided by
the time sampling system, which feeds the strategy
selector with two current times
𝑡
and
𝑡
.
𝑡
is a
modified time implicitly integrating the estimated
joints torques 𝜏̃.
𝑡
is given by the equation below:
𝑡
𝑡
𝑓
𝑠𝑔
𝜏
∗ ∆𝑡 ;
𝑡
𝑖
1
𝑇
𝑇
;
𝑡
𝑖
1
𝑇
(16)
Where 𝑓𝑠
𝑔𝜏
is a function outputting 0
or 1 considering a threshold for the mapped
estimated external torques 𝑔𝜏
.
𝑓
𝑠
𝑔𝜏
1;
|
𝑔𝜏
|
0.2
0;
|
𝑔
𝜏
|
0.2
(17)
𝑔𝜏
takes the estimated external torques
𝜏
deduced by the torque estimator and
produces a value ranging between 0,1
representing the relation between the estimated
torque and the maximum motors torques.
𝑔𝜏
𝜏
𝜏
𝑚
𝑚𝑖𝑛
𝜏
𝑚
𝑚𝑎𝑥
𝜏
𝑚
𝑚𝑖𝑛
(18)
𝑡
is given by “Equation_19”:
𝑡
𝑡
;𝑡
𝑇
𝑇
;𝑡
𝑇
(19)
𝑡
of “Equation_16” and
𝑡
of “Equation_19”
are fed to the strategy selector, which compares
𝑡
and 𝑡
, if those two are equals that means no collision
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
266
is detected, then the selection is made to take
𝑡
as an
interpolation time, in case of difference
𝑡
is
selected. In collision
𝑡
is always constant equals to
the time before the collision. This constant time
implies a constant trajectory during and after the
impact.
For illustration and presentation purposes, the
simulation results of the complete system are
presented in the following part.
6 SIMULATION RESULTS
The simulation of the collision detection and
compliance strategy was performed with robotics
conditions under gravitational force. The joint
positions were expected to be obtained by digital
encoders.
All joints velocities and accelerations were
acquired in two ways by numerical differentiation or
by numerical computation. Those mathematical
operations introduce a certain level of realistic noise
in the simulation.
The trajectory is generated between 𝑞
and 𝑞
,
representing two 𝑅
vectors with n=6. Where 𝑞
is
the initial starting joint robot positions at 𝑇
0 𝑠 and
𝑞
is the ending joint position at 𝑇
2 𝑠. The
desired articulations positions according to the two
strategies of “Figure 5” can be observed in “Figure
6”.
Figure 6: Trajectory deformation.
The deformation of the desired trajectory at
t=1.08s, as shown in “Figure 6”, helps to stop the
robot upon a collision. The strategy selector,
represented in “Figure 5”, switches the interpolation
time from 𝑡
to
𝑡
,
causing the time t to be constant
𝑡
𝑡
. As a result, the Feedforward system
maintains fixed torque values until the obstacle is
removed, or the contact between human-robot has
evolved (eg. pushing on the robot or evading the
contact).
Figure 7: Difference in articulation positions between
system 1: with the virtual SEA and system 2: without the
flexible components. It is illustrated on the first four axes
of the robot. Here q1 and q4 are the only ones impacted by
the strategy.
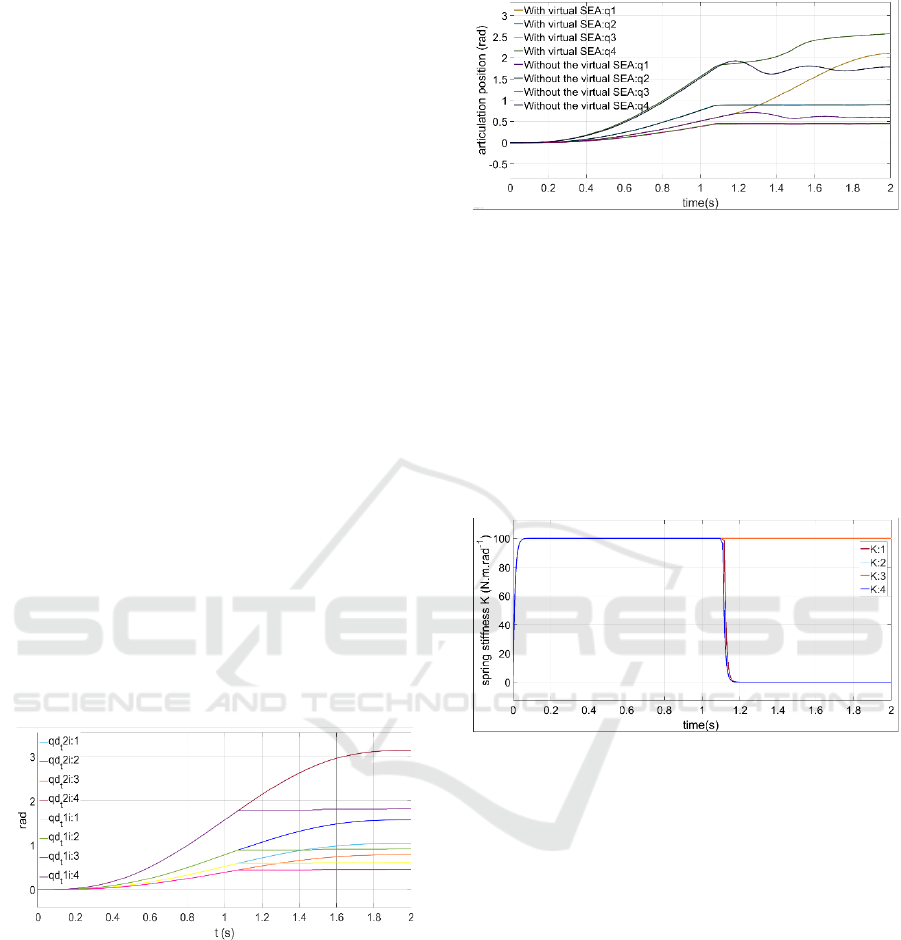
“Figure 7” shows the comparison of the robot
articulations positions between a system integrating
the virtual SEA and another without it.
The compliance in “Figure 7” is shown by the
increase of angular position of q1 and q4. This
angular growth is a response to the increase in joint
flexibility.
Figure 8: Spring stiffness, K.
“Figure 8” introduces the behaviors of the virtual
SEA in four regions, [0s, 0.2s], [0.2s, 1.08s], [1.08s,
1.2s] and [1.2s, 2s]. In these regions, the stiffness of
the springs varies; they increase in the first region,
until saturation with a maximale stiffness (Kmax) in
the second region, towards a rapid decrease during the
collision, and finally, they maintain a constant value
of the minimale stiffness (Kmin) after the collision.
The deflection angle
q
causes the variation
in K. In the first zone
q
decreases because in
this zone, rotors positions were following a fixed
reference 𝑞𝑞
. The saturation of K in the second
zone happened when the rotor and joint angular
differences are less than 0.0873 rad (about 5°). The
stiffness decreases in zone 3, due to the increase of
angular difference
q
. This zone represents the
collision zone, where the trajectory is modified, as
shown in “Figure 6”. The fixed trajectory implies a
fixe rotor angle, which is the leading cause of the
expansion of the gap between
q
shown in
PHRI Safety Control using a Virtual Flexible Joint Approach
267

“Figure 2”. In this case, the variation of q is induced
by Kmin nullifying torques values to the affected
joint. Rendering torques to 0 results in vast freedom
of movement of the joint. This freedom is highlighted
in the end zone, where K is fixed as Kmin.
“Figure 8” illustrates the trajectory issued from
“Equation_11”, and shows the effects of the
articulation flexibility on altering the joint trajectory.
The new trajectory generated by the flexible joint has
a direct effect on the forces between the end-effector
and the object. Those effects are shown in the
following figure, “Figure 9”.
Figure 9: The difference in reaction forces between the 2
systems.
“Figure 9” indicates the reduction of peak force
values on the impact. The variation of joint flexibility
shown in “Figure 8”, induced changes on the
Cartesian positions of the end-effector, this variation
leads to a new penetration value for “Equation_13”;
the joint flexibility induced by the virtual SEA insure
a smaller value of penetration for the first force
estimator giving in overall smaller reaction forces and
torques. “Figure 9” shows the main difference
between the two systems, the first one with the
variable stiffness (the red line) reduced the value of
reaction force to 0 at t=1.6s, while the second system
stiffness (the blue line) is oscillating with much
higher contact forces. The virtual SEA gives the
robot, in this case, the flexibility to move away from
the collision case.
7 COMPARATIVE DISCUSSIONS
From above, there is a two way to implement
compliance in a robotic using VIA or SEA systems.
Each type of those induced flexibilities holds
advantages and drawbacks.
In the case of SEA, robot compliance is ensured
by the control architecture. The controller varies the
actuation torque to reshape the desired path. Contrary
to VIA, SEA needs the presence of force/torque
sensors to trigger collision detection and re-
evaluation of the trajectory.
In other words, VIA acts directly on the path
while SAE needs a control loop to make a path
change.
Our approach combines the two above methods
by adding the VIA virtual component to the existing
SAE control loop, ensuring additional compliance in
the event of a collision, this additional layer makes
the robot softer in the event of a crash. It permits the
reduction of impact forces compared to the two
previous methods.
SEA benefits from active compliance induced by
an active controller which complexify the
implementation of such a solution. While VIA, due to
its passive compliance, does not need a complex
control scheme, facilitating its implementation in a
robotic application. Our solution, as mentioned
before, is the combination of both systems, which
gives this solution the benefice of the active control
scheme and virtual passive flexibility.
This approach makes the proposed compliance
more adjustable from the ordinary SEA controller, and
more controllable and reliable than a passive VIA.
Due to the uprising of COVID-19 pandemic, the
planned experiments in the laboratory on the robot
have been impossible to perform. We, therefore,
stayed on simulations. This way provides us with
enough data to be interpreted and brings promising
answers for the future validation on a real robot.
Fist, the simulated experiment was conducted to
highlight and to accentuate on the advantages of our
approach. This simulation concerns two cases: case
“A” showing pure SEA behaviour and case “B”
presenting the proposed solution. In “A”, the robot (a
UR3 from Universal Robots) is supposed to be
controlled using an impedance controller, while in
“B”, the robot is subjected to the same controller of
“A” plus a virtual VIA. In all experiments, a wall is
also supposed to be located at the proximity of the
robot. The wall is placed in a way that ensures a
collision with the moving the robot arm. In those
simulations, we will compare the insertion of the
robot end-effector into the wall, the force upon and
after the collision.
The robot's configuration on the collision is shown in
“Figure 10”:
Figure 10: Robot position in multiple configurations near
the right wall.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
268

The robot in “A” is controlled with impedance
control which tends to stop it on the desired position
where the contact point with the wall as shown in
“Figure 10”
.
While in “ B”, we can notice additional
compliance behaviour manifesting by the difference
in the configuration of the robot arm, as shown in
“Figure 10”.
In case “A” and “B” we notice the same
behaviour, were the robot kept it end effector on the
contact point with the wall.
The difference in the end effector position at the
end of the simulation is closely related to the virtual
VIA that has been introduced by the nonlinear
torsional spring. The figure highlights the role of the
stiffness in the flexibility of the articulation where we
can notice that the third and second articulation are
lower in B than A. This difference is the result of the
variation of the actuation torque 𝑓
𝜃
,𝑞
by
adjusting the stiffness in “Equation_10”.
In case of cobotic application maintaining a safe
distance in a collision is important, but the main
factor affecting the severity of the injury is how much
force was applied in the collision and when the robot
is stopped. The forces of cases “A” and “B’’ are
shown in “Figure 11”.
Figure 11: Robot forces upon and after the collision for the
case “A” and “B”.
“Figure 11” showcase robots end-effector’s
reaction forces in case “A” and “B”, where the
maximum impact forces differ from one situation to
another. In “A” the maximum impact forces
registered a value of 76 N, wherein “B” this value is
divided by 3, with maximum values of 26 N.
This difference in force values is not limited to the
impact; also an important reduction of its finale
values can be noticed, wherein “B” the Fext is around
2 N while in “A” Fext is approximately 8 N.
So in case of collision, the injury in case “A”
would be with much higher consequences while in
“B” the injury severity would be less.
Those two aspects of the case “B” answer the
safety factor of cobotic application, firstly by limiting
the robot action and displacement by fixing the robot
workspace to the position of the contact limiting the
risk of insertion, and by reducing the contact force,
the case “B” also reduces collision damages in
cobotics.
8 CONCLUSIONS
Concluding, we presented the feasibility of such an
integrated virtual SEA and its effect on robot joint
displacement without the need for altering the
existing robot joint.
The presented method combines the existent VIA
and SEA flexibility to produce a compliant robot. The
obtained simulation result validates the compliance
behaviour and could lead to a more secure robot,
which can reduce the stiffness of its joint at any
probable human risk, adding in a manner some of the
additional degrees of safety to the existent PHRI.
Another advantage of such a system is to adapt
the joint stiffness behaviour to suit not only one
specific profile but much more complex ones.
This method offers a promising new way of
reducing the forces on a collision subject, it is still in
development, in particular as for its adaptation to
different fields of application.
We intend in the future work to validate the
simulation result with experimental data. The next
step will be oriented towards applying this new
command law on a UR3 integrated into a complex
environment. The extracted experimental data will
help us to refine this strategy so that it will be safer
and more reliable for human-robot interaction.
ACKNOWLEDGMENTS
This work has been realized as part of an ANR
(French National Research Agency) SISCob project
ANR-14-CE27-0016.
PHRI Safety Control using a Virtual Flexible Joint Approach
269

REFERENCES
Ansarieshlaghi, Fatemeh, and Peter Eberhard. 2019.
“Hybrid Force/Position Control of a Very Flexible
Parallel Robot Manipulator in Contact with an
Environment.” ICINCO 2019 - Proceedings of the 16th
International Conference on Informatics in Control,
Automation and Robotics 2(Icinco): 59–67.
Bissell, C C. 2009. Springer Handbook of Automation
Springer Handbook of Automation. ed. Shimon Y. Nof.
Berlin, Heidelberg: Springer Berlin Heidelberg.
http://link.springer.com/10.1007/978-3-540-78831-7.
Bruno, Siciliano, and Khatib. 2013. 46 Choice Reviews
Online Springer Handbook of Robotics. eds. Bruno
Siciliano and Oussama Khatib. Berlin, Heidelberg:
Springer Berlin Heidelberg. http://link.springer.com/
10.1007/978-3-540-30301-5.
Collet, Alvaro, Dmitry Berenson, Siddhartha S. Srinivasa,
and Dave Ferguson. 2009. “Object Recognition and
Full Pose Registration from a Single Image for Robotic
Manipulation.” : 48–55.
Ebert, Dirk M., and Dominik D. Henrich. 2002. “Safe
Human-Robot-Cooperation: Image-Based Collision
Detection for Industrial Robots.” IEEE International
Conference on Intelligent Robots and Systems
2(October): 1826–31.
Forget, Florent et al. 2018. “Implementation, Identification
and Control of an Efficient Electric Actuator for
Humanoid Robots.” ICINCO 2018 - Proceedings of the
15th International Conference on Informatics in
Control, Automation and Robotics 2(Icinco): 29–38.
Haddadin, Sami, Alin Albu-Schäffer, Alessandro De Luca,
and Gerd Hirzinger. 2008. “Collision Detection and
Reaction: A Contribution to Safe Physical Human-
Robot Interaction.” 2008 IEEE/RSJ International
Conference on Intelligent Robots and Systems, IROS:
3356–63.
Kagami, Satoshi et al. 2003. “Humanoid Arm Motion
Planning Using Stereo Vision and RRT Search.” IEEE
International Conference on Intelligent Robots and
Systems 3(October): 2167–72.
Khalil, W., and J. Kleinfinger. “A New Geometric Notation
for Open and Closed-Loop Robots.” In Proceedings.
1986 IEEE International Conference on Robotics and
Automation, Institute of Electrical and Electronics
Engineers, 1174–79. http://ieeexplore.ieee.org/
document/1087552/.
Kufieta, Katharina. 2014. “Force Estimation in Robotic
Manipulators: Modeling, Simulation and
Experiments.” : 144.
Lenzi, Tommaso et al. 2011. “NEUROExos: A Variable
Impedance Powered Elbow Exoskeleton.” Proceedings
- IEEE International Conference on Robotics and
Automation: 1419–26.
De Luca, Alessandro. 2000. “Feedforward/Feedback Laws
for the Control of Flexible Robots.” Proceedings -
IEEE International Conference on Robotics and
Automation 1(April): 233–40.
De Luca, Alessandro, Alin Albu-Schäffer, Sami Haddadin,
and Gerd Hirzinger. 2006. “Collision Detection and
Safe Reaction with the DLR-III Lightweight
Manipulator Arm.” IEEE International Conference on
Intelligent Robots and Systems: 1623–30.
De Luca, Alessandro, and Raffaella Mattone. 2005.
“Sensorless Robot Collision Detection and Hybrid
Force/Motion Control.” Proceedings - IEEE
International Conference on Robotics and Automation
2005(April): 999–1004.
Maples, James A., and Joseph J. Becker. 1986.
“Experiments in Force Control of Robotic
Manipulators.” : 695–702.
Martinoli, Alcherio, Francesco Mondada, Nikolaus Correll,
and Grégory Mermoud. 2012. 83 STAR Springer Tracts
in Advanced Robotics Springer Tracts in Advanced
Robotics: Preface.
Morikawa, Sho, Taku Senoo, Akio Namiki, and Masatoshi
Ishikawa. 2007. “Realtime Collision Avoidance Using
a Robot Manipulator with Light-Weight Small High-
Speed Vision Systems.” Proceedings - IEEE
International Conference on Robotics and Automation
(April): 794–99.
Navarro, Benjamin et al. 2016. “An ISO10218-Compliant
Adaptive Damping Controller for Safe Physical
Human-Robot Interaction.” Proceedings - IEEE
International Conference on Robotics and Automation
2016-June: 3043–48.
———. 2018. “Physical Human-Robot Interaction with the
OpenPHRI Library To Cite This Version : HAL Id :
Hal-01823337 Physical Human-Robot Interaction with
the OpenPHRI Library Two-Layer Safe Damping
Control Framework.”
Nelson, Carl A, Laurence Nouaille, and Gérard Poisson.
2019. 73 Advances in Mechanism and Machine
Science. Springer International Publishing.
http://link.springer.com/10.1007/978-3-030-20131-9.
Pratt, Gill A., and Matthew M. Williamson. 1995. “Series
Elastic Actuators.” IEEE International Conference on
Intelligent Robots and Systems 1: 399–406.
Radomirovic, Dragi, and Ivana Kovacic. 2013. “Deflection
and Potential Energy of Linear and Nonlinear Springs:
Approximate Expressions in Terms of Generalized
Coordinates.” European Journal of Physics 34(3): 537–
46.
République Francaise. 2017. “Guide de Prévention à
Destination Des Fabricants et Des Utilisateurs Pour La
Mise En Oeuvre Des Applications Collaboratives
Robotisées-Edition 2017.” Ministère du travail.
https://travail-emploi.gouv.fr/IMG/pdf/guide_de_
prevention_25_aout_2017.pdf.
Sami Haddadin, Elizabeth Crof. 2008. “Handbook of
Robotics: Physical Human-Robot Interaction.”
Handbook of Robotics: 1835–74.
Schüthe, Dennis, Felix Wenk, and Udo Frese. 2016.
“Dynamics Calibration of a Redundant Flexible Joint
Robot Based on Gyroscopes and Encoders.” ICINCO
2016 - Proceedings of the 13th International
Conference on Informatics in Control, Automation and
Robotics 1(Icinco): 335–46.
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
270

Sebastián Arévalo, Laribi, Zeghloul, and Arsicault. 2019.
“On the Design of a Safe Human-Friendly Teleoperated
System for Doppler Sonography.” Robotics 8(2): 29.
Spong, M. W. 1987. “Modeling and Control of Elastic Joint
Robots.” Journal of Dynamic Systems, Measurement
and Control, Transactions of the ASME 109(4): 310–
19.
Tonietti, Giovanni, Riccardo Schiavi, and Antonio Bicchi.
2005. “Design and Control of a Variable Stiffness
Actuator for Safe and Fast Physical Human/Robot
Interaction.” Proceedings - IEEE International
Conference on Robotics and Automation 2005(April):
526–31.
Universal-Robots. 2012. “Ur Parameters for Kinematics
and Dynamics Calculations.” https://www.universal-
robots.com/how-tos-and-faqs/faq/ur-faq/parameters-
for-calculations-of-kinematics-and-dynamics-45257/.
Vanderborght, B. et al. 2013. “Variable Impedance
Actuators: A Review.” Robotics and Autonomous
Systems 61(12): 1601–14. http://dx.doi.org/10.1016/j.
robot.2013.06.009.
Whitney, Daniel E. 1985. “Historical Perspective and State
of the Art in Robot Force Control.” Proceedings - IEEE
International Conference on Robotics and Automation:
262–68.
Zeng, Ganwen, and Ahmad Hemami. 1997. “An Overview
of Robot Force Control.” Robotica 15(5): 473–82.
PHRI Safety Control using a Virtual Flexible Joint Approach
271
