
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect
Semantic and Topological Biological Communities
Marwa Ben M’Barek
1,2 a
, Amel Borgi
1,3
, Sana Ben Hmida
2 b
and Marta Rukoz
2
1
LIPAH, Facult
´
e des Sciences de Tunis, Universit
´
e de Tunis El Manar 2092, Tunis, Tunisia
2
LAMSADE CNRS UMR 7243, Paris Dauphine University, PSL Research University,
Place du Mar
´
echal de Lattre deTassigny, Paris, France
3
Institut Sup
´
erieur d’Informatique, Universit
´
e de Tunis El Manar, 1002, Tunis, Tunisia
marta.rukoz@lamsade.dauphine.fr
Keywords:
Community Detection, Biological Networks, PPI Networks, Genetic Algorithm, Heuristic Crossover.
Abstract:
Community detection aims to identify topological structures and discover patterns in complex networks. It
presents an important problem of great significance in many fields. In this paper, we are interested in the
detection of communities in biological networks. These networks represent protein-protein or gene-gene
interactions which corresponds to a set of proteins or genes that collaborate at the same cellular function.
The goal is to identify such semantic and/or topological communities from gene annotation sources such as
Gene Ontology. We propose a Genetic Algorithm (GA) based technique as a clustering approach to detect
communities from biological networks. For this purpose, we introduce four specific components to the GA: a
fitness function based on a similarity measure and the interaction value between proteins or genes, a solution
for representing a community with dynamic size, an heuristic crossover to strengthen links in the communities
and a specific mutation operator. Experimental results show the ability of our Genetic Algorithm to detect
communities of genes that are semantically similar or/and interacting.
1 INTRODUCTION
Community detection in networks is one of the most
popular topics of modern network science (Fortunato
and Hric, 2016). It deals with an interesting compu-
tational technique for the analysis of networks. It can
yield useful insights into the structural organization
of a network and can serve as a basis for understand-
ing the correspondence between structure and func-
tion (specific to the domain of the network).
In this paper, we are interested in detecting com-
munities in biological networks. These networks have
received much attention in the last few years since
they model the complex interactions occurring among
different components in the cell (Pizzuti and Rombo,
2014). We mainly focus on Protein-protein or Gene-
gene interaction networks
1
known as PPI networks.
Their nodes correspond to proteins or genes and the
a
https://orcid.org/0000-0002-8307-3533
b
https://orcid.org/0000-0003-4202-613X
1
Protein-protein or Gene-gene interaction networks are
mathematical representations of the physical contacts be-
tween proteins or genes in the cell.
edges correspond to pairwise interactions between
genes or proteins. These communities give us an idea
about the perception of the network’s structure. The
ultimate goal in biology is to determine how genes
or proteins encode function in the cell. This work is
multidisciplinary as it brings the field of biology and
computer science in the broad sense.
Thus, the goal is to find communities of genes
having a biological sense (that participate in the same
biological processes or that perform together specific
biological functions) from gene annotation sources.
To make this task, we have combined three levels of
information:
1. Semantic level: information contained in biologi-
cal ontologies such as Gene Ontology (GO) (Ash-
burner et al., 2000) and information obtained by
the use of a similarity measure such as GO-based
similarity of gene sets (GS2) (Ruths et al., 2009).
It assesses the semantic similarity between pro-
teins or genes.
2. Functional level: information contained in pub-
lic databases describing the interactions of pro-
teins or genes such as Search Tool for Recur-
Ben M’Barek, M., Borgi, A., Ben Hmida, S. and Rukoz, M.
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect Semantic and Topological Biological Communities.
DOI: 10.5220/0009779902950306
In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 295-306
ISBN: 978-989-758-443-5
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
295

ring Instances of Neighbouring Gene (STRING)
database (Mering et al., 2003).
3. Networks level: information contained in path-
way databases that present community of proteins
or genes such as Kyoto Encyclopedia of Genes
and Genomes (KEGG) database (Kanehisa and
Goto, 2000).
A lot of research effort has been put into community
detection in different academic fields such as physics,
mathematics and computer science. Meanwhile, var-
ious algorithms based on Genetic Algorithms (GA)
have been proposed. These algorithms are used to
overcome some drawbacks such as scaling up of net-
work size. Indeed, some of the community detec-
tion algorithms are unsuitable for very large networks
and require a priori knowledge about the community
structure, as the number and the size of communi-
ties which is not easy or impossible to obtain in real-
world networks (Tasgin et al., 2007). The algorithms
based on GA are very effective for community detec-
tion especially in very large complex networks (Jiao
et al., 2012). However, the vast majority of optimiza-
tion methods proposed to detect community in PPI
networks use graph topology and do not use similar-
ity measures between proteins or genes (Pizzuti and
Rombo, 2014).
This paper presents a new generic community de-
tection algorithm in PPI networks based on GA. The
proposed GA is parameterized according to the im-
portance affected to each measure criterion (semantic
measure and interaction measure). The aim is to de-
tect communities according to either both criteria, or
only one criterion. The obtained communities could
then be analyzed and compared for a better compre-
hension of the topological and similarity measures
and the relation between them. This work is a general-
ization of a previous method (named as GA-PPI-Net)
(Ben M’barek et al., 2019). Thus, we propose a GA
based approach that allows to find communities hav-
ing different sizes using the interaction and/or similar-
ity criterion. Alike the previous proposed algorithms,
the new proposed method uses the similarity mea-
sures as well as the interaction measure between pro-
teins or genes and tries to find the best proteins/genes’
community by maximizing the concept of community
measure. The main novelties of the approach can be
summarized as follows. We adopt a lighter represen-
tation of a community with dynamic size than the one
adopted in GA-PPI-Net, and we propose a new fitness
function that generalizes the previous one. It is still
based on the concept of community measure but it al-
lows to combine the semantic and the interaction cri-
terion by choosing their respective contribution to the
fitness function according to thresholds. This concept
provides a generic solution of a partitioning commu-
nities that are semantically similar or/and interacting.
Moreover, a new genetic operation that is a specific
heuristic crossover operator adapted to our problem
is introduced. This heuristic crossover help the GA
to build communities with high values of similarities
or/and interaction between genes. The algorithm out-
puts the final community by selectively exploring the
search space. Experiments on real datasets show the
ability of the proposed approach to correctly detect
communities having different sizes which are similar
and/or interact.
The contents of this paper are organized in six
main sections. The next section presents an overview
of the existing community detection algorithms. Sec-
tion 3 provides the problem definition. Section 4 de-
picts our main proposed algorithm for community de-
tection. In section 5, experimental results on real data
sets are presented and analyzed. Finally, section 6 re-
ports the conclusion.
2 COMMUNITY DETECTION
RELATED METHODS
Network community detection has an important role
in the networked data mining field. Community de-
tection helps to discover latent patterns in networked
data and it affects the ultimate knowledge presenta-
tion (Cai et al., 2016).
The task for network community detection is to
divide the whole network into small parts or groups
which are also called communities. There is no uni-
form definition for community in the literature, but in
academic domain, a community (also called a cluster
or a module) is a group of nodes that are connected
densely inside the group but connected sparely with
the rest of the network. Radicchi et al. (Radicchi
et al., 2004) propose two definitions of community.
These definitions are based on the degree of a node
(or valency)
2
. In the first definition, a community is a
subgraph in a strong sense: each node has more con-
nections within the community than the rest of the
graph. In the second definition, a community is a sub-
graph in a weak sense: the sum of all incident edges
in a node is greater than the sum of the out edges.
The problem of community detection has been re-
ceiving a lot of attention, in recent years, and many
different approaches have been proposed. The litera-
ture survey is divided into two categories: community
detection based on analytical approaches and those
2
The degree of a node is the number of edges incident
to the node.
ICSOFT 2020 - 15th International Conference on Software Technologies
296

based on evolutionary approaches (Pizzuti, 2018).
Analytical methods firstly split networks into sub-
groups according to their topological characteristics,
then the modularity assessment is carried out. The
modularity is defined as the fraction of edges inside
communities minus the expected value of the fraction
of edges, if edges fall at random without regard to the
community structure. Values of modularity approach-
ing 1 indicate strong community structure. A well
known algorithm in this category is the one presented
by Girvan and Newman (Girvan and Newman, 2002;
Newman and Girvan, 2004). It is a divisive hierarchi-
cal clustering method based on an iterative removal
of edges from the network. The edge removal splits
the network in communities. The removed edges are
chosen by using betweenness measures (that repre-
sents the number of shortest paths between all vertex
pairs that run along the edge). The idea underlying the
edge betweenness comes from the observation that if
two communities are joined by a few inter-community
edges, then all the paths from vertices in one commu-
nity to vertices in the must pass through these edges.
Paths determine the betweenness score to compute for
the edges. By counting all the paths passing through
each edge, and removing the edge scoring the max-
imum value, the connections inside the network are
broken. This process is repeated, thus dividing the
network into smaller components until a stop crite-
rion is reached. The criterion adopted to stop the di-
vision is the modularity. In (Newman, 2004), the au-
thor presents an agglomerative hierarchical algorithm
that optimizes the concept of modularity. Thus the
algorithm computes the modularity of all the clusters
obtained by applying the hierarchical approach, and
returns as result the clusters having the highest value
of modularity.
Analytical algorithms do not reach the expected
successful results in community detection from com-
plex networks. Therefore, various evolutionary based
algorithms (EAs) have been proposed to provide dif-
ferent approaches to solve the community detection
problem (Atay et al., 2017). Many community eval-
uation criteria have been proposed and quantities
of methods that combine either single objective or
multiobjective EAs with community detection have
emerged. Most if not all of these methods share
the common feature that they model the community
detection problem as an optimization problem (Cai
et al., 2016). The single objective methods optimize a
single property, while the multiobjective approaches
simultaneously optimize competing objectives. The
most popular single evaluation criterion is the modu-
larity proposed by Newman and Girvan (Newman and
Girvan, 2004). Since 2002, several methods that di-
vide networks into clusters according to the modular-
ity criterion have been developed (Atay et al., 2017).
In (Tasgin and Bingol, 2006) and (Liu et al., 2007),
the authors presented an approach based on a GA to
optimize the network modularity introduced by New-
man and Girvan (Girvan and Newman, 2002). How-
ever, some studies have indicated that the optimiza-
tion of modularity has several drawbacks (Cai et al.,
2016). First, it has the resolution limitation, i.e., max-
imising the modularity can fail in finding communi-
ties smaller than a fixed scale, even if these commu-
nities are well defined. The scale depends on the total
size of the network and the interconnection degree of
the communities (Fortunato and Barth
´
elemy, 2007).
Second, maximizing the modularity is proved to be
NP-hard (Cai et al., 2016). These drawbacks can con-
stitute a weakness for all those methods whose objec-
tive is to optimize the modularity. To avoid the reso-
lution limitation of modularity, many multi-resolution
models have been developped (Cai et al., 2016). Piz-
zuti (Pizzuti, 2008) has proposed an algorithm named
GA-Net and has used a special assessment function
called community score that uses only graph topol-
ogy. This community score takes one parameter r
which is hard to tune because higher values of r help
to detect communities and low values of this paramter
return no communities. A modification of the modu-
larity has been proposed in (Li et al., 2008) with the
concept of modularity density. The authors prove that
modularity density has a number of advantages with
respect to modularity, such as detecting communities
of different sizes.
Single objective optimization identifies a single
best solution that gives insights on the graph orga-
nization. However, this solution could be biased to-
ward a particular structure inherent inside the crite-
rion to optimize (Cai et al., 2016). These methods
have obtained very good results on both artificial and
real-world networks (Pizzuti, 2018). The intuitive no-
tion of community that the number of edges inside
a community should be much higher than the num-
ber of edges connecting to the remaining nodes of
the graph, has two different objectives: 1) maximiz-
ing the internal connection links and 2) minimizing
the external connection links (Pizzuti, 2018). Thus,
on the basis of these objectives, many multi-objective
community models have been established. The first
proposal framework to uncover community structure
has been presented by Pizzuti (Pizzuti, 2011; Pizzuti,
2009). In particular, the method introduces two objec-
tives: maximizing the community score proposed by
(Pizzuti, 2008) and minimizing the community fitness
put forward by (Lancichinetti et al., 2009). Then, the
fast elitist non-dominated sorting genetic algorithm
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect Semantic and Topological Biological Communities
297

(NSGA-II) proposed in (Deb et al., 2002) has been
applied. A variation of this method has been proposed
by Agrawal (Agrawal, 2011). The objectives to min-
imize are the modularity proposed by Newman and
Girvan (Girvan and Newman, 2002) and the commu-
nity score proposed by Pizzuti (Pizzuti, 2008). Sur-
veys on the selection of objective functions in multi-
objective community detection can be found in Shi et
al. (Shi et al., 2011; Shi et al., 2014).
Multi-objective evolutionary approaches, like the
single objective ones, are able to discover community
structures of quality comparable with, or even better
than, those obtained by analytical methods. Optimiz-
ing multiple objectives allows a simultaneous evalu-
ation of community structure from different perspec-
tives, then it is the user’s responsibility to choose a so-
lution (Cai et al., 2016). The choice of the objectives
to optimize should take into account the suggestions
given by Shi et al.(Shi et al., 2010), where a compari-
son of several objective functions in a multi-objective
framework has been performed (Pizzuti, 2018).
The use of evolutionary methods for community
detection presents a number of advantages (Pizzuti,
2018):
• During the search process, the communities’
number is generated automatically;
• Domain-specific knowledge can be incorporated
inside the method, such as biased initialization, or
specific variation operators instead of random, al-
lowing a more effective exploration of the state
space of possible solutions;
• The efficient implementations of population-
based models can be realized to deal with large
size networks.
Most evolutionary approaches to detect communities
have been applied in social networks and have used
only graphical topology and no semantic similarity
between nodes (Pizzuti and Rombo, 2014). In this
paper we propose a generic evolutionary algorithm to
detect semantic or/and topological communities in bi-
ological networks. This new algorithm tries to find the
best community by maximizing the concept of com-
munity measure. This measure is based on both the
graph topology (interaction) and the semantic simi-
larity between nodes. It is different to the community
score introduced by Pizzuti since it is not related to
the density introduced in (Pizzuti, 2008) and not re-
lated to the modularity of the sub-networks.
3 PROBLEM DEFINITION
The network of interactions between proteins is gen-
erally represented as an interaction graph G = (V,E)
where V is a set of objects, called nodes or vertices,
representing proteins and E is a set of links, called
edges, representing pairwise interactions. A commu-
nity (or cluster) in a network is a group of vertices
having a high density of edges within them, and a
lower density of edges between groups. In this work,
we design a community C as a group of genes or pro-
teins that are semantically similar and interact with
each other. A set of genes C = {G
1
,G
2
,...,G
n
} is a
community if it respects the following property:
∀ G
i
,G
j
∈ C, S(G
i
,G
j
) ≥ ∇
S
or I(G
i
,G
j
) ≥ ∇
I
(1)
Where:
• S(G
i
,G
j
): the similarity value between two genes
G
i
and G
j
. To calculate the similarity between
two genes, we need to use a measure allowing to
compare sets of terms that annotate these genes
thus we can quantify the similarity between these
sets. In this work, we use the semantic similar-
ity measure GS2 (GO-based similarity of gene
sets) (Ruths et al., 2009). This measure aver-
ages the similarity contributed by each gene in
C. Each gene is compared with the remaining set
of genes by calculating how closely that gene fol-
lows the functionality distribution of the remain-
ing genes. The functionality distribution is rep-
resented by the distribution of ancestor GO terms
for each gene (Ruths et al., 2009).
• I(G
i
,G
j
): the score of interaction between two
genes extracted from STRING Database (Mering
et al., 2003). This score explains the protein-
protein or the gene-gene associations known and
predicted according to different criteria in a bibli-
ographic reference.
• ∇
S
and ∇
I
are two thresholds. They are defined
for both the semantic and the interaction criterion
respectively. Their values are fixed according to
the recommendations of our biological expert.
• Each gene G can be annotated with a set of GO
(Gene Ontology) terms (Camon et al., 2003). We
use TP to denote the set of GO terms that annotate
a gene, this set is denoted by A(G). A(G).It con-
sists of an association between a gene and a GO
term. For example, the MEIKIN gene is identi-
fied by ID: 728637 and annotated by the follow-
ing sets: ”GO: 0007060”, ”GO: 0010789”, ”GO:
0016321”, ”GO: 0045143”, ”GO: 0051754”.
More formally,
A(G) =
{
T P that annotate G /T P ∈ GO
}
(2)
ICSOFT 2020 - 15th International Conference on Software Technologies
298

4 PROPOSED APPROACH
GAs have proved to be competitive alternative meth-
ods to traditional optimization and search techniques
and they have been applied to many problems in di-
verse research and application areas such neural nets
evolution, planning and scheduling, machine learning
and pattern recognition (Goldberg, 1989; Petrowski
and Ben-Hamida, 2017). Thus, it would be also suit-
able for solving the community detectionSIM group
problem.
We describe, in this section, the GA proposed in
this work as well as the genetic representation and the
variation operators that we propose.
The population is composed of individuals that are
the solutions of the problem. In our approach, an indi-
vidual is a set of proteins or genes that form a commu-
nity. A community may have different sizes. To eval-
uate a solution, we propose a fitness function based
on a community measure. The latter uses the simi-
larity value and the interaction score of every pair of
genes making up the solution. Moreover, we modify
the steps of GA to satisfy the needs of our algorithm.
Thus, we propose a new heuristic crossover operator,
a new mutation operator and insert some additional
steps during the population initialization. The algo-
rithm works as follows:
Algorithm 1: General Algorithm of the Generic GA-PPI-
Net approach.
Require: algorithm parameters, problem instance
Ensure: best solution to the optimization problem
Begin
1: Initialize population
2: Evaluate the initial population
3: for i = 1 to max iteration do
4: Select parents for mating
5: for each pair of candidates in the set of parents
do
6: Generate an offspring through genetic oper-
ator - crossover and mutation - with respec-
tively a probability p
c
and p
m
7: Evaluate the fitness of the offspring
8: Replace the worst existing individual in the
population by the obtained offspring
9: end for
10: end for
End
The various steps of the GA are described in the
following subsections.
4.1 Genetic Representation
A solution to our problem is a community of proteins
or genes. We represent it by a vector T. In this repre-
sentation, each individual stores: the size n of the cor-
responding community (= the number of proteins or
genes in the community) and the list of the n compo-
nents. Each component (gene or protein) is designed
by its name. A solution corresponds to an individual
in GA terms. Figure 1 illustrates the representation of
an individual adopted in our algorithm.
Figure 1: Example of individual representation designing a
community.
4.2 Population Initialization
In this work, the population is defined as a two-
dimensional array of individuals. It represents some
potential solutions of the problem. In order to initial-
ize this population, we first randomly recover com-
munities from the KEGG pathway database (Kane-
hisa and Goto, 2000). Then, we randomly create
the population with the recovered genes. The pop-
ulation is composed by individuals having different
sizes (Ben M’barek et al., 2019). Figure 2 presents an
example of an initial population with five individuals
having different sizes.
Figure 2: Example of an initial population.
4.3 Fitness Function
The fitness function relates to the ability of the candi-
date to survive and reproduce. It takes as input a can-
didate solution to the problem and produces as output
a performance measure of the solution with respect
to the considered problem. The choice of the fitness
function is a critical step for obtaining good solutions.
In the context of community detection, the most pop-
ular function is the modularity, originally introduced
by Girvan and Newman (Girvan and Newman, 2002).
In our work, we do not directly take into account the
modularity. Nevertheless, the topological propriety of
a community is taken into account through the inter-
action score between proteins or genes. Moreover,
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect Semantic and Topological Biological Communities
299

the fitness function is enriched with semantic infor-
mation. Indeed, we define a fitness function based on
the computation of similarity value and the interaction
score of each pair of genes in a community C. Thus,
as a first step for the fitness computation, a similar-
ity matrix is computed using the GS2 measure (sec-
tion 3). Likewise, an interaction matrix is computed
designing the interaction score between each pair of
genes. The proposed fitness function F is then defined
as follows:
F =
n
∑
i6= j,i=1, j=1
M
i j
(G
i
,G
j
) (3)
M
i j
(G
i
,G
j
) =
0 if S(G
i
,G
j
) ≤ ∇
S
or I(G
i
,G
j
) ≤ ∇
I
.
S(G
i
,G
j
) + I(G
i
,G
j
) otherwise.
(4)
Where:
• S(G
i
,G
j
) and I(G
i
,G
j
) are, respectively, the sim-
ilarity and the interaction values of each pair of
genes (G
i
,G
j
) introduced in section 3;
• ∇
S
and ∇
I
are two thresholds defining respec-
tively the topology and the semantic levels. Their
values are fixed in the beginning of the evolution.
This fitness function generalizes the previous
method that we proposed in (Ben M’barek et al.,
2019). The used fitness function in GA-PPI-Net was
based on the computation of the average similarity
value and the average interaction score of each two
genes existing in the community C. It is defined as fol-
lows (Ben M’barek et al., 2018; Ben M’barek et al.,
2019):
F1(C) = W
1
AVGS(C) +W
2
AVGI(C) (5)
With:
• AVGS and AVGI being the average similarity
value and the average interaction value of genes
in C respectively.
• W
1
and W
2
: weights ∈ [0,1].
F1 corresponds to a particular case of F when choos-
ing specific values of the thresholds (∇
S
= ∇
I
= 0).
4.4 Selection
In this stage of a GA loop, individuals are selected
from the population to be parents which mate and re-
combine to create offspring for the next generation.
Selection is very crucial to the convergence rate of
the GA as good parents drive individuals to fitter so-
lutions. The problem is how to select these individu-
als. In literature, there are many methods to select the
best individuals such as roulette wheel selection, tour-
nament selection, rank selection, elitism... (Goldberg
and Deb, 1991). For our problem we use the popular
tournament selection because it is highly efficient and
easy to implement (Goldberg and Deb, 1991).
4.5 Genetic Operators
After the generation of an initial population, a GA car-
ries out the genetic operators to generate offspring.
Once a new population is created, the genetic pro-
cess is performed iteratively until an optimal result is
found or a maximum number of generations is met.
Crossover and mutation are two basic operators of
GA. The algorithm performance depends tightly on
the choice of these operators. Indeed, crossover and
mutation operators guide the convergence of the algo-
rithm towards a solution for the problem. Their goal
is to both exploit the best solutions and explore the
search space.
For this work, we propose the use of two types
of crossover. The first one is the classic two-point
crossover. It is a generalization of the one-point
crossover. To apply this operator, two cross-points are
chosen randomly respecting the condition that their
positions do not exceed the longest parent size. Then,
the contents bracketed by these sites are exchanged
between two mated parents to get two new offspring.
A clean up phase is used in order to delete the redun-
dant gene in the created offspring. To better under-
stand this kind of crossover, a graphical illustration is
given in Figure 3. In this example, two sites are cho-
sen at random in position 1 and 4. Then two offspring
(Ch1,Ch2) are generated by exchanging the values of
the selected parents (P1,P2).
Figure 3: Example of a two points crossover operator.
The second crossover operator is a new heuristic
crossover. It is specific to our problem. The main
purpose of this operator is to create an offspring with
higher value of similarity or interaction or both sim-
ilarity and interaction. It is applied according to the
Algorithm 2.
The application of this heuristic crossover
helps the GA to build communities with high
values of similarities and interaction between
genes than the imposed thresholds. Figure 4
presents a graphical illustration to understand
the proposed heuristic crossover. Two individu-
als (P1,P2) are chosen randomly from the parent
population. This operator is usually applied with
ICSOFT 2020 - 15th International Conference on Software Technologies
300

Algorithm 2: Heuristic Crossover Algorithm.
1: Choose randomly two parents (P1,P2) from the
the parent population;
2: Merge the values of two parents (P1,P2) by re-
moving the redundant content (genes) to obtain
one individual P;
3: for each two genes G
i
and G
j
∈ P do
4: if i 6= j then
5: Compute the similarity Sim(G
i
,G
j
);
6: Compute the interaction Interaction(G
i
,G
j
);
7: end if
8: end for
9: for each two genes G
i
and G
j
∈ P do
10: if Sim(G
i
,G
j
) ≥ ∇
S
then
11: Add the genes to the first offspring Ch1;
12: end if
13: if Interaction (G
i
,G
j
) ≥ ∇
I
then
14: Add the genes to the second offspring Ch2;
15: end if
16: end for
17: Remove the redundant content (genes) to the ob-
tained offspring Ch1 and Ch2;
a high probability (p
c
) (Pizzuti, 2018). Then, the val-
ues of two parents (P1,P2) are merged by removing
the redundant content (genes) to obtain one individ-
ual P. After that two offspring (Ch1,Ch2) are created
according to the following conditions:
1. ∀i 6= j : G
i
,G
j
∈ P, if Sim(G
i
,G
j
) ≥ ∇
S
then add
the gene G
i
to the first offspring Ch1;
2. ∀i 6= j : G
i
,G
j
∈ P, if Interaction (G
i
,G
j
) ≥ ∇
I
then else add the gene G
i
to the second offspring
Ch2;
The mutation is an operator that acts in a rarer
fashion and in an unpredicted form to modify the
genes of the individual, promoting the diversification
of the population. However, the mutation must not be
too destructive and a speed bump for the process of
finding an optimal solution (Pizzuti, 2018). For these
purpose, we propose for the present problem a new
specific mutation operator called Optimized Commu-
nity Mutation (OCM). Mutation may be defined as a
small random tweak in the individual, to get a new so-
lution. It is used to maintain and introduce diversity in
the population and is usually applied with a low prob-
ability (p
m
). If the probability is very high, the GA
gets reduced to a random search (Pizzuti, 2018). We
present now the used mutation operator already de-
fined in our previous work (Ben M’barek et al., 2018).
Its goal is to maximize the chance of creating a better
solution than the original one. This operator can inte-
grate a new gene in order to replace a gene having a
poor quality or to enlarge the size of the community.
To mutate a solution C, the mutation operator alters
only one gene at a time and uses a score function, de-
noted GS, applied to each gene in C. This score helps
us to detect the gene having the best score in a com-
munity as well as the gene having the worst score. It
is equal to the sum of the average similarity and the
average interaction score of a gene in a community
(Ben M’barek et al., 2018). It is defined as follows:
AVGSim(G) =
n
∑
i=1
S(G,Gi)/n (6)
AVGInteraction(G) =
n
∑
i=1
I(G, G
i
)/n (7)
GS(G) = AV GSim(G) + AV GInteraction(G) (8)
Where:
• S(G, G
i
): The similarity value between a gene G
and the gene G
i
in the community C;
• I(G, G
i
): The interaction score of a gene G com-
pared to the gene G
i
in the community C.
• n: size of an individual (community).
The OCM mutation operator is applied according
to the following steps (Ben M’barek et al., 2019) pre-
sented in algorithm 3.
Algorithm 3: OCM algorithm.
1: Select in a solution C a gene having the highest
score GS that will be called ”bestGene”;
2: Randomly search a gene G
0
from the ”interac-
tion” table with which the ”bestGene” interacts
and G
0
/∈ C;
3: Get the gene having the lowest score GS in C, it
will be called ”worstGene”;
4: Fix a threshold θ (i.e θ = 0.5);
5: if GS(”worstGene”) ≤ θ then
6: replace the ”worstGene” by the gene G’ se-
lected in the second step;
7: else
8: Insert into the end position of the solution the
gene G’ selected in the second step and update
the size.
9: end if
5 EXPERIMENTAL RESULTS
In this section, we study the effectiveness of our
approach on real data sets (Pathways selected from
KEGG Pathway database). A set of preliminary tests
have been carried out to tune the GA parameters: pop-
ulation size, crossover and mutation rate and maxi-
mum number of generations. The retained values are
summarized in Table 1.
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect Semantic and Topological Biological Communities
301
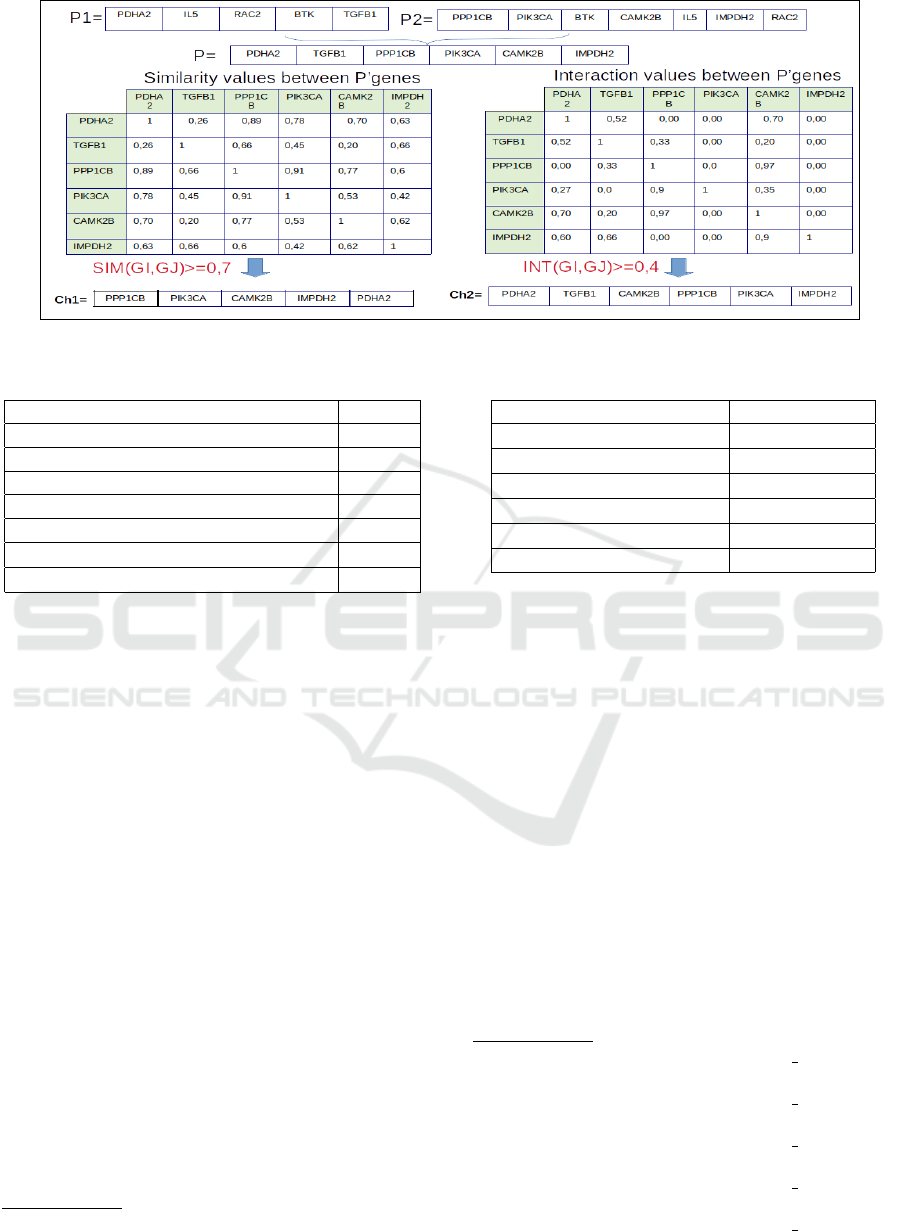
Figure 4: Example of an heuristic crossover operator (∇
S
= 0.7 and ∇
I
= 0.4).
Table 1: GA parameters.
Parameters Values
Population size 30
Generation number 100
Crossover rate 0.8
Mutation rate 0.01
Individual’size in the initial population [5,40]
∇
S
≥ 0.5
3
∇
I
≥ 0.4
3
A community of genes is accepted if the value of
the thresholds ∇
S
and ∇
I
are sufficient. The role of
these two thresholds is to vary the weight of the qual-
ity of a community. The ∇
S
allows to quantify the
similarity value. It is is set according to the GO an-
notations among a set of genes by averaging the con-
tribution of each gene’s GO terms and their ances-
tor terms with respect to the GO vocabulary graph
(Ben M’barek et al., 2018). If it is greater than or
equal to 0.5 then these two genes are similar, else they
are not (Ben M’barek et al., 2018). The ∇
I
refers to
the interaction value which defines the number of ci-
tation of this interaction in the literature. If this value
is greater than or equal to 0.4 then these two genes
have a strong interaction. The values of ∇
S
and ∇
I
are proposed by the biological expert and modified as
needed.
To check the capability of our approach to suc-
cessfully detect the communities of a network, we
pick a set of proteins or genes randomly from the
reference database KEGG pathway. More precisely,
our approach has been tested with five datasets pro-
posed by our biological expert. Their names and their
corresponding genes’ numbers are described in Ta-
ble 2. These datasets correspond to existing commu-
3
values proposed by the biological expert and modified
as needed
Table 2: The used datasets.
Datasets Genes’Number
Apoptosis
4
88
B cell receptor signalling
5
75
Purine metabolism
6
159
Rna degradation
7
159
Oocyte meiosis
8
114
Total 595
nities presented in KEGG pathway database.
The first evaluation consists to verify how the pro-
posed method is likely to find gene communities hav-
ing high similarity or/and high interaction.
The obtained communities are analyzed and com-
pared for a better comprehension of the topological
(interaction between genes) or/and the semantic sim-
ilarity measures. We performed tests with different
values of the proposed thresholds ∇
S
and ∇
I
of the
fitness function to determine communities of genes.
These values were proposed by the biological expert.
Actually, the tests showed that it was possible to de-
tect three types of existing communities of genes or
proteins having high interaction and/or high similar-
ity between their genes:
1. ∇
S
≥ 0.5 and ∇
I
= 0: detect similarity based
group of genes.
2. ∇
S
≥ 0.5 and ∇
I
≥ 0.4: detect similarity and in-
4
https://www.genome.jp/dbget-bin/www bget?
pathway:hsa04210
5
https://www.genome.jp/dbget-bin/www bget?
pathway:hsa04662
6
https://www.genome.jp/dbget-bin/www bget?
pathway:hsa00230
7
https://www.genome.jp/dbget-bin/www bget?
pathway:hsa03018
8
https://www.genome.jp/dbget-bin/www bget?
pathway:hsa04114
ICSOFT 2020 - 15th International Conference on Software Technologies
302

teraction based genes communities.
3. ∇
S
< 0.5 and ∇
I
≥ 0.4: detect interaction based
group of genes.
To determine these three types of communities, we re-
alized different experiments. We apply our approach
with proteins or genes chosen randomly from the five
proposed datasets (see Table 2). We vary the values
of the thresholds ∇
S
and ∇
I
in the range [0..1] and we
retained each time the best community. For the first
runs, we set the threshold values such that ∇
S
≥ 0.5
and ∇
I
≥ 0.4. We use ∇
S
= 0.6 and ∇
I
= 0.4. The
preliminary results showed clearly that our proposed
GA is able to detect similarity and interaction based
genes communities. For instance, Figure 5 clearly
shows a solution in these category of experiments
to detect communities of genes that are semantically
similar or/and interact (where the edge value I ≥ 0.4
and S ≥ 0.5).
Then, we test our GA with ∇
S
≥ 0.5 and ∇
I
= 0.
We turn our algorithm with values: ∇
S
= 0.6 and
∇
I
= 0. And, we obtain as result a group of genes
that are semantically similar and do not interact with
each other. One solution in these category of experi-
ments is shown in Figure 6 which represents a group
of genes having size 9.
For the last set of experiments, we set the thresh-
olds such as ∇
S
< 0.5 and ∇
I
≥ 0.4. We use ∇
S
= 0.3
and ∇
I
= 0.4. The obtained results show the capabil-
ity of the proposed GA to build an interaction based
group. Figure 7 illustrates an example of a detected
group of genes.
To conclude, the main goal by introducing thresh-
olds in the fitness function is to allow the GA to detect
three types of genes or proteins’ communities:
• a group of genes with high similarity (if ∇
S
≥
0.5).
• a group of genes with high interaction (if ∇
I
≥
0.4).
• a community of genes with high interaction and
high similarity (if ∇
S
≥ 0.5 and ∇
I
≥ 0.4).
To interpret biologically the obtained communities,
our biological expert proposed to evaluate them by
checking if they exist in KEGG or other biological
pathway databases. Each new community found by
our generic GA-PPI-Net is presented to the DAVID
tools (Database for Annotation Visualization and In-
tegrated Discovery) (Sherman et al., 2007), which
compares the founded community, denoted by Rnew,
with others in different databases and gives the per-
centage of Rnew genes that belong to the existing
communities in those databases. DAVID bioinfor-
matics resources consist of an integrated biological
knowledge-base and analytic tools that aim at sys-
tematically extracting biological meaning from large
gene/protein lists. It is the most popular functional an-
notation programs used by biologists (Sherman et al.,
2007). It takes a list of genes as input and exploits
the functional annotations available on these genes in
a public database such as, KEGG Pathways in order
to find common functions that are sufficiently specific
to these genes.
For each types of genes or proteins’ communities,
we run our approach 20 times with proteins or genes
chosen randomly from the five proposed datasets in
Table 2. And, we retained each time the best com-
munity. Thus, we have 20 best communities for
each type. We evaluate these obtained communi-
ties by checking if they exist in biological pathway
databases. The biological databases used to evaluate
our results are KEGG, Biocarta, Reactome, BBID and
EC Number. The results of this evaluation are shown
in Table 3 column Ben M’barek et al. 2020.
Our new approach is parameterized according to
the importance affected to each measure criterion (se-
mantic similarity measure and interaction measure).
This parameters allows us to detect communities ac-
cording to either both criteria, or only one crite-
rion. The results presented in Table 3 column Ben
M’barek et al. 2020 show that the new communi-
ties obtained by our algorithm correspond to some
”parts” of real networks existing in other biological
pathway databases, and in some cases to a complete
network (percentage 100%). The Generic GA-PPI-
Net achieves the highest percentage 80%, 90% and
100% when the fitness function is based on both sim-
ilarity and interaction values. And it achieves the per-
centage 90% and 100% when the fitness function is
based on semantic similarity criterion or interaction
criterion respectively.
These results are considered very satisfactory by
the biology expert. They constitute an initial valida-
tion of our algorithm and show the relevance of the
used fitness function. These tests should be supple-
mented on a larger scale with other datasets and dif-
ferent communities.
Moreover, we compare the results obtained by our
new algorithm with the one proposed in (Ben M’barek
et al., 2019). We design these approaches as Ben
M’barek et al. 2019 and Ben M’barek et al. 2020
respectively. A thorough comparison is not easy be-
cause the obtained communities for both propositions
haven’t the same sizes and the same constitution.
Hence, the same datasets proposed by the biological
expert in Table 2 and the same GA parameters were
used for both approaches. The two algorithms were
executed 20 times. We also used the DAVID tools
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect Semantic and Topological Biological Communities
303
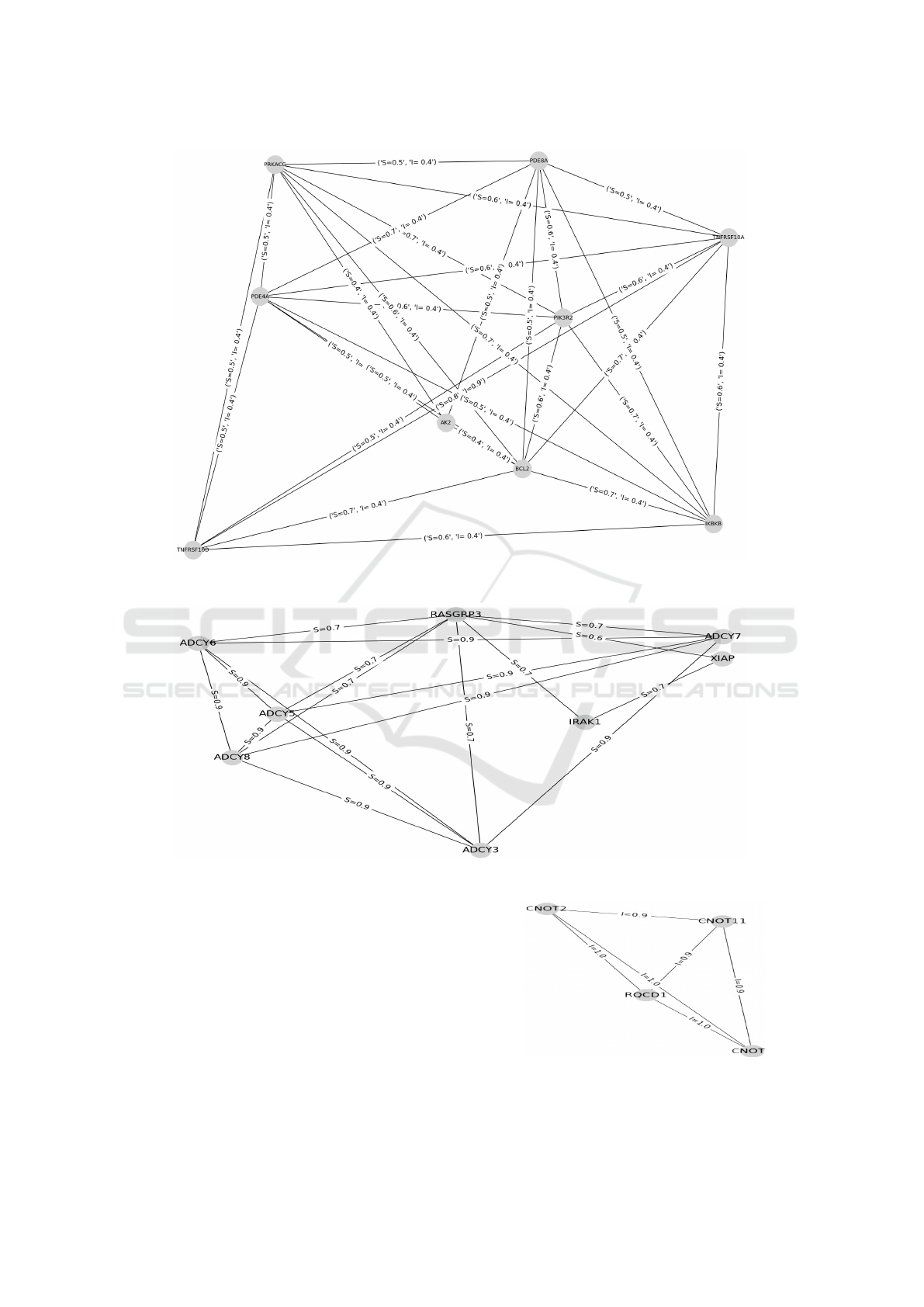
Figure 5: Example of a detected community of genes having high similarity and interaction scores (∇
S
≥ 0.5 and ∇
I
≥ 0.4).
Figure 6: Example of a detected similarity based groups of genes (∇
S
≥ 0.5 and ∇
I
= 0).
to estimate the recovery rate of the found commu-
nities with existing communities in different biolog-
ical databases. Table 3 column Ben M’barek et al.
2019 illustrates the results of the approach presented
in (Ben M’barek et al., 2019).
Table 3 shows how the present approach (Ben
M’barek et al. 2020) has additional abilities, accord-
ing to the use of thresholds in the fitness function, to
detect communities of genes based only on semantic
similarity or interaction criterion. Otherwise, accord-
ing to the results in the last two columns in Table 3,
the ability to detect communities based on both crite-
Figure 7: Example of a detected interaction based groups of
genes (∇
S
< 0.5 and ∇
I
≥ 0.4).
ICSOFT 2020 - 15th International Conference on Software Technologies
304

Table 3: Evaluation of the obtained communities. Comparison with Ben M’barek et al. 2019 approach.
Pathway DBs Ben M’barek et al. 2020 Ben M’barek et al. 2019
SIM groups INT groups SIM & INT communities
%Min %Max %Min %Max %Min %Max %Min %Max
BBIB 20% 45% 15% 50% 20% 90% 25% 50%
Biocarta 10% 70% 20 % 50% 20% 100% 20% 66%
EC Number 10% 90% 10% 60% 30% 100% 10% 100%
KEGG 9% 78% 10% 62% 11% 100% 15% 100%
Reactome 20% 75% 15% 100% 10% 80% 14% 100%
ria of the new GA is similar or better than the one of
Ben M’barek 2019 GA. Indeed, our new GA achieves
a higher percentage than Ben M’barek et al.2019 ap-
proach in 4 pathway databases: Kegg, Biocarta, BBIB
and Ec Number when the fitness function is based on
both similarity and interaction values. In other re-
spects, the Ben M’barek et al. 2019 approach has a
higher result than the Ben M’barek et al. 2020 ap-
proach in the Reactome pathway. Nevertheless, the
new GA keeps satisfactory percentage for the three
types of detected communities (75% for SIM groups
column, 100% for INT groups column and 80% for
SIM & INT communities column). The obtained per-
centage values corresponds to a complete communi-
ties or to some ”parts” of the real communities.
To conclude, the obtained results show the ability
of the GA proposed in this paper to effectively deal
with community detection in networks. Moreover,
the new GA allows to detect communities of genes
or proteins having different size according to the use
of thresholds in the fitness function. This thresholds
allows us to detect communities according to either
both criteria, or only one criterion. Thus, we obtain
three types of genes or proteins’ communities, which
improve that this approach is a generic approach of
Ben M’barek et al. 2019 approach. Further exten-
sions experiments will be carried out to detect com-
munities with larger size and identify new communi-
ties not yet known in the public biological databases.
6 CONCLUSIONS
In this paper, we have proposed a generic approach
based on GA to detect communities of interacting
genes or proteins. This approach is a generalization of
a previous work. It introduces the concept of commu-
nity measure and searches for an optimal partitioning
of the network by maximizing this measure. Our con-
tribution in this paper is threefold. First, we apply GA
to community detection in PPI networks. Second, we
modify the previous proposed fitness function to al-
low our GA to detect communities of genes that are
semantically similar and/or interacting. Third, we de-
fine a specific heuristic crossover operator adapted to
the considered biological problem. Dense communi-
ties existing in the network are obtained at the end
of the evolution by selectively exploring the search
space, without the need to know in advance the com-
munity size. The experimental results showed the
ability of the GA approach to correctly detect commu-
nities having different sizes which are semantically
similar and/or interacting. Future research will aim
at extending the proposed fitness function by adding
the modularity value and applying a multi-objective
optimization to improve the quality of the results.
ACKNOWLEDGEMENTS
We would like to show our gratitude to Dr. Walid
BEDHIAFI (Laboratoire de G
´
entique Immunologie et
Pathologies Humaines, Universit
´
e de Tunis El Manar)
for assistance to comprehend the biological fields and
for the interpretation of the results.
REFERENCES
Agrawal, R. (2011). Bi-objective community detection
(bocd) in networks using genetic algorithm. In In-
ter Conf on Contemporary Computing, pages 5–15.
Springer.
Ashburner, M., Ball, C. A., Blake, J. A., Botstein, D.,
Butler, H., Cherry, J. M., Davis, A. P., Dolinski, K.,
Dwight, S. S., Eppig, J. T., Harris, M. A., Hill, D. P.,
Issel-Tarver, L., Kasarskis, A., Lewis, S., Matese,
J. C., Richardson, J. E., Ringwald, M., Rubin, G. M.,
and Sherlock, G. (2000). Gene ontology: tool for
the unification of biology. The Gene Ontology Con-
sortium. Nat. Genet., 25(1):25–29.
Atay, Y., Koc, I., Babaoglu, I., and Kodaz, H. (2017). Com-
munity detection from biological and social networks:
A comparative analysis of metaheuristic algorithms.
Applied Soft Computing, 50:194–211.
Ben M’barek, M., Borgi, A., Bedhiafi, W., and Ben Hmida,
S. (2018). Genetic Algorithm for Community Detec-
tion in Biological Networks. Proc Computer Science,
126:195–204. Knowledge-Based and Intelligent In-
Generic GA-PPI-Net: Generic Evolutionary Algorithm to Detect Semantic and Topological Biological Communities
305

formation & Engineering Systems: Proc of the 22nd
Inter Conf, KES-2018, Belgrade, Serbia.
Ben M’barek, M., Borgi, A., Ben Hmida, S., and Rukoz,
M. (2019). Genetic algorithm to detect different
sizes’ communities from protein-protein interaction
networks. In Proc of the 14th Inter Conf on Software
Technologies - Volume 1: ICSOFT,, pages 359–370.
INSTICC, SciTePress.
Cai, Q., Ma, L., Gong, M., and Tian, D. (2016). A survey on
network community detection based on evolutionary
computation. Int. J. Bio-Inspired Comput., 8(2):84–
98.
Camon, E., Magrane, M., Barrell, D., Binns, D., Fleis-
chmann, W., Kersey, P., Mulder, N., Oinn, T., Maslen,
J., Cox, A., and Apweiler, R. (2003). The Gene
Ontology Annotation (GOA) Project: Implementa-
tion of GO in SWISS-PROT, TrEMBL, and InterPro.
Genome Res, 13(4):662–672.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
Nsga-ii. IEEE transactions on evolutionary compu-
tation, 6(2):182–197.
Fortunato, S. and Barth
´
elemy, M. (2007). Resolution limit
in community detection. PNAS, 104(1):36–41.
Fortunato, S. and Hric, D. (2016). Community detection in
networks: A user guide. Physics Reports, 659:1–44.
arXiv: 1608.00163.
Girvan, M. and Newman, M. E. J. (2002). Community
structure in social and biological networks. Proc. Natl.
Acad. Sci. U.S.A., 99(12):7821–7826.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, USA, 1st
edition.
Goldberg, D. E. and Deb, K. (1991). A comparative anal-
ysis of selection schemes used in genetic algorithms.
In Foundations of Genetic Algorithms, pages 69–93.
Morgan Kaufmann.
Jiao, X., Sherman, B. T., Huang, D. W., Stephens, R.,
Baseler, M. W., Lane, H. C., and Lempicki, R. A.
(2012). DAVID-WS: a stateful web service to fa-
cilitate gene/protein list analysis. Bioinformatics,
28(13):1805–1806.
Kanehisa, M. and Goto, S. (2000). KEGG: kyoto ency-
clopedia of genes and genomes. Nucleic Acids Res.,
28(1):27–30.
Lancichinetti, A., Fortunato, S., and Kertesz, J. (2009).
Detecting the overlapping and hierarchical commu-
nity structure in complex networks. New journal of
physics, 11(3):033015.
Li, Z., Zhang, S., Wang, R.-S., Zhang, X.-S., and Chen, L.
(2008). Quantitative function for community detec-
tion. Physical review E, 77(3):036109.
Liu, X., Li, D., Wang, S., and Tao, Z. (2007). Effective al-
gorithm for detecting community structure in complex
networks based on ga and clustering. In Inter Conf on
Computational Science, pages 657–664. Springer.
Mering, C. v., Huynen, M., Jaeggi, D., Schmidt, S., Bork, P.,
and Snel, B. (2003). STRING: a database of predicted
functional associations between proteins. Nucl. Acids
Res., 31(1):258–261.
Newman, M. E. J. (2004). Fast algorithm for detecting
community structure in networks. Physical Review E,
69(6). arXiv: cond-mat/0309508.
Newman, M. E. J. and Girvan, M. (2004). Finding and eval-
uating community structure in networks. Physical Re-
view E, 69(2). arXiv: cond-mat/0308217.
Petrowski, A. and Ben-Hamida, S. (2017). Evolutionary
Algorithms. John Wiley & Sons. Google-Books-ID:
fvRRCgAAQBAJ.
Pizzuti, C. (2008). Ga-net: A genetic algorithm for commu-
nity detection in social networks. In Inter conf on par-
allel problem solving from nature, pages 1081–1090.
Springer.
Pizzuti, C. (2009). A multi-objective genetic algorithm for
community detection in networks. In 2009 21st IEEE
Inter Conf on Tools with Artificial Intelligence, pages
379–386. IEEE.
Pizzuti, C. (2011). A multiobjective genetic algorithm to
find communities in complex networks. IEEE Trans-
actions on Evolutionary Computation, 16(3):418–
430.
Pizzuti, C. (2018). Evolutionary Computation for Commu-
nity Detection in Networks: A Review. IEEE Transac-
tions on Evolutionary Computation, 22(3):464–483.
Pizzuti, C. and Rombo, S. E. (2014). Algorithms and
tools for protein–protein interaction networks cluster-
ing, with a special focus on population-based stochas-
tic methods. Bioinformatics, 30(10):1343–1352.
Radicchi, F., Castellano, C., Cecconi, F., Loreto, V., and
Parisi, D. (2004). Defining and identifying communi-
ties in networks. PNAS, 101(9):2658–2663.
Ruths, T., Ruths, D., and Nakhleh, L. (2009). GS2: an ef-
ficiently computable measure of GO-based similarity
of gene sets. Bioinformatics, 25(9):1178–1184.
Sherman, B. T., Huang, D. W., Tan, Q., Guo, Y., Bour, S.,
Liu, D., Stephens, R., Baseler, M. W., Lane, H. C.,
and Lempicki, R. A. (2007). DAVID Knowledge-
base: a gene-centered database integrating heteroge-
neous gene annotation resources to facilitate high-
throughput gene functional analysis. BMC Bioinfor-
matics, 8:426.
Shi, C., Yu, P. S., Cai, Y., Yan, Z., and Wu, B. (2011).
On selection of objective functions in multi-objective
community detection. In Proc of the 20th ACM in-
ternational conference on Information and knowledge
management, pages 2301–2304. ACM.
Shi, C., Yu, P. S., Yan, Z., Huang, Y., and Wang, B. (2014).
Comparison and selection of objective functions in
multiobjective community detection. Computational
Intelligence, 30(3):562–582.
Shi, C., Zhong, C., Yan, Z., Cai, Y., and Wu, B. (2010). A
multi-objective approach for community detection in
complex network. In IEEE Congress on Evolutionary
Computation, pages 1–8. IEEE.
Tasgin, M. and Bingol, H. (2006). Community Detec-
tion in Complex Networks using Genetic Algorithm.
arXiv:cond-mat/0604419. arXiv: cond-mat/0604419.
Tasgin, M., Herdagdelen, A., and Bingol, H. (2007). Com-
munity Detection in Complex Networks Using Ge-
netic Algorithms. arXiv:0711.0491 [physics]. arXiv:
0711.0491.
ICSOFT 2020 - 15th International Conference on Software Technologies
306
