
Multi-view Clustering Analyses for District Heating Substations
Shahrooz Abghari
1 a
, Veselka Boeva
1
, Jens Brage
2
and H
˚
akan Grahn
1 b
1
Department of Computer Science, Blekinge Institute of Technology, Karlskrona, Sweden
2
NODA Intelligent Systems AB, Karlshamn, Sweden
Keywords:
Data Mining, Multi-view Clustering, Multi-layer Clustering, Time Series, District Heating Substation.
Abstract:
In this study, we propose a multi-view clustering approach for mining and analysing multi-view network
datasets. The proposed approach is applied and evaluated on a real-world scenario for monitoring and
analysing district heating (DH) network conditions and identifying substations with sub-optimal behaviour.
Initially, geographical locations of the substations are used to build an approximate graph representation of
the DH network. Two different analyses can further be applied in this context: step-wise and parallel-wise
multi-view clustering. The step-wise analysis is meant to sequentially consider and analyse substations with
respect to a few different views. At each step, a new clustering solution is built on top of the one generated
by the previously considered view, which organizes the substations in a hierarchical structure that can be used
for multi-view comparisons. The parallel-wise analysis on the other hand, provides the opportunity to analyse
substations with regards to two different views in parallel. Such analysis is aimed to represent and identify
the relationships between substations by organizing them in a bipartite graph and analysing the substations’
distribution with respect to each view. The proposed data analysis and visualization approach arms domain
experts with means for analysing DH network performance. In addition, it will facilitate the identification
of substations with deviating operational behaviour based on comparative analysis with their closely located
neighbours.
1 INTRODUCTION
District heating (DH) systems utilize hot water and
heat produced at a production unit for a number of
consumer units, i.e., buildings, in a limited geograph-
ical area through a distribution network. This part of
the system is referred to as the primary side. The con-
sumer unit itself consists of a heat exchanger, a circu-
lation network, and radiators for the rooms, which are
considered as the secondary side. The primary and
secondary sides are connected together through a sub-
station, which is responsible for adjusting the pressure
and the temperature of the supply water suitable for
the consumer unit.
In the DH domain, energy companies need to ad-
dress several conflicting goals such as satisfying con-
sumers’ heat demand including domestic hot water
(DHW) while minimizing production and distribu-
tion costs. Such complexity demands fault detection
and root cause analysis techniques for identification
of deviating behaviours and faults. Undetected faults
a
https://orcid.org/0000-0002-3010-8798
b
https://orcid.org/0000-0001-9947-1088
can lead to underlying problems, which in return can
increase the maintenance cost and reduce the con-
sumers’ satisfaction. When it comes to monitoring
of a DH network there are different features and char-
acteristics that one needs to consider. Domain experts
often analyse substations individually or in a group
with regard to one specific feature or a combination
of features. While this provides useful information
for the whole network it does not take into account
the location of the substations along the distribution
network and their neighbouring substations automat-
ically. In other words, the operational behaviours of
the DH substations need to be assessed jointly with
surrounding substations within a limited geographi-
cal distance. Due to the nature of the data and the
fact that different data representations can be used, the
process of monitoring and identifying faults and de-
viating behaviours of the DH system and substations
can be treated as a multi-view data analysis problem.
Multi-view datasets consist of multiple data repre-
sentations or views, where each one may contain sev-
eral features (Deepak and Anna, 2019). Multi-view
learning is a semi-supervised approach with the goal
158
Abghari, S., Boeva, V., Brage, J. and Grahn, H.
Multi-view Clustering Analyses for District Heating Substations.
DOI: 10.5220/0009780001580168
In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 158-168
ISBN: 978-989-758-440-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

to obtain better performance by applying the relation-
ship between different views rather than one to facil-
itate the difficulty of a learning problem (Blum and
Mitchell, 1998; Ando and Zhang, 2007; Xu et al.,
2013). Due to availability of inexpensive unlabeled
data in many application domains, multi-view unsu-
pervised learning and specifically multi-view cluster-
ing (MVC) attract great attention (Deepak and Anna,
2019). The goal of multi-view clustering is to find
groups of similar objects based on multiple data rep-
resentations.
We propose a multi-view clustering analysis ap-
proach for mining network datasets with multiple rep-
resentations. The proposed approach is used for mon-
itoring a DH network and identifying DH substa-
tions with sub-optimal operational behavior. We ini-
tially use geographical location of substations to di-
vide them into groups of similar substations based on
their distance and location. In that way, we are able
to: 1) group the substations (network nodes) based
on their location and distance, 2) build an approx-
imate graph representation of the DH network, and
3) order the substations using information about the
DH network structure and the average supply water
temperature for a specific period. Two different types
of analyses can then be applied in this scenario: i)
step-wise clustering to sequentially consider and anal-
yse substations with respect to a few different views;
ii) parallel-wise clustering to analyse substations with
regards to two different views in parallel.
2 RELATED WORK
MVC clustering algorithms have been proposed based
on different frameworks and approaches such as k-
means variants (Bickel and Scheffer, 2004; Cai et al.,
2013; Jiang et al., 2016), matrix factorization (Liu
et al., 2013; Zong et al., 2017), spectral methods (Ku-
mar and Daum
´
e, 2011; Wang et al., 2013) and
exemplar-based approaches (Meng et al., 2015; Wang
et al., 2015).
Bickel and Scheffers (Bickel and Scheffer, 2004)
proposed extensions to different partitioning and ag-
glomerative MVC algorithm. That study can proba-
bly be recognized as one of the earliest works where
an extension of k-means algorithm for two-view doc-
ument clustering is proposed. In another study (Cai
et al., 2013), the authors developed a large-scale
MVC algorithm based on k-means with a strategy for
weighting views. The proposed method is based on
the `
2,1
norm, where the `
1
norm is enforced on data
points to reduce the effect of outlier data and the `
2
norm is applied on the features. In a recent study,
Jiang et al. (Jiang et al., 2016) proposed an extension
of k-means with a strategy for weighting both views
and features. Each feature within each view is given
bi-level weights to express its importance both at the
feature level and the view level.
Liu et al. (Liu et al., 2013) proposed an MVC
algorithm based on joint non-negative matrix factor-
ization (NMF). The developed algorithm incorporates
separate matrix factorizations to achieve similar coef-
ficient matrices and further meaningful and compara-
ble clustering solution across all views. In a recent
study, Zong et al. (Zong et al., 2017) proposed an ex-
tension of NMF for MVC that is based on manifold
regularization. The proposed framework maintains
the locally geometrical structure of multi-view data
by including consensus manifold and consensus coef-
ficient matrix with multi-manifold regularization.
Kumar and Daum
´
e (Kumar and Daum
´
e, 2011)
proposed an MVC algorithm for two-view data by
combining co-training and spectral clustering. The
approach is based on learning the clustering in one
view to label the data and modify the similarity ma-
trix of the other view. The modification of the sim-
ilarity matrices are performed using discriminative
eigenvectors. Wang et al. (Wang et al., 2013) pro-
posed a variant of spectral MVC method for situations
where there are disagreements between data views us-
ing Pareto optimization as a means of relaxation of the
agreement assumption.
Meng et al. (Meng et al., 2015) proposed an MVC
algorithm based on affinity propagation (AP) for sci-
entific journal clustering where the similarity matrices
of the two views (text view and citations view) are in-
tegrated as a weighted average similarity matrix. In
another study, Wang et al. (Wang et al., 2015) pro-
posed a variant of AP where an MVC model consists
of two components for measuring 1) the within-view
clustering quality and 2) the explicit clustering con-
sistency across different views.
Fault detection and diagnosis (FDD) is an active
field of research and has been studied in different
application domains. Isermann (Isermann, 1997; Is-
ermann, 2006) provided a general review for FDD.
Katipamula and Brambley (Katipamula and Bramb-
ley, 2005a; Katipamula and Brambley, 2005b) con-
ducted an extensive review in two parts on fault de-
tection and diagnosis for building systems. Xue et
al. (Xue et al., 2017) applied clustering analysis and
association rule mining to detect faults in substations.
Sandin et al. (Sandin et al., 2013) used probabilistic
methods and heuristics for automated detection and
ranking of faults in large-scale district energy sys-
tems. Calikus et al. (Calikus et al., 2019) proposed an
approach for automatically 1) discovering heat load
Multi-view Clustering Analyses for District Heating Substations
159

patterns in DH systems and 2) identifying buildings
with abnormal heat profiles and unsuitable control
strategies.
In contrast to the above mentioned methods, this
study proposes a multi-view data analysis approach
that can be applied for monitoring, evaluating and
visualizing the operational behaviour of DH substa-
tions. The geographical location data is used as a
backbone of the analysis and the operational perfor-
mance of the substations is further assessed in con-
junction with their neighbours.
3 PROBLEM FORMALIZATION
We have a network with N nodes, e.g., a DH network
linking a set of substations located in some geograph-
ical region. Assume that each network node, substa-
tion, i (i = 1,2,... , N) is monitored under n differ-
ent conditions (i.e., the measurements of n different
features are collected) for a given time period, e.g.,
m days. Each monitored condition j ( j = 1,2,...,n)
contains the measured levels of the corresponding fea-
ture for a period of m days in t different time points.
This leads to a set of n time series data matrices D
j
( j = 1,2, . . . , n), one per feature, for each network
node.
This multi-view data context can additionally be
complicated in the case of a real-world scenario such
as one related to a DH network. For example, the
operational behaviour of the substations varies dur-
ing heating and non-heating seasons which requires
separate analysis. Therefore, for each substation two
datasets are usually collected and available for further
analysis and comparison. Notice that in this study,
we are only interested in the operational behaviour of
the DH substations during heating season due to the
importance of space heating.
The main challenge in the above multi-view con-
text is how to use all available measurements about
the substations’ operational behaviour and perfor-
mance for better understanding and improved main-
tenance of the DH network. Exploiting the whole po-
tential of these real-world datasets is not trivial and it
requires suitable data analysis techniques to prevent
information loss.
4 METHODS
4.1 Clustering Analysis
In this study, we are interested in identifying homoge-
neous groups of substations by considering their loca-
tions and additionally analysing them with respect to
different views (features). Due to unavailability of the
labeled data, clustering analysis is applied to explore
hidden structures within the data. We apply two clus-
tering algorithms as follows:
1. Minimum Spanning Tree Clustering: We use Van-
derPlas’ (VanderPlas, 2016) Python implantation of
the minimum spanning tree (MST) clustering algo-
rithm for grouping substations based on their geo-
graphical location. The algorithm is based on con-
structing an approximate Euclidean minimum span-
ning tree (EMST), which considers only k nearest
neighbours of each point for building the minimum
spanning tree rather than the entire set of edges in a
complete graph.
2. Affinity Propagation: We use the affinity prop-
agation (AP) algorithm (Frey and Dueck, 2007) for
clustering the time series based on their similarities.
AP works based on the concept of message pass-
ing between data points to first identify a suitable set
of exemplars and then to choose which data points
should pick which exemplars. One of the advantages
of AP, unlike other clustering algorithms, such as k-
means (MacQueen et al., 1967) which requires the
number of clusters as an input, is that it estimates the
optimal number of clusters from the data. In addition,
the chosen exemplars, the representative of the clus-
ters, are real data points which makes AP a suitable
clustering algorithm for this study.
4.2 Similarity Measures
We use different similarity measures, 1) to check the
similarity between daily time series profiles of each
feature, 2) to perform pairwise comparison between
exemplars of clustering solutions of different substa-
tions, and 3) to compute a similarity between two
clustering solutions by considering all pairs of mem-
bers. These similarity measures are as follows:
1. Dynamic Time Warping: Given two time series
Y = (y
1
,y
2
,..., y
n
) and Y
0
= (y
0
1
,y
0
2
,..., y
0
m
), the simi-
larity between Y and Y
0
can be measured using the dy-
namic time warping (DTW) algorithm. DTW is pro-
posed by Sakoe and Chiba (Sakoe and Chiba, 1978)
for spoken word detection with the focus of eliminat-
ing timing differences between two speech patterns.
In other words, DTW identifies an optimal match-
ing between the given sequences by warping the time
axis. In order to align the time series Y and Y
0
of
length n and m respectively, a cost matrix, Q
n×m
is
computed. Each element, q
i j
, of Q
n×m
corresponds
to the distance (often Euclidean) between y
i
and y
0
j
of
the two series. Using the cost matrix, the DTW tries to
find the best alignment path between these two time
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
160

series that is leading to minimum overall cost. The
best warping path should satisfy a different number of
conditions such as monotonicity, continuity, bound-
ary, warping window, and slope constraint.
2. Clustering Solution Similarities: Given two
clustering solutions C = {C
1
,C
2
,. . . ,C
n
} and C
0
=
{C
0
1
,C
0
2
,. . . ,C
0
m
} of datasets X and X
0
, respectively,
the similarity, C
S
w
, between C and C
0
can be assessed
as follows (Abghari et al., 2019):
C
S
w
(C,C
0
) =
∑
n
i=1
(min
m
j=1
w
i
.d(c
i
,c
0
j
))
2
+
∑
m
j=1
(min
n
i=1
w
0
j
.d(c
i
,c
0
j
))
2
,
(1)
where c
i
and c
0
j
are exemplars of the clustering solu-
tion C
i
and C
0
j
, respectively. The weights w
i
and w
0
j
indicate the relative importance of clusters C
i
and C
0
j
compared to other clusters in the clustering solution
C and C
0
, respectively. For example, a weight w
i
of
a cluster C
i
can be calculated as the ratio of its cardi-
nality with respect to the size of X, i.e., w
i
= |C
i
|/|X|.
The C
S
w
has values in a range of [0,1]. Scores equal to
zero imply identical performance while scores close
to one show significant dissimilarities.
3. Adjusted Rand Index: The quality of the results of
a clustering analysis can be validated by means of in-
ternal and external criteria. Internal criteria evaluate
the quality of the clustering solution produced by a
clustering algorithm that fits the data in terms of, e.g.,
compactness and separation by using the inherent in-
formation of the data. External criteria on the other
hand, can be used for measuring the level of agree-
ments between the results of a clustering algorithm in
comparison with ground truth, the results of another
clustering algorithm on the same data, or same clus-
tering algorithm but by considering different views.
In this study, we apply a symmetric external val-
idation index for assessing the similarity (consen-
sus) between two clustering results generated on the
studied DH substations with respect to two differ-
ent views. The adjusted Rand index (ARI) (Hubert
and Arabie, 1985) is a correction of the Rand in-
dex (RI) (Rand, 1971) that measures the similarity
between two clustering solutions by considering the
level of agreements between the two groups. ARI is
computed as follows:
ARI =
RI − ExpectedRI
Max(RI) − ExpectedRI
(2)
ARI scores are bound between -1 and +1. A score less
than or equal to 0 represents random labelling and 1
stands for perfect match.
5 PROPOSED APPROACH
Geographical locations of N substations are initially
used for building an approximate graph representa-
tion of the DH network. We refer to the geograph-
ical location of the substations as the Location view
(v
0
). This is performed by applying the MST cluster-
ing algorithm described in Section 4. The aim is to
connect substations based on their distance by build-
ing a minimum spanning tree and removing edges of
the tree with regard to a cut-off threshold. Therefore,
each cluster is represented by a tree that can be in-
terpreted as a representation of the DH network struc-
ture. In order to provide additional support for the do-
main experts, the graph representation can in turn be
used as a backbone for additional information about
the DH network, e.g., average yearly values and dif-
ferent forms of ranking.
On the foundation of the created grouping of the
substations we can perform further analysis by focus-
ing on a specific feature or subset of features and eval-
uate the substations’ operational behaviours in each
single location-based cluster. We study and evaluate
the following two scenarios:
1. Step-wise multi-view clustering (SW-MVC), we
can apply clustering analysis on substations that have
been grouped together at the previous step with re-
spect to a set of features, i.e., the substations can be
grouped by considering one feature at a time. This
scenario can be used when the domain experts are in-
terested in grouping similar substations based on their
performance with respect to one feature and then find-
ing similar substations in each group by using another
feature and so on. Figure 1 shows how the results of
this analysis can be visualized based on the location
of the substations and two features.
C
1m
C
12
C
11
C
1n
C
10
C
00
C
01
C
0n
…
…
…
C
20
C
21
V
0
: Location
V
1
: Feature 1
C
22
C
23
C
24
C
2q
C
2n
C
2m
V
2
: Feature 2
Figure 1: SW-MVC analysis, each view represents the clus-
tering analysis based on one feature. Every analysing step is
based on the results obtained on the previously considered
view. Triangles represent substations.
As an example, consider two substations s
i
and s
j
in the cluster C
00
from v
0
, where the similarity of the
two substations can be analysed in terms of their op-
Multi-view Clustering Analyses for District Heating Substations
161

erational behaviour, first based on Feature 1 (v
1
) and
then Feature 2 (v
2
). Here two scenarios can occur, ei-
ther s
i
and s
j
are grouped together with respect to v
1
,
since they performed similarly, or they are assigned
into different groups. In case of the first scenario, af-
ter applying the second step of the analysis (i.e., using
v
2
) if s
i
and s
j
are in the same group this shows that
the operational behaviour of the two substations are
similar with respect to v
1
and v
2
. Otherwise, the two
substations are only similar with regards to v
1
and dis-
similar with regards to v
2
. In case of the second sce-
nario, the substations are dissimilar with respect to
both views. Nevertheless, in all cases the domain ex-
pert might be interested to further analyse groups of
substations with a smaller size.
2. Parallel-wise multi-view clustering (PW-MVC), in
this scenario a group of substations can be studied by
considering different features in parallel. For exam-
ple, the substations can be clustered separately with
respect to two different features (or subsets of fea-
tures). The produced clustering solution can further
be compared and analysed to find out whether similar
substations, that have been grouped together based on
one feature, are still in the same group with respect to
the other feature. In addition, one can use a bipartite
graph, to present and visualize the relationships be-
tween a clustering solution based on one view and a
clustering solution produced on the other view. This
will provide domain experts more information by sup-
plying them with deeper insights about substations’
operational behaviours in different groups with re-
gards to two different views. For further analysis, one
can label clusters of each clustering solution with per-
formance indicators
1
and rank them from the highest
to the lowest performance.
The results of this pairwise comparison can be
used in conjunction with the SW-MVC analysis to
provide a better understanding of operational be-
haviour for each individual substation and the group
as a whole. Our initial assumption is that using the
SW-MVC analysis, one can construct a hierarchical
graph-model of a heating network for the area of
study. Those substations that are located in the same
cluster are assumed to share similar characteristics.
While the PW-MVC analysis focus is on identifying
a similar group of substations that are in the intersec-
tion of the two views.
1
The operational performance of a DH substation can be
evaluated with respect to different indicators, which are usu-
ally computed based on the quantitative relation between
the substation’s inputs and outputs.
6 EXPERIMENTS AND
EVALUATION
6.1 Dataset
The data used in this study is provided by an energy
company. The data consists of hourly average mea-
surements from 70 substations located in Southern
Sweden during 2015 to 2018. The dataset contains
eight features both from primary and secondary sides
of the DH network. The primary side data is always
available. The secondary side data on the other hand,
requires specific hardware to be extracted. Therefore,
in this study we mainly focus on primary side data to
analyse the operational behaviour of the DH substa-
tions.
Apart from these features there are two perfor-
mance indicators that are computed using both sides
of the DH network. The first indicator is called the
least temperature difference (Frederiksen and Werner,
2013) which represents the difference between pri-
mary and secondary return temperatures. The least
temperature difference of a substation can be greater
than or equal to zero, though it can go below zero
due to usage of DHW. A lower value of this indicator
implies better performance. The second indicator is
referred to as substation effectiveness. It is the ratio
of the difference between primary supply and return
temperatures to the difference between primary sup-
ply temperature and the secondary return temperature.
The efficiency of a well-performing substation should
be close to one in a normal setting. However, due to
the affect of DHW generation on the primary return
temperature, it can represent values above one. Ta-
ble 1 shows the dataset features and the performance
indicators.
Table 1: Features included in the dataset.
No. Feature Notation Unit
1 T
o
Outdoor temperature °C
2 T
s,1
st
Primary supply temperature °C
3 T
r,1
st
Primary return temperature °C
4 ∆T
1
st
Primary delta temperature °C
5 G
1
st
Primary mass flow rate l/h
6 Q
1
st
Primary heat kW
7 T
s,2
nd
Secondary supply temperature °C
8 T
r,2
nd
Secondary return temperature °C
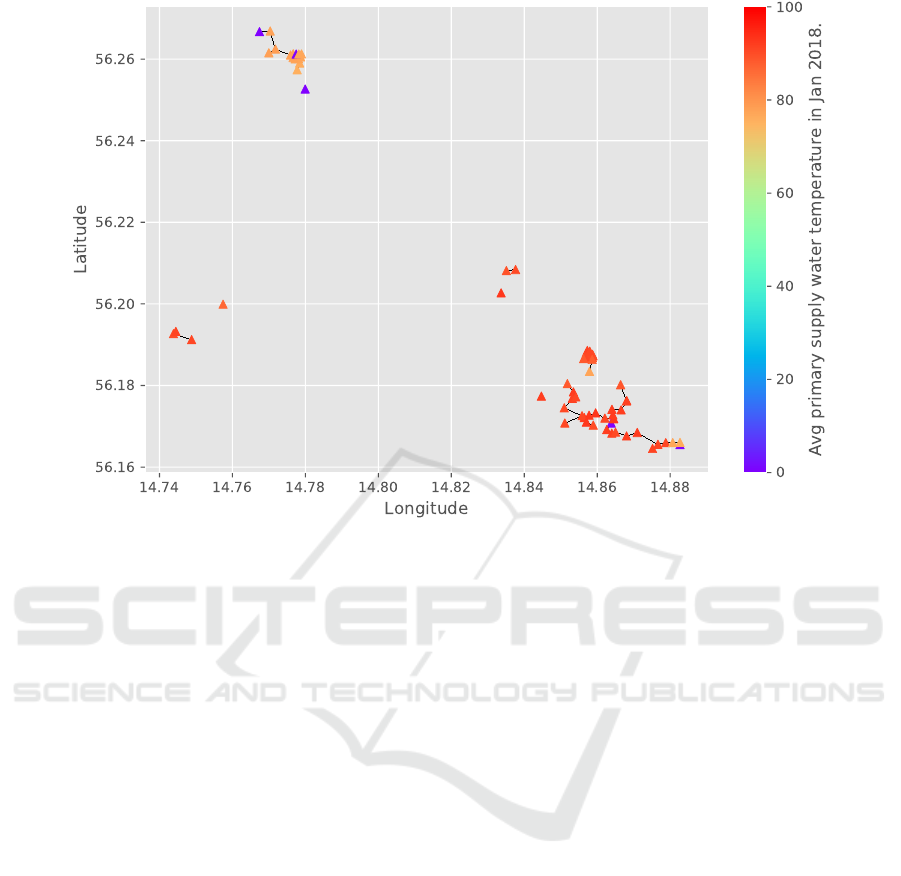
Figure 2 shows the groups and graph network rep-
resentation produced by applying MST clustering on
the above mentioned 70 substations. The substations
are partitioned into nine clusters by applying the MST
clustering algorithm while the cut-off parameter is set
to 500 meters. That is substations with distance less
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
162
0
1
2
3
4
5
6
7
8
Figure 2: 70 substations located in Southern Sweden are grouped into nine clusters using the MST clustering algorithm. The
geographical location of the substations is referred to as the Location view (v
0
). Substations with distance less than 500 meters
from their closest neighbours are grouped together. The color of the substations represents the average T
s,1
st
in January 2018,
which for most substations is around 87 °C.
than 500 meters from their closest neighbour(s) are
grouped together. Five clusters represent as a tree,
i.e., edges of the tree represent the distance between
the substations (the tree nodes) and the remaining four
clusters are singletons. The substations’ colors repre-
sent their received average T
s,1
st
(°C) in January 2018.
In order to make the data ready for the experi-
ment, first the duplicates are removed. Then we fo-
cused on extreme values which can appear as a result
of faults in measurement tools. We apply a Hampel
filter (Hampel, 1971) which is a median absolute de-
viation (MAD) based estimation to detect and smooth
out such extreme values. The filter is used with the
default parameters, i.e., the size of the window is set
to be seven and the threshold for extreme value detec-
tion is set to be three.
In the studied context, we have hourly measure-
ments data. This gives one time series every 24-hours
and in total 365 time series per year. Time series
with less than 24 measurement values are excluded.
Since we are expecting different behaviours from a
DH substation during heating and non-heating sea-
sons, the time series are divided into two groups with
respect to the outdoor temperature (T
o
). That is, if
the outdoor temperature is above a certain threshold,
T
o
threshold
, the DH substation behaviour can be cate-
gorized into the non-heating season otherwise to the
heating season. This threshold in Sweden can be set to
be T
o
threshold
= 10 °C. In order to assess each DH sub-
station’s operational behaviours during heating sea-
son and in comparison with other substations, the ex-
tracted time series are scaled with z-score normaliza-
tion. That is, each time series is scaled to have a mean
of zero and a standard deviation of one. Notice that in
the considered context the general shape of the time
series, rather than their amplitude, is important. Now
for every category, the time series related to one spe-
cific feature, i, can be compared in terms of similarity
with respect to a distance measure d(y
i
,y
0
j
), where d
in this study is DTW . This leads to a similarity ma-
trix, SM
i
. In the next step, SM
i
is fed to a clustering
algorithm. Here we aim to group time series based
on their similarities into a number of clusters. Con-
sidering each feature as one view, we can analyse the
operational behaviour of a set of DH substations by
using the explained evaluation scenarios in Section 5.
6.2 Implementation and Availability
The proposed approach is implemented in Python ver-
sion 3.6. The affinity propagation and the adjusted
Rand index are adopted from the scikit-learn mod-
ule (Pedregosa et al., 2011) and the MST clustering
algorithm is fetched from (VanderPlas, 2016). The
Multi-view Clustering Analyses for District Heating Substations
163
alignments between time series are identified using
dtwalign’s package
2
. The implemented code and the
experimental results are available at GitHub
3
.
7 RESULTS AND DISCUSSION
The initial view in our analyses is always the outcome
of the MST clustering, i.e., 70 substations in the stud-
ied area are grouped into nine clusters based on their
distances. We set the cut-off parameter to be 500 me-
ters which means any edges greater than 500 meters
are removed from the MST. The first three clusters
(0, 1, and 2) include 15, 32, and 14 substations, re-
spectively (in total 61 of 70 substations). The remain-
ing substations are grouped into 6 clusters as follows:
cluster 3 contains 2 substations, clusters 4, 5, 7, and 8
are singletons and cluster 6 has 3 substations.
In the remainder of this study we only consider
and discuss the results produced on clusters 0, 1, and
2, since the majority of the substations are distributed
in these clusters. Each analysis can be performed
based on different combinations of the features in Ta-
ble 1. However, due to the page limit, we only report
the results of the analyses with respect to T
r,1
st
and
∆T
1
st
(the difference between T
s,1
st
and T
r,1
st
).
7.1 SW-MVC Analysis
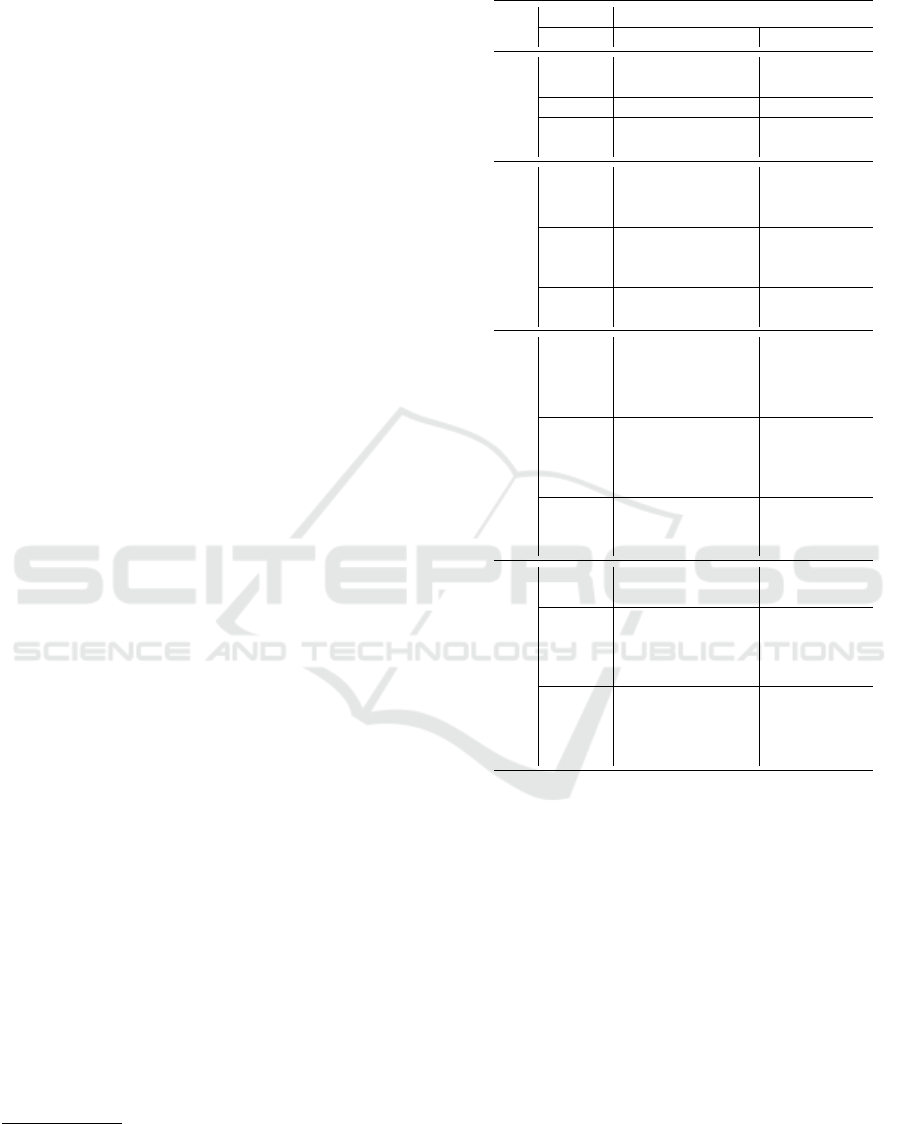
Table 2 shows the results of SW-MVC analysis for
61 substations throughout the heating seasons from
2015 to 2018. For each MST cluster (v
0
), initially
substations are grouped based on T
r,1
st
(v
1
) and then
for each created subgroup the clustering analysis is
performed using ∆T
1
st
(v
2
). The information in Ta-
ble 2 can be used in three different ways: column-
wise, row-wise, or both. In the column-wise case, one
can see how the substations in each MST cluster are
grouped based on the other two views (i.e., v
1
and v
2
)
in different years. The row-wise analysis shows how
the substations in each MST cluster are grouped step-
wise based on first v
1
and second v
2
. For example,
the domain experts might be interested in perform-
ing further analysis when the grouped substations in
v
1
are split into more subgroups based on v
2
. Num-
bers in bold in Table 2 represent the number of substa-
tions that are grouped into different clusters based on
v
2
as opposed to v
1
. By considering both cases one
can track the transition of the operational behaviour
of substations throughout the years.
2
https://github.com/statefb/dtwalign
3
https://github.com/shahrooz-abghari/MVC-DH-
Monitoring
Table 2: SW-MVC analysis based on T
r,1
st
and ∆T
1
st
from
2015 to 2018.
Year
v
0
: MST v
1
: T
r,1
st
v
2
: ∆T
1
st
Label #substations Label 0 1 2 Total
2015
0
5 0 5 5
10 1 1 9 10
1 32 0 11 12 9 32
2
5 0 3 2 5
9 1 6 3 9
2016
0
3 0 3 3
5 1 4 1 5
7 2 7 7
1
15 0 9 6 15
13 1 7 6 13
4 2 4 4
2
9 0 9 9
5 1 5 5
2017
0
8 0 8 8
1 1 1 1
5 2 5 5
1 3 1 1
1
11 0 8 3 11
4 1 1 3 4
16 2 8 8 16
1 3 1 1
2
2 0 2 2
9 1 9 9
3 2 3 3
2018
0
1 0 1 1
14 1 10 4 14
1
12 0 12 12
5 1 5 5
8 2 5 3 8
7 3 6 1 7
2
4 0 1 3 4
4 1 4 4
1 2 1 1
5 3 5 5
Note. Number of substations that are grouped into
different clusters based on v
2
as opposed to v
1
are
shown in bold.
Figure 3 depicts the SW-MVC analysis by consid-
ering T
r,1
st
as the first view (squares) and ∆T
1
st
as the
second view (circles) in the period from 2015 to 2018.
Figure 4 represents the SW-MVC analysis specifi-
cally for the MST cluster with label 0 during a period
covering 2017 and 2018. Notice, the color of squares
shows T
r,1
st
while the colored circles represent ∆T
1
st
.
These two features can be used as an assessment indi-
cator for the operational behaviour of the substations.
Technically, it is desired in a well performed substa-
tion that the T
r,1
st
has a lower value in comparison to
the T
s,1
st
. In other words, a greater delta means that
the substation is making more efficient use of the sup-
plied heat for space heating.
Table 3 provides the statistics, the average values
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
164
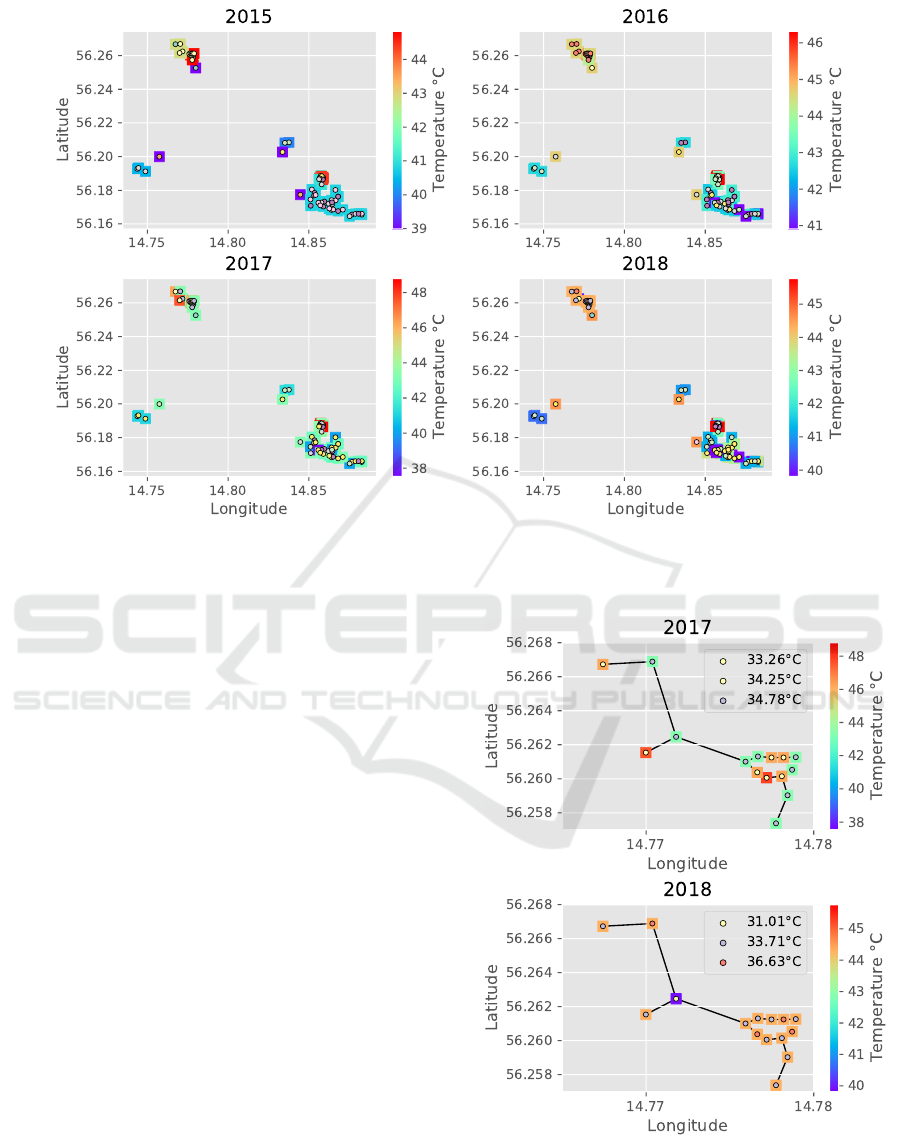
Figure 3: The results of SW-MVC analysis for the whole studied area contains 70 substations. Squares represent clusters of
substations based on the first view, T
r,1
st
, and circles represent groups of substations with respect to the second view, ∆T
1
st
.
Note that the substations with similar colors in different MST clusters are not related.
of the actual measurements and their standard devia-
tions, regarding the DH substations that are discussed
in Figure 4. As one can see in 2017, substations
are grouped into 4 clusters, where clusters 0 (green
squares) and 2 (orange squares) contains the major-
ity of substations, 8 and 5, respectively. The two
other clusters include only one substation each (red
squares). The average T
r,1
st
for cluster 0 is approxi-
mately 43 °C and for cluster 2 is around 46 °C. Clus-
ters 1 and 3 both show the average T
r,1
st
of 48 °C. All
the grouped substations in the previous step stayed to-
gether based on the ∆T
1
st
, i.e., no new cluster is cre-
ated. The cluster with 8 substations (grey circles in-
side green squares) represents the ∆T
1
st
of 34.79 °C,
while the cluster with 5 substations (yellow circles in-
side orange squares) shows the ∆T
1
st
of 33.26 °C. The
other two clusters (yellow circles inside red squares)
show the same value, 34.25 °C for the ∆T
1
st
.
In 2018, the same number of substations, 15, are
grouped into only two clusters with an average T
r,1
st
of approximately 40 °C for cluster 0 (purple square)
and 44 °C for cluster 1 (orange squares). A majority
of the substations, 13 out of 14, are grouped in clus-
ter 1. This cluster is further divided into two clusters,
one with 10 DH substations (grey circles inside or-
ange squares) and the average ∆T
1
st
of approximately
34 °C and the other with 4 substations (orange cir-
cles inside orange squares) and the average ∆T
1
st
of
Figure 4: The results of SW-MVC analysis for the MST
cluster with label 0 and 15 substations in 2017 (top) and
2018 (bottom). Colored squares represent groups of substa-
tions based on v
1
: T
r,1
st
and colored circles represent groups
of substations based on v
2
: ∆T
1
st
.
Multi-view Clustering Analyses for District Heating Substations
165

Table 3: SW-MVC analysis for the MST cluster with label 0, 2017 to 2018.
Year
v
0
: MST v
1
: T
r,1
st
v
2
: ∆T
1
st
Label Label #substations Avg(°C) SD(°C) Label #substations Avg(°C) SD(°C)
2017 0
0 8 43.31 5.39 0 8 34.78 4.13
1 1 47.88 - 0 1 34.25 -
2 5 46.23 3.35 0 5 33.26 3.01
3 1 47.61 - 0 1 34.25 -
2018 0
0 1 39.91 - 0 1 31.01 -
1 14 44.31 4.66
0 10 33.71 4.11
1 4 36.63 2.10
Note. Avg: average, SD: standard deviation
approximately 37 °C. Cluster 0 represents one sub-
station (yellow circle inside purple square) with the
average ∆T
1
st
of 31.01 °C. In both years there are sub-
stations that show slightly different operational be-
haviour in comparison to their neighbouring substa-
tions, e.g., the red substations in 2017 and the purple
substation in 2018. The domain experts can investi-
gate the reasons why these substations performed dif-
ferently in comparison to the majority of substations.
In addition, it is important to mention that the order
in which views are used for the SW-MVC analysis af-
fects the results, which can be decided based on the
domain expert’s preferences.
7.2 PW-MVC Analysis
The aim of this analysis is to group the substations
based on two different views (i.e., v
1
and v
2
) and com-
pare the results of the clustering solution to find out
which substations are similar based on both views.
Such analysis can provide useful information for the
domain experts while it applies for a period of time,
e.g., different years, where the transition of the opera-
tional behaviour of substations can be monitored. Ta-
ble 4 shows the distribution of the studied substations
based on PW-MVC analysis throughout the heating
season in the period from 2015 to 2018.
Figure 5 depicts the computed ARI scores for the
clustering solution based on T
r,1
st
and ∆T
1
st
of each
MST cluster in the period from 2015 to 2018. As
one can see, the ARI scores of the first three clus-
ters are absolutely dissimilar in 2015, 2016, and 2018.
However, cluster 2 with 14 substations shows the ARI
score of 0.71 in 2017, which means the majority of
DH substations in this cluster performed similarly.
Other clusters, 3 to 8 represent the adjusted Rand in-
dex of 1 for all the years.
Figure 6 shows the PW-MVC analysis for MST
cluster with label 1 with respect to T
r,1
st
and ∆T
1
st
in
the period from 2015 to 2018. The substations with
similar cluster labels with regard to both features are
shown in red. The insight provided by Figure 6 can
Table 4: PW-MVC analysis is performed based on T
r,1
st
and
∆T
1
st
separately from 2015 to 2018.
Year
v
0
: MST v
1
: T
r,1
st
v
2
: ∆T
1
st
Label #substation 0 1 2 3 0 1 2
2015
0 15 5 10 5 10
1 32 32 11 12 9
2 14 5 9 6 5 3
Total 70 51 19 31 27 12
2016
0 15 3 5 7 6 9
1 32 15 13 4 32
2 14 9 5 10 4
Total 70 36 23 11 57 13
2017
0 15 8 1 5 1 15
1 32 11 4 16 1 10 22
2 14 2 9 3 10 4
Total 70 30 14 24 2 44 26
2018
0 15 1 14 9 6
1 32 12 5 8 7 26 6
2 14 4 4 1 5 4 10
Total 70 26 23 9 12 48 22
Figure 5: PW-MVC analysis, the computed ARI scores for
T
r,1
st
and ∆T
1
st
throughout 2015 to 2018.
be used for analysing the difference between oper-
ational behaviour of the red substations against the
greys within one specific year. In addition, the transi-
tion of the substations from one color group to another
can be tracked and further analysed.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
166

Figure 6: The results of PW-MVC analysis for the MST cluster with label 1 and 32 substations. Substations in red are those
that are grouped with the same label according to the both views, namely T
r,1
st
and ∆T
1
st
from 2015 to 2018.
8 CONCLUSIONS
We have proposed a multi-view clustering approach
for analysing datasets that consist of different data
representations. The proposed approach has been ap-
plied for monitoring and analysing operational be-
haviour of district heating substations. We have ini-
tially used the substations’ geographical information
to build an approximate graph representation of the
DH network. This graph structure has been used as a
backbone for further analysis of the network perfor-
mance.
In the above context, we have proposed and dis-
cussed two different types of analysis: 1) step-wise
multi-view clustering that sequentially considers and
analyses the operational behaviour of the DH substa-
tions with respect to different views and organizes the
substations into a hierarchical structure. That is, at
each step a new clustering solution is built on top of
the one generated in the previous step with respect to
the considered view. 2) parallel-wise multi-view clus-
tering that analyses substations with regards to two
different views in side by side. This enables the iden-
tification of the relationships between neighbouring
substations by organizing them in a bipartite graph
and analysing their distribution with respect to the
two considered views. The proposed data analysis ap-
proach facilitates the visual analysis and inspections
of multi-view real-world datasets such as ones related
to the DH networks. For example, the proposed ap-
proach provides the opportunity to consider the DH
substations in close relation with their neighbours.
That is, those substations that demonstrate a deviat-
ing behavior from their neighbouring substations can
easily be identified for further investigation.
For future work, we are interested in expanding
our approach by adding a third scenario where the
clustering solution is the outcome of integration of
different views. We believe that the proposed ap-
proach provides a verity of analysis techniques to sup-
ply the domain experts with a complete picture about
the DH network operations. In addition, the proposed
approach can facilitate the identification of substa-
tions with deviating behaviours and suggest initiation
of further inspections by domain experts.
Multi-view Clustering Analyses for District Heating Substations
167

ACKNOWLEDGEMENTS
This work is part of the research project “Scal-
able resource-efficient systems for big data analyt-
ics“ funded by the Knowledge Foundation (grant:
20140032) in Sweden.
We would also like to thank Christian Johansson,
CEO of NODA Intelligent Systems, for his support
and valuable feedback.
REFERENCES
Abghari, S., Boeva, V., Brage, J., Johansson, C., Grahn,
H., and Lavesson, N. (2019). Higher order mining for
monitoring district heating substations. In 2019 IEEE
Int’l Conf. on Data Science and Advanced Analytics
(DSAA), pages 382–391. IEEE.
Ando, R. K. and Zhang, T. (2007). Two-view feature gener-
ation model for semi-supervised learning. In Proc. of
the 24th Int’l Conf. on Machine learning, pages 25–
32. ACM.
Bickel, S. and Scheffer, T. (2004). Multi-view clustering.
In ICDM, volume 4, pages 19–26.
Blum, A. and Mitchell, T. (1998). Combining labeled
and unlabeled data with co-training. In Proc. of the
eleventh annual Conf. on Computational learning the-
ory, pages 92–100.
Cai, X., Nie, F., and Huang, H. (2013). Multi-view k-
means clustering on big data. In Twenty-Third Int’l
Joint Conf. on artificial intelligence.
Calikus, E., Nowaczyk, S., Sant’Anna, A., Gadd, H., and
Werner, S. (2019). A data-driven approach for dis-
covery of heat load patterns in district heating. arXiv
preprint arXiv:1901.04863.
Deepak, P. and Anna, J.-L. (2019). Multi-View Clustering,
pages 27–53. Springer Int’l Publishing, Cham.
Frederiksen, S. and Werner, S. (2013). District Heating and
Cooling. Studentlitteratur AB.
Frey, B. J. and Dueck, D. (2007). Clustering by
passing messages between data points. Science,
315(5814):972–976.
Hampel, F. R. (1971). A general qualitative definition of
robustness. The Annals of Mathematical Statistics,
pages 1887–1896.
Hubert, L. and Arabie, P. (1985). Comparing partitions. J.
of classification, 2(1):193–218.
Isermann, R. (1997). Supervision, fault-detection and fault-
diagnosis methods—an introduction. Control engi-
neering practice, 5(5):639–652.
Isermann, R. (2006). Fault-diagnosis systems: an introduc-
tion from fault detection to fault tolerance. Springer
Science & Business Media.
Jiang, B., Qiu, F., and Wang, L. (2016). Multi-view cluster-
ing via simultaneous weighting on views and features.
Applied Soft Computing, 47:304–315.
Katipamula, S. and Brambley, M. R. (2005a). Methods
for fault detection, diagnostics, and prognostics for
building systems-A review, part I. Hvac&R Research,
11(1):3–25.
Katipamula, S. and Brambley, M. R. (2005b). Methods for
fault detection, diagnostics, and prognostics for build-
ing systems-A review, part II. Hvac&R Research,
11(2):169–187.
Kumar, A. and Daum
´
e, H. (2011). A co-training approach
for multi-view spectral clustering. In Proc. of the 28th
Int’l Conf. on machine learning (ICML-11), pages
393–400.
Liu, J., Wang, C., Gao, J., and Han, J. (2013). Multi-view
clustering via joint nonnegative matrix factorization.
In Proc. of the 2013 SIAM Int’l Conf. on Data Mining,
pages 252–260. SIAM.
MacQueen, J. et al. (1967). Some methods for classification
and analysis of multivariate observations. In Proc. of
the Fifth Berkeley Symp. on Mathematical Statistics
and Probability, volume 1, pages 281–297. Oakland,
CA, USA.
Meng, X., Liu, X., Tong, Y., Gl
¨
anzel, W., and Tan, S.
(2015). Multi-view clustering with exemplars for sci-
entific mapping. Scientometrics, 105(3):1527–1552.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,
Weiss, R., Dubourg, V., Vanderplas, J., Passos, A.,
Cournapeau, D., Brucher, M., Perrot, M., and Duch-
esnay, E. (2011). Scikit-learn: Machine learning in
Python. J. of Machine Learning Research, 12:2825–
2830.
Rand, W. M. (1971). Objective criteria for the evaluation
of clustering methods. J. of the American Statistical
association, 66(336):846–850.
Sakoe, H. and Chiba, S. (1978). Dynamic programming
algorithm optimization for spoken word recognition.
IEEE Transactions on Acoustics, Speech, and Signal
Processing, 26(1):43–49.
Sandin, F., Gustafsson, J., and Delsing, J. (2013). Fault de-
tection with hourly district energy data: Probabilistic
methods and heuristics for automated detection and
ranking of anomalies. Svensk Fj
¨
arrv
¨
arme.
VanderPlas, J. (2016). mst clustering: Clustering via eu-
clidean minimum spanning trees. J. Open Source Soft-
ware, 1(1):12.
Wang, C.-D., Lai, J.-H., and Philip, S. Y. (2015). Multi-
view clustering based on belief propagation. IEEE
Transactions on Knowledge and Data Engineering,
28(4):1007–1021.
Wang, X., Qian, B., Ye, J., and Davidson, I. (2013). Multi-
objective multi-view spectral clustering via pareto op-
timization. In Proc. of the 2013 SIAM Int’l Conf. on
Data Mining, pages 234–242. SIAM.
Xu, C., Tao, D., and Xu, C. (2013). A survey on multi-view
learning. arXiv preprint arXiv:1304.5634.
Xue, P., Zhou, Z., Fang, X., Chen, X., Liu, L., Liu, Y., and
Liu, J. (2017). Fault detection and operation optimiza-
tion in district heating substations based on data min-
ing techniques. Applied Energy, 205:926–940.
Zong, L., Zhang, X., Zhao, L., Yu, H., and Zhao, Q. (2017).
Multi-view clustering via multi-manifold regularized
non-negative matrix factorization. Neural Networks,
88:74–89.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
168
