In-memory k Nearest Neighbor GPU-based Query Processing

Polychronis Velentzas

, Michael Vassilakopoulos

and Antonio Corral

Data Structuring & Eng. Lab., Dept. of Electrical & Computer Engineering, University of Thessaly, Volos, Greece

Dept. of Informatics, University of Almeria, Spain

Keywords:

Nearest Neighbors, GPU Algorithms, Spatial Query, In-memory Processing, Parallel Computing.

Abstract:

The k Nearest Neighbor (k-NN) algorithm is widely used for classiﬁcation in several application domains

(medicine, economy, entertainment, etc.). Let a group of query points, for each of which we need to compute

the k-NNs within a reference dataset to derive the dominating feature class. When the reference points volume

is extremely big, it can be proved challenging to deliver low latency results. Furthermore, when the query

points are originating from streams, the need for new methods arises to address the computational overhead.

We propose and implement two in-memory GPU-based algorithms for the k -NN query, using the CUDA API

and the Thrust library. The ﬁrst one is based on a Brute Force approach and the second one is using heuristics

to minimize the reference points near a query point. We also present an extensive experimental comparison

against existing algorithms, using synthetic and real datasets. The results show that both of our algorithms

outperform these algorithms, in terms of execution time as well as total volume of in-memory reference points

that can be handled.

1 INTRODUCTION

Modern applications utilize big spatial or multidimen-

sional data. Processing of these data is demanding

and the use of parallel processing plays a crucial role.

Parallelism based on GPU devices is gaining popular-

ity during last years (Barlas, 2014). A GPU device

can host a very large number of threads accessing the

same device memory. In most cases, GPU devices

have much larger numbers of processing cores than

CPUs and faster device memory than main memory

accessed by CPUs, thus, providing higher computing

power. GPU devices that have general computing ca-

pabilities appear in many modern commodity com-

puters. Therefore, GPU-devices can be widely used

to efﬁciently compute demanding spatial queries.

Since GPU device memory is expensive in com-

parison to main memory, it is important to take advan-

tage of this memory as much as possible and scale-

up to larger datasets and avoid the need for costly

distributed processing. Distributed processing suffers

from excessive network cost which sometimes over-

comes the beneﬁts of distributed parallel execution.

The k Nearest Neighbor (k-NN) algorithm is

widely used for classiﬁcation in many problems areas

(medicine, economy, entertainment, etc.). For exam-

ple, k-NN classiﬁcation has been used for economic

forecasting, including bankruptcy prediction. (Chen

et al., 2011) present a model for bankruptcy predic-

tion using adaptive fuzzy k-NN, where k and the fuzzy

strength parameter are adaptively speciﬁed by particle

swarm optimization, while (Cheng et al., 2019) use k-

NN for predicting ﬁnancial distress (a key factor for

bankruptcy).

Let a group of query points, for each of which

we need to compute the k-NNs within a reference

dataset to derive the dominating feature class. When

the reference points volume is extremely big, it can

be proved challenging to deliver low latency results

and GPU-based techniques may improve efﬁciency.

Furthermore, when the query points are originating

fast from streams, the computational overhead is even

larger and the need for new parallel methods arises.

In this paper, We propose and implement two in-

memory GPU-based algorithms for the k-NN query,

using the CUDA API (NVIDIA, 2020) and the Thrust

library (Barlas, 2014). The ﬁrst one is Brute-force

based and the second one is using heuristics to mini-

mize the reference points near a query point.

We also present an extensive experimental com-

parison against existing algorithms, using synthetic

and real datasets. The results show that both of our

algorithms outperform these algorithms, in terms of

execution time as well as total volume of in-memory

310

Velentzas, P., Vassilakopoulos, M. and Corral, A.

In-memory k Nearest Neighbor GPU-based Query Processing.

DOI: 10.5220/0009781903100317

In Proceedings of the 6th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2020), pages 310-317

ISBN: 978-989-758-425-1

reference points that can be handled.

The rest of this paper is organized as follows. In

Section 2, we review related work and present the mo-

tivation for our work. Next, in Section 3, we present

the new algorithms that we developed for the k-NN

GPU-based Processing and in Section 4, we present

the experimental study that we performed for study-

ing the performance of our algorithms and for com-

paring them to their predecessors. Finally, in Sec-

tion 5, we present the conclusions arising form our

work and discuss our future plans.

2 RELATED WORK AND

MOTIVATION

In this section, we review the most representative al-

gorithms to solve k-NN queries in GPU. k-NN is typ-

ically implemented on GPUs using brute force (BF)

methods applying a two-stage scheme: (1) the com-

putation of distances and (2) the selection of the near-

est neighbors. For the ﬁrst stage, a distance matrix is

built grouping the distance array to each query point.

In the second stage, several selections are performed

in parallel on the different rows of the matrix.

There are different approaches for these two

stages. In (Kuang and Zhao, 2009), the distance

matrix is split into blocks of rows and each matrix

row is sorted using radix sort method. In (Garcia

et al., 2010), the previous distance matrix calcula-

tion scheme is used, but insertion sort method is ap-

plied instead of radix sort. (Liang et al., 2009) uses

the same approach as (Kuang and Zhao, 2009) and

(Garcia et al., 2010) to compute the distance matrix

and, for the selection phase, they calculate a local

k-NN for each block of threads and obtain a global

k-NN by merging. In (Komarov et al., 2014), for

the matrix computation uses the (Kuang and Zhao,

2009) and (Garcia et al., 2010) scheme and modi-

ﬁes the selection phase with a quicksort-based selec-

tion. Each block performs a selection operation with a

large number of threads per block. In (Sismanis et al.,

2012), the truncated sort algorithm was introduced in

the selection phase.

In (Areﬁn et al., 2012), the GPU-FS-kNN algo-

rithm was presented. It divides the computation of

the distance matrix into squared chunks. Each chunk

is computed using a different kernel call, reusing the

allocated GPU-memory. A selection phase is per-

formed after each chunk is processed.

In (Guti

errez et al., 2016), an incremental neigh-

borhood computation that eliminates the dependen-

cies between dataset size and memory is presented.

The iterative process copies several reference point

subsets into the GPU. Then, the algorithm runs the

local neighborhood search to ﬁnd the k nearest neigh-

bors from the query points to the reference point sub-

sets. Merging candidate result sets with new reference

point subsets is used to reach the ﬁnal solution.

In (Barrientos et al., 2011), a GPU heap-based al-

gorithm (called Batch Heap-Reduction) is presented.

Since it requires large shared memory, it is not able

to solve k-NN queries for high k values. In (Barri-

entos et al., 2017), new approaches to solving k-NN

queries in GPU using exhaustive algorithms based

on the selection sort, quicksort and state-of-the-art

heaps-based algorithms are presented.

(Kato and Hosino, 2012) proposes a new algo-

rithm that is also suitable for several GPU devices.

The distance matrix is split into blocks of rows. Each

thread computes the distances for a row. Parallel

threads push new candidates to a max-heap using

atomic operations. (Masek et al., 2015) presents a

multi-GPU implementation of a k-NN algorithm.

In (Li and Amenta, 2015), a new BF k-NN imple-

mentation is proposed by using a modiﬁed inner loop

of the SGEMM kernel in MAGMA library, a well-

optimized open source matrix multiplication kernel.

This brute force k-NN approach has been used in

(Singh et al., 2017) to accelerate calibration process

of a k-nearest neighbors classiﬁer using GPU.

Some of these algorithms (like the ones of (Gar-

cia et al., 2010) and their improved implementations

(Garcia et al., 2018)) consume a lot of device mem-

ory, since a Cartesian product matrix, containing the

distances of reference points to the query points, is

stored. In this paper, we present alternative algo-

rithms that focus on maximizing the total reference

points stored in the device memory, which could ac-

celerate execution by avoiding the creation of ex-

tra (unnecessary) data chunks and could scale-up to

larger reference datasets.

3 k-NN GPU-BASED

ALGORITHMS

In this section, we present the two new algorithms that

we developed and implemented using this library.

3.1 Thrust Brute-force

The ﬁrst method is based on a “brute force” algorithm

(Fig.1), using the Thrust library (denoted by T-BF).

Brute force algorithms are highly efﬁcient when ex-

ecuted in parallel. The algorithm has two input pa-

rameters, a dataset R consisting of m reference points

R = {r

..r

} in a 3d space and a dataset Q of

In-memory k Nearest Neighbor GPU-based Query Processing

311

Figure 1: Query point (red), k = 5 nearest neighbors (black).

n query points Q = {q

..q

} also in a three-

dimensional space. For every query point q ∈ Q, the

following steps are executed:

1. Calculate all the Euclidean distances between the

query point q and the reference points r E R. Store

the calculated distances in a dataset D consisting

of m distances D = {d

..d

}

2. Sort the distances D dataset

3. Create the KNN dataset K of the k nearest neigh-

bor points

K = {k

..k

}. These points contain the

sorted distances as well as the R dataset indices.

After n repetitions, all the KNN points will be calcu-

lated. Although the BF is perfectly suitable for a GPU

implementation, we noticed that the sorting step is

extremely GPU computationally bound. The CUDA

proﬁler revealed the 90% (or more in large datasets)

of the GPU computation is dedicated to sorting.

3.2 Thrust Distance Reﬁnement

The aforementioned method T-BF is memory efﬁcient

and well-performing but when the reference dataset

is extremely big, the distance sorting step deteriorates

the overall performance. This observation led us to

our next implementation, which radically reﬁnes the

nearest reference points.

The main concept of distance reﬁnement method

(denoted by T-DS) is that we can calculate the num-

ber of reference points by searching in concentric

ranges. We count the reference points of each con-

centric range until the total points counted exceed the

needed k points.

Our ﬁrst approach was to search in concentric

rings of equal width. The width of the ring l is con-

stant and is calculated as k times double the maximum

width of reference points area tmax, divided by the

number of reference points t p.

l = k ∗ 2t ∗ tmax/t p

Experimentation revealed that this approach was only

efﬁcient in dense and uniformly distributed reference

Figure 2: Distance Reﬁnement, query point in red, refer-

ence points in black, k = 10.

points without gaps. When we used synthetic or real

data, the results were the same or only a bit better than

the T-BF method. The problem was that the search

area did not scale quickly enough.

On our second approach, we used a hybrid area

incrementation step. Every two search rings, we dou-

bled the search ring width (Fig.2). This way the

search increment was semi-exponential. The algo-

rithm can scale quickly and produce excellent results

for all kinds of datasets.

By reﬁning the initial dataset, we create a very

small intermediate dataset that contains at least k ref-

erence points. This dataset will be used in the costly

sorting part of the algorithm and will speed up the ex-

ecution time (as we will experimentally show).

The algorithm has two input parameters, a dataset

R consisting of m reference points R = {r

..r

}

in a three-dimensional space and a dataset Q of n

query points Q = {q

..q

} also in a three-

dimensional space. For every query point q ∈ Q, the

following steps are executed:

1. Calculate the starting ring width l

2. Calculate all the Euclidean distances between the

query point q and the reference points r E R. Store

the calculated distances in a dataset D consisting

of m distances D = {d

..d

}

3. While the count of reference points c is less than

equal of k repeat

(a) If repetion%2 = 0, count the distance points

of the area ring between the circles with radius

repetion ∗ l and (repetition + 1) ∗ l

(b) If repetion%2 = 1, count the distance points

GISTAM 2020 - 6th International Conference on Geographical Information Systems Theory, Applications and Management

312

of the area ring between the circles with radius

repetion ∗l and (repetition +1)∗l. Double the

ring width l = 2 ∗ l

4. Reﬁne the distance points of less than or equal

to distance (repetition + 1) ∗ wr and copy them

to dataset DR consisting of c distances DR =

{dr

,dr

..dr

}

5. Sort the distances DR dataset

6. Create the KNN dataset K of the k nearest neigh-

bor points

K = {k

..k

}. These points contain the

sorted distances as well as the R dataset indices.

After n repetitions, all the KNN points will be calcu-

lated. For example in Figure 2, we calculated a dis-

tance reﬁnement of radius 4l resulting to a total of 12

distance points.

4 EXPERIMENTAL STUDY

We run a large set of experiments to compare the

repetitive application of the existing algorithms and

the newly implemented ones for processing batch

KNN queries. All experiments query at least 100K

reference points. We did not include less than 100K

reference points because we target the maximum

in-memory utilization and reference point less than

100K do not ﬁt in this context. The maximum refer-

ence points limit is 200M, which only our algorithm

T-DS achieved.

We have created random and synthetic clustered

datasets of 100.000, 250.000, 500.000 and 1.000.000

points. All the existing methods could only be ex-

ecuted with 100.000 reference points and only one

of them scaled to 1.000.000 points. Furthermore,

in order to check our method scaling we also cre-

ated random datasets of 10.000.000, 100.000.000 and

200.000.000 reference points. We also used three

big real datasets (Eldawy and Mokbel, 2015), which

represent water resources of North America (Water

Dataset) consisting of 5.836.360 line-segments and

world parks or green areas (Parks Dataset) consisting

of 11.503.925 polygons and world buildings (Build-

ings Dataset) consisting of 114.736.539 polygons. To

create sets of points, we used the centers of the line-

segment MBRs from Water and the centroids of poly-

gons from Park and Build. For all datasets the 3-

dimensional data space is normalized to have unit

length (values [0, 1] in each axis).

We run a series of experiments searching for 20

Nearest Neighbors (k = 20), using the aforementioned

datasets with groups of 1,10,100,250,500,750 random

query points. Every experiment was run at least 10

times and the mean of the experiment results were

calculated for every method.

All experiments were performed on a Dell In-

spiron 7577 laptop, running Windows 10 64bit,

equipped with a quad-core (8-thread) Intel I7 CPU,

16GB of main memory, a 256SSD disk used for the

operating system, a 1TB 7.2K SATA-3 Seagate HDD

storing our data and a NVIDIA Geforce 1060 (Mobile

Max-Q) GPU with 6GB of memory.

We run experiments to compare the performance

of batch KNN queries, regarding execution time as

well as memory utilisation. We tested a total of ﬁve

algorithms. Three of them are existing ones and the

other two are the new algorithms we implemented.

The list of algorithms is as follows:

1. BF-Global, Brute Force algorithm using the

Global memory (Garcia et al., 2010)

2. BF-Texture, using the GPU texture memory (Gar-

cia et al., 2018)

3. BF-Cublas, using CUBLAS (BLAS highly opti-

mized linear algebra library) (Garcia et al., 2010)

4. T-BF, Brute Force algorithm using Thrust library

5. T-DS, Distance Reﬁnement algorithm using

Thrust library

4.1 Random Reference Points

In our ﬁrst series of tests, we used random datasets for

the reference points. We created the datasets in vari-

ous volumes using normalized random points. The re-

sulting datasets’ density increased analogously to the

reference points cardinality. The datasets created are

near uniformly distributed.

In the ﬁrst chart (Fig. 3) with one query point,

we can see that our algorithms T-BF and T-DS are

extremely faster than the other methods. For one

query point T-BF ﬁnished in 0,53ms and T-DS in

0,59ms for the 100K reference points experiment.

The best of the other methods was BF-Texture achiev-

ing 39,68ms. It worths mentioning that the 100K ex-

periment was the only one that BF-Texture and BF-

Cublas ﬁnished. These two methods (BF-Texture and

BF-Cublas) could not scale at higher volumes of ref-

erence points, mainly due to execution exceptions re-

garding memory allocation problems. For the 1M ref-

erence points experiment the execution time differ-

ence is much greater, the BF-Global implementation

ﬁnished in 369,18ms while T-BF ﬁnished in 3,61ms

and T-DS in 0.92ms. The maximum speedup gain that

T-DS achieved was 529 (times faster) than BF-Global,

at 750K reference points (Table 1).

In the second chart with 10 query points, we can

observe about the same results as with the one query

In-memory k Nearest Neighbor GPU-based Query Processing

313

Figure 3: Random reference points, k = 20. X-axis: reference point cardinality, Y-axis: execution time measured in ms.

Table 1: Speedup gain of new methods T-BF,T-DS versus

BF-Global, using Random dataset.

Algo- Query Random Reference Points

rithm Points 100K 250K 500K 750K 1M

T-BF 1 117,27 101,69 123,58 122,25 102,41

T-DS 1 104,33 251,95 405,79 529,63 401,72

T-BF 10 15,36 11,62 11,98 13,82 10,47

T-DS 10 12,88 26,07 41,74 48,79 45,64

T-BF 100 1,80 1,24 1,40 1,38 1,15

T-DS 100 1,46 3,03 4,26 5,21 4,86

T-BF 250 0,86 0,54 0,59 0,63 0,71

T-DS 250 0,69 1,33 1,94 2,39 2,93

experiment. At 100K reference points, the best of

existing algorithms was again BF-Texture, ﬁnishing

at 40ms, while T-BF ﬁnished at 4.29ms and T-DS

at 5.11ms. For the 1M reference points experiment

the execution time difference is again much greater,

the BF-Global implementation ﬁnished in 377,91ms

while T-BF ﬁnished in 36.11ms and T-DS in 8.28ms.

T-DS was 45 times faster than BF-Global.

When reaching the group of 100 query points, we

can see that the execution time of T-BF is a slightly

better than the BF-Global. The overhead of sorting

large volumes of distance datasets begin to emerge.

The T-DS on the other hand continued its excellent

performance, ﬁnishing in 81.8ms at 1M reference

points, while BF-Global ﬁnished in 397.42ms.

In the following experiments, using groups of

250,500 and 700 query points, T-BF performance was

inferior compared to BF-Global. The T-DS algorithm

kept on outperforming the other ones, especially on

the large volumes of reference points.

In order to explore the limits of the algorithms,

we created random datasets ranging from 10M to

200M reference points (Fig. 4). The existing al-

gorithms could not scale higher than 1M reference

points. The T-BF reached 100M reference points.

The only algorithm that succeeded in 200M reference

points is T-DS. T-BF using one query point, executed

in 10M reference points in 28.96ms and T-DS in just

4.07ms. The T-DS ﬁnished in the 200M reference

points experiment in 61.93ms. The 10 points query

group, resulted analogously in 291.93ms for T-BF and

37.08ms for T-DS. All the other experiments resulted

to close linear performance, in respect to query points

groups. The T-DS implementation executed 10 times

faster than the T-BF one, in extremely large volumes

of reference datasets.

In terms of memory scaling the new algorithm T-

DS can compute up to 200M reference points. The

maximum reference points that other methods could

achieve are 1M reference points, thus our methods

can scale up to 200 times more than the other ones.

It worths mentioning that T-DS is much faster than

T-BF, because of the sorting overhead of T-BF.

GISTAM 2020 - 6th International Conference on Geographical Information Systems Theory, Applications and Management

314

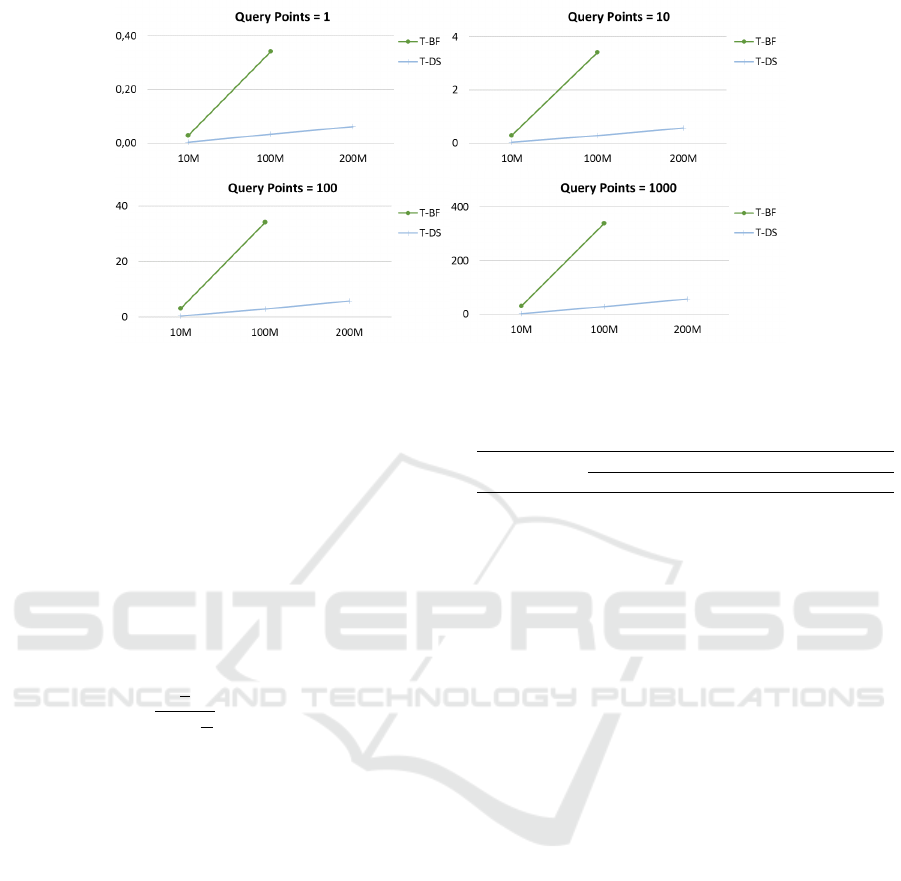
Figure 4: Maximum reference points, k = 20. X-axis: reference point cardinality, Y-axis: execution time measured in ms.

4.2 Synthetic Reference Points

We have also used synthetic datasets following dif-

ferent data distributions, and each data set contains

100.000, 250.000, 500.000, 750.000 and 1.000.000

points (Fig. 5). We have created these datasets be-

cause they are not uniformly distributed, like the ran-

dom ones and they resemble real-life data distribu-

tions. The synthetic reference points datasets are cre-

ated according to Zipf’s law. The Zipf distribution is

deﬁned as follows, and the value of z that we have

used is 0.7.

f (i) =

∑

j=1

,i = 1,2,· ·· ,n

The random experiment results are conﬁrmed in this

experiment. In the one query point experiment,

in ascending order, T-BF ﬁnished in 0.48ms, T-DS

in 0.65ms, BF-Texture in 49,76ms, BF-Global in

62.04ms and BF-Cublas in 74.41ms, for the 100K

reference dataset. The 1M experiment resulted to T-

DS 2.18ms, T-BF 3.56ms and BF-Global 367.57ms.

The maximum speedup gain that T-DS achieved was

270 (times faster) than BF-Global, at 750K reference

points (Table 2).

The 10 query point experiment resulted to a sim-

ilar outcome. The T-DS again was faster and out-

performed BF-Global by 25 times. When the query

points reached up to 100, we noticed that the perfor-

mance of T-BF is similar and slightly better than BF-

Global. On the other hand T-DS is still performing

good, especially for ≥ 500K reference points. Finally

in the 250 query points experiment, BF-Global sur-

passes T-BF, but is still slower than T-DS algorithm.

For one more time, T-DS is much faster than T-BF,

because of the sorting advantage reduction, as docu-

mented in the previous section.

Table 2: Speedup gain of new methods T-BF,T-DS versus

BF-Global, using Synthetic dataset.

Algo- Query Synthetic Reference Points

rithm Points 100K 250K 500K 750K 1M

T-BF 1 128,45 89,87 101,04 118,75 103,25

T-DS 1 94,57 134,70 196,90 270,53 168,76

T-BF 10 15,64 9,02 9,52 13,22 10,86

T-DS 10 10,34 11,56 20,48 25,04 24,58

T-BF 100 1,82 1,06 1,02 1,44 1,10

T-DS 100 1,20 1,21 1,94 3,65 2,54

T-BF 250 0,82 0,58 0,64 0,68 0,70

T-DS 250 0,54 0,66 1,25 1,44 1,74

4.3 Real Reference Points Comparison

We conducted 6 experiments using three different real

datasets using groups of query points of 10 and 100

points (Fig. 6). In order to compare all the algorithms

we created two reference datasets of 100K and 1M

points per every real dataset, by reducing them (the

real datasets) uniformly.

The only experiment that all the algorithms com-

pleted, is the one with 100K reference points. The

BF-Texture and BF-Cublas algorithm failed in all

subsequent experiments. The fastest algorithm in the

100K case was T-BF, ﬁnishing in 4.53ms (Water),

4.38ms (Parks) and 4.36ms (Buildings), while query-

ing 10 points and 43.78ms (Water), 43.99ms (Parks)

and 41.1ms (Buildings) while querying 100 points. In

the case of 1M reference points the T-DS was slightly

faster than T-BF. When we queried the hole datasets

the T-DS was about 2 times faster than T-BF.

The maximum speedup gain that T-DS achieved

was 391 (times faster) than BF-Global, at 1M water

reference points, using one query point (Table 3). Fur-

thermore, in the real dataset example, we certify once

more that T-DS is much faster than T-BF, because of

the sorting advantage.

In-memory k Nearest Neighbor GPU-based Query Processing

315

Figure 5: Synthetic reference points, k = 20. X-axis: reference point cardinality, Y-axis: execution time measured in ms.

Figure 6: Real reference points, k = 20. X-axis: reference point cardinality, Y-axis: execution time measured in ms.

Table 3: Speedup gain of new methods T-BF,T-DS versus BF-Global, using Real datasets.

Water Ref. Points Parks Ref. Points Buildings Ref. Points

Algorithm Query Points 100K 1M 100K 1M 100K 1M

T-BF 1 120,98 135,49 128,43 131,26 119,25 136,10

T-DS 1 38,31 391,19 74,74 102,16 78,85 352,03

T-BF 10 16,71 14,55 22,33 14,54 23,81 15,64

T-DS 10 5,55 15,73 11,07 16,95 10,97 32,28

T-BF 100 2,72 1,84 2,52 1,71 4,00 1,98

T-DS 100 1,14 1,81 1,53 2,31 2,19 3,22

T-BF 250 1,51 1,02 1,37 0,76 1,50 0,89

T-DS 250 0,61 1,08 0,79 1,04 0,80 1,47

GISTAM 2020 - 6th International Conference on Geographical Information Systems Theory, Applications and Management

316

5 CONCLUSIONS AND FUTURE

PLANS

In this paper, we presented new algorithms for k-NN

query processing in GPUs. These algorithms maxi-

mize the utilization of device memory, handling more

reference points in the computation. Through an ex-

perimental evaluation on synthetic and real datasets,

we concluded that these algorithms, not only work

faster than existing methods for small groups of query

points, but also scale-up to much larger reference

datasets. Moreover we validated that T-DS algorithm

is faster than T-BS, because of the extra reﬁnement

step minimizing the sorting overhead.

Future work plans include:

• Comparison of our algorithms to other algorithms

in the literature, regarding execution time and

scaling-up within the available device memory,

• Combination of GPU-based algorithms to data

stored in SSDs, using smart transferring of

data between the SSD, RAM and device mem-

ory (Roumelis et al., 2016) (without indexes),

(Roumelis et al., 2019) (using indexes),

• Testing the effectiveness of our algorithms on data

from other application domains, e.g. ﬁnancial

data (Cheng et al., 2019),

• Implementation of queries (like K-closest pairs),

based techniques utilized in this paper.

ACKNOWLEDGEMENTS

This research has been co-ﬁnanced by the European

Regional Development Fund of the European Union

and Greek national funds through the Operational

Program Competitiveness, Entrepreneurship and In-

novation, under the call RESEARCH – CREATE –

INNOVATE (project code:T1EDK-02161).

REFERENCES

Areﬁn, A. S., Riveros, C., Berretta, R., and Moscato, P.

(2012). Gpu-fs-knn: A software tool for fast and scal-

able knn computation using gpus. PloS ONE, 7(8):1–

13.

Barlas, G. (2014). Multicore and GPU Programming: An

Integrated Approach. Morgan Kaufmann, 1 edition.

Barrientos, R. J., G

omez, J. I., Tenllado, C., Prieto-Mat

ıas,

M., and Mar

ın, M. (2011). knn query processing in

metric spaces using gpus. In Euro-Par Conf., pages

380–392.

Barrientos, R. J., Millaguir, F., S

anchez, J. L., and Arias,

E. (2017). Gpu-based exhaustive algorithms process-

ing knn queries. The Journal of Supercomputing,

73(10):4611–4634.

Chen, H., Yang, B., Wang, G., Liu, J., Xu, X., Wang, S.,

and Liu, D. (2011). A novel bankruptcy prediction

model based on an adaptive fuzzy k-nearest neighbor

method. Knowl. Based Syst., 24(8):1348–1359.

Cheng, C., Chan, C., and Sheu, Y. (2019). A novel purity-

based k nearest neighbors imputation method and its

application in ﬁnancial distress prediction. Eng. Appl.

Artif. Intell., 81:283–299.

Eldawy, A. and Mokbel, M. F. (2015). Spatialhadoop: A

mapreduce framework for spatial data. In ICDE Conf.,

pages 1352–1363.

Garcia, V., Debreuve, E., Nielsen, F., and Barlaud, M.

(2010). K-nearest neighbor search: Fast gpu-based

implementations and application to high-dimensional

feature matching. In ICIP Conf., pages 3757–3760.

Garcia, V.,

Eric Debreuve, and Barlaud, M. (2018). Fast k

nearest neighbor search using gpu.

Guti

errez, P. D., Lastra, M., Bacardit, J., Ben

ıtez, J. M.,

and Herrera, F. (2016). Gpu-sme-knn: Scalable and

memory efﬁcient knn and lazy learning using gpus.

Inf. Sci., 373:165–182.

Kato, K. and Hosino, T. (2012). Multi-gpu algorithm for

k-nearest neighbor problem. Concurrency and Com-

putation: Practice and Experience, 24(1):45–53.

Komarov, I., Dashti, A., and D’Souza, R. M. (2014). Fast

k-nng construction with gpu-based quick multi-select.

PloS ONE, 9(5):1–9.

Kuang, Q. and Zhao, L. (2009). A practical gpu based knn

algorithm. In SCSCT Conf., pages 151–155.

Li, S. and Amenta, N. (2015). Brute-force k-nearest neigh-

bors search on the GPU. In SISAP Conf., pages 259–

270.

Liang, S., Wang, C., Liu, Y., and Jian, L. (2009). Cuknn:

A parallel implementation of k-nearest neighbor on

cuda-enabled gpu. In YC-ICT Conf., pages 415–418.

Masek, J., Burget, R., Karasek, J., Uher, V., and Dutta,

M. K. (2015). Multi-gpu implementation of k-nearest

neighbor algorithm. In TSP Conf., pages 764–767.

NVIDIA (2020). Nvidia cuda runtime api.

Roumelis, G., Corral, A., Vassilakopoulos, M., and

Manolopoulos, Y. (2016). New plane-sweep al-

gorithms for distance-based join queries in spatial

databases. GeoInformatica, 20(4):571–628.

Roumelis, G., Velentzas, P., Vassilakopoulos, M., Corral,

A., Fevgas, A., and Manolopoulos, Y. (2019). Parallel

processing of spatial batch-queries using xbr

-trees in

solid-state drives. Cluster Computing.

Singh, A., Deep, K., and Grover, P. (2017). A novel ap-

proach to accelerate calibration process of a k-nearest

neighbours classiﬁer using GPU. J. Parallel Distrib.

Comput., 104:114–129.

Sismanis, N., Pitsianis, N., and Sun, X. (2012). Parallel

search of k-nearest neighbors with synchronous oper-

ations. In HPEC Conf., pages 1–6.

In-memory k Nearest Neighbor GPU-based Query Processing

317