
Numerical Study of the Axial and Radial Forces,
the Stresses and the Strains in a High Pressure
Multistage Centrifugal Pump
Mohand-Amokrane Abdelouahab
1
, Guyh Dituba Ngoma
1
, Fouad Erchiqui
1
and Python Kabeya
2
1
University of Quebec in Abitibi-Témiscamingue, School of Engineering’s Department,
445, Boulevard de l’Université, Rouyn-Noranda, Quebec, J9X 5E4, Canada
2
University of Kinshasa, Department of Mechanical Engineering, Kinshasa, Democratic Republic of the Congo
Keywords: Multistage Centrifugal Pump, Axial and Radial Forces, Stress, Strain, CFX, Static Structural Analysis.
Abstract: This paper deals with the numerical study of the axial and radial forces, the stresses and the strains induced
by a liquid flow in a high pressure multistage centrifugal pump to improve their performances account for the
material of the shaft and the impellers. Indeed, a model of a 4-stage centrifugal pump is developed considering
a design point. The continuity and the Navier-Stokes equations are used for the liquid flow through the pump.
Additionally, the equations of the stresses and the strains are applied for the shaft and the impellers. The
obtained system of equations is solved by means of the CFX-code and the static structural analysis to
determinate the fields of velocity and pressure, the axial and radial forces, the stress and the strain on the
pump shaft. Moreover, numerical simulations are carried out to analyze the shaft behavior in terms of the
induced axial and radial forces, the stresses and the strains. The diffuser in the last pump stage is used as
parameter. Good trends are achieved comparing the obtained results with these found in the literature and
these calculated using the classical equations of the stresses and the strains.
1 INTRODUCTION
The growing technological development in the field
of liquid transportation in the mining sector is leading
pump manufacturers to design and develop high
pressure multistage centrifugal pumps that are
continually adapted to the industrial needs. Its
operation and its adequate life expectancy greatly
depend on the design and manufacture of its
components, such as, inter alia, the shaft, the
bearings, the impellers and the diffusers.
To better design and optimize the pump shaft and
the bearings of the multistage centrifugal pumps, the
axial and the radial forces acting on the impellers
must be known with accuracy to determinate the
bearing loads, the shafts stresses and the shaft
deflection accounting for the entire flow range. This
allows to avoid, mainly, the excessive bending of the
pump shaft, too high stresses on the pump shaft, and
the overloading of the axial and radial bearings. In
fact, several theoretical and experimental research
works have been done on the multistage centrifugal
pumps in the terms of the axial and radial forces, the
stresses and the strains acting on the pump shaft
(Karassik and McGuire, 1998; Gülich, 2010; Wang et
al., 2013; Watanabe, 2019; Gantar et al., 2002;
Bolade and Madki, 2015; TM.P. S.p.A.
Termomeccanica Pompe, 2003; Karassik et al., 2008;
Wang et al., 2014; and Suke et al., 2015).
In most previous study on the multistage
centrifugal pumps, the effects of the induced axial and
radial loads, the stresses and the strains accounting for
the diffuser return vanes and the diffuser in the last
pump stage in relation to the pump head, the brake
horsepower and the efficiency have been less
investigated (
Jino, T., 1980). Since the pump
performances of the multistage centrifugal pumps
depend, among other things, on the design of the
diffuser including the return vanes (Miyano et al.,
2008; and La Roche-Carrier et al., 2013), this is
essential to consider also the impact of the diffuser on
the axial and radial forces, the stresses and the strains
on the pump shaft.
Therefore, this research is focused to the
development of reliable and accurate numerical
models of a high pressure multistage centrifugal
Abdelouahab, M., Ngoma, G., Erchiqui, F. and Kabeya, P.
Numerical Study of the Axial and Radial Forces, the Stresses and the Strains in a High Pressure Multistage Centrifugal Pump.
DOI: 10.5220/0009783001810188
In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2020), pages 181-188
ISBN: 978-989-758-444-2
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

pump in order to study in-depth the axial and radial
forces, the stresses and the strains on the pump shaft
due to the liquid flow through the pump at varying
operating conditions using the 4-stage centrifugal
pump and the diffuser in the last pump stage as
parameter in relation to the pump performances.
The achieved results using two diffuser types for
the pump head, the brake horsepower and the
efficiency are compared. Furthermore, considering
the first pump stage, a good trend is obtained
validating the numerical results for the stresses on the
pump shaft from the determined axial and radial
forces by means of the classical equations of the
strength of materials and the mechanical design of
machine elements.
2 MODEL DESCRIPTION
Fig. 1 illustrates the components of the reference 4-
stage centrifugal pump considered in this study. It is
mainly composed of a shaft, four impellers and four
diffusers. The solid and fluid models of the 4-stage
centrifugal are shown in Fig. 2.
a) Shaft, impellers and diffuser with return vanes of type 1.
b) Pump stages: impeller and diffuser combined.
Figure 1: Components of a 4-stage centrifugal pump
(School of Engineering’s Department, Turbomachinery
laboratory, E-216, www.uqat.ca).
a) Solid model
b) Fluid model
Figure 2: 4-stage centrifugal pump models (Abdelouahab
M.-A., 2018).
Furthermore, relating to the pump diffuser, there are
some multistage centrifugal pumps that use another
type of the diffuser (La Roche-Carrier et al., 2013) as
indicated in Fig. 3. The performance comparison of
both diffuser types are done in this work.
a) Technosub Inc., www.technosub.net.
b) Diffuser solid model.
Figure 3: Diffuser with return vanes of type 2.
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
182

3 GOVERNING EQUATIONS
To determinate the fields of liquid flow velocity
and pressure in a multistage centrifugal pump, the
following hypotheses are considered (La Roche-
Carrier et al., 2013): (a) a steady state, three-
dimensional and turbulence flow using the k-
model is assumed; (b) the liquid is an
incompressible liquid; (c) it is a newtonian liquid;
and (d) the liquid’s thermophysical properties are
constant with the temperature.
Additionally, for the equations that govern the
solid mechanics for the calculation of the stresses
and the strains in the multistage centrifugal pump,
the applied assumptions are formulated as follows
(
Popov, 1999)
: (i) the material is considered
continuous, doesn't have cracks, nor cavities; (ii)
the material is homogeneous and presents the same
properties in all points; (iii) the material is
considered as isotropic; and (iv) no internal force
acts in the material before the application of the
external loads.
3.1 Liquid Flow Velocity and Pressure
The fields of liquid flow velocity and pressure are
found resolving the equations of the continuity and
the Navier-Stokes accounting for the corresponding
assumptions and using the ANSYS CFX-code
(
ANSYS inc.), based on the finite volume method (
La
Roche-Carrier et al., 2013)
. The boundary
conditions are formulated as follows: the static
pressure is given at the pump inlet, while the flow rate
is specified at the pump outlet. The frozen rotor
condition is used for the impeller-diffuser interface
per pump stage. A no-slip condition is set for the flow
at the wall boundaries.
Applying the coordinate system, the equations of
the continuity are given by:
0
z
w
y
v
x
u
(1)
where u(x,y,z), v(x,y,z) et w(x,y,z) are components of
the liquid flow velocity in the direction x, y and z.
Moreover, the equations of the Navier-Stokes are
expressed by:
222
222
2
222
222
( 2 )
eff
zx z
eff
uu u uuu
uvw
xy z
xyz
p
rv
x
vv v vvv
uvw
xy z
xyz
2
222
222
( 2 )
zy z
eff
p
ru
y
ww w www
uvw
xy z
xyz
p
z
(2)
where p is the pressure; is the density;
eff
is the
effective viscosity accounting for turbulence, it is
defined as
teff
. is the dynamic viscosity and
t
is the turbulence viscosity. It is linked to turbulence
kinetic energy k and dissipation ε.
The k- turbulence model is used in this work due
to the better convergence than with other turbulence
models.
To determinate the performance parameters of the
multistage centrifugal pump, the pump head is
described as H = (p
to
– p
ti
) / g, where p
ti
is the total
pressure at the pump inlet and p
to
the total pressure at
the pump outlet. The hydraulic power of the pump is
formulated as P
h
= QgH, where Q is the flow rate.
Moreover, the brake horsepower of the pump is given
by P
s
= T, where T is the impeller torque and is
the angular velocity. From the hydraulic power and
the brake horsepower, the efficiency of the pump can
be expressed as = P
h
/ P
s
.
3.2
Axial and Radial Forces
The axial forces is the result of unbalanced impeller
forces acting in the shaft axial direction. It is
composed of the force on the impeller’s front shroud
and hub shroud due to the static pressures on the
surface areas of the shrouds, and the momentum force
due to the change in direction of the liquid flow
through the impeller.
Furthermore, the radial force on the impeller
results from a non-uniform distribution of pressure on
the circumference of the impeller. The non-uniform
pressure distribution can be caused by: the
geometrical form of the diffuser for the multistage
centrifugal pumps; the non-symmetrical impeller
inflow; or the pump operating regime. It is to
highlight that the radial force depends on the time. Its
components are the static radial force and the
dynamic radial force. Generally, the static radial force
is greater than the dynamic radial force (Karassik and
McGuire, 1998; Gülich, 2010; Wang et al., 2013;
Numerical Study of the Axial and Radial Forces, the Stresses and the Strains in a High Pressure Multistage Centrifugal Pump
183

Watanabe, 2019; Gantar et al., 2002; Bolade and
Madki, 2015;TM.P. S.p.A. Termomeccanica Pompe,
2003; Karassik et al., 2008;
Jino, T., 1980; Abdelouahab
M.-A.,2018).
In this research, the axial and radial forces due to
the liquid flow through the multistage centrifugal
pump are determined using the ANSYS CFX-code.
3.3
Stress and Strains
The fundamental principles of the strength of
materials are accounted for the resolution of the
solid mechanics equations (
Popov, 1999
): the
superposition principle and the Saint-Venant
principle. The method of resolution of the
structural problems in the solid mechanics consists
of three steps: (i) the force analysis forces and the
equilibrium conditions; (2) the study of the
displacements and the geometric accounting; and
(iii) the application of the relations of forces and
displacements.
Neglecting the forces per unit of volume, the
equilibrium equations of elasticity in terms of three
normal and three shear stress components are
expressed by:
0
0
0
yx
xzx
xy y zy
yz
xz
z
xyz
xyz
xyz
(3)
Furthermore, the principal stresses, designed as
1
,
2
and
3
, are calculated from the
x
,
y
,
z
,
xy
,
xz
and
yz
. They are the invariants. Its values do not
depend on the orientation of the part with respect to
the xyz coordinate system. It is to highlight that the
principal stresses are available as individual result.
They are ordered such that
1
>
2
>
3
. These can be
given by:
1
1.5
2
22
10 3
1
1.5
2
22
20 3
1
1.5
2
22
30 3
1
2 cos arccos 0.5
33 3
1
2 cos arccos 0.5
33 3 3
1
2 cos arccos 0.5
33 3
JJ
J
JJ
J
JJ
J
3
(4)
where
0
222
2
222
3
000
1
3
; ;
xyz
xy yz zx xy yz zx
x y z x yz y zx z xy
xx yy zz
Jssssss
Jssssss
sss
(5)
Moreover, concerning the normal strains (
x
,
y
and
z
) and the shear strains (
xy
,
yz
and
zx
), they
can be written as:
; ;
; ;
xyz
xy yz zx
uvw
xzz
uu wv uw
x
yyzzx
(6)
where u, v and w are the displacements respectively
in the directions of x, y and z.
In addition, for the relationships between the
stresses and the strains, the generalized Hook’s law
for isotropic materials is used:
1
()
1
()
1
()
; ;
xxyz
yyzx
zzxy
xy yz
zx
xy yz zx
E
E
E
GGG
(7)
where E is the modulus of elasticity, G is the shear
modulus and is the Poisson’s ratio.
Inversely, the stresses can be expressed by:
(1 ) ( )
(1 )(1 2 )
(1 ) ( )
(1 )(1 2 )
(1 ) ( )
(1 )(1 2 )
; ;
xxyz
yyzx
zzxy
xy xy yz yz zx zx
E
E
E
GGG
(8)
The stress according to von Mises is selected for
the yield criteria. This stress is written as follows:
222
12 23 31
1
2
(9)
For the calculation of the stresses and strains,
the ANSYS-code for the structural static analysis
is used.
4 RESULTS AND DISCUSSION
Two cases are selected for examination of the shaft
behavior of a multistage centrifugal pump with
particular emphasis on the axial and radial forces, the
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
184

stresses and the strains due to the liquid flow through
the pump. The impact of the diffuser in the last pump
stage on the shaft is analyzed in different operating
conditions in terms of the flow rates.
Tabs. 1-4 indicate the reference data used for the
impeller, the diffuser and the shaft. The rotation speed
of the shaft is 1800 rpm and the flow rate range is
from 300 m³/h to 900 m³/h.
Table 1: Reference data of the impeller.
Inlet blade height b
1
[mm] 56
Outlet blade hei
g
ht b
2
[mm] 44,25
Hub diameter D
h1
[mm] 84,84
Inlet diameter D
h2
[mm] 194,95
Outlet diameter D
2
[mm] 401,3
Inlet blade angle β
b1
[°] 18
Outlet blade angle β
b2
[°] 22,5
Blade thickness e [mm] 7,94
Blade number Z
b
6
Table 2: Reference data of the diffuser (front side).
Inlet blade height b
3
[mm] 41,98
Outlet blade height b
4
[mm] 68,4
Inlet diameter D
3
[mm] 401,3
Outlet diameter D
4
[mm] 459
Inlet blade angle α
3b
[°] 16,44
Blade thickness e
3
[mm] 6,04
Blade numbe
r
Z
Le
11
Table 3: Reference data of the diffuser (rear side).
Return vane number Z
R
11
Outlet return vane height b
5
[mm]
24,4
Diameter at the inlet of the return
vane D
3
[mm]
459
Blade angle at the inlet of the
return vane α
5
[°]
17,04
Blade angle at the outlet of the
return vane α
6
[°]
93,84
Blade thickness of the return vane
e
3
[mm]
6,04
Table 4: Reference data of the shaft.
Length L [mm]
1000
Diameter d [mm] 71,12
Furthermore, the properties of the standard steel
and the water considered are indicated in Tabs. 5 and
6.
Table 5: Properties of the standard steel.
Module of the Young [Pa] 2x10
11
Poisson ratio 0,3
Com
p
ressibilit
y
module [Pa] 1,6667x10
11
Shear module [Pa] 7,6923x10
11
Resistance coefficient [Pa] 9,2x10
8
Ductility coefficient [Pa] 10
9
Yield stren
g
th [Pa] 2,5x10
8
Ultimate tensile stren
g
th [Pa] 4,6x10
8
Densit
y
[k
g
/m
3
] 7850
Table 6: Properties of water in 25 °C.
Density
[kg/m
3
]
Thermal
expansion
coefficient [
K
-1
]
Kinematic
viscosity
[m
2
/s]
997 2,57x10
-1
0,884x10
-6
4.1 Case Study
4.1.1 Effect of the Flow Rate
To analyze the effect of the flow rate on the radial
forces, the stresses and the strains on the shaft of the
4-stage centrifugal pump, the flow rate from 300 m³/h
to 900 m³/h are selected keeping the reference data as
constant.
Figs. 4-9 show the pump head, the brake
horsepower, the efficiency, the radial force, the stress
and the strain as a function of the flow rate. From
these figures, it is observed that the radial force
decreases and increases with growing flow rate. It is
the lowest in the best efficiency point (BEP) or in the
best efficiency zone, as indicated in Fig. 4. This can
be explain by the fact that the impeller is designed for
constant velocity near the best efficiency flow rate,
which yields an uniform static pressure around the
periphery of the impeller, at this flow rate. However,
as the flow rate moves away from the BEP, the
pressure distribution around the impeller changes,
resulting in high radial loads on the pump bearings.
Relating to the stress on the pump shaft, it
decreases, then it increases with rising flow rate. The
strain follows the same trend as the stress. At the low
flow rate and the high flow rate, the radial load on the
pump shaft is greater, this can lead to important stress
and the strain on the pump shaft. Thus, Figs. 4-9 are
relevant to better understanding the relationship
between the pump performances and the radial forces,
the stresses and the strains on the pump shat.
Numerical Study of the Axial and Radial Forces, the Stresses and the Strains in a High Pressure Multistage Centrifugal Pump
185

Figure 4: Head, stress, and radial force versus flow rate.
Figure 5: Brake horsepower, stress, and radial force versus
flow rate.
Figure 6: Efficiency, stress, and radial force versus flow
rate.
Figure 7: Head, strain, and radial force versus flow rate.
Figure 8: Brake horsepower, strain, and radial force versus
flow rate.
Figure 9: efficiency, strain, and radial force versus flow
rate.
4.1.2 Effect of the Diffuser in the Last Pump
Stage
To analyze the effect of the diffuser in the last pump
stage on the axial and radial forces on the shaft, two
models of the 4-stage centrifugal pump are selected
whose one having a diffuser in the last pump stage.
The reference data are kept as constant. Figs. 10-
14 present the pump head, the brake horsepower, the
efficiency, and the axial force and radial forces as a
function of the flow rate.
Fig. 10 indicates that the pump head with a
diffuser in the last pump stage is greater than the
without diffuser case. This can be explained by the
fact that a diffuser provides greater static pressure.
Moreover, it can be observed in Fig. 11 that the brake
horsepower for both cases is practically identical,
whereas the efficiency for the case of the last pump
stage with the diffuser is relatively higher than the
without diffuser case as shown in Fig. 12.
Relating to the axial force, it can be seen that the
use of the last pump stage without diffuser leads to
the greater axial force as illustrated in Fig. 13. In
addition, Fig. 14 presents the fact that the radial force
for the case of the last pump stage with the diffuser is
higher than the without diffuser case from 300 m³/h
to about 460 m³/h, whereas the radial force for the
case with the diffuser is lower than the without
diffuser case for the flow rate more than 460 m³/h.
Thus, the in-depth knowledge of the resulting
axial and radial forces acting on the shaft impellers of
the multistage centrifugal pump is essential to better
design and to optimize the shat bearings accounting
for the last pump stage configuration.
Figure 10: Head versus flow rate.
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
186
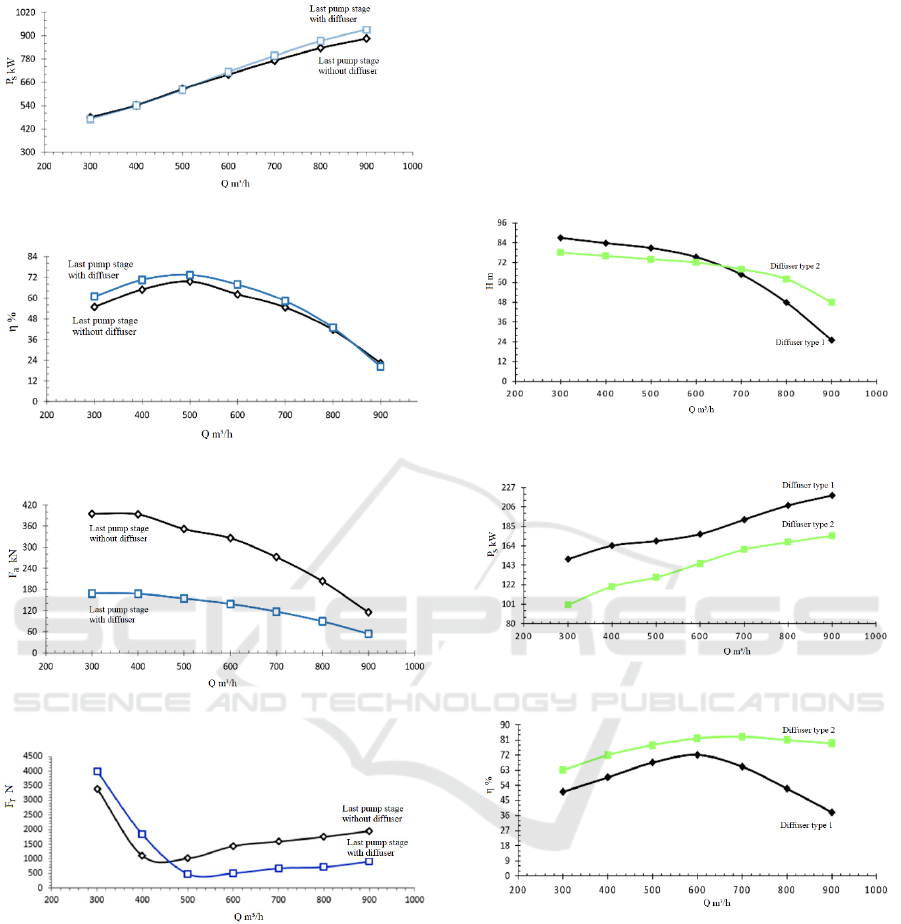
Figure 11: Brake horsepower versus flow rate.
Figure 12: Efficiency versus flow rate.
Figure 13: Axial force versus flow rate.
Figure 14: Radial force versus flow rate.
4.2 Comparison of the Results
4.2.1 Pump Performances According to the
Diffuser Type
The results of the pump head, the brake horsepower
and the efficiency relating to the diffuser of type 1 in
Fig. 1 are compared with the obtained results using
the diffuser of type 2 in Fig. 3.
Fig. 15 shows that the head achieved of the
diffuser in Fig. 1 is higher than that obtained with the
diffuser in Fig. 2 for the flow rate from 300 m³/h to
about 660 m³/h. Furthermore, Fig. 16 indicates that
the brake horsepower for the flow rate from 300 m³/h
to 900 m³/h for the diffuser in Fig. 1 are the highest.
In addition, the efficiency for the diffuser in Fig.
2 is better as depicted in Fig. 17. This comparison is
relevant to illustrate that the performances of a
multistage centrifugal pump can depend, inter alia, on
the used diffuser type.
Figure 15: Head versus flow rate.
Figure 16: Brake horsepower versus flow rate.
Figure 17: Efficiency versus flow rate.
4.2.2 Stress Results
The results of numerical simulations for the stresses
in this study are compared with the results for the
stresses using the classical equation for the first pump
stage. While confronting the curves in Fig. 18, the
trend of the classical and the numerical results are
similar. The gaps between the curves can be justified
by the different hypotheses used in terms of classical
calculations and numerical simulations.
Numerical Study of the Axial and Radial Forces, the Stresses and the Strains in a High Pressure Multistage Centrifugal Pump
187
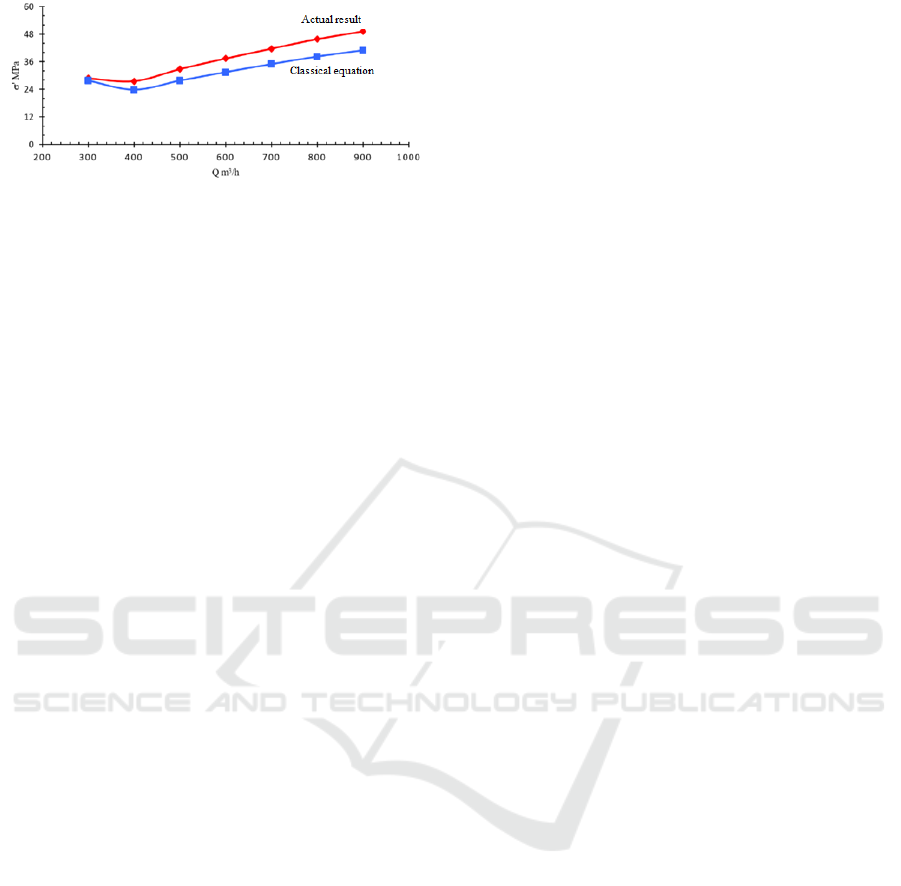
Figure 18: Stress versus flow rate.
5 CONCLUSION
This study focused on the numerical investigation of
the axial and radial forces, the stresses and the strains
on the shaft of a multistage centrifugal pump due to
the liquid flow through this pump. The continuity and
the Navier-Stokes equations are used for the liquid
flow in the pump. Moreover, the equations of the
stresses and the strains are applied for the shaft and
the impellers. The ANSYS CFX-code and the static
structural analysis code are used to determinate,
respectively, the fields of velocity and pressure for the
liquid flow, and the axial and radial forces, the
stresses and the strains for the shaft. Numerical
simulations are accomplished to examine the shaft
behavior in terms of the axial and radial forces acting
in the impellers, the stresses and the strains on the
shaft. For these simulations, inter alia, the diffuser in
the last pump stage is considered as parameter. This
is to find a relevant relationship between the pump
performances, the axial and radial loads, the stresses
and the strain on the shaft. The numerical results for
the pump performances using two diffuser types are
compared. In addition, the obtained numerical results
for the stresses on the shaft are validated considering
the first pump stage by means of the results found
applying the classical equations.
ACKNOWLEDGMENTS
The authors are grateful to the Technosub Inc.,
Industrial pumps manufacturing and distribution
(Rouyn-Noranda, Quebec, Canada).
REFERENCES
Karassik, I. J., McGuire, T., 1998. Centrifugal Pumps.
Springer-Verlag US.
Gülich, J. F., 2010. Centrifugal Pumps, second Edition,
Springer.
Wang C., Shi, W. and Zhang, L., 2013. Calculation
Formula Optimization and Effect of Ring Clearance on
Axial Force of Multistage Pump. Hindawi Publishing
Corporation, Mathematical Problems in Engineering,
Vol. 2013, Article ID 749375.
Watanabe, H., 2019. Prediction of flow phenomena,
performance and thrust forces of three-stage pump by
using URANS. IOP Conf. Series: Earth and
Environmental Science 240.
Gantar M., Florjancic D., and Sirok B., 2002. Hydraulic
Axial Thrust in Multistage Pumps - Origins and
Solutions. Journal Fluids Engineering, Vol. 124, Issue
2, 336-341, 6 pages.
Bolade, P. S., Madki, S. J., 2015. Analysis of Hydraulic
Thrusts in Centrifugal Pump to Increase the Bearing
Life. International Journal of Engineering Research &
Technology. ISSN: 2278-0181, Vol. 4 Issue 08.
TM.P. S.p.A. Termomeccanica Pompe, 2003.
TERMOMECCANICA Centrifugal pump handbook, La
Spezia – Italy.
Karassik, I. J., Messina, J. P., Cooper, P., Heald, C. C.,
2008. Pump Handbook. Fourth edition McGRAW-
HILL.
Wang, C., Shi, W., Si, Q., Zhou, L., 2014. Numerical
calculation and finite element calculation on impeller of
stainless steel multistage centrifugal pump. Journal of
Vibroengineering, Vol. 16, Issue 4, p. 1723-1734.
Suke, A. C., Londhe, B. P., Verma, A. B., 2015. Shaft
deflection Analysis of Multistage centrifugal Pump by
Finite element Method. International Journal of
Science, Engineering and Technology Research, Vol. 4,
Issue 7.
Jino, T., 1980. Hydraulic axial thrust in multistage
centrifugal pumps. Journal of Fluids Engineering,
Volume 102, Issue 1, 6 pages.
Miyano, M., Kanemoto, V, Kawashima, D., Wada, A.,
Hara, T., and K. Sakoda, K., 2008. Return vane
installed in multistage centrifugal pump. International
Journal of Fluid Machinery and Systems, vol. 1, no. 1,
pp. 57–63.
La Roche-Carrier N., Dituba Ngoma G., and Ghie W.,
2013. Numerical investigation of a first stage of a
multistage centrifugal pump: impeller, diffuser with
return vanes, and casing. ISRN Mechanical
Engineering, Vol. 2013, Article ID 578072, 15 pages.
School of Engineering’s Department, Turbomachinery
laboratory (E-216), University of Quebec in Abitibi-
Témiscamingue (UQAT), www.uqat.ca.
Abdelouahab M.-A., 2018. Étude des contraintes,
vibrations, poussées axiales et radiales induites par des
écoulements des liquides complexes dans une pompe
centrifuge multi-étage à grande pression et puissance.
Mémoire de mâitrise, Université du Québec en Abitibi-
Témiscamingue.
Popov E. P., 1999. Engineering Mechanics of Solids, 2nd
edition, Prentice Hall.
Technosub Inc., www.technosub.net.
ANSYS inc., www.ansys.com.
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
188
