
A Distributed Checkpoint Mechanism for Replicated State Machines
Niyazi
¨
Ozdinc¸ C¸ elikel
1
and Tolga Ovatman
2 a
1
Siemens R&D Center, Istanbul, Turkey
2
Department of Computer Engineering, Istanbul Technical University, 34469
˙
Istanbul, Turkey
Keywords:
Replicated State Machines, Distributed Checkpoints, Fault Tolerance.
Abstract:
This study presents preliminary results from a distributed checkpointing approach developed to be used with
replicated state machines. Our approach takes advantage from splitting and storing partial execution history
of the master state machine in a distributed way. Our initial results show that using such an approach provides
less memory consumption for both the running replicas and the restoring replica in case of a failure. On the
other hand for larger histories and larger number of replicas it also increases the restore duration as a major
drawback.
1 INTRODUCTION
Increasing popularity of serverless software hosting
services offered by major cloud vendors boosted the
usage of state machine models in various areas of
software development for cloud. Serverless comput-
ing offers software developers to eliminate the neces-
sity to take care of many layers/aspects of software
development stack and focus on developing and ex-
pressing tasks to be executed by cloud system. It is
possible to use different expression models; however,
using state machine models to express the functional-
ity is one of the frequently preferred approaches for
serverless computing.
As well as the independence form software stack,
serverless computing also offers non functional re-
quirements such as automatic scaling, fault tolerance,
etc.. Replicating a master state machine that is go-
ing to work in a distributed way to handle and syn-
chronously process requests is a widely used model
to provide fault tolerance. Naturally, this approach
has its own challenges and limitations. A major ap-
proach that can be used in fault tolerance is check-
pointing. Checkpointing involves saving the system
state in periodic intervals to boot the system back in
time of a failure. Application of checkpointing in
replicated state machines and increasing the effective-
ness of the process is an active research area in today’s
cloud computing systems.
In this study we investigate the idea of distributing
the state machine snapshot images among the state
a
https://orcid.org/0000-0001-5918-3145
machine replicas to decrease the amount of memory
overhead used by each replica when saving the system
state. Our approach involves striping the request his-
tory into many pieces during the checkpointing pro-
cess so that each replica is going to store a certain
piece of the history while the whole history can be
obtained from the overall system.
We have implemented our approach using Spring
state machine framework and compared our results
with the default mechanism which Spring SM uses
to provide fault tolerance for the state machine en-
sembles. By default Spring SM stores the whole his-
tory in the ensemble communication medium among
the state machines, which is used as an Apache
Zookeeper instance in our case. This makes the
Zookeeper system a single point of failure, whenever
a failure occurs in Zookeeper system loses the check-
point snapshots that has been taken so far.
Our preliminary results show that our approach
eliminates this single point of failure by distributing
the checkpoint snapshots among the replicas. By con-
trolling the amount of redundancy, distributed snap-
shots can be gathered even if more than one replica
fails at the same time, during executions. More-
over we also decrease the amount of memory over-
head needed for the checkpoint mechanism by split-
ting the snapshot information among the replicas.
Currently, our approach, in its preliminary state pro-
duces a heavy recovery-time overhead since the failed
replica needs to collect pieces from different replicas
in order to obtain a full history of execution. Such a
trade-off is unavoidable but our future study is aimed
Çelikel, N. and Ovatman, T.
A Distributed Checkpoint Mechanism for Replicated State Machines.
DOI: 10.5220/0009797405150520
In Proceedings of the 10th International Conference on Cloud Computing and Services Science (CLOSER 2020), pages 515-520
ISBN: 978-989-758-424-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
515

towards minimizing this overhead.
In the rest of the paper, we begin by summariz-
ing the related work. Afterwards we explain our dis-
tributed checkpointing mechanism and provide an ex-
emplary architecture and experimental environment
to evaluate out approach in Section. We finalize with
conclusions and planned future work.
2 RELATED WORK
Performance of the checkpointing has always been a
widely investigated topic in the distributed comput-
ing domain. There are numerous techniques to be
used as a solution in order to minimize checkpoint
and recovery costs. (Heo, Junyoung & Yi, Sangho &
Cho, Yookun & Hong,Jiman & Shin,Sung, 2006) pro-
poses a solution for minimizing checkpointing costs
in terms of storage aspects while (Mao, Yanhua and
Junqueira, Flavio and Marzullo, K., 2008) focuses on
high network performance, in terms of throughput.
(Mao, Yanhua and Junqueira, Flavio and Marzullo,
K., 2008) propose a high-performance replicated state
machine check-pointing and recovering approach de-
rived from Paxos consensus protocol, which is out
of scope for this research. (B. Ghit and D. H. J.
Epema, 2017) propose to checkpoint only straggling
tasks in order to minimize the number of checkpoints
and hence, overall checkpointing overhead. (Naksine-
haboon, Nichamon and Liu, Yudan and Leangsuksun,
C. and Nassar, Ruba and Paun, Mihaela and Scott,
S., 2008) propose a novel checkpointing mechanism
in order to reduce the checkpoint data size by check-
pointing only dirty pages that are modified since last
checkpoint time. This novel approach named as in-
cremental check-point model which involves a deci-
sion mechanism in order to persist the minimal nec-
essary data to be check-pointed since the last check-
point time in the execution history.
There are many other efforts which is targeted
for finding a way to efficiently implement the check-
pointing mechanism in system level (Gioiosa, R. and
Sancho, J.C. and Jiang, S. and Petrini, Fabrizio, 2005)
or user level (Sancho, J.C. and Petrini, Fabrizio and
Johnson, G. and Frachtenberg, Eitan, 2004). (Sancho,
J.C. and Petrini, Fabrizio and Johnson, G. and Fracht-
enberg, Eitan, 2004) states the user level approach
as checkpointing is performed explicitly by exter-
nal applications and propose the approach for deter-
mining optimal checkpoint frequency as a matter-of-
fact. (Gioiosa, R. and Sancho, J.C. and Jiang, S. and
Petrini, Fabrizio, 2005) defines the system-level ap-
proach as generally-applicable approach, which can
be defined as an application is unaware whether it
is checkpointed or not. Gioiose et al. also pro-
poses an innovative methodology called buffered co-
scheduling which is implemented at kernel level,
hence has unrestricted access to processor registers,
file descriptors, and states several check-pointing for-
mulations to be used, such as internal check-pointing
in which uses UNIX/LINUX signal mechanism.
The idea behind using replicated state machines in
order to model distributed check-pointing approach is
already stated by (Bolosky, William and Bradshaw,
Dexter and Haagens, Randolph and Kusters, Norbert
and Microsoft, Peng, 2011) and (Fred B. Schneider,
1990), replicated state machines can be made fault-
tolerant by running on multiple computers with feed-
ing the same inputs.
3 DISTRIBUTED
CHECKPOINTING
Distributed checkpointing approach for replicated
state machines utilizes the idea of each replica sav-
ing the state of execution history for a predesignated
period of time. This way each replica stores one or
more portions of the execution history locally, later to
be retrieved by a freshly booting replica.
Let’s assume that each state machine consists of
some states denoted as s
i
and some actions that trig-
ger transition between states such as s
i
a
k
−→ s
j
where
transition from state i to state j is triggered by action
k. These definitions result in a basic state machine
model in 1 that is going to be used in this paper’s con-
text. In this definition δ defines the transitions as a
function from state-action pairs to states.
M = {S, A}
S = {s
0
, s
1
, . . .}
A = {a
0
, a
1
, . . .}
δ = S × A → A
(1)
Regarding the definition in equation 1 we can ex-
emplify the execution history for a state machine as
in definition in equation 2 where the history begins
with a state and continues by action-state pairs where
each state is navigable by the related action in the state
machine definition. This example can be used to rep-
resent portions of history where the history may con-
tain only a portion of the full execution of the state
machine. However if the history begins by the initial
state (e.g. s
0
) than the history represents the full ex-
ecution history until the final state of the sequence in
the history.
H = s
i
, a
j
, s
k
, a
p
, s
r
, . . . (2)
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
516

The definition in equation 2 does not include
any temporal information about the execution history
other than the sequence of state transitions. To define
the time interval that the history belongs to we are go-
ing to use a superscript to indicate a discrete clock tick
interval that begins from 0 tick as the full execution’s
beginning time. In addition, we are going to use a
subscript to associate a history with the id of a replica
which currently stores the given partial history.
H
0−39
= s
0
, a
0
, s
1
, a
1
, s
2
, a
2
, . . . , s
19
, a
19
, s
20
H
0−9
0
= s
0
, a
0
, s
1
, a
1
, . . . , a
4
, s
5
H
10−19
1
= s
5
, a
5
, s
6
, a
6
, . . . , a
9
, s
10
H
20−29
2
= s
10
, a
10
, s
11
, a
11
, . . . , a
14
, s
15
H
30−39
3
= s
15
, a
15
, s
16
, a
16
, . . . , a
19
, s
20
(3)
For instance, the full history indicated as H
0−39
in equation 3 describes an execution history collected
between time ticks 0 and 39, where 21 different states
has been travelled, triggered by 20 different actions.
In order to be more illustrative all the actions and
states are chosen as distinct and numbered in se-
quence for the sake of this example. In a realistic
scenario there would have been arbitrary transitions
among the states of the state machine with arbitrary
incoming actions. In equation 3 the full history is kept
by four different replicas, each indicated with H
s−e
i
where i represents replica id, s represents beginning
time tick and e represents end time tick. The history
is divided into four different partial histories in this
example where each part is kept in a different replica.
In a replicated state machine, logically all the
replicas act as a logical master state machine where
any request, triggering an action, received by a replica
is synchronously communicated and reflected to other
replicas, causing the other replicas to execute the
same action in their local machines. This situation
results is a logical master history, which corresponds
to H
0−39
in our example, be shared between all the
replica state machines.
In our distributed checkpointing, approach we
have implemented the underlying mechanism for the
replicated machines to synchronously store, collect
and merge this logical history by the currently run-
ning replicas. Since there is a single logical history
for all the replicas, it is not required to store a real
time clock to perform fair sharing of the execution
histories; instead it is sufficient to count the number
of actions in current partial history to decide when to
start/stop storing a partial history by each replica.
Briefly, our distributed checkpointing approach
utilizes the discrete time depending on executing ac-
tions in replicated state machines to distribute the
Figure 1: Overall Architecture.
checkpoint storing responsibility between the current
members of an ensemble (replica group). In this paper
we investigate the advantages and overhead of per-
forming such a distribution in a replica group. We can
perform many additional tasks such as re-distributing
histories to load balance for replicas that has just
joined an ensemble or storing redundant partial his-
tories to eliminate single point of failure in a replica
group.
4 SYSTEM ARCHITECTURE
AND EXPERIMENTAL
ENVIRONMENT
In our system architecture illustrated in Figure 1,
replicated state machines perform simplified opera-
tions on its own local variables, such as incrementing
and decrementing, and also updates shared variables
while passing from one state to another. Once all the
replicated state machines are started to run, they waits
events to be triggered in order to perform transitions
between states. When the first event is forwarded to
any of the state machines, it processes this event, per-
forms necessary operations on its local variables, up-
dates shared variables which is shared among states
and finishes its execution in order to process the in-
coming event. Once the processing of the event is fin-
ished, all the state machines will be in the same state
and then will wait next event to process. The syn-
chronization between states is established by master
machine.
In our experimentation environment base func-
tionalities used for executing distributed checkpoint-
ing mechanism are built. There are three clients
which executes replicated state machines in Figure 2
A Distributed Checkpoint Mechanism for Replicated State Machines
517
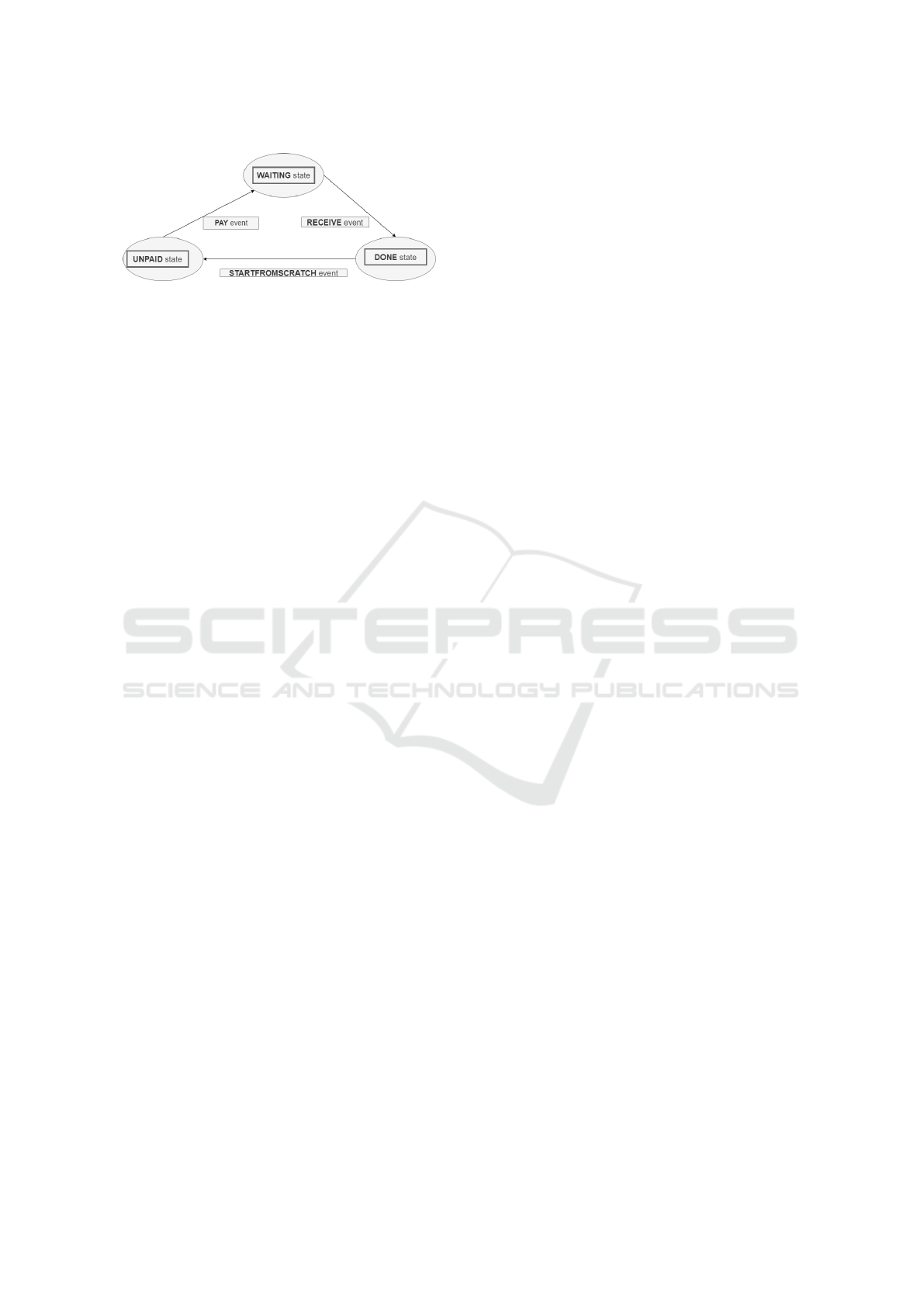
Figure 2: States and transitions of the replicated state ma-
chines.
and one master machine which hosts the Apache
Zookeeper binaries and provides coordination mech-
anism for replicated state machines.
Each of these clients and master machine runs as
containers in Docker Engine. The aim of using docker
containers is simplifying the connections between the
clients and master in an isolated network structure.
Our proposed mechanism do not need to be run in-
side containers; it can be applied to any replicated
state machine implementation. In our experimental
implementation we have chosen to use containers to
host the replicas. Moreover, by using containerization
phenomenon, clients and master can be started up in
repetition by using minimal resources of the machine
which hosts docker daemon. All the clients and mas-
ter machine runs as lightweight linux containers. In
addition to that, with the aim of starting and stopping
containers, starting and stopping replicated state ma-
chines inside containers, docker-compose tool is used
for orchestration purposes.
An example docker-compose file is provided in or-
der to start replicated state machines inside contain-
ers:
version: "3"
services:
smoc1:
build:
context: .
dockerfile: smoc/Dockerfile
networks:
- distributedWan
hostname: ${HOSTNAME_SMOC1}
environment:
- EXCHANGE=${IPC_EXCHANGE_FOR_SMOC1}
- QUEUE=${IPC_QUEUE_FOR_SMOC1}
smoc2:
build:
context: .
dockerfile: smoc/Dockerfile
networks:
- distributedWan
hostname: ${HOSTNAME_SMOC2}
environment:
- EXCHANGE=${IPC_EXCHANGE_FOR_SMOC2}
- QUEUE=${IPC_QUEUE_FOR_SMOC2}
networks:
distributedWan:
external:
name: loadbalancer_isolatedNetwork
Distributed checkpointing is continuously being
performed during the life-cycle of the replicated state
machines. Each of the state machines being executed
in each clients, does not store whole execution his-
tory -which includes state transitions, states, local and
shared variables-, they only store minimal portion of
the execution history. Once an event is forwarded to
any of replicated state machines inside the ensemble,
it is stored locally by the state machine which pro-
cessed this event on its local context. Context for
the replicated state machines can be modelled as in-
put -incoming event, event timestamp, source event-
and as output -local and shared variables, destination
state- and be stored as a whole. Hence, the replica
which processes the event is responsible for storing
related artifacts regarding this event. As a result of
checkpointing process in each client, whole execution
history is persisted in distributed manner in different
containers.
In case of any failure in any of replicated
state machines, execution history can be gath-
ered from non-faulty clients via a broadcast
message.Communications between client machines
which hosts replicated state machines are established
via remote procedure calls using the RabbitMQ mes-
sage broker tool. Once the faulty client processed the
incoming messages, sorted and applied in the exe-
cuted order on its own state machine, it is ready to
re-join the cluster again.
From that point on, experimental setup is pre-
sented. A debian-based machine is used for con-
ducting our experiments, which is equipped with
2.60 GHz Intel i5 CPU, 4 GB RAM and 100 GB
SSDs. The communication medium among contain-
ers are established via network features of the docker-
compose tool. The master node hosts the Zookeeper
binaries whereas client nodes -which are based on
alpine base image- serve as hosts for the replicated
state machines.
5 EVALUATION
We have conducted experiments with 4, 8, 12 and
16 replicas in an experiment environment described
in the previous section and measured the amount of
difference between memory consumption and restore
duration.
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
518

Figure 3: Memory consumption difference of the replica
being restored.
(a) 96 requests
(b) 960 requests
Figure 4: Replica restore durations.
In Figure 3, we present the difference in mem-
ory consumption of the replica that is being restored
with and without using distributed checkpoints. Each
bar in the figure represents the difference of mem-
ory consumption between conventional checkpoint-
ing and distributed checkpointing. Distributed check-
pointing mechanism provided around 17 kilobytes of
advantage compared to the conventional checkpoint
mechanism present in Spring state machine frame-
work.
In Figure 4, we present the restore duration for a
history with 96 different requests and 960 requests re-
spectively. We have used a ten-fold input in terms of
number of requests to observe the effect of large num-
ber of requests on restore duration during our compar-
ison. It can be seen that even though our approach
provides comparable results for small histories and
small number of replicas as the amount of communi-
cation need increases our approach starts to perform
poorly.
We would also like to note that using distributed
checkpoints also decreased the memory consumption
from 2 up to 7 kilobytes in each replica for the exper-
iments above. Even though there exists an advantage
in using distributed checkpoints in terms of memory
consumption, still the trade-off for restore duration
seems to be high for larger systems.
6 CONCLUSION AND FUTURE
WORK
In this preliminary work we have proposed a dis-
tributed checkpoint mechanism that can be used in
replicated state machines. Our work relies on split-
ting execution histories into multiple parts during the
execution so that each part can be stored by another
replica. This approach also allows redundant storage
of partial histories to reduce the number of critical
replicas that may render the system useless in case
of failure. Besides the mentioned advantage, our ap-
proach provided less memory usage in present repli-
cas and in the replica which is being recovered. In its
current form, recovery time is increased because of
the extra communication overhead needed for collect-
ing partial histories from replicas. We plan to work on
decreasing this overhead as much as possible to pro-
vide a better trade-off for distributed checkpointing.
Another possible area of extension is balancing the
amount of checkpoint data stored in each replica with
the addition of new replicas to an existing ensemble.
ACKNOWLEDGEMENTS
This study is supported by the scientific and tech-
nological research council of Turkey (TUBITAK),
within the project numbered 118E887
REFERENCES
B. Ghit and D. H. J. Epema (2017). Better safe than sorry:
Grappling with failues of in-memory data analytics
frameworks. HPDC, pages 105–116.
Bolosky, William and Bradshaw, Dexter and Haagens,
Randolph and Kusters, Norbert and Microsoft, Peng
(2011). Paxos replicated state machines as the basis of
a high-performance data store. NSDI’11: Proceedings
A Distributed Checkpoint Mechanism for Replicated State Machines
519

of the 8th USENIX conference on Networked systems
design and implementation, pages 141–154.
Fred B. Schneider (1990). Implementing fault-tolerant ser-
vices using the state machine approach: A tutorial.
ACM Computing Surveys, 22:299–319.
Gioiosa, R. and Sancho, J.C. and Jiang, S. and Petrini, Fab-
rizio (2005). Transparent, Incremental Checkpointing
at Kernel Level: a Foundation for Fault Tolerance for
Parallel Computers. SC ’05: Proceedings of the 2005
ACM/IEEE Conference on Supercomputing, pages 9–
9.
Heo, Junyoung & Yi, Sangho & Cho, Yookun &
Hong,Jiman & Shin,Sung (2006). Space-efficient
page-level incremental checkpointing. Journal of In-
formation Science and Engineering, 22:237–246.
Mao, Yanhua and Junqueira, Flavio and Marzullo, K.
(2008). Mencius: Building Efficient Replicated State
Machine for WANs. OSDI’08: Proceedings of the 8th
USENIX conference on Operating systems design and
implementation, pages 369–384.
Naksinehaboon, Nichamon and Liu, Yudan and Leangsuk-
sun, C. and Nassar, Ruba and Paun, Mihaela and
Scott, S. (2008). Reliability-Aware Approach: An
Incremental Checkpoint/Restart Model in HPC Envi-
ronments. IEEE International Symposium on Cluster
Computing and the Grid (CCGRID), pages 783–788.
Sancho, J.C. and Petrini, Fabrizio and Johnson, G. and
Frachtenberg, Eitan (2004). On the feasibility of
incremental checkpointing for scientific computing.
Proceedings - International Parallel and Distributed
Processing Symposium, IPDPS 2004 (Abstracts and
CD-ROM), 18:58–.
CLOSER 2020 - 10th International Conference on Cloud Computing and Services Science
520
