
Functions Approximation using Multi Library Wavelets and
Least Trimmed Square (LTS) Method
Abdesselem Dakhli
1a
, Maher Jbeli
1
and Chokri Ben Amar
2b
1
Ha’il University, Kingdom of Saudi Arabia
2
Research Groups on Intelligent Machines (REGIM), ENIS, University of Sfax, Tunisia
Keywords: Wavelet Neural Networks, Least Trimmed Square, Multi Library Wavelet Function, Beta Wavelets.
Abstract: Wavelet neural networks have recently aroused great interest, because of their advantages compared to
networks with radial basic functions because they are universal approximators. In this paper, we propose a
robust wavelet neural network based on the Least Trimmed Square (LTS) method and Multi Library Wavelet
Function (MLWF). We use a novel Beta wavelet neural network BWNN. A constructive neural network
learning algorithm is used to add and train these additional neurons. The general goal of this algorithm is to
minimize the number of neurons in the network during the learning phase. This phase is empowered by the
use of Multi Library Wavelet Function (MLWF). The Least Trimmed Square (LTS) method is applied for
selecting the wavelet candidates from the MLWF to construct the BWNN. A numerical experiment is given
to validate the application of this wavelet neural network in multivariable functional approximation. The
experimental results show that the proposed approach is very effective and accurate.
1 INTRODUCTION
The approximation of a function makes it possible to
estimate the underlying relationship from a set of
input-output data constituting the fundamental
problem of various applications, for example the
classification of models, the extraction of data, the
reconstruction of signals and identification of systems
(Chen, Jain, 1994),(Hwang ,Lippman ,1994).
For instance, the problem and the purpose of the
identification system are used to estimate the
characteristics of the underlying system using
empirical input-output data from the system.
The problem of pattern recognition is a mapping
of functions whose purpose is to assign each pattern
in a characteristic space to a specific label in a group
space (class).
The aim of signal processing is to determine
adaptively no stationary system parameters through
the input-output signals.
In the literature (Sontag, 1992), (Park, Sandberg,
1991), the feed forward neural network is applied as
a method to resolve the interpolation and the function
adjustment problems. However, in several studies
a
https://orcid.org/0000-0001-5789-9430
b
https://orcid.org/0000-0002-0129-7577
(Yang, Wang, Yan, 2007), (Chui, Mhaskar,1994), it
has been shown that the ability to approximation
using neural network depends on kind of training
algorithm, such as, the BP algorithm. However, the
learning algorithms are often eventually turned into
optimization problems. The neural network learning
by the BP algorithm often causes the instability of this
network. Indeed, in the process of finding the optimal
value, the different partial optimal value is often
obtained and not the overall optimal value.
Recently, problems of approximation of
univariate functions have been studied by
constructive feed forward neural networks. The use of
these networks for multivariate functions has had a
limit, which concerns the convergence conditions and
the actual operation, which becomes relatively
difficult (Muzhou, Yixuan, 2009),(Dakhli, Bellil, Ben
Amar, 2014),(Llanas, Sainz, 2006).
In the literature (Han, Hou, 2007), (Xu, Cao,
2005), the authors proved that the connection weight
of RBF neural networks can be obtained through
several learning algorithms. Therefore, the weight has
some instability.
468
Dakhli, A., Jbeli, M. and Ben Amar, C.
Functions Approximation using Multi Library Wavelets and Least Trimmed Square (LTS) Method.
DOI: 10.5220/0009802604680477
In Proceedings of the 22nd International Conference on Enterprise Information Systems (ICEIS 2020) - Volume 1, pages 468-477
ISBN: 978-989-758-423-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The Multilayer Perceptrons (MLPs) and the
Radial Basic Function Networks (RBFN) are applied
to solve the problem of approximating functions.
They produce a generic black-box functional
representation and have been displayed to be capable
for approximating any continuous function defined
with arbitrary accuracy, (Miao, Chen, 2001),
(Kreinovich, 1991).
Other literatures (Han, Hou, 2008), (Huang, Chen,
2008), (Mai-Duy, Tran-Cong, 2003) have used
constructive feedforward RBF neural networks to
solve approximation problems of quasi-
interpolations. Mulero Martínez (Mulero-Martinez,
2008) applied Gaussian RBF neural networks with
uniformly spaced nodes.
The obtained results showed a better
approximation. Ferrari et al. (Ferrari, Maggioni,
Borghese, 2004) have addressed the problem of
multi-scale approximation with the use of
hierarchical RBF neural networks. However, these
methods have the same defects of the BP algorithm.
They are either unstable or complicated and slow.
Several algorithms that are used to calculate the
network parameters perform the wavelet network
training. These parameters are the biases and the
weights, the parameters of the wavelet function
(translation and dilation parameters). Nevertheless,
there are numerous studies on training WNNs.
Derivative-based learning methods including
Gradient Descent, Back Propagation, etc. are the most
frequently-used methods in the previous works of
WNN training, (Hwang, Lav, Lippman, 1994), (Lin,
2006).
In addition, derivative-free methods, as
evolutionary algorithms (Eftekhari, Bazoobandi,
2014), (Bazoobandi, Eftekhari, 2015), (Ganjefar,
Tofighi, 2015), (Tzeng,2010), have also been
previously used. The learning method proposed in the
well-known Back propagation method for neural
networks.
Other approaches applied a fuzzy WNN learning
method, which uses a gradient-based adaptive
approach to adjust and evaluate all network
parameters, (Abiyev, Kaynak, 2008), (Chen, Bruns,
1995), (Zhang, Benveniste, 1992).
Evolving WNN is an evolutionary algorithm (EA)
for WNN training. Yao, et al., have used this
algorithm, for the first time (Yao, Wei, He, 1996).
The evolution of the WNN showed a good precision
in the simulations.
Yet, Tzeng's research is another important effort
related to the application of evolutionary algorithms.
A genetic algorithm (GA) adjusts and evaluates all
the parameters of the fuzzy WNN (FWNN-GA)
(Tzeng, 2010).
Hashemi et Al. applied another version of GA for
the training of WNN parameters. The SLFRWNN is
a Single Hidden Layer Fuzzy Recurrent Wavelet
Neural Network (WNN) that uses a two-phase
learning algorithm. At first, a GA was used to
initialize the network settings. Then, back
propagation learning based on the chain
differentiation rule was applied to adjust and evaluate
wavelet functions and weight parameters,
(Karamodin, Haji Kazemi, Hashemi, 2015),
(Ganjefar, Tofighi, 2015).
Schmidt et al. (Schmidt, Kraaijveld, Duin, 1992)
used a Neural Network with Random Weights
(NNRW). This network is formed by a unique hidden
layer, where input weights and biases are randomly
assigned, and the output weights are evaluated using
the resolution of a least square linear problem in one
step. This network could not guarantee the universal
approximation ability.
Another type of Network Applied Random
Vector Functional Link Network (RVFL), developed
by Pao and Takefujiand Pao et al.(Pao, Takefuji,
1992), (Pao, Park, Sobajic, 1994) who developed
further (McLoone, Brown, Irwin, Lightbody, 1998);
the method is called Extreme Learning Machine
(ELM) in more recent searches (Huang, Zhu, Siew,
2006), (Igelnik, Pao, 1995).
The overall goal of our work is to use a
constructive algorithm that minimizes the number of
neurons in the network during the learning phase. At
first, the construct starts with a single neuron on the
hidden layer during the training process. When the
learning process stabilizes, that is, the improvement
the error compared to the previous step is less than a
given threshold, it adds a new neuron to the hidden
layer of the frozen network and the weights of the last
added neuron are corrected during the restart of the
phase learning.
The addition of wavelet in the layer is done from
a wavelet library using a selection method called
Least Trimmed Squares (LTS). This estimator will
have to choose the wavelet functions Beta suitable for
building our Wavelet Network.
This study is structured as follows: section 1
introduces a literature review of principal approaches.
Section 2 describes the wavelet decomposition and
the structure of wavelet neural networks. Section 3
presents our proposed approach. Section 4 deals with
the experimental results of this approach. Section 5
ends up with a conclusion and a discussion.
Functions Approximation using Multi Library Wavelets and Least Trimmed Square (LTS) Method
469
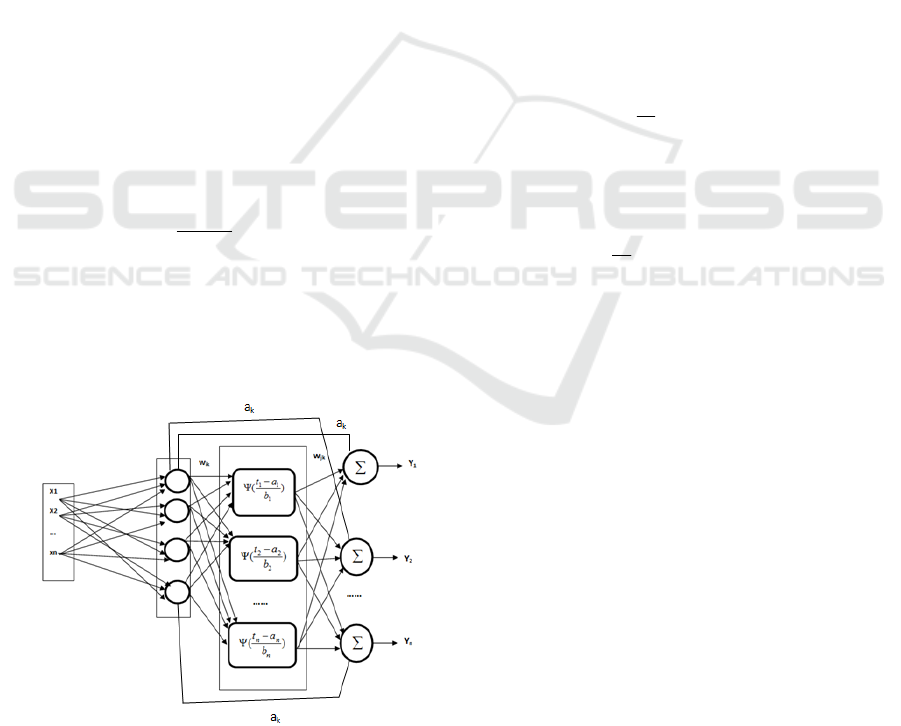
2 WAVELET NEURAL
NETWORK
In 1992, Benveniste and Zhang defined the WNN
(Zhang, Benveniste, 1992). WNNs are the
combination of two signal processing techniques
"wavelet transforms and artificial neural networks"
whose activation functions are based on a family of
wavelets. WNN has successfully found in several
applications in almost every field of engineering and
science. The Wavelet Neural Networks has recently
attracted much attention for its able to correctly
identify non-linear dynamic systems with
inconsistent information (Zhang, 1997), (Dakhli,
Bellil, Ben Amar 2016).
The WNN is constructed by the combination of
the wavelet transform and the artificial neuron
networks (Charfeddine, El’arbi, Ben Amar, 2014).
The WNN structure is composed of three layers (an
input layer, a hidden layer and an out layer). The
salaries of the weighted outputs are added. Each
neuron is connected to the other following layer. The
WNN (Fig. 2) is defined by pondering a set of
wavelets dilated and translated from one wavelet
candidate with weight values to approximate a given
signal f. The overall response of the WNN is:
iw
N
k
kk
i
i
N
i
i
xa
a
bx
y
01
ˆ
(1)
Where (x1, x2,…,xNi ) is the vector of the input,
Nw is the number of wavelets and y is the output of
the network. The output can have a component refine
in relation to the variables of coefficients ak (k = 0,
1... Ni) (Fig.1).
Figure 1: Wavelet Neural Network structure.
The wavelet mother is selected from the MLWF,
is defined by dilation (ai) which controls the scaling
parameter and translation (bi) which controls the
position of a single function )(x . A WNN is used
to approximate an unknown function:
)(xfy
(2)
Where f is the regression function and
is the
error term.
The discretization of the wavelet transform must
be elaborated if we want to obtain a non-redundant
transformation. To do this discrete decomposition, we
must take into consideration the values taken by the
two wavelet parameters (ai; bi). These parameters
must take values in a discrete subset of
. This
discretization often uses the sets of parameters a and
b defined by a=
m
a
0
and b=
m
anb
00
with (m; n)
,
the set of integers
1
0
a
,
0
0
b
(Daubechies, 1992),
(Antonini, Barlaud, Mathieu, Daubechies, 1992),
(Payan, Antonini, 2006).
The family of analyzing functions
nm,
is then
given by:
)(
00
2
0,
nbxaa
m
m
nm
(3)
Thus, for a signal constituting
j
a
0
points we
calculate then only the coefficients:
j
a
i
m
m
nbxaxfabaW
0
1
00
2
0
)()(),(
(4)
With
jm ,...,1
and
mj
an
0
,...,1
In fact, the properties of the approximation
obtained are elaborated by the selection of the
parameters (a; b). Analyzing functions elaborate
information redundant when a is near to 1 and b is
near to 0. If we choose a
0
= 2 and b
0
= 1, then we
speak of a dyadic transform.
As part of our work, we want to implement the
architecture of a wavelet network that will use the
beta wavelet as a function transfer in the hidden layer.
The structure of this network must be constructed in
a constructive and incremental way. To validate the
performance of our network, we must use it to
approximate unknown functions.
This relation (1), which represents a finite sum, is
considered to be an approximation of an inverse
transform or a decomposition of a function into a
weighted sum of wavelets, where each ci is
proportional to W(a,b). Therefore, the realization of
an approximation of a function defined on a finite
domain. The wavelet transform of this function exists,
and its reconstruction is possible.
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
470

3 PROPOSED APPROACH
This paper presents a new approach based on the
wavelet neural network and constructed by using the
Multi Library Wavelet Function (MLWF). The
CBWNN structure is solved by using the LTS
method. Our approach is divided into two steps: the
construction of the Multi Library Wavelet Function
(MLWF) and the construction of Beta Wavelet
Neural Networks (BWNN) using MLWF and the LTS
Method (Dakhli, Bellil, Ben Amar, 2016), (Wali,
Aoun, Karray, Ben Amar, Alimi, 2010).
3.1 Beta Wavelets
The Beta Wavelet is a parameterizable function that
is defined by
)()(
,,,
10
xx
qpxx
(Othmani,
Bellil., Ben Amar, Alimi,2010), (ElAdel, Ejbali,
Zaied, Ben Amar, 2016) (Dakhli, Bellil, Ben Amar,
2016),with x0, x1, p and q real parameters verifying:
10
xx and
qp
qxpx
x
c
01
. We will have to limit
ourselves to the only case where p> 0 and q> 0. The
Beta function is defined as follows:
0
1
01
01
() ,
0otherwise
pq
cc
xx
xx
xx xx
Beta x if x x x
(5)
According to the different forms of the beta
function, we find again that this function is only
canceled in x0 and x1. Therefore, it does not verify
the oscillation property but it has been proved in the
works (Boughrara, Chtourou, Ben Amar, 2012), that
all derivatives of the beta function are admissible
wavelets. The modifications of the functional
parameters of the beta function x0, x1, q and p allow
us to obtain the different wavelets. The derivative n
of a beta wavelet one-dimensional (1D) is elaborated
by the following expression:
xxP
x
nin
C
xxPxPx
x
nn
dx
xd
x
n
i
in
in
n
i
n
n
nn
n
n
n
n
1
1
1
1
1
0
1
1
1
1
0
x
q!1
)x-(x
p!
1
)()(
x
q!
x-x
p!
)1(
)(
)(
(6)
With:
Figure 2: Different wavelet forms of derivatives of the Beta
function.
These different wavelet derivative forms of the
beta function satisfy the following properties:
admissibility, finite energy, zero momentum,
compactly supported and translation and dilation;
For all n
N and
0n
the function
n
n
n
dx
xd
x
satisfies the admissibility
condition:
dw
w
wTF
n
2
(7)
A wavelet has finite energy if:
0
dxx
(8)
All derivatives of the beta function have been
proved to satisfy the finite energy condition for all n
N and .0
n
0
)(
dxxxPdx
dx
xd
n
n
n
(9)
It has been shown that the derivative n of the beta
function has n null moments:
0
1
0
dxxxPx
x
x
n
n
(10)
All the wavelets derived from the Beta function
have a support:] x0; x1 [. Derivatives of the beta
function verify translation and expansion (dilation)
properties.
Functions Approximation using Multi Library Wavelets and Least Trimmed Square (LTS) Method
471
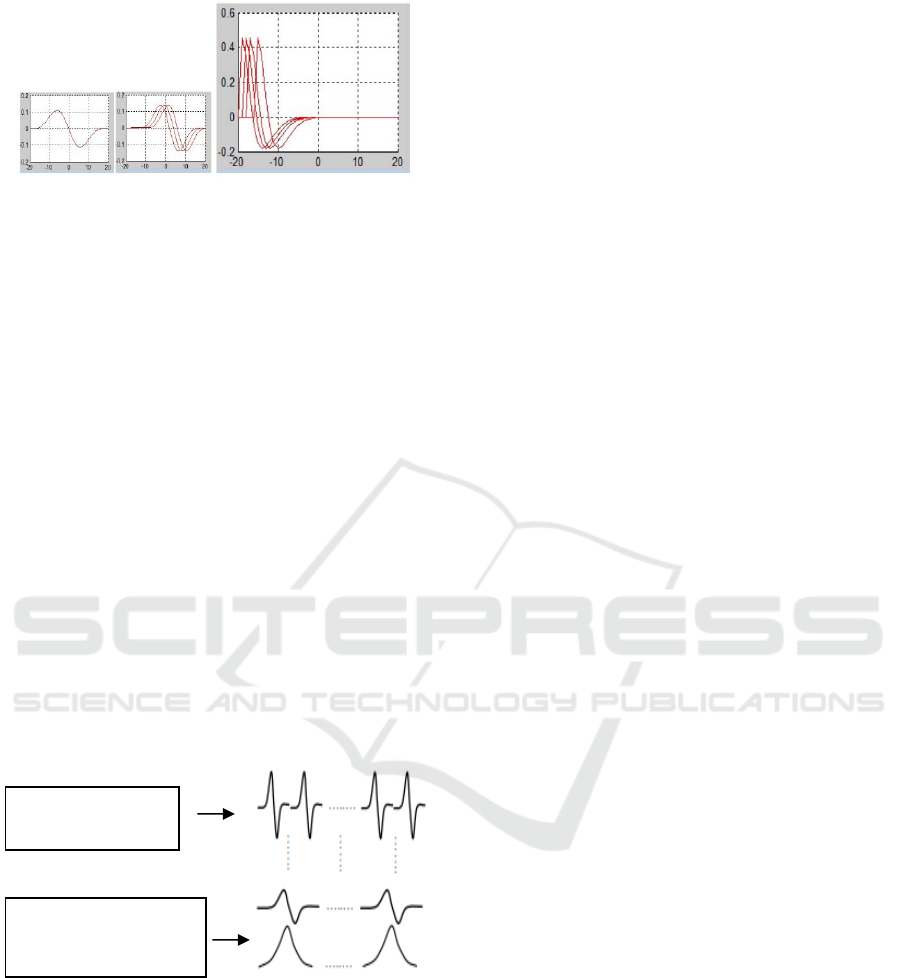
Figure 3: Translation and dilation of derivatives of the Beta
function.
3.2 Construction of Multi Library
Wavelet Function (MLWF)
The wavelet library MLWF contains a set of
candidates regressors. This library must be a finite
number of wavelets (Bouchrika, Zaied, Jemai, Ben
Amar, 2012) (Dhibi, Ben Amar, 2019), as little as
possible, so that the procedure for selecting candidate
wavelets can be used effectively. Given a wavelet
function w, the construction of the library W consists
in choosing a subset of the family that is
parameterized continuously.
.,:
d
babxa
(11)
The construction of the wavelet library MLWF,
generated from the family of mother wavelets, is
defined as:
ii
M
ii
iiii
j
bxabxa
MjbabxaMLWF
,...,
,...,1,,,
1
*
(12)
Figure 4: The wavelet library MLWF according to the
number of levels of decomposition for the wavelet
transforms.
The wavelet library contains candidate wavelets.
They are used to build the wavelet array. These
wavelets are used as activation functions for the
wavelet network. The construction of the wavelet
library candidate to join our wavelet network is based
on the principle of sampling on a dyadic grid of
parameters of expansion and translation is preceded.
When the length of the signal f to be approximated is
equal to n, the sampling produced in the first scale n /
2 of the wavelets. So, the number of wavelets is
halved each time we climb a ladder (Dakhli, Ben
Amar, 2019). The sampling stops at any scale i with i
≤ m but we complete the library by the corresponding
scale functions of the last scale. The number of
functions in this library is equal to n.
We apply the inverse transform to discrete
wavelets that can be interpreted as the output of a
wavelet array and then we can build the wavelet
library. The coefficients of expansion (a) and
translation (b) are evaluated by the following
expressions:
.
0
m
aa
.
00
m
anbb
With a> 1 and b> 0. Dyadic sampling is done
when a
0
= 2 and b
0
= 1.
3.3 Wavelet Network Construction
using the LTS Method
The technique of selecting wavelets from an already
built library plays a very important role. It improves
the performance of the wavelet network from the
point of view of complexity and decision, especially,
in the classification field (Teyeb, Jemai, Zaied, Ben
Amar, 2014).
In fact, the selection method makes it possible to
choose the most significant wavelets to build the
wavelet network, that is to say the wavelets that
improve the performance and the objective of the
network. The use of the selection techniques is due to
the large number of wavelets in the library. Therefore,
the method of choice must select a determined
number (Nw) of the wavelets from an element
number (Mw) in the library. Several selection
techniques make it possible to manage the choice of
wavelets, for example, the orthogonalization
selection technique.
After the construction of the wavelet library, we
try to build our wavelet network. The hidden layer of
our network must be composed of suitable wavelet
functions to improve the network performance and
efficiency. To select these functions, we must use the
Least Trimmed Square method, which is used to
initialize and to build our wavelet neural network.
The residual (or error) ei at the output (
i
y
ˆ
) of the
WNN due to the ith example is defined by:
niyye
iii
,
ˆ
(13)
First scale
[n/2 wavelets]
Scale number i
[n/2
i
wavelets andn/2
i
scaling function]
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
472

The Least Trimmed Square estimator is applied to
choose the WNN weights that minimize the total sum
of trimmed squared errors:
p
k
n
i
iktotal
eE
11
2
2
1
(14)
The notation for the ordered absolute residuals is
e(i) , so
....2)1( neee
The number of wavelets, M, is chosen as the
minimum of the so-called Akaike’s final prediction
error criterion (FPE):
2
1
ˆ
2
1
/1
/1
ˆ
n
k
kk
pa
pa
PFE
yxf
nnn
nn
fJ
(15)
Where npa is the number of parameters in the
estimator.
3.4 Proposed Algorithmic Approach
To build the topology of the wavelet network, we will
apply an ascending (incremental) approach. Indeed,
the construction of our network using this approach is
obtained by adding wavelets and connection within
the hidden layer. The addition is made when the
network used produces errors. In this approach, the
initial structure comprises a small number of neurons,
usually an input layer and an output layer. Therefore,
our problem is focused on building the hidden layer
using the proper wavelets that can improve the
performance of our network.
To solve this problem, at first we built a library
containing a finite number of wavelets that are subject
to the selection procedure. Then, we used an
estimator to select at each step the relevant wavelet
function to join the network. This estimator is called
Least Trimmed Squares (LTS).
Consider y = F (x), which maps an input vector x
to an output vector y. The set of available input-
output data for the approximation is as follows:
Input Signal:
Nix
m
i
,...,2,1,
Desired Response:
Nid
i
,...,2,1,
1
Note that the output is assumed to be one
dimensional. Let the approximating function be
denoted by f (x). The function (xi; f (xi)) is used to
compute a new estimate
f
ˆ
as an approximation of
the function f.
In this section, we propose an algorithmic
approach to build CBWNN in an incremental way.
The details of our approach are as follows:
Step 1. At first, the candidate wavelet library is
constructed to be selected as the wavelet network
activation functions. This step is the following:
Select the mother wavelet that can cover the entire
support of the signal to be analyzed.
Use the discrete wavelet transform using dyadic
sampling of the continuous wavelet transform to
construct the wavelet library.
Step 2. Apply the Least Trimmed Square method to
choose the correct wavelet to initialize and build our
wavelet neural network.
Step 3. Use an Emin error between the input and the
network output as a stopping condition for learning.
Step 4. Select the next wavelet from the wavelet
library (MLWF). The addition of wavelet is done
incrementally (the selection is sequential). The
learning (Mejdoub, FontelesBen Amar, Antonini,
2009) is incremental and repeat the following steps:
Step 5. Evaluate the dual basis of activation wavelet
of the hidden layer of the wavelet neural network and
select a new wavelet from the wavelet library
(MLWF).
Step 6. If the error Emin is reached then it is the end
of the learning, otherwise, a new wavelet of the
library is chosen and one returns to the step 2.
4 RESULTS AND DISCUSSION
In this study, we attempted to approximate
(reconstruct) three signals F1(x), F2 (x) and F3(x)
which are defined by the equations (16), (17) and
(18).
5.2,5.2)sin()cos(5.1)(1 xforxxxF
(16)
5.2,5.2)5.1sin()(2 xforxxF
(17)
)33(
13
x
exxF
(18)
The result (Table 1) below shows the MSE after
100 training for classical wavelet neural networks
(CWNN)[49] and only 50 iterations for BWNN for
the F1and F2 signals.
Experiment results are performed to prove the
effectiveness of our proposed approach. The
evaluation metrics, namely, the Mean Square Error
(MSE) and the training time are used to compare our
approach
(BWNN) with the classical wavelet
neural networks (CWNN) approaches.
Functions Approximation using Multi Library Wavelets and Least Trimmed Square (LTS) Method
473
The Mean Square Error (MSE) is defined by:
N
i
i
yxf
N
MSE
1
2
)(
ˆ
1
(19)
Table 1: Comparison between BWNN and CWNN (Bellil,
Ben Amar, Alimi, 2006) in term training time.
Functions
Methods
F1 F2
Average
training
time(sec)
CWNN 0.45212 0.04582 80
BWNN 0.17251 0.00742 66.5
For F1, the MSE for CWNN is 0.45212, comparing
to 0.17251 for BWNN. For F2, the MSE using CWNN
is equal to 0.045282, comparing to 0.00742 for our
proposed approach BWNN. Finally, the average
learning time for the CWNN (80 sec) is higher than our
proposed approach (66.5 sec) (Table 1).
Table 2: Comparison between BWNN and WNN in term of
MSE for F3 functions approximation.
Model Basis Function MSE
WNN (Zainuddin,
Pauline,2008)
Gaussian Wavelet 0.0210695
Mexican Hat 9.41899e-005
Morlet 4.11055e-005
BWNN Beta1 wavelet 1,01305e-005
From Table 2, BWNN with Beta wavelet as the
basis function gives the best performance. Our
approach (BWNN) approximates an exponential
function well. Hence, in this case where a 1-D
exponential function is used, BWNN outperforms
WNN.
The Mean Square Error (MSE) of the Mexican hat
WNN is 0,53645 compared to 0,00384 the BW2
BWNN achieved. From these simulations, we can
deduce the efficiency of Beta wavelet in term of
function approximation. The table 3 below gives the
Mean Square Error using traditional wavelets and
Beta wavelet with the Least Trimmed Square (LTS)
method.
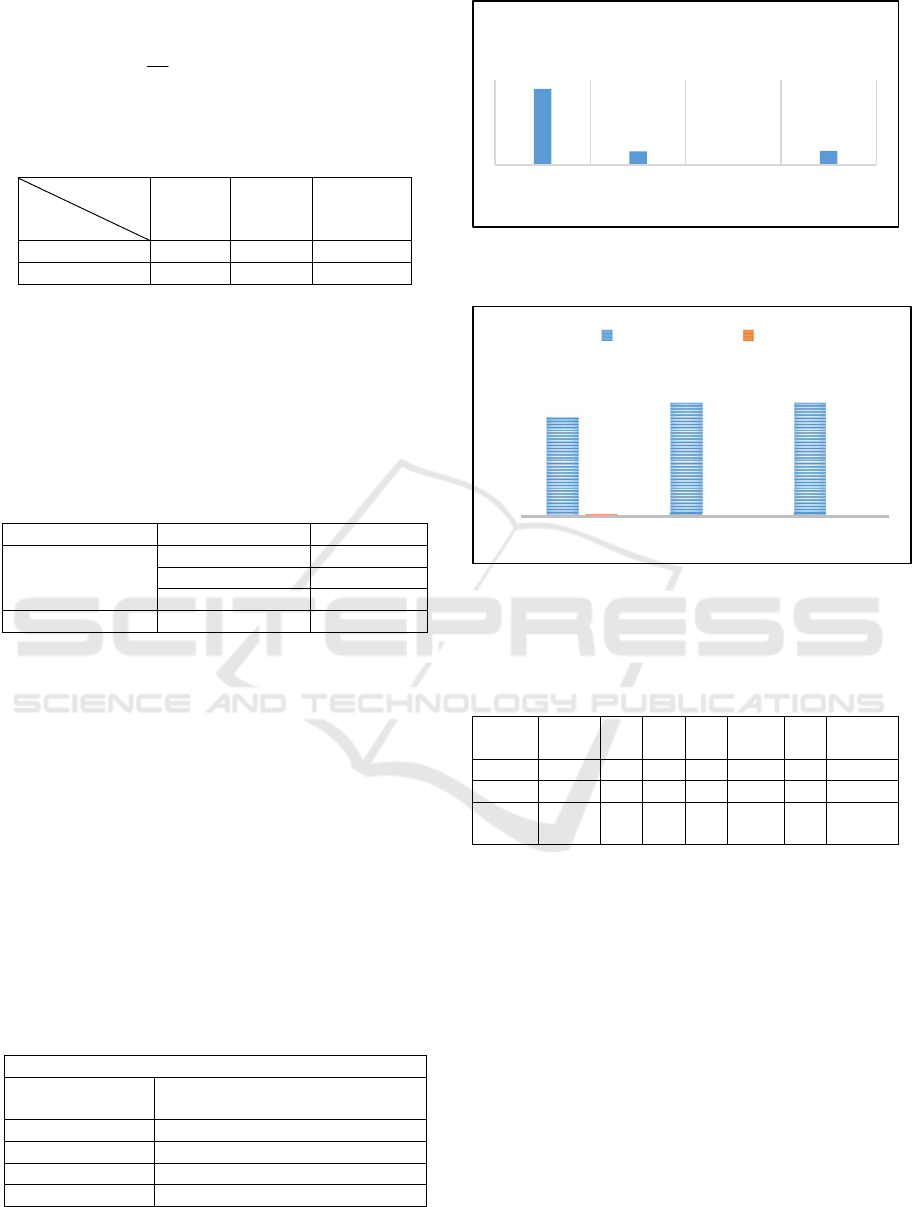
Table 3: Comparison of MSE for Beta wavelets and
Mexican hat type in term of 1 -D approximation.
The Least Trimmed S
q
uare
(
LTS
)
metho
d
Mother wavelet
functions
MSE
Mexican hat 0,53645
Beta1 wavelet 0,0945
Beta2 wavelet 0,00384
Beta3 wavelet 0,09856
Figure 5: Comparison of MSE for Beta wavelets and
Mexican hat type.
Figure 6: Evolution of mean square error as a function of
the number of wavelets selected using The Least Trimmed
Square (LTS) method.
Table 4: Selected mother wavelets and Mean Square Error
(MSE) using The Least Trimmed Square (LTS) method.
Functions
Nb of
wavelets
Beta1 Beta2 Beta3 Mexhat Slog MSE
F1 7 1 2 2 1 1 0.17251
F2 8 2 2 2 1 1 0.00742
F3 8 3 2 1 1 1
0,000010
1305
Table 4 shows that the F1 signal is reconstructed
with a Mean Square Error (MSE) of 0.17251 using 7
wavelets in hidden layer. The best regressors for Multi
Library Wavelet Function (MLWF) are: 1 wavelet
from Beta1, 2 wavelets from Beta2, 2 wavelets from
Beta3, 1 wavelet from the Mexhat wavelet and 1
wavelet from Slog wavelet. The Least Trimmed
Square (LTS) method has a better performance to
choose the mother wavelet from the Multi Library
Wavelet Function (MLWF). Our approach proves to be
effective to choose a suitable wavelet.
Table 4 shows that the F2 signal is reconstructed
with a Mean Square Error (MSE) of 0.00742 using 8
wavelets in hidden layer. The best regressors for
Multi Library Wavelet Function (MLWF) are: 2
wavelets from Beta1, 2 wavelets from Beta2, 2
wavelets from Beta3, 1 wavelet from the Mexhat
0,53645
0,0945
0,00384
0,09856
MEXICAN
HAT
BETA1
WAVELET
BETA2
WAVELET
BETA3
WAVELET
MSE
7
88
0,17251
0,00742
1,01305E‐
05
0
2
4
6
8
10
F1 F2 F3
Nbofwavelets MSE
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
474

wavelet and 1 wavelet from Slog wavelet. Table 5
shows the Residual Based Regressor Selection
(RBRS) which is used to select the mother wavelet
from the Multi Library Wavelet Function (MLWF) to
construct the WNN. This neural network has many
mother wavelets. On the other hand, the LTS selects
a small number of wavelets to build a wavelet
network. So, this observation shows the performance
of LTS to build a wavelet network and consequently
this approach improves the completeness and the
performance of our network.
Table 5: Selected mother wavelets and Mean Square Error
(MSE) using Residual Based Regressor Selection (RBRS).
Functions
Nb of
wavelets
Beta1 Beta2 Beta3 Slog MSE
F1 12 3 2 3 1 0.85231
F2 11 2 3 2 2 0.62531
F3 12 3 3 2 2 0.78563
The results presented in table 5 also show the
performance of our approach which used The Least
Trimmed Square (LTS) method as a selection method
to choose the suitable wavelets from the wavelet
library in order to build the Wavelet Neural networks.
5 CONCLUSIONS
This paper presents function approximation by using
a new approach for constructing a Beta Wavelet
Neural Networks (BWNN). We have investigated the
universal approximation theory of wavelet neural
networks whose transfer functions are Beta Wavelet
(Beta1.Beta2...). The problem was to find the optimal
network structure. In order to determine the optimal
network, a constructive neural network-learning
algorithm is used to add and train these additional
neurons. The general goal of this algorithm is to
minimize the number of neurons in the network
during the learning phase. This phase is empowered
by the use of the Multi Library Wavelet Function
(MLWF).
The Least Trimmed Square (LTS) method is
applied for selecting the wavelet candidates from the
MLWF to construct the BWNN. Comparing to the
classical algorithms, the results show a significant
improvement in the resulting performance and
topology.
These results have been realized thanks to many
capacities that are listed as:
The capacity of the Multi Library Wavelet
Function (MLWF) contended the wavelet
candidates used to construct the BWNN.
The capacity of the Least Trimmed Square
(LTS) method, which is applied, for selecting the
wavelet candidates from the MLWF to construct
the BWNN.
There are promising directions for future work.
We want to explore the optimal approximation of
more general and typical functions to validate our
approach. We plan to extend the optimal
approximation to functions with larger entries.
ACKNOWLEDGEMENTS
We would like to acknowledge the financial support,
under the form of grant, from the General Direction of
Scientific Research (DGRST), Tunisia.
REFERENCES
Chen, D. S., & Jain, R. C. (1994). A robust backpropagation
learning algorithm for function approximation. IEEE
Transactions on Neural Networks, 5(3), 467-479.
Hwang, J. N., Lay, S. R., & Lippman, A. (1994).
Nonparametric multivariate density estimation: a
comparative study. IEEE Transactions on Signal
Processing, 42(1 0), 2795-2810.
Sontag, E. D. (1992). Feedforward nets for interpolation
and classification. Journal of Computer and System
Sciences, 45(1), 20-48.
Park, J., & Sandberg, I. W. (1991). Universal
approximation using radial-basis-function
networks. Neural computation, 3(2), 246-257
Yang, G. W., Wang, S. J., & Yan, Q. X. (2007). Research
of fractional linear neural network and its ability for
nonlinear approach. Chinese Journal of Computers-
Chinese Edition-, 30(2), 189.
Chui, C. K., Li, X., & Mhaskar, H. N. (1994). Neural
networks for localized approximation. Mathematics of
Computation, 63(208), 607-623.
Muzhou, H., Xuli, H., & Yixuan, G. (2009). Constructive
approximation to real function by wavelet neural
networks. Neural Computing and Applications, 18(8),
883.
Dakhli, A., Bellil, W., &Ben Amar, C. (2014).
Classification DNA Sequences of Bacterias using Multi
Library Wavelet Networks.
Llanas, B., & Sainz, F. J. (2006). Constructive approximate
interpolation by neural networks. Journal of
Computational and Applied Mathematics, 188(2), 283-
308.
Han, X., & Hou, M. (2007, August). Neural networks for
approximation of real functions with the Gaussian
functions. In Third International Conference on Natural
Computation (ICNC 2007) (Vol. 1, pp. 601-605).
IEEE.
Functions Approximation using Multi Library Wavelets and Least Trimmed Square (LTS) Method
475

Xu, Z. B., & Cao, F. L. (2005). Simultaneous Lp-
approximation order for neural networks. Neural
Networks, 18(7), 914-923.
Miao, B. T., & Chen, F. L. (2001). Applications of radius
basis function neural networks in scattered data
interpolation. Journal-China University Of Science
And Technology, 31(2), 135-142.
Kreinovich, V. Y. (1991). Arbitrary nonlinearity is
sufficient to represent all functions by neural networks:
a theorem. Neural networks, 4(3), 381-383.
Han, X., &Hou, M. (2008, April). Quasi-interpolation for
data fitting by the radial basis functions.
In International Conference on Geometric Modeling
and Processing (pp. 541-547). Springer, Berlin,
Heidelberg.
Huang, G. B., & Chen, L. (2008). Enhanced random search
based incremental extreme learning
machine. Neurocomputing, 71(16-18), 3460-3468.
Mai-Duy, N., &Tran-Cong, T. (2003). Approximation of
function and its derivatives using radial basis function
networks. Applied Mathematical
Modelling, 27(3),197-220.
Mulero-Martinez, J. I. (2008). Best approximation of
Gaussian neural networks with nodes uniformly
spaced. IEEE transactions on neural networks, 19(2),
284-298.
Ferrari, S., Maggioni, M., & Borghese, N. A. (2004).
Multiscale approximation with hierarchical radial basis
functions networks. IEEE Transactions on Neural
Networks, 15(1), 178-188.
Hwang, J. N., Lay, S. R., &Lippman, A. (1994).
Nonparametric multivariate density estimation: a
comparative study. IEEE Transactions on Signal
Processing, 42(10), 2795-2810.
Lin, C. J. (2006). Wavelet neural networks with a hybrid
learning approach. Journal of information science and
engineering, 22(6), 1367-1387.
Eftekhari, M., & Bazoobandi, H. A. (2014). A differential
evolution and spatial distribution based local search for
training fuzzy wavelet neural network. International
Journal of Engineering, 27(8), 1185-1194.
Bazoobandi, H. A., & Eftekhari, M. (2015). A fuzzy based
memetic algorithm for tuning fuzzy wavelet neural
network parameters. Journal of Intelligent & Fuzzy
Systems, 29(1), 241-252.
Ganjefar, S., & Tofighi, M. (2015). Single-hidden-layer
fuzzy recurrent wavelet neural network: Applications to
function approximation and system
identification. Information Sciences, 294, 269-285.
Tzeng, S. T. (2010). Design of fuzzy wavelet neural
networks using the GA approach for function
approximation and system identification. Fuzzy Sets
and Systems, 161(19), 2585-2596.
Abiyev, R. H., & Kaynak, O. (2008). Fuzzy wavelet neural
networks for identification and control of dynamic
plants—a novel structure and a comparative
study. IEEE transactions on industrial
electronics, 55(8), 3133-3140.
Chen, J., & Bruns, D. D. (1995). Wave ARX neural network
development for system identification using a
systematic design synthesis. Industrial & engineering
chemistry research, 34(12), 4420-4435.
Zhang, Q., & Benveniste, A. (1992). Wavelet
networks. IEEE transactions on Neural Networks, 3(6),
889-898.
Yao, S., Wei, C. J., & He, Z. Y. (1996). Evolving wavelet
neural networks for function
approximation. Electronics Letters, 32(4), 360.
Tzeng, S. T. (2010). Design of fuzzy wavelet neural
networks using the GA approach for function
approximation and system identification. Fuzzy Sets
and Systems, 161(19), 2585-2596.
Karamodin, A., Haji Kazemi, H., &Hashemi, S. M. A.
(2015). Verification of an evolutionary-based wavelet
neural network model for nonlinear function
approximation. International Journal of
Engineering, 28(10), 1423-1429.
Ganjefar, S., & Tofighi, M. (2015). Single-hidden-layer
fuzzy recurrent wavelet neural network: Applications to
function approximation and system
identification. Information Sciences, 294, 269-285.
Schmidt, W. F., Kraaijveld, M. A., & Duin, R. P. (1992,
August). Feed forward neural networks with random
weights. In International Conference on Pattern
Recognition (pp. 1-1). IEEE Computer Society Press.
Pao, Y. H., & Takefuji, Y. (1992). Functional-link net
computing: theory, system architecture, and
functionalities. Computer, 25(5), 76-79.
Pao, Y. H., Park, G. H., & Sobajic, D. J. (1994). Learning
and generalization characteristics of the random vector
functional-link net. Neurocomputing, 6(2), 163-180.
McLoone, S., Brown, M. D., Irwin, G., & Lightbody, A.
(1998). A hybrid linear/nonlinear training algorithm for
feedforward neural networks. IEEE Transactions on
Neural Networks, 9(4), 669-684.
Huang, G. B., Zhu, Q. Y., &Siew, C. K. (2006). Extreme
learning machine: theory and
applications. Neurocomputing, 70(1-3), 489-501.
Igelnik, B., &Pao, Y. H. (1995). Stochastic choice of basis
functions in adaptive function approximation and the
functional-link net. IEEE Transactions on Neural
Networks, 6(6), 1320-1329.
Zhang, Q., & Benveniste, A. (1992). Wavelet
networks. IEEE transactions on Neural Networks, 3(6),
889-898.
Dakhli, A., Bellil, W., &Ben Amar, C. (2016, November).
DNA Sequence Classification Using Power Spectrum
and Wavelet Neural Network. In International
Conference on Hybrid Intelligent Systems (pp. 391-
402). Springer, Cham.
Zhang, Q. (1997). Using wavelet network in nonparametric
estimation. IEEE Transactions on Neural
networks, 8(2), 227-236.
Dakhli, A., & Bellil, W., Ben Amar, C. (2016). Wavelet
neural networks for DNA sequence classification using
the genetic algorithms and the least trimmed
square. Procedia Computer Science, 96, 418-427.
Daubechies, I. (1992). Ten lectures on wavelets (Vol. 61).
Siam.
ICEIS 2020 - 22nd International Conference on Enterprise Information Systems
476

Antonini, M., Barlaud, M., Mathieu, P., & Daubechies, I.
(1992). Image coding using wavelet transform. IEEE
Transactions on image processing, 1(2), 205-220.
Payan, F., & Antonini, M. (2006). Mean square error
approximation for wavelet-based semiregular mesh
compression. IEEE transactions on visualization and
computer graphics, 12(4), 649-657.
Wali, A., Aoun, N. B., Karray, H., Ben Amar, C., & Alimi,
A. M. (2010, December). A new system for event
detection from video surveillance sequences.
In International Conference on Advanced Concepts for
Intelligent Vision Systems (pp. 110-120). Springer,
Berlin, Heidelberg.
Mejdoub, M., Fonteles, L., Ben Amar, C., & Antonini, M.
(2009). Embedded lattices tree: An efficient indexing
scheme for contentbased retrieval on image
databases. Journal of Visual Communication and Image
Representation, 20(2), 145-156.
Boughrara, H., Chtourou, M., & Ben Amar, C. (2012,
May). MLP neural network based face recognition
system using constructive training algorithm. In 2012
International Conference on Multimedia Computing
and Systems (pp. 233-238). IEEE.
Dakhli, A., Bellil, W., & Ben Amar, C. (2016, October).
Wavelet Neural Network Initialization Using LTS for
DNA Sequence Classification. In International
Conference on Advanced Concepts for Intelligent
Vision Systems (pp. 661-673). Springer, Cham.
Teyeb, I., Jemai, O., Zaied, M., & Ben Amar, C. (2014,
July). A novel approach for drowsy driver detection
using head posture estimation and eyes recognition
system based on wavelet network. In IISA 2014, The
5th International Conference on Information,
Intelligence, Systems and Applications (pp. 379-384).
IEEE.
Othmani, M., Bellil, W., Ben Amar, C., &Alimi, A. M.
(2010). A new structure and training procedure for
multi-mother wavelet networks. International journal
of wavelets, multiresolution and information
processing, 8(01), 149-175.
Charfeddine, M., El’arbi, M., & Ben Amar, C. (2014). A
new DCT audio watermarking scheme based on
preliminary MP3 study. Multimedia tools and
applications, 70(3), 1521-1557.
Bouchrika, T., Zaied, M., Jemai, O., & Ben Amar, C. (2012,
December). Ordering computers by hand gestures
recognition based on wavelet networks.
In CCCA12 (pp. 1-6). IEEE.
El Adel, A., Ejbali, R., Zaied, M., & Ben Amar, C. (2016).
A hybrid approach for Content-Based Image Retrieval
based on Fast Beta Wavelet network and fuzzy decision
support system. Machine Vision and
Applications, 27(6), 781-799.
Dakhli, A., & Ben Amar, C. (2019). Power spectrum and
dynamic time warping for DNA sequences
classification. Evolving Systems, 1-10.
Dhibi, N,, Ben Amar, C. (2019),Multi-mother wavelet
neural network-based on genetic algorithm and
multiresolution analysis for fast 3D mesh deformation.
IET Image Processing 13(13): 2480-2486.
Bellil, W., Ben Amar, C. & Alimi, A. M. (2006).
Comparison between beta wavelets neural networks,
RBF neural networks and polynomial approximation
for 1D, 2D functions approximation. International
Journal of Applied Science, Engineering and
Technology, 13, 33-38.
Functions Approximation using Multi Library Wavelets and Least Trimmed Square (LTS) Method
477
