
Chalcogenide All-solid Hybrid Microstructured Optical Fiber
with Flattened Normal Dispersion and High Birefringence
in the mid-IR Region
Hoang Tuan Tong, Hoa Phuoc Trung Nguyen, Takenobu Suzuki and Yasutake Ohishi
Research Center for Advanced Photon Technology, Toyota Technological Institute,
2-12-1 Hisakata, Tempaku, Nagoya, 468-8511, Japan
Keywords: Chalcogenide Microstructured Optical Fibers, Chromatic Dispersion, Birefringence Fiber, Supercontinum
Generation.
Abstract: We propose in this work a new chalcogenide hybrid microstructured optical fiber with all-solid structure to
realize a flattened normal chromatic dispersion profile in a broad wavelength range which is important for
highly coherent and broad bandwidth supercontinuum generation in the mid-infrared window. The
calculated results show that the normal dispersion regime can be obtained from 4.5 to 13 µm with the
flatness of 4 ps/km-nm. In addition, the birefringence properties of the proposed fiber are investigated. The
effects of breaking the symmetry of the fiber structure and increasing the refractive index difference
between the core and the cladding solid rods can make the phase birefringence reach the values of the order
of 10
-3
.
1 INTRODUCTION
Mid-infrared supercontinuum (MIR SC) light
sources are expected to have many potential
applications, such as bio-photonic diagnostics
(Verdonck, 2016), spectroscopy (Cruz, 2015) and
infrared imaging (Su, 2014) due to the presence of
unique molecular absorption bands in the MIR
region. Among a variety of nonlinear optical fibers
which have been widely studied for the generation
of MIR SC, chalcogenide optical fibers have great
advantages because they have wide transmission
window up to around 18 μm and high nonlinearity
(Kohoutek, 2013; Zakery, 2003; Romanova, 2014).
Aiming at the generation of very broad SC spectral
bandwidth, a great number of studies on SC
generation by pumping highly nonlinear optical
fibers in the anomalous dispersion regime have been
demonstrated. However, the generated SC spectra
are usually incoherent and the output SC pulses have
complex temporal properties (Dudley, 2006). More
recently, several studies showed that highly coherent
SC generation could be achieved by pumping in the
normal dispersion regime to overcome the low
coherence and complex temporal properties
(Klimczak, 2014; Liu, 2016; Klimczak, 2016), but
this pumping scheme drastically reduced the SC
spectral bandwidth. To maintain the high coherence
and improve the spectral bandwidth of SC, a broad
and flattened chromatic dispersion in the normal
dispersion regime is important. In addition, to
minimize detrimental effects such as, polarization
mode dispersion, polarization noise and instability,
polarization-maintaining chalcogenide fibers which
have high birefringence are potential candidates
(Caillaud, 2016; Ghosh, 2019). However, high
birefringence properties were demonstrated by using
photonic crystal fibers with very complex elliptical
air-hole structures which are very difficult to
fabricate (Dabas, 2011; Yue, 2007; Hui, 2018; Saha,
2019).
In our previous work (Nagasaka, 2017), it was
shown that a broadband and highly coherent MIR
SC can be generated in a chalcogenide double-clad
fiber using femtosecond pulses to pump in the
normal dispersion regime. The fiber was
experimentally fabricated by using As
2
Se
3
, AsSe
2
and As
2
S
5
chalcogenide glasses. In this work, we
propose a new chalcogenide all-solid hybrid
microstructured optical fiber (Ch-ASHMOF) with
only one ring of 6 circular solid rods in the cladding
and a high-index circular core in the center to obtain
Tong, H., Nguyen, H., Suzuki, T. and Ohishi, Y.
Chalcogenide All-solid Hybrid Microstructured Optical Fiber with Flattened Normal Dispersion and High Birefringence in the mid-IR Region.
DOI: 10.5220/0009804500930098
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - DCNET, OPTICS, SIGMAP and WINSYS, pages 93-98
ISBN: 978-989-758-445-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
93

a more flattened chromatic dispersion in a broad
wavelength range of the normal dispersion regime.
Due to the absence of complex air-hole structures,
the fiber fabrication is more feasible than using
complex elliptical air-hole structures. The results
show that flattened chromatic dispersion can be
obtained from 4.5 to 13 µm with the flatness of 4
ps/km-nm. In addition, the birefringence properties
of the fiber are investigated by tuning the
geometrical parameters and increasing the refractive
index difference between the core and cladding rods.
As a result, the phase birefringence can reach the
values of the order of 10
-3
.
2 MATERIAL PROPERTIES
Figure 1a shows the refractive index profiles of
As
2
Se
3
, AsSe
2
and As
2
S
5
chalcogenide glasses. They
were measured by using ellipsometry method. The
refractive index difference between As
2
Se
3
and
As
2
S
5
is as large as 0.6 whereas refractive indices of
As
2
Se
3
and AsSe
2
are close. Based on the measured
refractive index data in Fig. 1a, the material
dispersions of those glasses were calculated and are
shown in Fig. 1b. The zero-dispersion wavelengths
of As
2
Se
3
, AsSe
2
and As
2
S
5
glasses were 6.5, 7.2
and 5.2 µm, respectively. The material
dispersion of As
2
S
5
rapidly increases beyond 5 µm
but material dispersions of As
2
Se
3
and AsSe
2
gradually increase beyond 6 µm. In Fig. 1c,
transmission spectra of As
2
Se
3
, AsSe
2
and As
2
S
5
glasses are shown. The transmission spectra were
measured using a UV/VIS/NIR spectrometer (Perkin
Elmer, Lambda 900) and an FTIR spectrometer
(Perkin Elmer, Spectrum 100) with 1 mm-thick
samples. As
2
Se
3
and AsSe
2
glasses are still
transparent (higher than 40%) beyond 13 µm,
whereas As
2
S
5
glass is not transparent over 13 µm.
An absorption band above 9 µm of As
2
S
5
glass is
caused by the As-S bonds. Absorption bands from
14 to 16 µm and above 17 µm of As
2
Se
3
and AsSe
2
glasses are caused by the As-Se bonds. An
absorption peak at 12 µm which is caused by the Se-
OH bonds is found only for AsSe
2
.
3 FIBER DESIGN
3.1 Flattened Chromatic Dispersion
In our previous work (Nagasaka, 2017), we
demonstrated a chalcogenide double cladding fiber
Figure 1: (a) Refractive index, (b) material dispersion and
(c) transmission properties of As
2
Se
3
, AsSe
2
and As
2
S
5
chalcogenide glasses, respectively.
(Ch-DCF) whose core, first cladding and second
cladding layers were made of the As
2
Se
3
, AsSe
2
and
As
2
S
5
glasses, respectively, The diameters of the
core and first cladding were D
core
= 7.8 µm and D
clad1
= 30.7 µm, respectively. Its schematic cross-section
image is shown in Fig. 2 and its calculated
chromatic dispersion profile is shown in Fig. 3. A
normal dispersion regime is obtained from 4.5 to
12.5 µm with a minimum of -12.5 ps/km-nm at 9.4
µm and anomalous chromatic dispersion is realized
beyond 12.5 µm. Using 2.8-cm-long section of this
fiber, we demonstrated SC generation extending
from 2 to 14 μm at the -40 dB level by using the
pump wavelength of 10 μm and the coupled pump
peak power of 1.3 MW (Nagasaka, 2017).
To make the normal dispersion profile more
flattened, a Ch-ASHMOF with an As
2
Se
3
core,
AsSe
2
cladding and a ring of 6 As
2
S
5
rods is
OPTICS 2020 - 11th International Conference on Optical Communication Systems
94

proposed in this work. The diameters of the core,
solid rods and pitch are D
core
=8.0, d=1.9 and =13
µm, respectively, as shown in Fig. 2. Using this Ch-
ASHMOF, a normal dispersion regime whose flatness
is approximately 4 ps/km-nm can be obtained from
4.5 to 13 µm as calculated and shown in Fig. 3.
Figure 2: Schematic cross-sectional images of
chalcogenide double-clad fiber (Ch-DCF) and
chalcogenide all-solid hybrid microstructured optical fiber
(Ch-ASHMOF).
Figure 3: Calculated chromatic dispersion profiles of the
Ch-DCF and Ch-ASHMOF which are depicted in Fig. 2.
The calculations of chromatic dispersion profile were
performed by using a commercial software (Mode
Solution) from the Lumerical company.
3.2 Birefringence Properties
The phase birefringence B(
) is defined as the
difference between n
x
and n
y
which are the real part
of the effective refractive indices of x-polarized
fundamental modes HE
11
(slow axis) and y-polarized
fundamental modes HE
11
(fast axis) (Caillaud, 2016;
Ghosh, 2019). It is calculated by using Eq. 1
() n() n()
xy
B
(1)
Therefore, the key point of realizing the
birefringence is to destroy the symmetry of fiber
structure and increase the effective index difference
between the two orthogonal polarization modes
(Dabas, 2011). For microstructured optical fibers,
high birefringence can be achieved by designing an
asymmetric arrangement of air holes, not only by
altering the air holes size near the core area
(Caillaud, 2016; Ortigosa, 2000; Ju, 2003), but also
by changing the shape of air holes (Yue, 2007), or
by introducing mechanical stress as demonstrated in
(Schreiber, 2005). In our work, the symmetry of the
solid-rod structure is broken by modifying the
properties of the L and R rods which take the core as
a reflecting point as shown in Fig. 4.
Figure 4 shows the geometrical changes in the
cross-sectional structures of the Ch-ASHMOFs from
S0 to S1, S2a and S3a. In fact, the changes occur
only for the L and R rods whereas other components
keep constant. In S1 and S3a, the diameters of the L
and R rods increase from 1.9 to 4 and 8 µm,
respectively, as compared to that in S0. Furthermore,
in S2a, the distances from the core to the centers of
Figure 4: Schematic cross-sectional images of Ch-
ASHMOFs (S0, S1, S2a and S3a). The two As
2
S
5
(L and
R) rods in these structures were modified to study their
effects on the phase birefringence of the fiber.
As
2
Se
3
AsSe
2
As
2
S
5
D
clad1
Ch-DCF
D
core
d
D
core
As
2
Se
3
As
2
S
5
AsSe
2
Ch-ASHMOF
123456789101112131
4
-40
-30
-20
-10
0
10
20
Ch-DCF
Ch-ASHMOF
Dispersion (ps/km-nm)
Wavelength (um)
~4 ps/km-nm
S0
LR
S1
S2a
n
S3a
n
Chalcogenide All-solid Hybrid Microstructured Optical Fiber with Flattened Normal Dispersion and High Birefringence in the mid-IR
Region
95

the L and R rods become shorter and the diameters
of the L and R rods are 4 µm.
The calculated wavelength dependence of the
phase birefringence profiles corresponding to S0,
S1, S2a and S3a fiber structures are shown in Fig. 5.
It can be noticed that the phase birefringence
increases significantly as depicted by the red line
(S2a) when the L and R rods get closer to the core
because the symmetry of the fiber structure is
strongly destroyed. Besides, the phase birefringence
can be very high as shown by the blue line (S3a)
when the diameters of the L and R rods become very
different from the other As
2
S
5
rods. As a result, the
phase birefringence can reach 3.6 x10
-3
at 12 µm.
Figure 5: Calculated phase birefringence of Ch-
ASHMOFs (S0, S1, S2a and S3a) whose cross-section
structures were depicted in Fig. 4, respectively.
To further increase the phase birefringence, we
investigate the effect of increasing the refractive
index difference (n) between the core and the solid
rods in the cladding. Figure 6 illustrates the
schematic cross-sectional images of S2a, S2b and
S2c structures. These structures have an identical
geometry, but the refractive index of the solid rods
in the cladding is assumed to be different from that
of S2a, S2b and S2c. The small-grid pattern in S2b
indicates that the refractive index of the solid rods in
the cladding of S2b decreases by 0.05 as compared
to that of the As
2
S
5
in S2a. The large-grid pattern in
S2c indicates that the refractive index of the solid
rods in the cladding of S2c decreases by 0.1 as
compared to that of the As
2
S
5
in S2a. In other words,
the n increases by 0.05 and 0.1 in S2b and S2c as
compared to S2a, respectively. The calculated
wavelength dependence of the phase birefringence
profiles corresponding to S2a, S2b and S2c fiber
structures are shown in Fig. 7 as the red solid line,
dashed line and dotted line, respectively. It is
obvious that the phase birefringence increases when
n increases, especially at wavelengths longer than
7 µm.
Figure 6: Schematic cross-sectional images of Ch-
ASHMOFs (S2a, S2b and S2c). The refractive indices of 6
rods in the cladding of the S2b and S2c structures were
assumed to decrease by 0.05 and 0.1, respectively, as
compared to the measured refractive index of As
2
S
5
glass
which was used in the S2a structure.
Figure 7: Calculated phase birefringence of Ch-
ASHMOFs (S2a, S2b and S2c) whose cross-section
structures were depicted in Fig. 6.
Figure 8: Schematic cross-sectional images of
Ch-ASHMOFs (S3a, S3b and S3c). The refractive indices
of 6 rods in the cladding of the S3b and S3c structures
were assumed to decrease by 0.05 and 0.1, respectively, as
compared to the measured refractive index of As
2
S
5
glass
which was used in the S3a structure.
Similarly, the effect of increasing n was
investigated for the S3a fiber structure. The change
in refractive index of the rods in the cladding is
indicated by the small and large grid patterns in
Fig. 8. The calculated wavelength dependence of
3456789101112
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Phase birefringence (x10
-3
)
Wavelength (um)
S0
S1
S2a
S3a
S2a
n
S2b
n+0.05
S2c
n+0.1
3456789101112
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Phase birefringence (x10
-3
)
Wavelength (um)
S2a (
n)
S2b (
n+0.05)
S2c (
n+0.1)
S3a
n
S3b
n+0.05
S3c
n+0.1
OPTICS 2020 - 11th International Conference on Optical Communication Systems
96
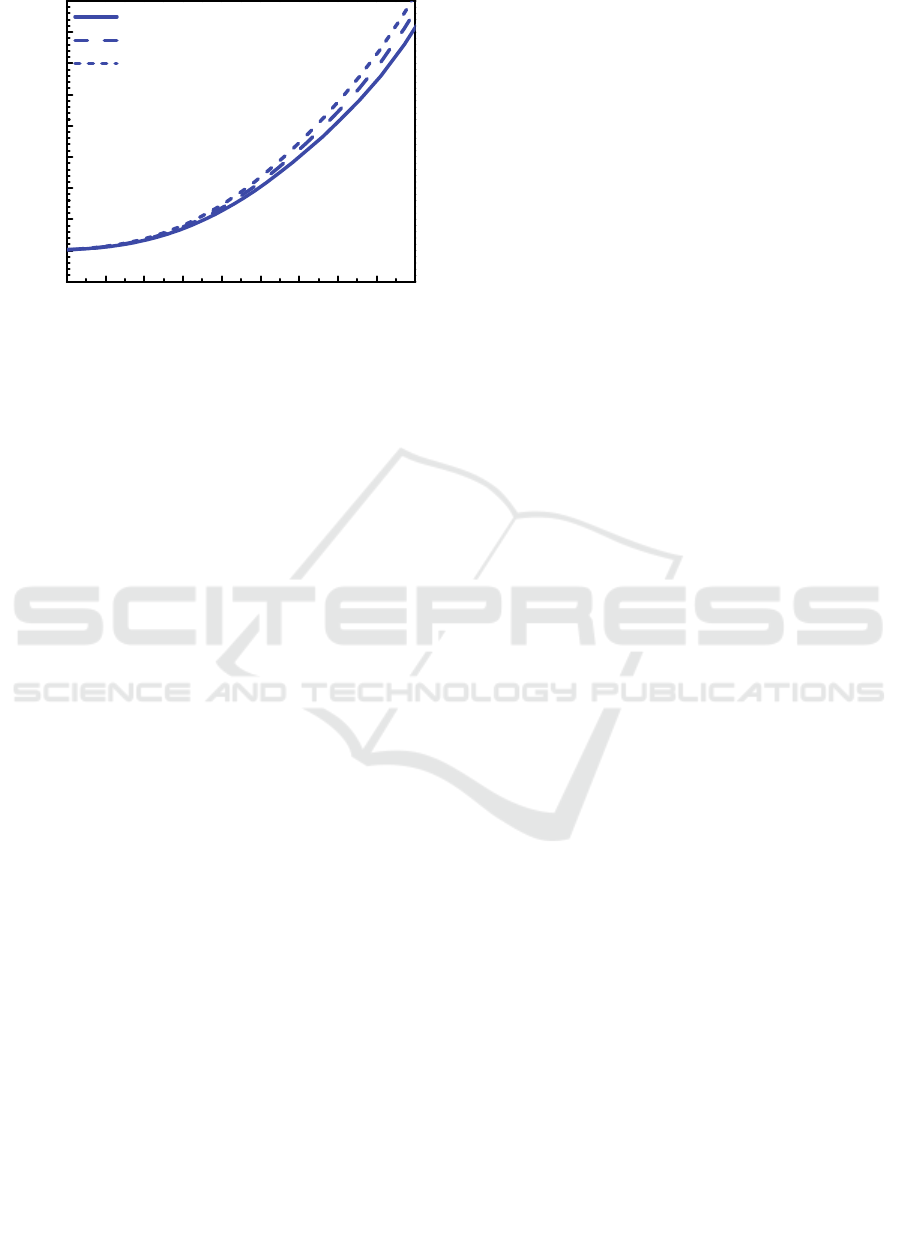
Figure 9: Calculated phase birefringence of Ch-
ASHMOFs (S3a, S3b and S3c) whose cross-section
structures were depicted in Fig. 8.
the phase birefringence profiles corresponding to the
S3a, S3b and S3c fiber structures are shown in Fig. 9
as the blue solid line, dashed line and dotted line,
respectively. As can be seen, the phase birefringence
can be larger than 4.0x10
-3
in case of the S3c
structure.
4 CONCLUSIONS
In this work, a new Ch-ASHMOF made of As
2
Se
3
,
AsSe
2
and As
2
S
5
glasses with all-solid structure was
proposed to realize a flattened chromatic dispersion
in a broad wavelength range of the normal
dispersion regime. The calculated results show that
the normal dispersion regime can be obtained from
4.5 to 13 µm with the flatness of 4 ps/km-nm. In
addition, the birefringence properties of the fiber
were investigated by changing the diameter of two
solid rods in the cladding to break the symmetry of
the fiber structure and by increasing the refractive
index difference between the core and the rods in the
cladding. The combination of these effects can make
the phase birefringence reach the values of the order
of 10
-3
. Due to the feasible fabrication process,
flattened chromatic dispersion and the ability of
controlling phase birefringence, the proposed Ch-
ASHMOF can be a good candidate to realize MIR
SC generation with broad bandwidth and high
coherence for many potential applications.
ACKNOWLEDGEMENTS
This work was supported by the Japan Society for
the Promotion of Science (JSPS) KAKENHI (Grant
Number 15H02250, 17K18891 and 18H01504).
REFERENCES
Verdonck, M., Denayer, A., Delvaux, B., Garaud, S., De,
W. R., Desmedt, C., Sotiriou, C., Willard, G. K. and
Goormaghtigh, E., 2016. Characterization of human
breast cancer tissues by infrared imaging, Analyst,
141, 606-619.
Cruz, F. C., Maser, D. L., Johnson, T., Ycas, G., Klose,
A., Giorgetta, F. R., Coddington, I. and Diddams, S.
A., 2015. Mid infrared optical frequency combs based
on difference frequency generation for molecular
spectroscopy, Opt. Express, 23, 26814-26824.
Su, R., Kirillin, M., Chang, E. W., Sergeeva, E., Yun, S.
H. and Mattsson, L., 2014. Perspectives of mid-
infrared optical coherence tomography for inspection
and micro metrology of industrial ceramics, Opt.
Express, 22. 15804-15819.
Kohoutek, T., Orava, J., Greer, A. L. and Fudouzi, H.,
2013. Submicrometer soft lithography of a bulk
chalcogenide glass, Opt. Express, 21, 9584-9591.
Zakery, A. and Elliott, S. R., 2003. Optical properties and
applications of chalcogenide glasses: a review, J. Non-
Cryst. Solids, 330, 1–12.
Romanova, E. A., Kuzyutkina, Y. S., Konyukhov, A. I.,
Abdel M. N., Seddon, A. B., Benson, T. M., Guizard,
S. and Mouskeftaras, A., 2014. Nonlinear optical
response and heating of chalcogenide glasses upon
irradiation by the ultrashort laser pulses, Opt. Eng., 53,
071812.
Dudley, J. M., Genty, G. and Coen, S., 2006.
Supercontinuum generation in photonic crystal fiber,
Rev. Mod. Phys., 78, 1135–84.
Klimczak, M., Siwicki, B., Skibinski, P., Pysz, D.,
Stȩpien, R., Heidt, A., Radzewicz, C. and Buczynski,
R., 2014. Coherent supercontinuum generation up to
2.3 μm in all-solid softglass photonic crystal fibers
with flat all-normal dispersion, Opt. Express, 22,
18824-18832.
Liu, L., Cheng, T., Nagasaka, K., Tong, H.T., Qin, G.,
Suzuki, T. and Ohishi, Y., 2016. Coherent mid-
infrared supercontinuum generation in all-solid
chalcogenide microstructured fibers with all-normal
dispersion, Opt. Lett., 41, 392-395.
Klimczak, M., Siwicki, B., Zhou, B., Bache, M., Pysz, D.,
Bang, O. and Buczynski, R., 2016. Coherent
supercontinuum bandwidth limitations under
femtosecond pumping at 2 μm in all-solid soft glass
photonic crystal fibers, Opt. Express, 24, 29406-
29416.
Caillaud, C., Gilles, C., Provino, L., Brilland, L., Jouan,
T., Ferre, S. and Troles, J., 2016. Highly birefringent
chalcogenide optical fiber for polarization-maintaining
in the 3-8.5 µm mid-IR window, Opt. Express, 24,
7977-7986.
Ghosh, A. N., Meneghetti, M., Petersen, C. R., Bang, O.,
3456789101112
-0.5
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Phase birefringence (x10
-3
)
Wavelength (um)
S3a (
n)
S3b (
n+0.05)
S3c (
n+0.1)
Chalcogenide All-solid Hybrid Microstructured Optical Fiber with Flattened Normal Dispersion and High Birefringence in the mid-IR
Region
97

Brilland, L., Venck, S. and Sylvestre, T., 2019.
Chalcogenide-glass polarization-maintaining photonic
crystal fiber for mid-infrared supercontinuum
generation, J. Phys. Photonics, 1, 044003.
Dabas, B. and Sinha, R. K., 2011. Design of highly
birefringent chalcogenide glass PCF: A simplest
design, Opt. Commun., 284, 1186-1191.
Yue, Y., Kai, G., Wang, Z., Sun, T., Jin, L., Lu, Y. and
Yuan, S., 2007. Highly birefringent elliptical-hole
photonic crystal fiber with squeezed hexagonal
lattice, Opt. Lett., 32(5), 469-471.
Hui, Z., Yang, M., Zhang, Y. and Zhang, M., 2018. Mid-
infrared high birefringence As2Se3-based PCF with
large nonlinearity and distinctive dispersion by using
asymmetric elliptical air hole cladding, Mod. Phys.
Lett. B, 32, 1850023.
Saha, R., Hossain, M.M., Rahaman, M.E. and Mondal,
H.S., 2019. Design and analysis of high birefringence
and nonlinearity with small confinement loss photonic
crystal fiber, Front. Optoelectron., 12, 165-173.
Nagasaka, K., Liu, L., Tuan, T. H., Cheng, T., Matsumoto,
M., Tezuka, H., Suzuki, T. and Ohishi, Y., 2017.
Supercontinuum generation in chalcogenide double-
clad fiber with near zero-flattened normal dispersion
profile. J. Opt, 19, 095502.
Ortigosa, B. A., Knight, J. C., Wadsworth, W. J., Arriaga,
J., Mangan, B. J., Birks, T. A. and Russell, P. S. J.,
2000. Highly birefringent photonic crystal fibers,
Opt. Lett., 25, 1325-1327.
Ju, J., Jin, W. and Demokan, M. S., 2003. Properties of a
highly birefringent photonic crystal fiber,
IEEE Photon. Technol. Lett., 15, 1375-1377.
Yue, Y., Kai, G., Wang, Z., Sun, T., Jin, L., Lu, Y.,
Zhang, C., Liu, J., Li, Y., Liu, Y. and Yuan, S., 2007.
Highly birefringent elliptical-hole photonic crystal
fiber with squeezed hexagonal lattice, Opt. Lett., 32,
469-471.
Schreiber, T., Röser, F., Schmidt, O., Limpert, J., Iliew,
R., Lederer, F., Petersson, A., Jacobsen, C., Hansen,
K.P., Broeng, J. and Tünnermann, A., 2005. Stress-
induced single-polarization single-transverse mode
photonic crystal fiber with low nonlinearity, Opt.
Express, 13, 7621-7630.
OPTICS 2020 - 11th International Conference on Optical Communication Systems
98
