Free-form Trap Design for Vibratory Feeders

using a Genetic Algorithm and Dynamic Simulation

Daniel Franz

een Haraldson

, Lars Carøe Sørensen

and Simon Mathiesen

SDU Robotics, The Maersk McKinney Moller Institute, University of Southern Denmark, 5230 Odense M, Denmark

Keywords:

Self-adaptive Genetic Algorithm, Dynamic Simulation, Part Feeding, Vibratory Feeders, Optimization.

Abstract:

The task of feeding parts into a manufacturing system is still extensively handled using classical vibratory bowl

feeders. However, the task of designing these feeders is complex and largely handled by experience and trial-

and-error. This paper proposes a Self-Adaptive Genetic Algorithm based learning strategy that uses dynamic

simulation to validate feeder designs. Compared to previous approaches of ensuring parts are oriented to a

desired orientation by both deciding on a set of suitable mechanisms and then optimizing them to the speciﬁc

part, this strategy learns a free-form design needing little prior domain knowledge from the designer. This

novel approach to feeder design is validated on two different parts and it creates designs of hills and valley

that reorients the parts to a single orientation. The found designs are validated both in simulation and with

real-world experiments and achieve high success rates for reorienting the parts.

1 INTRODUCTION

Within the domain of assembly automation, the sub-

parts of an assembly need to be physically available

for the system. Whether assembly is done using a

robot or a simpler type of manipulator, the parts need

to be: 1) within reach, 2) singulated enough to be

grasped, and 3) presented to the manipulator in a suf-

ﬁciently accurate position and orientation for the as-

sembly to be carried out successfully. This prepara-

tion task for the parts is typically referred to as Part

feeding, and can often be the bottleneck which limits

the performance of a manufacturing system. There-

fore, efﬁcient solutions are highly sought after. Al-

though ﬂexible feeder systems utilizing computer vi-

sion exist, the classical part feeding techniques of

mechanically ensuring parts always are ready to be

picked from a known position and orientation, are

broadly applied in the manufacturing industry. In

practice, this is often done using Vibratory Feeders

(VFs), either as Vibratory Bowl Feeders (VBFs) or as

Vibratory Linear Feeders (VLFs).

These vibratory feeders feed parts from bulk, us-

ing high-frequency micro-vibrations to convey parts

along a helical track to a speciﬁc location at the outlet

https://orcid.org/0000-0003-2049-336X

https://orcid.org/0000-0003-4165-5719

https://orcid.org/0000-0002-7764-5849

of the feeder from which the parts can then be further

manipulated. While conveying, the parts encounter a

series of passive mechanical orienting devices, called

traps, consisting of geometric features such as: pro-

trusions, narrowings of the track, and steps. The VBF

is a popular approach e.g due to its robustness and

simplicity under operation. However, a feeder is ded-

icated to a speciﬁc part, thus requiring new designs

for new part types. Additionally, this design process

is often associated with high complexity, which in to-

tal this leads to high costs due to the time a designer

must spend on each design. The complexity espe-

cially comes from the process generally being driven

by experience-based trial-and-error approaches, and

thus addressing this issue with a method for facilitat-

ing the design will thereby reduce costs and enable

deployment across a wider range of feeding tasks.

This paper addresses this problem by com-

bining simulation-based evaluation, with a Self-

Adaptive (Meyer-Nieberg and Beyer, 2007) Genetic

Algorithm (GA) (Whitley, 1994), and in doing so it

will be shown that the geometric features needed for

orienting the parts can be learned. This is achieved

by representing the feeder track, as a surface of con-

nected vertices. The shape, and thereby the behav-

ior of the feeder track, can be changed by manipu-

lating the position of these vertices. The task is thus

reduced to the problem of ﬁnding a vertex conﬁgu-

ration which reliably aligns the parts. The resulting

294

Haraldson, D., Sørensen, L. and Mathiesen, S.

Free-form Trap Design for Vibratory Feeders using a Genetic Algorithm and Dynamic Simulation.

DOI: 10.5220/0009816402940304

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 294-304

ISBN: 978-989-758-442-8

Figure 1: The two feeder tracks that was generated using

the Free-Form Trap Designer presented in this paper along

with their respective parts moving clockwise.

track surface then becomes a mixture of valleys and

hills which redirects and reorient the part by taking

advantage of its geometric features and mass distribu-

tion. Examples of two feeder designs generated with

the approach presented in this paper can be seen in

Figure 1. It should be noted that this approach does

not rely on any existing trap design, but rather builds

its own custom orienting features, and as a result pro-

vides a new method for generating reorienting traps

requiring little to no domain speciﬁc knowledge from

the designer.

The paper is structured as follows: Section 2 go

through the related work. Section 3 provides an

overview of the learning strategy as well as describing

the tools used for the implementation. Next, Section 4

describes how the GA was adapted to the domain, fol-

lowed by an elaboration on the self-adapting features

of the GA in Section 5. Furthermore, Section 6 and

Section 7 serves to evaluate and discuss the perfor-

mance of the approach, respectively. Finally, the con-

clusion and proposed future work will be presented in

Section 8 and 9, respectively.

2 RELATED WORK

Even though the design of vibratory part feeders are

traditionally done more or less ad hoc, and that solu-

tions are developed from the experience of the artisan

making them, there have been attempts to formalize

the process.

In this context, one must mention the extensive

work of (Boothroyd, 2005). This work describes the

mechanics of the VF and presents a system for classi-

fying parts based on their geometric envelope together

with a method to match these classiﬁcations to spe-

ciﬁc trap types. There are also guidelines and assistive

functions for adjusting the parameters of a limited set

of traps, but using them requires considerable domain

knowledge and is not completely straight forward.

In order to approach a black box system for sim-

pler trap design, which requires little human interven-

tion or prior knowledge, simulation based approaches

have been pursued in the past. This goes back to

the work of (Berkowitz and Canny, 1996; Berkowitz

and Canny, 1997), which modeled the feeding process

with dynamic simulation and found good correspon-

dence between the simulated results and real world

experiments, however, not without some discrepan-

cies.

In more recent work (Stocker and Reinhart, 2016),

the authors investigate a trap type called a Step. The

interaction between the step and a part is modeled

through simulation, where they perform a sensitivity

analysis for varying parameter settings of both trap

and part geometry to map the behavior. This work

illustrates that even simple traps with one parameter

can have complex behavior, and that it would be bene-

ﬁcial to have automated optimization methods for the

design problem.

Earlier work has pursued optimization methods to

apply to generic trap principles. In (Hofmann et al.,

2013) a Random Search Algorithm is presented. The

algorithm is tested on a Step trap and optimizes this

one parameter trap from a sample space of 13 discrete

values for step height. However, it seems likely that

the approach will struggle with multi-parameter traps

(and thereby larger parameter spaces) and either will

perform insufﬁcient evaluation of the parameter space

or require large amounts of samples.

Another approach to simulation-based optimiza-

tion of traps can be found in (Mathiesen et al., 2018).

This work presents an approach based in Bayesian

Optimization with neighborhood approximation from

Kernel Density Estimation. The approach works on

simple data from the simulation with the evaluation

providing a purely binomial outcome, i.e. did the trap

perform as it should, resulting in a success, or did it

fail. The approach is validated by attempting to orient

a part with four different multi-parameter trap prin-

ciples, these having 1-4 parameters, and with a pa-

rameter space of 19600 points for the trap having the

largest solution space. Although this approach was

able to solve the task within a feasible time frame,

and being generically applicable to any trap principle,

it still only works on speciﬁc traps with speciﬁc sets

of associated parameters. Thus, a designer either has

to choose which trap is useful for orienting the part in

question, or try out all of them.

Another branch of approaches to trap design

started with (Berretty et al., 1999) and was further ex-

tended in (Berretty et al., 2001). These works present

dedicated algorithms to four speciﬁc trap principles,

which ﬁnd good values for their inherent design pa-

Free-form Trap Design for Vibratory Feeders using a Genetic Algorithm and Dynamic Simulation

295

(a) 2D-points. (b) Cross-section. (c) Feeder segment. (d) Triangulation. (e) Surface.

Figure 2: Illustrates how a sequence of 2D-points and lengths gets translated in to its respective feeder design.

rameters under the assumption that parts move along

a linear track, singulated, and at a constant velocity.

The principle of the presented traps all relies on parts

falling through gaps in the track. Similar work (Goe-

mans et al., 2006), and (Goemans et al., 2007) and

(Goemans and van der Stappen, 2008), later intro-

duced additional traps and algorithms, but all these

works also model part motion as quasi-static which

does not account for the uncertainty in part motion

caused by the vibrations. When they in (Goemans and

van der Stappen, 2008) ﬁnd discrepancies between

model and experiments this is accredited to unreal-

istic part motion.

The approach presented in this paper uses dy-

namic simulation similar to (Hofmann et al., 2013)

and (Mathiesen et al., 2018), which we believe bet-

ter encapsulates the stochastic nature of part motion

in the real feeder. However, our approach differs

from all previously mentioned automated design ap-

proaches as it requires no prior knowledge, or deci-

sions, by the designer on how the part is to be ori-

ented, but rather lets the Genetic Algorithm ﬁnd out

on its own.

Genetic algorithms have previously been applied

to the domain of part feeder design, but on the dif-

ferent issue of trap sequencing. The work of (Chris-

tiansen et al., 1996) applied a GA to this problem.

The GA worked on a set of pre-computed matrices de-

scribing the transition of the parts orientations when

subjected to a trap, and efﬁciently combined these to

form a sequence of traps that fully oriented the part to

one speciﬁc orientation. It should be mentioned that

further work has been done on this topic in (Math-

iesen and Ellekilde, 2017) and recently in (Stocker

et al., 2019), but as this is not directly connected to

the topic of this paper, we will merely leave these ref-

erences for completeness.

3 LEARNING STRATEGY AND

TOOLS

This section serves to provide an overview of the ap-

plied strategy to learn a functional feeder design. As

mentioned earlier, the strategy is based on a genetic

algorithm which evaluates a feeder design using dy-

namic simulation. The overall structure of the strat-

egy is as follows:

1. Initialize random population of P individuals

2. For each generation:

(a) For each individual, perform:

i. Feeder Construction.

ii. Feeder Simulation.

iii. Fitness Computation.

(b) Repeat P times to form the new generation:

i. Select a parent-pair.

ii. Generate child from parent chromosomes.

iii. Add child to the new generation.

The core of the learning strategy lies in the genetic al-

gorithm which explores the feeder design space. This,

and details on chromosome encoding, are described

in Section 4, whereas the following subsections elab-

orate on the feeder construction and simulation ap-

proaches used to evaluate the speciﬁc designs formed

by the GA.

3.1 Feeder Construction

The feeder constructor takes as input a structured list

of 2D-points and distances, and converts it to a 3D-

model that can be simulated. Figure 2 shows the over-

all construction process.

First, a list of 2D-points seen in Figure 2a can be

used to draw a closed shape in 2D by connecting each

point with its two neighbors in the list. This shape will

be referred to as a feeder cross-section, and an exam-

ple of this process can be seen in Figure 2b. A wire-

frame can now be formed from introducing additional

cross-sections (displaced along, and with its surface

normal along, the direction of conveying), and con-

necting the points in the cross-sections which share

Please note that when referring to populations and gen-

erations the population is always currently existing. The

term generation is used when referring to the population in

chronological context i.e. past, present, and future genera-

tions.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

296

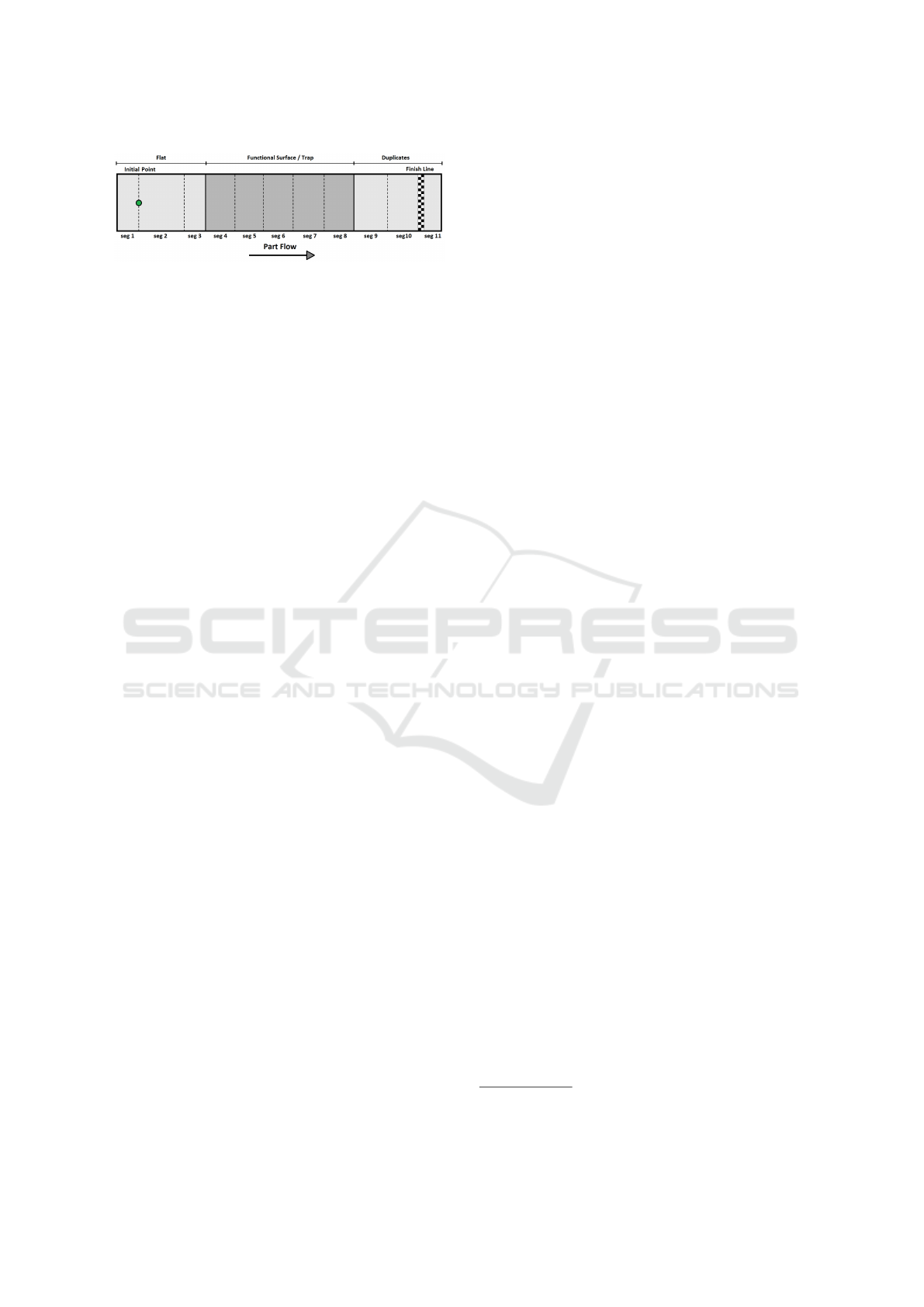
Figure 3: Illustration of the feeder layout showing the initial

point from where parts start and the ﬁnish line. Marked in

dark gray is the functional surface on which the constructed

trap is located.

the same index. This forms a structure which will be

referred to as a feeder segment. An example of this is

found in Figure 2c. Each set of four adjacent points in

the wire-frame are then closed using two triangles as

seen in Figure 2d. Finally, segments are combined

to form the feeder surface as shown in Figure 2e.

All segments in the feeder have a speciﬁed Segment

Height, Segment Width. Additionally, we also con-

straint the length of th the feeder by a Min Segment

Length and Max Segment Length (length being in the

direction of part ﬂow). For convenience our expla-

nation of feeder construction assumes a linear track,

but bowl feeders are easily formed from this when the

direction of conveying instead is transformed to the

tangent of a circle. This naturally also introduces the

Bowl Radius as a design parameter.

The track constructor works with three different

types of sections, which relative placement to each

other is shown in Figure 3:

• Flat - The section which leads the parts from start

to the trap. This section forms a ﬂat track.

• Functional Surface/Trap - The section which the

GA will mold into a trap that orients the part. This

surface is deﬁned by its Number of Cross Sections,

along with the number of Points pr. Cross Section.

• Duplicates - The section which leads the reori-

ented parts away from the feeder. Here each cross-

section is a copy of the last cross-section in the

functional trap.

3.2 Track Surface Smoothing

The feeder constructor tends to form surfaces with

abrupt transitions and sharp edges which in gen-

eral makes the designs fragile and hard to produce.

This issue is addressed through the development of

a smoothing operator, as an attempt to push the

search space exploration towards better designs. The

smoothing operator works by removing points in all

cross-sections of the feeder. Excluding the four cor-

ner points which are kept ﬁxed, the smoothing op-

erator goes through each point on the feeder surface

and removes it at a probability p

, thus simplifying

the surface and dampening the undesired features. To

keep the same number of points for the next genera-

tion, the removed points are reconstructed through a

linear interpolation using the points that persisted.

Therefore a p

of 0 will have no impact on the

surface, whereas a p

of 1 will construct a completely

ﬂat surface deﬁned by the four corner points of the

surface. How the GA adapt this parameter dynami-

cally to create good feeder tracks will be described in

greater detail in Section 5.

3.3 Feeder Simulation

The constructed tracks are evaluated using dynam-

ics simulation. The implementation is based on the

robotics simulation framework RobWorkSim (Joer-

gensen et al., 2010), which provides an interface to,

among others, the physics engine ODE

. RobWork-

Sim also contains efﬁcient methods for collision de-

tection and contact generation, which as such pro-

vides a simulation environment sufﬁciently fast and

accurate to model the dynamics of the system in ques-

tion (Mathiesen et al., 2018).

The parts move by oscillating the feeder with a si-

nusoidal motion both vertically and in the direction

of part ﬂow. Forward conveying is therefore purely

a result of the impact force and friction between the

track and the parts. Although the simulation is inher-

ently deterministic, this approach together with small

perturbations on the initial conditions allows it to suf-

ﬁciently incorporate the stochastic nature of the parts

as they move along the feeder track, and thus provides

a realistic environment for the GA.

3.4 Evaluation by Simulation

The simulation procedure used to evaluate the perfor-

mance of a feeder design is broken up into the follow-

ing steps:

1. The part is spawned at the initial point shown in

Figure 3 with a random orientation as close to the

surface as possible.

2. The simulation runs until it reaches a termination

criteria.

3. The part’s initial and ﬁnal state is saved.

The simulation terminates if one of the following cri-

teria are met:

1. The part reached the ﬁnish line.

2. The part fell off the track.

The Open Dynamics Engine manual can be found at:

http://ode.org/wiki/index.php?title=Manual

Free-form Trap Design for Vibratory Feeders using a Genetic Algorithm and Dynamic Simulation

297

3. The simulation time exceeds a predeﬁned thresh-

old, hence the part got stuck on the track.

The initial state of the part represents its position

and orientation (pose) at the initial point, whereas the

part’s ﬁnal state is its pose when it got the farthest

on the feeder (ideally reaching the ﬁnish line). The

overall layout of the track can be seen in Figure 3.

The feeder will be evaluated over N simulations.

Each successful simulation will thus produce two

transformation matrices, namely the initial transform

and the ﬁnal transform T

, organized as a 2 × N

matrix:



i,1

i,2

··· T

i,N

f ,1

f ,2

··· T

f ,N



(1)

4 THE GENETIC ALGORITHM

A part starts on the feeder in some random orienta-

tion. Looking at the orientations of all the parts be-

ing fed, they occur with some probability distribu-

tion that we denote as the initial distribution of ori-

entations. The purpose of the genetic algorithm is to

transform this distribution of orientations, into an as

concentrated a ﬁnal (post trap) distribution as possi-

ble. In this work we do not use the notion of a ﬁnite

set of distinguishable orientations, as doing so will

inhibit any attempts to directly obtain a quantiﬁable

measure of how close two orientations are to one an-

other. Therefore, part orientations are treated as rota-

tions about the origin in three-dimensional Euclidean

space. Thus, the GA has to cluster these rotation as

densely as possible and into as few disconnected clus-

ters as possible. Albeit there are other components,

this makes up the main part of the ﬁtness function

with which the algorithm operates.

4.1 The Fitness Function

This GA uses a multi-objective ﬁtness function, from

which the total ﬁtness is calculated as the summed to-

tal of three individual ﬁtness scores. The three ﬁtness

functions are a collision-based ﬁtness F

, a distance-

based ﬁtness, F

and an orientation-based ﬁtness F

The collision-based ﬁtness F

is computed as the

amount of triangles in the feeder being in collision

(overlaps) with one another, negated. Feeder de-

signs with fewer collisions c, will thus have a higher

collision-based ﬁtness described by:

= −c (2)

The distance-based ﬁtness F

is computed as the

average distance between the part at its ﬁnal state, and

the goal, measured in segments along the direction of

part ﬂow.

This can be calculated as shown in:

= −

∑

i=1

(3)

N is the total number of simulations and d

is the dis-

tance from the part’s ﬁnal positions to the ﬁnish line.

As an example, a score of F

= −1.3 would indi-

cate that, on average, each part failed to pass the last

segment plus the remaining 30 percent of the second

to last segment. The part’s positions will be derived

from the result matrix of (1).

The orientation-based ﬁtness F

is computed by

measuring the average distance between all pairs of

orientations. This is done by computing the difference

between the concentration of the initial orientations

O(i), relative to that of the ﬁnal orientations, O( f ).

This results in:

= O(f) − O(i) (4)

Here, f and i represents the ﬁnal and initial state being

the rows in the result matrix of (1). A positive F

will,

therefore, indicate that the set of parts terminated in a

more ordered state compared to when they entered the

feeder.

The distance between any pair of orientations are

found by computing the rotation between the two rep-

resented as an Axis-Angle rotation (AA

rot

), thus ob-

taining the smallest possible rotation that separates

them. The concentration of a set of orientations can

then be computed as:

O(x) = −

− N

N−1

∑

j=1

∑

k= j+1

rot

x, j

, T

x,k

) (5)

The square root of the distance between orientations

reward grouping orientations together, over simply

moving all orientations closer to a mean. A perfectly

concentrated set of orientations will therefore have an

O(x) = 0 and decrease as the orientations becomes

more misaligned.

4.2 The Parameter Encoding

All parameters for the optimization are stored as a

binary string, which will be referred to as the Chro-

mosome. Thus, each individual in a population has

its own chromosome. Furthermore, the full chromo-

some holds multiple Genes, that is, sub-strings con-

taining parameters of a speciﬁc type or length, which

again can be further subdivided in to single param-

eters. Breaking the genetic material up into smaller

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

298

Figure 4: Representation of the chromosome structure.

components creates structure and also allows for the

use of customized crossover and/or mutation schemes

(see Section 4.3.3).

Each gene represents a decimal number (referred

to as a double), ranging from 0 − 1, and its binary

string is encoded using b bits of reﬂected binary code

(Gray code). The feeder segments are made from

cross-sections of connected 2D-points, each point is

encoded as two doubles representing its two compo-

nents x an y respectively.

4.2.1 The Problem Encoding

The constructed feeders presented later in Section 6

uses the 3-gene setup represented in Figure 4. The

ﬁrst gene holds the points used to represent each

cross-section in the feeder. The second gene holds

the distances between each cross-section. Both the

ﬁrst and second gene is encoded as doubles of length

b = 10, and the third gene holds the strategy param-

eters used for generating the children/individuals of

the next generation. These values are encoded using

doubles of length b = 20.

4.3 The Strategy Parameters

After the evaluation of all individuals of the current

generation, denoted g

, a number of individuals are

chosen using a tournament-based selection strategy.

These are paired for the recombination step, where

each parent-pair is subjected to a crossover and a mu-

tation scheme to create the children, which make up

generation g

i+1

4.3.1 The Selection Scheme

The Genetic Algorithm uses a deterministic tourna-

ment selection with no elitism. The tournament selec-

tion is applied to an evaluated population and works

by randomly picking s individuals with replacement.

The winner of this tournament is determined as the in-

dividual with the highest ﬁtness, which then becomes

one of two parents needed for recombination. This

process is repeated to gain the second parent forming

a parent-pair. This parent-pair gets one child for the

new generation. This process is then repeated until

the size of the new generation |g

i+1

| is equal to |g

Algorithm 1: The State-Based Crossover Scheme used dur-

ing recombination.

1: // Both parent and child holds a chromosome,

represented as a list of bits

3: procedure SBX(parent

, parent

, p

)

4: child = parent

5: crossoverState = true

6: for i = 1 → |parent

| do

7: if randReal(0, 1) < p

then

8: crossoverState = randBool()

9: end if

10: if crossoverState then

11: child[i] = parent

[i]

12: end if

13: end for

14: return child

15: end procedure

4.3.2 The Crossover Scheme

We refer to the crossover scheme used for this im-

plementation as State-Based Crossover, or SBX. This

crossover strategy allow for multiple crossover points

so that with probability p

any point in the gene be-

comes a crossover point. The implementation of this

scheme is shown in Algorithm 1.

4.3.3 The Mutation Schemes

The mutation scheme takes as input a string of bi-

nary numbers (a gene) and manipulates it, using a

mutation probability/rate p

. This p

, is the sum of

two mutation probabilities, namely a dynamic muta-

tion probability p

, and a static mutation probability

. The dynamic mutation probability is the muta-

tion rate that will be regulated by the Genetic Algo-

rithm’s self-adaption, which will be described in de-

tail in Section 5. The static mutation probability is a

constant value ensuring p

> 0, which otherwise re-

sults in mutation becoming impossible for an individ-

ual. Otherwise, if the mutation rate would become 0

for a signiﬁcant part of the population it could result

in the learning going into stagnation. This GA im-

plementation applies two different mutation schemes,

that is Binary Uniform Mutation and 2D-Point Muta-

tion.

Binary Uniform Mutation (BUM) This mutation

scheme works by iterating through each bit in the

gene, and with probability p

, replacing that bit with

a random binary number. The Binary Uniform Mu-

tation scheme is applied to the genes containing the

Free-form Trap Design for Vibratory Feeders using a Genetic Algorithm and Dynamic Simulation

299

distances between each cross-section, and the genes

containing the strategy parameters (gene

and gene

2D-Point Mutation (2DPM) Instead of going

through each bit, mutating them one by one as in

the Binary Uniform Mutation, the 2D-Point Mutation

scheme operates on all bits of a single point (i.e. the

x- and y-component) at the same time. A mutation of

the point can happen up b times with p

probability.

When a mutation happens it draws two random bit in-

dices (one for x and another for y) and replaces the

value of each bit with a random binary number.

5 SELF-ADAPTION STRATEGY

A general drawback when using Genetic Algorithms

is that its performance is sensitive to the tuning

of its strategy parameters. To remedy the prob-

lem, this implementation uses a self-adaption strat-

egy. This means that the GAs strategy parameters

will be tuned automatically, while solving the task.

This self-adaption use individual level self-adaption

as described in (Meyer-Nieberg and Beyer, 2007).

These strategy parameters are: the crossover rate p

the dynamic mutation rate p

, and the smooth rate

. Including p

allows for the algorithm to au-

tonomously exploit the smoothing property to ﬁrst

generate smooth, but functional, feeders faster, and

subsequently turn down the smoothing to opt for more

detailed geometries. These strategy parameters are lo-

cated at the third gene of each individual, and will be

optimized along with the rest of their chromosome,

using the ﬁtness scores in combination with the se-

lection scheme. The self-adaption is therefore said to

operate on an empirical update rule as described in

(Meyer-Nieberg and Beyer, 2007).

A clear advantage of the self-adaption strategy is

that it makes the GA more robust and simpler to oper-

ate from a user perspective. However, the additional

overhead added to the learning problem effectively

slows down the algorithm as more generations now

will be needed solve the same problem.

The GA’s self-adaption mechanisms are applied

when the new generation is formed. The strategy val-

ues of each parent forms the basis for the strategy val-

ues of their child. This is found by computing the

geometric mean between the parents’ strategy values

by:

A(x

, x

, ...x

) =

∏

i=1

(6)

The result is subjected to crossover and mutation to

form the new strategy values, which are then used to

Algorithm 2: The transition function (TF) that passes ge-

netic material from parents to child.

1: // Deﬁne Parents as Arrays of the 3 Genes

2: parent

[3] = {gene

, gene

}

3: parent

[3] = {gene

, gene

}

5: procedure TF(parent

, parent

, p

)

6: // Deﬁne Child as Array of 3 Genes

7: child[3] = {gene

, gene

}

9: // Decode Strategy Values from each Parent

10: [p

, p

dm1

, p

] ← decode(parent

[3])

11: [p

, p

dm2

, p

] ← decode(parent

[3])

12:

13: // Compute the Geometric Mean

14: p

= A(p

, p

)

15: p

= A(p

dm1

, p

dm2

)

16:

17: // Generate Child’s New Strategy Values

18: child[3] = SBX(parent

[3], parent

[3], p

)

19: child[3] = BUM(child[3], p

+ p

)

20: [p

, p

] ← decode(child[3])

21:

22: // Recombination, Mutation and Smoothing

23: child[2] = SBX(parent

[2], parent

[2], p

)

24: child[2] = BUM(child[2], p

+ p

)

25:

26: child[1] = SBX(parent

[1], parent

[1], p

)

27: child[1] = 2DPM(child[1], p

+ p

)

28: child[1] = Sur f aceSmoothing(child[1], p

)

29: return child

30: end procedure

generate the remaining (gene

and gene

) genes by

applying SBX, mutation, and ﬁnally smoothing.

This is done when applying the transition function

of Algorithm 2 to the parent-pairs chosen by the selec-

tion scheme. The function takes as input two parents

(each with the three genes), and the static mutation

rate p

6 RESULTS

This section presents the result from testing the feeder

design approach on two parts, whereas Section 7 will

serve to discuss these result. The two parts are: 1) A

4 × 8 × 12 mm solid plastic Cube and 2) an industrial

brass part which will be referred to as Cone. The two

parts can be seen in Figure 5, placed on a ﬂat track,

in the simulation environment, oriented in their stable

poses.

The vibratory drive unit used for the experiments

is a BF40 vibration drive, controlled using a Fre-

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

300

Figure 5: The two parts, the cube (top) and the cone (bot-

tom) in their poses. The parts’ stable poses are numbered

from left to right.

Table 1: The list of manual settings used for learning the

designs for both the cube and the cone.

Cube Cone

Number of Cross Sections 5 5

Points pr. Cross Section 8 8

Min Segment Length 15 mm 22 mm

Max Segment Length 36 mm 36 mm

Segment Width 60 mm 60 mm

Segment Height 30 mm 30 mm

Bowl Radius 175 mm 175 mm

Simulations/Evaluation [N] 100 100

Population Size [P] 100 100

Tournament Size [s] 6 6

Static Mutation Rate [p

] 0.002 0.001

quency control unit SIGA, from the manufacturer

Afag Automation AG

. The drive has a vibration angle

of 12

◦

and operates at 50Hz full-wave motion. The

physical properties: parts mass, friction coefﬁcient,

and restitution coefﬁcient between part and feeder has

been determined experimentally. All these parameters

are used to model the system in simulation.

The GA and feeder track constructor also has a list

of settings. The chosen settings for the two test-cases

can be seen in Table 1.

6.1 Learning Feeder Designs

The GA is used to learn a feeder design for each part.

The graphs in Figure 6 show how the ﬁtness evolve

over time for the cone part. The learning graphs

for the cube was left out intentionally, as it has very

similar characteristics. However, it convergence on

a working design around generation 60. Here each

graph shows the learning curve of the best performing

individual in a population, along with the arithmetic

See https://www.afag.com/

mean of the top 30th percentile of the population.

Figure 7 shows how the strategy values adapt over

time. This is shown with the geometric mean of the

top 30th percentile of the population.

The learning is time-consuming, mainly due to the

evaluation step, so evaluations are run in parallel on a

computer cluster

. The learning ran for a total exe-

cution time of 16.5h and 35.5h, for the cube and the

cone, respectively, which resulted in 467 generations

for both.

6.1.1 Selecting the Final Solutions

At the end of each generation, the highest perform-

ing individual in the population is stored, effectively

forming a list of population winners. The highest

scoring individuals in this list are reevaluated each

with 1000 simulations and a new winner is chosen as

the best feeding solution.

The best solution for the cube was found in gener-

ation 439 and in generation 462 for the cone. The cor-

responding model of these feeder designs can be seen

in Figure 8. 3D-printed

versions of these solutions

were used for validation with real-world experiments

and are shown in Figure 1.

6.2 Feeder Validation

The best feeder designs were validated through real-

world experiments on the physical feeder. This was

done using the stable poses for the cube (6 poses) and

the cone (4 poses) shown in Figure 5, and testing suc-

cess rate over a ﬁxed number of experiments for each

stable pose. A success is deﬁned as the part ending up

in the expected orientation.

Results comparing simulation and real-world ex-

periments for both the cube feeder and the cone feeder

is found Table 2 and Table 3, respectively. Here, T is

the number of Tests performed, F counts the number

tests which Failed, and the Performance P is the suc-

cess rate measured in percent. A failed test is deﬁned

as when the part does not ends up in the expected ori-

entation (as shown in Figure 8).

7 DISCUSSION

The learning curves in Figure 6 show that the GA

manages to improve the feeder design across the gen-

The cluster consists of ten PCs each with an Intel Core

i7-3770 CPU@3.40 GHz with 4 cores and 8 threads.

The feeders were printed using a consumer-grade 3D-

printer, and lightly post-processed to remove the uninten-

tional layer lines that occurs when using an FDM printer.

Free-form Trap Design for Vibratory Feeders using a Genetic Algorithm and Dynamic Simulation

301

Figure 6: The learning for the cone part. The learning curve is split up into each of the three ﬁtness scores for transparency.

This is shown for the best performing individual of each generation (blue) and the average score computed from the top 30th

percentile in each generation (red). Note that for the collision based score, the curves are close together.

Figure 7: The evolution of the strategy values over time.

The strategy values were computed as the geometric mean

of the populations top 30th percentile of the population.

This is shown on a logarithmic scale.

Figure 8: The ﬁnal feeder designs for the cube (top), and

the cone (bottom). The rightmost part on each shows the

expected ﬁnal orientation of the part.

erations. The algorithm quickly ﬁnds a design with-

out collisions in its internal model. In around gener-

ation 50 the design also allows the part to move all

the way from its initial starting position to the ﬁnish

line. From the orientation based learning curve it can

be seen that the GA steadily forms a feeder which re-

duces the variance of the cones orientation distribu-

tion, and that from around generation 250 the rate of

convergence decreases.

Looking at Figure 7, it can also be seen that the

strategy values for Mutation and Smooth rate go to-

wards a speciﬁc range, indicating convergence, how-

ever, with some noise (which is to be expected when

Table 2: The cube feeder test results.

Simulation Physical

Pose T F P T F P

1 1000 0 100.0% 100 0 100%

2 1000 10 99.0% 100 0 100%

3 1000 5 99.5% 100 0 100%

4 1000 9 99.1% 100 0 100%

5 1000 7 99.3% 100 0 100%

6 1000 7 99.3% 100 0 100%

Total 6000 38 99.4% 600 0 100%

Table 3: The cone feeder test results.

Simulation Physical

Pose T F P T F P

1 1000 25 97.5% 100 1 99%

2 1000 40 96.0% 100 3 97%

3 1000 37 96.3% 100 2 98%

4 1000 24 97.6% 100 0 100%

Total 4000 126 96.9% 400 6 98.5%

the self-adaption tries to improve). These strategy

values gradually become less aggressive as the GA

converges on a useful feeder design. However, the

crossover rate behaves more erratic at the end of the

learning curve. This can be explained by the fact that

the individuals in the population become very similar

over time. When this happens the crossover scheme

will have little impact and thus the self-adaption strat-

egy will not be able to make meaningful adjustments

to this strategy parameter.

From Table 2 and Table 3 it can be seen that

both feeder designs perform re-orientations with a

high success rate, however, not without notable er-

rors. This is especially clear for the cone feeder de-

sign scoring a 98.5% success rate for the experiments

on the physical feeder. It should be noted that the real

feeders seem more forgiving than the simulation and

achieves better performance. This could simply be

due to uncertainties from the limited data-set of the

manual experiments, but previous experience has also

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

302

shown that the simulation has a tendency to empha-

size some errors that are otherwise dampened by the

real feeder.

The learned feeder designs presented in Figure 1

and 8 reorients the parts by exploiting their mass dis-

tribution and attempt to topple them into one orien-

tation. The track shape is then held constant to keep

the parts in their new orientation. This removes the

need for a designer to make informed decisions on

the orientation strategy, both in terms of deciding on

a suitable trap type, as well as deciding which part ori-

entation to optimize the feeder towards. This results

in a system which is easier to use for non-experts.

8 CONCLUSION

In this paper, a new approach to vibratory feeder de-

sign has been presented. The approach is based on a

Genetic Algorithm with self-adaption of its strategy

values. The approach creates working designs that

attempt to reorient all parts in the feeder to a single

orientation. The novelty of the approach is that it can

grow free-form features adapted to the speciﬁc part,

which is a clear distinction from previous methods,

that optimizes ﬁxed designs by varying their inherent

parameters. The design approach was used to learn

designs for two parts, where it in both cases formed

features that toppled the parts and subsequently held

them in place in their new orientation. The obtained

designs yielded promising results with high success

rates making the presented approach a solid basis for

future work.

9 FUTURE WORK

There are multiple open issues that can be addressed

with future work. Most notable is that the results do

not provide 100% successful reorientation, and for the

designs to be used in industry this needs to be han-

dled. Moreover, the simulation accuracy, although

producing useful realistic results, is not perfect. An

approach to address this could be adding controlled

noise to the sensitive parameters such as geometry,

mass distribution, friction, etc., forcing the learning to

adapt the design to account for these variations, and

thus creating a more robust result.

Furthermore, the simulation involves only one

part on the track. This neglects the inﬂuence of part

interaction on the learned design and the effect this

has is an open question that must be addressed in the

future.

Additionally, even with a perfect simulation, there

is no inherent guarantee in the algorithm, that it ﬁnds a

perfect design using only the current strategy of reori-

enting the parts. Thus, it could be necessary to extend

the design method with another strategy which more

aggressively optimizes towards rejecting parts in all

but one orientation.

It is also likely that better performance can be

achieved by having speciﬁc strategy parameters of

each individual gene, as e.g. the optimal value for mu-

tation rate could be different for the distance between

segments and the 2D-points of the cross-sections. In-

vestigating this in the future could lead to faster con-

vergence and improved performance and is essen-

tially free to investigate due to the GA’s self-adaption.

Naturally, the settings in Table 1 also affect over-

all performance and should be addressed with a clear

policy on how to set them.

Lastly, the approach should also be validated on

more test cases in the future, but in its current state,

this feeder design approach shows promising results.

ACKNOWLEDGMENTS

This work was supported by Innovation Fund Den-

mark as a part of the project “MADE Digital”.

REFERENCES

Berkowitz, D. R. and Canny, J. (1996). Designing parts

feeders using dynamic simulation. In Proceedings, In-

ternational Conference on Robotics and Automation,

volume 2, pages 1127–1132. IEEE.

Berkowitz, D. R. and Canny, J. (1997). A comparison of

real and simulated designs for vibratory parts feeding.

In Proceedings, International Conference on Robotics

and Automation, volume 3, pages 2377–2382. IEEE.

Berretty, R.-P., Goldberg, K., Overmars, M. H., and van der

Stappen, A. F. (1999). Geometric algorithms for trap

design. In Proceedings of the ﬁfteenth annual sym-

posium on Computational geometry, pages 95–104.

ACM.

Berretty, R.-P., Goldberg, K., Overmars, M. H., and van der

Stappen, A. F. (2001). Trap design for vibratory bowl

feeders. The International Journal of Robotics Re-

search, 20(11):891–908.

Boothroyd, G. (2005). Assembly Automation and Product

design. CRC Press, 2nd ed. edition.

Christiansen, A. D., Edwards, A. D., and Coello, C. A. C.

(1996). Automated design of part feeders using a ge-

netic algorithm. In Proceedings, International Con-

ference on Robotics and Automation, volume 1, pages

846–851. IEEE.

Free-form Trap Design for Vibratory Feeders using a Genetic Algorithm and Dynamic Simulation

303

Goemans, O. C., Anderson, M. T., Goldberg, K., and

van der Stappen, A. F. (2007). Automated feeding of

industrial parts with modular blades: Design software,

physical experiments, and an improved algorithm. In

International Conference on Automation Science and

Engineering, pages 318–325. IEEE.

Goemans, O. C., Goldberg, K., and van der Stappen, A. F.

(2006). Blades: a new class of geometric primitives

for feeding 3d parts on vibratory tracks. In Proceed-

ings, International Conference on Robotics and Au-

tomation, pages 1730–1736. IEEE.

Goemans, O. C. and van der Stappen, A. F. (2008). On

the design of traps for feeding 3d parts on vibratory

tracks. Robotica, 26(4):537–550.

Hofmann, D., Huang, H., and Reinhart, G. (2013). Auto-

mated shape optimization of orienting devices for vi-

bratory bowl feeders. Journal of Manufacturing Sci-

ence and Engineering, 135(5):051017.

Joergensen, J. A., Ellekilde, L.-P., and Petersen, H. G.

(2010). Robworksim - an open simulator for sensor

based grasping. In ISR 2010 (41st International Sym-

posium on Robotics) and ROBOTIK 2010 (6th Ger-

man Conference on Robotics), pages 1–8. VDE.

Mathiesen, S. and Ellekilde, L.-P. (2017). Automatic selec-

tion and sequencing of traps for vibratory feeders. In

7th International Conference on Simulation and Mod-

eling Methodologies Technologies and Applications

(SIMULTECH), pages 145–154. SCITEPRESS Dig-

ital Library.

Mathiesen, S., Sørensen, L. C., Kraft, D., and Ellekilde, L.-

P. (2018). Optimisation of trap design for vibratory

bowl feeders. pages 3467–3474.

Meyer-Nieberg, S. and Beyer, H.-G. (2007). Self-adaptation

in evolutionary algorithms. In Parameter setting in

evolutionary algorithms, pages 47–75. Springer.

Stocker, C. and Reinhart, G. (2016). Sensitivity analysis of

the dynamic behavior of transported material in vibra-

tory bowl feeders using physics simulation. Applied

Mechanics & Materials, 840.

Stocker, C., Schmid, M., and Reinhart, G. (2019). Rein-

forcement learning–based design of orienting devices

for vibratory bowl feeders. The International Journal

of Advanced Manufacturing Technology, pages 1–12.

Whitley, D. (1994). A genetic algorithm tutorial. Statistics

and computing, 4(2):65–85.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

304