Computational Music Thinking Patterns: Connecting Music

Education with Computer Science Education through the Design of

Interactive Notations

Alexander Repenning, Jürg Zurmühle, Anna Lamprou and Daniel Hug

University of Applied Sciences and Arts Northwestern Switzerland, FHNW School of Education,

Bahnhofstrasse 6, Windisch, Switzerland

Keywords: Computational Thinking, Computational Music Thinking, K-12 Computer Science Education, Music

Education, Elementary School Pre-service Teacher Education.

Abstract: Computational Music Thinking combines computing education and music education with the goal to

overcome common aptitudinal and attitudinal challenges. Many students, and teachers, believe that writing

programs or performing music is beyond their natural abilities. Instead of trying to teach computing and music

separately, Computational Music Thinking employs the design of interactive notations as a synergistic activity

to learn simultaneously about computation and music. On the one hand, music can turn abstract computational

concepts into enjoyable concrete experiences. Computation, on the other hand, can expand students’ notion

of music education well beyond music performance. A course with elementary school pre-service teachers

explored the teaching of Computational Music Thinking through a small set of constructs called

Computational Music Thinking Patterns. These patterns are centered around educational activities to design

interactive notations in accessible as well as engaging ways. Computational Music Thinking Patterns expand

our previous work on Computational Thinking Patterns used in game design and simulation authoring

activities. Data collected from the course suggest highly positive effects on teachers' attitudes towards

believing that Computational Music Thinking is important to their teaching, that Computational Music

Thinking helps the comprehension of computer science and that Computational Music Thinking helps the

comprehension of music.

1 INTRODUCTION

In most elementary schools around the world teachers

are required to teach a wide range of subjects

including language, math, science, and art including

music. Recently, some countries such as Switzerland,

have made computing education, consisting of

programming and Computational Thinking (CT)

(Repenning, Lamprou, Petralito, & Basawapatna,

2019), mandatory. Many schools and teachers

perceive this as a challenge (Gander et al., 2013)

because this requirement adds another subject to the

list of courses to teach. Moreover, unlike the more

traditional subjects’ teachers typically do not have

any programming background and, consequently,

feel ill prepared to teach CT-related courses. Even

pre-service teachers – most of them are recent high

school graduates in their twenties – who are being

trained at a school of education to become teachers,

typically have no experience in computer science. At

the School of Education PH FHNW in Switzerland

pre-service teachers were over 10 times less likely to

have had previous experience in programming

compared to the average Swiss population. A dismal

fraction of 0.2% of these teachers had any

programming experience. Clearly, the majority of

pre-service teachers are not planning to become

teachers because of computation but rather in spite of

it.

Hug has started to explore Computational Music

Thinking (CMT) (Hug et al., 2017) as a notion

combining programming with music through a small

set of manageable constructs called Computational

Music Thinking Patterns that are accessible and

engaging. By pattern we mean design patterns (Lea,

1994) that are reusable forms of a solution common

to design problems. This paper describes five patterns

common to computation and music.

Repenning, A., Zurmühle, J., Lamprou, A. and Hug, D.

Computational Music Thinking Patterns: Connecting Music Education with Computer Science Education through the Design of Interactive Notations.

DOI: 10.5220/0009817506410652

In Proceedings of the 12th International Conference on Computer Supported Education (CSEDU 2020), pages 641-652

ISBN: 978-989-758-417-6

641

The idea to teach CT as an interdisciplinary

connection between Computer Science (CS) and

other subjects is not new (Lee, Martin, & Apone,

2014) Examples include the connection of CS with

Math (e.g., (Papert, 1980)), language (e.g. through

storytelling (Werner, Denner, Bliesner, & Rex,

2009)), craft (e.g., (Kafai et al., 2014)), Sports (e.g.,

(Floyd & Sorbara, 2019) and art (e.g., (Knochel &

Patton, 2015). Most of our own experience is rooted

in game design (e.g., (Repenning, 2014)) and

simulation building (e.g., (Basawapatna, Repenning,

Koh, & Savignano, 2014)). Game Design has been

well received by in-service teachers (Repenning et

al., 2015) but Repenning found that while most pre-

service school teachers enjoy game design activities

some are surprisingly skeptical (Repenning et al.,

2019) towards the use of game design activities to

teach CT. One concern is mostly of a pragmatic

nature. In spite of game design being immensely

popular with K-12 students (Alexander, 2014;

Werner et al., 2009; Kafai, 2006), it is not a subject

that elementary school teachers are expected to teach.

However, most elementary school teachers do need to

teach subjects such as Music. Combining CT with

Music into CMT is highly compelling to teachers as

it suggests hitting two birds with one stone. More

importantly, however, computation and music share

important conceptual roots that could significantly

increase students’ fundamental understanding of

systems and notations.

We conceptualize CMT as a highly synergistic

framework supporting students’ interlinked

understanding of CT and music through the

exploration of a collection of CMT constructs that we

call Computational Music Thinking Patterns. These

patterns, in turn, are extensions of the repertoire of

Computational Thinking Patterns (Basawapatna,

2011) originally developed to find universal patterns

describing phenomenalistic object interactions

(Michotte, 1963) common to game design and

simulation building. Some practical definitions of CT

break it down into low level programming concepts

such as sequences, conditionals, and iteration

(Brennan & Resnick, 2012) and even try to assess CT

performance through instruments counting the

presence of these concepts in code (Moreno-León,

Robles, & Román-González, 2015) Frameworks

based on patterns, in contrast, operate at a higher level

by conceptualizing combinations of programming

elements that can add up to a higher goal.

Learning activities are centered around

Computational Music Thinking Patterns make

students design interactive notations. The key idea of

a notation is the affordance to separate representation

and interpretation. Figure 1 shows a music box

containing a cylinder representing a specific song.

This cylinder can be exchanged with a different one

to play a different melody with the same

interpretation mechanism. To use, and more

importantly to design, these kinds of notations

provides a deep understanding of powerful ideas that

are common between music and programming.

Designing interactive notations provides

affordances to make learning activities even more

engaging. Students not only design static

representations of existing songs but can interact with

an ongoing process of music playing through mouse

or keys input changing the notation in real time.

A Computational Music Thinking pilot course

was conducted in the Fall of 2019 with 9 pre-service

elementary teachers. The course covered five

Computational Music Thinking Patterns:

Interpretation, Interaction, Chance, Hierarchy and

Rewrite Rules. In the first part of the 14-week course

the pre-service teachers learned to implement these

patterns. In the second part they started to work in

pairs to develop Zones of Proximal Flow tutorials

(Basawapatna, Repenning, & Savignano, 2019) to

teach K-12 students some of these patterns. This

paper outlines some related work, describes the

patterns and presents course evaluation results.

2 RELATED WORK

There are large bodies of literature in both Music

education with digital technologies (Ruthmann,

Heines, Greher, Laidler, & Saulters, 2010; Cano,

Dittmar, Abeßer, Kehling, & Grollmisch, 2018; King

& Himonides, 2016) and Computational Thinking

(Wing, 2006; Grover & Pea, 2013) education. The

combination of music and computation based on

programming, however, has received much less

attention particularly at the elementary school level.

Discussion of related work here is limited to the

elementary school level.

2.1 Combining CT with Music

The idea of connecting Computational Thinking with

Music has been explored from multiple angles.

Algorithmic composition, for instance, explores the

composition based on formal methods and

computation. Edwards describes computational

notations going back to the “Musikalisches

Würfelspiel” (“musical dice game”, attributed,

among others, to Mozart) based on chance (Edwards,

2011). Aleatoric composition was explored in

CSME 2020 - Special Session on Computer Supported Music Education

642

particular in the 20th century, both driven by the

artistic questioning of musical traditions and the

advent of computers, and the related use of

computation as means of composing and generating

music (Schulze, 2000). The core mechanism is for

computers to play sounds based on rules, which are

based on musical principles. Sequences of sounds, for

instance melodies, are represented as functions

playing a series of (pitched, tonal) sounds. Music can

be composed by composing functions, i.e., functions

calling other functions. This composition process can

be done virtually, that is by writing code representing

functions calling other functions, or tangibly, by

arranging physical objects into compositions. These

objects, in turn, may be passive such as traditional

LEGO bricks representing a music notation (Baratè,

Ludovico, & Malchiodi, 2017) or active such as the

tangible music blocks in the Algo.Rythm system

based on Arduino circuit boards (Peng, 2012).

The use of Computational thinking has also been

proposed specifically in music education (Ruthmann

et al., 2010; Greher & Heines, 2014). The main

motivation and goal also here are to support STEAM

(STEM education with Arts added: Science,

Technology, Engineering, Art, Math) education and

promoting related digital skills in the arts, but with a

stronger focus on musical learning. Greher & Heines

for instance propose Scratch for musical

programming. Their pedagogy makes use of

preparatory exercises, which employ visual symbols

drawn on paper representing musical actions, that

then are executed by children with musical

instruments or objects. When programming musical

code with Scratch, however, they have to rely on

abstract representations of musical processes.

This work also builds on previous work by some

of the authors exploring approaches to CMT with

secondary school children in a workshop setting (Hug

et al., 2017). This work showed that children were

highly motivated to use visual programming

environments to create music and attitudes both

towards music and CS improved.

2.2 Approaches to Programming

With a target audience of elementary school students,

a key challenge in supporting algorithmic

composition is the difficulty of dealing with text-

based programming languages and abstractions of

musical processes. For instance, SonicPI (Sam

Aaron, 2016; Samuel Aaron, Blackwell, & Burnard,

2016) is a powerful life coding environment suitable

even for upper primary school classes but relies on a

specific set of commands aimed exclusively at

providing musical functions. Blocks-based

programming languages such as AgentSheets, Alice,

Scratch and AgentCubes help to overcome syntactic

challenges (Alexander Repenning, 2017). Many

blocks-based programming languages, including

AgentCubes and Scratch, feature music functions

such as MIDI sound tools to trigger sounds. Other

languages such as the Blockly-based tool created by

Baratè et al. (Baratè, Formica, Ludovico, &

Malchiodi, 2017) feature functions to compose

melodies. The goal of this system is to facilitate re-

coding (Nake & Grabowski, 2017) activities where

students are provided a given song which then they

have to re-code by using composing functions

including loops. Another approach is presented by

EarSketch (Freeman & Magerko, 2016; Xambó,

Freeman, Magerko, & Shah, 2016) which presents a

“Computational Music Remixing” environment

which combines the familiar multitrack environment

for playback of audio with coding facilities that can

be used for rule-based playback.

2.3 Interactive Notation Design as

Emergent Principle

Our approach to CMT integrates the creation of

symbols representing musical actions of varying

complexity with the actual coding process. Through

the use of the programming environment

AgentCubes, which employs a blocks-based coding

environment, but also supports the creation of visual

sprites that become rule-based agents, it is possible to

combine the best of two worlds, which turned out to

be a key benefit of the system during the course. We

call the emerging underlying principle “Interactive

Notation Design” (IND) and use it as the main

activity that students engage in to become

Computational Music Thinkers. The focus on

notation is similar to the LEGO Music Notation

project (Baratè, Formica, et al., 2017). Unlike with

the LEGO Music Notional project, however,

notations are not provided for the students. Instead,

students are expected to become Computational

Music Thinkers by experimenting with their own

interactive notations. These notations could be one,

two or even three dimensional. Students design

notations by drawing their own symbols and define

the meaning of their notation through programming.

Moreover, students design interactive notations

including the affordance to interact with the notation

at run time. That is, while the music is playing users

could change the notation by editing, that is moving

and changing symbols, in real time. Students can also

program interactive symbols that are symbols

Computational Music Thinking Patterns: Connecting Music Education with Computer Science Education through the Design of Interactive

Notations

643

reacting to user input such as key events from

keyboards or external input devices such as Makey

Makeys.

3 INTERVENTION: DESIGNING

INTERACTIVE NOTATIONS

Nine pre-service elementary school teachers studying

at the School of Education participated in an elective

course where they were taught five different

Computational Music Thinking Patterns. These pre-

service teachers are, technically speaking, bachelor’s

degree students. Henceforth, and for the sake of

brevity the paper refers to them simply as students.

The course itself consisted of 14 lessons. Each lesson

briefly introduced each Computational Music

Thinking Patterns with the necessary theory and

historical background from music and computation.

The connection between thinking in music and CT

gives students new insights into both topics. They

learn that music is also based on rules that can be

made explicit. Scales and chords are built according

to certain rules, rhythms function according to

hierarchies of emphases, pieces of music are divided

into hierarchical parts. On the other hand,

programmed agents can trigger and influence musical

actions. Melodies or rhythms can be programmed, or

random sound sequences can be invented. The

students learn and experience playfully connections

between music and programming.

The students develop musical games for children

based on the five patterns. This enables the children

to learn about music and about programming by

trying and playing.

In a second step, students explore the pedagogy of

CMT, i.e., the experience of how to teach CMT, by

writing and evaluating ZPF tutorials (Zone of

Proximal Flow Tutorials (Basawapatna et al., 2019).

To build successful ZPF tutorials students must think

about how to provide tiered instructions supporting

differentiation. These ZPF tutorials enable children to

build and program their own worlds in AgentCubes.

The students learn in terms of content about the

relationship between music and computational

thinking. They learn and know rules for programming

music. Methodically, students learn forms of project-

like learning, explorative learning and the concept of

Productive Failure (Kapur, 2008). They mainly work

independently in small project groups and are

supported by the lecturers only as needed.

Participants start with simple programming of

agents in AgentCubes using the first CMT pattern

“interpretation”. They distinguish between a form of

notation (representation) and rules of execution

(interpretation). For many students it was new that

music can be represented not only in classical

notation, but also as pins on a cylinder (music box),

as bars in a sequencer program or as holes in a paper

strip. For programming, a distinction had to be made

between the note and the player. In a sequence of

symbols, the note represents a sequence of sounds.

The player interprets the symbols according to certain

rules and moves through the sequence. First,

individual sounds were assigned to the symbols, then

chords or changing sounds. Even through these

simple programming, very different musical works

became possible.

In the following lessons the students were

introduced to all five CMT patterns and developed

their own projects. The projects were presented in the

group and received feedback for further work. The

sequence and contents of the lessons are shown in

Table 1 below.

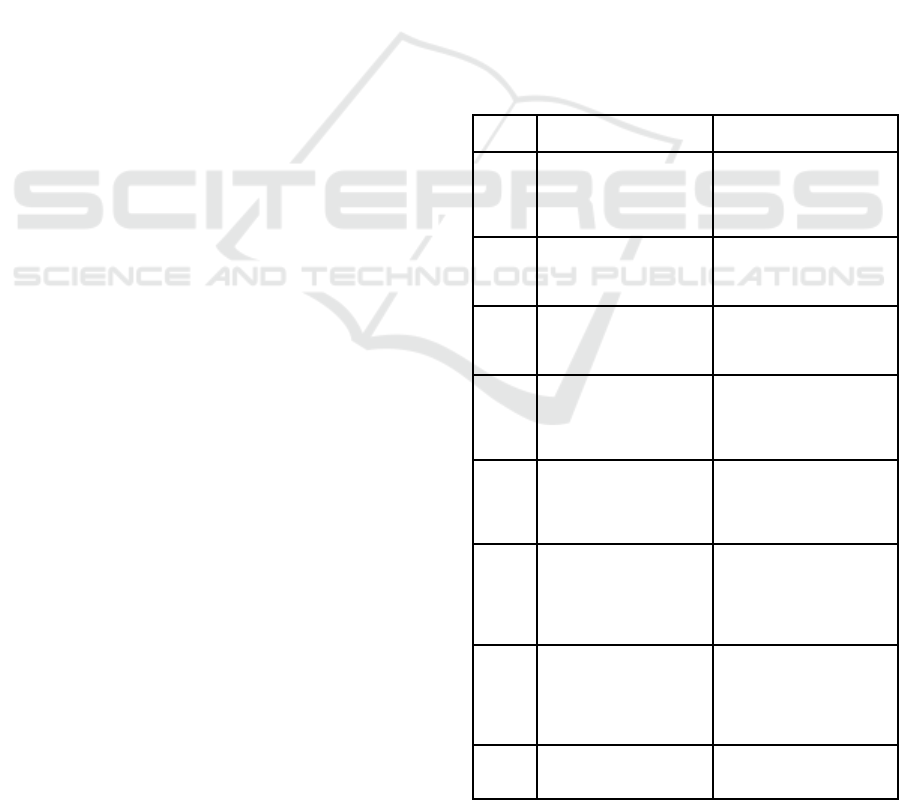
Table 1: Computational Music Thinking Course Outline.

Week Theory Practice

1 Introduction:

Music and Computational

Thinking

Recreation of a simple melody

with five notes.

Creation of different kinds of

agents in AgentCubes

2 CMT Pattern 1: Interpretation

Creation of Symbols and Rules of

interpretation

Creation and programming an

own melody

3 CMT Pattern 1:

Interpretation cont.

Playtime

Programming different

Possibilities (Melodies and Chords)

4 CMT Pattern 2: Interaction

Musical elements and parameters

Musical form

Small interaction Projects: Using

keyboard commands and

interfaces (Makey Makey) to

influence the music live.

5 CMT Pattern 3: Chance Programming probabilities

(%change) Music pieces became

unpredictable and therefore more

interesting.

6 CMT Pattern 4: Hierarchy

Pentatonic Sound Systems

The pieces of music followed a

certain form (Rondo) A B A C A

D. The individual parts A B C etc.

then control a certain sequence of

sounds.

7 CMT Pattern 5: Rewriting rules Programming of larger pieces like

a blues or song accompaniment

with chord progressions or more

complex pieces of music

Start with Pitch Project

8 Layers in music: Melody,

Harmony, Rhythm, Bass

Presentation Pitch Project

Peer Review

CSME 2020 - Special Session on Computer Supported Music Education

644

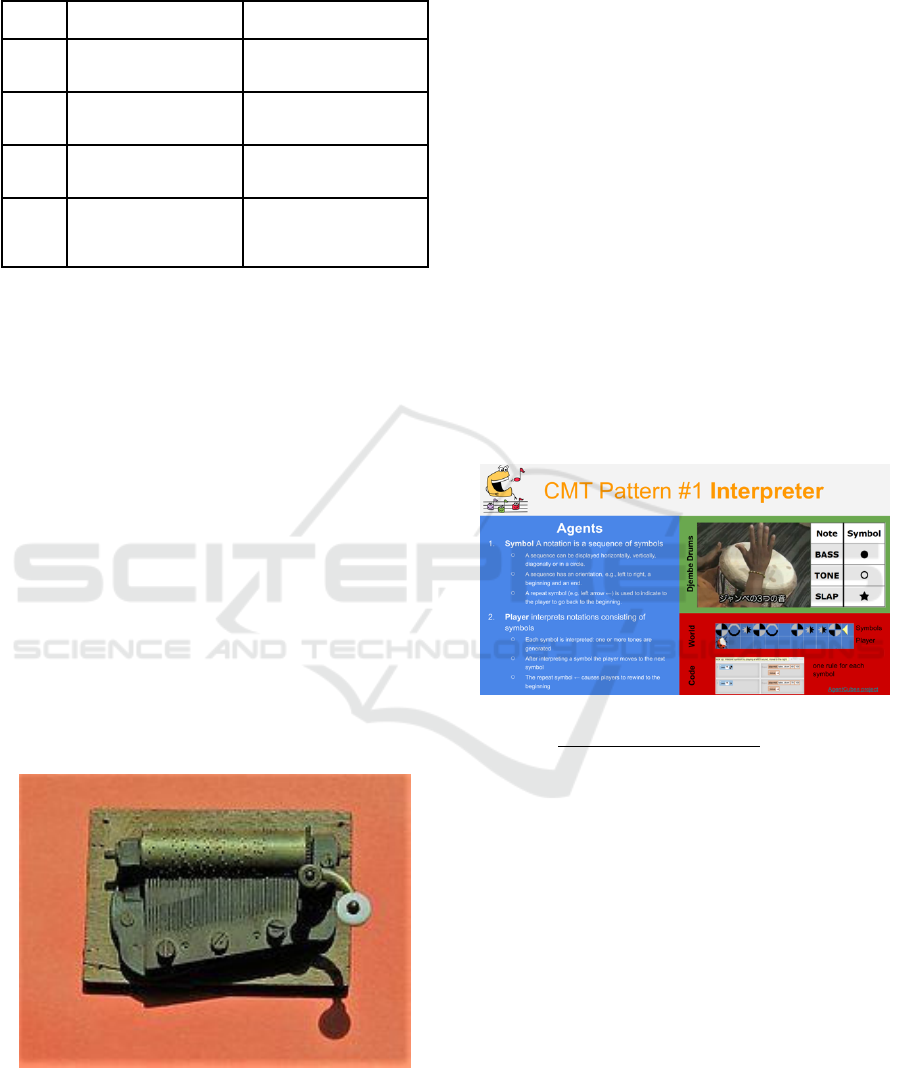
Table 1: Computational Music Thinking Course Outline

(cont.).

Week Theory Practice

9 Hierarchy in rhythm (Measure,

metre, rhythm)

Presentation of Project sketches

Decision for final projects

10-12 Introduction: ZPF Tutorials

Evaluation: Interviews

Work on own Project

Presentation and feedback

13 Presentation Project

Peer Review

14 Evaluation: Questionnaire

Introduction: Other Programs

for Music

All learning activities are based on the design of

interactive notation and evolve from simple rule

replication (procedural programming) to the

development of new rules (declarative

programming).

3.1 Five Computational Music

Thinking Patterns

Below are the detailed descriptions of five

Computational Music Thinking Patterns used in the

course. No claims are made that this list is exhaustive.

3.1.1 Pattern #1: Interpreter

The interpreter pattern is the main Computational

Music Thinking Pattern. It is very powerful in itself

but also serves as the basis for most of the other

Computational Music Thinking Patterns. To that end,

it makes sense in this paper, but also when teaching

students, to spend more time introducing this pattern.

Figure 1: A music box (example from around 1900)

combines notation with interpretation.

The interpreter is used to represent a basic melody,

rhythm or program as a sequence of symbols which

can be executed. In music, the interpreter pattern can

be viewed as an abstraction of a music box (Figure 1).

Music boxes, in turn, are a form of automation. A

music box is a musical instrument producing musical

notes by sensing the presence of pins on a revolving

cylinder or disk. The presence of a pin will trigger a

sound by putting tiny metal rods, which are tuned as

tones of a scale, into vibration. These tuned rods are

arranged in a comb. Abstractly, the pins on a cylinder

serve as notation that gets interpreted by the music

box. Automation and abstraction are key components

of Computational Thinking (Wing, 2006). In

computing, computer programs are sequences of

instructions that are interpreted. Again, there is the

idea of a notation that gets interpreted. Independent

of their manifestations–either as physical

manifestations such as cylinders, disks, and punch

cards found in 19th century music boxes, or as virtual

manifestations such as text based and blocks-based

programming languages found in 21th century

programming languages–the fundamental idea of

interpretation is the same in music and computing.

Figure 2: Computational Music Thinking Pattern #1.

Interpreter: https://go.fhnw.ch/QCQzJK.

To build an interpreter a student first designs a

number of symbols by drawing 2D or 3D shapes (see

World in Figure 2) representing individual sounds.

For instance, students would design three symbols to

represent the three basic sounds of a djembe drum:

bass, tone, and slap. Then, students arrange these

symbols into one, two or even three-dimensional

notations. For instance, they could arrange the

djembe sound symbols into a one-dimensional left to

right sequence representing a rhythm or even a basic

melody. Finally, students program a so-called player

agent (Repenning, Smith, Owen, & Repenning, 2012)

by writing simple rules to interpret the melody like

this:

IF I see the bass symbol THEN I play the

bass sound, and I move to the right.

A rule is needed for each symbol and one more rule

is needed when there is no symbol. When the program

Computational Music Thinking Patterns: Connecting Music Education with Computer Science Education through the Design of Interactive

Notations

645

is run the player agent will play the melody and move

from left to right. Students can change the melody by

rearranging symbols even while the music is playing.

Figures 2-6 illustrate the CMT patterns. They are

meant to work as slides and not as paper Figures.

Each pattern follows a simple color-coding scheme:

blue describes agents with their interactions; green

describes real world analogies; red describes

snapshots of the programming world and code. Some

patterns do not feature all these parts. Some of their

content, particularly the code, requires readers to

zoom. We present the first, and most important

pattern in two column mode for readability but will

have to keep the remaining ones in one column mode

due to paper size limitations. Alternatively, links

below each pattern Figure provide full access to slides

including the project links and the full source code.

3.1.2 Pattern #2: Interaction

Interaction (Figure 3) enables users to actively

engage with the music making process. That is, the

computer does not just autonomously play previously

composed songs from beginning to end but reacts to

input from the user. This kind of interaction can

unfold at different levels. For instance, at a low level,

a user could press one key causing the computer to

produce one sound. To make this more entertaining

computer keyboards can be replaced with Makey

Makeys (Graves, 2014) which could be connected to

various pieces of fruit in order to create something

called the Banana Piano. Using drum sounds instead

of piano sounds could turn a Banana Piano into a

drum kit where the touch of each fruit plays a

different drum kit sound. However, at a higher level

of abstraction, one would want to establish a more

sophisticated mapping between input and output. One

input should result in many outputs. A groovebox, for

instance, is an electronic or digital musical instrument

featuring pads (large keys optimized for music

applications) that can trigger entire sequences of

sounds.

Figure 3: Computational Music Thinking Pattern #2.

Interaction: https://go.fhnw.ch/2sbSd3.

The interaction pattern, extending the interpreter

pattern, features an interactive symbol reacting to user

input. For instance, this symbol could represent a

traffic light, controlled by the user, toggling between

two states: red and green. The player agent would be

blocked when seeing a red traffic light. It would have

to wait for the user to press a key to make the light

turn green. Traffic light symbols can be put

anywhere, typically at the beginning of a sequence,

but also anywhere in the midst of a sequence to

control music. Notations, extended by interactive

symbols such as the traffic light, turn into powerful

interactive notations enabling users to control music.

3.1.3 Pattern #3: Chance

Chance (Figure 4) in computational music production

often is seen as means to provide elements of surprise

and stimulate creativity and thus plays an important

role in computational music thinking both at

composition time as well as performance time in

particular in post-war “aleatoric” music (Boehmer,

1988; Schulze, 2000). Chance is relatively simple to

compute but harder to employ meaningfully in music.

For instance, a sequence of MIDI instruments playing

at random pitches is not likely to result in great

sounding melodies. Early uses of chance in music

include random dice compositions attributed, for

instance to Mozart (Cope, 1989) mapping the sum of

two dice to a number, between 2 and 12, used as an

index to play one out of 11 different sequences of

sounds. A simple extension to our notation is the

introduction of random split symbol-making the

player moves up or down, with equal chance, to a

different sequence of symbols. Splits could be further

combined into a binary tree of random choices.

Figure 4: Computational Music Thinking Pattern #3.

Chance: https://go.fhnw.ch/eu7o1y.

3.1.4 Pattern #4: Hierarchy

Hierarchies (Figure 5) are fundamental concepts in a

wide variety of fields not only music and CS. A

hierarchy is a representation differentiating at least

CSME 2020 - Special Session on Computer Supported Music Education

646

two different levels. A higher level may contain, or

control, a lower level. In music, a hierarchical

notation would allow a higher level of representation

to control a lower level. An analogy reaching back to

musical boxes (Figure 1) would expand on the notion

of triggering a sound. A master music box would

control a number of subservient music boxes.

Metaphorically speaking, instead of a pin on the

musical cylinder triggering a single sound it would

trigger one of these subservient music boxes. These

subservient music boxes, in turn, would play an entire

melody. Hierarchies can be nested. That is, the lower

level could serve as the higher level to an even lower

level and so on.

Hierarchical control distinguishes two important

cases: synchronous and asynchronous control.

Synchronous control of music boxes suggest that the

master box triggers a subservient music box and then

awaits the completion of the song. Only then does it

continue moving its cylinder. Asynchronous control,

in contrast, does not wait for the completion of the

song of the subservient music box. To reflect this

interaction our notation must provide at least two

levels of interpretation. A higher-level player

interprets high level symbols. Instead of just playing

a sound this interpretation of the higher level activates

a low-level player. In the synchronous case the high-

level player and the low-level player need to

implement some form of handshaking so that the

high-level player can wait for the low-level player to

finish a loop. In the asynchronous case no

handshaking is needed. The high-level player simply

continues. The hierarchy pattern can be used, for

instance, to explore the musical notion called the

rondo. A rondo is a musical form combining

recurring sequences of music serving as main themes,

sometimes called refrains, with contrasting themes,

sometimes called episodes. These various themes are

represented as character symbols, e.g., A and B. A

rondo is then expressed as sequences of these

symbols. Classical rondos include ABA, ABBA,

ABACA, or ABACABA. Figure 5 outlines some

basic rondos. These rondos are played synchronously.

3.1.5 Pattern #5: Rewrite-rules

Graphical rewrite-rules (Figure 6) are declarative

music notations. In blues, chord rewrite-rules, have

been used to create chord progressions producing

boogie woogie. Patterns 1 to 4 define music

procedurally. That is, procedural notations include an

explicit notion of control flow suggesting where the

computation currently is, what to do next and, most

importantly,

how to do it. The player agent can be

Figure 5. Computational Music Thinking Pattern #4.

Hierarchy: https://go.fhnw.ch/6EDCPo.

viewed as the state of the computation indicating how

far along one is to interpret a notation. Through the

process of interpretation, the player explicitly maps

the symbols to instructions such as playing a certain

sound. Declarative programming, captured by pattern

5, in contrast, describes desired outcomes without

specifying how to get there by capturing logic as

IF/THEN rules. In music a graphical rewrite rule

establishes a mapping between sequences of sounds

that have been played with sequences of sounds that

will be played. In other words, a rule describes

IF I heard sound 1, followed by sound

2, followed by sound …

THEN I will play sound a, followed by

sound b, followed by sound c…

Figure 6 shows two rules. The blocks on the left-hand

side of the red arrow denote sounds played in the past.

Blocks on the right-hand side of the arrow denote

sounds that will be played in the future. Rules are

tested from top to bottom. If there is a rule that

matches, that is it’s

IF sequence of sounds matches exactly

the sequence of sounds just played

THEN the then sequence of sounds will

be played.

Figure 6: Computational Music Thinking Pattern #5.

Rewrite-Rules: https://go.fhnw.ch/Evwjtl.

Both, the user, by pressing keys, and the system, by

executing rules, can produce new sounds. User

Computational Music Thinking Patterns: Connecting Music Education with Computer Science Education through the Design of Interactive

Notations

647

suggested sounds have a higher priority than system

suggested sounds. Users and the system react to each

other similar to musicians participating in a jam

session.

3.1.6 Implementing Patterns

Computational Music Thinking Patterns are a

growing collection of combinable constructs that can

be implemented in AgentCubes but also any other

Computational Thinking Tool (Repenning,

Basawapatna, & Escherle, 2016; Repenning,

Basawapatna, & Escherle, 2017) supporting sound

output, mouse and keyboard input. Combinations of

patterns can produce hierarchies that feature chance,

chance controlled by interaction, or rewrite-rules

including chance. Some patterns are simpler to

implement than others. The interpreter, chance and

interaction patterns could be implemented by all

students with very little code. The handshaking of the

hierarchy pattern proved too complex for students

with no programming experience. Finally, the

rewrite-rule pattern requires complex programming

implementing an entire rule-based programming

language. Activities based on rewrite-rules were

limited to students experimenting with their own

rules and not writing their own rule interpreter. This

was because the implementation of a rule interpreter

system requires advanced programming

understanding, e.g., the understanding of recursion,

which our students did not have.

4 METHODS

The paper is based on a variety of data collected

during the 2019 fall semester: Survey data, interviews

and course evaluation data. The following sections

describe in detail the methods used for the study.

Students’ participation in the study was voluntary.

4.1 Procedure

The course comprised 14 sessions. Survey data were

collected from the participants during the first and last

sessions. All surveys were conducted on a computer

in the classroom. For each course the first (pre)

electronic survey was completed by participants in

the beginning of the first introductory lesson, which

represents the baseline pre-data of this study. The

same participants completed a second (post)

electronic survey at the end of the last session (after

14 weeks), representing the post-data. Interviews

were conducted with the students in the same final

session. Finally, a course evaluation (survey data)

was run by the university for all courses including this

one.

4.2 Participants

The sample comprises a total of nine pre-service

primary-level teacher students, six male and three

females. The students were in their fifth semester and

all but two had previously taken the obligatory CS

module consisting of two courses one in the subject

of CS and one in the CS didactics.

4.3 Measures

The pre- and post-surveys consisted of 22 identical

items and contained three groups of questions (see

Table 2): attitude (abb. Att.), skills, and aptitude (abb.

Apt.). A set of twelve 4-point Likert- scale items

(1=strongly disagree, 4=strongly agree) consisted of

questions with regards to the participants’ attitudes

and contained three subgroups: attitude towards

music (five items (Q1, Q2, Q7, Q11, Q17), e.g.

“Learning music is boring for me”), attitude towards

CS (four items (Q3, Q8, Q12, Q21), e.g. “I think that

CS is difficult for me to learn”) and attitude towards

the combination of CS and music (three items (Q4,

Q5, Q6), e.g. “I believe that the combination of CS

and music helps to better understand music”). A

second set of seven 4-point Likert- scale items

(1=strongly disagree, 4=strongly agree) consisted of

questions with regard to the participants’ skills and

consisted also of three subgroups: CS skills (two

items (Q16, Q19), e.g. “I can program”), music skills

(four items (Q14, Q15, Q18, Q20), e.g. “I play an

instrument”) and skills combining music and CS (one

item (Q13): “I make music with the computer”).

Finally, a set of two 4-point Likert- scale items

(1=strongly disagree, 4=strongly agree) consisted of

questions with regards to the participant’s self-

reported aptitude. One with regards to music (Q9): “I

consider myself unmusical” and one with regards to

CS (Q10): “I don't consider myself a computer whiz”.

The survey also contained one open-ended question:

What do you understand by the term "Computational

Music Thinking"?

The interviews consisted of eight open ended

questions that complimented the survey and focused

on motivational aspects.

During the implementation of the course, all

courses at the School of Education were also

evaluated. This evaluation was of a general nature and

mostly targeted the quality of the course and the

teaching. It asked about the design of the course, the

CSME 2020 - Special Session on Computer Supported Music Education

648

pace, difficulty and scope of the material, the quality

of the lecturers and the focus on the students. The

survey consisted of 24 5-point Likert-scale items

grouped in five groups: course (nine items), speed,

difficulty and amount of material (three items),

lectures (six items), students (five items) and overall

evaluation (one item). Because we did not conduct

this evaluation, we do not have access to the data but

only to the results, some of which we present here.

5 RESULTS

At the beginning of our course the participants

indicated on a Likert-Scale from 1 to 4 that music is

very important for them (Q1: M =3.89) and that both

music and CS are quite important for their job as

teachers (Q2, Q3, M= 3.33) while the combination of

the two seems to be less important (Q4, M = 2.78).

The students had a positive attitude towards the

learning benefits of the combination of music and CS.

They seem to believe however, that the combination

helps to understand music more (Q6, M= 3.22) than

it helps to understand CS (Q5, M= 3). They further

believed that CS (Q8, M=2.67) is more difficult to

learn than music is (Q7, M=2). They do not think they

are non-musical (Q9, M=1.56) but they think on

average that they do not have computer affinity (Q10,

M= 2.44). They find learning music (Q11, M=1.89)

less boring than learning CS (Q12, M=2.22). With

regards to music skills, our students indicated good

skills with regards to playing an instrument (Q14,

M=3.22), but they indicate less than average skills

with regards to understanding music (Q18, M=2.33)

and more than average with music theory knowledge

and good singing (Q20, Q15 M=2.78). Furthermore,

even though they indicated an average fascination

with computers and technology (Q21, M=2.56), their

computer gaming skills are average (Q16, M=2.33)

and their programming skills are low (Q19, M =

1.78). Finally, they do not make music with the

computer (Q13, M=1.89).

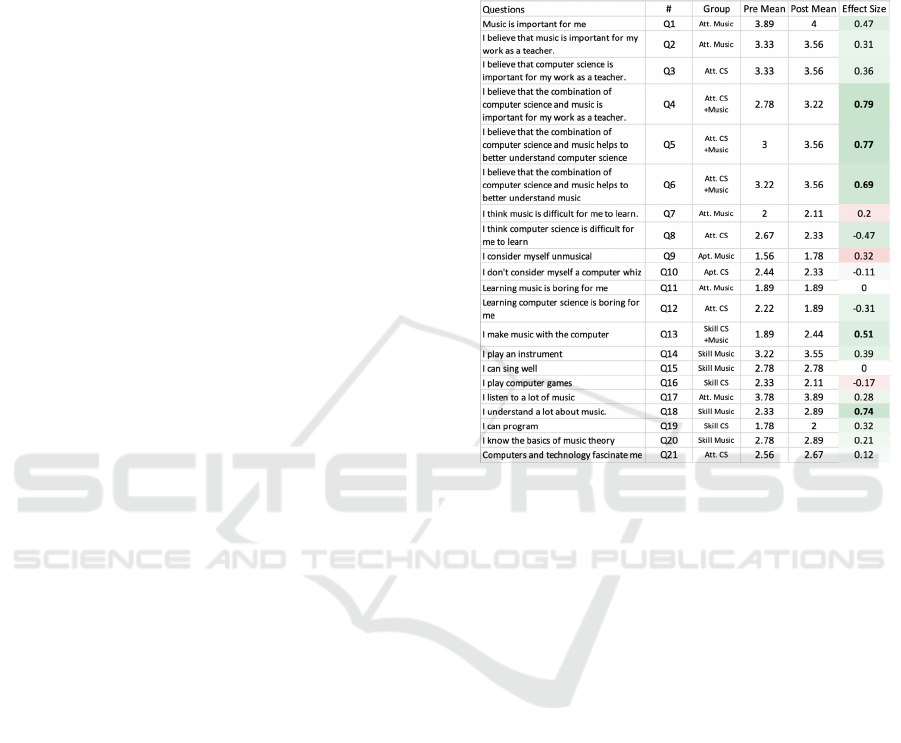
5.1 Pre-post and Effect Sizes

The table below (Table 2) shows the means and the

effect sizes from the pre-post responses. Positive

effects (positive or negative effect sizes suggesting

more desirable, or less undesirable effects) are

marked green. Negative effects (less desirable, or

more undesirable) are marked red. Color saturation is

proportional to effect size (Cohen's d is small: [0.2,

0.5], medium [0.5, 0.8], and large ≥ 0.8). Effects that

are medium and large (|d| ≥ 0.49), are marked bold.

With the exception of Q7, Q9 and Q16 all other post-

means indicate positive shifts after the course.

Table 2: Pre- Post means and effect sizes. Small: [0.2, 0.5),

medium: [0.5, 0.8), large: > 0.8. Desirable effects in Green,

undesirable effects in Red.

5.2 Course Evaluation

As the evaluation was conducted by the school, we

have no access to the raw data but only to the results,

which paint a very positive picture for the course.

Overall our students assessed the course as very good

(M= 4.5, scale 1 to 5). They indicated that the course

provided good practical references for their future

profession (M=3.9) while most importantly they

found the course very important for their professional

practice (M=4.2). The students also felt not only that

they gained a very good insight but that the course

raised their interest in the topic (both M= 4.3).

6 DISCUSSION

Overall, the strongest positive change based on effect

size was in attitudes towards the combination of

music and computer science (Q4, Q5, Q6). The

combination of music and computer science for the

importance for the work as a teacher in general is

rated higher by the students at the end of the course

than at the beginning with an effect size of 0.79. We

assume that the cooperation of two disciplinary

experts had a positive effect on this assessment by the

Computational Music Thinking Patterns: Connecting Music Education with Computer Science Education through the Design of Interactive

Notations

649

students and that the course was successful in

showing how the interdisciplinary combination in the

form of computational music thinking can contribute

to learning in general. This also resonates with the

effect that CS is considered somewhat less difficult to

learn in post. The integration also supported a better

understanding of computer science (effect size 0.77)

and music (effect size 0.69) individually, which

indicates that the interdisciplinary approach also

supports disciplinary development.

The effect size of 0.51 regarding making music

with the computer (Q13), is interesting, as it suggests

that the course supported the notion that

programming can be used to create music, and helped

the participants to discover new ways of making

music with the computer beyond using dedicated

musical software. This is particularly encouraging, as

for most of the participants making music with

programming and without instruments or singing was

something new and unfamiliar before they started the

course.

Looking at the skill related questions, the effect

on programming skills (Q19) was small. In context of

the higher effect on musical competences, this

suggests that the intervention can profit from

previous knowledge of the participants, a finding also

shown in earlier related work (Hug et al., 2017). Out

of the 9 participants 2 had no programming

experience. Initially our programming course

(Repenning et al., 2019) was stated as a requirement.

However, the two participants with no previous

programming experience did not have a problem

picking up programming skills through CMT.

The results of a formal course evaluation showed

high scores in the assessment of the course design (a

good learning atmosphere and active participation)

and in promoting interest in the topic.

At the end of the course an interview was made

with the participants. In this interview the students

indicated high interest in applying the topic in class

and that they could imagine ways to integrate CMT

in their teaching practice, without having to give up

other musical activities they enjoy and feel competent

in executing with the children at school. But also,

some challenges could be identified. Not all schools

have a sufficient number of computers, up-to-date

software or a stable and fast network for several

children to work on projects, and activities can be

relatively time consuming, which requires careful

scaffolding. This concern regarding the application in

the classroom was also reflected in the course

evaluation questionnaire, with a large dispersion of

the rating results in this regard. However, regarding

the specific activities presented in the course, not only

did some students express their confidence in being

able to bring CMT to the classroom, some even

reported positive results from already implementing

CMT pilots in their classrooms.

7 CONCLUSIONS

The combination of music and computational

thinking by two experts in a course for primary

teachers enabled students to learn both subjects

individually and in an interdisciplinary way. Five

Computational Music Thinking Patterns–

interpretation, interactivity, chance, hierarchy and

rewrite-rules–represent high level constructs

integrating fundamental concepts of computation and

music. Students were able to design interactive

notations by using AgentCubes to create their own

worlds, design and animate agents and create and

design sounds as melodies, chords and rhythms. Data

collected from the course suggest significant positive

effects on teachers' attitudes towards believing that

Computational Music Thinking is important to their

teaching, that Computational Music Thinking helps

the comprehension of computer science and that

Computational Music Thinking helps the

comprehension of music.

The mixture of instruction, playtime and project

development with regular peer feedback enabled the

students to develop individual learning paths and

unconventional projects that they could implement

for or with children in school. The participants

developed new perspectives on informatics and

musical thinking and used the computer as a musical

instrument with codes and rules.

Future work will further analyze qualitative data

gathered in the interviews to gain a better

understanding of the attitudes and perspectives in

terms of applying Computational Music Thinking,

designing interactive notations and gaining teaching

practice. In addition, the final projects of the students

are available, which have not yet been systematically

evaluated. All projects were designed and worked in

AgentCubes, different Computational Music

Thinking patterns were applied, and musical topics

were worked on. An important aspect is to better

understand the actual musical concepts embodied in

the participant’s creation in order to integrate it with

specific musical learning goals.

Finally, future work will address the theory-based

further development of the Computational Music

Thinking patterns and the principle and application

Interactive Notation Design as means to integrate

computational thinking and musical thinking. A

CSME 2020 - Special Session on Computer Supported Music Education

650

particular focus lies on enabling the transfer into

teaching practice and applicability in classroom

situations.

Therefore, a second edition of the course is

planned for Fall 2020 and will offer the opportunity

to adapt the course design and fine tune the data

gathering process. Also, collaborations with schools

for pilot courses with children are being prepared in

order to further develop the transfer from teacher

education to classroom application.

ACKNOWLEDGMENTS

This project has been funded by the Hochschullehre

2025 FHNW Lehrfond. The use of AgentCubes was

funded by the Hasler Foundation.

REFERENCES

Aaron, S. (2016). Sonic Pi–performance in education,

technology and art. International Journal of

Performance Arts and Digital Media, 12(2), 171-178.

Aaron, S., Blackwell, A. F., & Burnard, P. (2016). The

development of Sonic Pi and its use in educational

partnerships: Co-creating pedagogies for learning

computer programming. Journal of Music, Technology

and Education, 9(1), 75-94.

Baratè, A., Formica, A., Ludovico, L. A., & Malchiodi, D.

(2017, April). Fostering computational thinking in

secondary school through music-an educational

experience based on google blockly. In International

Conference on Computer Supported Education (Vol. 2,

pp. 117-124). SCITEPRESS.

Baratè, A., Ludovico, L. A., & Malchiodi, D. (2017).

Fostering computational thinking in primary school

through a LEGO®-based music notation. Procedia

computer science, 112, 1334-1344.

Basawapatna, A., Koh, K. H., Repenning, A., Webb, D.C.,

& Marshall, K. S. (2011, March). Recognizing

Computational Thinking Patterns. In Proceedings of

the 42nd ACM technical symposium on Computer

science education (pp. 245-250).

Basawapatna, A., Repenning, A., Koh, K. H., & Savignano,

M. (2014, March). The Consume-Create Spectrum:

Balancing Convenience and Computational Thinking

in STEM Learning. In Proceedings of the 45th acm

technical symposium on computer science education

(pp. 659-664).

Basawapatna, A., Repenning, A., & Savignano, M. (2019,

February). The Zones of Proximal Flow Tutorial:

Designing Computational Thinking Cliffhangers. In

Proceedings of the 50th ACM Technical Symposium on

Computer Science Education (pp. 428-434).

Boehmer, K. (1988). Zur Theorie der offenen Form in der

neuen Musik (2. Auflage ed.). Darmstadt: Tonos.

Brennan, K., & Resnick, M. (2012, April). New

frameworks for studying and assessing the

development of computational thinking. In

Proceedings of the 2012 annual meeting of the

American educational research association,

Vancouver, Canada (Vol. 1, p. 25).

Cano, E., Dittmar, C., Abeßer, J., Kehling, C., &

Grollmisch, S. (2018). Music Technology and

Education. In R. Bader (Ed.), Springer Handbook of

Systematic Musicology (pp. 855-871). Berlin,

Heidelberg: Springer Berlin Heidelberg.

Cope, D. (1989). Experiments in musical intelligence

(EMI): Non‐linear linguistic‐based composition.

Journal of New Music Research, 18(1-2), 117-139.

Edwards, M. (2011). Algorithmic composition:

computational thinking in music. Communications of

the ACM, 54(7), 58.

Floyd, S. P., & Sorbara, L. (2019, February). Sports

Analytics as a Context for Computational Thinking in

K-12 Education. In Proceedings of the 50th ACM

Technical Symposium on Computer Science Education

(pp. 1282-1282).

Freeman, J., & Magerko, B. (2016). Iterative composition,

coding and pedagogy: A case study in live coding with

EarSketch. Journal of Music, Technology and

Education, 9(1), 57-74.

Gander, W., Petit, A., Berry, G., Demo, B., Vahrenhold, J.,

McGettrick, & Meyer, B. (2013). Informatics

education: Europe cannot afford to miss the boat.

Report of the joint Informatics Europe & ACM Europe

Working Group on Informatics Education.

Graves, C. (2014). Teen experts guide makerspace

makeover.

Knowledge Quest, 42(4), 8.

Greher, G. R., & Heines, J. M. (2014). Computational

thinking in sound: teaching the art and science of music

and technology. New York: Oxford University Press.

Grover, S., & Pea, R. (2013). Computational Thinking in

K–12 A Review of the State of the Field. Educational

Researcher, 42(1), 38-43.

Hug, D., Petralito, S., Hauser, S., Lamprou, A., Repenning,

A., Bertschinger, D., … & Cslovjecsek, M. (2017,

August). Exploring Computational Music Thinking in

a Workshop Setting with Primary and Secondary

School Children. In Proceedings of the 12th

International Audio Mostly Conference on Augmented

and Participatory Sound and Music Experiences (pp. 1-

8).

Kafai, Y. (2006). Playing and Making Games for Learning.

Games and Culture, 1(1), 36-40.

Kafai, Y. B., Lee, E., Searle, K., Fields, D., Kaplan, E., &

Lui, D. (2014). A crafts-oriented approach to

computing in high school: Introducing computational

concepts, practices, and perspectives with electronic

textiles. ACM Transactions on Computing Education

(TOCE), 14(1), 1-20.

Kapur, M. (2008). Productive failure. Cognition and

instruction, 26(3), 379-424.

King, A., & Himonides, E. (2016). Music, technology and

education: critical perspectives (A. King & E.

Computational Music Thinking Patterns: Connecting Music Education with Computer Science Education through the Design of Interactive

Notations

651

Himonides Eds.). Abingdon, Oxon; New York, NY:

Routledge.

Knochel, A. D., & Patton, R. M. (2015). If art education

then critical digital making: Computational thinking

and creative code. Studies in Art Education, 57(1), 21-

38.

Lea, D. (1994). Christopher Alexander: An introduction for

object-oriented designers. ACM SIGSOFT Software

Engineering Notes, 19(1), 39-46.

Lee, I., Martin, F., & Apone, K. (2014). Integrating

computational thinking across the K--8 curriculum.

Acm Inroads, 5(4), 64-71.

Michotte, A. (1963). The Perception of Causality (T. R.

Miles, Trans.). London: Methuen & Co. Ltd.

Moreno-León, J., Robles, G., & Román-González, M.

(2015). Dr. Scratch: Automatic analysis of scratch

projects to assess and foster computational thinking.

RED. Revista de Educación a Distancia, (46), 1-23.

Nake, F., & Grabowski, S. (2017). Think the Image, Don't

Make It! On Algorithmic Thinking, Art Education, and

Re-Coding. Journal of Science and Technology of the

Arts, 9(3), 21-31.

Papert, S. (1980). Mindstorms: Children, computers, and

powerful ideas: New York: Basic Book.

Peng, H. (2012, February). Algo. Rhythm: computational

thinking through tangible music device. In Proceedings

of the Sixth International Conference on Tangible,

Embedded and Embodied Interaction (pp. 401-402).

Repenning, A. (2014, January). Scalable Game Design:

Broadening Participation by Integrating Game Design

and Science Simulation Building into Middle School

Curricula. Paper presented at the Future Directions in

Computing Education, Summit Meeting, Orlado,

Florida.

Repenning, A. (2017). Moving Beyond Syntax: Lessons

from 20 Years of Blocks Programming in AgentSheets.

Journal of Visual Languages and Sentient Systems,

3(July), 68-89.

Repenning, A., Basawapatna, A., & Escherle, N. (2016,

September). Computational Thinking Tools. In 2016

IEEE Symposium on Visual Languages and Human-

Centric Computing (VL/HCC) (pp. 218-222). IEEE.

Repenning, A., Lamprou, A., Petralito, S., & Basawapatna,

A. (2019, July). Making Computer Science Education

Mandatory: Exploring a Demographic Shift in

Switzerland. In Proceedings of the 2019 ACM

Conference on Innovation and Technology in Computer

Science Education (pp. 422-428).

Repenning, A., Smith, C., Owen, B., & Repenning, N.

(2012, June). AgentCubes: Enabling 3D Creativity by

Addressing Cognitive and Affective Programming

Challenges. In EdMedia+ Innovate Learning (pp. 2762-

2771).

Repenning, A., Webb, D. C., Koh, K. H., Nickerson, H.,

Miller, S. B., Brand, C., . . . & Gutierrez, K. (2015).

Scalable Game Design: A Strategy to Bring Systemic

Computer Science Education to Schools through Game

Design and Simulation Creation. Transactions on

Computing Education (TOCE), 15(2), 1-31.

Repenning A., Basawapatna A. R., & Escherle, N. A.

(2017). Principles of Computational Thinking Tools. In

H. C. Rich P. (Ed.), Emerging Research, Practice, and

Policy on Computational Thinking. Educational

Communications and Technology: Issues and

Innovations (pp. 291-305): Springer, Cham.

Ruthmann, A., Heines, J. M., Greher, G. R., Laidler, P., &

Saulters, C. (2010, March). Teaching computational

thinking through musical live coding in scratch. In

Proceedings of the 41st ACM technical symposium on

Computer science education (pp. 351-355).

Schulze, H. (2000). Das aleatorische Spiel: Erkundung und

Anwendung der nichtintentionalen Werkgenese im 20.

Jahrhundert. München: Fink.

Werner, L., Denner, J., Bliesner, M., & Rex, P. (2009,

April). Can middle-schoolers use Storytelling Alice to

make games?: results of a pilot study. In Proceedings

of the 4th International Conference on Foundations of

Digital Games. (pp. 207 - 214).

Wing, J. M. (2006). Computational Thinking.

Communications of the ACM, 49(3), 33-35.

Xambó, A., Freeman, J., Magerko, B., & Shah, P. (2016).

Challenges and New Directions for Collaborative Live

Coding in the Classroom. In International Conference

of Live Interfaces (ICLI 2016). Brighton, UK.

CSME 2020 - Special Session on Computer Supported Music Education

652