
A Learning Automata-based Algorithm for Energy-efficient Elastic
Optical Networks
Georgia A. Beletsioti
1 a
, Georgios I. Papadimitriou
1 b
, Petros Nicopolitidis
1 c
,
Emmanouel Varvarigos
2 d
and Stathis Mavridopoulos
1 e
1
Department of Informatics, Aristotle University of Thessaloniki, Thessaloniki, GR-54124, Greece
2
School of Electrical and Computer Engineering, National Technical University of Athens, Athens, GR-15780, Greece
Keywords:
Adaptivity, Elastic Optical Network, Energy-efficiency, Learning Automata.
Abstract:
Efficient use of available bandwidth plays an important role in performance enhancement due to the wide
penetration of high-bandwidth demanding services. The flexible nature of elastic optical networks (EONs)
effectively uses spectral resources for communication by allocating the minimum required bandwidth to cus-
tomer requirements. Since the energy consumption of such networks scales with the magnitude of bandwidth
demand, many studies have addressed the issue of energy wastage in optical networks. Learning Automata
are Artificial Intelligence tools that have been used in networking algorithms where adaptivity to the charac-
teristics of the network environment can result in a significant increase in network performance. This work
introduces a new adaptive power-aware algorithm, which selectively switches off bandwidth variable optical
transponders (BVTs) under low utilization scenarios supporting energy efficiency. A novel algorithm which
uses LA technology and significantly reduces the total energy consumption, while maintaining low bandwidth
blocking probability (BBP), is proposed. LA mechanism applied in this work, aims to find the best number of
BVTs to be switched off so as for the BBP not to be affected. Simulation results are presented, which indicate
that the proposed algorithm achieves a power saving of up to 50%, compared to non-adaptive solutions.
1 INTRODUCTION
The demand for bandwidth grows exponentially ev-
ery year, driven by a growing number of global in-
ternet users. Furthermore, high capacity-demanding
technologies, including autonomous vehicles, the in-
ternet of things, high bandwidth enhanced video, and
virtual reality, will also drive future needs. According
to Cisco, global IP traffic stood at 122 Exabytes in
2017 and it is estimated that these numbers will triple
by 2022 (Cisco, 2019).
Elastic optical networks (EON), as a novel con-
cept of WDM networks, are considered the most
suitable architecture for backbone and next gen-
eration metropolitan networks as they are charac-
terized by high spectral efficiency and adaptability
(Jinno, 2017). EONs which are based on orthog-
a
https://orcid.org/0000-0002-1895-094X
b
https://orcid.org/0000-0001-9529-9380
c
https://orcid.org/0000-0002-5059-3145
d
https://orcid.org/0000-0002-4942-1362
e
https://orcid.org/0000-0002-7058-3147
onal frequency-division multiplexing (OFDM) (Dao
et al., 2018) support lightpaths with different bitrates,
exploit the flexible grid technology where the spec-
trum is split into 25, 12.5 GHz or less slots compared
to coarser splitting of 50 GHz or 100 GHz of tradi-
tional WDM networks. Hence, the slots are com-
bined to create channels, which are not overlapping
due to OFDM’s orthogonality capacity, of the desired
size using bandwidth what is strictly necessary for the
transmission spectrum (Soumplis, 2017).
The energy consumed by ICT (Information and
Communication Technology) equipment, which is
rapidly expanding (Belkhir and Elmeligi, 2018),
(Beletsioti et al., 2016), causes a significant economic
and environmental problem. According to European
Framework Initiative for Energy and Environmental
Efficiency in the ICT Sector, ICTs account for 8-10%
of the European electricity consumption and up to 4%
of its carbon emissions. Furthermore, the network in-
frastructure is becoming a large portion of the energy
footprint in ICT. Thus, the concept of energy efficient
or green networking has been emerged as a research
topic. The issue of energy saving in IP Over WDM
Beletsioti, G., Papadimitriou, G., Nicopolitidis, P., Varvarigos, E. and Mavridopoulos, S.
A Learning Automata-based Algorithm for Energy-efficient Elastic Optical Networks.
DOI: 10.5220/0009819400270034
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - DCNET, OPTICS, SIGMAP and WINSYS, pages 27-34
ISBN: 978-989-758-445-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
27

networks has been extensively studied during the pre-
vious years (Shen and Tucker, 2009), (Chabarek et al.,
2008), (Melidis et al., 2019), (Dharmaweera et al.,
2014).
Various power-efficient algorithms considering
the design of IP over EON (Zhu et al., 2019) can be
found in the literature. A fairly common, yet effective
method of energy saving is the extensive application
of optical bypass, reducing thus the number of high
energy-consuming optical-electrical-optical (O-E-O)
conversions, as the signal can be transported, ampli-
fied and switched directly in the optical domain. In
(Zhang et al., 2015), energy efficient traffic grooming
in IP-over-elastic optical networks taking into account
sliceable optical transponders is studied. MILP mod-
els among their corresponding heuristics are imple-
mented, for each of three different types of bandwidth
variable transponders, and investigated in terms of en-
ergy efficiency. Based on traffic and optical groom-
ing methods, Selene heuristic (Kyriakopoulos et al.,
2018) is an online algorithm which exploits the in-
novative Signal Overlap technique for power savings
in EONs. The work in (Vizca
´
ıno et al., 2012) is dedi-
cated to the study of energy efficiency in optical trans-
port networks, comparing the performance of an in-
novative flexible network grid based on Orthogonal
Frequency Division Multiplexing (OFDM) with that
of Wavelength Division Multiplexing (WDM) with
a Single Line Rate (SLR) and a Mixed Line Rate
(MLR) operation. Energy-aware heuristic algorithms
are proposed for resource allocation both in static
(offline) and dynamic (online) scenarios with time-
varying demands for the Elastic-bandwidth OFDM-
based network and WDM networks (with SLR and
MLR). Lopez et al. in (Vizcaino et al., 2012), pro-
vides an in depth energy efficient comparison between
conventional path protection schemes for fixed-grid
(WDM) and flexible-grid (EON) networks.
Besides the above mentioned techniques, a con-
siderable number of published articles pertaining to
artificial intelligence (AI) approaches in conjunction
with energy efficiency issues in optical networks can
be found in the literature (Musumeci et al., 2018),
(Mata et al., 2018). Kyriakopoulos et al. in (Kyr-
iakopoulos et al., 2014) propose a heuristic method
based on ant colony optimization to reduce network
energy footprint by exploiting the basic principles
of swarm intelligence for finding the most energy-
efficient routes from source to destination nodes. In
addition, a multi-objective genetic algorithm is pro-
posed by Fern
´
andez et al. in (Fern
´
andez et al., 2012)
to design virtual topologies in order to reduce both
energy consumption and network congestion.
Optical switching node
Line amplifier
IP routers
IP Layer
Optical Layer
BVT
Figure 1: IP-Over-EON Architecture.
2 NETWORK MODEL
2.1 IP Over EON Architecture
A typical IP Over EON architecture, as shown in Fig.
1, is considered. The IP Over EON consist of two lay-
ers, the IP and the optical layer. In the IP layer, each
node is equipped with a central IP router, while the
optical layer consists of the optical switching nodes
connected with fiber optic cables. The optical layer
offers the link between the IP routers. In each node
multiple traffic streams from access network enters
the IP router. Each IP router port is connected to the
optical switching node through BVTs. At the start-
ing point of the data transmission, BVTs are responsi-
ble to convert the electrical flows from the IP layer to
optical flows (E/O conversion), then the traffic enters
the optical domain and is routed in all optical con-
nections over the optical network. When all optical
traffic traveling along the lightpath reaches its desti-
nation, the BVTs converts the signal back to electrical
(O/E conversion) and finally reaches the end point at
the IP layer. Data are then forwarded and handled by
the corresponding IP router. Finally, to enable optical
signals to travel over long distances, erdium doped
fiber amplifiers (EDFAs) are used in fiber optic con-
nections.
2.2 Elastic Optical Transponder
Technologies
Two types of transponder technologies according to
their sliceability degree can be categorised as follows.
Non-Sliceable BVT. This type of transponder is de-
signed to provide flexible lightpaths. NS-BVT allows
any optical channel with any spectral width and cen-
tral frequency to be established. NS-BVT has only
one slice and it is exclusively used to serve one light-
path, and thus it is called non-sliceable. Due to its
high available bandwidth it is offered to serve future
DCNET 2020 - 11th International Conference on Data Communication Networking
28

demands (i.e 400 Gbps). However, it often suffers
from low utilization.
Sliceable BVT. To overcome the above inflexibility of
NS-BVT, sliceable BVT were proposed in the litera-
ture (Sambo et al., 2017), (Jinno et al., 2012). Unlike
NS-BVT, this type of transponder which is also de-
signed to provide flexible lightpaths, allows more than
one lightpath to be established in the same transpon-
der. A physical transponder can be logically sliced
into multiple sub-transponders, each of which can
serve an independent lightpath between source and
destination nodes without electric processing at inter-
mediate nodes. As a result, various optical flows can
be aggregated into one optical transponder in order
to improve its utilization. This feature of S-BVT en-
ables optical grooming (Zhang et al., 2015), which
can additionally, significantly improve energy effi-
ciency, since no new transponders required for new
connections to be accommodated.
3 POWER CONSUMPTION
ANALYSIS
The main components, used in this study, which can
influence the amount of power consumption on an IP
Over EON are the IP router ports, the S-BVTs and
the EDFAs. A 400 Gbps IP router port, which con-
nects the IP router to the BVT is considered. An IP
router port consumes 560 W (1) (Zhang et al., 2015).
The power consumption of a BVT can be expressed
as in (2) according to (Zhang et al., 2015). TR rep-
resents the transmission rate of the optical transpon-
der, where in case of a sliceable transponder indicates
the sum of transmission rates of all sub-transponders.
An additional 20% of power consumption is consid-
ered as an overhead contribution for each transponder.
Moreover, it is assumed that the energy consumption
of the transmitter and the receiver are identical and are
equal to half of the power consumption of a transpon-
der. Erbium Doped Fiber Amplifiers are considered
as amplifiers in this study. The power of the EDFA is
represented in Equation (3), in which X is the spec-
trum width for amplifying. An inline amplifier is de-
ployed every 80km along the fiber, while a postampli-
fier as well as a pre amplifier are required at the ends
of the fiber link. The total power consumption is cal-
culated by adding the total energy consumption of the
BVTs, the EDFAs and the IP router ports (4).
PC
IP
= 560(Watt) (1)
PC
BV T
= 1.683 ×T R(Gb/s) + 91.333(Watt) (2)
PC
EDFA
= 0.0075 × X(GHz)(Watt) (3)
PC
total
= PC
IP
+ PC
BV T
+ PC
EDFA
(Wat t) (4)
4 THE LEARNING ENERGY
SAVING ALGORITHM (LESA)
4.1 Learning Automata Mechanism
Learning Automata (LA) are artificial intelligence
tools that can be applied to learn the characteristics
of a system’s environment. One major advantage of
LA is that they do not need to have any knowledge of
the environment they operate or any analytical knowl-
edge of the task to be optimized. A LA is a finite state
machine tool which improves its performance by in-
teracting with the random environment in which it op-
erates. The main purpose of a LA is to find within
a set of actions the optimal one, that is the action
that causes the minimum average penalty received by
the environment (or the maximum average reward re-
ceived by the environment). The low computational
complexity that a LA exhibits enables it to rapidly
converge to the best action of the environment with
which it interacts.
Figure 2 illustrates the operation of a typical LA,
in which there is a set of possible actions a
1
, a
2
,.., a
M
as well as the corresponding probabilities p. P(n) =
p
1
(n), p
2
(n),..., p
M
(n) constitutes a vector which rep-
resents the probability distribution for M actions at
each instant n. It holds that
∑
M
i=1
p
i
(n) = 1. At first,
the LA has no specific knowledge about the environ-
ment it operates and as a consequence all initial prob-
abilities are considered to be equal. At each instant
n, an action a
i
1 ≤ i ≤ M is selected with probability
p
i
(n). The action chosen by the automaton responds
with a stohastic reaction β
i
(n), which is used to up-
date the probability vector P. Upon completion of
this update, the LA selects the next action based on
the updated probability vector p
(n+1)
. This means that
the probabilities of some actions are increased or de-
creased according to the feedback received from the
environment.
4.2 Adaptive Model Formulation using
Learning Automata
Regarding the use of LA, in the context of this study,
is the detection of an acceptable number of BVTs that
should be switched off so that one manages to achieve
important energy savings while maintaining the BBP
A Learning Automata-based Algorithm for Energy-efficient Elastic Optical Networks
29
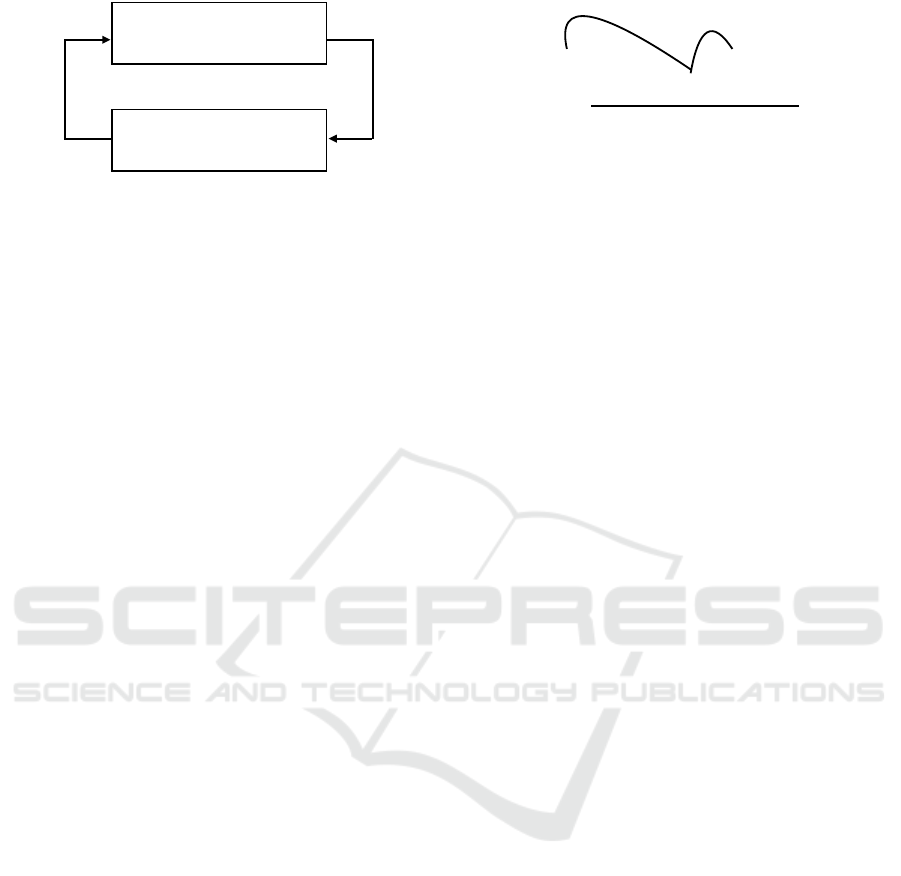
Random Environment
Learning Automaton
ai(n)
βi(n)
pi(n)
Figure 2: Operation of a Learning Automaton.
at low levels. In short, there are 2 actions that lead to
the next or previous state. This way the LA, based on
the corresponding probabilities, estimates where the
transition will take place. Equations (5) - (12) cor-
responds to the probability updating scheme of the
learning automaton that was described in the previous
section. At each cycle n, the basic choice probability
P of the selected action a is updated according to the
network feedback reaction. P
+1
(t) refers to action
+1
,
P
−1
(t) refers to action
−1
, whereas the term state (S)
refers to the number of BVTs switched off from net-
work nodes (i.e. S
5
corresponds to 50% of free dis-
abled BVTs per node), as it could be seen in Figure 3.
LA can then choose, based on P, whether to increase
the number of BVTs to be switched off (S
+1
) per node
by action
+1
, or decrease the number of BVTs to be
switched off (S
−1
) per node by action
−1
. At first, the
ratio of energy savings to BBP is estimated for a spe-
cific state. Afterwards, the LA checks if this ratio of
the state is greater than the calculated ratio of the pre-
vious state. Should the ratio be greater or equal than
the previously estimated ratio the basic choice proba-
bility of a increases according to (5), (6), (9) and (10).
Otherwise, the basic choice probability of a decreases
according to (7), (8), (11) and (12). L is a parameter
that governs the speed of the automaton convergence.
Two L values are used in this study, L
1
= 0.01 and
L
2
= 0.05.
For example, it is assumed that at a certain cycle
n, the LA is found at state 3 (S
3
), the corresponding
actions are action
−1
with P
−1
= 0.45, action
+1
with
P
+1
= 0.55 and the ratio of energy savings to BBP is
r. At cycle n + 1, the LA chooses the action with the
greater probability, P
+1
(action
+1
) and the new state
is 4. Then the ratio r
0
for state 4 is estimated and
compared to previously estimated ratio r. Should the
ratio r
0
be greater than r, the LA receives a rewarding
response and as a consequence updates the probabil-
ity scheme using (5) and (6). Finally, the LA is now at
state 4 and the probabilities for action
−1
and action
+1
are P
−1
= 0.4455 and P
+1
= 0.5545 respectively. This
procedure is repeated until the LA converges to a cer-
tain state.
State
action+1action-1
P(+1)(t)
P(-1)(t)
Figure 3: LESA learning mechanism.
P
(+1)u
(t + 1) = P
(+1)
(t) + L
1
× (1 − P
(+1)
(t)) (5)
P
(−1)u
(t + 1) = 1 − P
(+1)
(t) (6)
P
(+1)d
(t + 1) = P
(+1)
(t) − L
2
× P
(+1)
(t) (7)
P
(−1)d
(t + 1) = 1 − P
(+1)
(t) (8)
P
(−1)u
(t + 1) = P
(−1)
(t) + L
1
× (1 − P
(−1)
(t)) (9)
P
(+1)u
(t + 1) = 1 − P
(−1)
(t) (10)
P
(−1)d
(t + 1) = P
(−1)
(t) − L
2
× P
(−1)
(t) (11)
P
(+1)d
(t + 1) = 1 − P
(−1)
(t) (12)
4.3 Algorithm Description
The main idea of the proposed algorithm, namely
LESA, is the design of an energy efficient scheme
which manages to reduce the total energy con-
sumption during network’s operation, by adaptively
switching off a number of BVTs in low-use scenar-
ios without affecting the BBP. LESA algorithm con-
sists of two separate periods. The first period involves
the observation phase of the algorithm, during which
calculations are made regarding the utilization of the
BVTs. The second period refers to the use of LA
for estimating the relation between the energy sav-
ings achieved and BBP under a different number of
excluded BVTs (learning phase). Finally, the value
that was indicated by the LA, constitutes the most pre-
ferred one between the energy savings achieved and
BBP. That is, the number of BVTs to be switched off
in order for the BBP not to be affected significantly.
During the observation period, the algorithm starts
routing the traffic demands which arrive dynamically
in the network. LESA calculates the shortest paths
between the node pairs, using the k-shortest path
method, and routes the demands according to the First
Fit algorithm, while ensuring the continuity and conti-
guity constraint. During this phase, the existing BVTs
on the physical topology, as well as the BBP are moni-
tored for a fixed number of arrivals. Transmitters’ and
receivers’ utilization percentages for each node in the
physical topology have been calculated. Afterwards,
DCNET 2020 - 11th International Conference on Data Communication Networking
30

the mean BVT utilization per node is estimated. In the
final step of this period, the power consumption, using
(1), (2) and (3), as well as the BBP of the initial phys-
ical topology are estimated. In addition, the algorithm
outputs the number of free BVTs and the total num-
ber of BVTs per node after a certain percentage of the
free BVTs have been removed. Observation’s phase
output is used as an input to phase two of the algo-
rithm, the decision making with Learning Automaton
phase (learning phase).
Algorithm 1 shows the pseudocode of the pro-
posed algorithm LESA during the learning phase with
a learning automata mechanism. Tran
0
[i][x], is an ar-
ray which constitutes the number of BVTs per node,
where x indicates the node on the physical topology,
when i% of the free BVTs have been removed, i.e.
i = 0%, 10%, 20%,.., 100%. This array corresponds
to the states that the learning automaton can be found.
In detail, S
2
corresponds to i = 20%, while S
8
corre-
sponds to i = 80%. LA may chose to either increase
the number of removed BVTs, action
(+1)
, from the
physical topology with P
(+1)
, or decrease the num-
ber of removed BVTs, action
(−1)
, from the physical
topology with P
(−1)
. Firstly, the algorithm chooses
randomly a state sr and calculates BBP
0
for this state,
as well as the energy gains (ES
0
) of this state in com-
parison to PC
total
given from phase 1. Then the al-
gorithm retrieves the action with the highest probabil-
ity from ActionVector (lines 10 and 21), action
(+1)
or action
(−1)
which corresponds to S
sr+1
or S
sr−1
re-
spectively, runs the simulation for a fixed number of
arrivals and estimates the new BBP
00
for the current
state, as well as the energy gains (ES
00
) of this state
in comparison to PC
total
given from phase 1. Should
the ratio
ES
00
BBP
00
be greater or equal to
ES
0
BBP
0
, the learning
automaton updates the updating probability scheme
according to (5), (6), (9) and (10). Equations (5)
and (6) are applied when the LA rewards the incre-
ment of the switched off BVTs, while (9) and (10)
when the LA rewards the decrement of the switched
off BVTs. Otherwise, the LA updates the updating
probability scheme using (7), (8), (11) and (12). By
the end of this period, the algorithm ends up (conver-
gence of LA) with the estimated value of percentage
of switched off BVTs (S).
5 PERFORMANCE EVALUATION
A set of simulation experiments were conducted, in
order to evaluate the performance of the proposed al-
gorithm LESA. To estimate the overall power con-
sumption of different design solutions, the metropoli-
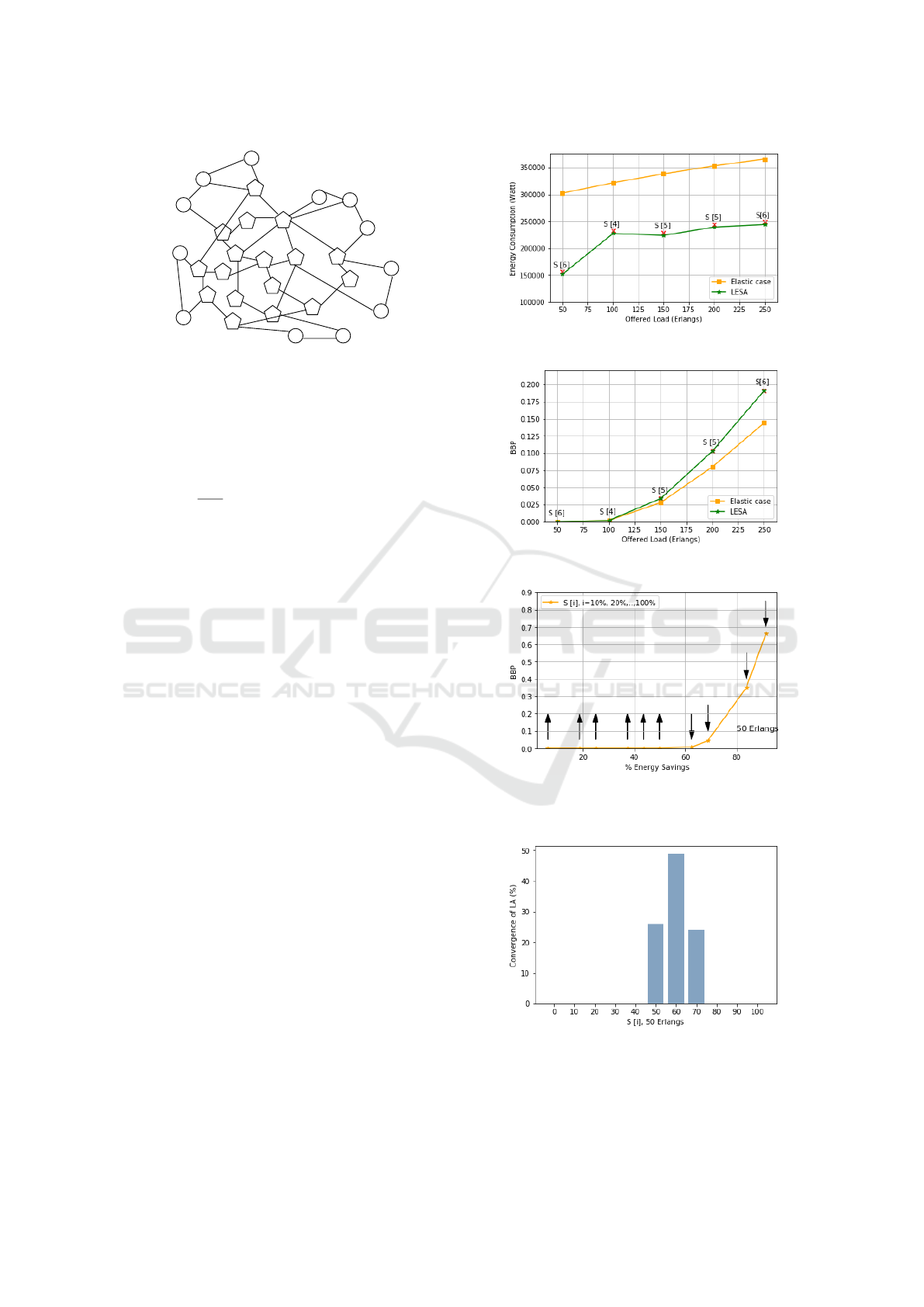
tan mesh network (Antoniades et al., 2004) of Figure
Algorithm 1: LESA, Learning Phase.
Input:
G(N, L): Physical Topology
N: Set of nodes in the network
L: Set of links in the network
PC
total
: Total PC from Phase 1
Total BBP from Phase 1
Tran
0
[i][x]: Number of BVTs per node
x ∈ N according to i
1: i ← removedtransponders 0%, 10%, .. , 100%
2: S ← Tran
0
[i]
3: ActionVector ← [S,action
(−1)
,action
(+1)
]
4: action
(−1)
← P
(−1)
5: action
(+1)
← P
(+1)
6: Choose state (S) sr randomly
7: Calculate ES
0
compared to initial PC
total
for S
sr
8: Calculate new BBP
0
for S
sr
9: while y ≤ trainingLA,y = 0 do
10: if ActionVector[2] ≥ ActionVector[1] then
11: sr ← sr + 1
12: Run Simulation for S
sr
13: Calculate new ES
00
and BBP
00
14: if
ES
00
BBP
00
≥
ES
0
BBP
0
then
15: Estimate P
(+1)u
(t + 1) using (5)
16: Estimate P
(−1)u
(t + 1) using (6)
17: else
18: Estimate P
(+1)d
(t + 1) using (7)
19: Estimate P
(−1)d
(t + 1) using (8)
20: end if
21: else
22: sr ← sr − 1
23: Run Simulation for S
sr
24: Calculate new ES
00
and BBP
00
25: if
ES
00
BBP
00
≥
ES
0
BBP
0
then
26: Estimate P
(−1)u
(t + 1) using (9)
27: Estimate P
(+1)u
(t + 1) using (10)
28: else
29: Estimate P
(−1)d
(t + 1) using (11)
30: Estimate P
(+1)d
(t + 1) using (12)
31: end if
32: end if
33: y ← y + 1
34: end while
Output:
Convergence of LA
4, which consists of 29 nodes and 41 links was con-
sidered.
5.1 Simulation Parameters and
Assumptions
An elastic optical network simulator has been im-
plemented, using Python 3.7 on Spyder. The num-
ber of frequency slots (FS) on a link equals to 160.
A Learning Automata-based Algorithm for Energy-efficient Elastic Optical Networks
31
1
2
3
4
5
67
8
9
10
11
12
13
14
15
17
18
19
20
21
22
23
24
25
16
27
28
29
26
Figure 4: Mesh based Metropolitan network.
The granularity of FS is 25 GHz, while the modula-
tion format used in every connection is assumed to
be the same during the whole simulation. Also, one
FS as a guard-band associated with each of the con-
nections is considered. Connection requests follow
a Poisson process with an average connection’s inter
arrival time (IAT) equals to 1 (λ), while their hold-
ing time follows a negative exponential distribution
with mean value (µ) and the offered load is deter-
mined by λ / µ (Erlangs). The latter is tuned to achieve
the desired traffic load (Comellas and Junyent, 2015).
The number of FSs per connection corresponds to the
uniform distribution, while each new coming connec-
tion can take any value from 1 to 9 with a uniformly
distributed probability (Comellas and Junyent, 2015).
The source and destination nodes of a request are ran-
domly and independently selected from the network
topology. K-shortest path, with k=3, and the First Fit
scheme, are used for solving the RSA problem. 400
Gbps slicable-BVTs which can launch 10 sub-carriers
(a sub-carrier is associated to a FS) enabling optical
grooming, and each sub-carrier can carry a 40-Gbps
signal are considered in this study. The number of S-
BVTs per node is assumed to be 15. Results presented
below are averaged over 3 × 10
5
connection requests
per simulation and the LA training number is assumed
to be 100.
5.2 Simulation Results
In order to measure the energy-saving potential
of LESA, a simple non-energy aware routing and
spectrum assignment approach, namely Elastic case
(Comellas and Junyent, 2015), has been implemented.
Figure 5 depicts the total energy consumption versus
the offered load (Erlangs) between LESA and Elastic
case algorithm. Each point in the graph (concerning
the LESA algorithm) corresponds to the energy con-
sumption when using the value (S) obtained by LA
mechanism after a training time (x symbol indicates
the state S LA finds). The energy consumption of
Figure 5: Energy consumption (in Watt) of LESA.
Figure 6: BBP performance of LESA.
(a) Percentage of energy savings (%) and BBP for
50 Erlang under different states in LESA opera-
tion.
(b) Convergence of basic probabilities for different
states in LESA operation.
Figure 7: LESA performance for 50 Erlang.
DCNET 2020 - 11th International Conference on Data Communication Networking
32
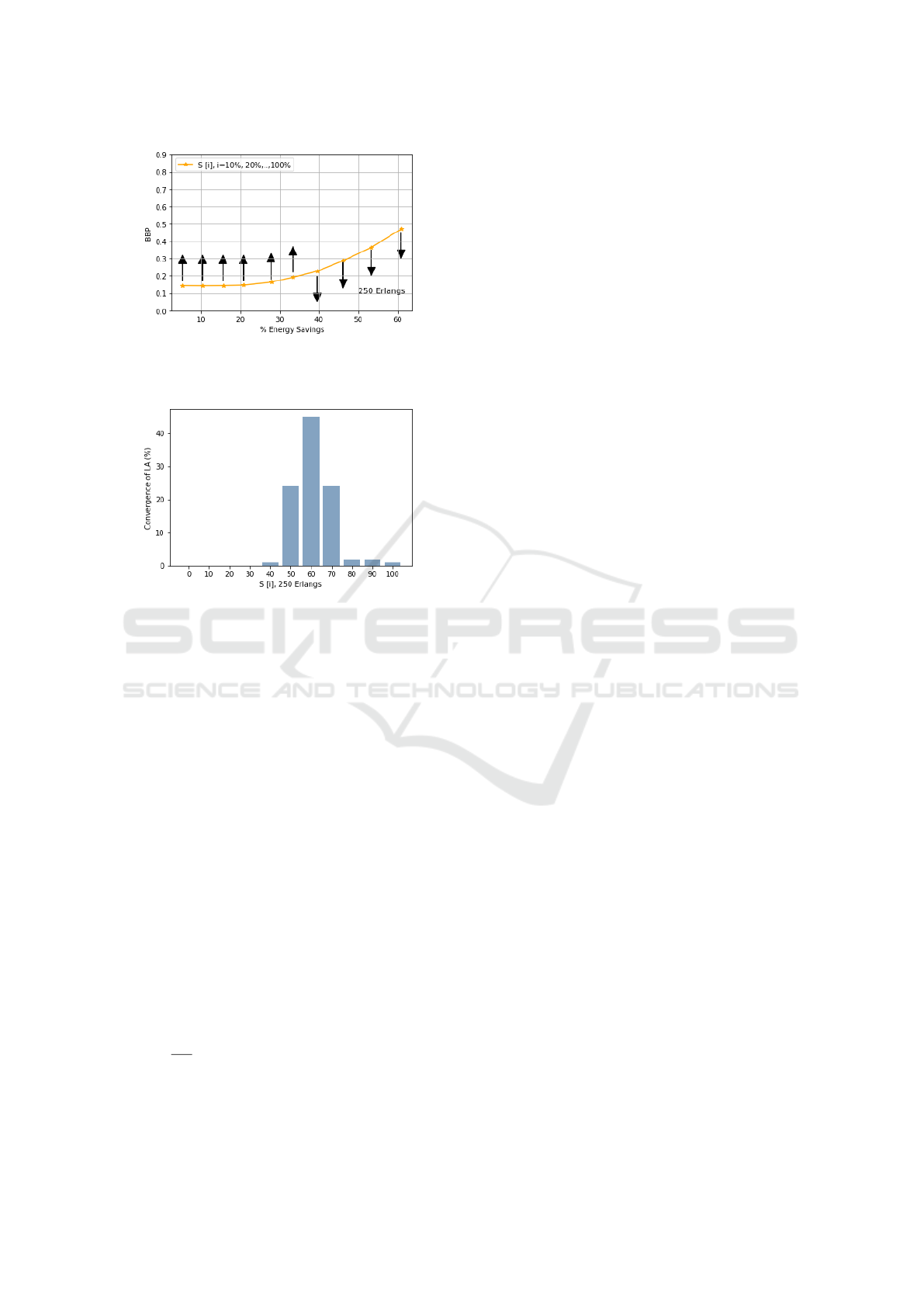
(a) Percentage of energy savings (%) and BBP for
250 Erlang under different states in LESA opera-
tion.
(b) Convergence of basic probabilities for different
states in LESA operation.
Figure 8: LESA performance for 250 Erlang.
each compared methods rises in a common way as
the offered load increases. It is worth noticing that
LESA always outperforms the reference Elastic case
algorithm. Corresponding results obtained in terms
of power savings are summarized in Figures 7a and
8a for 50 and 250 Erlangs, respectively. These results
are translated into profit by up to 50% and 33% Er-
langs, respectively.
Figures 7 and 8 illustrate the obtained results of
the proposed algorithm under different traffic loads.
More specifically, Figures 7 and 8 show the perfor-
mance evaluation of LESA for 50 and 250 Erlangs,
respectively. For each traffic load, two subfigures are
presented, with the first (7a and 8a) representing the
percentage of energy savings under the different states
of the algorithm versus the BBP, whereas the sec-
ond (7b and 8b) representing the convergence of basic
choice probabilities of LA towards different levels of
energy-saving. The arrows shown in the line graphs
(7a and 8a) correspond to the increase or decrease in
the ratio
ES
BBP
compared to the previous state.
An energy saving from 6% to 90% is achieved un-
der the offered load of 50 Erlangs, while the BBP
takes values from 0% to 66%, for states S
1
= 10%
to S
10
= 100%, respectively (Figures 7a and 7b). In
detail, for the first six states (S
1
- S
6
) of the simulation
the BBP remains at zero levels, while the percentage
of power gain rises progressively as the number of
the switched off BVTs increases, since a significant
number of BVTs as well as IP router ports is reduced.
For the rest of the states, the graph’s curve changes
significantly, as the BBP shifts at a faster rate than
the energy savings. As a result, the most acceptable
value of the free BVTs that should be switched off is
60% or S
6
. Should 60% of free BVTs per node will
be switched off from the physical topology, a power
saving of about 50% is achieved, while the BBP still
remains at zero levels. Observations are verified on
Figure 7b which report the convergence of the LA.
As it could be clearly seen, the LA chooses the pre-
ferred value of S
6
most of times with a percentage of
49%. Similar results, pertaining to 250 Erlangs can
be seen in Figure 8.
Finally, BBP, in linear scale, versus the increas-
ing offered load is depicted in Figure 6. BBP of
both algorithms increases when the traffic load in-
creases. As it could be seen, BBP remains the same
as long as the offered load is up to 100 Erlangs for
both LESA and Elastic case algorithm. Although, as
expected in higher offered load values the Elastic case
algorithm results in lower BBP, as the lightpaths have
more chances to be accommodated in a network with
a greater number of BVTs. However, the proposed
algorithm manages to save important amounts of en-
ergy without significantly increasing the BBP.
6 CONCLUSIONS
A novel algorithm which makes use of Learning Au-
tomata (LA) in a mechanism that selectively switches
off BVTs in low-load scenarios to achieve energy sav-
ings, is presented in this work. LA, based on BBP ob-
servations, aims at finding the most acceptable num-
ber of BVTs that should be switched off so that there
is a noticeable increase in terms of energy gains with-
out affecting the BBP. Simulation results verified that
the proposed algorithm can achieve by up to 50% of
energy savings while keeping the BBP at low levels.
ACKNOWLEDGEMENTS
This research has been cofinanced by the Euro-
pean Union and Greek national funds through the
Operational Program Competitiveness, Entrepreneur-
ship and Innovation, under the call RESEARCH-
CREATE-INNOVATE (project code:T1EDK-05061).
A Learning Automata-based Algorithm for Energy-efficient Elastic Optical Networks
33

REFERENCES
Antoniades, N., Roudas, I., Ellinas, G., and Amin, J. (2004).
Transport metropolitan optical networking: evolving
trends in the architecture design and computer model-
ing. Journal of lightwave technology, 22(11):2653.
Beletsioti, G. A., Papadimitriou, G. I., and Nicopolitidis,
P. (2016). Energy-aware algorithms for ip over wdm
optical networks. Journal of Lightwave Technology,
34(11):2856–2866.
Belkhir, L. and Elmeligi, A. (2018). Assessing ict global
emissions footprint: Trends to 2040 & recommenda-
tions. Journal of Cleaner Production, 177:448–463.
Chabarek, J., Sommers, J., Barford, P., Estan, C., Tsiang,
D., and Wright, S. (2008). Power awareness in net-
work design and routing. In IEEE INFOCOM 2008-
The 27th Conference on Computer Communications,
pages 457–465. IEEE.
Cisco (2019). Cisco visual networking index: Forecast and
trends, 2017 - 2022. Technical report.
Comellas, J. and Junyent, G. (2015). Improving link
spectrum utilization in flexgrid optical networks.
IEEE/OSA Journal of Optical Communications and
Networking, 7(7):618–627.
Dao, H., Morvan, M., and Gravey, P. (2018). An effi-
cient network-side path protection scheme in ofdm-
based elastic optical networks. International Journal
of Communication Systems, 31(1):e3410.
Dharmaweera, M. N., Parthiban, R., and S¸ekercio
˘
glu, Y. A.
(2014). Toward a power-efficient backbone network:
The state of research. IEEE Communications Surveys
& Tutorials, 17(1):198–227.
Fern
´
andez, N., Dur
´
an, R. J., de Miguel, I., Merayo, N.,
Aguado, J. C., Fern
´
andez, P., Jim
´
enez, T., Rodr
´
ıguez,
I., S
´
anchez, D., Lorenzo, R. M., et al. (2012). Surviv-
able and impairment-aware virtual topologies for re-
configurable optical networks: A cognitive approach.
In 2012 IV International Congress on Ultra Modern
Telecommunications and Control Systems, pages 793–
799. IEEE.
Jinno, M. (2017). Elastic optical networking: Roles and
benefits in beyond 100-gb/s era. Journal of Lightwave
Technology, 35(5):1116–1124.
Jinno, M., Takara, H., Sone, Y., Yonenaga, K., and Hirano,
A. (2012). Multiflow optical transponder for efficient
multilayer optical networking. IEEE Communications
Magazine, 50(5):56–65.
Kyriakopoulos, C. A., Papadimitriou, G. I., and Nicopoli-
tidis, P. (2018). Exploiting the signal overlap tech-
nique for energy efficiency in elastic optical networks.
In 2018 International Conference on Computer, Infor-
mation and Telecommunication Systems (CITS), pages
1–5. IEEE.
Kyriakopoulos, C. A., Papadimitriou, G. I., Nicopolitidis,
P., and Varvarigos, E. M. (2014). Energy-aware light-
path routing in optical networks based on adaptive
heuristics. In 2014 6th International Congress on Ul-
tra Modern Telecommunications and Control Systems
and Workshops (ICUMT), pages 15–22. IEEE.
Mata, J., De Miguel, I., Duran, R. J., Merayo, N., Singh,
S. K., Jukan, A., and Chamania, M. (2018). Artificial
intelligence (ai) methods in optical networks: A com-
prehensive survey. Optical switching and networking,
28:43–57.
Melidis, P., Nicopolitidis, P., and Papadimitriou, G. (2019).
Reserved energy-aware virtual topology management
for ip-over-wdm optical networks. Optical Switching
and Networking, 31:72–85.
Musumeci, F., Rottondi, C., Nag, A., Macaluso, I., Zibar,
D., Ruffini, M., and Tornatore, M. (2018). An
overview on application of machine learning tech-
niques in optical networks. IEEE Communications
Surveys & Tutorials, 21(2):1383–1408.
Sambo, N., Giorgetti, A., Cugini, F., and Castoldi, P. (2017).
Sliceable transponders: pre-programmed oam, con-
trol, and management. Journal of Lightwave Technol-
ogy, 36(7):1403–1410.
Shen, G. and Tucker, R. S. (2009). Energy-minimized de-
sign for ip over wdm networks. Journal of Optical
Communications and Networking, 1(1):176–186.
Soumplis, P. (2017). Routing and spectrum allocation al-
gorithms in elastic optical networks. PhD thesis.
Vizcaino, J. L., Ye, Y., L
´
opez, V., Jim
´
enez, F., Duque, R.,
and Krummrich, P. (2012). On the energy efficiency
of survivable optical transport networks with flexible-
grid. In European Conference and Exhibition on Opti-
cal Communication, pages P5–05. Optical Society of
America.
Vizca
´
ıno, J. L., Ye, Y., and Monroy, I. T. (2012). Energy ef-
ficiency analysis for flexible-grid ofdm-based optical
networks. Computer Networks, 56(10):2400–2419.
Zhang, J., Zhao, Y., Yu, X., Zhang, J., Song, M., Ji, Y., and
Mukherjee, B. (2015). Energy-efficient traffic groom-
ing in sliceable-transponder-equipped ip-over-elastic
optical networks. IEEE/OSA Journal of Optical Com-
munications and Networking, 7(1):A142–A152.
Zhu, M., Sun, Q., Zhang, S., Gao, P., Chen, B., and Gu,
J. (2019). Energy-aware virtual optical network em-
bedding in sliceable-transponder-enabled elastic opti-
cal networks. IEEE Access, 7:41897–41912.
DCNET 2020 - 11th International Conference on Data Communication Networking
34
