Stability of Barrier Model Predictive Control

Maxime Pouilly-Cathelain

1,2

, Philippe Feyel

, Gilles Duc

and Guillaume Sandou

Safran Electronics & Defense, Massy, France

Universit

e Paris-Saclay, CNRS, L2S, CentraleSup

elec, Gif-sur-Yvette, France

Keywords:

Model Predictive Control, Nonlinear Constraints, Barrier functions, Stability Analysis, Invariant Set.

Abstract:

In the last decades, industrial problems have tried to take into account constraints explicitly in the design of the

control law. Model Predictive Control is one way to do so and has been extensively studied. However, most

papers related to constrained Model Predictive Control often omit to consider nondifferentiable constraints and

stability is not ensured when constraints are not satisﬁed. The aim of this paper is to propose a formulation of

the cost function of a Model Predictive Control to ensure stability in face with input and state nondifferentiable

constraints. For this purpose, a set where all constraints are satisﬁed is deﬁned by means of the invariant set

theory. Once this set is deﬁned, the system is enforced to reach it and stay in, while guaranteeing stability

thanks to the choice of a well suited Lyapunov function based on the cost function.

1 INTRODUCTION

In industrial problems, system design is usually based

on high-level system speciﬁcations. In order to reach

these speciﬁcations with high performances, require-

ments have to be taken into account during the design

of the control law. Model Predictive Control (MPC) is

one way to control systems with state and input con-

straints. In this paper, we aim to design a stabilizing

controller for a discrete linear system subject to non-

differentiable constraints.

As presented in (Rawlings et al., 2017), MPC

method elaborates the control input as the result of

an optimization problem. At each time step, a vec-

tor of future inputs is determined to get the optimal

predicted behavior of the system on a ﬁnite predic-

tion horizon according to a cost function. Following

the principle of the receding horizon, only the ﬁrst in-

put of the obtained input sequence is applied to the

system. Stability, feasibility and constraint consider-

ations are important points that have been studied in

MPC theory. The following paragraphs present some

works related to these topics in order to capture the

underlying context of our study.

To begin with, MPC stability has been extensively

studied in recent decades. (Chen and Shaw, 1982) is

one of the ﬁrst papers using a terminal constraint and

a Lyapunov function based on the cost function of the

MPC in order to prove stability. At this point no con-

straint was taken into account. (Keerthi and Gilbert,

1988) extended this work by using an equality termi-

nal constraint and a Lyapunov function to prove the

stability for a nonlinear discrete time varying system

subject to constraints. An equality constraint is in

general really challenging for an optimization algo-

rithm. Proof given in previous cited articles suppose

that the system is able to reach the target state be-

fore the end of the prediction horizon in order to avoid

the problem of recursive feasibility. More recently, in

order to relax the terminal constraint while keeping

stability, (Rawlings and Muske, 1993) have used the

cost of the inﬁnite horizon problem to deﬁne a termi-

nal cost. The proof of stability is based on the use of

a ﬁnal controller related to the inﬁnite horizon control

problem. (Chisci et al., 1996) and (Scokaert et al.,

1999) impose a terminal set where a state feedback

controller stabilizes the system. One drawback of this

method is the need to reach this set before the end of

the prediction horizon.

Next, one main issue of constrained MPC is the

feasibility of the problem because infeasibility can

lead to instability. In fact, in presence of constraints,

the system can be unable to reach the target point, this

deﬁnes MPC infeasibility. Recursive feasibility is an

important point, meaning that if the system can reach

the target point at a given time step, the problem is

also feasible at the next time step. To obtain this,

some improvements of the MPC problem have been

proposed. To avoid infeasibility to reach an imposed

terminal set, (Michalska and Mayne, 1993) propose a

150

Pouilly-Cathelain, M., Feyel, P., Duc, G. and Sandou, G.

Stability of Barrier Model Predictive Control.

DOI: 10.5220/0009821001500158

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 150-158

ISBN: 978-989-758-442-8

solution with a prediction horizon of variable length.

In this case, the problem is that the prediction hori-

zon could become really large and the optimization

algorithm could be unable to ﬁnd a solution. In or-

der to relax the problem, it is possible to use slack

variables, as presented in (Camacho and Bordons,

2007). The main drawback of this method is that it

increases the number of optimization parameters. Fi-

nally, (Zeilinger et al., 2010) propose to relax the ter-

minal set constraint that can grow to make the prob-

lem feasible.

Barrier model predictive control (BMPC) has

emerged in order to take into account constrains di-

rectly in the cost function. Barrier functions method is

similar to the use of slack variables in that it permits to

relax constraints. The ﬁrst proposition has been done

by (Wills and Heath, 2004) for differentiable con-

straints. Regardless of BMPC, economic MPC has

been developed to enforce reduction of some quan-

tities. According to (Amrit et al., 2011), economic

MPC minimizes a cost function that includes convex

constraints. (M

uller et al., 2014) presents a formula-

tion that permits to take into account the mean value

of a state in the cost function.

Stability of BMPC has already been studied sev-

eral times. For instance in (Wills and Heath, 2004) the

stability has been proven by using a quadratic upper

bound of the barrier function and an ellipsoidal termi-

nal set. The same method has been used in (Feller and

Ebenbauer, 2015) with a polytopic terminal set. This

work is extended to suboptimal solution in (Feller

and Ebenbauer, 2017) where polytopic constraints on

states and inputs are included in the cost function us-

ing relaxed logarithmic barrier. Furthermore, (Pet-

sagkourakis et al., 2019) propose conditions to ensure

robust stability according to system uncertainties, yet

this paper only deals with differentiable constraints.

To the best of our knowledge, there is no literature

dealing with BMPC and nondifferentiable constraints.

Moreover, the case where the system is far from the

set where all constraints are satisﬁed is often omitted.

In this paper, we aim to propose a BMPC for lin-

ear discrete systems that can deal with any evaluable

constraint, being differentiable or not, by means of

barrier functions. For this purpose, a gradient free

optimization algorithm is needed to deal with any for-

mulation of barrier function. For instance, differen-

tial evolution algorithms (Price et al., 2006) are inter-

esting candidates to solve this problem. This choice

has been done in (Merabti and Belarbi, 2014) with a

multi-objective model predictive control using meta-

heuristic. Nevertheless this solution is only suitable

for a relatively small number of constraints, as the

difﬁculty of choosing the best solution in the Pareto

front increases with the number of objectives.

In addition to the proposed methodology, a proof

of stability using Lyapunov and invariant set theories

is also established in the case of linear discrete sys-

tems under some realistic assumptions. The proposed

method is based on the following steps:

1. Constraints formulation. Constraints directly re-

sult from the initial set of speciﬁcations and no

reformulation should be required at this stage.

2. Constraints classiﬁcation. Constraints are clas-

siﬁed into two different categories and some of

them are used in the cost function as barrier func-

tions. This classiﬁcation is important for stability

purpose as it will be shown in the sequel.

3. Unconstrained set deﬁnition. Speciﬁcations per-

mit to deﬁne a set where all constraints are sat-

isﬁed and the corresponding backward reachable

set. These sets are deﬁned in such a way that the

stability can be proven.

4. Cost function deﬁnition. The cost function is de-

ﬁned by using barrier functions deﬁned in step (2)

and according to sets deﬁned in step (3).

This paper is organized as follows. First of all, we

will introduce some notations in section 2. Section 3

introduces conditions about the barrier functions to

be chosen. Then, section 4 is related to the determi-

nation of the maximal unconstrained set. The cost

function of the proposed BMPC is developed in sec-

tion 5. Thereafter, section 6 provides a proof of sta-

bility based on the Lyapunov theory. An application

of the proposed BMPC is given in section 7. Finally,

section 8 concludes and proposes some future works.

2 NOTATIONS

Linear discrete-time systems of interests in this paper

are deﬁned by (1).

K`1

“ Ax

`Bu

“ Cx

`Du

. (1)

where K P N is the time index, x

PX Ď R

(n P N

P U Ď R

(p P N

), y P R

(m P N

), A P R

nˆn

B P R

nˆp

, C P R

mˆn

and D P R

mˆp

. X and U are

two compact sets. Without any loss of generality, the

system will be stabilized at the origin. Assumption 1

and 2 are considered for the system.

Assumption 1. pA, Bq is controllable.

Assumption 2. A is non singular. Among others, this

is the case for systems obtained by discretization of

continuous systems without time delay.

Stability of Barrier Model Predictive Control

151

Our prediction model is deﬁned by (2) where pre-

dicted states and outputs will be respectively denoted

by ¯x and ¯y.

@k PJ0; N ´1K,

¯x

k`1

“ A ¯x

`Bu

¯y

“ C ¯x

`Du

. (2)

¯x

P R

is the initial state of the system and ¯x

P R

the ﬁnal predicted state where N PN

is the prediction

horizon. It is assumed that the state at time K, x

, can

be measured thus ¯x

“ x

. The vector of predicted

states is

x “ r¯x

, . . . , ¯x

denotes the cost function. Mathematical for-

matting of the cost function will be more precisely

presented in section 5. We also deﬁne the optimal

cost J

and the problem P

q which is solved by

the MPC optimizer at each time step as (3).

q : J

q “ min

x, uq | u PU

(

. (3)

u P U

denotes the vector of inputs. According to

the receding horizon principle, the ﬁrst component of

the vector u is applied to the system and (3) is solved

again at the following time step.

}x}

denotes the norm of x P R

deﬁned by

}x}

“ x

Qx where Q P R

nˆn

is a symmetric strictly

deﬁnite positive matrix.

@x P R

, dpx, Sq “ inf tN px, sq|s PSu represents

the distance between x and the set S where N is a

norm on R

. For instance, N could be the Euclidean

norm.

The following operator can be applied to sets:

@pA, Bq Ď R

ˆR

, AzB “ tx |x PA and x R Bu.

(4)

3 FORMULATION OF THE

BARRIER FUNCTIONS

System design is often based on end-user speciﬁca-

tions. Only speciﬁcations that can be mathematically

formatted as constraints are considered in this paper.

The main goal of this section is to present a way to

consider constraints as barrier functions that will be

used in the proposed BMPC. Properties required for

sake of stability proof (section 6) are also provided.

Once constraints are satisﬁed, the goal is to make the

system remain as long as possible inside the corre-

sponding set; in the case where the initial system state

does not satisfy the constraints, the goal is to reach the

feasible set.

We only consider inequality constraints deﬁned by

ď c

max

(5)

where

X is any set of states evaluated at any sample

time and

U is any set of inputs evaluated at any sample

time and c

max

P R.

We admit that all constraints are at least satisﬁed

at the origin pc p0, 0q ď c

max

which is the target point.

Equality constraints are unusual in industrial prob-

lems and can be easily converted into inequality con-

straint using (6), where ε P R

is a small number.

“ 0 Ñ

›

´ε ď 0 (6)

Constraints can be classiﬁed into two categories:

1. Constraints that are applied independently to each

predicted state. For instance, an upper bound on a

given state variable.

2. Constraints that are applied to a combination of

different predicted states. For instance, the vari-

ance of a state over the predicted horizon.

The total number of constraints and the number

of constraints which belong to the ﬁrst type will be

respectively denoted by N

and N

In the following, the constraint u PU is not consid-

ered using a barrier function because the search space

of a gradient free optimization algorithm is usually a

compact set.

The largest set included in X where all constraints

are satisﬁed will be denoted by

C Ď X.

For stability purpose (see section 6), only con-

straints that belong to the ﬁrst type will be taken into

account in the cost function of the MPC as barrier

functions. However, all constraints will be taken into

account during the determination of

C .

It is worth emphasizing that barrier functions are

only here to penalize the cost function when con-

straints are not satisﬁed, thus it cannot be ensured

that constraints will always be satisﬁed. Moreover,

because barrier functions can only be evaluated on

the prediction horizon we cannot guarantee that con-

straints will be satisﬁed from a global point of view.

Yet, increasing the value of N can increase probability

to globally fulﬁll requirements.

The use of barrier functions permits to relax the

MPC problem and improve feasibility. This relax-

ation permits to always ﬁnd a trajectory to reach the

target point even if all constraints are not satisﬁed.

We will now give some properties required to

prove stability of the proposed BMPC. The barrier

function l

for constraint c should be deﬁned to sat-

isfy:

@pu, kqPU

ˆJ0; NK,

p¯x

, uq “ 0 if ¯x

p¯x

, uq ě 0 if ¯x

(7)

where

is the set where the constraint c is satisﬁed.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

152

is deﬁned as the global barrier function:

@pu, kq PU

ˆJ0; NK, l

p¯x

, uq“

c“1

p¯x

, uq. (8)

Using (7) the following property holds:

@pu, kqPU

ˆJ0; NK,

p¯x

, uq “ 0 if ¯x

p¯x

, uq ě 0 if ¯x

(9)

where

C is deﬁned by (10).

C “

c“1

. (10)

Since l

is a barrier function that may be applied to

all elements of the predicted state vector

x, the no-

tation l

x, uq will be used in the sequel. Properties

presented in (9) still hold true for each element ¯x

the predicted state

4 DETERMINATION OF THE

UNCONSTRAINED SET

In this section a method to determine a set C as an

approximation of

C is presented. This set C has to

be included or equal to

C and to be positive invariant.

Positive invariant sets correspond to deﬁnition 1 be-

low, which will be used in section 6 to prove stability.

Deﬁnition 1. A set C is positive invariant with re-

spect to the system x

K`1

“ Ax

`Bu

for the control

law u

“

if for a state x

PC then for all i P N

K`i

P C .

The set which corresponds to the set of all points

that can reach C in N steps is denoted by C

pNq. The

following property 1 holds true and the corresponding

proof is given by proof 1.

Property 1. If C is positive invariant then, for all

pNq, it exists u

such that x

K`1

“Ax

`Bu

pNq.

Proof 1. Let x

be an element of C

pNq. It means

that it exists an input sequence u “ ru

, . . . , u

N´1

which leads to a ﬁnal predicted state ¯x

P C . It has

been supposed that the predictor is identical to the

system thus, at the next time step, the current state

will be x

K`1

“ ¯x

“ A ¯x

`Bu

. Because C is pos-

itive invariant with respect to u

“

, it exists

P U such that ¯x

“ A ¯x

`Bu

P C . Therefore,

the control vector u

“

, . . . , u

N´1

, u

‰

leads to

¯x

P C . Thus for all x

P C

pNq, it exists u

such

that x

K`1

“ Ax

`Bu

P C

pNq. ˝

4.1 First Approximation of

C :

To begin with, by taking into account all speciﬁca-

tions, a ﬁrst approximation

C of

C should be de-

termined. This ﬁrst approximation is not necessarily

positive invariant. In some cases and particularly in

the case of nonlinear constraints, the set

where a

constraint c is satisﬁed is difﬁcult to compute. That is

why a set

is used as an approximation. Thus,

a ﬁrst approximation

C of

C is:

C “

c“1

. (11)

For all constraint c, assumption 3 is done on

Assumption 3. Every set

contains the origin. As a

consequence, 0 P

C which means that

C is not empty.

As an example, in a stochastic context, consider-

ing a constraint on the variance σ

over the prediction

horizon of the ﬁrst element ¯x

of the predicted state

`“

¯x

, . . . , ¯x

‰˘

ď a. (12)

where a P R

, a set

for this constraint can be de-

ﬁned by:

“

, @k PJ0; NK , ¯x

P R , |¯x

| ď

(

. (13)

4.2 Deﬁnition of the Set C

In this part, it is supposed that the ﬁrst approximation

C Ď

C is known. In the following, we will deal with

a convex polytope approximation of

C . Convex poly-

tope approximations of sets are discussed in (Bron-

stein, 2008).

The maximal positive invariant set C included

C is determined using an algorithm described

in (Gilbert and Tan, 1991) for the system deﬁned

by (14). K

is computed by solving a Linear

Quadratic problem.

K`1

“ Ax

`BpK

“ Cx

`DpK

. (14)

This method will be illustrated by the example in

section 7.

In the following, it is assumed that C is known

and deﬁned, therefore property 1 holds for C

pNq.

Remark 1. Equation (9) still holds by substituting

for C because C Ď

C .

Stability of Barrier Model Predictive Control

153

5 DEFINITION OF THE COST

FUNCTION

5.1 Theoretical Concept

We would like to ensure that ¯x

will reach C when the

current state x

“ ¯x

is in XzC . The set of trajectories

corresponding to N steps forward from ¯x

such that

dp¯x

, C q ă dp¯x

, C q is denoted by T. T

ĂT denotes

the set of trajectories such that ¯x

P C which means

that dp¯x

, C q “ 0.

Assumption 4 is considered.

Assumption 4. ¯x

is in the maximal controllable set

included in X. As a consequence, T is not empty.

Furthermore, by deﬁnition of C

pNq, T

is not

empty if and only if the current state x

“ ¯x

is in

pNq.

The two following cases are considered:

1. If T

is empty, then a LQ control law is applied.

With this control law, the state is ensured to reach

pNq

2. If T

is not empty, then the best trajectory in T

is found according to the cost function and con-

straints that belong to the ﬁrst category presented

in section 3.

Figure 1 shows the different cases for a two states

system.

Following statements propose a mathematical for-

mulation of the cost function that can be used as the

criterion to be optimized in both cases.

5.2 Mathematical Formulation

When ¯x

R C , convergence has to be prioritized

against constraints thus a terminal constraint is added

on ¯x

. This terminal constraint can be formulated by a

cost function presented in section 5.2.1. If this termi-

nal constraint is satisﬁed a cost function that includes

barrier functions is used as presented in 5.2.2. The

problem is ﬁnally formulated as a single optimization

problem in section 5.2.3.

5.2.1 Mathematical Formulation of the Terminal

Constraint

In this case, we have to ﬁnd if it exists a trajectory that

can reach C which means that dp¯x

, C q “ 0 thus the

cost function is required to be the distance dp¯x

, C q:

x, uq “ dp¯x

, C q. (15)

With this cost function the optimization algorithm

is enforced to ﬁnd a trajectory with the ﬁnal predicted

state in (or at least as close as possible to) the set C

where all constraints are satisﬁed. This is equivalent

to a terminal constraint.

Case 1

pNq

LQ trajectory

¯x

Case 2

pNq

¯x

Possible trajectory

Selected trajectory

Figure 1: Graphic presentation of the two different cases.

5.2.2 Mathematical Requirements for Finding

the Best Trajectory with Regard to

Constraints

In the case of x

“ ¯x

P C

pNq ô J

x, uq “ 0, it is

required to ﬁnd the best trajectory in T

according to

the classical MPC cost function and the barrier func-

tions. Thus, the cost function to be minimized is de-

ﬁned by (16).

x, uq “

N´1

k“0

lp¯x

, u

q`l

p¯x

q`l

x, uq. (16)

where lp¯x

, u

q “ }¯x

}

`}u

}

is the classical MPC

cost, l

p¯x

q is a terminal cost and l

corresponds to

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

154

barrier functions (deﬁned in section 3).

5.2.3 Mathematical Formatting of the Cost

Function

We want to consider one single optimization problem

thus a cost function that takes into account both cases

presented in section 5.1 is deﬁned. For this purpose,

a positive and a negative cost function will be respec-

tively used for the ﬁrst and the second case by using

the involutory

transformation t deﬁned by (17).

@x PR

, tpxq “ ´1{x. (17)

The optimization process is ﬁnally based on the

global cost function J

deﬁned by (18).

x, uq “

x, uq if ¯x

R C

pNq

t pJ

x, uqq if ¯x

P C

pNq and J

x, uq ‰ 0

´8 if ¯x

P C

pNq and J

x, uq “ 0

(18)

In the next section, it will be shown how this cost

function permits to impose stability.

Remark 2. This methods bears similarities with the

one proposed in (Feyel, 2017) where H

controllers

are tuned using stochastic algorithms. The ﬁrst step of

the method consists of reducing the distance between

the largest magnitude of eigenvalues of the closed

loop and the unit circle and the second optimization

step consists of ﬁnding the best controller according

to speciﬁcations.

6 ASYMPTOTIC STABILITY

To begin with, as presented in (Mayne et al., 2000),

the cost function deﬁned by (16) is not sufﬁcient to

prove stability because it requires to assume that the

barrier function deﬁned by (8) is decreasing along

the prediction horizon. This assumption is unsatis-

fying when we deal with some speciﬁc constraints

such as standard deviation of the output which can

only grow if the system starts from a stationary state.

That is why the cost function (18), using a terminal

constraint, has been proposed.

In this section assumption 5 is considered.

Assumption 5. The optimization algorithm always

ﬁnds the global minimum of P

deﬁned by (3).

In practice it is almost impossible to ﬁnd the ex-

act global solution at each step thus some works have

been done in order to prove stability without assump-

tion 5, (Reble and Allg

ower, 2012), (Allan et al.,

An involutory transformation deﬁnes a transformation

that is its own inverse.

2017), (Scokaert et al., 1999). Using these works, the

following proof can be modiﬁed to tackle suboptimal

solutions given by the optimizer. This point will be

tackled in future works.

In order to prove stability, we need to ensure that

the following properties hold when solving P

p¯x

1. If ¯x

is not in C

pNq, the convergence to C

pNq of

the system state is ensured.

2. If ¯x

is in C

pNq we have Lyapunov stability.

With these two statements it is possible to prove

that the system will reach the unconstrained set C and

that the system is stable in the sense of Lyapunov in

pNq.

Remark 3. The decrease of the distance in the ﬁrst

statement (section 5.2.1) does not imply that the value

of the cost function decreases.

6.1 Convergence for x

“ ¯x

R C

pNq

The cost function has been formulated in order to

ﬁrstly determine a trajectory such that dp¯x

, C q “ 0,

but in case where x

“ ¯x

R C

pNq such a trajectory

does not exist. In practice, it corresponds to a positive

cost at the end of the optimization. In this case, a LQ

control law is applied to the system. With this law, the

system state is ensured to converge to C

pNq.

Remark 4. The idea that consists of applying the se-

quence of input determined by the MPC algorithm

that decreases the distance from C is not sufﬁcient

to ensure convergence thus it is not a viable solution.

6.2 Convergence for x

“ ¯x

P C

pNq

We now tackle the second point. To begin with, the

following function V is deﬁned.

x, uq P C

pNq

N`1

ˆU

V p

x, uq “t pJ

x, uqq “

´1

x,uq

(19)

By simpliﬁcations using the fact that ¯x

P C

pNq

and (18):

x, uq P C

pNq

N`1

ˆU

V p

x, uq “ J

x, uq

“

N´1

k“0

lp¯x

, u

q`l

p¯x

q`l

x, uq.

(20)

Because l and l

are positive functions on

X ˆU and l

is a positive function on X

N`1

ˆU

we can conclude that V is a positive function on

pNq

N`1

ˆU

. Moreover, V p0, 0q “ 0.

Stability of Barrier Model Predictive Control

155

We can choose similarly to the warm start method

presented in (Rawlings et al., 2017) (see Fig. 2):

@k PJ0; N ´2K, u

“ u

k`1

, (21)

N´1

is chosen such that ¯x

P C . The existence of

N´1

such that ¯x

P C is directly derived from deﬁ-

nition 1 and property 1. The optimization algorithm

could ﬁnd an other vector u

, but this solution can

only be better in terms of cost function (thanks to as-

sumption 5) thus the proof proposed below still holds.

pNq

¯x

“ ¯x

¯x

“ ¯x

¯x

“ ¯x

¯x

“ ¯x

¯x

“ ¯x

¯x

“ ¯x

¯x

Trajectory from ¯x

Figure 2: Example for N “ 6

The next predicted state vector corresponding

to u

will be denoted by

. By deﬁnition,

“

¯x

, . . . , ¯x

, ¯x

‰

. The function V evaluated at

the next time step is thus V p

, u

We now evaluate V p

, u

q´V p

x, uq,

V p

, u

q´V p

x, uq

“

N´1

k“0

lp¯x

, u

q`l

p¯x

q`l

, u

„

N´1

k“0

lp¯x

, u

q`l

p¯x

q`l

x, uq



“

N´1

k“0

“

lp¯x

, u

q´lp¯x

, u

‰

` l

, u

q´l

x, uq

` l

p¯x

q´l

p¯x

(22)

As a reminder, only barrier functions that correspond

to constraints that belong to the ﬁrst category pre-

sented in section 3 are taken into account. Moreover,

“

¯x

, . . . , ¯x

, ¯x

‰

by deﬁnition. Thus, the expres-

sion l

, u

q´l

x, uq that appears in (22) can be

simpliﬁed by looking only on inﬂuence of the ﬁrst

component: ¯x

and the last one: ¯x

. In order to make

it appears explicitly, we will note:

, u

q´l

x, uq “ l

p¯x

, u

q´l

p¯x

, uq. (23)

Moreover, by using (21), we can simplify (22):

V p

, u

q´V p

x, uq “ lp¯x

N´1

, u

N´1

q´lp¯x

, u

` l

p¯x

, u

q´l

p¯x

, uq

` l

p¯x

q´l

p¯x

(24)

By deﬁnition of C , ¯x

P C ñ l

p¯x

, u

q “ 0

(see (9)). We ﬁnally have

V p

, u

q´V p

x, uq “ lp¯x

N´1

, u

N´1

q´lp¯x

, u

´ l

p¯x

, uq

` l

p¯x

q´l

p¯x

(25)

From (9), l

is a positive function thus:

V p

, u

q´V p

x, uq

ď l

p¯x

q´l

p¯x

q`lp¯x

N´1

, u

N´1

q´lp¯x

, u

(26)

The right part of inequality (26) corresponds to the

classical equation that is found in the proof of stability

of the original Model Predictive Control. According

to (Rawlings et al., 2017), if we choose for instance

p¯x

q “ ¯x

P ¯x

where P is the positive deﬁnite solu-

tion of the Ricatti equation:

P “ Q `A

PA ´A

PBpB

PB `Rq

´1

PA, (27)

we can prove that

p¯x

q´l

p¯x

q`lp¯x

N´1

, u

N´1

q´lp¯x

, u

q ă 0

(28)

From (26), we ﬁnally have V p

, u

q´V p

x, uq ă 0.

To conclude, V is a positive decreasing function

with V p0, 0q “ 0 thus V is a Lyapunov function and

we can conclude that the proposed BMPC is Lya-

punov stable on C

pNq.

7 APPLICATION EXAMPLE

In this example, a motor with angular position and ve-

locity respectively denoted by θ and Ω is considered.

The considered motor can be modeled by a ﬁrst order

transfer function: θpsq{upsq “ 0.9{ps ˚p1 `0.015sqq

The sampled time is chosen to be T

“ 1ms and the

whole state is measured. The corresponding state

space representation is:

’

K`1

“

1.0 1.0e ´3

0 9.4e ´1

1.0e ´4

5.8e ´2

“

1 0

0 1

(29)

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

156

where x

“

Ω

It is assumed that the set of constraints

C is de-

ﬁned for all K in N by

0 1

0 ´1

. (30)

Furthermore, @K P N, ´10 ď u

ď 10.

In this particular case, all constraints are taken into

account in the cost function because they all belong to

the ﬁrst category presented in section 3. In this exam-

ple, exponential barrier functions deﬁned by (31) have

been used.

x, uq “ α max

0, exp

β max

kPJ1,NK

tdpΩ

, X

Ω

´ 1

(31)

where α and β are two tuning parameters respec-

tively ﬁxed to 5 and 1000. X

Ω

is the set where con-

straints on Ω are satisﬁed.

Algorithm developed by (Gilbert and Tan, 1991)

is now applied to ﬁnd a set C Ď

C that is positive in-

variant. As a result, the algorithm has converged in

14 steps to C , this result is presented in Fig. 3. More-

over, algorithms developed by (Herceg et al., 2013)

have been used to compute all sets.

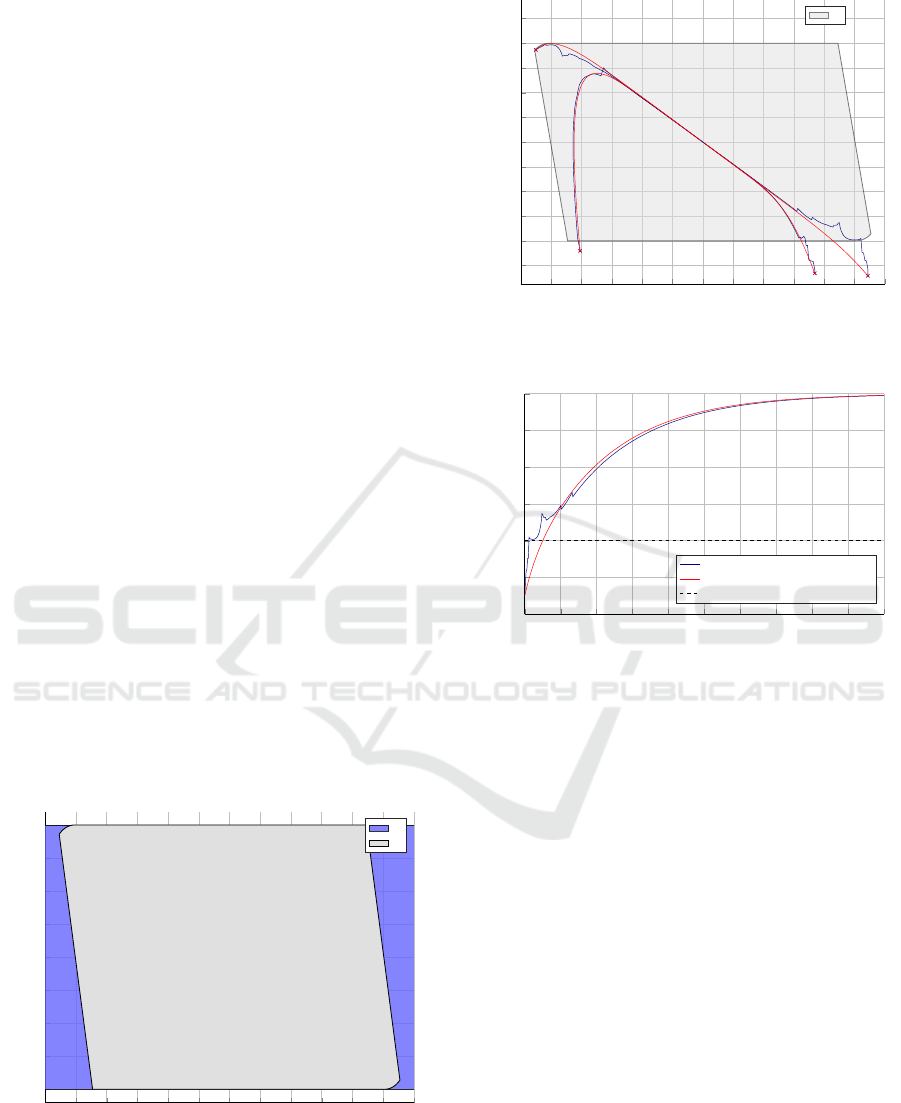
Figure 4 shows some trajectories from different

initial points of the proposed algorithm. The BMPC

problem is solved using Perturbed Differential Evo-

lution algorithm proposed in (Feyel, 2015) which is

known to give results with small standard deviation

from a run to the next. In order to emphasize the in-

terest of the cost function deﬁned by (18), Fig. 4 also

shows results obtained without using the barrier func-

tion. Finally, as it can be seen in Fig. 5, constraints are

satisﬁed faster with the proposed method than without

using barrier functions.

´1.2 ´1 ´0.8

´0.6

´0.4 ´0.2 0 0.2 0.4

0.6

0.8 1 1.2

´8

´6

´4

´2

Position (θ)

Velocity (Ω)

Figure 3: C computed by algorithm developed by (Gilbert

and Tan, 1991).

´1.2 ´1 ´0.8

´0.6

´0.4 ´0.2 0 0.2 0.4

0.6

0.8 1 1.2

´10

´8

´6

´4

´2

Position (θ)

Velocity (Ω)

Figure 4: Trajectories using the same initial point using the

proposed algorithm (in blue) and without using it (in red).

5 ¨10

´2

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45 0.5

´12

´10

´8

´6

´4

´2

Time (s)

Velocity pΩq

Using the proposed method

Without using the proposed method

Constraint

Figure 5: Temporal comparison of trajectories using the

proposed method or not.

8 CONCLUSION

We have proposed a MPC which can handle any kind

of nonlinear constraints by including barrier functions

in a particular cost function. Using this method re-

quires to deﬁne a set C where all constraints are sat-

isﬁed. Some important properties of the set have been

presented and a method to deﬁne it has also been pro-

vided. Furthermore, we have proposed a proof of sta-

bility for our Barrier Model Predictive Control. The

interest of the method has been shown on a numerical

example.

In return of the use of a gradient free optimiza-

tion algorithm, real time implementation will need

an efﬁcient code optimization for parallelization, or

the use of a compact algorithm if the memory is lim-

ited. Moreover the characterization of C is sometimes

difﬁcult and can lead to conservative results. Future

works will deal with a more efﬁcient determination of

this set.

Stability of Barrier Model Predictive Control

157

This paper is restricted to the case of linear

systems because application of algorithm developed

by (Gilbert and Tan, 1991) and by extension deﬁnition

of C is not direct for nonlinear systems. That is why

future works will also deal with extension to nonlin-

ear systems. We will also extend stability to the case

of suboptimal solution given by the optimizer and im-

prove robustness with respect to system uncertainties.

REFERENCES

Allan, D. A., Bates, C. N., Risbeck, M. J., and Rawlings,

J. B. (2017). On the inherent robustness of optimal

and suboptimal nonlinear MPC. Systems & Control

Letters, 106:68 – 78.

Amrit, R., Rawlings, J. B., and Angeli, D. (2011). Eco-

nomic optimization using model predictive control

with a terminal cost. Annual Reviews in Control,

35(2):178 – 186.

Bronstein, E. M. (2008). Approximation of convex sets

by polytopes. Journal of Mathematical Sciences,

153(6):727–762.

Camacho, E. F. and Bordons, C. (2007). Model predictive

control, Second Edition. Springer International Pub-

lishing.

Chen, C. and Shaw, L. (1982). On receding horizon feed-

back control. Automatica, 18(3):349–352.

Chisci, L., Lombardi, A., and Mosca, E. (1996). Dual-

receding horizon control of constrained discrete time

systems. European Journal of Control, 4(2):278–285.

Feller, C. and Ebenbauer, C. (2015). Weight recentered bar-

rier functions and smooth polytopic terminal set for-

mulations for linear model predictive control. In 2015

American Control Conference (ACC), pages 1647–

1652. IEEE.

Feller, C. and Ebenbauer, C. (2017). A stabilizing iteration

scheme for model predictive control based on relaxed

barrier functions. Automatica, 80:328–339.

Feyel, P. (2015). Perturbed differential evolution algorithm–

enhancing the differential evolution algorithm by per-

turbing the mutants.

Feyel, P. (2017). Robust Control Optimization with Meta-

heuristics. John Wiley & Sons.

Gilbert, E. G. and Tan, K. T. (1991). Linear systems with

state and control constraints: The theory and applica-

tion of maximal output admissible sets. IEEE Trans-

actions on Automatic control, 36(9):1008–1020.

Herceg, M., Kvasnica, M., Jones, C., and Morari, M.

(2013). Multi-Parametric Toolbox 3.0. In Proc. of

the European Control Conference, pages 502–510,

urich, Switzerland. http://control.ee.ethz.ch/mpt.

Keerthi, S. a. and Gilbert, E. G. (1988). Optimal inﬁnite-

horizon feedback laws for a general class of con-

strained discrete-time systems: Stability and moving-

horizon approximations. Journal of optimization the-

ory and applications, 57(2):265–293.

Mayne, D. Q., Rawlings, J. B., Rao, C. V., and Scokaert,

P. O. (2000). Constrained model predictive control:

Stability and optimality. Automatica, 36(6):789–814.

Merabti, K. and Belarbi, H. (2014). Multi-objective pre-

dictive control: a solution using metaheuristics. Inter-

national Journal of Computer Science & Information

Technology (IJCSIT).

Michalska, H. and Mayne, D. Q. (1993). Robust re-

ceding horizon control of constrained nonlinear sys-

tems. IEEE transactions on automatic control,

38(11):1623–1633.

uller, M. A., Angeli, D., Allg

ower, F., Amrit, R., and

Rawlings, J. B. (2014). Convergence in economic

model predictive control with average constraints. Au-

tomatica, 50(12):3100–3111.

Petsagkourakis, P., Heath, W. P., Carrasco, J., and Theodor-

opoulos, C. (2019). Input-output stability of barrier-

based model predictive control.

Price, K., Storn, R. M., and Lampinen, J. A. (2006). Differ-

ential evolution: a practical approach to global opti-

mization. Springer Science & Business Media.

Rawlings, J. B., Mayne, D. Q., and Diehl, M. (2017). Model

Predictive Control: Theory, Computation, and De-

sign. Nob Hill Publishing.

Rawlings, J. B. and Muske, K. R. (1993). The stability of

constrained receding horizon control. IEEE transac-

tions on automatic control, 38(10):1512–1516.

Reble, M. and Allg

ower, F. (2012). Unconstrained

model predictive control and suboptimality estimates

for nonlinear continuous-time systems. Automatica,

48(8):1812–1817.

Scokaert, P. O., Mayne, D. Q., and Rawlings, J. B. (1999).

Suboptimal model predictive control (feasibility im-

plies stability). IEEE Transactions on Automatic Con-

trol, 44(3):648–654.

Wills, A. G. and Heath, W. P. (2004). Barrier function based

model predictive control. Automatica, 40(8):1415–

1422.

Zeilinger, M. N., Jones, C. N., and Morari, M. (2010).

Robust stability properties of soft constrained mpc.

In 49th IEEE Conference on Decision and Control

(CDC), pages 5276–5282. IEEE.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

158