Proactive-cooperative Navigation in Human-like Environment for

Autonomous Robots

Wanting Jin

, Paolo Salaris

and Philippe Martinet

Chorale Team, INRIA Sophia Antipolis, Valbonne, France

Keywords:

Human-robot Interaction, Proactive Planning, Cooperative Behavior, Social Force Model.

Abstract:

This work

deals with the problem of navigating a robot in a constrained human-like environment. We provide

a method to generate a control strategy that enables the robot to proactively move in order to induce desired

and socially acceptable cooperative behaviors in neighboring pedestrians. Contrary to other control strategies

that simply aim to passively avoid neighboring pedestrians, this approach aims to simplify the navigation task

of a robot by looking for cooperation with humans, especially in crowded and constrained environments. The

co-navigation process between humans and a robot is formalized as a multi-objective optimization problem

and a control strategy is obtained through the Model Predictive Control (MPC) approach. The Extended

Headed Social Force Model with Collision Prediction (EHSFM with CP) is used to predict the human motion.

Different social behaviors of humans when moving in a group are also taken into account. A switching strategy

between purely reactive and proactive-cooperative planning depending on the evaluation of human intentions

is also furnished. Validation of the proactive-cooperative planner enables the robot to generate more socially

and understandable behaviors is done with different navigation scenarios.

1 INTRODUCTION

In order to enable the robot to establish a cooperative

behavior with humans in a constrained environment,

the robot not only should be able to plan its motion in

the presence of humans but also to predict human ac-

tions. The problem has two main parts: Human Aware

Navigation and Human Motion Prediction.

Human Aware Navigation. Reactive planning treats

pedestrians as static or moving obstacles in the envi-

ronment (Bevilacqua et al., 2018). However, proac-

tive planning extends reactive planning by taking into

account that humans can see the robot and react ac-

cordingly. In (Ferrer and Sanfeliu, 2019) authors pro-

pose an Anticipative Kino-dynamic Planner, where

the reaction of the human towards robot motion has

been taken into account. In (Truong and Ngo, 2017),

the robot motion is planned by using the Hybrid Re-

ciprocal Velocity Obstacle (Snape et al., 2011), which

is known as a proactive velocity-based approach.

https://orcid.org/0000-0002-3399-0499

https://orcid.org/0000-0003-1313-5898

https://orcid.org/0000-0001-5827-0431

This work is funded by MOBI-DEEP project

(ANR-17-CE33-0011) and CROWDBOT project (H2020

n.779942).

However, in previous works, human motion is only

a passive reaction to the robot one. It is worth not-

ing that besides passively move to avoid the collision,

humans are also able to understand others’ navigation

intentions and actively move to give convenience to

others. In (Che et al., 2020), the robot expresses its

navigation desire through explicit and implicit com-

munication. In (Khambhaita and Alami, 2020), both

human and robot trajectories are optimized during the

cooperation process.

Human Motion Prediction. The microscopic human

motion model can be roughly classiﬁed as physics-

based, planning-based and learning-based. For the

planning-based methods, humans behave like plan-

ners by ﬁnding an optimal path during navigation

(Mombaur et al., 2010). In (Trautman et al., 2013),

human motion is modeled as an Interacting Gaussian

Process. However, such methods require a lot of data

for training and do not generalize to different envi-

ronments. Among the physics-based models, the So-

cial Force Model (SFM) is the most used one (Hel-

bing and Moln

ar, 1995) which is a simple and uni-

versal method that could provide valid motion pre-

dictions by taking into account the interactions with

the environment. In the case of cooperation, human

behaviors are not only based on the information per-

412

Jin, W., Salaris, P. and Martinet, P.

Proactive-cooperative Navigation in Human-like Environment for Autonomous Robots.

DOI: 10.5220/0009822004120419

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 412-419

ISBN: 978-989-758-442-8

ceived from surrounding but also depend on their in-

tentions. In (Tamura et al., 2012), the sub-goals are

set based on human intentions. In (Zanlungo et al.,

2011), the authors improve the initial SFM by adding

the explicit collision prediction (CP). In this paper,

we choose a suitable cost function and deﬁne a con-

strained optimization framework to generate both re-

active and proactive-cooperative motions for a mo-

bile robot in human-like environments. We extend

the SFM framework and show by simulations that it

is able to give reasonable and useful predictions of

human motions, even during the cooperative phase.

We also provide a switching strategy between reactive

and proactive-cooperative planning depending on the

human availability to collaborate. Finally, we test the

performances of the proposed machinery under differ-

ent and signiﬁcant human-robot interaction scenarios,

especially where the cooperation and the communi-

cation of intentions are important (Khambhaita and

Alami, 2017).

2 NAVIGATION STRATEGY

In this section, our proactive-cooperative planning is

described and the switching strategy for passing from

purely reactive strategy to a proactive one is provided.

2.1 Multi-objective Optimization

For simplicity reasons, both humans and robots are

modeled as cylinders with radius r

and r

, respec-

tively. The conﬁguration of the vehicle is described

by q

(t) = (p

(t),θ

(t)), where p

(t) = (x

(t),y

(t))

is the position of the vehicle, and θ

(t) is the vehi-

cle heading angle. The input of the vehicle is de-

noted by u

= [v

(t),ω

(t)]

with v

(t) and ω

(t) the

forward and angular velocity respectively. We also

deﬁne v

as the robot linear velocity. In this

paper, we use a kinematic and nonholonomic model

for our robot but any other model can be used. Let

us also consider humans moving on the same plane

around the robot and represent the state of the i-th per-

son as q

(t) = (p

(t),θ

(t),v

(t),ω

(t)), where

(t) = (x

(t),y

(t))

and θ

(t) are deﬁned similar as

the conﬁguration of robot. And ω

is the angular ve-

locity. We will assume the following dynamic model

for each person in the environment:

˙x

= v

cosθ

− v

sinθ

; ˙y

= v

sinθ

+ v

cosθ

(t) = ω

; ˙v

(t) =

; ˙v

(t) =

;

(t) =

(1)

where u

= [u

]

are the inputs used to generate

the predicted trajectory. The mass and the inertia of

the i-th person are deﬁned as m

and I

. We deﬁne

as the human linear velocity expressed on the

plan of motion.

The motion planning problem can be hence for-

malized as a constrained multi-objective optimization

problem (see Sec. 4) that smoothly adapts to different

social scenarios by changing the weights of the linear

scalarization applied to the cost function. As a con-

sequence, in a generic form, the constrained multi-

objective optimization problem can be formalized as

∗

=argmin

t+T

∑

(τ),q

(τ),...,q

(τ)) dτ

s.t. g

g(u

(t),q

(t),.. . , q

(t)) ≤ 0

(2)

where

t is the current time, T is the whole horizon

time, N is the total number of pedestrians in the neigh-

boring, γ

are the weights to be adapted depending

on the current scenario, F

(·) are the cost functions

(see Sec. 4.1), g

g(·) are the several constraints (see

Sec. 4.2). As it will be clear in Sec. 4, the optimiza-

tion problem (2) will be solved by adopting the Model

Predictive Control (MPC).

2.2 Proactive-cooperative Planning

A reactive action consists in a local path correspond-

ing to an instantaneous reaction to sensory feedback.

An action can be deﬁned instead as proactive if it

has the ability of creating or controlling a situa-

tion rather than just responding to it after it hap-

pened. To be proactive a robot has to act with the aim

of creating or controlling a situation that, e.g., may

facilitate a subsequent phase of cooperation and/or

the robot (human) objective. Differently from reac-

tive planning, proactive one must take into account

if the human is willing to cooperate or not by ob-

serving how he/she reacts. In the starting stage of

the proactive-cooperative planning, the robot should

proactively generate actions to express its willingness

to cooperate and intentions clearly. Once the hu-

man understands the robot’s objective and is willing

to cooperate, the cooperation phase starts (see Fig-

ure 1). The main difference between reactive and

proactive-cooperative planning is that, the latter up-

dates the predicted human trajectory simultaneously

with the planned robot trajectory. Hence, both human

and robot future trajectories are taken into account for

the optimization process (see the two-way arrows be-

tween the ”Human State Prediction” and ”Proactive-

Cooperative Planning” blocks in Figure 1).

Proactive-cooperative Navigation in Human-like Environment for Autonomous Robots

413

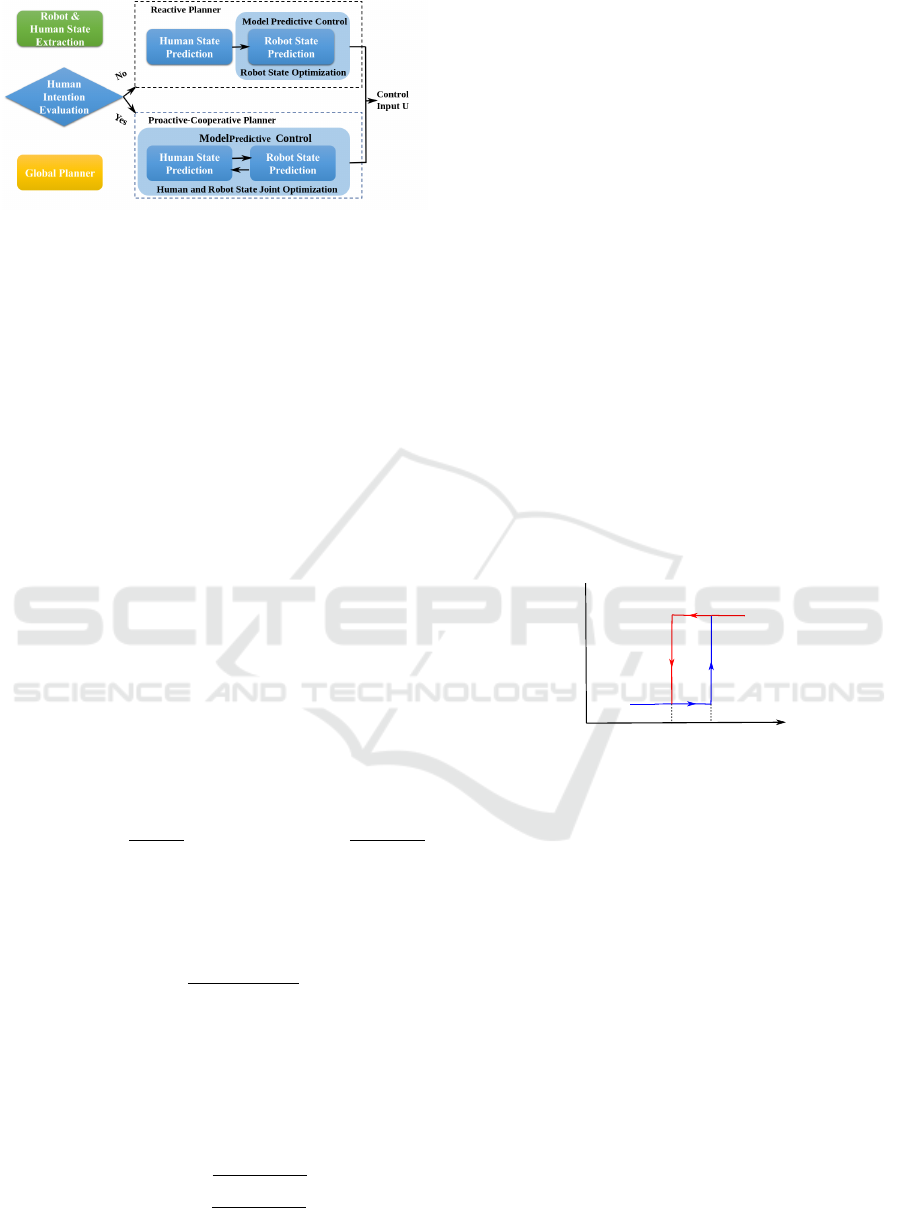
Figure 1: Local planning framework.

2.3 Switching Strategy

Based on previous analysis, it is clear that the

robot must be able to switch between reactive and

cooperative-proactive strategies depending on the re-

sult of the evaluation of human intentions. For sim-

plicity reasons, we consider only two possible human

intentions (denoted by int):

• iff int = 0: human does not see the robot or is not

willing to cooperate;

• iff int = 1: human sees the robot and is willing to

cooperate;

Let us introduce now the conﬁdence of human inten-

tions Con

int

= g(ms), as a function of ms which can be

considered as the ”measurement” of human reaction

to robot movements. ms is deﬁned as a binary func-

tion which depends on the difference between the ob-

servation of the real human trajectories

real

and the

predicted one during cooperation q

coop

as:

• ms = 0: when



real

− q

coop



> e

thres

• ms = 1: when



real

− q

coop



< e

thres

where, e

thres

is a threshold parameter.

Odd(int) =

p(int=1)

p(int=0)

and Odd(int|ms) =

p(int=1|ms)

p(int=0|ms)

are deﬁned as the ratio between the possibility of hav-

ing int = 1 and int = 0 before and after ms is updated.

Its form can be simpliﬁed through Bayes rule and ap-

ply log operator to both sides as

logOdd(int|ms) = log

p(ms|int = 1)

p(ms|int = 0)

+ logOdd(int)

(3)

We use the value of log Odd(int) to represents the

conﬁdence of human intentions Con

−

int

before updat-

ing ms, and logOdd(int|ms) to represent the updated

conﬁdence Con

int

after updating ms. Previous equa-

tion (3) becomes Con

int

= Con

−

int

+ lomeas, with:

lomeas =

(

lonot = log

p(ms=0|int=1)

p(ms=0|int=0)

∈ (−1,0)

losee = log

p(ms=1|int=1)

p(ms=1|int=0)

∈ (0,1)

(4)

where lomeas is a predeﬁned value indicating how

the Con

int

should be updated depending on the ”mea-

surement” ms. During the interaction process be-

tween the human and the robot, the robot will have

a new ms at each time step, and Con

int

will be up-

dated continuously through the whole interaction pro-

cess. To avoid jerky motion during switching, hys-

teresis is introduced. When the robot and a per-

son meet, the robot is not sure about human inten-

tions. The robot needs to clearly show its cooperative

willingness and checks the human ones for cooper-

ation. The conﬁdence Con

int

is initially set higher

than a given conﬁdence threshold Con

thres−

, to en-

able the proactive-cooperative behavior. If the hu-

man responds to the robot motion accordingly then

ms is set to 1 and the conﬁdence Con

int

keeps to in-

crease and rests bigger Con

thres−

: the cooperative pro-

cess ﬁnally starts. If the human does not respond to

robot suggestions or he/she decides to stop the coop-

eration then ms = 0, the conﬁdence Con

int

decreases

and falls down Con

thres−

. The robot switches to reac-

tive planning to guarantee safety. During the reactive

planning, if the conﬁdence Con

int

increases beyond

Con

thres+

, the robot switches again to the proactive-

cooperative planning (Figure 2).

Planning Strategy

Reactive

Planning

Proactive-

Cooperative

Planning

Con

int

Con

thres+

Con

thres-

Figure 2: Switching strategy.

3 HUMAN MOTION

The robot needs to predict the human motion under

different navigation scenarios. The Extended Headed

Social Force Model (EHSFM) with Collision Pre-

diction (CP) is proposed as a combination of three

state of the art works built upon the SFM frame-

work: The Headed Social Force Model (HSFM) (Fa-

rina et al., 2017), the Extended Social Force Model

(ESFM) (Ferrer and Sanfeliu, 2019) and the collision

prediction (CP) (Zanlungo et al., 2011).

3.1 Headed Social Force Model

The HSFM expands the SFM by taking into account

that pedestrians usually move along its heading direc-

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

414

tion. The control input u

is hence computed as

= f

= β

( f

)

− β

= −β

(θ

− θ

) − β

(5)

Deﬁnitions of the parameters are the same as in (Fa-

rina et al., 2017). The interaction force between

pedestrian i and agent z (z can be an obstacle o, a wall

w and other pedestrians j) is

= A

−diz)/B

(6)

where A

reﬂects the strength of interaction, B

corre-

sponds to the interaction range. r

= r

is the sum

of their radius. d

= kp

− p

k denotes the distance

between their centers. n

denotes the normalized co-

ordinates pointing from agent z to pedestrian i.

3.2 EHSFM with Collision Prediction

The EHSFM with CP extends the HSFM by including

the ESFM to take into account the inﬂuence of robot

motion on human one. The human ability of collision

prediction is also added. The behaviors of humans

when walking in a group are also introduced. Let u

the input as deﬁned in 5. The deﬁnition of the social

force is extended by introducing the effect of human-

robot interactions, the range of view and the effects of

people walking as a group. The total social force f

= f

+ f

grp

. (7)

In real cases, a group of people can separate for

a while in order to avoid collision and then again

come back in formation depending on the relation-

ship between the members of the group (Bruneau

et al., 2015). In our work, group behavior is mod-

eled by considering a spring between a couple of peo-

ple. When the members get closer or separate be-

cause of external force generated by the environment,

the spring will push or bring them back to a comfort-

able distance. The group force and the stiffness of the

spring s

are deﬁned as follows:

grp

= s

grp

− l

grp

with s







1+cos(∠v

)

grp

−v

if d

grp

< 2l

grp

0 otherwise

(8)

where d

grp

is the current distance between a couple

of members and l

grp

is the initial distance before the

interaction with the robot. Parameter κ represents

the relationship between two persons. Its value for

a group of mother and son should be higher than for

a group of friends. The stiffness of the spring should

reduce to model the intention of the member of sepa-

rating each other, thus it is also a function of the dif-

ference between two members’ heading direction and

the magnitude of the velocity. When d

grp

> 2l

grp

couple of people are not treated as a group anymore.

The updated external force f

is deﬁned as:

∑

j(6=i)∈N

i j

∑

w∈W

∑

o∈O

∑

r∈R

(9)

where N, O, R are the sets of pedestrians, obstacles

and robots in the environment. w

takes into account

the anisotropy effect of the interaction force (Johans-

son et al., 2007) caused by the human’s limit ﬁeld of

view and it is deﬁned as:

= (λ + (1 − λ)

1 + cos(ψ

)

), cos(ψ

) = e

· n

(10)

where ψ

is the angle between human forward direc-

tion e

and normalized distance vector n

. λ ∈ [0, 1]

is a parameter which grows with the strength of inter-

actions from behind.

The interaction force generated by the robot f

added to model the effects of the robot motion on the

human one. The interaction force f

deﬁned in (6) is

not enough to model human intention during cooper-

ation since it models human motion as a pure reaction

to changes in the environment. In order to model the

cooperative behavior between humans and the robot,

the human’s ability of Collision Prediction (CP) to

solve potential collisions is taken into account. The

interaction force with CP f

(z can be obstacles o,

walls w, pedestrians j and robots r ) is

(

{

}

{

}

) = A

−d

)

(11)

The parameters are deﬁned similarly to (Zanlungo

et al., 2011). The comparison between f

and f

showed in Figure 3. Under the scenario where agent

i and j meet face to face in a corridor, f

i j

is along

continuous lines which depend on the current relative

positions. This leads both agents to decelerate but

cannot generate signiﬁcant lateral motion until they

are very close. f

i j

is instead along the dashed lines

which depend on the future point of potential colli-

sion. This leads the two agents to move in the lateral

direction and gives the way to the others.

4 PROBLEM DEFINITION

The optimization problem is now formalized by using

the MPC which solves an optimal control problem for

Proactive-cooperative Navigation in Human-like Environment for Autonomous Robots

415

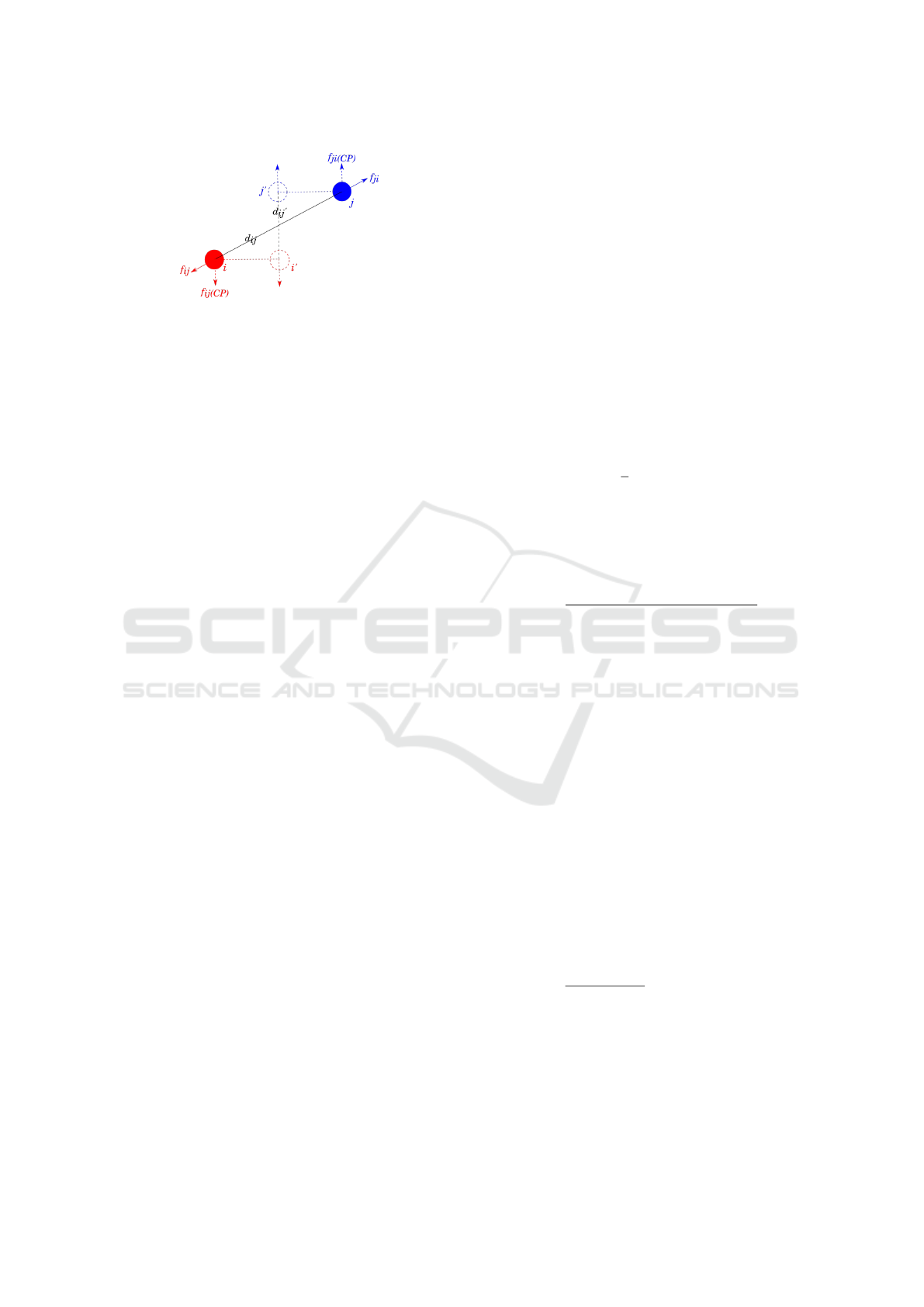
Figure 3: Comparison between f

i j

and f

i j

when two

agents i and j meet face to face in a corridor

a ﬁnite horizon time window T , using the state of the

system of the current time

t as the initial state. The

horizon time is hence divided into h steps of ﬁxed

length ∆t, such that h∆t = T . k is then used to rep-

resent each time step with k ∈ {0,1, .. ., h}.

Reactive Planning. For reactive planning, the robot

motions do not inﬂuence the human ones. Thus, once

the robot detects a person in the environment, it pre-

dicts the human future state by using HSFM and then

modiﬁes its own trajectory to avoid collisions. The

optimization problem can be deﬁned as:

argmin

{

(0)···u

(h)

}

∑

k=0

goal

(k) + γ

energy

(k) (12)

s.t. Model: q

(k + 1) = q

(k) +

(k))4t

Constraints: g

(k); g

(k)

State feedback:

(

(0) =

(

{

(0)···q

(h)

}

{

(

t)···

(

t + h)

}

Proactive-cooperative Planning. For proactive-

cooperative planning, the robot not only needs to ac-

complish its navigation task as for the reactive plan-

ning but also to express its cooperation willingness

clearly while, at the same time, maximizing the hu-

man comfort by respecting social rules. The predicted

human trajectories and the robot ones are updated at

the same time by using the EHSFM with CP. The op-

timization problem is deﬁned as:

argmin

{

(0)···u

(h)

}

∑

k=0

goal

(k) + γ

energy

(k) + γ

indiv

(k)

+γ

dir

(k) + γ

ttc

(k) + γ

group

(k)

(13)

s.t. Model:

(

(k + 1) = q

(k) +

(k))4t

(k + 1) = q

(k) +

(k), q

(k))4t

Constraints: g

(k); g

(k)

State feedback:

(

(0) =

(

(0) =

(

4.1 Cost Function

In (12) and (13), the cost function is composed of:

Reach the Goal. The robot has to reach a given goal

or a close area around it.

goal

(k) =



(k) − p

goal

(



(14)

Energy Consuming. The energy at each time step k:

energy

(k) =

(k)

(15)

Individual Comfort. The inﬂuence of the robot mo-

tion on each person is modeled by the interaction

force. The cost function for individual comfort is:

indiv

(k) =



(k)



(16)

Group Comfort. The cost to separate or compress the

group because of robot motion can be formalized by

the potential energy of the spring in the group:

group

(k) =

grp

(k) − l

grp

)

(17)

Directionality. The directional cost function penal-

izes the face to face behavior between humans and the

robot to increase the legibility of robot motion. The

evaluation parameter of directional cost is (Khamb-

haita and Alami, 2020)

dir

(k) =

(k) ·

−−→

(k) + v

(k) ·

−−→

(k)

C(k)

(18)

where C is the distance between robot and human i.

The penalty cost function for directionality is F

dir

(k)



(ζ

dir

+ ε) − c

dir

(k) if c

dir

(k) < (ζ

dir

+ ε

dir

)

0 otherwise

(19)

where ζ

dir

is a threshold of activation, ε is a parameter

that takes into account the accuracy of the directional

estimation. Notice that, higher relative velocity and

shorter distance means a higher penalty. The direc-

tional cost function sets up the tread-off between the

effect of slowing down and changing the path.

Time to Collision. The robot is expected to look

ahead and anticipate its actions clearly. The minimum

distance between the robot and human i in a future

time window η is

ttc

(k) = min

∈(0,η)

+ v

) − (p

+ v

)

(20)

while the cost function corresponding to the minimum

human-robot distance within η is

ttc

(k) =

(

(ρ

ttc

+ε)−d

ttc

(k)

C(k)

if d

ttc

(k) < (ρ

ttc

+ ε)

0 otherwise

(21)

If d

ttc

is smaller than a certain threshold ρ

ttc

, then the

cost function is activated and, if minimized, pushes

the robot to move sideways in head of time η. There-

fore, the robot clearly suggests a solution to the hu-

man on how reducing the risk of a potential collision.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

416

4.2 Constraint

The constraints that guarantee safety and comfort are:

Proxemic constraint. The proxemics theory intro-

duced in (Twitchell Hall, 1966) deﬁnes areas around

people with different distances of interaction w.r.t. the

others, e.g. the intimate space is within 0.45m and

the personal space is within 1.2m. Since the scenario

for our task is extremely constrained, the robot may

go into the pedestrian’s personal space but it should

never violate the intimate space to guarantee comfort.

Thus, the distance between pedestrian i (with i ∈ N)

and the robot should be bigger than the intimate space

radius ξ

per

, i.e.

(k) : r

+ r

+ ξ

per

−

(k) − p

(k)

< 0 (22)

Safety Distance Constraint to Walls. The robot

should stay sufﬁciently far from walls. The walls are

deﬁned as line segments in 2D. The distance d

be-

tween each wall w (with w ∈ W ) and the robot must

be bigger than the safety distance ξ

wall

. Moreover, the

robot motion should not push the human i too close to

the wall. Thus, these constraints are:

(k) : r

+ ξ

wall

− d

(k) < 0 (23)

(k) : r

+ ξ

wall

− d

(k) < 0 (24)

Safety Distance Constraint to Obstacles. Each obsta-

cle is deﬁned as a circumscribing disc-shaped object

with center position p

and radius r

. The deﬁnition

of safety constraint to obstacles are similar to safety

constraint to walls.

(k) : r

+ ξ

obs

− d

(k) < 0 (25)

(k) : r

+ ξ

obs

− d

(k) < 0 (26)

5 RESULTS AND ANALYSIS

Simulations are done in Matlab



. The total simula-

tion time is 10s. The size of the horizon time window

is T = 5s. At each time step, the future control input

consists of a sequence of 10 piece-wise constant val-

ues. As a consequence, ∆t = 0.1s. Three scenarios of

interactions between one single person and one single

robot have been considered. Scenario 1: one single

person and one robot meet face to face in a corridor;

Scenario 2: one single person and one robot perform

a 90

path-crossing; Scenario 3: as in scenario 1 with

an obstacle partially blocking the way. For these sce-

narios, a comparison between reactive and proactive-

cooperative planning has been done. Finally, in Sce-

nario 4 one robot meets a group of persons.

Model Parameter. As mentioned in (Khambhaita

and Alami, 2017), the parameter re-tuning or learn-

ing under different scenarios is required for every

state of the art human motion prediction method

since humans behave differently in different situa-

tions. The parameters used in each scenario (see Ta-

ble 1) are tuned manually. More reasonable values

can be learned through data analysis of real experi-

ments (Ferrer and Sanfeliu, 2019) in future works.

Table 1: Parameters of Human Motion Model.

Scenario N

◦

(1) 250 6 250 6 0 0 2000 0.08

(2) 250 15 250 15 0 0 2000 0.08

(3) 250 12 250 12 400 0.5 2000 0.08

(4) 250 6 250 6 0 0 2000 0.08

(5) 250 6 250 6 0 0 2000 0.08

Optimization Parameters. The weighting parameters

and penalty thresholds for each cost function need to

be re-tuned for each scenario in order to have proper

behavior. The parameters used in this paper are in Ta-

ble 2. The proxemics distance is set to ξ

per

= 0.45 m.

The safety distance between human (robot) and the

wall and the obstacle are set to ξ

wall

= 0.2 m, ξ

obs

0.1 m. The collision time window is set to η = 8 s.

Table 2: Weighting Parameters and Penalty Thresholds.

Scenario N

◦

dir

ttc

(1) 1 1 0.005 200 200 0 0.5 2

(2) 0.1 1 0.05 100 100 0 1 1

(3) 1 1 0.05 100 100 0 0.5 2

(4) 1 1 0.005 200 200 0 0.5 2

(5) 1 1 0 100 100 1 0.5 2

Human and Robot Characteristic. Human mass is

75 kg and inertia I

= 0.045 kg m

. Humans radius

is r

= 0.3 m. We assume that humans reach the de-

sired velocity of 1.5 m/s in φ = 0.5 s. Robot radius

is 0.3 m. The linear velocity v

∈ [0, 2] and angular

velocity w

∈ [−1,1].

Environment Parameters. The origin of the world

reference frame is ﬁxed at the bottom left corner of the

wall on the left, with x

and y

axis along with the

horizontal and vertical directions, respectively. The

length and width of the corridor are 15 m and 5 m, re-

spectively. The 90

cross path takes place in a square

of 15 × 15 m.

5.1 Simulation Results

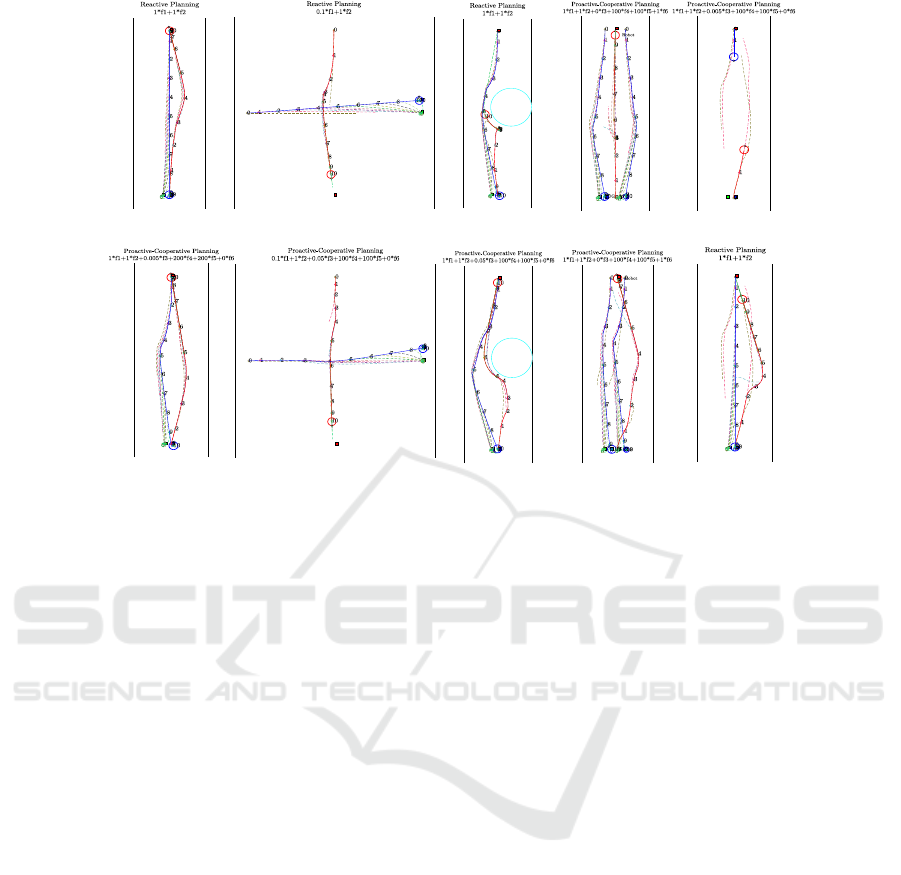
The simulation results are reported in Figure 4. The

red (denoted by G

) and blue (denoted by G

hAct

)

squares mark the position of the robot and human ac-

tual goal, respectively. In order to introduce some

noise in the human motion prediction, the predicted

Proactive-cooperative Navigation in Human-like Environment for Autonomous Robots

417

hAct

hPre

Human

Robot

hAct

hPre

Human

Robot

hAct

hPre

Human

Robot

hAct

hPre

Human

Robot

hAct

hPre

Human

Robot

hAct

hPre

Human

Robot

gAct

gPre

gAct

gPre

hAct

hPre

Human

Robot

gAct

gPre

gAct

gPre

hAct

hPre

Human

Robot

)

) (e

)

Figure 4: Simulation results for the four scenarios (a,b,c,d): Reactive (above) and proactive-cooperative (below); Switching

strategy (e): 0-2s proactive-cooperative planning (above) and 3-10s reactive planning (below).

human navigation goal is set differently and marked

with a green square (denoted by G

hPre

). The red and

the blue continuous curves (dashed curves) are then

executed (planned) robot trajectory and the simulated

(predicted) human trajectory, respectively. The col-

ored circles on the red and blue continuous curves

represent the robot and human positions at each sec-

ond (with the number indicate the time).

Scenario 1. The human starts at the top middle of

the corridor and plans to cross the corridor and reach

his/her goal at the bottom middle(see Figure 4-(a)).

The robot starts at the opposite position of the corri-

dor and plans to reach the top middle of the corridor.

The predicted human goal is 0.5m left of the actual

goal. For the reactive planner, the robot detours to

respect proxemics distance when it is close to the hu-

man. This may make human confused and threatened

by the robot motion. By using proactive-cooperative

planning (see Figure 4-(a), bottom), the robot deceler-

ates while approaching the human and deviates to the

lateral side to clearly show its cooperative intentions

to the human. After the interaction, the robot accel-

erates again to reach its goal. Hence, the trajectory

generated by our proactive-cooperative planning has

higher legibility and is more socially acceptable.

Scenario 2. The human starts at the left middle of

the square and plan to reach the right middle. The

robot starts at the top middle of the square and plans to

reach the bottom middle. The predicted human goal

is 0.5m above the actual goal. By using reactive plan-

ning, the robot starts with high speed and then slows

down and detours on the back of the human (almost

at 4 s of the simulation). On the contrary, by using

proactive-cooperative planning (see Figure 4-(b), bot-

tom), the robot slows down initially as well as moving

straight towards its navigation goal to show its inten-

tions and let the human pass ﬁrst. Once human passes

the crossing point, the robot accelerates to reach its

goal. During the interaction process, no confusion

seems to be generated as the robot shows its naviga-

tion goal clearly and human accelerates to pass the

crossing point and gives the way to the robot.

Scenario 3. The obstacle is a cylinder with center at

= [3.5,8]

and radius r

= 1.5m. Since the robot

assumes the human will not give the way, during the

time window 3s-8s the robot cannot ﬁnd a feasible

trajectory to reach the goal (see Figure 4-(c)). The

robot has to turn around and move to the right side to

respect the proxemic constraint during the time win-

dow 5s-6s. Indeed, the predicted human trajectories

are different from real ones. By using our proactive-

cooperative planning (see Figure 4-(c) bottom), the

robot reaches the navigation goal much more efﬁ-

ciently. Moreover, it slows down and moves to the

lateral side to clearly express its politeness. The hu-

man passes ﬁrst the bottleneck created by the obstacle

and gives enough space to the robot that clearly ex-

pressed to the human its navigation goal.

Scenario 4. The navigation scenario is as for Sce-

nario 1. For the group of mother and son (see Fig-

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

418

ure 4-(d) bottom), κ = 100 and l

= 1 m. For the

group of friends (see Figure 4-(d) top), κ = 10 and

= 2 m. For the ﬁrst case, when the robot meets

a group of mother and son, since the spring stiffness

is very high and may cost much energy to separate

them, the robot detours from outside. However, in the

second case, when the robot meets a group of friends,

the robot passes through the group to save energy.

Switching strategy. The result for the corridor sce-

nario is showed in Figure 4-(e). All the parameters for

reactive and proactive-cooperative planner are ﬁxed

to correctly compare the performance of these two

strategies. In real application, for reactive planning,

the robot motion should be more conservative, with

∈ (0,1] and the proxemic distance ξ

per

= 1.2 m.

For the switching parameters, the initial conﬁdence

Con

int

= 20, Con

thres+

= 10, Con

thres+

= 7, e

thres

= 1,

lonot = 2 and losee = 1. In Figure 4-(f) on the top,

at the beginning the robot proactively communicates

with the human its willingness. During this phase, the

robot evaluates human intentions. Until 2s of simula-

tion, the conﬁdence Con

int

is still beyond the thresh-

old Con

thres−

, thus the robot maintains a proactive and

cooperative behavior. However, in the following (see

Figure 4-(f) bottom), the real human trajectory dif-

ferentiates from the predicted one, thus Con

int

falls

below the conﬁdence threshold Con

thres−

: the robot

switches to reactive planning to guarantee safety.

6 CONCLUSIONS

A Proactive-cooperative planning for a mobile robot

and a switching strategy to pass from a purely reac-

tive to a proactive behavior depending on the conﬁ-

dence about human intentions is provided. Simula-

tions show the effectiveness of our method. The many

parameters introduced for modeling the human mo-

tion model in different situations are the main draw-

back of our method. Future works will be dedicated

to include some learning strategies (e.g. (Ferrer and

Sanfeliu, 2019) and (Che et al., 2020)) to determine

these parameters and automatically adapt the method

to any situation. Moreover, a simulator for taking onto

account more realistic human motions will be consid-

ered. Finally, real experiments are required to deﬁ-

nitely validate the proposed machinery.

REFERENCES

Bevilacqua, P., Frego, M., et al. (2018). Reactive planning

for assistive robots. IEEE Robotics and Automation

Letters, 3(2):1276–1283.

Bruneau, J., Olivier, A., and Pettr

e, J. (2015). Going

through, going around: A study on individual avoid-

ance of groups. IEEE Trans. on Visualization and

Computer Graphics, 21(4):520–528.

Che, Y., Okamura, A. M., and Sadigh, D. (2020). Efﬁcient

and trustworthy social navigation via explicit and im-

plicit robot–human communication. IEEE Transac-

tions on Robotics, pages 1–16.

Farina, F., Fontanelli, D., et al. (2017). Walking ahead: The

headed social force model. PLOS ONE, 12(1):1–23.

Ferrer, G. and Sanfeliu, A. (2019). Anticipative kino-

dynamic planning: Multi-objective robot navigation

in urban and dynamic environments. Autonomous

Robots, 43(6):1473–1488.

Helbing, D. and Moln

ar, P. (1995). Social force model for

pedestrian dynamics. Physical Review E, 51:4282–

4286.

Johansson, A., Helbing, D., and Shukla, P. K. (2007). Spec-

iﬁcation of the social force pedestrian model by evo-

lutionary adjustment to video tracking data. Advances

in Complex Systems, 10:271–288.

Khambhaita, H. and Alami, R. (2017). Assessing the social

criteria for human-robot collaborative navigation: A

comparison of human-aware navigation planners. In

Proc. IEEE ISRHIC, pages 1140–1145.

Khambhaita, H. and Alami, R. (2020). Viewing robot navi-

gation in human environment as a cooperative activity.

In Robotics Research, pages 285–300.

Mombaur, K., Truong, A., and Laumond, J.-P. (2010). From

human to humanoid locomotion—an inverse optimal

control approach. Autonomous Robots, 28(3):369–

383.

Snape, J., van den Berg, J. P., et al. (2011). The hybrid

reciprocal velocity obstacle. IEEE Transactions on

Robotics, 27:696–706.

Tamura, Y., Le, P. D., et al. (2012). Development of pedes-

trian behavior model taking account of intention. In

IEEE/RSJ IROS, pages 382–387.

Trautman, P., Ma, J., et al. (2013). Robot navigation in

dense human crowds: the case for cooperation. In

Proc. IEEE ICRA, pages 2153–2160.

Truong, X. and Ngo, T. D. (2017). Toward socially aware

robot navigation in dynamic and crowded environ-

ments: A proactive social motion model. IEEE TASE,

14(4):1743–1760.

Twitchell Hall, E. (1966). The hidden dimension. Garden

City, N.Y., Doubleday.

Zanlungo, F., Ikeda, T., and Kanda, T. (2011). Social force

model with explicit collision prediction. EPL (Euro-

physics Letters), 93:68005.

Proactive-cooperative Navigation in Human-like Environment for Autonomous Robots

419