
On Generating Efficient Data Summaries for Logistic Regression: A
Coreset-based Approach
Nery Riquelme-Granada, Khuong An Nguyen and Zhiyuan Luo
Department of Computer Science, Royal Holloway University of London, Egham, Surrey, TW20 0EX, U.K.
Keywords:
Coresets, Data Summaries, Logistic Regression, Large-data, Computing Time.
Abstract:
In the era of datasets of unprecedented sizes, data compression techniques are an attractive approach for
speeding up machine learning algorithms. One of the most successful paradigms for achieving good-quality
compression is that of coresets: small summaries of data that act as proxies to the original input data. Even
though coresets proved to be extremely useful to accelerate unsupervised learning problems, applying them to
supervised learning problems may bring unexpected computational bottlenecks. We show that this is the case
for Logistic Regression classification, and hence propose two methods for accelerating the computation of
coresets for this problem. When coresets are computed using our methods on three public datasets, computing
the coreset and learning from it is, in the worst case, 11 times faster than learning directly from the full input
data, and 34 times faster in the best case. Furthermore, our results indicate that our accelerating approaches
do not degrade the empirical performance of coresets.
1 INTRODUCTION
Classification is one of the most fundamental machine
learning problems: given labeled data D, we aim to
efficiently learn a model that predicts properties of un-
seen data with minimal error. This leads to the fol-
lowing dilemma: on one hand, our learning process
benefits greatly as the size of the input data grows; on
the other hand, the computational cost of our leaning
algorithms grows at least linearly with the input data
size. Hence, large-scale datasets tend to provide rich
knowledge to the learning process at the cost of very
high computing time.
The classic approach for tackling the above chal-
lenge in the algorithmic field of Computer Science
is through the design of new algorithms with better
running times (i.e. an efficient new algorithm which
scales with the input data). A more recent, novel
approach involves using the same (potentially ineffi-
cient) algorithm over a reduced version of the input
data (i.e. compressing the input data so that the same
algorithm may complete faster).
One of the most popular frameworks to achieve
a compression of (large-scale) input data is that of
‘coresets’ (or core-sets) (Har-Peled and Mazumdar,
2004), which allows us to identify and remove less
important information from our input data while re-
taining certain properties. Roughly speaking, a core-
set is a small weighted subset of data
1
that prov-
ably correctly approximates the original input data
(Phillips, 2016). After obtaining a coreset, we
may safely discard the original input data and run
our learning algorithm over the weighted data sum-
mary, dramatically reducing storage and computa-
tional overheads.
In this paper we investigate the performance of
coresets for Logistic Regression (LR) and show that
careless use of coresets may result in devastating im-
pact for the learning process. More concretely, we
empirically show that clustering, which is used as a
subroutine in the coreset construction, imposes a se-
vere bottleneck on the coreset computation for LR.
To circumvent the above problem, we present a
method called ‘Accelerated Clustering via Sampling’
(ACvS), and shall demonstrate that it greatly acceler-
ates the coreset construction. Additionally, we intro-
duce the Regressed Data Summarisation Framework
(RDSF), a meta procedure that not only accelerates
the coreset construction process, but also opens a new
perspective for coresets: we apply machine learning,
in the form of regression, to decide what input infor-
mation is important to include in the data summary.
Thus, RDSF “learns” the importance of each input
point and allows us to retain this knowledge in the
1
Although this can be relaxed.
78
Riquelme-Granada, N., Nguyen, K. and Luo, Z.
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach.
DOI: 10.5220/0009823200780089
In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 78-89
ISBN: 978-989-758-440-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

form of a trained linear regressor. The latter can be
extremely useful for deciding the importance of pre-
viously unseen points in almost constant time.
We summarise our contributions as follows:
• We show the existence of a heavy bottleneck
in the clustering step of the coreset construction
algorithm for LR. In response, we empirically
demonstrate that this issue can be mitigated by
taking the clustering over small uniform random
samples of the input data. We call this method
Accelerated Clustering via Sampling (ACvS), and
we show that using it alongside coresets greatly
accelerates the coreset computation while retain-
ing the coreset performance.
• Piggybacking on ACvS, we propose the method
of Regressed Data Summarisation Framework
(RDSF) to output coreset-based summaries of
data. In essence, given a dataset D and a core-
set construction algorithm A, we can plug-in A
into RDSF to obtain (i) a small summary of D
(ii) a trained regression model capable of identify-
ing important points in unseen data. Thus, RDSF
adds an extra layer of information to the whole
data compression process.
• We shed light on the empirical performance of
coresets for Logistic Regression with and without
our methods; for this, we measure their perfor-
mance not only in terms of computing time, but
also in terms of classification accuracy, F1 score
and ROC curves.
The rest of the paper is organised as follows: Sec-
tion 2 gives a gentle introduction to coresets and dis-
cusses the coreset inefficiencies for the defined learn-
ing problem. Section 3 provides a full description of
our two methods: ACvS and RDSF. Our empirical
evaluations are presented in Section 4. Finally, we
conclude our work in Section 5.
2 BACKGROUND AND PROBLEM
In this section we give a gentle introduction to core-
sets. We define the classification problem of Logistic
Regression in the optimisation setting, for which we
present the state-of-the-art algorithm for constructing
coresets. Finally, we show the computational bottle-
neck imposed by computing a clustering of the whole
input data as part of the LR coreset construction algo-
rithm.
2.1 Coresets
Coresets are a data approximation framework that has
been used to reduce both the volume and dimension-
ality of big and complex datasets. We can formally
define a coreset as follows: let function f be the ob-
jective function of some learning problem and let D
be the input data. We call C an ε-coreset for D if the
following inequality holds:
| f (D) − f (C )| ≤ ε f (D) (1)
where ε is the error parameter. This expression es-
tablishes the main error bound offered by coresets.
Hence, coresets are lossy compressed versions of the
input data D and the amount of information loss is
quantified by ε. Note that we need |C | << |D|.
The design of an algorithm to construct a set C
that fulfils (1) depends naturally on the function f . In
machine learning, f is defined as the objective func-
tion of the learning problem of interest. Thus, we
consider f as the function that minimises the log-
likelihood, which corresponds to learning a Logistic
Regression classifier.
Even though coresets have been widely studied in
the context of clustering (Feldman et al., 2013) (Har-
Peled and Mazumdar, 2004) (Bachem et al., 2017)
(Zhang et al., 2017) (Ackermann et al., 2012), their
uses remain largely unexplored for supervised learn-
ing problems. In this light, the most studied problem
in the coreset community is Logistic Regression (LR)
(Huggins et al., 2016) (Munteanu et al., 2018). Cur-
rent coreset construction algorithms for this problem
also rely on solving a clustering problem under the
hood. Specifically, the current state-of-the-art core-
set algorithm for LR (Huggins et al., 2016) showed
good speed-ups in the Bayesian setting (i.e. Bayesian
Logistic Regression), where posterior inference al-
gorithms are computationally demanding. However,
these computing-time gains can easily vanish as we
move to a non-Bayesian setting due to the computa-
tional cost incurred in clustering.
2.2 Logistic Regression
We define Logistic Regression in the optimisation set-
ting and hereafter we will refer to the below defi-
nition simply as LR. Let D := {(x
n
,y
n
)}
N
n=1
be our
input data, where x
n
∈ R
d
is a feature vector and
y
n
∈ {−1, 1} is its corresponding label. We de-
fine the likelihood of observation y
n
, given some
parameter θ ∈ R
d+1
, as p
logistic
(y
n
= 1|x
n
;θ) :=
1/(1 + exp(−x
n
· θ)) and
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach
79

p
logistic
(y
n
= −1|x
n
;θ) := 1 −
1
(1 + exp(−x
n
· θ))
=
exp(−x
n
· θ)
(1 + exp(−x
n
· θ))
=
1
(1 + exp(x
n
· θ))
. (2)
Therefore, we have p
logistic
(y
n
|x
n
;θ) :=
1/(1 + exp(−y
n
x
n
· θ)) for any y
n
and define the
log-likelihood function LL
N
(θ|D) as in (Shalev-
Shwartz and Ben-David, 2014):
LL
N
(θ|D) :=
N
∑
n=1
ln p
logistic
(y
n
|x
n
;θ)
= −
N
∑
n=1
ln(1 + exp(−y
n
x
n
· θ)) (3)
which is the objective function for the LR problem.
The optimal parameter
ˆ
θ can be estimated by max-
imising LL
N
(θ|D). In other words, we want to min-
imise L
N
(θ|D) :=
∑
N
n=1
ln(1 + exp(−y
n
x
n
· θ)) over
all θ ∈ R
d+1
. Finally, our optimisation problem can
be written as:
ˆ
θ := arg min
θ∈R
d+1
L
N
(θ|D), (4)
where
ˆ
θ is the best solution found. Once we have
solved Equation (4), we use the estimated
ˆ
θ to make
label predictions for each previously unseen data
point.
A Bayesian approach to Logistic Regression re-
quires us to specify a prior distribution for the un-
known parameter θ, p(θ) and derive the posterior dis-
tribution p(θ|D) by applying Bayes’ theorem:
p(θ|D) =
p(D|θ)p(θ)
p(D)
=
p(D|θ)p(θ)
R
p(D|θ)p(θ)dθ
.
Notice that both the Bayesian and optimisation
settings require the computation of the likelihood
function. However, the Bayesian framework needs
to use posterior inference algorithms to estimate
p(θ|D), hence high computational cost incurred as no
closed form solution can be found.
Having defined LR and contrasted it to the
Bayesian framework, we can now proceed to present
the state-of-the-art coreset construction for this par-
ticular classification problem.
2.3 The Sensitivity Framework
We focus on the state-of-the-art coreset algorithm for
LR classification propossed by Huggins et al. (Hug-
gins et al., 2016), to which we shall refer as Core-
set Algorithm for Bayesian Logistic Regression (CA-
BLR). Designed for the Bayesian setting, this algo-
rithm uses random sampling for constructing small
coresets that approximate the log-likelihood function
on the input data.
Before describing CABLR in detail, however, it
is important to shed some light on the roots of this
algorithm in order to understand why the method can
easily become computationally unfeasible for LR in
the optimisation setting as defined in Section 2.2.
To design CABLR, Huggins et al. followed
a well-established framework for defining coresets
commonly know as the sensitivity framework (Feld-
man and Langberg, 2011). This framework provides a
systematic general approach for constructing coresets
for different instances of clustering problems e.g. K-
means, K-median, K-line and projective clustering. In
essence, this abstract framework consists in reducing
coresets to the problem of finding an ε-approximation
(Mustafa and Varadarajan, 2017), which can be com-
puted using non-uniform sampling. Hence, the sen-
sitivity framework falls under the random-sampling
category for defining coresets. The non-uniform dis-
tribution is based on the importance of each data
point, in some well-defined sense
2
. Hence, each
point in the input data is assigned an importance
score, a.k.a. the sensitivity of the point. To com-
pute such importance scores, the framework requires
an approximation to the optimal clustering of the in-
put data. Then, for each input point, the sensitiv-
ity score is computed by taking into account the dis-
tance between the point and its nearest (sub-optimal)
cluster centre obtained from the approximation. The
next step is to sample M points from the distribu-
tion defined by the sensitivity scores, where M is the
size of the coreset. Finally, to each of the M points
in the coreset, a positive real-valued weight is as-
signed by taking the inverse of the point’s sensitiv-
ity score. Hence, the sensitivity framework allows us
to design coreset construction algorithms that return a
coreset consisting of M weighted points. The theoret-
ical proofs and details can be found in (Feldman and
Langberg, 2011).
The sensitivity framework proved to be an ex-
tremely powerful tool for constructing coresets for
many clustering instances as the time required for
computing the necessary clustering approximation is
small compared to the time needed for clustering the
full input data.
Huggins et al. made the first incursion in using the
sensitivity framework to design a coreset algorithm
for the supervised learning problem of Bayesian Lo-
gistic Regression, proving that CABLR indeed pro-
duce ε-coresets of size M with probability 1 − δ.
However, their algorithm still depends on approxi-
2
for our discussion, it is enough to state that the sensi-
tivity score is a real value in the half-open interval [0,∞)
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
80

mating the clustering of the input data. This is not
a major problem in the Bayesian setting, as posterior
inference algorithms are computationally expensive.
Careless use of this algorithm in the optimisa-
tion setting, as we shall see in the next section, may
be devastating as computing the clustering of the in-
put data, even for the minimum number of iteration,
can be too expensive. The description of CABLR is
shown in Algorithm 1.
Input: D: input data, Q
D
: k-clustering of D
with |Q
D
| := k, M: coreset size
Output: ε-coreset C with |C | = M
1 initialise;
2 for n = 1,2, ..., N do
3 m
n
← Sensitivity(N,Q
D
) ;
// Compute the sensitivity of
each point
4 end
5 ¯m
N
←
1
N
∑
N
n=1
m
n
;
6 for n = 1,2, ..., N do
7 p
n
=
m
n
N ¯m
N
; // compute importance
weight for each point
8 end
9 (K
1
,K
2
,...,K
N
) ∼ Multi(M,(p
n
)
N
n=1
) ;
// sample coreset points
10 for n = 1,2, ..., N do
11 w
n
←
K
n
p
n
M
; // calculate the weight
for each coreset point
12 end
13 C ← {(w
n
,x
n
,y
n
)|w
n
> 0};
14 return C
Algorithm 1: CABLR: an algorithm to construct coresets
for Logistic Regression.
Remark. In the description of Algorithm 1, we hide
the coreset dependence on the error parameter ε, de-
fined in Section 2.1. There is a good reason for do-
ing this. When theoretically designing a coreset al-
gorithm for some fixed problem, there are two error
parameters involved: ε ∈ [0, 1], the “loss” incurred
by coresets, and δ ∈ (0, 1), the probability that the al-
gorithm will fail to compute a coreset. Then, it is nec-
essary to define the minimum coreset size M in terms
of these error parameters. The norm is to prove there
exists a function t : [0,1] × (0,1) → Z
+
, with Z
+
be-
ing the set of all positive integers, that gives the corre-
sponding coreset size for all possible error values i.e.
t(ε
1
,δ
1
) := M
1
implies that M
1
is the minimum num-
ber of points needed in the coreset for achieving, with
probability 1 − δ, the guarantee, defined in inequality
(1), for ε
1
. However, in practice, one does not worry
about explicitly giving the error parameters as inputs;
since each coreset algorithm comes with its own defi-
nition of t, one only needs to give the desired coreset
size M and the error parameters can be computed us-
ing t. Finally, t defines a fundamental trade-off for
coresets: the smaller the error parameters, the bigger
the resulting coreset size i.e. smaller coresets may po-
tentially lose more information than bigger coresets.
3
Notice that Algorithm 1 implements the sensitiv-
ity framework almost as described in Section 2.3: k
cluster centres, Q , from the input data are used to
compute the sensitivities; then, sensitivities are nor-
malised and points get sampled; finally, the weights,
which are inverse proportional to the sensitivities, are
computed for each of the sampled points. Thus, even
though the obtained coreset is for LR, CABLR still
needs a clustering of the input data as is common for
any coreset algorithms designed using the sensitivity
framework.
2.4 The Clustering Bottleneck
Clustering is known to be a computationally hard
problem (Arthur and Vassilvitskii, 2007). This is why
approximation and data reduction techniques are use-
ful for speeding up existing algorithms. The sen-
sitivity framework, originally proposed for design-
ing coresets for clustering problems, requires a sub-
optimal clustering of the input data D in order to com-
pute the sensitivity for each input point. This require-
ment transfers to CABLR, described in the previous
section. In the Bayesian setting, the time necessary
for clustering D is strongly dominated by the cost of
posterior inference algorithms (see (Huggins et al.,
2016)). However, if we remove the burden of pos-
terior inference and consider the optimisation setting,
then the situation is dramatically different.
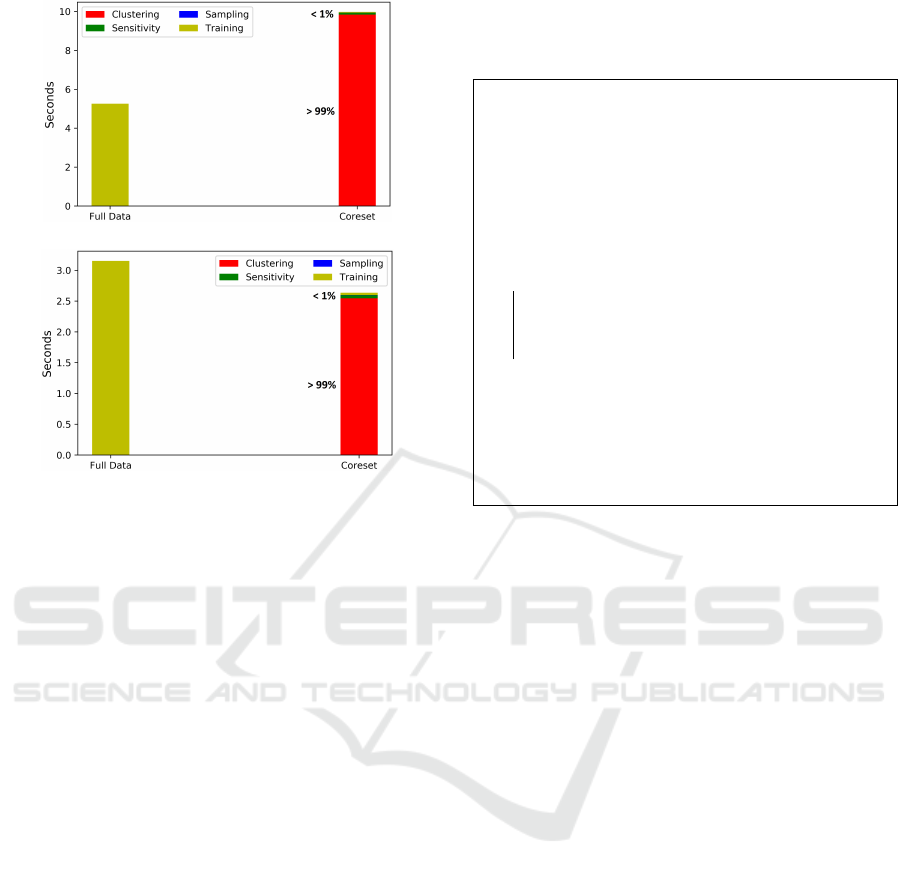
Figure 1 sheds some light on the clustering time
with respect to all the other steps taken by CABLR to
construct a coreset, namely: sensitivity computation
and sampling. The time spent on learning from the
coreset is also included.
We can clearly see that obtaining the clustering
can be dangerously impractical for constructing core-
sets for LR in the optimisation setting as it severely
increases the overall coreset-construction time. Even
worse, constructing the coreset is slower than learn-
ing directly from D, defeating the purpose of using
the coreset as an acceleration technique.
3
For CABLR, Huggins et al. proved that t(ε, δ) :=
d
c ¯m
N
ε
2
[(D + 1)log ¯m
N
+ log(
1
δ
)]e, where D is the number of
features in the input data, ¯m
N
is the average sensitivity of
the input data and c is a constant. The mentioned trade-off
can be appreciated in the definition of t.
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach
81
(a) Webspam
(b) Covertype
Figure 1: Comparison of the computing time needed for
constructing LR coresets for the Webspam and Covertype
datasets. The clustering process consumed the majority of
the processing time.
Rather than giving up on coresets for LR, we pro-
pose the following research question: ‘Can we still
benefit from good coreset acceleration in the optimi-
sation setting?’
We give an affirmative answer to this question
through two approaches described in the next section.
The key ingredient for both methods is the use of Uni-
form Random Sampling.
3 PROPOSED PROCEDURES
In this section, we propose two different procedures
for efficiently computing coresets for Logistic Re-
gression in the optimisation setting. Both approaches
are similar in the following sense: they both make use
of Uniform Random Sampling (URS) for speeding up
the coresets computation. This is not the first time that
the concept of URS comes up alongside coresets; in
fact, URS can be seen as a naive approach for com-
puting coresets and it is the main motivation for deriv-
ing a more sophisticated sampling approach (Bachem
et al., 2017). In our procedures, however, we see URS
as a complement to coresets, not as an alternative to
them, which is usually the case in coresets works.
3.1 Accelerating Clustering via
Sampling
Input: CABLR: coreset algorithm, D: input
data, A: a clustering algortithm, k:
number of cluster centres, b |D|:
number of samples
Output: C : coreset
1 initialise;
2 S ←
/
0;
3 B ← |S|;
4 while B < b do
5 s ← SamplePoint(D) // Sample
without replacement
6 S ← S ∪ {s} // Put s in S
7 end
8 Q
S
← A(S,k) // Run Clustering
algorithm on S
9 C ← CABLR
M
(D,Q
S
) // Run Coreset
Algorithm
10 return C
Algorithm 2: ACvS procedure.
To recap, we are interested in efficiently learning a
good linear classifier using Logistic Regression in the
optimisation setting, as defined in Section 2.2. Fur-
thermore, we want the learning process to be as com-
putationally efficient as possible. Coresets allow us to
achieve this, at the cost of compromising on the qual-
ity of the resulting classifier. The good news is that
coresets maintain this quality loss bounded.
For LR classification, however, the state-of-the-art
algorithm to compute a coreset, CABLR, is not ade-
quate for our optimisation setting. Specifically, the
computing time required to compress the input data
overshadows the time needed for learning from the
compressed data. We identified that the source of such
inefficiency comes from the clustering step and hence
we reduced the problem of speeding-up CABLR to
the problem of accelerating the clustering phase.
Our first procedure, Accelerated Clustering via
Sampling (ACvS), uses a straightforward application
of URS. The procedure is described in Algorithm 2.
First, we extract b input points from D and put them
into a new set S. We require that b N, where
N := |D|. Then, we cluster S to obtain k cluster cen-
tres, namely Q
S
with |Q
S
| := k. We finally run the
CABLR algorithm using Q
S
as input and compute a
coreset. Since we have that |S| |D|, obtaining Q
S
is substantially faster than obtaining Q
D
. Notice that
the coreset algorithm CABLR is parameterised by the
coreset size M. As a simple example, say we have a
large dataset that we would like to classify using lo-
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
82

gistic regression, and to do it quite efficiently, we de-
cide to compress the input data into a coreset. The
standard coreset algorithm for LR dictates that we
have to find a clustering of our dataset as the very first
step; then we use the clustering to compute the sensi-
tivity of each point; the next step is to sample points
according to their sensitivity and to put them in the
coreset, and finally we compute the weight for each
point in the coreset. What ACvS proposes is: instead
of computing the clustering of our dataset, compute
the clustering of a very small set of uniform random
samples of it, then proceed as the standard coreset al-
gorithm dictates.
We designed this procedure based on the follow-
ing observation: uniform random sampling can pro-
vide unbiased estimation for many cost functions that
are additively decomposable into non-negative func-
tions. We prove this fact below.
Let D be a set of points and let n := |D|; also, let Q
be a query whose cost value we are interested in com-
puting. We can define a cost function which is decom-
posable into non-negative functions as cost(D, Q) :=
1
n
∑
x∈D
f
Q
(x).
Many machine learning algorithms can be cast to
this form. Here, we are mainly concerned about k-
means clustering, where Q is a set of k points and
f
Q
(x) := min
q∈Q
||x − q||
2
2
. Let us now take a random
uniform sample S ⊂ D with m := |S|, and define the
cost of query Q with respect to S as cost(S,Q) :=
1
m
∑
x∈S
f
Q
(x). To show that cost(S, Q) is an unbi-
ased estimator of cost(D, Q) we need to prove that
E[cost(S, Q)] = cost(D,Q)
Claim. E[cost(S,Q)] = cost(D, Q)
Proof. By definition, we have that cost(S,Q) :=
1
m
∑
x∈S
f
Q
(x). Expanding this, we get
E[cost(S, Q)] = E[
1
m
∑
x∈S
f
Q
(x)] (5)
The crucial step now is to compute the above ex-
pectation. To do this, it is useful to construct the set
S that contains all the possible subsets S in D. The
number of such subsets has to be
n
m
, which implies
|S| :=
n
m
. Then, computing the expectation over S
and re-arranging some terms we get
1
n
m
1
m
∑
S∈S
∑
x∈S
f
Q
(x) (6)
Next, we get rid of the double summation as fol-
lows: we count the number of times that f
Q
(x) is com-
puted. By disregarding overlapping computation of
f
Q
(x) due to the fact that a point x can belong to multi-
ple subsets S ∈ S, we can quickly obtain that the count
has to be
(n−1)
(m−1)
. Then, we can write (6) as
1
n
m
1
m
(n − 1)
(m − 1)
∑
x∈D
f
Q
(x) (7)
Notice that now we have a summation that goes
over our original set D. Finally, by simplifying the
factors on the left of the summation we have
1
n
∑
x∈D
f
Q
(x)
= cost(D,Q)
(8)
which concludes the proof.
The imminent research question here is: how does
using the ACvS procedure affect the performance of
the resulting coreset? We shall show in Section 4 that
the answer is more benign than we originally thought.
3.2 Regressed Data Summarisation
Framework
Our second method builds on the previous one and it
gives us at least two important benefits on top of the
acceleration benefits given by ACvS:
• sensitivity interpretability: it unveils an existing
(not-obvious) linear relationship between input
points and their sensitivity scores.
• instant sensitivity-assignment capability: apart
from giving us a coreset, it gives as a trained re-
gressor capable of assigning sensitivity scores in-
stantly to new unseen points.
Before presenting the method, however, it is use-
ful to remember the following: the CABLR algorithm
(Algorithm 1) implements the sensitivity framework,
explained in Section 2.3, and hence it relies on com-
puting the sensitivity (importance) of each of the input
points.
We call our second procedure Regressed Data
Summarisation Framework (RDSF). We can use this
framework to (i) accelerate a sensitivity-based core-
set algorithm; (ii) unveil information on how data
points relate to their sensitivity scores; (iii) obtain a
regression model that can potentially assign sensitiv-
ity scores to new data points.
The full procedure is shown in Algorithm 3:
RDSF starts by using ACvS to accelerate the cluster-
ing phase. The next step is to separate the the input
data D in two sets: S, the small URS picked during
ACvS, and R, all the points in D that are not in S.
The main step in RDSF starts at line 12: using the
clustering obtained in the ACvS phase, Q
S
, we com-
pute the sensitivity scores only for the points in S and
place them in a predefined set Y . A linear regression
problem is then solved using the points in S as feature
vectors and their corresponding sensitivity scores in
Y as targets. This is how RDSF sees the problem of
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach
83

Input: D: input data, A: clustering
algortithm, k: number of cluster
centres, b |D|: number of samples
in the summary, M: coreset size
Output:
˜
C : Summarised Version of D, φ:
Trained Regressor
1 initialise;
2 S ←
/
0;
3 B ← |S|;
4 N ← |D|;
5 while B < b do
6 s ← SamplePoint(D) // Sample
without replacement
7 S ← S ∪ {s} // Put s in S
8 end
9 Q
S
← A(S,k) // Run Clustering
algorithm on S
10 R ← D \ S;
11 Y ←
/
0;
12 for n = 1,2, ..., b do
13 m
n
← Sensitivity(b,Q
S
) // Compute
the sensitivity of each point
s ∈ S
14 Y ← Y ∪ {m
n
};
15 end
16
ˆ
Y , φ ← PredictSen(S,Y,R) // Train
regressor on S and Y , predict
sensitivity for each r ∈ R
17 Y ← Y ∪
ˆ
Y ;
18 ¯m
N
←
1
N
∑
y∈Y
y;
19 for n = 1,2, ..., N do
20 p
n
=
m
n
N ¯m
N
; // compute importance
weight for each point
21 end
22 (K
1
,K
2
,...,K
N
) ∼ Multi(M,(p
n
)
N
n=1
) ;
// sample coreset points
23 for n = 1,2, ..., N do
24 w
n
←
K
n
p
n
M
; // calculate the weight
for each coreset point
25 end
26
˜
C ← {(w
n
,x
n
,y
n
)|w
n
> 0};
27 return
˜
C ,φ
Algorithm 3: The Regressed Data Summarisation Frame-
work (RDSF) uses a coreset construction to produce
coreset-based summaries of data.
summarising data as the problem of ‘learning’ the
sensitivity of the input points. The result of such
learning process is a trained regressor φ and RDSF
uses it to predict the sensitivities of all the points in R.
Hence, RDSF uses S as training set and R as test set.
We finally see that after merging the computed and
predicted sensitivities of S and R (line 16 in Algo-
rithm 3), respectively, RDSF executes the same steps
as CABLR i.e. compute the mean sensitivity (line 19),
sample the points that will be in the summary (line 22)
and compute the weights (line 23).
It is worth noting that we avoid using the term
coreset for RDSF’s output; this is because, strictly
speaking, the term coreset implies that a theoreti-
cal guarantee of the kind presented in formula (1) is
proven. We shall see in the next section that the sum-
maries produced by RDSF indeed perform as good as
coresets; however, the prove of theoretical guarantees
for our summaries are left as a future work.
4 EXPERIMENTS & RESULTS
In this section, we present our empirical evaluations.
It is worth mentioning that we investigate coresets
(and coresets-based approaches) using a set of metrics
that are standard in machine learning, and to the best
of our knowledge, no previous research work shows
how coresets respond to this kind of evaluation.
4.1 Description
For illustration purposes, we tested our procedures on
3 datasets shown in Table 1. These chosen datasets
are publicly available
4
and well-known in the coreset
community.
Table 1: Overview of the datasets used for the evaluation of
our methods.
Dataset Examples Features
Webspam 350,000 254
Covertype 581,012 54
Higgs 11,000,000 28
We are interested in analysing the following five
different approaches:
• Full: no coreset or summarisation technique is
used. We simply train a LR model on the entire
training set and predict the labels for the new in-
stances in the test set.
• CABLR: we make use of coresets via the CA-
BLR algorithm (Algorithm 1). Thus, we obtain a
clustering of the training data and run CABLR to
obtain a coreset. We then train a LR model on the
coreset to predict the test labels.
4
https://www.csie.ntu.edu.tw/
∼
cjlin/libsvmtools/
datasets/ - last accessed in 2/2020.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
84

• ACvS: we use our procedure ‘Accelerated Clus-
tering via Sampling’, described in Algorithm 2, to
accelerate the coreset computation. Once we have
obtained the coreset in the accelerated fashion, we
proceed to learn a LR classifier over it.
• RDSF: summaries of data are generated via the
‘Regressed Data Summarisation Framework’, de-
scribed in Algorithm 3. That is, we compute sen-
sitivity scores only for a handful of instances in
the training set. Then, we train a regressor to pre-
dict the sensitivity scores of the rest instances. We
sample points according to the sensitivities, com-
pute their weights and return the data summary.
We then proceed as in the previous coreset-based
settings.
• URS: for the sake of completeness, we include
‘Uniform Random Sampling’ as a baseline for re-
ducing the volume of input data; we simply pick
M input points uniformly at random and then train
a LR classifier over them.
For each of the above approaches, and for each
dataset in Table 1, we take the following steps:
(a) data shuffling: we randomly mix up all the avail-
able data.
(b) data splitting: we randomly select 50% of the
data to use as training set and leave the rest for
testing. It is the training set to which we refer as
input data D.
(c) data compressing: we proceed to compress the
input data: CABLR approach computes a core-
set without any acceleration, ACvS computes a
coreset by using CABLR with accelerated cluster-
ing phase, RDSF compresses the input data into a
small summary data in an accelerated fashion, and
URS performs a naive compression by taking an
uniform random sample of the input data. Full
Data is the only approach not relying on com-
pressing the input data.
(d) data training: we train a Logistic Regression
classifier on the input-data compression obtained
in the previous step. Again, the Full Data ap-
proach trains the classifier on the full input data
D.
(e) data assessing: we finally use the trained Logis-
tic Regression classifier to predict the labels in the
test set and apply our performance metrics, de-
tailed in Section 4.2.
We applied the above strategy 10 times for each
of the five different approaches. Regarding the hard-
ware, our experiments were performed on a single
desktop PC running the Ubuntu-Linux operating sys-
tem, equipped with an Intel(R) Xeon(R) CPU E3-
1225 v5 @ 3.30GHz processor and 32 Gigabytes of
RAM.
Lastly, for coresets, we adapted to our needs the
CABLR algorithm implementation and shared by its
authors
5
. All our programs were written in Python.
The algorithm used for clustering the input data is the
well-known K-means algorithm and, finally, RDSF
uses linear regression to learn sensitivities.
4.2 Evaluation
As we previously mentioned, the empirical perfor-
mance of coresets has mainly remained as a grey area
in the past years. We apply the following performance
metrics in order to shed some light on, first, the per-
formance of coresets in general, second, the perfor-
mance of our proposed methods. The following 5 per-
formance metrics are considered:
• Computing time (seconds): our main goal is
to accelerate the coreset computation to con-
sequently speed-up the learning process when
coreset-based approaches are applied. We distin-
guish 5 phases for which we measure time:
(a) Clustering: the time needed to obtain the k-
centres for coreset-based approaches.
(b) Sensitivity: the time required to compute the
sensitivity score for each input point.
(c) Regression: the time needed for training a re-
gressor in order to predict the sensitivity scores
for input points. The prediction time is also
taken into account.
(d) Sampling: the time required to sample input
points.
(e) Training: the time required for leaning an LR
classifier.
Notice that the Training phase is the only one
present in all our approaches. Hence, for exam-
ple, the coreset approach does not learn any re-
gressor and thus it is assigned 0 second for that
phase. The URS approach does not perform any
clustering or sensitivity computation, hence those
phases get 0 second for this method, etc.
• Classification Accuracy: is given by the percent-
age of correctly classified test examples and it is
usually the baseline metric for measuring perfor-
mance.
• F1 Score: is the harmonic average of precision
and recall (Goutte and Gaussier, 2005).
5
https://bitbucket.org/jhhuggins/lrcoresets/src/master -
last accessed in 2/2020
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach
85

• Area Under the ROC Curve (AUROC): pro-
vides an aggregate measure of performance across
all possible classification thresholds.
4.3 Results
We categorise our results according to the four differ-
ent metrics considered. Notice that our performance
metrics are shown as functions of the size of the sum-
maries used for training the LR classifier. For exam-
ple, if we look at Figure 5, we see that summaries cor-
respond to very small percentages of the Higgs dataset
i.e. 0.005 %, 0.03 %, 0.06 %. and 0.1 %. For Web-
spam and Covertype, we show results for summary
sizes of 0.05 %, 0.1 % , 0.3 %, 0.6 % and 10 % of the
total input data.
Due to limited space, and given that the perfor-
mance of all the methods follows similar patterns with
respect to accuracy, F1 socre and AUROC, we only
show figures for one (random) dataset for these partic-
ular metrics; however, the tables in Section 4.4 show
results for all datasets in a more detailed fashion.
4.3.1 Computing Time
Figure 2 summarises our results in terms of comput-
ing time. We show in the stacked-bars plots the time
spent for each phase of the different approaches.
We can clearly see that the CABLR approach,
which applies coresets in their original form, is not
suitable for the optimisation setting we are consider-
ing. Specifically, with respect to the Full method, we
notice that for the Covertype dataset, the coreset ap-
proach gives a modest acceleration of approximately
1.2 times. The situation becomes more severe for the
Webspam and Higgs datatsets, where using the tra-
ditional coreset approach incurs in a learning process
which is about 1.9 and 1.3 times slower than not using
coreset at all, respectively.
Hence, by removing the bottleneck produced by
the clustering phase, our two proposed methods show
that we can still benefit from coreset acceleration to
solve our particular problem; that is, our methods
take substantially shorter computing time when com-
pared to both the CABLR and Full Data approaches.
In particular, and with respect to Full Data approach,
our approach ACvS achieves a minimum acceleration
of 17 times (Webspam) and a maximum acceleration
of 34 times (Higgs) across our datasets. Regarding
RDSF, the minimum acceleration obtained was 11
times (Webspam) and the maximum was 27 times
(Covertype).
Notice that our accelerated methods are only
beaten by the naive URS method, which should most
certainly be the fastest approach.
(a) Webspam
(b) Covertype
(c) Higgs
Figure 2: Comparison of the computing time of different
methods.
Finally, notice that the RDSF approach is slightly
more expensive than ACvS. This is the computing
price we pay for obtaining more information i.e.
RDSF outputs a trained regressor that can immedi-
ately assign sensitivities to new unseen data points;
this can prove extremely useful in settings when
learning should be done on the fly.
The natural follow-up question now is whether our
methods’ resulting classifiers perform well. We ad-
dress this question in great detail in the following sec-
tions.
4.3.2 Accuracy
We first look into the baseline metric for measuring
the success of a classifier: the accuracy. Tables 2, 3
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
86
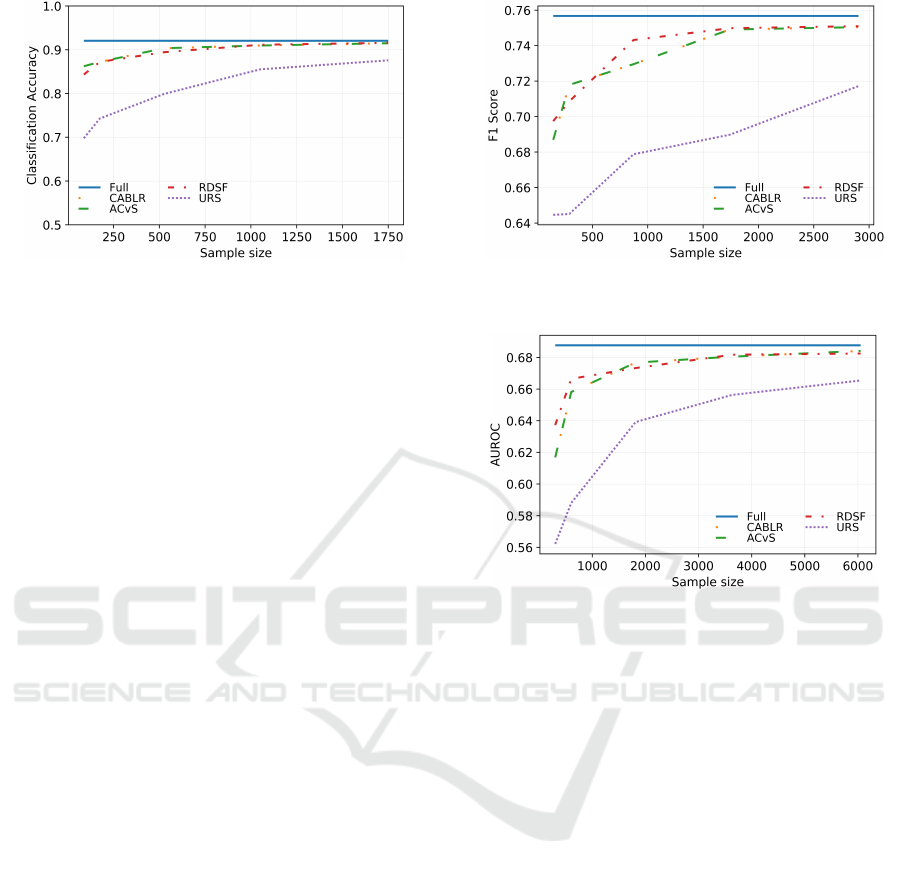
Figure 3: Comparison of the prediction accuracy for all
methods on the Webspam dataset.
and 4 show how the accuracy of the methods changes
as the sample sizes increase on different datasets. To
recall, each of the different methods considered relies
on reducing the input data via a coreset-based com-
pression or a random uniform sample, as described in
Section 4.1. Hence, we here report the different accu-
racy scores obtained by training our LR classifier on
different samples sizes. As reference, we also include
the accuracy of the Full Data method as a straight
line, see Figure 3 for an example.
The first observation is that all the methods per-
form better as the sample sizes increase. Quite sur-
prisingly, we see that in all cases, without exceptions,
the ACvS approach achieves the exact same accu-
racy that the CABLR approach achieves, for all sam-
ple sizes. Hence, for coresets, clustering over a sub-
sample of the input data does not seem to deteriorate
the rate of correct predictions of the resulting classi-
fiers, and greatly accelerates the overall coreset com-
putation, as we could appreciate in the previous sec-
tion.
We also see that the RDSF approach performs
as good as the rest of the coreset-based approaches,
with accuracy never lower than the baseline approach
URS. On this regard, it is common for coreset to be
lower bounded in performance by the URS approach:
that is, we expect coresets to outperform URS in
most situations. Finally, we see that, as sample sizes
increase, the gap between coreset performance and
URS performance reduces (i.e. they both get closer
and closer to the Full Data approach).
4.3.3 F1 Score
We now present the results of applying the F1-score
metric to our LR classifiers for different sample sizes,
see Figure 4.
The very first observation is that, similar to the
previous metric results, ACvS and CABLR obtain ex-
actly the same scores, and RDSF remains competitive
Figure 4: Comparison of the F1 score for all methods on the
Covertype dataset.
Figure 5: Comparison of the area under the ROC curve for
all methods on the Higgs dataset.
against them. Furthermore, it is fair to say that for the
Covertype dataset, RDSF has preferable performance
compared to the rest of the coreset-based approaches.
Hence, we once more see that the advantages of core-
sets are available in our setting as long as we carefully
accelerate the underlying algorithm.
Finally, our experiments reveal that the perfor-
mance gap between URS and the rest of the ap-
proaches becomes even greater for the F1 Score;
showing that classifiers trained over coresets are more
useful and informative than the ones trained over uni-
formly randomly selected samples.
4.3.4 AUROC
Lastly, we present the AUROC score for each of our
5 approaches. Figure 5 shows comparison of the AU-
ROC scores for all methods. The picture is similar
to that of F1-score and Accuracy: coreset-based ap-
proaches consistently outperform URS. We see in-
deed that ACvS and RDSF perform as well as the
traditional coreset approach, achieving their perfor-
mance in substantially less computing time than core-
sets (see Section 4.3.1).
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach
87

4.4 Summary of Results
This section provides detailed performance metrics of
our proposed methods on the Covertype, Webspam,
and Higgs datasets (see Tables 2, 3 and 4). Overall,
the empirical results demonstrated that our proposed
ACvS and RDSF run significantly faster than the tra-
ditional Coreset approach, while maintaining compet-
itive performance, in all datasets considered.
Table 2: Performance comparison on the Covertype dataset
where size is the percentage of training data. “M” stands
for “Methods”, “A” stands for “Accuracy” and “T” stands
for “Time”.
Size (%) M F1 AUROC A T(secs)
0.05 Full 0.76 0.83 0.76 3.35
0.05 CABLR 0.69 0.75 0.69 2.78
0.05 ACvS 0.69 0.75 0.69 0.12
0.05 RDSF 0.70 0.76 0.69 0.12
0.05 URS 0.65 0.71 0.63 0.04
0.3 Full 0.76 0.83 0.76 3.31
0.3 CABLR 0.73 0.81 0.73 2.78
0.3 ACvS 0.73 0.81 0.73 0.13
0.3 RDSF 0.74 0.81 0.74 0.13
0.3 URS 0.68 0.77 0.69 0.05
1 Full 0.76 0.83 0.76 3.71
1 CABLR 0.75 0.82 0.75 3.38
1 ACvS 0.75 0.82 0.75 0.18
1 RDSF 0.75 0.82 0.75 0.18
1 URS 0.72 0.80 0.73 0.07
5 CONCLUSION
Under the presence of ever growing input data, it is
absolutely necessary to accelerate the learning time
of machine learning algorithms. Instead of improv-
ing the algorithms, there are less direct approaches
that involve reducing the input data and hence learn
from smaller data. Coreset approach is one of such
methods. As coresets were originally proposed to
be used to solve computationally hard problems,
like clustering, they should be carefully applied in
computationally-less-demanding scenarios, like clas-
sification. However, it is not obvious how to do this.
We proposed two methods that can bring all the ben-
Table 3: Performance comparison on the Webspam dataset
where size is the percentage of training data. “M” stands
for “Methods”, “A” stands for “Accuracy” and “T” stands
for “Time”.
Size (%) M F1 AUROC A T(secs)
0.05 Full 0.92 0.94 0.97 5.39
0.05 CABLR 0.86 0.89 0.92 10.15
0.05 ACvS 0.86 0.89 0.92 0.31
0.05 RDSF 0.84 0.87 0.90 0.49
0.05 URS 0.70 0.79 0.88 0.05
0.3 Full 0.92 0.94 0.97 6.54
0.3 CABLR 0.90 0.92 0.96 13.40
0.3 ACvS 0.90 0.92 0.96 0.41
0.3 RDSF 0.89 0.91 0.95 0.64
0.3 URS 0.80 0.85 0.92 0.06
1 Full 0.92 0.94 0.97 6.35
1 CABLR 0.92 0.93 0.97 13.44
1 ACvS 0.92 0.93 0.97 0.45
1 RDSF 0.92 0.93 0.97 0.68
1 URS 0.88 0.90 0.95 0.08
efits of coresets to Logistic Regression classification
in the optimisation setting: Accelerating Clustering
via Sampling (ACvS) and Regressed Data Summari-
sation Framework (RDSF). Both methods achieved
substantial overall learning acceleration while main-
taining the performance accuracy of coresets.
Our results clearly show that coresets can be used
to learn a logistic regression classifier in the optimi-
sation setting. It is enlightening to observe that, even
though CABLR needs a clustering of the input data,
this can be largely relaxed in the practical sense. Fur-
thermore, our calculations indicate that CABLR must
be used with the clustering done over a small sub-
set of the input data in the optimisation setting (i.e.
our ACvS approach). Regarding RDSF, this opens a
new direction for perceiving coresets: we could pose
the computation of data summary as solving a small-
scale learning problem in order to solve a large-scale
one. It is illuminating to see that the sensitivities
can be largely explained by a simple linear regressor.
Most importantly, we believe that this method may be
very powerful for the online learning setting (Shalev-
Shwartz et al., 2012), since RDSF returns a trained re-
gressor capable of assigning sensitivity scores to new
incoming data points. We leave as future work the use
of these methods in different machine learning con-
texts.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
88

Table 4: Performance comparison on the Higgs dataset
where size is the percentage of training data. “M” stands
for “Methods”, “A” stands for “Accuracy” and “T” stands
for “Time”.
Size (%) M F1 AUROC A T(secs)
0.005 Full 0.68 0.69 0.64 89.22
0.005 CABLR 0.62 0.62 0.59 112.44
0.005 ACvS 0.62 0.62 0.59 2.61
0.005 RDSF 0.62 0.64 0.60 4.16
0.005 URS 0.58 0.56 0.54 1.12
0.03 Full 0.68 0.69 0.64 92.22
0.03 CABLR 0.67 0.68 0.633 121.25
0.03 ACvS 0.67 0.68 0.63 2.70
0.03 RDSF 0.67 0.67 0.63 4.46
0.03 URS 0.66 0.64 0.60 1.20
0.1 Full 0.68 0.69 0.64 90.18
0.1 CABLR 0.68 0.68 0.64 123.97
0.1 ACvS 0.68 0.68 0.64 2.61
0.1 RDSF 0.68 0.68 0.64 4.50
0.1 URS 0.69 0.67 0.62 1.29
ACKNOWLEDGMENTS
We thank the reviewers for their helpful and thorough
comments. Our research is partially supported by As-
tra Zeneca and the Paraguayan Government.
REFERENCES
Ackermann, M. R., M
¨
artens, M., Raupach, C., Swierkot,
K., Lammersen, C., and Sohler, C. (2012).
Streamkm++: A cluste ing algorithm for data streams.
Journal of Experimental Algorithmics (JEA), 17:2–4.
Arthur, D. and Vassilvitskii, S. (2007). k-means++: The
advantages of careful seeding. In Proceedings of the
eighteenth annual ACM-SIAM symposium on Discrete
algorithms, pages 1027–1035. Society for Industrial
and Applied Mathematics.
Bachem, O., Lucic, M., and Krause, A. (2017). Practi-
cal coreset constructions for machine learning. arXiv
preprint arXiv:1703.06476.
Feldman, D. and Langberg, M. (2011). A unified frame-
work for approximating and clustering data. In Pro-
ceedings of the forty-third annual ACM symposium on
Theory of computing, pages 569–578. ACM.
Feldman, D., Schmidt, M., and Sohler, C. (2013). Turning
big data into tiny data: Constant-size coresets for k-
means, pca and projective clustering. In Proceedings
of the twenty-fourth annual ACM-SIAM symposium on
Discrete algorithms, pages 1434–1453. SIAM.
Goutte, C. and Gaussier, E. (2005). A probabilistic interpre-
tation of precision, recall and f-score, with implication
for evaluation. In European Conference on Informa-
tion Retrieval, pages 345–359. Springer.
Har-Peled, S. and Mazumdar, S. (2004). On coresets for
k-means and k-median clustering. In Proceedings of
the thirty-sixth annual ACM symposium on Theory of
computing, pages 291–300. ACM.
Huggins, J., Campbell, T., and Broderick, T. (2016). Core-
sets for scalable bayesian logistic regression. In Ad-
vances in Neural Information Processing Systems,
pages 4080–4088.
Munteanu, A., Schwiegelshohn, C., Sohler, C., and
Woodruff, D. (2018). On coresets for logistic regres-
sion. In Advances in Neural Information Processing
Systems, pages 6561–6570.
Mustafa, N. H. and Varadarajan, K. R. (2017). Epsilon-
approximations and epsilon-nets. arXiv preprint
arXiv:1702.03676.
Phillips, J. M. (2016). Coresets and sketches. arXiv preprint
arXiv:1601.00617.
Shalev-Shwartz, S. and Ben-David, S. (2014). Understand-
ing machine learning: From theory to algorithms.
Cambridge university press.
Shalev-Shwartz, S. et al. (2012). Online learning and on-
line convex optimization. Foundations and Trends
R
in Machine Learning, 4(2):107–194.
Zhang, Y., Tangwongsan, K., and Tirthapura, S. (2017).
Streaming k-means clustering with fast queries. In
Data Engineering (ICDE), 2017 IEEE 33rd Interna-
tional Conference on, pages 449–460. IEEE.
On Generating Efficient Data Summaries for Logistic Regression: A Coreset-based Approach
89
