Deﬁnition of a Walking with Starting and Stopping Motions for the

Humanoid Romeo

A. Kalouguine

1,2 a

, V. de-Le

on-G

omez

, C. Chevallereau

1 b

, S. Dalibard

2 c

and Y. Aoustin

1,∗ d

Laboratoire des Sciences du Num

erique de Nantes, CNRS UMR 6004, Ecole Centrale de Nantes,

Universit

e de Nantes, France

SoftBank Robotics, 43, Rue du Colonel Pierre Avia, 75015, Paris, France

Keywords:

Humanoid Robot, Starting Motion, Stopping Motion, Center of Mass, Zero Moment Point, Essential Model.

Abstract:

The aim of this paper is to develop a complete walking with a starting, periodic and stopping motion for a 3D

humanoid robot with n actuated variables. The dynamic behaviour of the center of mass of the humanoid robot

is deﬁned by a model called Essential model. The ZMP is imposed, the horizontal position of the CoM is free.

The n − 2 other generalized variables of the humanoid robot are controlled and their trajectories can be for

example chosen as a sinusoidal function of time. The gait parameters are determined based on data obtained

from human walking. Numerical tests are presented for a complete walking motion. The perspectives are to

test the obtained trajectories experimentally.

1 INTRODUCTION

Designing a walking trajectory for a humanoid robot

entails strong difﬁculties such as unilateral constraints

with the ground, numerous joints, respecting the dy-

namic equilibrium, among others. There exist several

popular methods, which are based on the relation be-

tween the zero moment point (ZMP) and the center of

mass (CoM), to develop walking trajectories for ex-

periments with humanoid robots, for example (Kajita

et al., 2014), (Kaneko et al., 2004). Their main ad-

vantage is to not require a lot of information about

the dynamic behavior of each of the robot’s bodies.

However during a walking, an important ﬂexion of

the knee joint for the stance leg is actually not human-

like. Also, the results are based on a simpliﬁed model,

thus the walking stability is not ensured for a robot

with small feet. With the linear inverted pendulum

(LIP) model, walking motions based on capture point

regulation are developed in order to exploit the nat-

ural dynamic of the pendulum to stop it. The cap-

ture point is the location on the ground where a biped

needs to step in order to come to a stop. The CoM

motion freely converges to the capture point, see (En-

https://orcid.org/0000-0003-3092-9534

https://orcid.org/0000-0002-1929-5211

https://orcid.org/0000-0001-8655-8619

https://orcid.org/0000-0002-3484-117X

∗

Corresponding author

glsberger et al., 2001) and (Pratt et al., 2012). But

its theoretical concept is mainly based on the assump-

tion that the altitude of the CoM is constant, i.e. the

linear inverted pendulum (LIP) assumption. A walk-

ing gait based on human-like virtual constraints has

been investigated in (Ames et al., 2012) for the robot

Nao; Sakka in (Sakka, 2017) also performed this type

of study for an online human motion imitation with

Nao for slow motions. Another approach employed

to generate walking patterns for biped robots is based

on central pattern generators (CPGs) and does not re-

quire any physical model of the biped; see (Behnke,

2006), (Graf et al., 2009) or (Shachykov, 2019). How-

ever they request the tuning of a lot of parameters.

The parametric optimisation can also be used to de-

ﬁne ofﬂine walking trajectories for humanoid robots,

for example (Bessonnet et al., 2002), (Tlalolini et al.,

2010), or (Ames et al., 2012). The main advantage

of parametric optimization is that energy consump-

tion can be minimized. But this method requests a lot

of computation efforts. The reference motion of the

biped can also be based on a record of human mo-

tion (Powell et al., 2013), (Tomic et al., 2014). By

deﬁnition, a human is a perfect model to deﬁne a hu-

manoid walking. Nevertheless, making the correla-

tion between the human motion and the robot joints

is not so easy. Despite these interesting contributions,

to our best knowledge there are few papers about the

design of a complete walking motion, taking into ac-

Kalouguine, A., de-León-Gómez, V., Chevallereau, C., Dalibard, S. and Aoustin, Y.

Deﬁnition of a Walking with Starting and Stopping Motions for the Humanoid Romeo.

DOI: 10.5220/0009827000470055

In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 47-55

ISBN: 978-989-758-442-8

count the constraints on ZMP trajectory, with a start-

ing, a periodic and a stopping motion. An interest-

ing investigation was done in (Ames, 2014) but the

approach was more hybrid, without double support

phases. In (Khusainov et al., 2017), desired foot po-

sitions of the humanoid robot are generated for any

given trajectory by taking into account kinematic lim-

its in robot legs. In but to our best knowledge for hu-

manoid robots there are no extract trajectories from

human data.

The contribution of this paper is to ﬁll this gap.

Our main objective is to ﬁnd feasible walking trajec-

tories for a given robot, taking into account these dy-

namic characteristic, i.e. with unilateral ground con-

tact forces and ensure dynamic equilibrium. More-

over, the proposed trajectories are inspired by aver-

age human motion, copying a particular human gait,

chosen to translate an emotion like joy or fatigue, or

dedicated to a task like carrying loads, etc. A com-

plete walking motion is deﬁned for Romeo, a hu-

manoid robot with n = 31 joints. This complete walk-

ing, which is composed of double support (DS) and

single support (SS) phases is calculated by using the

Essential model, which models the relation between

ZMP and CoM by considering the complete dynamic

of the robot unlike the LIP model, i.e. a determin-

ing feature of human gait, (De-Le

on-G

omez et al.,

2019). Vukobratovic (Vukobratovic et al., 2012) en-

lighten us on biomechanical inspiration of this feature

to carry out biped robot motion such as posture real-

ization, gait synthesis. The trajectory of the ZMP is

here imposed, the horizontal position of the CoM of

the humanoid robot is free to adapt to the ZMP evolu-

tion. The n−2 remaining generalized coordinates are

given functions of time (often sinusoidal functions),

whose parameters are inspired by data extracted from

human walking. The CoM is thus computed from

the knowledge of the evolution of the ZMP and these

n − 2 remaining generalized coordinates. The n joint

variables of the robot are deduced from this calcula-

tion. From the inverse dynamic model it is possible to

deduce the torques to carry out this complete walking.

The paper is outlined as follows. The humanoid

robot Romeo is described in section 2. The Essential

model is presented in section 3. The boundary value

problem to obtain a periodic walking motion is stated

in section 4. The starting and stopping phases are de-

tailed in section 5. The results of the numerical tests

are presented in section 6. Section 7 offers our con-

clusions and perspectives.

2 ROMEO

The humanoid robot considered in this study is

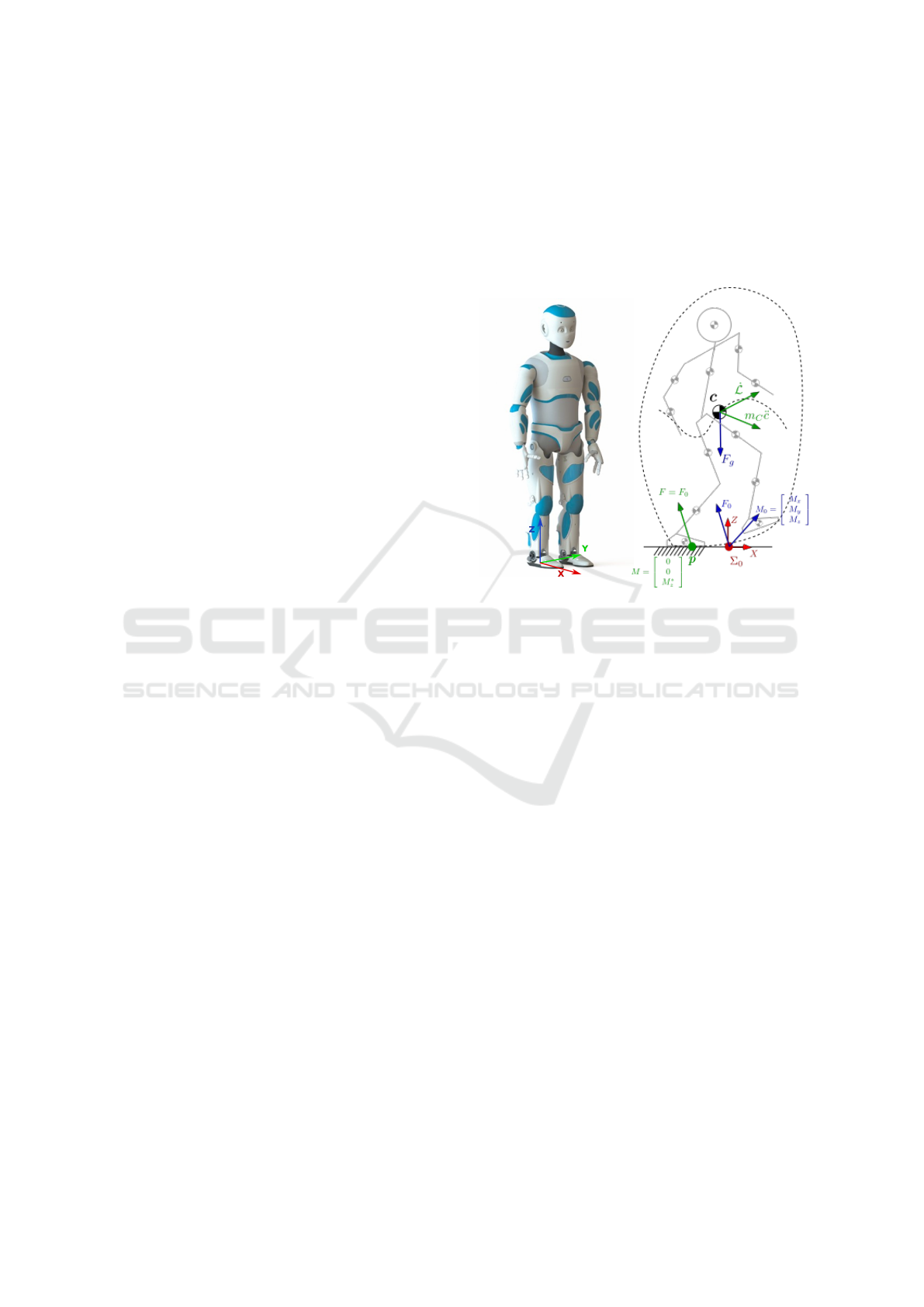
Romeo, a prototype platform developed by the com-

pany Softbank Robotics, see ﬁg. 1 a). It is 1.47m

tall, weighs 36 kg and features 31 degrees of freedom

(DoF) gathered into the conﬁguration vector q.

Figure 1: A) Photography of Romeo. b) Illustration of the

global equilibrium.

3 ESSENTIAL MODEL

The objective of the Essential model is, instead of im-

posing as many trajectories as there are degrees of

freedom (DoFs), to leave two DoFs free to allow for a

chosen placement of the ZMP. Since the relation be-

tween ZMP and CoM is considered as a determining

feature of human gait (Kajita et al., 2014), (Koolen

et al., 2012), and the positions of CoM and ZMP are

strongly linked, we choose to ”set free” the horizontal

coordinates r

= (x, y) of the CoM in order to adapt

to the imposed trajectory of the ZMP.

In order to take inspiration from the human motion,

let us introduce r ∈ R

31×1

r = (r

, r

)

= (x,y, z(t), x

(t), y

(t), z

(t), ψ

(t), θ

(t),

(t), ψ

(t), θ

(t), φ

(t), q

(t), ·· · , q

(t))

(1)

We deﬁne r

as the vector of the 29 variables of r

for which the trajectories are imposed. z(t) deﬁnes

the desired altitude of the CoM. x

(t), y

(t), z

(t) and

(t), θ

(t), φ

(t) describe the desired position and

orientation of the free foot, and ψ

, θ

, φ

give the de-

sired orientation of the torso link. The upper-body

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

variable joints are deﬁned by q

to q

. The desired

trajectory for r

(t) is deﬁned based on human motion.

The robot conﬁguration can be deﬁned by the joint

vector q ∈ R

31×1

or by the vector r, and a geometric

model can be built. Let q = g(r

, r

) be, ˙q and ¨q are

deduced thanks to the kinematic models as follows:

˙q = J

˙r

, ¨q = J

¨r

˙r

¨r

˙r

. (2)

Here J

∈ R

31×2

and J

∈ R

31×29

. In this study the

evolution of r

is chosen as a function of time, thus

the joint evolution can be expressed as function of

, ˙r

, ¨r

and t only :

q = g(r

,t), ˙q = J

˙r

+ v(t, r

¨q = J

¨r

˙r

+ a(t, r

, ˙r

(3)

To assess the feasibility of a walking trajectory,

it is necessary to calculate the external forces act-

ing on the humanoid robot. These external forces

here are the gravity force F

and the ground reac-

tion forces applied on each foot (see ﬁg. 1 b). The

resulting ground reaction is deﬁned by the wrench ∈

6×1

, M

)

= (F

, F

, M

)

in a refer-

ence frame Σ

. The global equilibrium of the robot

can be written as :









¨q +



(q, ˙q)



(4)

where q ∈ R

31×1

is the joint vector of the robot.

Using (3), the global equilibrium (4) can be

rewritten:







(t, r

)

(t, r

)



¨r



(t, r

, ˙r

)

(t, r

, ˙r

)



(5)

Let p = (p

, p

, 0)

be the global zero moment point

(ZMP). Its coordinates p

and p

satisfy :

+ M

= 0, F

− M

= 0.

(6)

, p

) must be inside the convex hull of support at

all times in order to satisfy the dynamic equilibrium

condition (Vukobratovic and Borovac, 2004). We im-

pose a desired evolution of the ZMP px(t) and py(t)

inside the convex hull of the support foot (or feet in

DS) in order to satisfy the equilibrium condition. Dur-

ing the SS phase the desired motion of the ZMP is a

migration of the ZMP from the heel to the toe of the

stance foot. In DS phase the desired motion of the

ZMP is deﬁned by a linear evolution from the ﬁnal

position of the ZMP at the end of the SS phase on the

stance foot, until the initial position of the ZMP at the

beginning of the SS on the next stance foot. By using

the 3

, 4

, and 5

lines of (5), we rewrite (6) as:

Frz

(t, r

)¨r

+ d

Frz

(t, r

, ˙r

)) p

(t)+

Mry

(t, r

)¨r

+ d

Mry

(t, r

, ˙r

) = 0,

Frz

(t, r

)¨r

+ d

Frz

(t, r

, ˙r

)) p

(t)−

Mrx

(t, r

)¨r

− d

Mrx

(t, r

, ˙r

) = 0.

(7)

These two scalar equations (7) isolate the essential

characteristic of the walking that is the relationship

between the ZMP and the CoM. Solving (7) gives

the Essential model describing the acceleration of the

horizontal positions x and y of the CoM, that are de-

ﬁned to achieve the imposed evolution of the ZMP:

¨r

= f (r

, ˙r

,t, p

(t), p

(t)). (8)

By integration of (8) from initial conditions we

can calculate the current values of ˙r

, i.e. ˙x, ˙y, and

, i.e x, and y. To sum up, the evolution of x and y is

not imposed in order to allow them to adapt to the im-

posed evolution of the ZMP. With this strategy to de-

ﬁne a reference trajectory of walking, which is based

on the Essential model (8) and r

(t), no approxima-

tions are made to the dynamic model when designing

the humanoid walking. The method ensures the fea-

sibility of a walking trajectory from the point of view

of the condition on the ZMP.

The choice of the height z(t) of the CoM allows to

satisfy the positivity of the vertical component of the

resultant ground reaction force during the walking. It

is sufﬁcient to satisfy

¨z(t) > −g

The condition of no slipping can be checked based on

the knowledge of ¨r

and ¨z. It is sufﬁcient to satisfy

||¨r

(t)|| < µ(¨z(t) − g)

where µ is the friction coefﬁcient. The numerical val-

idation of these conditions is presented in ﬁg. 9.

3.1 Torques and Ground Forces in SS

and DS

By now, the torques required to produce the motion

have to be calculated. During the SS phase, by con-

sidering the stance foot motionless on the ground, we

can deﬁne the dynamic behavior of the robot:

τ = A

(t, r

f )¨r

+ d

(t, r

, ˙r

) (9)

In DS phase, the effort wrench (F

ext

, M

ext

)

applied

on the second leg, (9) becomes

τ = A

(t, r

)¨r

+ d

(t, r

, ˙r

) + J

ext



ext



. (10)

The global equation gives the global reaction effort

, M

, but the distribution on both legs is free and

will modify the actuation torque. During a DS, the

global ZMP is the barycentre of the two local ZMPs

on each foot, this implies that the global ZMP and the

local ZMPs are aligned. In DS, the choice of local

ZMPs p

and p

is used to calculate the distribution

Deﬁnition of a Walking with Starting and Stopping Motions for the Humanoid Romeo

of efforts. This choice must limit the internal forces

useless to the motion in order to avoid increasing the

joint torques. We can then calculate the vertical reac-

tion force F

and F

on legs 1 and 2 by solving this

system:

+ p

+ F

= p

+ p

+ F

= p

(11)

To limit the risk of slipping, the ratio between tangen-

tial and normal forces for the global equilibrium is

chosen equal for each leg. The components F

, F

, and F

are calculated to satisfy:

+ F

(12)

By using (11) and (12) we ﬁnd M

= M

+ M

. The

moment around the z axis is also shared between the

two legs by using a similar distribution to the force

components (12) as follows:

+ M

+ F

(13)

In this study, two types of DS phases are consid-

ered.

• DS during the walking phase which allows to join

two phases of SS with foot positions offsets along

the x and y axes. We want to have a continuous

evolution of the ZMP, which results in continuous

joint torques and avoids high jerk. We choose an

evolution of the global ZMP in order that during

the DS phases, the two local ZMPs keep a con-

stant pose corresponding to the ﬁnal pose of the

ZMP in SS: p

, and the initial pose of the ZMP

for the next SS: p

. This implies that the global

ZMP evolves linearly between the ﬁnal pose of

the ZMP during the previous SS and the initial

pose of the ZMP during the next SS.

• For the initial DS in starting phase, or the ﬁnal DS

in stopping phase, on the contrary, we have the

two feet aligned along the x-axis and a non-linear

evolution of the global ZMP (Jian et al., 1993).

The local ZMPs will then be chosen to yield the

current value of the global ZMP along the x-axis

while remaining within the surface of the corre-

sponding foot. In addition, when stationary, we

want an identical distribution of forces over the

two feet, we choose a position of the CoM accord-

ing to the y-direction between the two feet and a

y-position of the local ZMPs in the center of the

feet. A linear ZMP evolution along the y-axis is

chosen. The aim is to ensure continuity and to

minimize the lateral torque on the ankle. An illus-

tration is shown in ﬁg. 8 for the case studied.

4 PERIODIC WALKING MOTION

The periodic motion is composed of SS phases and

DS phases with ﬂat foot contacts on the ground. There

is no impact at the end of the SS phase, since the ve-

locity of the swing foot is imposed to be zero when

it touches the ground. A quadratic-cycloidal function

is used to deﬁne the trajectory of the swing foot. The

orientation of its sole is varying during motion, but

parallel to the ground during DS phases. Sinusoidal

functions are used to deﬁne the motions of the arms

and the trunk. The parameters of these functions are

tuned based on observations of human motions (Win-

ter, 1992). To deﬁne a periodic walking motion for

Romeo, the step width D and the step length S are

adapted to its physical characteristics and the limits of

its actuators. The step width D is chosen to be 0.20m

to satisfy a safe clearance between Romeo’s ankles.

The step length S is chosen in the range 0.15 to 0.20m,

which corresponds to a 0.30-0.40m displacement of

the swing foot and a velocity of 0.83 to 1.1km/h re-

spectively. The duration of one DS phase is chosen to

be close to 12% of the cycle (2 steps) duration 2 · T ,

where T = T

. T

= 0.15s and T

= 0.60s are

the chosen durations of the DS phases and SS phases.

In SS, the ZMP evolution is chosen as linear along the

x axis and centered in the middle of the foot along the

y axis. In DS, the ZMP evolves linearly between its

ﬁnal position in the previous SS and its initial position

in the next SS as explained in section 3.1.

To ﬁnd the periodic motion, a boundary value

problem is stated and solved as follows. Let

(x(t

), y(t

), ˙x(t

), ˙y(t

)) be the components in the hor-

izontal plane of the position and velocity of the COM

at the beginning of a current step of the walking mo-

tion. The periodic condition is

(x(t

), y(t

), ˙x(t

), ˙y(t

)) =

(x(t

+ T ), y(t

+ T ), ˙x

+ T ), ˙y

+ T ))

(14)

by taking into account the change of the reference

frame when the two legs switch their roles just at the

beginning of the current step. So ˙x

+ T ), ˙y

T ) are the initial velocities of the COM in SS of the

next step. The boundary value problem is stated as:

what are x(t

), y(t

), ˙x(t

) and ˙y(t

) such that after in-

tegration of (8) over the time interval [t

+ T ] the

periodic condition (14) is satisﬁed.

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

5 STARTING AND STOPPING

MOTIONS

In order to perform the target periodic walking mo-

tion experimentally, it is necessary to add starting and

stopping motions, which are composed of DS phases

and SS phases. This allows the robot to start from

(resp. to stop in) a resting position. Each resting posi-

tion is deﬁned to be a static equilibrium where the ver-

tical projection of the CoM on the ground is merged

with the ZMP close to the center of the convex hull

of support. From the observation of data from human

walking (Grundy et al., 1975) a ZMP trajectory is de-

ﬁned by using piecewise polynomial functions to be

adapted to a humanoid robot. A sequence of starting

phase (DS

, SS

, and DS

), a periodic walking motion

(SS and DS) and a stopping phase (SS

n−1

, DS

n−1

, SS

and DSS

) is shown in ﬁg. 2.

For the starting motion control points are intro-

duced:

• P

ZMP at the start of DS

• P

ZMP in the middle of DS

• P

ZMP at the transition between DS

and SS

• P

ZMP at the transition between SS

and DS

• P

ZMP at the end of the DS

phase

These control points are used to deﬁne the evolution

of ZMP during starting phase. They are illustrated on

ﬁg. 2

In DS

phase p

and p

are both deﬁned as

quadratic functions of time going from P

to P

with

the intermediate point P

. In SS

and DS

phases p

and p

are deﬁned as linear functions of time con-

necting, respectiively, P

to P

and P

to P

. P

imposed by the chosen periodic trajectory.

For the stopping motion, the strategy to deﬁne the

ZMP trajectory is similar. We deﬁne:

• P

ZMP at the transition between SS

n−1

and

n−1

• P

ZMP at the transition between DS

n−1

and SS

• P

ZMP at the transition between SS

and DS

• P

ZMP in the middle of DS

• P

ZMP at the end of the DS

phase

At the start of SS

n−1

phase, the ZMP position is

(taking into account the change of reference frame)

the same as in P

because of the periodic nature of

the trajectory before SS

n−1

. We can therefore denote

this point as P

as well. In SS

n−1

phase, p

and p

are

therefore deﬁned as linear functions to connect P

. In DS

n−1

and SS

phases, p

and p

are deﬁned as

linear functions of time to connect P

to P

, P

to P

respectively. In DS

phase p

and p

are deﬁned as

quadratic functions of time connecting P

to P

with

an intermediate point P

The stopping phase with two DS phases and two

SS phases is not symmetric with respect to the start-

ing phase with two DS phases and only one SS phase

in order to mimic easier the motion of the ZMP in hu-

mans during the starting and stopping motions. The

step width D and the step length S are given but

not necessarily similar between the starting, stopping

and periodic motions. A boundary value problem is

solved to deﬁne the starting and stopping motions.

This boundary value problem is stated as follows:

Starting Motion. Let us consider the known two co-

ordinates of the horizontal position of the CoM,

which is also the ZMP position P

. Their two

velocities are equal to zero. Let us consider the

known two coordinates of the horizontal position

of the CoM at the end of DS

phase and their two

velocities. These two coordinates and two veloc-

ities are also the state of the periodic horizontal

motion of the CoM at the beginning of the SS

phase.

Let us take into account the essential model

(8) and T

start

the duration of the starting mo-

tion. What are the four possible variables

to carry out the starting motion by integra-

tion of (8) from (X(0),Y (0),

X(0),

Y (0))

(X(T

start

),Y (T

start

X(T

start

Y (T

start

))

? We

choose the components p

and p

of the two con-

trol points P

, and P

of the ZMP trajectory, to

solve this boundary problem. A SQP method (Se-

quential Quadratic Programming) with fmincon of

Matlab

 is used to ﬁnd the coordinates of P

and P

in order to easier ensure that the ZMP is

always inside of the convex hull of the support

area. The Essential model dynamics are then in-

tegrated from the starting state (r

(0), ˙r

(0))

for

this COM, to the ﬁnal state (r

start

), ˙r

start

))

of the starting motion. This ﬁnal state is compared

to the target state (r

des

start

), ˙r

des

start

))

by us-

ing a Mean Square criterion (optionally weighed

to emphasize the importance of one of the dimen-

sions):

J = (X(T

start

) − X

des

start

))

(Y (T

start

) −Y

des

start

))

(

X(T

start

) −

des

start

))

(

Y (T

start

) −

des

start

))

(15)

Stopping Motion. The strategy is similar to that of

the starting motion. For the four possible vari-

ables to carry out the stopping motion we choose

Deﬁnition of a Walking with Starting and Stopping Motions for the Humanoid Romeo

the components p

and p

of the two control

points P

to P

of the ZMP trajectory, to solve this

boundary problem. An equivalent criterion to (5)

is calculated with respect to the two coordinates

of the horizontal resting position of the CoM and

their two respective velocities.

J = (X(T

stop

) − X

des

stop

))

(Y (T

stop

) −Y

des

stop

))

X(T

stop

)

Y (T

stop

)

(16)

Figure 2: Sequence starting motion, cycling walking stop-

ping motion.

All joint trajectories also need to be continuous

during this transition. And since there is no impact

in our gait, this is equivalent to imposing that the

evolution of r

be continuous. The sinusoidal func-

tions, which deﬁne the actuated joints of the arms and

trunk, are multiplied by a piecewise polynomial cut-

off function which is equal to 1 during the periodic

motion and smoothly goes to 0 during the starting and

stopping phases in order to start and to stop with a null

velocity and null acceleration.

6 NUMERICAL RESULTS

6.1 Periodic Motion

We choose a ZMP trajectory close to the one that is

observed in humans. Since we do not have foot roll-

off motion, we avoid the ZMP reaching the edges of

the foot. That way, the non-tilting condition is safely

satisﬁed.

The evolution of ZMP in DS phase is chosen as

follows:

• In x-direction, from p

= 0 (under the ankle) to

= 0.10m (in the toes of the foot).

• In y-direction, p

= 0 (center of the foot).

The corresponding COM trajectory is represented

on ﬁg. 3. We observe that the COM trajectory in

the horizontal plane is not far from a sinus func-

tion, which is what is observed for humans (Rose and

Gamble, 2006).

However, when calculating the torque values for

this trajectory, we observe that the torques are not

Figure 3: COM trajectory corresponding to a human-like

evolution of the ZMP.

Figure 4: Torques at both knees for a human-like ZMP tra-

jectory. The dashed line marks the end of the SS phase

(swing foot contact), and the red dashed lines show the max-

imum acceptable torque for Romeo. It is interesting to note

that these limits are not constant - this is because of a speci-

ﬁcity of the knee joint in Romeo: the maximum torque de-

pends on the joint position.

compatible with the hardware of Romeo, as shown

in ﬁg. 4. In order to reduce these torques, we need

to make some adaptations to the original parameters.

We analyzed the effect of various parameters on the

torques, and observed that the most efﬁcient way to

inﬂuence the knee torques is to modify the ZMP tra-

jectory. The result of this adaptation is presented in

the following section, and the trajectory used in the

rest of the paper is the modiﬁed one.

6.2 Effect of ZMP Evolution on Torques

The results presented above correspond to an evolu-

tion of the ZMP going from the heel to the tip of each

foot (see ﬁg. 3). The torque at the ankle is directly

affected by the pose of the ZMP. It can be seen in ﬁg.

5 (2

image), that the propulsive torque at the ankle

is low at the beginning of the step. As a consequence,

a high propulsive torque is required at the knee joint

(ﬁg. 5 (3

image)). In fact this high torque exceeds

the limits of the actuator (shown in dotted line) of the

robot Romeo. We explored the effect of the inﬂuence

of ZMP evolution. The results show that a modiﬁca-

tion of the ZMP trajectory inﬂuences the torques in

the support knee and in the support ankle. A ZMP

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

that has a constant position in front of the foot allows

a higher propulsive force in the ankle at the beginning

of the SS, and thus allows to decrease the propulsive

force at knee, and then produces a knee torque com-

patible with the actuator of Romeo.

Figure 5: Joint torques (N.m) versus time (s): comparison

of the torque in the lower part of the robot for two periodic

trajectories with a step size of 0.20 m and a period of 0.75 s.

The trajectory in green is with a human like ZMP evolution

in DS, and the trajectory in blue has a ZMP constrained to

the front of the foot.

6.3 Complete Motion

The synthesised walking trajectory is such that the

step width parameter D is the same for the starting,

periodic and stopping motions. The step length pa-

rameter S is chosen to be 0.16m, 0.15m and 0.20m

for the starting, periodic and stopping motions respec-

tively. For this synthesised trajectory, the trajectories

of the horizontal position of the CoM and the ZMP

are shown ﬁg. 6. The starting motion and the stop-

ping phases are respectively composed of three and

four phases. Four steps make up the periodic mo-

tions. During this periodic motion the step size equals

0.15m. We can observe that the COM and ZMP evo-

lutions are continuous from the starting conﬁguration

to the stopping conﬁguration.

A focus of the starting and stopping phases is pre-

sented ﬁg. 7. The horizontal position of the CoM and

the ZMP position coincide well at the starting and

stopping conﬁgurations. The control points to solve

the two boundary value problems are depicted with

green stars.

In the ﬁrst and last DS phases, the ZMP follows

a more complex trajectory. It is therefore necessary

Figure 6: Imposed ZMP trajectory (orange) and corre-

sponding COM (blue). The dashed rectangles represent the

foot placements.

Figure 7: Imposed ZMP trajectory (orange) and horizontal

position of the corresponding COM (blue).

to deﬁne a non constant local ZMP for each foot. We

choose at all times to keep the same x coordinate as

the global ZMP, and stay as close as possible to the

center of each foot in y direction to improve walking

stability. The resulting local ZMP trajectories are pre-

sented in ﬁg. 8.

We can also verify that the non slipping condition

is fulﬁlled. This condition is the fact that the ratio be-

tween the tangential and normal forces does not ex-

ceed the friction coefﬁcient. This friction coefﬁcient

is chosen equal to 0.7 here. Both of these forces are

calculated with (4). The sinusoidal-like shape of the

normal reaction force observed in ﬁg. 9 is linked to

the oscillations of the height z the COM F = m¨z +mg.

Deﬁnition of a Walking with Starting and Stopping Motions for the Humanoid Romeo

Figure 8: Evolution of the local ZMP (red) for each foot

respectively during the ﬁrst and last DS phases of the start-

ing (a) and stopping (b) motions. The blue line indicates

the corresponding COM evolution, resp. starting and stop-

ping in the middle of both feet. The dashed lines show the

distribution of the global ZMP and its relation to the COM

position.

Figure 9: Normal (top plot) and tangential (bottom) com-

ponents of the reaction force. The red dashed line repre-

sents the maximum acceptable tangential force without risk

of slipping.

We compute the torque value for all of the joints.

However, we choose to only present in ﬁg. 10 the

torques on both legs in the joints in the sagittal plane.

Indeed, these are the torques that require the highest

magnitude. It can be observed that the torques are in-

side to motor limits for the studied robot. The torque

required for starting, periodic, and stopping motions

are of similar magnitude.

Figure 10: The torque at the ankle, knee and hip joints, in

the sagittal plane for the complete motion.

7 CONCLUSIONS

A complete walking with a starting motion and a stop-

ping motion is deﬁned thanks to a strategy based on

the Essential model. This methodology ensures the

ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics

feasibility of the walking trajectory with respect to

the condition on the ground reaction force: take off,

slipping and rotation of the support foot are avoided.

The ZMP trajectory is ensured to be inside a convex

hull of the support surface. The parameters of trajec-

tories of the swing leg ankle, the trunk and the arms

are tuned thanks to observations from human walking.

The effect of the choice of the ZMP evolution on the

required torque is investigated. A correlation between

the pose of the ZMP in sagittal plane and torque at an-

kle and knee in saggital plane has been shown. The

perspectives are to test this complete walking motion

experimentally.

REFERENCES

Ames, A. D. (2014). Human-inspired control of bipedal

walking robots. IEEE Transactions on Automatic

Control, 59(5):1115–1130.

Ames, A. D., Cousineau, E. A., and Powell, M. J. (2012).

Dynamically stable bipedal robotic walking with nao

via human-inspired hybrid zero dynamics. In Proc. of

the 15th ACM int. conf. on Hybrid Systems: Compu-

tation and Control, pages 135–144. ACM.

Behnke, S. (2006). Online trajectory generation for om-

nidirectional biped walking. In Proc. Int. Conf.

on Robotics and Automation (ICRA), pages 1597–

1603, Orlando, USA.

Bessonnet, G., Chesse, S., and Sardin, P. (2002). Generating

optimal gait of a human-sized biped robot. In Proc. of

the ﬁfth Int. Conf. on Climbing and Walking Robots,

pages 717–724.

De-Le

on-G

omez, V., Luo, Q., Kalouguine, A., P

amanes,

J. A., Aoustin, Y., and Chevallereau, C. (2019). An es-

sential model for generating walking motions for hu-

manoid robots. Robotics and Autonomous Systems,

112:229–243.

Englsberger, J., Ott, C., Roa, M. A., Albu-Sh

affer, A., and

Hirzinger, G. (2001). Bipedal walking control based

on capture point dynamics. In Proc. Int. Conf. on

Intelligent Robots and Systems (IROS), pages 4420–

4427, San Francsico, USA.

Graf, C., H

aryl, A., R

ofer, T., and Laue, T. (2009). A ro-

bust closed-loop gait for the standard platform league

humanoid. In Proc. Workshop on Humanoid Soc-

cer Robots of the IEEE-RAS Int. Conf. on Humanoid

Robots, pages 30–37, Paris, France.

Grundy, M., Tosh, P., McLeish, R., and Smidt, L. (1975).

An investigation of the centres of pressure under the

foot while walking. J. of bone and joint surgery.

British volume, 57(1):98–103.

Jian, Y., Winter, D. A., Ishac, M. G., and Gilchrist, L.

(1993). Trajectory of the body cog and cop during

initiation and termination of gait. Gait & Posture,

1(1):9–22.

Kajita, S., Hirukawa, H., Harada, K., and Yokoi, K.

(2014). Introduction to humanoid robotics, volume

101. Springer.

Kaneko, K., Kanehiro, F., Kajita, S., Hirukawa, H.,

Kawasaki, T., Hirata, M., K.Akachi, and Isozumi, T.

(2004). Humanoid robot hrp-2. In Proc. IEEE Int.

Conf. on Robotics and Automation ICRA, pages 1083–

1090, New-Orleans, Louisiana, USA.

Khusainov, R., Sagitov, A., Klimchik, A., and Magid, E.

(2017). Arbitrary trajectory foot planner for bipedal

walking. In ICINCO (2), pages 417–424.

Koolen, T., de Boer, T., Rebula, J., Goswami, A., and Pratt,

J. (2012). Capturability-basd analysis and control of

legged locomotion, part 1: Theory and application to

three simple gait models. Int. J. of Robotics Research,

31(09):1094–1113.

Powell, M. J., Heraeid, A., and Ames, A. D. (2013). Speed

regulate in 3d robotic walking through motion transi-

tions between human-inspired partial hybrid zero dy-

namics. In Proc. IEEE Int. Conf. on Robotics and Au-

tomation (ICRA), pages 4803–4810, Karlsruhe, Ger-

many.

Pratt, J. E., Koolen, T., de. Boer, T., Rebula, J. R., Cotton,

S., Carff, J., Johnson, M., and Neuhaus, P. D. (2012).

Capturability-based analysis and control of legged lo-

comotion, part 2: application to m2v2, a lower-body

humanoid. The International Journal of Robotic Re-

search, 31(10):1117–1133.

Rose, J. and Gamble, J. G. (2006). Human walking.

Williams & Wilkins, 3 edition.

Sakka, S. (2017). Imitation des mouvements humains par un

robot humano

ıde sous contrainte d’

equilibre. HDR,

Universit

e Pierre et Marie Curie (UPMC).

Shachykov, A. (2019). Biomedical signals analysis and

neural modeling of motor coordination in Parkinson’s

disease. PhD thesis, Universit

e de Lorraine France.

Tlalolini, D., Aoustin, Y., and Chevallereau, C. (2010).

Design of a walking cyclic gait with single support

phases and impacts for the locomotor system of a

thirteen-link 3d biped using the parametric optimiza-

tion. Multibody System Dynamics, 23(1):33–56.

Tomic, M., Vassallo, C., Chevallereau, C., Rodic, A., and

Potkonjak, V. (2014). Arms motion of a humanoid

inspired by human motion. In Proc. Int. Conf. Medi-

cal and Service Robotics (MESROB 2014), Lausanne,

Switzerland.

Vukobratovic, M. and Borovac, B. (2004). Zero-moment

point-thirty ﬁve years of its life. Int. J. of Humanoid

Robotics, 1(1):157–173.

Vukobratovic, M., Borovac, B., Rodic, A. and, K. D., and

Potkonjak, V. (2012). A bio-inspired approach to the

realization of sustained humanoid motion. Int. J. of

Advanced Robotic System, 9(201):1–16.

Winter, D. A. (1992). Foot trajectory in human gait: a pre-

cise and multifactorial motor control task. Physical

therapy, 72(1):45–53.

Deﬁnition of a Walking with Starting and Stopping Motions for the Humanoid Romeo