Local Rotation Pattern: A Local Descriptor of Color Textures
Hela Jebali
1
, No
¨
el Richard
2
and Mohamed Naouai
1
1
Faculty of Science of Tunis, University Campus El Manar, Tunisia
2
University of Poitiers, XLIM UMR CNRS 6172, France
Keywords:
Color Texture, Descriptor, Quaternion Rotation, Geodesic Distance, Classification.
Abstract:
Describing color textures is an extremely challenging problem in pattern recognition and computer vision. In
this paper, a new texture feature is proposed and investigated for color texture image classification. Based on
quaternion representation of color images and quaternion rotation, a Local Rotation Pattern descriptor (LRP)
is proposed. Using quaternion to represent color images is done by encoding the three RGB channels into the
three imaginary parts of a quaternion. The distance between two color can be expressed as the angle of rotation
between two unit quaternions using the geodesic distance to obtain finally our LRP histograms. Performance
in texture classification is assessed for three challenging datasets: Vistex, Outex-TC13 and USPtex databases
facing to the recent results from the state-of-the-art. Results show the high efficiency of the proposed approach.
1 INTRODUCTION
Colour is an important characteristic of digital images
which has received significant interest from the re-
search community. This fundamental image property
has been widely used in many applications such as
object recognition, skin detection and image retrieval.
Although, a large variety of efficient texture descrip-
tors has been developed in the literature.
Cooccurrence matrix and Run-Length Matrix
(RLM)(Xiaoyan et al., 2009) are good descriptors of
texture content. Some years later, Ojala (Ojala et al.,
2002) expanded the local binary pattern (LBP) as a
powerful and successful texture descriptor in pattern
recognition and many computer vision applications.
The Local Binary Pattern descriptor has been used
successfully in texture classification (Guo et al., 2012)
, face recognition (Timo et al., 2004) and image re-
trieval (Penatti et al., 2012). Several research works
have proposed to transpose the texture analysis from
gray-level to colour images (Guo et al., 2010)(Guo
et al., 2010)(Mehta and Egiazarian, 2016). Several
colour texture expression are induced by the analy-
sis of color as a combination of three gray-level tex-
ture affected to the three colour channel. It exists few
works express the vectorial processing of color tex-
ture.
For research in computer graphics and computer
vision, Rotations in three-dimensional space are com-
monly represented as unit quaternions in a relatively
simple way. In this work, based on a local pattern en-
coding scheme and the quaternion representation, we
propose to use the rotation notion to process the dis-
tance between colors. Therefore, a new vector texture
feature: Local Rotation Pattern (LRP) is suggested.
This paper is organised as follow: in the following
sections, the mathematical definition of quaternion
and its properties are recalled. Then, we detailed
the Local Rotation Pattern (LRP) proposition and the
associated feature. Finally, the performance of our
proposed descriptor is evaluated on three challenging
datasets: Vistex, Outex-TC13 and USPtex databases.
2 QUATERNION ALGEBRA
2.1 Definition
Quaternions were discovered by William Hamilton in
1843 (Rowan, 1866) with the aim of generalize com-
plex numbers in three dimensional space. Quater-
nions form a four dimensional noncommutative alge-
bra. Extended from the complex numbers, any quater-
nion q ∈ H can be written in its Cartesian form as:
q = w + xi + y j + zk (1)
where w,x,y,k ∈ R and i, j,k are complex operators
that are roots of −1 satisfying:
i
2
= j
2
= k
2
= i jk = −1 (2)
(i j = −ji = k), ( jk = −k j = i), (ki = −ik = j) (3)
The real number a is called a real (or scalar) part
of q and is denoted R (q). The quaternion with real
Jebali, H., Richard, N. and Naouai, M.
Local Rotation Pattern: A Local Descriptor of Color Textures.
DOI: 10.5220/0009827805670573
In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 567-573
ISBN: 978-989-758-443-5
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
567

part w = 0, called pure quaternion (q = xi + y j + zk),
is an imaginary (or vector) part of q and is denoted
I (q). We can thus write q = R (q)+ I (q).
The quaternion conjugate is q = R (q) −I (q) and the
modulus of a quaternion is given by:
|q| =
p
w
2
+ x
2
+ y
2
+ z
2
=
p
qq (4)
Any quaternion with a norm |q| = 1 is named a
unit quaternion. The inverse of any quaternion is de-
fined as q
-1
=
q
|q|
, such that qq
-1
= 1. Hence, any
quaternion may be represented in the polar form:
q = |q|exp
µθ
= |q|(cos θ + µsinθ) (5)
Where µ =
xi+y j+zk
√
xi+y j+zk
and θ = arccos(
w
|q|
) represent a
real angle.
2.2 Quaternion RGB Images
Sangwine (Sangwine, 1996) was the first to demon-
strate the applicability of a quaternion Fourier trans-
form to color images. A color containing only three
components in the RGB space, Sangwine proposed to
describe the color information on the imaginary part
of the pure quaternion. Any pixel of a image I at the
coordinates (x,y) will therefore be coded as follows:
I(x,y) = 0 + R(x,y)i + Gx,y) j + B(x,y)k (6)
Where R(x,y),G(x,y) and B(x, y) represent the com-
ponents Red, green and blue respectively. Figure 1
illustrates the quaternion representation of RGB color
images.
Figure 1: Quaternion Representation of RGB color image.
Quaternions are compactly represent the RGB
color space. Therefore, the color interaction that ex-
ists between different channels is incorporated in any
processing at the image level.
2.3 Distance between Quaternions as
Rotations
Rotation in three-dimensional space can be repre-
sented in various forms. The Euler angles and quater-
nions are the two commonly used forms in computer
vision applications. In this work, we interested to the
quaternion representation. Any rotation R can be de-
scribed using a unit quaternion r (with norm equal to
1) as follows:
r = cos(
θ
2
) + v sin(
θ
2
) (7)
Where θ and v are respectively the angle and axis
of the rotation R.
In the unit-quaternion system, the concept of the
distance between two rotations can be described by
the angle between them. In geometry, this distance is
the length of the shortest geodesic path on the man-
ifold H between both quaternions. This distance is
called the Riemannian distance between two quater-
nions q
1
and q
2
is given by:
dist
H
(q
1
,q
2
) = klog(q
−1
1
q
2
)k (8)
Where log(q
i
) gives the rotation axis and angle of the
rotation matrix. The k.k above gives the magnitude
of the rotation angle. This Riemannian metric is well
known in the case of unit quaternions. The property
of the invariance to inversion of q
−1
1
q
2
6= q
2
q
−1
1
gives:
klog(q
−1
1
q
2
)k = klog(q
1
q
−1
2
)k (9)
Angulo in (Jes
´
us, 2014) proposed a symmetrized ver-
sion of the geodesic distance between two unit quater-
nions as follows:
dist
H
(q
1
,q
2
) = klog(q
−
1
2
1
q
2
q
−
1
2
1
)k (10)
Where the norm represent the usual Euclidean norm.
This geodesic distance gives values in the range [0, π].
3 PROPOSED METHOD
3.1 Local Rotation Pattern (LRP)
In this section, we describe the proposed vector fea-
ture for color texture: Local Rotation Pattern LRP.
Our proposed pattern intends to explore the difference
between two adjacent color pixels based on quater-
nion representation. Suppose q
i
and q
j
are two quater-
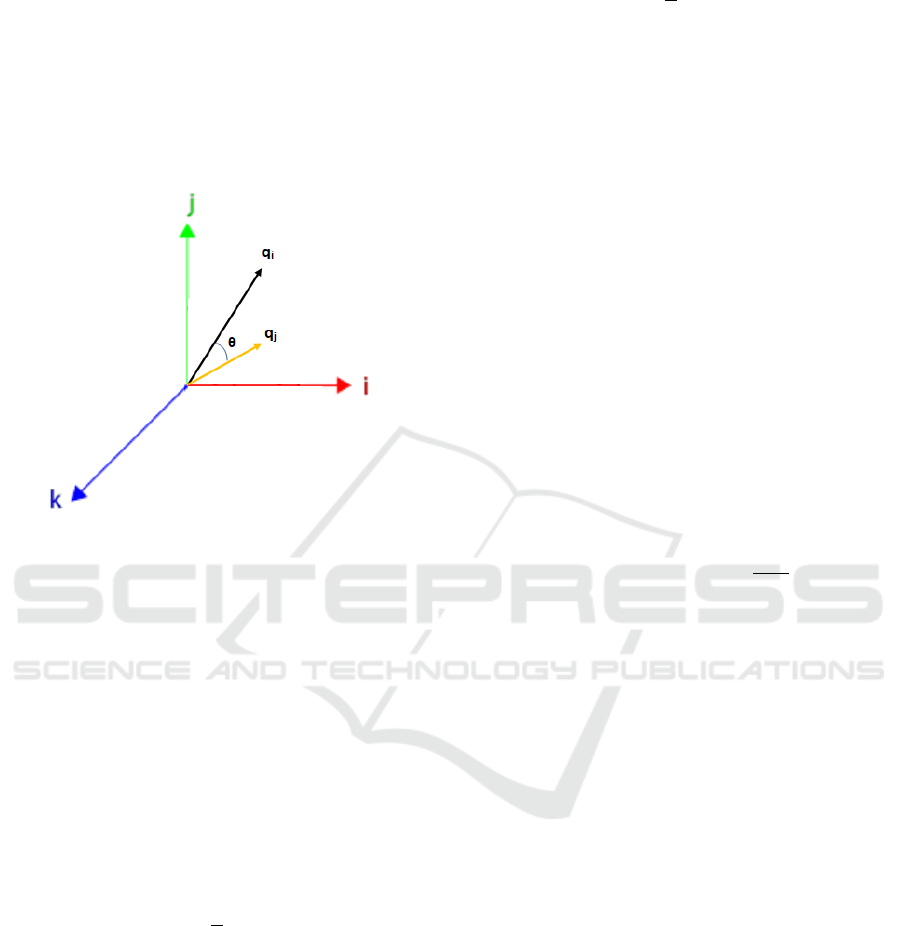
nions in color image, Figure 2 shows that the two
quaternions differ in their amplitudes as well as in the
phase θ that exists between them. Therefore, there are
two options to process the difference or the similarity
ICSOFT 2020 - 15th International Conference on Software Technologies
568

between two color pixels: the first one is the modulus
as following:
h(q
i
,q
j
) = |q
i
|−|q
j
| (11)
Furthermore the modulus, the phase between the
two quaternions can also be used to express the dif-
ference between them using the Eq. 10. In the case of
two similar quaternions, we found that the modulus
difference and the phase θ are equal to zero.
Figure 2: Illustration of the difference between two quater-
nion q
i
and q
j
.
Following, based on quaternion representation of
color image, two local pattern are used to coded our
proposed Local Rotation Pattern LRP: one for the
norms LRP
N
and the other for the angle of rotation
LRP
A
. Given a color image I represented in a quater-
nion form. Based on the local pattern scheme, let q
c
the quaternion central pixel of 3 ×3 block with P = 8
neighbors and q
i
are the surrounding pixels. The local
pattern of norms LRP
N
of the central pixel is replaced
by the mean of the various norm difference calculated
using Eq. 11.
More details of our local pattern value for LRP
N
are given in Figure 3 using the Eqs. 12 and 13.
LRP
N
(q
c
) =
1
P
P−1
∑
i=0
h(q
i
,q
c
) (12)
Hist(LRP
N
) = {prob(LRP
N
= a),∀a ∈ [0,255]}
(13)
In other hand, considering color as a unit quater-
nion, it can represent a rotation in three dimensional.
Therefore, the distance between central pixel and its
surrounding are expressed as a distance between two
rotations using the geodesic distance using Eq. 10.
Finally, the Local Pattern value of LRP
A
of the central
pixel q
c
is then coded with the average value of the
different angles rotation, as given by:
LRP
A
(q
c
) =
1
P
P−1
∑
i=0
dist
H
(q
i
,q
c
) (14)
Hist(LRP
A
) = {prob(LRP
A
= a),∀a ∈ [0,π]} (15)
Eventually, the LRP signature of texture I is de-
fined by concatenate the two histograms of two local
patterns LRP
A
and LRP
N
as:
Hist(LRP) = {Hist(LRP
A
),Hist(LRP
N
)} (16)
The process of encoding LRP is illustrated in Fig-
ure 3.
3.2 Similarity Measure between LRP
Similarity measure plays an important role to retrieve
textures. Many distance functions can be used to
measure similarities, between features. Considering
the LRP as probability density function, the mostly
used similarity measure is the Kullback-Leibler di-
vergence. The Kullback-Leibler measure of informa-
tion KL(P/Q) assess the quantity of information lost
when Q is used to estimate P (Eq. 17) (Kullback and
Leibler, 1951).
KL(P/Q) =
Z
∞
−∞
p(x)ln(
p(x)
q(x)
)dx (17)
where p and q are the respective densities of P and Q.
In order to define a similarity measure, the Kullback-
Leibler divergence is defined as the sum of the mea-
sure of information of P relative to Q and the measure
of information of Q relative to P.
D
KL
(P,Q) = KL(P/Q) + KL(Q/P) (18)
4 EXPERIMENTS AND
DISCUSSION
This section provides several experimental results to
demonstrate the effectiveness of the proposed LRP.
We evaluate the proposed color feature using a chal-
lenging problems: color image classification. In order
to assess classification performances of the suggested
LRP feature, we used the standard protocol used in
(Maliani et al., 2014). Images of each databases
are divided into two sub-sets, where 50% are used
for training phase and the other 50% for validation.
Each image of the test set is the classified through the
nearest neighbor class (1-NN) with the less Kullback-
Leibler divergence (D
KL
distance).
Local Rotation Pattern: A Local Descriptor of Color Textures
569

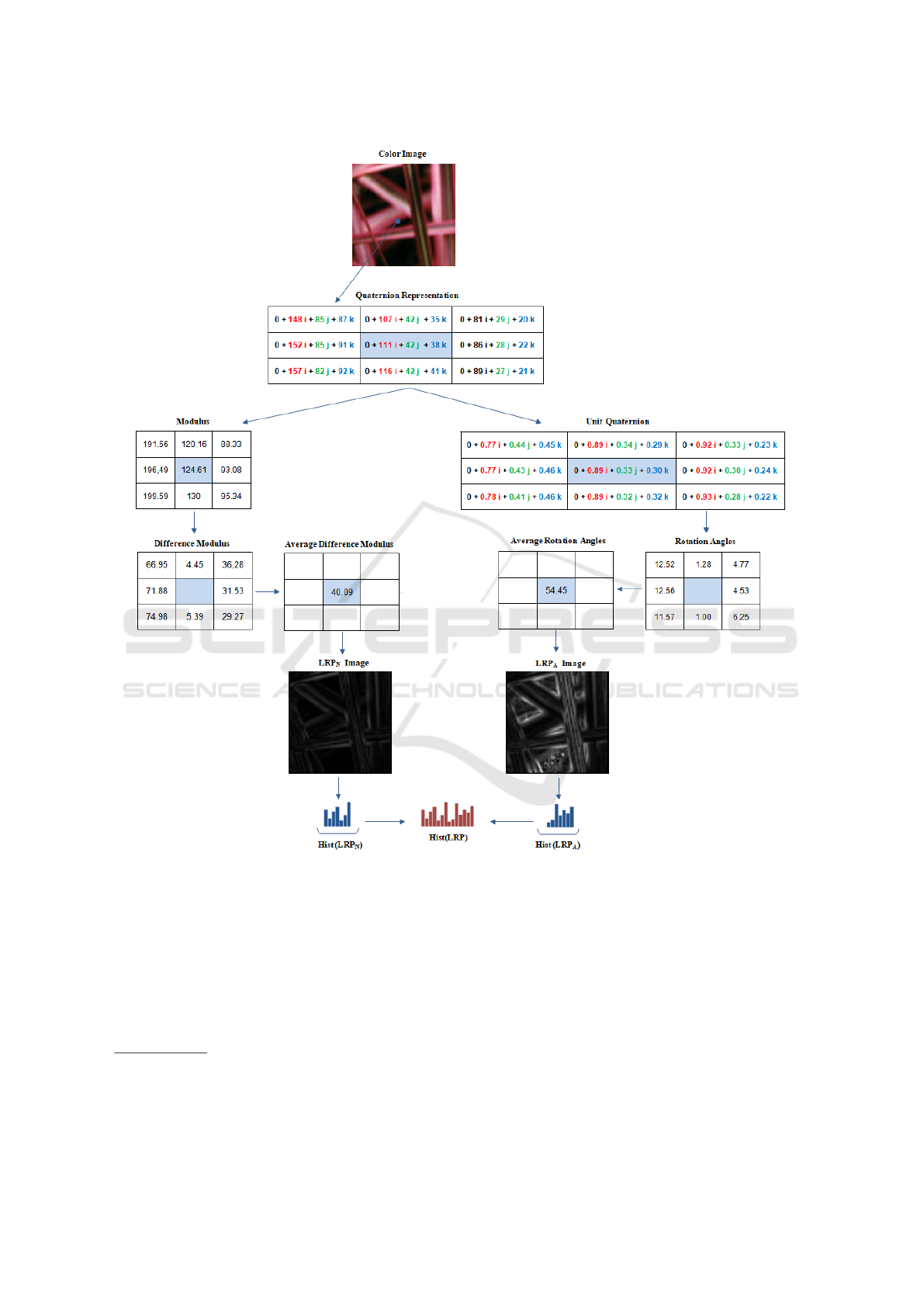
Figure 3: The basic LRP descriptor with P = 8.
4.1 Dataset and Results
For experimentation and in order to show the high ef-
ficiency of the proposed descriptor, three following
popular color texture databases from the literature are
used: Vistex
1
, Outex-TC13
2
, and USPtex
3
databases:
Vistex is one of the most used dataset for com-
parative study. It is built of 54 colour images of size
1
http://vismod.media.mit.edu/vismod/imagery/
VisionTexture
2
http://www.outex.oulu.fi
3
http://fractal.ifsc.usp.br/dataset/USPtex.php
512 ×512 pixels, these images are acquired using un-
controlled conditions. Each colour image was divided
into 16 sub-images of 128 ×128 pixels, resulting 432
images. The Figure 4 presents some classes of Vistex
dataset with their two local patterns LRP
N
and LRP
A
,
which the inter and intra-class D
KL
distance between
them are shows in Table 1.
The distance between classes varies according to
the similarity between them while the inter-class dis-
tance is equal zero. Following distances, there are re-
semblance between Fabric and the Food (251.72).
USPtex dataset (Andre et al., 2012) contains 191
ICSOFT 2020 - 15th International Conference on Software Technologies
570

Figure 4: Some color textures from Vistex dataset with their
LRP
A
and LRP
N
.
classes of natural colored textures, found on a daily
basis. The original images of size 512 ×384 are di-
vided into 12 samples of size 128 ×128, so 2292 im-
ages in total. Figure 5 shows three different color tex-
tures from this database (Brick, Leaves and Grass tex-
tures) and the Table 2 presents the similarity measure
between them.
Table 1: Inter and intra-class D
KL
distance for images of
Vistex database.
Vistex Fabric Flowers Food
Fabric 0 593.65 949.83
Flowers 593.65 0 251.72
Food 949.83 251.72 0
Table 2: Inter and intra-class D
KL
distance for color images
of Outex-TC13 database.
USPtex Brick Leaves Grass
Brick 0 3171.95 3826.54
Leaves 3171.95 0 1396.28
Grass 3826.54 1396.28 0
The Outex database contains 1360 images divided
into 68 classes with 20 samples per class of size 128×
128 pixels. Figure 6 shows some color textures of
Outex database with their two local patterns LRP
N
and
LRP
A
.
Visually, we can observe the great similarity be-
tween the two Barleyrice classes. This similarity is
validated by the estimated Kullback-Leibler Diver-
Figure 5: Some color textures from USPtex dataset with
their LRP
A
and LRP
N
.
gence D
KL
= 632.75 (see Table 4). On the other
hand the Barley 09 texture is far from the Canvas tex-
ture visually, that is expressed by the distance value
D
KL
= 3448.59.
Figure 6: Some color textures from Outex-TC13 dataset
with their LRP
A
and LRP
N
.
Local Rotation Pattern: A Local Descriptor of Color Textures
571

Table 3: Classification rates (%) achieved by the proposed LRP on Vistex, Outex-TC13 and USPtex databases in front of
results previously published. Best results reached are highlighted by bold text.
Methods Vistex Outex-TC13 USPtex
LSTM network (Byeon et al., 2014) 99.09 94.70 -
SMGD (Maliani et al., 2014) 97.50 89.70 -
Local jet+ Fourier (Oliveira et al., 2015) 97.84 87.16 89.63
C
2
O (Martinez et al., 2015) 99.30 82.64 -
CLP (Richard et al., 2016) 97.70 82.10 -
LED+ED (Minh-Tan et al., 2017) 94.70 76.67 90.50
LNDP (Manisha and Balasubramanian, 2017) - 77.16 80.66
SMO (Neiva et al., 2018) 99.54 86.47 91.49
LDTP (Khadiri et al., 2018) 75.82 80.32 84.11
Relocated C
2
O (Jebali et al., 2018) 100 92.40 -
LCCMSP (Merabet and Ruichek, 2018) - 84.87 90.01
ARCS-LBP (Merabet et al., 2019) - 85.72 88.88
Proposed LRP 99.54 94.90 93.20
Table 4: Inter and intra-class D
KL
distance for color images
of Outex-TC13 database.
Outex Canvas Barley 08 Barley 09
Canvas 0 1781.34 3448.59
Barley 08 1781.34 0 632.75
Barley 09 3448.59 632.75 0
4.2 Performance in Classification
To have a fair comparison of our obtained classifica-
tion rates in front of those previously published, we
used the same databases and the same schemes of par-
titions used for training and testing as in the recent
published methods (Maliani et al., 2014), (Richard
et al., 2016), (Jebali et al., 2018), (Neiva et al., 2018)
and (Merabet et al., 2019).
A comparative analysis of obtained classification
rates by the proposed texture descriptor and some
state-of-the-art texture descriptors summarized in Ta-
ble 3. The highest result of each dataset is high-
lighted in bold type. Firstly, for the Vistex database,
the best classification rate is achieved by two meth-
ods: the Relocated C
2
O with 100% and the second
row is achieved by the proposed LRP with 99.54%.
For USPtex dataset, the lowest results are obtained
by the integrative methods LNDP, LDTP and ARCS-
LBP (around 80.66%, 84.11% and 88.88%). The
highest result is obtained using the proposed method
achieving 93.20% of accuracy rate.
In terms of color texture characterization, Outex-
TC13 is the hardest database as results shows. More-
over, on this dataset the performance of LSTM net-
work method around 94.70%. The Local directional
ternary pattern (LDTP) and the Colour local pattern
(CLP) descriptor presents the lowest accuracies, with
80.32% and 82.10% respectively. The highest per-
formance is obtained by the proposed Local Rotation
Pattern (LRP) with 94.90%.
5 CONCLUSION
In this paper, we proposed a new vector texture fea-
ture using the quaternion rotation. Unlike the existing
texture feature, the proposed one enables the implicit
use of the color interaction between color components
in color images. The experiment results show the ef-
ficiently of our proposed texture descriptor for color
texture image classification. Our proposed method
was tested on three databases, the VisTex, Outex, and
USPtex databases, yielding correct classification rates
of 99.54%, 94.90% and 93.20% respectively. Future
works will be devoted to improving the robustness of
our proposed descriptor to color image changes (Ro-
tation, scaling change, illuminance change).
REFERENCES
Andre, B., Dalcimar, C., and Odemir, B. (2012). Color
texture analysis based on fractal descriptors. Pattern
Recognition, 45:1984–1992.
Byeon, W., Liwicki, M., and Breuel, T. (2014). Texture
classification using 2d lstm networks. IEEE, 22nd Int.
C. Pattern Recogn. (ICPR).
Guo, Y., Zhao, G., and Pietikinen, M. (2012). Discrimina-
tive features for texture description. Pattern Recogni-
tion, 45(10):3834 – 3843.
Guo, Z., Zhang, L., and Zhang, D. (2010). A completed
modeling of local binary pattern operator for texture
classification. IEEE Transactions on Image Process-
ing, 19(6):1657–1663.
Guo, Z., Zhang, L., and Zhang, D. (2010). Rotation in-
variant texture classification using lbp variance (lbpv)
ICSOFT 2020 - 15th International Conference on Software Technologies
572

with global matching. Pattern Recognition, 43(3):706
– 719.
Jebali, H., Richard, N., Chatoux, H., and Naouai, M.
(2018). Relocated colour contrast occurrence ma-
trix and adapted similarity measure for colour texture
retrieval. In Advanced Concepts for Intelligent Vi-
sion Systems, pages 609–619, Cham. Springer Inter-
national Publishing.
Jes
´
us, A. (2014). Riemannian l (p) averaging on lie group
of nonzero quaternions. Advances in Applied Clifford
Algebras, 24.
Khadiri, I. E., Chahi, A., Merabet, Y. E., Ruichek, Y., and
Touahni, R. (2018). Local directional ternary pat-
tern: A new texture descriptor for texture classifi-
cation. Computer Vision and Image Understanding,
169:14 – 27.
Kullback, S. and Leibler, R. (1951). On information and
sufficiency. Ann. Math. Statist, 22(1):79–86.
Maliani, A. D. E., Hassouni, M. E., Berthoumieu, Y.,
and Aboutajdine, D. (2014). Color texture classifi-
cation method based on a statistical multi-model and
geodesic distance. Journal of Visual Communication
and Image Representation, Elsevier.
Manisha, V. and Balasubramanian, R. (2017). Local neigh-
borhood difference pattern: A new feature descriptor
for natural and texture image retrieval. Multimedia
Tools and Applications, pages 1–25.
Martinez, R., Richard, N., and Fernandez, C. (2015). Al-
ternative to colour feature classification using colour
contrast ocurrence matrix. Proc. SPIE 9534, Twelfth
International Conference on Quality Control by Arti-
ficial Vision.
Mehta, R. and Egiazarian, K. (2016). Dominant rotated
local binary patterns (drlbp) for texture classification.
Pattern Recognition Letters, 71:16 – 22.
Merabet, Y. E. and Ruichek, Y. (2018). Local concave-and-
convex micro-structure patterns for texture classifica-
tion. Pattern Recognition, 76:303 – 322.
Merabet, Y. E., Ruichek, Y., and Idrissi, A. E. (2019).
Attractive-and-repulsive center-symmetric local bi-
nary patterns for texture classification. Engineering
Applications of Artificial Intelligence, 78:158 – 172.
Minh-Tan, P., Grgoire, M., and Lionel, B. (2017). Color
texture image retrieval based on local extrema features
and riemannian distance. Journal of Imaging, 3(4).
Neiva, M. B., Vacavant, A., and Bruno, O. M. (2018).
Improving texture extraction and classification using
smoothed morphological operators. Digital Signal
Processing, 83:24 – 34.
Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-
tiresolution gray-scale and rotation invariant texture
classification with local binary patterns. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
24(7):971–987.
Oliveira, M. W. D. S., da Silva, N. R., Manzanera, A., and
Bruno, O. M. (2015). Feature extraction on local jet
space for texture classification. Physica A: Statistical
Mechanics and its Applications, 439:160 – 170.
Penatti, O. A., Valle, E., and da S. Torres, R. (2012). Com-
parative study of global color and texture descriptors
for web image retrieval. Journal of Visual Communi-
cation and Image Representation, 23(2):359 – 380.
Richard, N., Martinez, R., and Fernandez, C. (2016).
Colour local pattern: a texture feature for colour im-
ages. Journal of the International Colour Association,
16:56–68.
Rowan, H. W. (London 1866). Elements of Quaternions.
Longmans Green.
Sangwine, S. J. (1996). Fourier transforms of colour images
using quaternion or hypercomplex, numbers. Elec-
tronics Letters, 32(21):1979–1980.
Timo, A., Abdenour, H., and Matti, P. (2004). Face recog-
nition with local binary patterns. In Pajdla, T. and
Matas, J., editors, Computer Vision - ECCV 2004,
pages 469–481, Berlin, Heidelberg. Springer Berlin
Heidelberg.
Xiaoyan, S., Shao-Hui, C., Jiang, L., and Frederic, M.
(2009). Automatic diagnosis for prostate cancer using
run-length matrix method. Medical Imaging. Procced-
ing of SPIE, 7260.
Local Rotation Pattern: A Local Descriptor of Color Textures
573