Linear Generalized ElGamal Encryption Scheme

Pascal Lafourcade

1 a

, L

eo Robert

1 b

and Demba Sow

2 c

Universit

e Clermont Auvergne, LIMOS CNRS (UMR 6158), Campus des C

ezeaux, Aubi

ere, France

LACGAA, Universit

e Cheikh Anta Diop de Dakar, Senegal

Keywords:

Cryptography, Partial Homomorphic Encryption, Linear Assumption, ElGamal Encryption Scheme.

Abstract:

ElGamal public key encryption scheme has been designed in the 80’s. It is one of the ﬁrst partial homomorphic

encryption and one of the ﬁrst IND-CPA probabilistic public key encryption scheme. A linear version has been

recently proposed by Boneh et al. In this paper, we present a linear encryption based on a generalized version

of ElGamal encryption scheme. We prove that our scheme is IND-CPA secure under linear assumption. We

design a generalized ElGamal scheme from the generalized linear. We also run an evaluation of performances

of our scheme. We show that the decryption algorithm is slightly faster than the existing versions.

1 INTRODUCTION

In 2009 in his thesis (Gentry, 2009), G. Grentry pro-

posed the ﬁrst fully homomorphic encryption scheme.

It was a revolution and it solves an open problem

already stated by Rivest Shamir and Adelman when

they invented RSA in (Rivest et al., 1978). Many ad-

vances have been done and nowadays we have some

efﬁcient implementations like for instance SEAL de-

veloped by Microsoft (SEAL, 2019). However for

some applications like the inversion of a large ma-

trix or multiplications of large matrices fully homo-

morphic encryption schemes can be very slow or pro-

duce large ciphertext or even be inexact. It is why

all partial homomorphic encryptions like RSA (Rivest

et al., 1978), GM (Goldwasser and Micali, 1982),

ElGamal (Elgamal, 1985), Benaloh (Benaloh, 1999;

Fousse et al., 2011), Okamoto-Uchiyama (Okamoto

and Uchiyama, 1998), Naccache-Stern (Naccache

and Stern, 1998), Paillier (Paillier, 1999) or Gal-

braith (Galbraith, 2002), are still widely used. They

can be used to solve such problems in reasonable

among of time like in (Ciucanu et al., 2019).

Many cryptosystems rely on the Difﬁe-Hellman

decision problem (DDH) (Boneh, 1998; Joux and

Guyen, 2006) assumption, notably the ElGamal en-

cryption scheme and the Cramer-Shoup encryption

scheme (Cramer and Shoup, 1998). In (D. Boneh and

Shacham, 2004b), Boneh et al. introduced the Deci-

https://orcid.org/0000-0002-4459-511X

https://orcid.org/0000-0002-9638-3143

https://orcid.org/0000-0002-1917-2051

sional Linear Assumption (DLA) and a variation of

ElGamal encryption scheme. Our aim is to improve

this linear version of ElGamal encryption scheme us-

ing the same approach proposed in (Sow and Sow,

2011).

Contributions. We propose the following results:

• Most of today’s public key cryptosystems are re-

sistant to various types of attacks and are effec-

tive. Their main role is the protection of commu-

nications so they guarantee the security of the data

exchanged or stored. Thus, it will always be inter-

esting to ﬁnd a new encryption scheme or to im-

prove a known one. It is in this context that we

propose a linear Generalized ElGamal encryption

scheme. The modiﬁcations are about the key gen-

eration which lead to a different encryption and

decryption algorithms. Like linear ElGamal en-

cryption, the linear Generalized ElGamal encryp-

tion scheme is IND-CPA secure under (DLA).

• We also propose the ElGamal and the Generalized

ElGamal schemes from the generalized linear.

• We implement the algorithms and compare their

performances with the original algorithms. Our

performance evaluations show that the decryption

algorithm is faster. We also demonstrate that our

key generation algorithm is slower, but this is not

a problem since this operation is usually done

only once.

372

Lafourcade, P., Robert, L. and Sow, D.

Linear Generalized ElGamal Encryption Scheme.

DOI: 10.5220/0009828703720379

In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 372-379

ISBN: 978-989-758-446-6

Related Works. In 1985, Taher ElGamal (Elgamal,

1985) proposed an encryption and signature scheme

called ElGamal scheme.

In (Hanoymak, 2013), Turgut Hanoymak proves

the security of ElGamal encryption scheme which

is based on the hardness to solve the Computa-

tional Difﬁe-Hellman (CDH) and Decisional Difﬁe-

Hellman (DDH) problems.

In (D. Boneh and Shacham, 2004b), Boneh et al.

proposed a linear encryption scheme based on the El-

Gamal encryption scheme. The linear ElGamal en-

cryption scheme is IND-CPA secure under the (DLA).

In (Sow and Sow, 2011), a modiﬁed variant of

the ElGamal scheme is presented, and it is called

Generalized ElGamal. As ElGamal’s scheme, the

Generalized ElGamal scheme is based on Decisional

Difﬁe-Hellman Problem (DDH). In the Generalized

ElGamal scheme, the decryption key size is smaller

than those of ElGamal scheme. Hence the General-

ized ElGamal scheme is more efﬁcient than ElGamal

scheme; since the decryption process is a bit faster.

The encryption mechanism has the same efﬁciency

than ElGamal encryption mechanism. But, the key

generation algorithm is slower than the key genera-

tion algorithm of ElGamal scheme. However, this is

not a problem since the key generation is done only

once.

Outline of Paper. In Section 2, we present the orig-

inal ElGamal encryption scheme and the Generalized

ElGamal encryption scheme. In Section 3, we present

the Linear assumption, the linear ElGamal encryp-

tion scheme and the ElGamal encryption scheme from

the generalized linear. In Section 4, we propose the

linear Generalized ElGamal encryption scheme and

the Generalized ElGamal encryption scheme from the

generalized linear. In Section 5, we propose a com-

plexity analysis of our scheme. In Section 6.1, we

present the curves showing the average time of the

key generation, encryption and decryption algorithms

of the ElGamal encryption scheme and the General-

ized ElGamal encryption scheme. In Section 6.2, we

also present the curves showing the average time of

the key generation, encryption and decryption algo-

rithms of the Linear ElGamal encryption scheme and

the Linear Generalized ElGamal encryption scheme.

Note that a full version with the security proofs is

available on (Extended Version, ).

2 ElGamal AND GENERALIZED

ElGamal ENCRYPTION

SCHEMES

We recall the ElGamal encryption scheme (Elga-

mal, 1985) and the Generalized ElGamal encryption

scheme (Sow and Sow, 2011).

2.1 The ElGamal Encryption Scheme

Given a computational group scheme G, the ElGamal

public-key encryption is deﬁned as follow (Elgamal,

1985):

Key Generation Algorithm. For the creation of a

public/secret key, Bob should do the following:

1. Select a ﬁnite cyclic group G of order d

with generator g.

2. Select a random integer a such that 2 < a < d.

3. Compute h = g

in G.

4. The public key is pk = (G,d, g,h) and the

secret key is sk = a.

Encryption Algorithm. To encrypt a message m

for Bob, Alice should do the following:

1. Take pk = (G, d,g,h), the Bob’s public key;

2. Select a random integer r such that

1 < r < d = #G;

3. Compute c

= g

and c

= m · h

in G;

4. The ciphertext is c = (c

Decryption Algorithm. To decrypt a ciphertext c,

Bob should do the following:

1. Take sk = a the secret key.

2. Compute m =

)

, we note that m ∈ G.

3. The plaintext is m.

Security Proof of ElGamal Encryption. We recall

some theorems, which show the security of ElGamal

encryption scheme under the CDH and DDH assump-

tions. Let GP an algorithm which takes 1

and re-

turns the public key pk = (G,d,g,h) of the ElGamal

encryption scheme.

I One-wayness under the CDH Assumption. If

the CDH assumption holds with respect to GP,

then the ElGamal encryption scheme is one-way.

Theorem 2.1. Let adversary A be a probabilis-

tic polynomial-time algorithm against the ElGa-

mal encryption scheme (Elgamal, 1985) in the

OW-CPA sense. Then there is a probabilistic

Linear Generalized ElGamal Encryption Scheme

373

polynomial-time algorithm B against GP solving

the CDH problem such that:

Adv

CDH

GP ,B

(k) = Adv

OW−CPA

Π,A

(k).

I Indistinguishability under the DDH Assump-

tion. If the DDH assumption holds with respect

to G P , then the ElGamal encryption scheme is

indistinguishable under chosen-plaintext attacks,

i.e., it is IND-CPA secure.

Theorem 2.2. Let adversary A be a probabilis-

tic polynomial-time against the ElGamal encryp-

tion scheme in the IND-CPA sense. Then there

is a probabilistic polynomial-time algorithm B

against GP solving the DDH problem such that:

Adv

DDH

GP ,B

(k) =

· Adv

IND−CPA

Π,A

(k).

I Semantic Security. In (J. Katz, 2008), Katz and

al. prove the semantic security of the ElGamal

encryption scheme.

Theorem 2.3. Under the DDH assumption, El-

Gamal encryption scheme is semantically secure.

2.2 Generalized ElGamal Encryption

Scheme

We give a key generation mechanism and a public key

encryption algorithm (Sow and Sow, 2011), which

can be view as a slight modiﬁcation of ElGamal’s

schemes (Elgamal, 1985).

Key Generation Algorithm. To create a pair of

public and private key, we do the following:

1. Select a cyclic group G with sufﬁciently large or-

der d = #G such that G = hgi.

2. Select two random integers r and k sufﬁciently

large such that 2 < k < d and r of size half the

size of d with d = #G. Compute kd.

3. Compute with euclidean division algorithm, the

pair (s,t) such that kd = rs + t where t = kd

mod s.

4. Compute γ = g

and δ = g

in G; Note that γ 6= 1

and δ 6= 1.

Then public key is ((γ,δ),G) and the private key is

(r,G).

Encryption Algorithm. To encrypt a message with

the public key ((γ,δ),d,G), we do the following:

1. Select a random integer 2 < α < d = #G such that

α and #G are co-prime.

2. Compute c

= γ

and λ = δ

in G, hence c

6= 1

and λ 6= 1.

3. Transform the message m as an element of G and

compute c

= λm in G.

The ciphertext is (c

Decryption Algorithm. To decrypt a ciphertext of

the form (c

) that is encrypted with the public

key ((γ,δ), d,G) and knowing the associate secret key

(r,G), we just need to compute c

Provable Security of the Generalized ElGamal En-

cryption Scheme.

I One-wayness under the CDH Assumption.

Theorem 2.4. Under the CDH Assumption, the

Generalized ElGamal encryption scheme is One-

Way secure under Chosen Plaintext Attack (OW-

CPA). That is, for a security parameter k, if there

is an attacker A that inverse the Generalized El-

Gamal encryption then we can build an algorithm

B that solves CDH, it means that

Adv

CDH

GP ,B

(k) = Adv

OW−CPA

Π,A

(k).

I Indistinguishability under the DDH Assump-

tion.

Theorem 2.5. Under the DDH Assumption, the

Generalized ElGamal encryption scheme is indis-

tinguishable under Chosen Plaintext Attacks, i.e.,

it is IND-CPA secure. So we have:

Adv

DDH

GP ,B

(k) =

· Adv

IND−CPA

Π,A

(k),

where A is an attacker of the Generalized ElGa-

mal encryption and k the security parameter.

To justify the performance of Generalized ElGa-

mal encryption scheme described in (Sow and Sow,

2011) with respect to ElGamal encryption scheme,

comparison curves in execution time of the key gen-

eration, encryption and decryption algorithms are per-

formed (see Figure 1, Figure 2 and Figure 3).

3 LINEAR ENCRYPTION

Boneh et al. (D. Boneh and Shacham, 2004b) in-

troduced a decisional assumption, called Linear, in-

tended to take the place of DDH in groups - in partic-

ular, bilinear groups (Joux and Nguyen, 2003) - where

DDH is easy. For this setting, the Linear problem has

desirable properties, as they have shown: it is hard if

DDH is hard, but, at least in generic groups (Shoup,

1997), it remains hard even if DDH is easy. Letting G

be a cyclic multiplicative group of prime order p, and

SECRYPT 2020 - 17th International Conference on Security and Cryptography

374

letting g

, and g

be arbitrary generators of G, we

consider the following problem:

Linear Problem in G: Given g

, g

∈ G

as input, output yes if a+b = c and no otherwise. The

advantage of an algorithm A in deciding the Linear

problem in G is denoted by Adv

linear

and it is equal

to:

|Pr[A(g

a+b

) = yes :

← G,a, b

← Z

]

−Pr[A(g

,η) = yes :

,η

← G,a, b

← Z

with the probability taken over the uniform random

choice of the parameters to A and over the coin tosses

of A. We say that an algorithm A(t, ε)-decides Linear

in G if A runs in time at most t, and Adv

linear

is at

least ε.

Deﬁnition 3.1. We say that the (t,ε)-Decision Linear

Assumption holds in G if no algorithm (t, ε)-decides

the Decision Linear problem in G.

The Linear problem is well deﬁned in any group

where DDH is well deﬁned. It is mainly used in

bilinear groups like in (Boneh and Franklin, 2003;

D. Boneh and Shacham, 2004a; Paterson, 2005).

3.1 Linear ElGamal Encryption Scheme

Boneh et al proposed a linear encryption scheme

based on the ElGamal encryption scheme. Given a

computational group scheme G, the Linear ElGamal

encryption scheme is deﬁned as follows:

LE.Gg(1

): Choose a random generator g

← G and

← Z

, and set g

← g

−1

and g

← g

−1

. The

public key is pk = (g

) ∈ G

; the secret key

is sk = (x

) ∈ Z

LE.Enc(pk, M): To encrypt a message M ∈ G, parse

pk = (g

) ∈ G

, choose random exponents

← Z

, and set: u

← g

and u

← g

and

← Mg

. The ciphertext ct = (u

) ∈

LE.Dec(sk, ct): Parse the private key sk as (x

) ∈

and the ciphertext ct as (u

) ∈ G

and

compute M ← u

−x

Correctness of Decryption Process. Since u

and u

= g

, u

= Mg

we have:

/(u

) = Mg

/((g

)

= (Mg

)/(g

) = M

Theorem 3.2. Under the Linear Assumption, ElGa-

mal Encryption Scheme is IND-CPA secure (D. Boneh

and Shacham, 2004b).

3.2 ElGamal from Generalized Linear

We deﬁne three functions: the setup function, denoted

LE.Gg(), the encryption function, denoted LE.Enc()

and the decryption function, denoted LE.Dec().

We now describe how these functions works.

LE.Gg(1

) : Choose a random generator g

← G

and x

,..., x

n−1

← Z

, and set: g

← g

1/x

← g

1/x

, . .., g

n−1

← g

1/x

n−1

. The public key

is pk = (g

,..., g

) ∈ G

; the secret key is

sk = (x

,..., x

n−1

) ∈ Z

n−1

LE.Enc(pk, M): To encrypt a message M ∈ G, parse

pk = (g

,..., g

) ∈ G

, choose random ex-

ponents r

,..., r

n−1

← Z

, and set: u

←

, u

← g

,...u

← Mg

+...+r

n−1

. the ci-

phertext ct = (u

,..., u

) ∈ G

LE.Dec(sk, ct): Parse the private key sk as (x

...,x

n−1

) ∈ Z

n−1

and the ciphertext ct as (u

...,u

) ∈ G

and compute :

M ← u

/(u

...u

n−1

)

4 LINEAR GENERALIZED

ElGamal ENCRYPTION

SCHEME

We present the Linear Generalized ElGamal encryp-

tion scheme, its security and the Generalized ElGamal

encryption scheme from the generalized linear.

4.1 Algorithms

Given a computational group scheme G, the Lin-

ear Generalized ElGamal encryption scheme is com-

posed of the following three functions: the setup func-

tion, denoted LGE.Gg(), the encryption function, de-

noted LGE.Enc() and the decryption function, de-

noted LGE.Dec().

We now describe how these functions works.

LGE.Gg(1

): Choose a random generator g

← G

and k

← Z

, r

← Z

d/2

Compute (s,t) ∈ Z

such that s ← b

c and t ←

kd mod r and set g

← g

, g

← g

, and g

← g

The public key is pk = (g

) ∈ G

and the

secret key is sk = (r, s,t) ∈ Z

d/2

× Z

Linear Generalized ElGamal Encryption Scheme

375

LGE.Enc(pk, M): To encrypt a message M ∈ G,

parse pk = (g

) ∈ G

, choose random ex-

ponents α

,α

← Z

, and set

← g

and c

← g

and c

← Mg

+α

;

the ciphertext ct = (c

) ∈ G

LGE.Dec(sk, ct): Parse the private key sk as (r, s,t) ∈

d/2

×Z

and the ciphertext ct as (c

) ∈ G

and compute M ← c

Before proving the security of our scheme in The-

orem 4.1, we give its correctness.

Correctness of Decryption Process. Since c

, c

= g

and c

= Mg

+α

, we have:

= g

+α

= Mg

(α

+α

= Mg

(rs+t)(α

+α

)

= Mg

kd(α

+α

)

= M

Theorem 4.1. The Linear Generalized ElGamal En-

cryption Scheme is IND-CPA secure under the Deci-

sional Linear Assumption (DLA).

4.2 Generalized ElGamal from

Generalized Linear

Given a computational group scheme G, the Gener-

alized ElGamal encryption scheme from the general-

ized linear is deﬁned as follows:

LGE.Gg(1

): Choose a random generator g

← G

and k, r

← Z

× Z

d/2

, compute (s

) ∈ Z

such

that s

← b

c and t

← kd mod r

, 1 ≤ i ≤

and

set for 0 ≤ k ≤

− 1: g

3k+1

← g

k+1

, g

3k+2

←

k+1

and g

3k+3

← g

k+1

. The public key is pk =

,..., g

n−2

n−1

) ∈ G

and the secret

key is sk = (r

) ∈ Z

d/2

× Z

,1 ≤ i ≤

LGE.Enc(pk, M): . To encrypt a message M ∈

G, parse pk = (g

,..., g

n−2

n−1

) ∈ G

choose random exponents α

,α

,..., α

n−1

← Z

and set 0 ≤ k ≤

− 1 : c

3k+1

← g

3k+1

, c

3k+2

←

3k+2

, c

3k+3

← Mg

3k+1

+α

3k+2

3k+3

. The ciphertext ct

is (c

3k+1

3k+2

3k+3

) ∈ G

LGE.Dec(sk, ct): Parse the private key sk as (r

)

∈ Z

d/2

× Z

, 1 ≤ i ≤ n/3 and the ciphertext ct as

,..., c

) ∈ G

and compute

M ←

∏

k=1

k+1

3k+1

k+1

3k+2

3k+3

Table 1: Comparison of Linear ElGamal and Linear Gen-

eralized ElGamal for each algorithm in terms of computa-

tional cost.

Linear ElGamal Linear General-

ized ElGamal

Size Key secret key ∈ Z

q = o(G)

secret key ∈ Z

d = o(G)

Key Gen P = 2, M = 0,

nP = 3, nS = 2

P = 3, M = 1,

nP = 3, nS = 3

Encryption P = 3, M = 1 P = 3, M = 1

Decryption P = 2, M = 2,

I = 2

P = 2, M = 2,

I = 0

5 COMPLEXITY EVALUATION

We present a complexity comparison between the

Linear ElGamal and the Linear Generalized ElGamal

schemes. We give in this section a theoretical com-

plexity where we study the number of computations

needed in each algorithm (key generation, encryption

and decryption). Let us set the following parameters:

• P = power’s number (exponent),

• M = multiplication’s number,

• S = sum’s number,

• I = inverse’s number,

• nP = number of parameters of the public key,

• nS = number of parameters of the private key.

To present the performance of the two encryp-

tion schemes, we study the number of operations per-

formed (according to the parameters described) in the

key generation, encryption and decryption processes.

From the comparative Table 1, we can clearly see

that Linear Generalized ElGamal encryption scheme

is slower at generating keys but is faster for decryp-

tion the exponent used in the decryption algorithm has

a size half of the order of the group. Moreover, we see

that there is no inverse computed (even though this

difference brings only a slight improvement).

6 PERFORMANCE

EVALUATIONS

All our algorithms have been programmed with Sage-

Math (The Sage Developers, 2020). The tests are per-

formed with security parameters of size 32, 64, 128,

512, 1024 bits. Some even go up to 2048 bits. We

start by comparing ElGamal and Generalized ElGa-

SECRYPT 2020 - 17th International Conference on Security and Cryptography

376

0.2

0.4

0.6

0.8

1.2

·10

−3

Size of security parameter

Time in seconds

Key Generation algorithm, 1000 trials

ElGamal

Generalized ElGamal

Figure 1: Average time of key generation algorithm depend-

ing on the size of security parameter.

mal

before comparing Linear ElGamal and Linear

Generalized ElGamal.

6.1 ElGamal and Generalized ElGamal

We present the curves showing the execution time

of the key generation, encryption and decryption al-

gorithms of the ElGamal encryption scheme and the

Generalized ElGamal encryption scheme.

The execution time of those two schemes is car-

ried out under the same conditions in terms of gen-

eration of the values and sizes of the security param-

eters. Indeed, given a size of a security parameter,

there are 1000 trials where new parameters (such as

prime number and messages) are computed for each

trial.

We give a detailed execution time for the key gen-

eration in Figure 1 and 4, the encryption algorithm in

Figure 2 and 5 and the decryption algorithm in Fig-

ure 3 and 6.

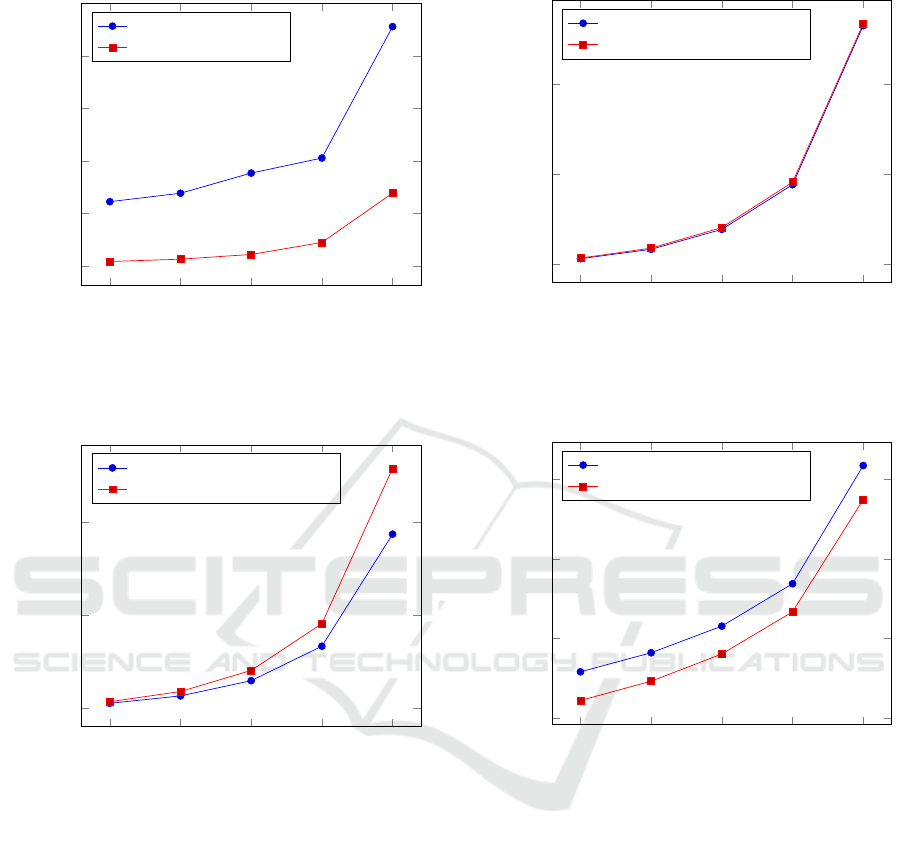
Key Generation Algorithms. The curves of Fig-

ure 1 show the execution time of key generation al-

gorithms for the ElGamal encryption scheme and for

Generalized ElGamal encryption scheme. We show

that the two algorithms are similar. When the key size

increases then the Generalized ElGamal is a bit faster.

Encryption Algorithms. The curves of Figure 2

show the execution time of encryption algorithms of

the ElGamal encryption scheme and Generalized El-

Gamal encryption scheme. We observe that the Gen-

Surprisingly this performance evaluation has not been

done in (Sow and Sow, 2011).

0.5

·10

−3

Size parameter

Time in seconds

Encryption algorithm, 1000 trials

ElGamal

Generalized ElGamal

Figure 2: Average time of encryption algorithm depending

on the size of security parameter.

eralized ElGamal encryption is always faster that El-

Gamal encryption. Indeed, we observe empirically

that computations of γ

and computations of δ

for

Generalized ElGamal have the same execution time

than the term h

for the standard ElGamal. Yet, the

computations of the term g

is slower than the three

others. Thus, the overall execution time of encryption

algorithm for the Generalized scheme is less than the

one for the standard ElGamal.

Decryption Algorithms. The curves given in Fig-

ure 3 show the execution time of decryption algo-

rithms of the ElGamal encryption scheme and Gen-

eralized ElGamal encryption scheme. We can see that

the Generalized ElGamal decryption is always signif-

icantly faster that ElGamal decryption.

6.2 Linear ElGamal and Linear

Generalized ElGamal

We studied the performance of Linear Generalized El-

Gamal encryption scheme with respect to Linear El-

Gamal encryption scheme. We present the execution

time evaluations of the key generation in Figure 4, en-

cryption in Figure 5 and decryption in Figure 6.

Key Generation Algorithms. The curves given in

Figure 4 show the execution time of key generation

algorithms of the Linear ElGamal encryption scheme

and Linear Generalized ElGamal encryption scheme.

We can see that our algorithm for key generation is

clearly slower than the one proposed by Boneh et al. It

is the price to pay in order to have a faster encryption

and decryption algorithms. It is not an issue because

Linear Generalized ElGamal Encryption Scheme

377

0.2

0.4

0.6

0.8

·10

−3

Size parameter

Time in seconds

Decryption algorithm, 1000 trials

ElGamal

Generalized ElGamal

Figure 3: Average time of decryption algorithm depending

on the size of security parameter.

·10

−3

Size of security parameter

Time in seconds

Key Generation algorithm 100 trials

Linear ElGamal

Linear Generalized ElGamal

Figure 4: Average time of key generation algorithm depend-

ing on the size of security parameter.

the key generation is in general done only once while

the encryption and decryption algorithms are more of-

ten used.

Encryption Algorithms. The curves of Figure 5

give the execution time of encryption algorithms of

the Linear ElGamal encryption scheme and Linear

Generalized ElGamal encryption scheme. Accord-

ing to the complexity analysis the timings are similar

since the number of exponentiations are similar. Em-

pirically, we observe that they are similar.

Decryption Algorithms. The curves of Figure 6

represent the execution time of decryption algorithms

of the Linear ElGamal encryption scheme and Linear

·10

−3

Size of security parameter

Time in seconds

Encryption algorithm with 100 trials

Linear ElGamal

Linear Generalized ElGamal

Figure 5: Average time of encryption algorithm depending

on the size of security parameter.

·10

−3

Size of security parameter

Time in seconds

Decryption algorithm, 100 trials

Linear ElGamal

Linear Generalized ElGamal

Figure 6: Average time of decryption algorithm depending

on the size of security parameter.

Generalized ElGamal encryption scheme. We clearly

see that the decryption is faster using our scheme,

which conﬁrms the complexity analysis of the previ-

ous section.

7 CONCLUSION

We have proposed a faster Linear Generalized ElGa-

mal encryption scheme based on the Generalized El-

Gamal encryption scheme. We prove that our linear

scheme is IND-CPA secure under the Linear problem

like the linear encryption scheme based on the ElGa-

mal encryption scheme. It also has a faster encryption

and decryption algorithms.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

378

In the future, we would like to see how our ap-

proach can be applied to improved other schemes.

ACKNOWLEDGEMENT

This study was partially supported by the French

ANR project ANR-18-CE39-0019 (MobiS5).

REFERENCES

Benaloh, J. (1999). Dense probabilistic encryption.

Boneh, D. (1998). The decision difﬁe-hellman problem.

In In Proceedings of the Third Algorithmic Number

Theory Symposium, volume 1423, pages 48–63.

Boneh, D. and Franklin, M. (2003). Identity-based en-

cryption from the weil pairing. SIAM J. Computing,

32(3):586–615.

Ciucanu, R., Giraud, M., Lafourcade, P., and Ye, L. (2019).

Secure strassen-winograd matrix multiplication with

mapreduce. In Obaidat, M. S. and Samarati, P.,

editors, Proceedings of the 16th International Joint

Conference on e-Business and Telecommunications,

ICETE 2019 - Volume 2: SECRYPT, 2019, pages 220–

227. SciTePress.

Cramer, R. and Shoup, V. (1998). A practical public key

cryptosystem provably secure against adaptive chosen

ciphertext attack. In Proc. of the 18th Annual Interna-

tional Cryptology Conference on Advances in Cryp-

tology, CRYPTO’98.

D. Boneh, B. L. and Shacham, H. (Sept. 2004a). Short

signatures from the weil pairing. J. Cryptology,

17(4):297–319.

D. Boneh, X. B. and Shacham, H. (Aug. 2004b).

Short group signatures. In In M. Franklin, edi-

tor,Proceedings of Crypto 2004, volume 3152, pages

41–55.

Elgamal, T. (1985). A public key cryptosystem and a sig-

nature scheme based on discrete logarithms. IEEE

Transactions on Information Theory, 31(4):469–472.

Extended Version. https://sancy.iut-clermont.uca.fr/

∼

lafourcade/PAPERS/PDF/Secrypt-long2020.pdf.

Fousse, L., Lafourcade, P., and Alnuaimi, M. (2011). Be-

naloh’s Dense Probabilistic Encryption Revisited. In

Progress in Cryptology - AFRICACRYPT 2011 - 4th

Conference on the Theory and Application of Crypto-

graphic Techniques in Africa, volume 6737 of Lecture

Notes in Computer Science, pages 348–362. Springer.

Galbraith, S. D. (2002). Elliptic curve paillier schemes. J.

Cryptol., 15(2):129–138.

Gentry, C. (2009). A Fully Homomorphic Encryption

Scheme. PhD thesis, Stanford, CA, USA.

Goldwasser, S. and Micali, S. (1982). Probabilistic encryp-

tion and how to play mental poker keeping secret all

partial information. In Proceedings of the Fourteenth

Annual ACM Symposium on Theory of Computing,

STOC ’82.

Hanoymak, T. (2013). On provable security of crypto-

graphic schemes. International Journal of Informa-

tion Security Science, 2, No.2.

J. Katz, Y. L. (2008). Introduction to modern cryptography.

CRC PRESS.

Joux, A. and Guyen, K. (2006). Separating decision diffe-

hellman to diffe hellmann in cryptographie groups.

Joux, A. and Nguyen, K. (Sept. 2003). Separating deci-

sion difﬁe-hellman from computational difﬁe-hellman

in cryptographic groups. J. Cryptology, 16(4):239–47.

Naccache, D. and Stern, J. (1998). A new public key cryp-

tosystem based on higher residues. In Proceedings of

the 5th ACM Conference on Computer and Commu-

nications Security, CCS ’98, page 59–66, New York,

NY, USA. Association for Computing Machinery.

Okamoto, T. and Uchiyama, S. (1998). A new public-key

cryptosystem as secure as factoring. In Nyberg, K.,

editor, Advances in Cryptology — EUROCRYPT’98,

pages 308–318, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Paillier, P. (1999). Public-key cryptosystems based on com-

posite degree residuosity classes. In Stern, J., editor,

Advances in Cryptology — EUROCRYPT ’99, pages

223–238, Berlin, Heidelberg. Springer Berlin Heidel-

berg.

Paterson, K. (2005). Cryptography from pairings. Cam-

bridge University Press, 317 of London Mathematical

Society Lecture Notes:215–51.

Rivest, R. L., Shamir, A., and Adleman, L. (1978). A

method for obtaining digital signatures and public-key

cryptosystems. Commun. ACM, 21(2):120–126.

SEAL (2019). Microsoft SEAL (release 3.4). https:

//github.com/Microsoft/SEAL. Microsoft Research,

Redmond, WA.

Shoup, V. (May 1997). Lower bounds for discrete log-

arithms and related problems. In In W. Fumy, edi-

tor, Proceedings of Eurocrypt 1997, volume 1233 of

LNCS, pages 256–66.

Sow, D. and Sow, D. (2011). A new variant of el gamal’s en-

cryption and signatures schemes. Journal of Algebra,

Number Theory and Applications, 20(1):21–39.

The Sage Developers (2020). SageMath, the Sage

Mathematics Software System (Version 9.0).

https://www.sagemath.org.

Linear Generalized ElGamal Encryption Scheme

379