Modeling and Simulation of Long Boom Manipulator based on
Geometrically Exact Beam Theory
Lingchong Gao
1
, Yingpeng Zhuo
2
, Michael Kleeberger
1
, Haijun Peng
2
and Johannes Fottner
1
1
Chair of Materials Handling, Material Flow, Logistics, Technical University of Munich, Garching, Germany
2
Department of Engineering Machenics, Dalian University of Technology, Dalian, P.R. China
Keywords:
Long Boom Manipulator, Geometrically Exact Beam, Multi-body Dynamic, Nonlinear System.
Abstract:
The boom system of the aerial platform vehicle and the fire-rescue turntable ladder can be considered as
a long boom manipulator. Due to the slenderness of the boom structure, there are always some vibrations
occurring during the operation. In order to control the vibration, reliable dynamic modeling and simulation
are necessary. In this paper, we propose a model of the long boom manipulator, especially the folding boom
system, as a flexible-rigid coupled multi-body system. And the flexible long boom structure is formulated
as a geometrically exact Euler-Bernoulli beam with hybrid interpolation for discretization. The governing
equations of the system dynamics are established according to the principle of virtual power. A dynamic
simulation of the spatial motion of the long boom manipulator is performed and the results are analyzed.
1 INTRODUCTION
Aerial platform vehicle and fire rescue turntable lad-
der are usually equipped with long boom systems to
help personal to reach a high position. In order to
make the boom as long as possible without compro-
mising the mobility of the carriage vehicle, the boom
is designed as a telescopic boom or folded boom. The
boom system can be fully unfolded for operation in
the meanwhile be folded for transitions on the road
network. The boom system is normally equipped with
a hydraulic system to provide power for actions and
can be considered as a hydraulic manipulator with a
long boom structure. The long boom manipulator is
designed with a long and slender boom structure so
that the weight can be controlled to fit the limit of
bearing capacity of the vehicle axle. However it leads
to another problem, the vibration occurs during the
operation due to the flexibility of the boom structure.
Such vibration can be stimulated by the change of the
motion status, such as sudden acceleration or declara-
tion, or the change of the external forces. Therefore
the topics of dynamic simulation and vibration control
of this kind of long boom manipulator have attracted
some researchers to investigate.
In the work of Zuyev (Zuyev, 2005), the boom
structure of the fire-rescue turntable ladder was mod-
eled as a flexible multi-body system with the passive
joint for the stabilization of the boom system, and
the hydraulic component was included in the math-
ematical model of the system (Sawodny et al., 2002).
Pertsch applied the assumption of the Euler-Bernoulli
beam theory on the description of the dynamic behav-
ior of the fire-rescue turntable ladder as a distributed
parameter model (Pertsch et al., 2009). The model
has been further developed for the coupled bending-
torsional vibration that occurs in the slewing motion,
and the corresponding active control for the vibration
damping was also developed and tested in real opera-
tion (Pertsch and Sawodny, 2016). Nguyen developed
a multi-body dynamic model with a chain of rigid
bodies connected to each other end by end with ro-
tational spring and dampers to reflect the flexibility of
the ladder. He also included a model of rope in the
system to investigate the effect of the pre-tensioned
rope to the vibration of the ladder structure during the
luffing operation (Nguyen et al., 2019). In our recent
work (Gao et al., 2019), we investigated the dynamic
response of the long boom manipulator with the con-
sideration of the hydraulic drive system. The math-
ematical models of the hydraulic system and boom
structure, which was modeled as a planar Timoshenko
beam, were established as port-Hamiltonian formu-
lation and a co-simulation of this structure-hydraulic
system is performed in the environment of Simulink.
An accurate dynamic model of the long boom ma-
nipulator is the prerequisite for the control design
to suspension the vibration. Based on our previous
Gao, L., Zhuo, Y., Kleeberger, M., Peng, H. and Fottner, J.
Modeling and Simulation of Long Boom Manipulator based on Geometrically Exact Beam Theory.
DOI: 10.5220/0009830402090216
In Proceedings of the 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2020), pages 209-216
ISBN: 978-989-758-444-2
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
209

work, we would like to investigate the spatial dynamic
performance of the long boom manipulator. Then we
need a suitable description for the dynamical behavior
of the flexible boom in space. The deformation of the
boom is considerably small compared with the length
of the boom and the rotation and the displacement of
the rigid body are rather large. This flexible-rigid cou-
pled problem of geometrical non-linearity involving
small flexible deformation draws our attention to the
achievement of the development of geometrically ex-
act beam element formulation.
The geometrically exact beam theory was pro-
posed and developed by Reissner (Reissner, 1973)
(Reissner, 1972) and Som (Simo, 1985) (Simo and
Vu-Quoc, 1986) (Simo, 1988) model the geometri-
cally nonlinear beams. The formulation of a geomet-
rically exact beam can be described by the position
vector of the beam centerline with a rotation matrix of
the rotation of a cross-section. The curvature vector
is used to describe the rotational strain (bending and
torsion) of the beam. The shear-locking problem for
slender beam due to the independent interpolations
of displacement and rotation can be avoided by the
modification of the formulation of the geometrically
exact beam element. Shabana (Shabana and Yakoub,
2001) and Yakouba (Yakoub and Shabana, 2001) de-
veloped a formulation called absolute nodal coordi-
nate for the beam element by selection 12 degrees of
freedom for each node including position vectors and
nine slopes. The shape function they designed can
represent arbitrary large rigid body motions exactly.
Zupan proposed a beam element formulation based on
the interpolation of the curvatures, a strain measure-
interpolation based element (Zupan and Saje, 2003).
Zhang (Zhang et al., 2015) presented a coupled inter-
polation of the centerline position vector and the ori-
entation vector of the cross-section to avoid the ”shear
lock” problem. Fang (Fang and Qi, 2016) a hybrid in-
terpolation method, using Hermitian interpolation of
the centerline to calculate the curvatures of the two
end nodes and a second interpolation for the internal
curvatures.
In this paper, the long boom manipulator with a
folding boom system is investigated. The boom struc-
ture is modeled as a flexible spatial beam, meanwhile,
the hydraulic cylinder and the luffing links are treated
as rigid bodies. The governing equations of the entire
manipulator are formulated according to the multi-
body formulation with constrains. The flexible body
is considered as geometrically exact Euler-Bernoulli
beam, and a hybrid interpolation is proposed. Each
beam is meshed by nodes that have the given global
position vectors. And the derivatives of the curvatures
of the beam centerline at these inner nodes are deter-
mined by the values of the two end nodes according
to the cubic spline interpolation. The virtual power of
each element can be formulated by the Gauss integra-
tion using the selected Gauss points. The parameters
at these Gauss points between the two adjacent nodes
can be described as the polynomials of the node pa-
rameters. Then the governing equations of the manip-
ulator can be derived from the sum virtual power of
the flexible beams and the rigid bodies.
2 MULTI-BODY DYNAMIC OF
LONG BOOM MANIPULATOR
As shown in Fig. (1), the folding boom manipulator
consists of two boom structure with the correspond-
ing luffing mechanism. The luffing mechanism for the
first boom (attached on the turntable) is a single hy-
draulic cylinder and the one for the second boom a hy-
draulic cylinder combining with two rigid links. The
luffing operation means to change the angle between
the boom and the horizontal level. The slew operation
is the rotation motion of the turntable around the rota-
tion axis. For simplicity, the original boom structure
is modeled as a homogeneous flexible beam, and the
hydraulic cylinders and the links are modeled as rigid
bodies.
旵⋶䅨Ṓ
Ř
Ś
ś
š
ŝ
Ŝ
ř
濄濄
Ľ
Ŀ
ş
݊
ଵ
݊
ଶ
݊
ଷ
Figure 1: A folding boom system.
2.1 Multi-body Dynamics Formulation
with Constraints
As marked in Fig. (1), body 2,5,7 and 10 are consid-
ered as flexible bodies, and body 1,3,4,6,8,9 and 11
are considered as rigid bodies. The body-fixed frames
for the bars are defined as: 1) the origin is set at one
end of the bar with rotational joint; 2) the first frame
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
210

vector is set along the bar at inertial time; 3) the third
frame vector is set vertical to the luffing plane.
The origin of the body-fixed frame can be defined
as
r
r
r
j,0
= r
r
r
k,0
+ x
j
n
n
n
1
k
+ y
j
n
n
n
2
k
(1)
where (x
j
,y
j
) is the origin coordinate of frame j in
frame k.
For each rigid body, its moment of inertia relative
to its own frame is J
j,c
, and its mass center can be
expressed as
r
r
r
j,c
= r
r
r
j,0
+ u
j
n
n
n
1
j
+ v
j
n
n
n
2
j
(2)
where (u
j
,v
j
) is the coordinate of the mass center in
frame j.
The virtual power equation of each body can be
expressed as
δp
j
= δ

˙
r
r
r
j,0
ω
ω
ω
j

T

M
M
M
j

¨
r
r
r
j,0
˙
ω
ω
ω
j

+ F
F
F
j

(3)
The relationship between virtual velocity and gen-
eralized virtual velocity is
δ

˙
r
r
r
j,0
ω
ω
ω
j

T
= T
T
T
j
δ
˙
q
q
q,

¨
r
r
r
j,0
˙
ω
ω
ω
j

= T
T
T
j
¨
q
q
q + α
α
α
j
(4)
where T
T
T
j
is the transfer matrix and α
α
α
j
=
˙
T
T
T
j
˙
q
q
q.
Then the virtual power equation of all the bodies
in the generalized coordinate can be expressed as
δp = δ
˙
q
q
q
T
(M
M
M
¨
q
q
q + F
F
F) (5)
where M
M
M =
∑
T
T
T
T
j
M
M
M
j
T
T
T
j
,F
F
F =
∑
T
T
T
T
j
F
F
F
j
T
T
T
j
The virtual equation of hydraulic cylinder can be
simplified as
δp
f
= δ ˙s(ks +c ˙s) (6)
where k is the equivalent stiffness, c is the equivalent
dumping coefficient and s is the distant between the
two joints on the cylinder.
The bodies of the system are connected by rota-
tional or transnational joints. These kinematic con-
straints can be described as
Φ
Φ
Φ(q
q
q,t) = 0
0
0,
˙
Φ
Φ
Φ = Φ
Φ
Φ
q
˙
q
q
q+υ
υ
υ = 0,
¨
Φ
Φ
Φ = Φ
Φ
Φ
q
¨
q
q
q+γ
γ
γ = 0 (7)
where υ
υ
υ = ∂Φ
Φ
Φ/∂t, γ
γ
γ =
˙
Φ
Φ
Φ
q
˙
q
q
q +
˙
υ
υ
υ and Φ
Φ
Φ
q
is the Jaco-
bian matrix of the constraints.
By using the stabilization of constraints proposed
by Baumgerte(Baumgarte, 1972), the constraint equa-
tion of the acceleration can be rewritten as
Φ
Φ
Φ
q
¨
q
q
q +
˙
Φ
Φ
Φ
q
˙q +
˙
Φ
Φ
Φ
t
+ 2ξ
1
˙
Φ
Φ
Φ + ξ
2
Φ
Φ
Φ = 0 (8)
where ξ
1
and ξ
2
are the stabilization coefficients.
2.2 Geometrically Exact
Euler-Bernoulli Beam
2.2.1 The Geometric Configuration of a Spatial
Beam
The main assumption of a 3D Euler-Bernoulli beam
theory is that arbitrary cross sections of the beam al-
ways maintain rigid and perpendicular to the tangent
vector of the central line of the beam. The position
vector r
r
r(s) of the beam central line is defined with
the arc-length coordinate of the beam central line s.
ࢋ
ଵ
ࢋ
ଶ
ࢋ
ଷ
࢔
ଵ
࢔
ଶ
࢔
ଷ
࢘ ݏ,t
ࢍ
ଵ
ࢋ
ଶ
ࢋ
ଵ
ࢋ
ଷ
ࢍ
ଶ
ࢍ
ଷ
݋
Figure 2: Geometic configuration of a Euler-Bernulli beam.
The basis frame of the cross section is define as
[e
e
e
1
,e
e
e
2
,e
e
e
3
], in which e
e
e
1
is parallel to the tangent vector
of the beam central line r
r
r
0
.
e
e
e
1
= r
r
r
0
/


r
r
r
0


(9)
And the other two orientaiton vectors are atteched
on the cross section and denoted by the right-handed
orthogonal rule.
e
e
e
T
2
r
r
r
0
= e
e
e
T
3
r
r
r
0
= 0 (10)
The normal vector of the cross section can be ex-
pressed as (s
i
= sinϕ
i
,c
i
= cosϕ
i
)
e
e
e
1
= c
2
c
3
n
n
n
1
+ s
3
n
n
n
2
− s
2
c
3
n
n
n
3
(11)
and the Euler angles can be calculated as
ϕ
2
= acrtan(−n
n
n
T
3
e
e
e
1
/n
n
n
T
1
e
e
e
1
)
ϕ
3
= acrsin(n
n
n
T
2
e
e
e
1
)
(12)
The rotation matrix of the coordinate system of
the cross section with respect ot the basis frame of the
beam can described by Euler angles as
e
e
e
i
= R
R
Rn
n
n
i
=

e
e
e
1
e
e
e
2
e
e
e
3

n
n
n
i
(13)
Modeling and Simulation of Long Boom Manipulator based on Geometrically Exact Beam Theory
211

2.2.2 The Formulation of Angle Velocity of the
Cross-section
The time derivative of the base vectors of the refer-
ence frame on the cross section can be obtained by
the cross product of its angle velocity and the base
vectors
˙
e
i
=
e
ω
ω
ωe
i
= ω
ω
ω × e
i
(14)
The angle velocity vector of the cross section can
be expressed as
ω
ω
ω = ω
e1
e
e
e
1
+ ω
e2
e
e
e
2
+ ω
e3
e
e
e
3
(15)
in which the weight value can be calculated as
ω
e1
= e
e
e
T
3
˙
e
e
e
2
,ω
e2
= e
e
e
T
1
˙
e
e
e
3
,ω
e3
= e
e
e
T
2
˙
e
e
e
1
(16)
Then the formulation of the angle velocity of cross
section can be written as
ω
ω
ω = T
T
T
ϕ
˙
ϕ
ϕ
ϕ (17)
where
T
T
T
ϕ
=


1 s
3
0
0 c
1
c
3
−s
1
0 −s
1
c
3
−c
1


=

p
p
p
1
p
p
p
2
p
p
p
3

p
p
p
1
,p
p
p
2
and p
p
p
3
are the weight vectors of three rotation
axis in the frame of the cross section.
The angler accelerations of the cross section can
be expressed as
˙
ω
ω
ω = T
T
T
ϕ
¨
ϕ
ϕ
ϕ +
˙
T
T
T
ϕ
˙
ϕ
ϕ
ϕ (18)
2.2.3 The Formulation of Strain Vector of the
Cross-section
The curvature vector of the cross section represents
the bending and torsion of the centerline of the beam.
And the arc-length derivative of the base vectors of
the reference frame on the cross section can be ob-
tained by the cross product of the curvature vector and
the base vectors
e
0
i
=
e
κ
κ
κe
i
= κ
κ
κ × e
i
(19)
The curvature vector on the cross section can be
expressed as
κ
κ
κ = κ
e1
e
e
e
1
+ κ
e2
e
e
e
2
+ κ
e3
e
e
e
3
(20)
κ
e1
= e
e
e
T
3
e
e
e
0
2
,κ
e2
= e
e
e
T
1
e
e
e
0
3
,κ
e3
= e
e
e
T
2
e
e
e
0
1
(21)
κ
κ
κ = T
T
T
ϕ
ϕ
ϕ
ϕ
0
(22)
The time derivatives of κ
κ
κ and κ
κ
κ
0
are
˙
κ
κ
κ = T
T
T
ϕ
˙
ϕ
ϕ
ϕ
0
+ φ
φ
φ(ϕ
ϕ
ϕ
0
)
˙
ϕ
ϕ
ϕ (23)
where
φ
φ
φ(ϕ
ϕ
ϕ
0
) =
h
∂p
p
p
2
∂ϕ
1
ϕ
0
2
+
∂p
p
p
3
∂ϕ
1
ϕ
0
3
0
0
0
∂p
p
p
2
∂ϕ
3
ϕ
0
2
i
According to the geometrically exact beam theory,
the generalized strains can be classified as axial strain
and the three weights of curvature vector in the frame
of cross-section.
ε
1
= kr
r
r
0
k − 1 (24)
and its time derivatives can be expressed as
˙
ε
1
= T
T
T
ε
˙
r
r
r
0
(25)
in which
T
T
T
ε
= (1 + ε
1
)
−1
(r
r
r
0
)
T
The derivative of the normal vector with the re-
spect of the arc-length is
e
e
e
0
1
= (1 + ϕ
1
)
−1
(r
r
r
00
− ε
0
1
e
e
e
1
) = b
b
b
2
ϕ
0
2
+ b
b
b
3
ϕ
0
3
(26)
in which
b
b
b
2
= −s
2
c
3
n
n
n
1
− c
2
c
3
n
n
n
3
b
b
b
3
= −c
2
s
3
n
n
n
1
+ c
3
n
n
n
2
+ s
2
s
3
n
n
n
3
Then the arc-length derivatives of Euler angles can
be acquired as
ϕ
0
2
= b
b
b
T
2
e
e
e
1
,ϕ
0
3
= b
b
b
T
3
e
e
e
1
(27)
The time derivative of normal vector can be ex-
pressed as
˙
e
e
e
1
= (1 + ε
1
)
−1
(E
E
E − e
e
e
1
e
e
e
T
1
)
˙
r
r
r
0
= b
b
b
2
˙
ϕ
2
+ b
b
b
3
˙
ϕ
3
(28)
then the time derivative of Euler angles can be ex-
pressed as
˙
ϕ
2
= b
b
b
T
2
˙
e
e
e
1
= T
T
T
ϕ
2
˙
r
r
r
0
,
˙
ϕ
3
= b
b
b
T
3
˙
e
e
e
1
= T
T
T
ϕ
3
˙
r
r
r
0
(29)
where the transfer matrices are
T
T
T
ϕ
2
= b
b
b
T
2
(1 + ε
1
)
−1
(E
E
E − e
e
e
1
e
e
e
T
1
)
T
T
T
ϕ
3
= b
b
b
T
3
(1 + ε
1
)
−1
(E
E
E − e
e
e
1
e
e
e
T
1
)
The further arc-length derivative can be expressed
as
˙
ϕ
0
2
= T
T
T
ϕ
2
˙
r
r
r
00
+ T
T
T
0
ϕ
2
˙
r
r
r
0
,
˙
ϕ
0
3
= T
T
T
ϕ
3
˙
r
r
r
00
+ T
T
T
0
ϕ
3
˙
r
r
r
0
(30)
where
T
T
T
0
ϕ
2
= (1 + ε
1
)
−1
(b
b
b
0T
2
− ε
0
1
T
T
T
ϕ
2
)
T
T
T
0
ϕ
3
= (1 + ε
1
)
−1
(b
b
b
0T
3
− ε
0
1
T
T
T
ϕ
3
)
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
212

2.2.4 Discretization Method
The main idea of the discretization is to add n − 1
nodes on the beam centerline and to mesh the whole
beam into n elements. In order to reduce the num-
ber of system variables, the position vectors r
r
r
i
of all
nodes and the arc-length derivatives of the position
vectors r
r
r
0
0
,r
r
r
0
n
of two boundary nodes are selected.
And the arc-length derivatives of position vectors of
the inner nodes (r
r
r
0
i
,i = 1,2, ...,n − 1) can be acquired
by the following equations with cubic spline interpo-
lation
[r
r
r
0
]A
A
A = a[r
r
r]B
B
B + [
r
r
r
0
0
r
r
r
0
n
]C
C
C (31)
where a = L
−1
, [r
r
r
0
] = [
r
r
r
0
0
r
r
r
0
1
... r
r
r
0
n
] and [r
r
r] =
[
r
r
r
0
r
r
r
1
... r
r
r
n
]
Then time derivations of the curvature of the in-
ner nodes can be expressed by the parameters of the
boundary nodes as
˙
r
r
r
0
i
= Γ
Γ
Γ
i
˙
q
q
q
e
(32)
and
¨
r
r
r
0
i
= Γ
Γ
Γ
i
¨
q
q
q
e
+ γ
γ
γ
i
(33)
where γ
γ
γ
i
is the acceleration margin and the details are
not expanded.
The arc-length coordinate of the node i on the cen-
troid line of the beam can be given as
s
i
= iL
0
/n (34)
in which L
0
is the original length of the beam and n is
the number of the elements meshed on the beam.
The position vector of the point between each two
nodes on the centerline of the beam can be described
by the polynomials as
r
r
r
ξ
= N
1
r
r
r
i
+ LN
2
r
r
r
0
i
+ N
3
r
r
r
i+1
+ LN
4
r
r
r
0
i+1
(35)
where L = L
0
/n and the shape functions are
N
1
= 1 − 3ξ
2
+ 2ξ
3
,N
2
=

ξ − 2ξ
2
+ ξ
3

N
3
= 3ξ
2
− 2ξ
3
,N
4
=

ξ
3
− ξ
2

(36)
And the normalized variables are defined as
ξ = L
−1
(s − s
1
) (37)
Furthermore, the curvature on the centerline of the
beam between two nodes and its arc-length deriva-
tion can be expressed with the derivations of the shape
functions. The overall idea of the hybrid interpolation
of an entire Euler-Bernoulli beam is show as Fig. (3).
Then the time derivative of the position vector at the
point between each nodes can be expressed as
˙
r
r
r
ξ
= T
T
T
r
˙
q
q
q
e
,
¨
r
r
r
ξ
= T
T
T
r
¨
q
q
q
e
+ a
a
a
r
(38)
in which
T
T
T
r
= N
1
G
G
G
i
+ N
3
G
G
G
i+1
+ L(N
2
Γ
Γ
Γ
i
+ N
4
Γ
Γ
Γ
i+1
)
a
a
a
r
= L(N
2
Γ
Γ
Γ
i
+ N
4
Γ
Γ
Γ
i+1
)
•
!
•
"
•
#
$
!
$
"
$
#
%
&
, %
&
'
(
!
(
"
(
#
)
%
*
, %
*
'
%
+
%
+-!
%
.
Figure 3: Hybrid interpolation of an Euler-Bernoulli beam.
2.2.5 The Virtual Power of the Beam Element
The virtual power of the entire beam is formed by the
sum of virtual power from each element.
The virtual power of inertial forces
δp
tra
= m
Z
1
0
δ
˙
r
r
r
ξ
T
(
¨
r
r
r
ξ
− g
g
g)dξ
= δ
˙
q
q
q
T
e
(M
M
M
e,tra
¨
q
q
q
e
+ F
F
F
e,tra
)
(39)
where
M
M
M
e,tra
= mL
Z
1
0
T
T
T
T
r
T
T
T
r
dξ
F
F
F
e,tra
= mL
Z
1
0
T
T
T
T
r
(a
a
a
r
− g
g
g)dξ
The virtual kinetic power of rotation can be ex-
pressed as
δp
rot
= L
Z
1
0
δω
ω
ω
T

J
J
J
ρ
˙
ω
ω
ω +
e
ω
ω
ωJ
J
J
ρ
ω
ω
ω

dξ
= δ
˙
q
q
q
T
e
(M
M
M
e,rot
¨
q
q
q
e
+ F
F
F
e,rot
)
(40)
where
M
M
M
e,rot
= L
Z
1
0
T
T
T
T
ϕ
R
R
R
T
J
J
J
ρ
R
R
RT
T
T
ϕ
dξ
F
F
F
e,rot
= L
Z
1
0
T
T
T
T
ϕ

R
R
R
T
J
J
J
ρ
R
R
R
˙
T
T
T
ϕ
˙
q
q
q
e
+
e
ω
ω
ωJ
J
J
ρ
ω
ω
ω

dξ
The strain vector is
ε
ε
ε =

ε
1
κ
1
κ
2
κ
3

T
(41)
The internal virtual power can be express as
δp
int
= L
Z
1
0
δ
˙
ε
ε
ε
T
D
D
Dε
ε
εdξ = (δ
˙
q
q
q
e
)
T
F
F
F
e,int
(q
q
q
e
) (42)
where D
D
D = diag(EA,GJ,EI
2
,EI
3
) and F
F
F
e,int
(q
q
q
e
) is
called generalized nodal forces
F
F
F
e,int
(q
q
q
e
) = L
Z
1
0
(
∂ε
ε
ε
∂q
q
q
e
)
T
D
D
Dε
ε
εdξ (43)
Modeling and Simulation of Long Boom Manipulator based on Geometrically Exact Beam Theory
213

The external virtual power can be written as
δp
ext
= δ
˙
r
r
r
T
i
f
f
f
i
+ δω
ω
ω
T
i
m
m
m
i
+
Z
1
0
δ
˙
r
r
r
ξT
f
f
f (ξ)dξ (44)
where f
f
f
i
and m
m
m
i
are the concentrated forces and mo-
ments on the element node i and f
f
f (ξ) is the dis-
tributed force. The virtual work of the external forces
can be reformed as
δp
ext
= δ
˙
q
q
q
e
T
(F
F
F
c
+ F
F
F
d
) = δ
˙
q
q
q
e
T
F
F
F
e,ext
(45)
where the generalized external forces are
F
F
F
c
= F
F
F
i
+ R
R
R
T
T
T
T
T
ϕ
M
M
M
i
,F
F
F
d
=
Z
1
0
T
T
T
r
f
f
f (ξ)dξ
2.3 The Governing Dynamic Equation
According to the virtual power principle, the virtual
power equation of a single beam element is
δp
p
p
int
+ δp
p
p
ine
= δp
p
p
ext
(46)
By submitting the internal virtual power, inertial
virtual power and the external virtual power, the equa-
tion yields as
δ
˙
q
q
q
T
e
(M
M
M
e,ine
¨
q
q
q
e
+ F
F
F
e,ine
+ F
F
F
e,int
− F
F
F
e,ext
) = 0 (47)
the the governing dynamic equation of beam element
can be expressed as
M
M
M
e
¨
q
q
q
e
+ F
F
F
e
= 0 (48)
where F
F
F
e
= F
F
F
e,ine
+ F
F
F
e,int
− F
F
F
e,ext
.
The general coordinate is defined as q
q
q, and the the
coordinate of the nodes in the element form can be
written as
q
q
q
e,i
= T
T
T
i
q
q
q,
˙
q
q
q
e,i
= T
T
T
i
˙
q
q
q,
¨
q
q
q
e,i
= T
T
T
i
¨
q
q
q +
˙
T
T
T
i
˙
q
q
q (49)
The original dynamic equation of multi-body sys-
tem can be expanded to a dynamic equation of
flexible-rigid multi-body system with constraints by
using Lagrange multiplier as
M
M
M
¨
q
q
q − F
F
F = Φ
Φ
Φ
T
q
λ (50)
where
M
M
M =
∑
T
T
T
T
i
M
M
M
e,i
T
T
T
i
+
∑
T
T
T
T
j
M
M
M
j
T
T
T
j
,
F
F
F =
∑
T
T
T
T
i
(M
M
M
e,i
˙
T
T
T
i
˙
q
q
q + F
F
F
e,i
) +
∑
T
T
T
T
j
F
F
F
j
T
T
T
j
Then, the governing equation can be rewritten as

M
M
M Φ
Φ
Φ
T
q
Φ
Φ
Φ
q
0

¨
q
q
q
−λ

=

F
F
F
−
˙
Φ
Φ
Φ
q
˙q −
˙
Φ
Φ
Φ
t
− 2ξ
1
˙
Φ
Φ
Φ − ξ
2
Φ
Φ
Φ

(51)
which can be transferred into the order ordinary dif-
ferential equations (ODEs) about q and can be solved
by ODE solvers.
3 SIMULATION AND ANALYSIS
3.1 Initial Configuration and
Parameters
The linear motions of two hydraulic cylinders and ro-
tational motion of the turntable are designed as fol-
lowing functions of velocity and acceleration, which
are given as
v(t) =



v
0
t
2
(3t
1
− 2t) /t
3
1
0 < t < t
a
v
0
t
a
< t < t
b
v
0
(t
1
+t
2
+t
3
−t) /t
3
t
b
< t < t
c
a(t) =



6v
0
t (t
1
−t) /t
3
1
0 < t < t
a
0 t
a
< t < t
b
−v
0
/t
3
t
b
< t < t
c
(52)
where t
a
= t
1
, t
b
= t
1
+t
2
and t
c
= t
1
+t
2
+t
3
.
The parameters of the rigid bodies, such as the
hydraulic cylinders and the rigid links are chosen as
follows: the masses of the cylinders and the pistons
are both 10kg, the radiuses of the cross-section of the
cylinders and the pistons are 0.05m and 0.035m, the
linear density and the radius of the links are 61.5kg/m
and 0.05m. And the parameters of the flexible bod-
ies are selected as: the radius of the cross-section
is 0.15m; the linear density is 544.6kg/m; the elas-
tic modulus is 2.11×10
11
Pa and the Poisson’s ratio is
0.3.
The initial configuration of the manipulator is de-
signed as Fig. (4). Both hydraulic cylinders are re-
tracted, the first boom is at horizontal position and
the second boom is folded and coinciding with the
first boom. The luffing plane is set in XY-plane.
Figure 4: The initial configuration of the manipulator.
The Fig. (5) presents the deployment sequence of
the manipulator in the designed scenario. First, the
first boom is driven to luff, when the first hydraulic
cylinder is fully extended, the first boom arrives at
the designed angle displacement (stage 1). Then the
turntable rotates clockwise 90
◦
and changes the luff-
ing plane from X-Y plane to X-Z plane (stage 2). At
last, the second boom starts and the first boom re-
mains static and the tip of the second boom reaches
the highest position at last (stage 3).
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
214

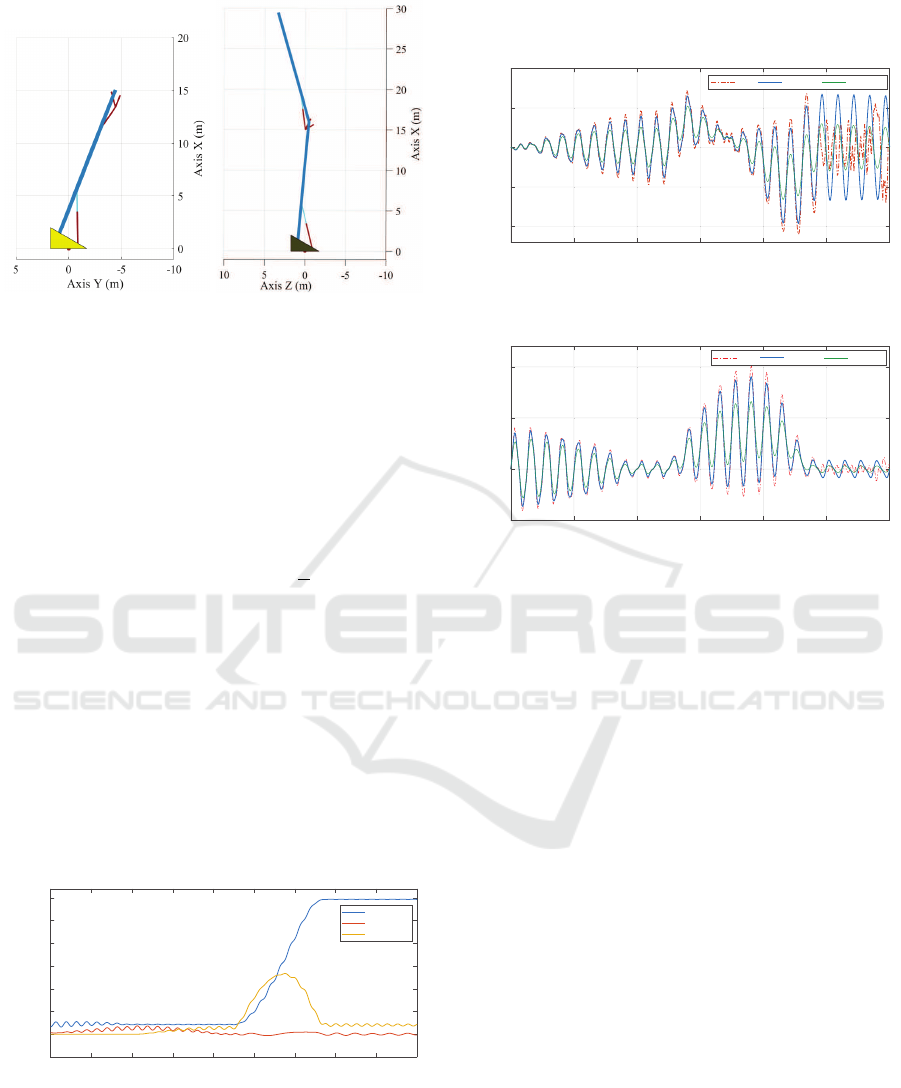
Figure 5: Four configurations of the manipulator during the
operation.
3.2 Simulation Results and Analysis
The dynamic equations of the flexible multi-body sys-
tem are usually stiff differential equations. Differ-
ent from the common numerical method to solve stiff
equations using numerical damping to filter the high
frequency, we apply the method presented by Qi (Qi
et al., 2018) to filter the high-frequency part during
the modeling stage. The main idea of this method is
to use the average value of the stress σ in the time in-
terval (t,t +h) to approximate the instantaneous stress
σ as
¯
σ , h
−1
Z
t+h
t
σ
τ
dτ ≈ σ
t
+ h
˙
σ
t
/2 + h
2
¨
σ
t
/6 (53)
then, the filtered equation can be solved by regular
ODE solver in MATLAB, such as solver ODE45.
The motion designed in section 3.1 is simulated
and solved with ODE45 in MATLAB. The coefficient
is selected as 0.005. The curves in Fig. (6) show the
displacements of the tip of the second boon in the co-
ordinate space.
0 5 10 15 20 25 30 35 40 45
Time (s)
-5
0
5
10
15
20
25
30
Displacement of the tip of
the second boom (m)
X direction
Y direction
Z direction
Figure 6: The displacement of the boom’s tip.
The Fig.(7) and Fig.(8) represent the results with
different selection of the value of h. The solid line
is the results solved by ode45 with h = 0.001 and
h = 0.002 which means the frequencies higher than
1000Hz and 500Hz have been filtered. The dotted
line is the results solved by stiff solver ode15s. In
this caparison, we simulated the luffing process only.
0 5 10 15 20 25 30
Time (s)
-10
-5
0
5
10
Velocity in the Y-deriction (m/s)
h=0 h=0.001 h=0.005
Figure 7: The velocity of the tip of the second boom in the
Y direction.
0 5 10 15 20 25 30
Time (s)
-5
0
5
10
Velocity in the X-deriction (m/s)
h=0 h=0.001 h=0.005
Figure 8: The velocity of the tip of the second boom in the
X direction.
The above figures show that some high frequen-
cies parts of the stiff system have been filtered, espe-
cially at the rare part of the simulation when no more
input motion occurs. The amplitude of the dynamic
response is also reduced as long as the coefficient h
increases.
4 CONCLUSION AND OUTLOOK
In this paper, we introduce the basic theory of the
geometrically exact Euler-Bernoulli beam and apply
a hybrid interpolation method to discrete the beam.
The cubic spline interpolation is used to reduce the
number of the system variables by describing the arc-
length derivatives of the inner nodes with the posi-
tion vectors of all the nodes and the arc-length deriva-
tives of the two boundary nodes. The virtual power of
the element is formulated by the Gauss integration be-
tween each adjective two nodes. The system parame-
ters inside the element are presented as the interpola-
tion using the Gauss points between the two nodes of
the element. Then the governing equations of the flex-
ible bodies can be derived, and combining the govern-
ing equations of the rigid bodies and constrains func-
tion, the dynamic governing equations of the folding
boom system are formulated with a method of fil-
Modeling and Simulation of Long Boom Manipulator based on Geometrically Exact Beam Theory
215

tering high frequency vibrations and solved by ODE
solver. The dynamic simulation of the designed long
boom manipulator in a process with luffing and slew-
ing motions is accomplished.
The following topics are considered as our further
research with the object to control the vibration of the
long boom manipulator in the operation:
1).In the current model, the elasticity of the hy-
draulic cylinder is simplified as constant spring stiff-
ness. In reality, the oil inside the chambers of the hy-
draulic cylinder performs as a nonlinear elastic body.
The equations describing the dynamics of the hy-
draulic system will be included in the model of the
long boom manipulator to acquire a more accurate dy-
namic response of the system.
2). Although the motions of the manipulator are
designed to be smooth, the dynamic response of the
boom system is still remarkable due to the large flex-
ibility of the structure. The mathematical description
of the system will be reformed as an optimal control
problem to investigate the solution of vibration con-
trol. The optimal control problem can be proposed as
a path-following problem to optimize the dynamic re-
sponse of the boom structure to fit the trajectory of the
motion of the model with a rigid body assumption.
ACKNOWLEDGEMENTS
The research is supported by Deutsche Forschungs-
gemeinschaft (FO 1180 1-1) and National Science
Foundation of China (11761131005).
REFERENCES
Baumgarte, J. (1972). Stabilization of constraints and
integrals of motion in dynamical systems. Com-
puter methods in applied mechanics and engineering,
1(1):1–16.
Fang, H. and Qi, Z. (2016). A hybrid interpolation method
for geometric nonlinear spatial beam elements with
explicit nodal force. Mathematical Problems in En-
gineering, 2016.
Gao, L., Wang, M., Kleeberger, M., Peng, H., and Fottner,
J. (2019). Modeling and discretization of hydraulic
actuated telescopic boom system in port-hamiltonian
formulation. Modeling and Discretization of Hy-
draulic Actuated Telescopic Boom System in Port-
Hamiltonian Formulation. In Proceedings of the 9th
International Conference on Simulation and Modeling
Methodologies, Technologies and Applications, (69-
79):SCITEPRESS–Science and Technology Publica-
tions, Lda.
Nguyen, V. T., Schmidt, T., and Leonhardt, T. (2019). Ef-
fect of pre-tensioned loads to vibration at the ladder
tip in raising and lowering processes on a turntable
ladder. Journal of Mechanical Science and Technol-
ogy, 33(5):2003–2010.
Pertsch, A. and Sawodny, O. (2016). Modelling and con-
trol of coupled bending and torsional vibrations of an
articulated aerial ladder. Mechatronics, 33:34–48.
Pertsch, A., Zimmert, N., and Sawodny, O. (2009). Mod-
eling a fire-rescue turntable ladder as piecewise euler-
bernoulli beam with a tip mass. In Proceedings of the
48h IEEE Conference on Decision and Control (CDC)
held jointly with 2009 28th Chinese Control Confer-
ence, (pp. 7321-7326).
Qi, Z., Cao, Y., and Wang, G. (2018). Model smoothing
methods in numerical analysis of flexible multibody
systems. Chinese Journal of, 50(4):863–870.
Reissner, E. (1972). On one-dimensional finite-strain beam
theory: the plane problem. Zeitschrift fuer ange-
wandte Mathematik und Physik ZAMP, 23(5):p 795–
804.
Reissner, E. (1973). On one-dimensional large-
displacement finitestrain beam theory. Studies in Ap-
pliedMathematics, 52(2):p 87–95.
Sawodny, O., Aschemann, H., and Bulach, A. (2002).
Mechatronical designed control of fire-rescue
turntable-ladders as flexible link robots. IFAC
Proceedings Volumes(35):509–514.
Shabana, A. A. and Yakoub, R. Y. (2001). Three dimen-
sional absolute nodal coordinate formulation for beam
elements: theory. J. Mech. Des., 123(4):606–613.
Simo, J. C. (1985). A finite strain beam formulation.
the three-dimensional dynamic problem. i. Com-
puter methods in applied mechanics and engineering,
49(1):55–70.
Simo, J. C. (1988). On the dynamics in space of rods under-
going large motions—a geometrically exact approach.
Computer methods in applied mechanics and engi-
neering, 66(2):125–161.
Simo, J. C. and Vu-Quoc, L. (1986). A three-dimensional
finite-strain rod model. part ii: Computational aspects.
Computer methods in applied mechanics and engi-
neering, 58(1):79–116.
Yakoub, R. Y. and Shabana, A. A. (2001). Three dimen-
sional absolute nodal coordinate formulation for beam
elements: implementation and applications. J. Mech.
Des., 123(4):614–621.
Zhang, Z., Qi, Z., Wu, Z., and Fang, H. (2015). A spatial
euler-bernoulli beam element for rigid-flexible cou-
pling dynamic analysis of flexible structures. Shock
and Vibration, 2015.
Zupan, D. and Saje, M. (2003). Finite-element formulation
of geometrically exact three-dimensional beam theo-
ries based on interpolation of strain measures. Com-
puter methods in applied mechanics and engineering,
192(49-50):5209–5248.
Zuyev, A. (2005). Stabilization of a flexible manipulator
model with passive joints. IFAC Proceedings Volumes,
38(1):784–789.
SIMULTECH 2020 - 10th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
216