
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing
Problem
Jamila Sassi
a
, Ines Alaya
b
and Moncef Tagina
COSMOS-ENSI, National School of Computer Sciences, University of Manouba 2010, Tunisia
Keywords:
Combinatorial Multi-objective Optimization, Artificial Bee Colony Algorithm (ABC), Multi-objective
Vehicle Routing Problem with Time Window (VRPTW).
Abstract:
The vehicle routing problem has attracted a lot of interest during many decades because of its wide range
of applications in real life problems. This paper aims to test the efficiency and capability of bee colony
optimization for this kind of problem. We present a Bee-route algorithm: a multi-objective artificial Bee
Colony algorithm for the Vehicle Routing Problem with Time Windows. We have performed our experiments
on well known benchmarks in the literature to compare our proposed algorithm results with other state-of-the-
art algorithms.
1 INTRODUCTION
The vehicle routing problem (VRP) is a part of a
large application domain. It could be applied to var-
ious fields such as transportation, network connec-
tion, health management techniques, recycling meth-
ods, etc. The VRP aims at finding an optimal set of
routes for a number of vehicles, initially located at a
depot, to serve a given set of customers. Each vehi-
cle leaving the depot returns to the initial depart af-
ter having completed its tour in a certain time slot.
The cumulative demand of customers visited by a ve-
hicle must not exceed its capacity. We introduce in
this article a multi-objective artificial Bee Colony al-
gorithm for Vehicle Routing Problem with Time Win-
dows (VRPTW) called Bee-route algorithm. In the
multi-objective VRPTW, we consider two objectives
to be optimized: the first is to minimize the number of
vehicles used to deliver the demand of customers and
the second objective is to minimize the total distance
of the routes.
Approaches proposed in recent decades have been
characterized by prioritizing customers, and for time
optimization, reaching a reasonable time frames. The
problem of Vehicle Routing Problems with Time
Windows (VRPTW) constitutes a generalization of
the VRP in which each customer has a window of
time within this time the customer must be served.
a
https://orcid.org/0000-0002-9857-6467
b
https://orcid.org/0000-0002-7037-3326
The VRPTW aims to determine optimal routes for a
number of vehicles when serving a set of customers
within predefined time intervals (the time windows).
The main formulation of the VRPTW was proposed in
1987 by (Solomon, 1987) where the time constraints
must be respected by each vehicle. In fact, it has been
shown that the classic VRP problem is NP-hard, and
this result could be extended to the VRPTW. While
it is quite possible to determine an optimal solution
for small instances, it quickly becomes unfeasible for
medium or large instances.
Given the complexity of the VRPTW, many res-
olution methods have been developed. In (Lim and
Zhang, 2007), proposed a two-stage algorithm for
the VRPTW. The authors extended the VRPTW algo-
rithm for m-VRPTW. Vehicle routing problem with
both time window and limited number of vehicles.
The m-VRPTW is an useful extension of VRPTW
problem in real applications. The algorithm first mini-
mizes the number of vehicles with an ejection pool to
hold temporarily unserved customers which enables
the algorithm to go through the infeasible solution
space. (Ghoseiri and Ghannadpour, 2010) have pro-
posed a goal programming approach for the formula-
tion of the VRPTW and an adapted efficient genetic
algorithm for it in which the decision maker speci-
fies optimistic aspiration levels to the objectives (total
distance and number of vehicles) and the deviations
from those aspirations are minimized. (Tsung-Che
and Wei-Huai, 2014) have presented an evolutionary
algorithm to find a set of Pareto optimal solutions.
Sassi, J., Alaya, I. and Tagina, M.
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing Problem.
DOI: 10.5220/0009831303070318
In Proceedings of the 15th International Conference on Software Technologies (ICSOFT 2020), pages 307-318
ISBN: 978-989-758-443-5
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
307

They incorporate problem specific knowledge into the
genetic operators. The objectives are to minimize the
number of vehicles and the total distance simultane-
ously.
In recent years, swarm intelligence has also at-
tracted the interest of many researches from several
scientific areas (Alzaqebah et al., 2018), (Alaya I.,
2003), (Zouari W., 2017) : biology, ethology, com-
puter science , etc. Many researchers have success-
fully proposed Artificial Bee Colony (ABC) algo-
rithm to quickly find good quality solutions to prob-
lems. An ABC has been proposed by (Ghaleini E. N.,
2018) in the network application, to optimize weight
and biases of artificial neural networks to receive
higher levels of accuracy and performance prediction.
They combined artificial bee colony and neural net-
work for the specific purpose of approximating the
safety factor of retaining walls. (Alzaqebah and Sana,
2016) investigate the use of bee algorithms (BA) to
address the VRPTW and identify their strengths and
weaknesses. The strength of BA is that the algorithm
has both global exploration performed by Scout bees
and local exploitation performed by recruiter bees.
Then again the weakness of the algorithm is that it
is parameter dependent, so each instance may require
different parameter values. The proposed work in
(Alzaqebah and Sana, 2016) involves the recruitment
of additional Employed bees and applies local search
to a set of elite solutions, which are considered the
most promising solutions in the search space. (Shao-
qiang and Linjie, 2016) has been presented a real
western-style food delivery problem in Dalian city,
China, which can be described as a vehicle routing
problem with time windows. An integer linear model
for the problem is developed, and an improved arti-
ficial bee colony algorithm, which possesses a new
strategy called an adaptive strategy, a crossover op-
eration, and a mutation operation, which are pro-
posed for the problem. (Yao, 2017) propose an im-
proved artificial bee colony (IABC) algorithm for the
VRPTW.The ABC algorithm is improved by a local
optimization based on a crossover operation borrowed
from the genetic algorithm and a scanning strategy.
(Alzaqebah and Sana, 2016) proposed a Modified
ABC algorithm to improve the solution quality of the
original ABC. In the Modified ABC a list of aban-
doned solutions is used by the scout bees to memo-
rise the abandoned solutions. This algorithm using a
memory by scout bees. They can memorise the aban-
doned solutions and select one of these solutions to
be replaced by a new generated solution. They re-
placed all the abandoned solutions by randomly gen-
erated solutions as in the original ABC algorithm.
In this paper, we are interested in introducing a
new algorithm that solves the multi-objective vehi-
cle routing problem with time windows (VRPTW)
with the artificial bee colony optimization. Since
we consider the VRPTW as a multi-objective prob-
lem, in which we have to minimize the number of
vehicles and the total distance, optimizing one ob-
jective usually leads to degrading the other objec-
tive. The conventional single-objective approaches
for VRPTW, and even some approaches that claims
to be multi-objective, are unable to explore this con-
flicting behaviour of objectives and return a single
best solution. Whereas for multi-objective problems,
there is a set of optimal solutions and not a single
best solution, called the non-dominated solutions or
the Pareto optimal solutions. A feasible solution is
non-dominated if it does not exist another feasible so-
lution better than the current one in some objective
function without worsening other objective function.
Our algorithm approximates this set of Pareto opti-
mal solutions, since it is based on a metaheuristic ap-
proach, considering both of the objectives at the same
time. In fact, in the proposed algorithm, we propose
to employ a weighted approach called Bee-route al-
gorithm: a multi-objective artificial Bee Colony algo-
rithm for Vehicle Routing Problem with Time Win-
dows. This approach will solve the problem consid-
ering the two objectives simultaneously relatively to
different weight vectors.
The remaining parts of the paper are organized as
follows: In section 2, we will describe the formula-
tion of VRPTW. Our approach will be defined with
more details in section 3. In section 4 we will present
our experiments and results. Finally, we will draw the
conclusion and we will provide further research per-
spectives.
2 FORMULATION OF THE
VRPTW
In our approach, we aim at the vehicle routing prob-
lem with time window (VRPTW). This problem is
a variant of the well-kown VRP complemented by
a time window in which each customer should be
served. Formally, we present the problem description
of the VRPTW as follows:
The VRPTW is defined by a directed graph G
= (V,E), where V ∈ {0, 1, ..., n} is the node set and
E ∈ {(i, j) : 0 ≤ i, j ≤ n, i 6= j} is the arc set. Node
0 is the depot and N = V \{0} denotes the set of cus-
tomers. For customer i, a vehicle may arrive before
the start time of window e
i
and wait until e
i
to start the
service, but it may not arrive after l
i
the end of time.
At the same time, each customer can only call for
ICSOFT 2020 - 15th International Conference on Software Technologies
308

one vehicle but the same vehicle is allowed to serve
more than one customer. Each customer i has a re-
quired service time s. In Solomon’s benchmark, the
service time for each customer for the time taken to
load/unload is also measured, which is considered to
be unique regardless of the demand size. All the vehi-
cles are the same with load capacity Q. The total de-
mand of the customers served by each vehicle cannot
exceed the maximum capacity Q. We also use the fol-
lowing notations for the formulation of VRPTW. The
set K = (k
1
, k
2
, ..., k
n
), homogeneous vehicles based
in the depot. The Decision variable: x
k
i j
{ 1: if vehi-
cle k visits node j immediately after node i, i 6= j, 0 :
otherwise}
Based on the conditions aforementioned, the
objective function of the VRPTW is to minimize the
distance. c
i j
is the distance to travel from node i
to j, i.e the distance between them. The demand of
customer i is d
i
, the travel time from customer i to
customer j is t
i j
. The starting time of vehicle k for
customer i is b
ik
. All the routes must start from the
depot b
0k
= e
0
, go to a number of customers and
end at the depot. It prohibits the vehicle which runs
from customer i to j from arriving at the customer j
before the time b
ik
+ t
i j
: The mathematical equation
of VRPTW can be defined as follows:
a- Minimize number of vehicles
Min
∑
k∈K
x
k
i j
; ∀i, j ∈ N (1)
b- Minimize total distance
Min
∑
(i, j)∈N
c
i j
∑
k∈K
∑
j∈N
x
k
i j
; ∀i, j ∈ N (2)
subject to
∑
k∈K
∑
j∈N
x
k
i j
= 1; ∀i ∈ N (3)
∑
i∈N
d
i
∑
j∈N
x
k
i j
≤ Q; ∀k ∈ K (4)
∑
j∈N
x
k
0 j
≤ 1; ∀k ∈ K (5)
∑
i∈N
x
k
i j
−
∑
i∈N
x
k
ji
= 0; ∀ j ∈ N, ∀k ∈ K (6)
∑
i∈N
x
k
i,n
= 1; ∀k ∈ K (7)
x
k
i j
(b
ik
+t
i j
+ s − b
jk
) ≤ 0; ∀(i, j) ∈ N, ∀k ∈ K (8)
e
i
(
∑
j∈N
x
k
i j
) ≤ b
ik
≤ l
i
(
∑
j∈N
x
k
i j
); ∀i ∈ N, ∀k ∈ K (9)
x
k
i j
∈ {0, 1}; ∀(i, j) ∈ N, ∀k ∈ K (10)
Constraints (3)restrict the assignment of each cus-
tomer is visited exactly once. Next, constraints (4),(8)
guarantee schedule feasibility with respect to time
considerations and capacity restriction, respectively.
Additionally, constraints (5)-(7) ensure that each ve-
hicle k starts serving from the distribution center and
returns to the distribution center after finishing its
work.Note that for a given k, constraints (9) force
b
ik
= 0 whenever customer i is not visited by vehi-
cle k. Finally, (10) impose binary conditions on the
flow variables. The binary conditions (10) allow con-
straints (8) to be linearized as:
b
ik
+t
i j
+ s − b
jk
≤ (1 − x
k
i j
)M
i j
;∀(i, j) ∈ N, ∀k ∈ K
(11)
where M
i j
are large constants. Furthermore, M
i j
can
be replaced by max{ b
i
+ t
i j
+ s − e
j
, 0} (i, j) ∈ E,
and constraints (8) or (11) need only be enforced for
arcs (i, j) ∈ N, such that M
i j
>0; otherwise, when
max{ b
i
+ t
i j
+ s − e
j
, 0} , these constraints are sat-
isfied for all values of b
ik
, b
jk
and x
k
i j
.
We have to design routes, in such a way that there
should be a minimum number of vehicles and ti mini-
mize the amount of distance traveled. So we consider
VRPTW as a bi-objective problem. Other consider-
able objectives may be :
- Minimizing the waiting time, delay time, service
time, etc. . . ;
- Minimizing the total cost of the tour;
- Maximizing the vehicle load used in the tour etc...;
3 THE BEE-ROUTE ALGORITHM
We describe in this section the details of our pro-
posed algorithm based on the artificial bee colony al-
gorithm for the multi-objective vehicle routing prob-
lem with time window, called Bee-route. We describe
in the second paragraph the proposed algorithm using
a weighted approach and we explain the main idea of
the algorithm.
In order to find solutions for our multi-objective
problem, we use a weighted approach. We consider
the bi-objective VRPTW problem, where the objec-
tive function is obtained by linear scalarization. In
our problem the coefficients w
1
, weighting the num-
ber of vehicles and w
2
, weighting the total distance,
are chosen randomly in such a way that w
1
+ w
2
= 1.
At each iteration we choose a different pair of values
for w
1
and w
2
To apply ABC to the VRPTW, we consider that
the food source represents the candidate solution and
the quantity of the nectar of the food source represents
the quality of the solution (the aggregated objective
function).
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing Problem
309

The Bee-route algorithm, as it uses the ABC
scheme, is divided in three phases: Phase of Em-
ployed Bees, phase of Onlooker Bees and phase of
Scout Bee.
- Employed Bees: transmit and share information
about a particular source, its location relatively to the
hive. The number of employed bees is equal to the
number of food sources around the hive.
- Onlooker Bees: are looking for a source of food to
exploit. The onlookers check the dance of the em-
ployed bees within the hive, to select a food source.
- Scout Bees: If a food source is abandoned, its
employed bee becomes a scout to explore new food
sources randomly.
In the ABC algorithm, the number of food sources
(that is the employed or onlooker bees) is equal to the
number of solutions in the population. Whereas the
quality of nectar of a food source represents the fit-
ness cost of the associated solution. The ABC algo-
rithm is described as follows:
In the initialization, the positions of the food sources
are randomly selected by the bees. The employed
bees go around the food sources to find a better source
than the one visited. Then, they share the quality of
the source with the onlookers bee. The latter focus
mainly on higher quality food sources. When a food
source has been sufficiently explored, it is abandoned
and the explorers go out in search of a new source.
The ABC algorithm repeats the three phases (em-
ployed, onlooker and scout) until reaching a desired
solution quality or a maximum number of cycles. The
Bee-route algorithm is outlined in Algorithm 1.
For each food source, only one bee is affected.
The quality of a food source depends on several fac-
tors such as proximity and amount of nectar. Con-
sequently, the employed bees whose food source is
deleted becomes a scout bee.
Initially, the initial solution of the algorithm is ran-
domly generated. The positions of the food sources
(customers) are randomly selected by the bees at the
initialization stage and their nectar qualities are mea-
sured. Thus, each employed bee starts with a random
initial solution. The algorithm begins with the initial
population of food sources and their evaluation while
checking the constraint of capacity in vehicles and the
constraints of time windows to customers.
Secondly, in the employed bees phase, each bee
tries to improve its situation by a local search. They
modify the current solution based on the fitness value
(amount of nectar) of the new solution. The quality of
the food sources of the employed bees is measured by
using a fitness value calculated as follows:
Fitness =
1
the ob jective f unction
(12)
Algorithm 1: The Bee-route algorithm.
Initialize the population Archive with n random solutions
(food sources) by checking the capacity constraints and the
time window constraints.
Initialize Pareto set ←
/
0
Repeat{
For each employed bee {
Produce a solution S
0
from the neighborhood of S
using the 2-opt method
if ( f itness(S’) > f itness(S))then{
Update the best solution.
Memorize the solution.
trial = 0}
Else
trial = trial +1
}
For each onlookers bee {
Choose a solution S
0
with probability P
i
(13)
Create a solution S
00
from the neighborhood of S
0
using
the 2-opt method
if (fitness(S
00
) > fitness(S
0
))then {
Update the best solution.
trial = 0 }
Else
trial = trial +1
}
if (trial = limit) then {
Replace the not improved solution through the scout
bee with a random solution S.
}
Save Archive (set of solutions)
Update Pareto set (set of non-dominated solutions)
} Until ( a maximum number of cycles is reached)
Return Pareto.
}
*fitness= 1 / (w
1
∗ numbero f vehicles + w
2
∗ distance)
where w
1
randomly ∈ [0, 1] and w
2
= 1 − w
1
Where the objective function is a weighted aggre-
gation between functions (1) and (2). So, the em-
ployed bees phase consists in improving solutions by
a local search. In our algorithm the 2-opt method
(Br
¨
aysy and Gendreau, 2005) is used. For each solu-
tion, a neighborhood exploration is made to find a best
solution in the neighborhood. Afterwards, the number
of food sources is reduced by keeping only the best
one. The main idea of 2-opt is to check pairs of non-
adjacent arcs in a given route, rearranging these pairs
by exchanging the terminal nodes of the two arcs in
each pair and finally computing the improvement in
the route length to obtain a shorter tour until we have
found a local optimum. Thus, every employed bee,
during each iteration, finds a new food source using
2-opt. The nectar amount (fitness) of the new food
source is then evaluated. If the new food source has
more nectar than the old one, then the old one is re-
placed by the new one, otherwise the new food source
is abandoned. The employed bee memorizes the
ICSOFT 2020 - 15th International Conference on Software Technologies
310

food source position. The Bee-Route algorithm com-
bines the global search and local search methods
which allows the bees in the two aspects of the ex-
ploration and exploitation of food sources to achieve
a better balance. Each vehicle spends one-time slot
(time unit) to travel one distance unit, so the speed
of the vehicle is assumed to be constant. The time
window boundaries are defined by the earliest and lat-
est arrival times (the time interval); in which the ve-
hicle must arrives at the customer’s place before the
latest arrival time. The vehicle should wait in cases
where it arrives before the earliest arrival time. The
service time of the customer must be taken into ac-
count, which represents the time that is spent to load
or unload demands. The demand size is considered
same for all customers. All routes have to be finished
by the upper limit of the depot time window.
After all employed bees have finished with the
above exploitation process, they share the nectar in-
formation of the food sources with the onlookers.
Then, in the onlooker bees phase, the food sources are
selected according to a probability. Each onlooker bee
chooses another food source in the neighborhood of
the one currently in her memory based on the fitness
function. The probability is calculated as follows:
P
i
=
f
i
∑
N
i=1
f
j
(13)
Where f
i
is the fitness value of the i
th
solution in
the swarm. As seen, the better the solution Si is, the
higher the probability (P
i
) of the i
th
food source se-
lected is. Thus, this method promotes the best solu-
tions adopted, in the same time it gives a chance to the
others. In Bee-Route, both of the employed bees and
the onlookers have the responsibility to execute bal-
ance between exploitation and exploration since the
weighted approach allows the search to go in different
directions and the local search intensify the search in
each direction. However the responsibility of scouts
is to perform only exploration. Finally, the scout bee
phase is made to replace the undeveloped solutions. If
the number of trials for a food source is greater than a
given “limit”, a new food source will be obtained ran-
domly in the search space. Moreover, the scout bees
replace the one abandoned by the onlooker bees. If
certain food sources are not improved during several
cycles, the scout bee is converted into an employed
bee.
4 EXPERIMENTATION
In this section, we show the experimental results
found by our algorithm when applied to well-
known benchmarks of VRPTW. We compare these
results with the multi-objective evolutionary algo-
rithms from literature MOV-GP (Ghoseiri and Ghan-
nadpour, 2010), KBEA (Tsung-Che and Wei-Huai,
2014), IABC (Yao, 2017), Modified ABC (Alzaqebah
and Sana, 2016) and the Best Known results of the
Solomon VRPTW benchmark (Solomon, 1987). We
have chosen these algorithms since they use a multi-
objective approach and returns a set of non-dominated
solutions while most of the other approaches return a
single solution. We use also the Best Known solution
from the benchmark as a reference. For the three al-
gorithms, each Solomon instance is run 10 times. The
values of our algorithm parameters are fixed experi-
mentally as follows: the maximum number of cycles
NCmax=1000, the number of customers=100 (the
largest in-stance of multiobjective VRPTW) and the
trial count when solution has not improved, limit=10.
In the following, we describe, first, the Solomon
benchmark instances. Then, we report the computa-
tional results obtained by our algorithm and compare
them to the state-of-the art algorithms.
4.1 Benchmark Problems
We use in the experimentation the standard
Solomon’s benchmark for multi-objective VRPTW
problem (Solomon, 1987). The instances have
different customer numbers (25, 50, 75 and 100). We
tested our approach on the largest instances with 100
clients. They are divided into six groups: C1, C2,
R1, R2, RC1, RC2, each of them containing between
8 and 12 instances. The groups are based on three
types of the customer locations: (C), (R) and (RC).
Each type has a set of 2 groups. In sets C1 and C2 the
customers are positioned in groups. In sets R1 and R2
the customers’ position is created randomly through
a uniform distribution. In sets RC1 and RC2, part of
the customers is placed randomly and part is placed
in groups. In each Solomon instance, customers’
location is given by the coordinates in a 2-dimensions
space, which are then used to calculate the Euclidean
distance using two decimal places. All instances
of the same group have the same customers’ loca-
tion, number of available vehicles (25) and service
time(10); thus they only differ in value of capacity
of available vehicles (200,1000), demand and time
windows between instances. In these experiments,
we haven’t use C1 and C2 instances sets since they
contain very small number of routes. Results are thus
reported for R1 (12 instances), R2 (11 instances),
RC1 (8 instances) and RC2 (8 instances).
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing Problem
311

4.2 Computational Results
To test the efficiency of Bee-route, we compare, first
the numerical results of the non-dominated solutions
found by Bee-route with those found by the evolu-
tionary algorithms and the Best Known solution. Sec-
ond, We compare also the performance of our algo-
rithm with the other algorithms using the Hypervol-
ume metric. Then, we perform a statistical test to
verify if our algorithm is significantly better than the
other algorithms. Finally, we compare the CPU time
taken by the different algorithms.
4.2.1 Non Dominated Solutions’ Comparison
In this section, we enumerate all the approximate
Pareto sets found by the different algorithms since,
for the VRPTW, the number of non-dominated solu-
tions is generally not large because there isn’t, usu-
ally, a big difference in the number of vehicles be-
tween solutions. So we show in the tables 1, 2, 3, and
4 the results for benchmark sets, respectively, R1, R2,
RC1 and RC2 of our algorithm Bee-route, the evo-
lutionary algorithms MOV-GP (Ghoseiri and Ghan-
nadpour, 2010), KBEA (Tsung-Che and Wei-Huai,
2014), IABC (Yao, 2017), Modified ABC (Alzaqe-
bah and Sana, 2016) and the single Best Known
(Solomon, 1987) solutions reported in the literature.
In these tables, we report in the column “NV” the val-
ues of the objective number of vehicles, and in the
column “T.dis” the values of the objective total dis-
tance of the VRPTW instances.
In Table 1, we can see that Bee-route can provide
the best results for most instances of the R1 set. In
fact, considering the two objectives: the minimum
number of vehicles and the total distance, the non-
dominant solutions obtained by our algorithm are ei-
ther identical or better than the best known solutions
(Solomon, 1987) reported in the literature, MOV-
GP (Ghoseiri and Ghannadpour, 2010), IABC (Yao,
2017), modified ABC (Alzaqebah and Sana, 2016)
and also KBEA (Tsung-Che and Wei-Huai, 2014) in
the cases R102,R103,R109,R110. From Table 1 we
can see that for instance R101, all but one of the so-
lutions found by the authors are dominated by The
IABC solution. We remark also that our algorithm
finds the largest approximate Pareto sets for most of
the instances and have a competitive results for re-
maining instances.
According to Table 2, that shows the results of
Bee-route for 3 instances in R2, we remark that the
Pareto front returned by our algorithm dominates
those found by MOV-GP (Ghoseiri and Ghannad-
pour, 2010), Modified ABC (Alzaqebah and Sana,
2016) and KBEA (Tsung-Che and Wei-Huai, 2014)
for R202 and R203, where the number of vehicles and
the total distance is reduced. For others instances,
Bee-Route present a competitive Pareto set compar-
ing the results of the algorithms in the state-of-the-art.
In Tables 3 and 4, the non-dominated solutions of
Bee-route are competitive with the other algorithms.
In these tables, the Pareto front of Bee-route domi-
nates the other fronts for 5 instances(RC102,RC108
in table3 and RC204,RC207 and RC208 in table 4)
of both of the two sets. In Table 3, the solution
of RC108 instance, in our algorithm with 9 vehicles
dominates the solution found by KBEA, Best Known,
MOV-GP and Modified ABC. However, the solution
with 10 vehicles found by KBEA dominates our so-
lution with 10 vehicles. In the same case for the
RC102 instance, Bee-route with 11 vehicles domi-
nates all other algorithms in comparison. However,
the solution with 12 vehicles found by KBEA dom-
inates our solution with 12 vehicles. On the other
hand, we note that the non-dominated solutions re-
turned by our algorithm are competitive for other
algorithms. In Table 4, the solution of RC204 in-
stance, in our algorithm with 2 vehicles dominates
the solution found by KBEA,Best Known, MOV-GP
and Modified ABC. However, KBEA with 3 vehicles
dominates Bee-route. In RC208 instance, Bee-route
with 2 and 4 vehicles dominates the solution found
by KBEA. But the solution with 3 vehicles found by
KBEA dominates our solution. We note also that
our algorithm finds the largest approximate Pareto
sets for most of the instances in MOV-GP (Ghoseiri
and Ghannadpour, 2010), IABC (Yao, 2017), Modi-
fied ABC (Alzaqebah and Sana, 2016) and the Best
Known (Solomon, 1987).
4.3 Hypervolume Comparison
The most widely used indicator to evaluate the per-
formance of search algorithms is the hypervolume in-
dicator (Zitzler, 2001). It measures the volume of the
dominated portion of the objective space and is of ex-
ceptional interest as it possesses the highly desirable
feature of strict Pareto compliance. Table 1 shows the
results of the hypervolume metric for Bee-route and
the other evolutionary algorithms. We present in the
first row of Table 1 the algorithms by comparing. For
the first column we find the instances tested. For the
other columns for each algorithm, we show after exe-
cution of the hypervolume code on the Pareto sets of
R1, R2, RC1 and RC2 the results found. We first no-
tice that our algorithm finds hypervolume values that
are largely better than MOV-GP(Ghoseiri and Ghan-
nadpour, 2010), IABC (Yao, 2017), Modified ABC
(Alzaqebah and Sana, 2016) and Best-Known algo-
ICSOFT 2020 - 15th International Conference on Software Technologies
312

Table 1: Comparison of non dominated solutions sets of Bee-route and evolutionary algorithms on the R1 instances set.
Bee-route MOV-GP Best Known KBEA IABC Modified ABC
NV T.dis NV T.dis NV T.dis NV T.dis NV T.dis NV T.dis
R101 17 1631.6 17 1618.3
18 1626.2
19 1618.6 19 1677 19 1650.8 19 1650.8
20 1613.8 20 1651.1 20 1642.8 20 1643.1
R102 16 1440.9
17 1434.2 17 1486.1 17 1486.1 17 1465
18 1425.1 18 1511.8 18 1472.6 18 1480.7
19 1422.8 19 1494.7
R103 12 1229.9
13 1292.6 13 1292.6 13 1207
14 1221.9 14 1287 14 1213.6 14 1240.8
15 1264.2
R104 9 1007.3 9 1007.3
10 1026.4 10 974.2 10 974.2 10 996.2 10 996.2
11 956.1
12 1047.0 12 1047.0
R105 14 1377.1 14 1377.11 14 1390.5
15 1340.5 15 1424.6 15 1360.7
16 1339.1 16 1382.5 16 1369.5
17 1323.5
R106 11 1263.1
12 1252.0 12 1252.0
13 1235.3 13 1270.3 13 1239.9 13 1271.1
14 1227.8
R107 10 1104.6 10 1104.6 10 1126.3
11 1067.8 11 1108.8 11 1074.2
12 1129.9
R108 9 960.8 9 958.6 9 927.8
10 903.1 10 971.9 10 942.8
11 1004.1
R109 11 1061.1 11 1194.7 11 1194.7
12 1040.1 12 1212.3 12 1101.9 12 1028.5
13 1170.5
14 1206.7
R110 10 1112.9 10 1118.8 10 1118.8 10 1088.2
11 1086.8
12 1027.5 12 1156.5 12 1123.3
R111 10 1096.7 10 1096.7 10 1099.4
11 1111.9 11 1054.2
12 1037.1 12 1053.5 12 1101.5
13 1020.8
R112 9 1066.5 9 982.1 9 982.1
10 1044.0 10 1036.9 10 960.5 10 960.6
11 829.0 11 1011.5 11 1019.8
rithms on all the instances. Comparing it with the
KBEA(Tsung-Che and Wei-Huai, 2014) algorithm,
we find that Bee-route results are better except for the
R2 instances, where the approximate Pareto sets of
KBEA(Tsung-Che and Wei-Huai, 2014) are larger but
do not dominate those of Bee-route. On the contrary,
we recall that the non dominated solutions returned by
our algorithm dominates those of KBEA(Tsung-Che
and Wei-Huai, 2014) even for these instances.
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing Problem
313

Table 2: Comparison of non dominated solutions sets of Bee-route and evolutionary algorithms on the R2 instances set.
Bee-route MOV-GP Best Known KBEA Modified ABC
NV T.dis NV T.dis NV T.dis NV T.dis NV T.dis
R201 4 1221.2 4 1351.4 4 1252.3 4 1252.3
5 1181.7 5 1193.2
6 1175.8 6 1171.2
8 1150.9 8 1185.5
9 1148.4
R202 2 1178.6
3 1158.3 3 1191.7 3 1191.7
4 1035.7 4 1091.2 4 1079.3
5 1041.1
7 1037.5 7 1103.1
R203 2 961.1
3 930.6 3 1041 3 939.5 3 939.5
4 927.1 4 901.2
5 877.3 5 995.8 5 890.5
6 978.5 6 874.8 6 958.9
R204 2 812.1 2 825.5 2 825.5
3 1130.1 3 749.4
4 755.8 4 927.7 4 743.2 4 818.4
5 732.8 5 831.8 5 735.8
R205 2 1108.3
3 990.8 3 994.4 3 994.4
4 1087.8 4 959.7
5 954.1
6 826.2 6 1020.5
R206 3 879.1 3 1422.3 3 906.1 3 906.1
3 940.1
4 859.7 4 889.3
5 879.8 5 960.2
R207 2 864.6 2 890.6 2 890.6
3 855.3 3 904.9 3 812.7
4 800.7
5 905.7
R208 2 769.2 2 726.8 2 726.8
3 774.1 3 706.8
4 764.9
R209 3 853.5 3 909.1 3 909.1
4 844.7 4 1008 4 864.1
5 837.9 5 859.3
6 943.1
R210 3 929.3 3 938.5 3 939.3 3 938.5
4 905.5 4 924.7
5 879.6 5 922.2
6 912.5 6 1003.9
R211 2 856.9 2 885.7 2 885.7
3 848.0 3 1101.5 3 778.0
4 778.0 4 1101.5 4 755.9
5 837.6
ICSOFT 2020 - 15th International Conference on Software Technologies
314

Table 3: Comparison of non dominated solutions sets of Bee-route and evolutionary algorithms on the RC1 instances set.
Bee-route MOV-GP Best Known KBEA Modified ABC
NV T.dis NV T.dis NV T.dis NV T.dis NV T.dis
RC101 14 1696.9 14 1650.1
15 1636.5 15 1690.6 15 1624.9
16 1629.4 16 1678.9 16 1634.5
17 1615.2
RC102 11 1586.0
12 1571.18 12 1554.7 12 1554.7
13 1509.4 13 1477.5
14 1442.0 14 1461.3
15 1493.2 15 1492.8
RC103 11 1261.6 11 1261.6
12 1331.8
13 1334.5
14 1273.9
RC104 10 1153.5 10 1135.4 10 1135.4
11 1147.7 11 1177.2 11 1215.6
12 1126.7
RC105 13 1629.4 13 1629.4
14 1592.7 14 1540.1
15 1578.5 15 1611.5 15 1519.2 15 1546.4
16 1536.5 16 1589.4 16 1518.6
RC106 11 1424.7 11 1424.7
12 1385.2 12 1394.4
13 1362.9 13 1437.6 13 1377.3
14 1351.1 14 1425.3 14 1423.1
RC107 11 1222.1 11 1230.4 11 1222.1
12 1263.0 12 1212.8 12 1300
13 1229.7
RC108 9 1153.8
10 1141.2 10 1139.8 10 1139.8
11 1111.2 11 1156.5 11 1117.5
12 1193.6
4.4 Statistical Test
We perform in this section a statistical test to verify
if the results returned by Bee-route are significantly
better than those returned by the the algorithms MOV-
GP (Ghoseiri and Ghannadpour, 2010), IABC (Yao,
2017), Modified ABC (Alzaqebah and Sana, 2016)
and KBEA (Tsung-Che and Wei-Huai, 2014). We use
the Wilcoxon test (Riquelme and Baran, 2005) with a
level of significance (α = 0.05). We test the set of
non-dominated solutions of all instances of R1, R2,
RC1 and RC2 since the approximate Pareto sets of
each instance is not large enough to test each instance
separately.
Table 6 shows that Bee-route algorithm returns
non dominated solutions that are significantly better
than the other evolutionary algorithms almost for
all the instances in both the objectives Number of
Vehicles (N.v) and Total distance (T.d). Thus, the
Wilcoxon Test confirms the performance of our algo-
rithm and show that our algorithm is significantly bet-
ter when compared to the state-of-the-art algorithms
for the multi-objective VRPTW except for some in-
stances where the results are very close and the dif-
ference is not significant.
4.5 CPU Time Comparison
Table 7 shows the average computation time, the
number of runs, and the computing environment for
the compared algorithms Bee-route, MOV-GP (Gho-
seiri and Ghannadpour, 2010), IABC (Yao, 2017) and
KBEA (Tsung-Che and Wei-Huai, 2014). We note
that these values are given as an indication since the
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing Problem
315

Table 4: Comparison of non dominated solutions sets of Bee-route and evolutionary algorithms on the RC2 instances set.
Bee-route MOV-GP Best Known KBEA IABC Modified ABC
NV T.dis NV T.dis NV T.dis NV T.dis NV T.dis NV T.dis
RC201 4 1423.7 4 1406.9 4 1406.9 4 1258.6
5 1298.9 5 1279.6
6 1279.9
7 1254.3 7 1273.5
8 1272.2 8 1308.7
RC202 3 1384.1 3 1365.6 3 1365.6
4 1057.7 4 1369.8 4 1162.5
5 1118.6
6 1020.1
8 1099.5 8 1167
RC203 3 1069.1 3 1049.6 3 1049.6 3 1083.6
4 1045.4 4 1060 4 945.1
5 1039.1 5 926.8
6 906.5 6 1014.7
RC204 2 926.5
3 819.3 3 901.4 3 798.4 3 798.4 3 799.1
4 788.6 4 881.8
RC205 4 1282.2 4 1410.3 4 1297.6 4 1297.6 4 1321.3
5 1246.2 5 1236.7
6 1187.9
7 1161.8 7 1210.6
RC206 3 1146.3 3 1146.3 3 1171.2
4 1095.7 4 1194.8 4 1081.8
5 1012.6 5 1068.7
6 1112.3
7 1054.6
RC207 2 1028.9
3 1014.5 3 1061.1 3 1061.1 3 1096.5
4 998.7 4 1040.6 4 1001.8
5 982.5
6 966.3
7 1059.6
RC208 2 909.1
3 856.4 3 898.5 3 828.1 3 828.1 3 833.9
4 845.9 4 783.1
5 882.1
different algorithms are tested on different comput-
ers. However, Bee-route demonstrates the ability to
produce high quality solutions in shorter CPU times.
5 CONCLUSION
This article proposes a Bee-route algorithm based on
the artificial bee colony metaheuristic for the multi-
objective vehicle routing problem with time win-
dow. The proposed algorithm Bee-route is applied
on a well-known benchmark of VRPTW. Experiments
show that the algorithm returns non dominated solu-
tions that are significantly better than those obtained
by evolutionary algorithms from the state of the art
and also the best solution reported by the benchmarks.
In fact the non-dominated solutions returned by Bee-
route dominate those returned by the other algorithms
for most of the tested instances.
The proposed algorithm finds the largest approximate
Pareto sets almost at all times, and a well distributed
front. But KBEA finds a set of non-dominated
solutions larger than that of D-MABC for 18 in-
stances. However, hybridizing our algorithm with
ICSOFT 2020 - 15th International Conference on Software Technologies
316
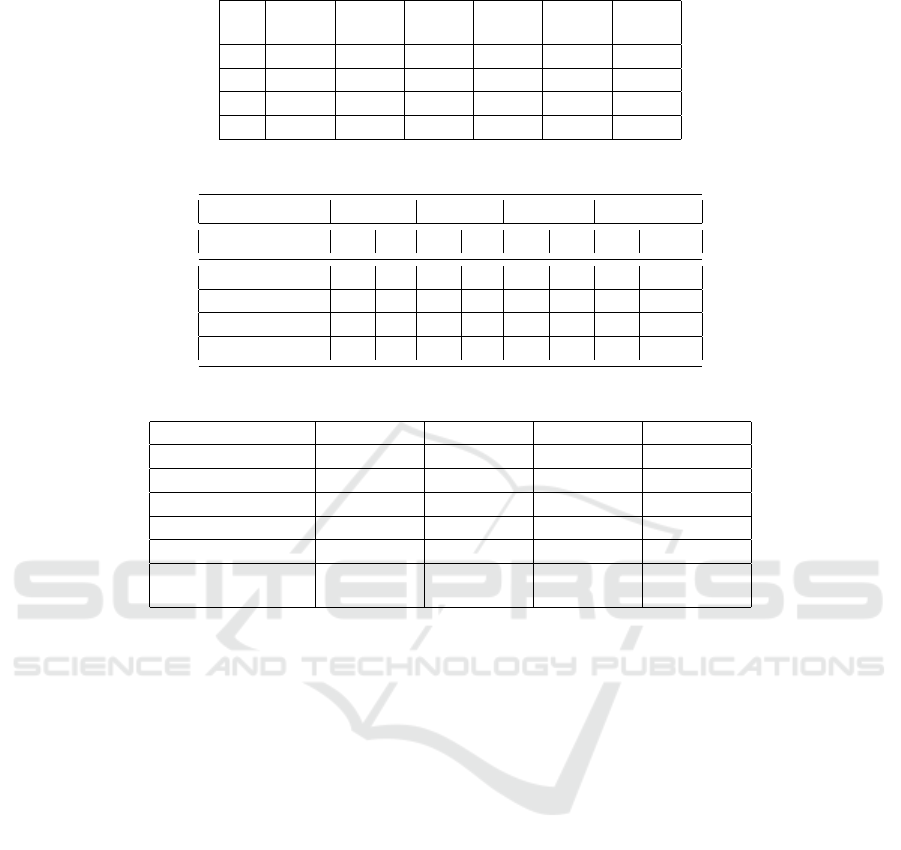
Table 5: Hypervolume metric values for Bee-route and evolutionary algorithms.
Bee-
route
MOV-
GP
Best-
Known
KBEA IABC Modified
ABC
R1 6.71E+05 6.70E+05 5.96E+05 6.60E+05 4.67E+05 6.57E+05
R2 8.31E+04 4.20E+04 2.00E+04 9.54E+04 n/a 7.58E+04
RC1 4.72E+05 4.32E+05 3.33E+05 4.60E+05 n/a 4.18E+05
RC2 8.56E+04 4.32E+04 2.25E+04 8.37E+04 2.11E+04 8.37E+04
Table 6: Comparative set of distance solutions in Bee-route and evolutionary algorithms with Wilcoxon Test.
W.TEST MOV-GP KBEA IABC Modified ABC
N.v T.d N.v T.d N.v T.d N.v T.d
Bee-route R1 + + + + + + + +
Bee-route R2 + + + - n/a n/a + +
Bee-route RC1 + + + + n/a n/a + +
Bee-route RC2 + + + + + + + +
Table 7: Average computation time, computing environments, and number of runs.
Algorithm MOV-GP KBEA Bee-route IABC
Avg comput time (s.) R1 > 500 11.7 9.9 39.98
R2 > 900 22.7 16.2 n/a
RC1 > 500 10.4 7.6 n/a
RC2 > 1300 19.1 10.3 22.5
runs 10 10 10 20
CPU/Language 1.6
GHz(Matlab)
Intel i7-3770
3.4 GHz (C++)
Intel i5-2520M
2.5 GHz (C++)
n/a
other heuristics could diversify more the approximate
Pareto sets and large the number of non dominated
solutions. Bee-route could also be a promising ap-
proach for other multi-objective problems with more
than two objectives to optimize. In future works, we
want to combine our algorithm with other heuristics
of the state of the art. We can combine the ABC algo-
rithm with other metaheuristics in order to widen the
space of the Pareto front. Also we can solve other ver-
sions of the problem of VRP like the Vehicle Routing
Problem with Pickup and Delivery, the Vehicle Rout-
ing Problem with Multiple Trips, the Open Vehicle
Routing Problem, etc.
REFERENCES
Alaya I., Sammoud O., H. M. G. K. (2003). Ant colony
optimization for the k-graph partitioning problem. In
The 3rd Tunisia-Japan Symposium on Science and
Technology (TJASST).
Alzaqebah, Malek. Salwani, A. and Sana, J. (2016). Modi-
fied artificial bee colony for the vehicle routing prob-
lems with time windows. In SpringerPlus. 5(1398),
1-12.
Alzaqebah, M., Jawarneh, S., Sarim, H. M., and Abdullah,
S. (2018). Bees algorithm for vehicle routing prob-
lems with time windows. International Journal of Ma-
chine Learning and Computing, 8(3):236–240.
Br
¨
aysy, O. and Gendreau, M. (2005). Vehicle routing prob-
lem with time windows, part i: Route construction and
local search algorithms. In Transportation science.
39(1), 104-118.
Ghaleini E. N., Koopialipoor M., M. M. S. M. E. M. T. G. B.
(2018). A combination of artificial bee colony and
neural network for approximating the safety factor of
retaining walls. In Engineering with Computers. 8(8),
1-12.
Ghoseiri, K. and Ghannadpour, S. (2010). Multi-objective
vehicle routing problem with time windows using goal
programming and genetic algorithm. In Applied Soft
Computing. 10(4), 1096-1107.
Lim, A. and Zhang, X. (2007). A two-stage heuristic with
ejection pools and generalized ejection chains for the
vehicle routing problem with time windows. In IN-
FORMS Journal on Computing. 19(3), 443-457.
Riquelme, N., V. L. C. and Baran, B. (2005). Perfor-
mance metrics in multi-objective optimization. In
Latin American Comp. Conf. (CLEI). 10(13), 1-11.
Shaoqiang, Y. Cuicui, T. Y. L. and Linjie, G. (2016). An im-
proved artificial bee colony algorithm for vehicle rout-
ing problem with time windows, a real case in dalian.
In Advances in Mechanical Engineering. 8(8), 1-9.
Solomon, M. (1987). Algorithms for the vehicle routing and
Bee-route: A Bee Algorithm for the Multi-objective Vehicle Routing Problem
317

scheduling problem. In Operations Research. 35(2),
254-265.
Tsung-Che, C. and Wei-Huai, H. (2014). A knowledge-
based evolutionary algorithm for the multiobjective
vehicle routing problem with time windows. In Com-
puters and Operations Research. 45(4), 25-37.
Yao, B. Yan, Q. Z. M. Y. Y. (2017). Improved artificial
bee colony algorithm for vehicle routing problem with
time windows. In PLoS ONE. 12(9).
Zitzler, E., r. (2001). Hypervolume met-
ric calculation. In Computer Engi-
neering and Networks Laboratory (TIK).
ftp://ftp.tik.ee.ethz.ch/pub/people/zitzler/hypervol.c.
Zouari W., Alaya I., T. M. (2017). A hybrid ant colony al-
gorithm with a local search for the strongly correlated
knapsack problem. In AIEEE/ACS 14th International
Conference on Computer Systems and Applications.
527-533.
ICSOFT 2020 - 15th International Conference on Software Technologies
318
