
Interval-based Sound Source Mapping for Mobile Robots
Axel Rauschenberger and Bernardo Wagner
Real-Time Systems Group (RTS), Institute for Systems Engineering,
Leibniz Universit
¨
at Hannover, Appelstraße 9A, D-30167, Hannover, Germany
Keywords:
Mobile Robotics, Sound Source Mapping, Robot Audition, Interval Analysis.
Abstract:
Auditory information can expand the knowledge of the environment of a mobile robot. Therefore, assigning
sound sources to a global map is an important task. In this paper, we first form a relationship between the
microphone positions and auditory features extracted from the microphone signals to describe the 3D position
of multiple static sound sources. Next, we form a Constraint Satisfaction Problem (CSP), which links all
observations from different measurement positions. Classical approaches approximate these non-linear system
of equations and require a good initial guess. In contrast, in this work, we solve these equations by using
interval analysis in less computational effort. This enables the calculation being performed on the hardware of
a robot at run time. Next, we extend the approach to model uncertainties of the microphone positions and the
auditory features extracted by the microphones making the approach more robust in real applications. Last,
we demonstrate the functionality of our approach by using simulated and real data.
1 INTRODUCTION
Auditory perception has an important meaning in hu-
man life. In order to improve the human-robot inter-
action (HRI), robots also need to be capable of an-
alyzing acoustic signals. Thus, much research has
been done in the field of Robot Audition (Argentieri
et al., 2015), (Rascon and Meza, 2017). For vari-
ous tasks it is important to estimate the direction to a
sound source, which is addresses in the field of Sound
Source Localization (SSL). Recently, Sound Source
Mapping (SSM) became a new challenge. Here, the
goal is to assign the position of sound sources to a
map. Possible applications are localization of miss-
ing people in a disaster scenario. Overall, the result
of the mapping approach depends on:
1. Knowledge about the positions of the microphone
in a global map.
2. Auditory features extracted from the microphone
signals. Here, a major role depends on the Time
Difference of Arrival (TDoA), which describes the
time offset a signal reaches a pair of microphones.
However, the listed items cannot be determined with-
out any error, due to measurement and modeling un-
certainty.
For instance, the localization result of a mobile
robot in a global map deviates from its true position.
x
map
y
map
Robot Position
Robot Position:
Estimated by
Localization
Sound Source
Front-back
ambiguity
Direction towards
sound source
Estimated Direction
towards sound source
(a) Challenges of SSM. (b) Interval-based approach.
Figure 1: Challenges of SSM and our solution.
Therefore, a direction measurement to a sound
source does not correspond to the true origin (cf. Fig.
1a). Consequently, the result of combined direction
measurements from different positions (e.g. by trian-
gulation) contains an error. Another problem occurs,
if the microphone positions are incorrectly specified
according to the reference coordinate system of the
mobile robot. This systemic error influences the di-
rection measurement.
Further on, due to typical geometrical symme-
tries of the arrangement of microphones, ambigui-
ties can arise, making it impossible to distinguish be-
tween a sound source coming from the front or the
back (Front-back ambiguity). Specifically, the field
of Binaural Audition, which uses only a single pair of
microphones (representing human ears), suffers from
this problem.
Unfortunately, in the classical approaches less at-
Rauschenberger, A. and Wagner, B.
Interval-based Sound Source Mapping for Mobile Robots.
DOI: 10.5220/0009832803350345
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 335-345
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
335

tention is paid to address the uncertainties leading to
the mentioned problems. Therefore, in this paper,
an approach for mapping the 3D position of multiple
sound sources is developed, which is able to tackle
the aforementioned issues. Hereby, we will focus on
static sound sources.
First, we describe the physical relationship be-
tween the microphone positions and the TDoA mea-
surements (cf. Section 4). This relationship takes the
front-back ambiguity into account. However, solving
the resulting non-linear system of equations is a chal-
lenging task. Fortunately, by using methods based on
a special case of computation on sets (introducing in
Section 3.1) - so called interval analysis (Jaulin et al.,
2001) - we are able to solve the equations without
any approximation and less computational effort com-
pared to classical approaches. This is an important re-
quirement for performing the 3D SSM using the hard-
ware of a mobile robot at run time. Next, Section 5
shows our interval-based approach to solve the cor-
responding Constraint Satisfaction Problem (CSP).
As a consequence, the sound source positions are de-
scribed by boxes, depicted in Figure 1b). Afterwards,
we use another benefit of the interval analysis and ex-
tend our approach to model the uncertainty of the mi-
crophone positions (cf. Section 6). Next, we propose
a novel method to estimate the TDoA from the micro-
phone signals and describe their uncertainty (cf. Sec-
tion 7). By doing this, our approach is getting more
robust in real applications. Finally, Section 8 presents
an evaluation in the simulation and in a real experi-
ment, which shows the feasibility of our approach (cf.
Section 8).
In summary, the main contributions of our
Interval-Based Sound Source Mapping (IB-SSM)
are:
• Taking front-back ambiguity into account
• Low computational effort, making it applicable
using on the hardware of a robot
• Novel method for estimating the TDoA from di-
rection measurements
• Modeling uncertainty of microphone positions
and TDoA using intervals
2 RELATED WORK
Existing approaches for SSM can be divided into two
categories. The first category based on ray trac-
ing. These approaches assume, that the origin of a
sound source corresponds to a visible feature in a
map. Therefore, a so-called occupied grid is used,
which contains the information if grids of a geomet-
ric map are occupied or free. Next, due to SSL the
directions to the sound sources are estimated. Grids
intersecting by a ray toward this direction are assigned
with a probability representing the position of a sound
source. The main advantage of this approach is, that
with a single measurement may calculate the position
of a source. Therefore, (Kallakuri et al., 2013) uses
a 2D LiDAR to generate the occupied grid. How-
ever, the approach fails if sound sources are outside
the plane of the LiDAR (e.g. loud speaker on a table
or mounted on the ceiling). Therefore, (Even et al.,
2017) extend the approach by using a 3D LiDAR.
Disadvantages are larger cost of computation and in-
tegration of additional hardware, which cannot be ex-
tended to all existing robotic systems. Moreover, it is
assumed that sound can not pass occupied grids. As a
result, acoustical transparent materials or low walls in
front of a sound source, will be assigned with a high
probability representing a sound source.
The second category based on localization strate-
gies as Triangulation (Sasaki et al., 2010), FastSLAM
(Hu et al., 2011), Monte Carlo localization (Sasaki
et al., 2016) and Particle Filter (Evers et al., 2017). In
contrast to the first category, measurements from vari-
ous directions need to be conducted. To overcome this
drawback (Su et al., 2016) a three layered approach is
proposed, which combines acoustic ray casting with
triangulation from (Sasaki et al., 2010). However, the
triangulation approach assumes that most cross-points
of different directions are close to the true sound po-
sition which may not be true. Further on, both cate-
gories do not address the front-back ambiguity. More-
over uncertainties for the microphone position and the
TDoA are not fully taken into account. (Sasaki et al.,
2016) models the uncertainty of a direction measure-
ment with an zero-mean Gaussian distribution. How-
ever, if the measurements are biased (i.e. they exhibit
a systematic error, due to e.g. inaccurate knowledge
about the microphone positions) this assumption will
not be true.
3 INTERVAL ANALYSIS
After introducing the interval analysis, we motivate
their usage for the task of sound source mapping.
3.1 Basics
The accuracy of a distance measurement with a fold-
ing ruler is usually ±1 mm. Here, the idea of interval
analysis arises (Jaulin et al., 2001). Instead of speci-
fying an exact value or a stochastic distribution, lower
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
336

and upper bounds are used, defined respectively by x
and x. We assume the true measurement is enclosed
in the interval [x] = [x,x]. However, no assumption is
made as to which value is most likely. By conducting
the intervals of two distance measurements A = [9,10]
and B = [2, 3] from the same reference point, we cal-
culate their interval distance as follows:
[9,10]− [2,3] = [9 − 3,10 − 2] = [6,8]. (1)
Hence, it is guaranteed that the distance is between
6 and 8. More dimensional intervals are represented
as an interval vector [x], resulting in an interval box.
Furthermore, given a measurement Y ∈ R
m
(e.g. the
TDoA) and a non-linear measurement function f :
R
n
→ R
m
the relationship to an unknown set X (e.g.
the position of the sound sources) is characterized as
follows:
X = {x ∈ R
n
| f(x) ∈ Y} = f
−1
(Y). (2)
The unknown set X can be calculated with a branch
and bound algorithm Set Inversion Via Interval Anal-
ysis (SIVIA) (Jaulin et al., 2001). Another approach
is to formulate f as a Constraint Satisfaction Prob-
lem (CSP) and use so-called contractors (Chabert and
Jaulin, 2009). The main idea is to start with an initial
search space containing a set of boxes. On each box
a calculation is performed and inconsistent parts are
removed, resulting in a smaller box.
3.2 Application to SSM
As we will show in Section 5, the main advantage of
using interval analysis in SSM is the simple method-
ology of solving the CSP resulting from the relation-
ship between the microphone signals (represented by
the TDoA) and their position. The solution (possible
position of sound sources) is represented by a set of
interval boxes. After conducting a subsequent mea-
surement from a different position, a new restriction is
added to the CSP. Fortunately, by using interval anal-
ysis, this process can be performed by the intersection
of the interval boxes of the previous solution. Impor-
tantly, both the microphone position and the TDoA
can also be modeled as interval boxes. By doing this,
the solution of the CSP will result in larger interval
boxes, compared to fixed values for both quantities.
However, uncertainties can be modeled in a simple
manner, making it applicable for real scenarios.
First, the accuracy of the transformation between
the microphones and the reference coordinate sys-
tem at the robot is affected by the used calibration
method. This knowledge needs to be integrated to
the transformation by specifying an interval box [x].
Next, the localization accuracy of the robot within the
map depends on the used sensor and the resolution
of the map. (Langerwisch and Wagner, 2012) pro-
pose an interval-based approach for guaranteed robot
localization. In (Sliwka et al., 2011) interval meth-
ods are used in the context of robust localization of
underwater robots. Furthermore, extracting multiple
TDoA’s from the microphone signals in a noisy envi-
ronments is a challenging task. In many cases an es-
timation is given by extracting peaks from the cross-
correlation function. However, signals are sampled
at a discrete timestamp. Therefore, the uncertainty of
the TDoA highly depends on the sampling frequency.
A interval-based method to estimate the timestamps
between two sensors are proposed in (Voges and Wag-
ner, 2018).
4 PROBLEM DEFINITION AND
NOTATION
Let us assume, various sound sources s ∈ {1,...,n
s
}
are emitting acoustical signals with the velocity of
sound c in the current environment. n
s
is the total
number of sources, which is unknown in advance.
Their positions are characterized by x
s
∈ R
3
. Fur-
ther, a mobile robot perceives these acoustic signals
using a microphone array, equipped with n
m
micro-
phones. We model the relationship between micro-
phone pairs. Therefore, we denote the first and second
position of a microphone pair i ∈ {1,..., n
p
} as x
(n)
m
P
i,1
and x
(n)
m
P
i,2
∈ R
3
. n
p
is the total number of used micro-
phone pairs. Due to the movement of the robot, the
positions of the microphones are changing. There-
fore, the superscript n ∈ {1,.., n
l
} denotes the index
of location and n
l
is the total number of locations.
Moreover, the time a signal arrives at the first and
the second microphone results in a time difference -
so-called Time Difference of Arrival (TDoA) - which
we denote as
(s)
∆t
(n)
i
. The superscript s indicates the
TDoA resulting from source s. Further, the TDoA
depends on the position of microphone pair i at loca-
tion index n. Finally, we form a relationship between
the position of a microphone pair and the TDoA mea-
sured for a single source s as followed:
||x
(n)
m
P
i,1
− x
s
||
2
− ||x
(n)
m
P
i,2
− x
s
||
2
=
(s)
∆t
(n)
i
· c. (3)
For an easier understanding we show the relation-
ship in Fig. 2a dropping the superscript (n). It can
be noted that, the left-hand side of Equation (3) con-
tains the geometrical properties of the microphone
configuration, whereas the right-hand side includes
the measurements of the microphone pair in form of
Interval-based Sound Source Mapping for Mobile Robots
337
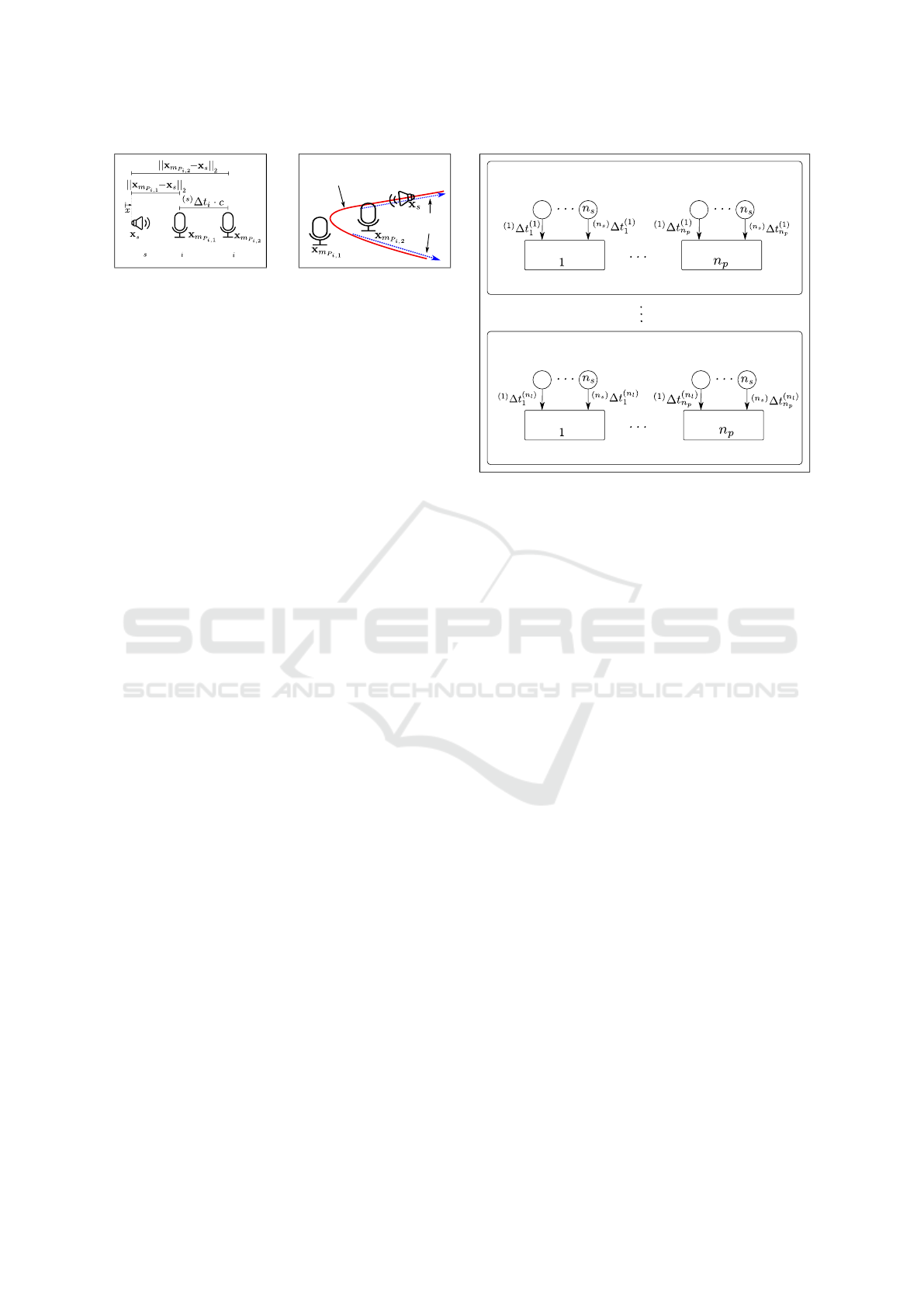
First microphone
from pair
Second microphone
from pair
Sound
Source
(a) Relationship between the position
of a microphone pair and the TDoA
given in Equation (3).
Possible position of
sound source s
Front-back
ambiguity
(b) The position of a sound source is
located on a hyperbolic curve (red) for
a given TDoA.
Figure 2: Relationship between microphone signals and
their position.
the TDoA. As indicated in Figure 2b the solution of
Equation (3) for a fixed TDoA is located on a hyper-
bolic curve. By making the assumption that a sound
source is far away (far field assumption), two feasi-
ble directions towards the sound sources can be occur,
which represents the front-back ambiguity (cf. Fig.
2b). In contrast to presented methods in Section 2, we
do not restrict our approach to these directions. In-
stead we use the information of the hyperbolic func-
tion to infer the sound position.
Next, Equation (3) only describes the relation-
ship between a single microphone pair for one sound
source at one measurement position. However, each
microphone pair perceives various sound sources at
different measurement positions (cf. Fig. 3). Thus,
the total number n
t
of equations is stated as follows:
n
t
= n
s
· n
p
· n
l
. (4)
Therefore, we integrate all equations into a mathemat-
ical system, which needs to be solved. Due to the high
non-linearity and restriction between all equations,
this is a challenging task. Classical approaches lin-
earize each equation through a second order Taylor-
series expansion (Foy, 1976), but suffer from inten-
sive computation and require a good initial guess. In
contrast to these approaches an interval-based method
is proposed in (Reynet et al., 2009). Though, Equa-
tion (3) is solved in a different context of localizing
the origin of an electromagnetic wave emitting source
by using three static receivers for a known TDoA. We
found that this approach can be applied to our prob-
lem. Therefore, we define the methodology in the
next Section.
5 RESULTING CONSTRAINT
SATISFACTION PROBLEM
In this Section we calculate a set of interval boxes
which includes all sound sources positions of the en-
vironment.
Sound Sources
1
Microphone pair
Measurement position 1
Sound Sources
1
Microphone pair
Measurement position n
l
Sound Sources
1
Microphone pair
Sound Sources
1
Microphone pair
Figure 3: Equation (3) needs to be fulfilled for all micro-
phone pairs, all sound sources at all measurement positions.
Therefore, we formulate Equation (3) as a CSP as
follows:
H :
Variables: x
s
Constants: x
(n)
m
P
i,1
,x
(n)
m
P
i,2
,
(s)
∆t
(n)
i
,c
Contraints:
1. ||x
(n)
m
P
i,1
− x||
2
− ||x
(n)
m
P
i,2
− x||
2
=
(s)
∆t
(n)
i
· c
Domains: [x
s
],[x
(n)
m
P
i,1
],[x
(n)
m
P
i,2
],[
(s)
∆t
(n)
i
],[c]
Depending on the assignment of the domain, we are
able to model uncertainties. Furthermore, if the do-
main of the values are selected in a proper way, it can
be guaranteed that the true solution is included. How-
ever, specifying these bounds is a challenging task.
The bounds of the velocity of sounds c depend on the
range of temperature in the environment. In this work,
we set the bounds for the microphone positions as ex-
plained in Section 6. In Section 7, we show the pro-
cess of estimating the bounds for the TDoA from the
microphone signals.
To solve the CSP H we use the branch and bound
algorithm Set Inversion Via Interval Analysis (SIVIA)
(Jaulin et al., 2001) and a forward-backward contrac-
tor (Chabert and Jaulin, 2009), which we denote with
(s)
C
(n)
i
. The main idea is that we start with an ini-
tial box [x] containing the full dimension of the con-
sidered environment. Afterwards, we perform calcu-
lations on [x] using the contractor
(s)
C
(n)
i
, which re-
moves inconsistent parts of [x].
The formulated CSP describes the position of a
single sound source s according to one microphone
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
338

pair i at the measurement position n. However, the
position of s needs to be included in all equations cor-
responding to the other microphone pairs. Therefore,
in the first step we need to identify all equations at
the position n describing the relationship to the sound
source s (cf. Section 7). Afterward, due to the ben-
efits of interval analysis, we form a single contractor
for all of these microphone pairs, by intersection of
the corresponding contractors:
Contractor Source s:
(s)
C
(n)
=
n
p
\
i=1
(s)
C
(n)
i
. (5)
To visualize the applied methodology, we illus-
trate the mapping of a sound source in the schematic
draw in Fig. 4. The signals of two sources s
1
and
s
2
are perceived by a mobile robot at position n and
n + 1. Additionally, at position n a reflection s
r
from
sound source s
2
occurs. At each position and for each
sound source a contractor
(s)
C
(n)
is calculated. Using
each contractor separately on [x] results in five areas,
which are not linked. To solve this, we first combine
all contractors corresponding to the same position, by
calculating the union as follows:
Contractor at Position n: C
(n)
=
n
s
[
s=1
(s)
C
(n)
. (6)
Last, intersecting both contractor at position n and
n + 1, results in the final contractor, which is used
to calculate the solution after collecting all measure-
ments.
Final Contractor: C =
N
l
\
n=1
C
(n)
. (7)
It is important to note, that these approach enable
to handle wrong direction measurements caused by
reflections. As, calculating the intersection results in
an empty set for areas corresponding to the reflec-
tions.
In summary, our Interval-Based Sound Source
Mapping (IB-SSM) is shown in Algorithm 1. After
conducting a measurement at position n (cf. line 4)
the intervals for the microphone positions (cf. line 5)
and for the TDoA (cf. line 6) are estimated. Next, the
contractor from Equation (6) is calculated (cf. line 7).
Afterward, the previous solution (or the initial domain
if first measurement is conducted) is reduced by using
the contractor and SIVIA (cf. line 8). In contrast to
building the final contractor C from Equation (7) after
conducting all measurements, the proposed algorithm
benefits from new information directly after conduct-
ing a measurement. This enables optimal positions to
be calculated at run-time making it feasible to result
in a more accurate solution.
Robot at
Position n
Robot at
Position n+1
x
map
y
map
Sound
Source s
2
Sound
Source s
1
Trajectory
from Position
n to n+1
Reflection of s
2
Figure 4: Simplified representation of the contracted areas.
Algorithm 1: Pseudo-Code: IB-SSM.
Input: Initial Domain: [x], Number of Positions: n
l
Output: Contracted Domain [x
c
]
1: for n = 1 to n
l
do
2: p ← getNextMeasurementPosition(n)
3: driveToPosition(p)
4: z ← takeMeasurement(p)
5: [m] ← calcIntMicPos(p) cf. Section 6
6: [t] ← calcIntTDoA(z) cf. Section 7
7: C ← buildContractor([m],[t]) cf. Section 5
8: [x
c
] ← contractBoxes(C ,[x]) cf. Section 5
9: [x] ← [x
c
]
10: end for
6 INTERVAL-BASED
MICROPHONE POSITION
In order to solve the CSP from Section 5 the micro-
phone positions need to be known. In our proposed
approach we model the following aspects:
1. Error of microphone position in the coordinate
system of the mobile platform
2. Localization error of the mobile platform
First, we measure the translation t
m
i
∈ R
3
between a
fixed coordinate system on the platform to the center
of a microphone membrane m
i
. This translation is the
outcome of a calibration process. Here, we do not as-
sume any directivity of the microphones, therefore no
orientation is modeled. Last, depending on our cal-
ibration method we extend t
m
i
in all dimension with
an uncertainty t
u
m
i
∈ R
3
and model the result as an in-
terval box [t
m
i
− t
u
m
i
,t
m
i
+ t
u
m
i
]. Great attention has to
be given to these bounds. However, even for a poor
Interval-based Sound Source Mapping for Mobile Robots
339
calibration it can be guaranteed, that the true position
of the sound sources are included in the result of our
SSM approach, if proper bounds are selected.
Second, the transformation from the coordinate sys-
tem of the mobile platform to a global map is given
as:
(map)
x
m
i
= R
map
rob
·
(rob)
x
m
i
+t
map
rob
. (8)
t
map
rob
denotes the translation from the mobile coordi-
nate system to the map coordinate system.
R
map
rob
∈ SO(3) models the rotation. Because the
movement of the mobile platform is restricted to the
XY-plane, a rotation only occurs around the z-axis.
Thus, R
map
rob
can be described as follows:
R
map
rob
=
cos(α) −sin(α) 0
sin(α) cos(α) 0
0 0 1
. (9)
Depending on the used localization algorithm the
translation t
map
rob
is extended with an uncertainty e.g.
described above. Here, special consideration needs to
be paid to the resolution of the used map. Next, the
bounds for the angle α need to be specified.
7 INTERVAL-BASED TIME
DIFFERENCE OF ARRIVAL
The time differences of microphone pairs are required
in order to solve the CSP in Section 5. Fig. 3 shows
that a single microphone pairs needs to distinguish
TDoA’s corresponding to n
s
different sources. With-
out any additional knowledge about the characteris-
tics of the signals it is a challenging task. Follow-
ing approaches can be used to address the problem of
finding intervals for the TDoA:
1. Interval-based approach using the raw micro-
phone signals
2. Direction measurements through state-of-the-art
methods from the field of Sound Source Localiza-
tion (SSL) combined with tracking methods
It should be noted, that the first approach is the best
choice in order to calculate guaranteed bounds for the
time differences.
However, addressing this problem without any
knowledge about the characteristics (e.g frequency
range of signals) is hard to handle. We do not as-
sume about these characteristics, resulting in a higher
range of applications. Due to the robustness against
noise in real applications, by using tracking methods
with existing SSL, we focus on the second approach.
By doing this, existing SSL systems can be easily
extended to perform SSM. The most promising ap-
proaches for SSL are subspace methods derived from
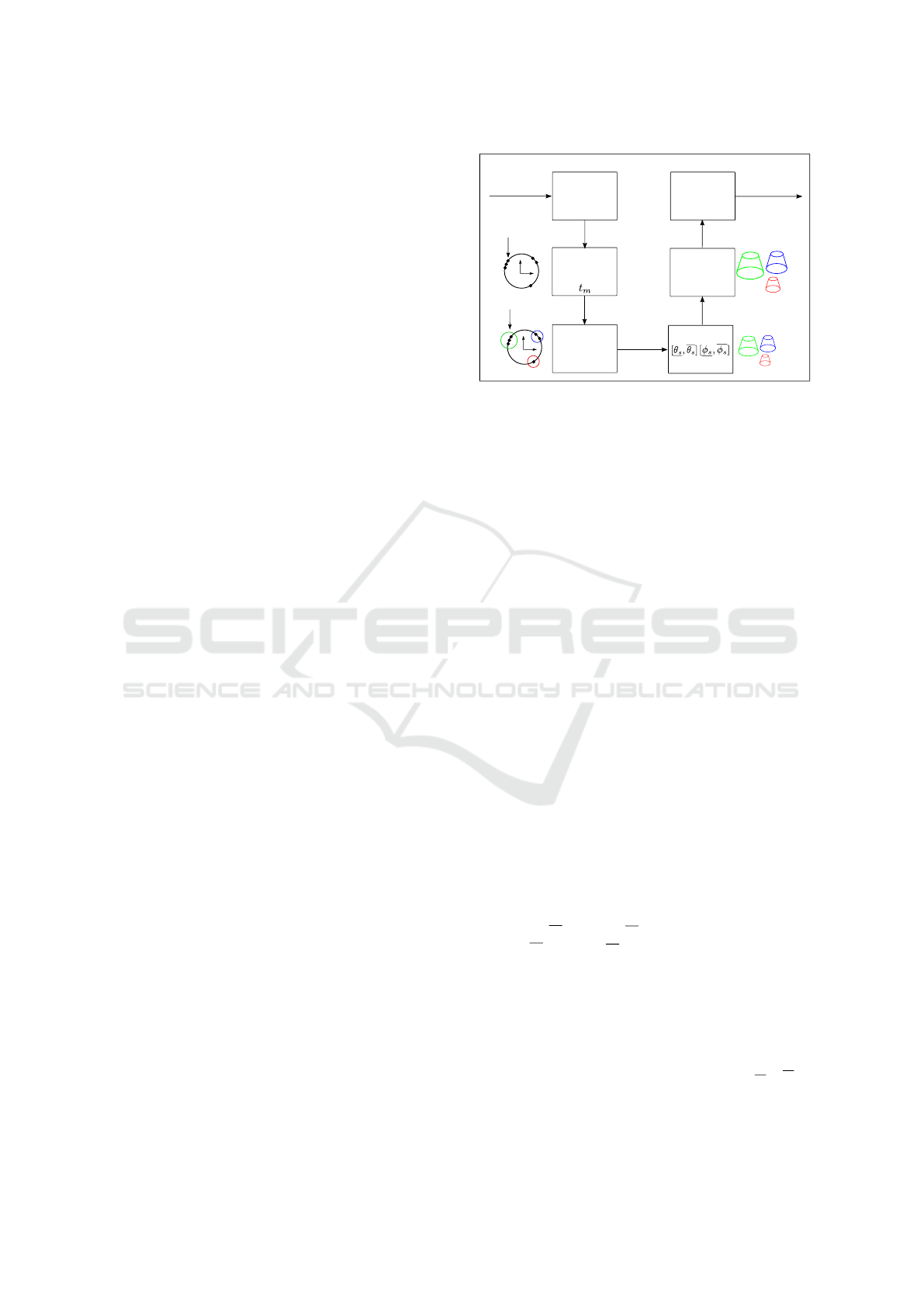
Input:
Microphone
Signals
SSL
(e.g. SRP-PHAT,
MUSIC)
+
M3K method
Tracked
Directions
Collect
Directions
Measurement
Duration:
Collected
Directions
Cluster
Directions
K-mean
Clustering
Clustered
Directions
Calculate
Angle Bounds
for each cluster
s
Add System
bounds
SSL-Resolution
Calculate
Time Difference
+
Append
Sampling Error
Extended Cone
Segments
Cone
Segments
x
y
x
y
Direction projected
on unit sphere
Cluster
Output:
Time Difference
Interval for each
Cluster
Figure 5: Pipeline for calculating the time difference inter-
vals.
MUSIC (Schmidt, 1986) e.g. GEVD-MUSIC (Naka-
mura et al., 2009) and beamforming-based methods
e.g. SRP-PHAT (Do et al., 2007). A comprehen-
sive review of existing SSL approaches is given in
(Rascon and Meza, 2017). These approaches esti-
mate the Direction of Arrival (DoA) to a sound source
s represented by azimuth (horizontal angle) θ
s
and
φ
s
(vertical angle). The angle conventions are given
in Fig. 6. However, the direct result of these algo-
rithms without any post-processing is not practical in
real experiments. For this reason, we use a modified
3D Kalman (M3K) method proposed in (Grondin and
Michaud, 2019). The direction of the SSL is classified
as three possible states: diffuse noise, emitting from
a new sound source, or emitting from a tracked sound
source. For the following and our experiments in Sec-
tion 8.2 we only use directions from tracked sources.
Furthermore, using SSL algorithms in practice,
the system is getting more robust against noise by col-
lecting various measurements in a specific duration of
time t
m
. We assume all sound sources s being active
for at least 20 percent of this time. A set of direc-
tions is computed after the measurement (see Fig. 5).
Hence, we cluster these directions characterized by
projecting the directions on a unit sphere - by the k-
mean algorithm.
We calculate for each cluster the bounds for the
angles [θ
s
,θ
s
] and [φ
s
,φ
s
] by selecting the minimal
and maximal values. Attention should be paid to
the angle resolution of the used SSL algorithm and
it needs to be appended at the intervals for θ
s
and φ
s
.
In order to prevent collisions with the sound
sources and to eliminate disturbances by the
robot/sensor setup itself we restrict all sound sources
s being located at least with the minimal distance r
s
to
the microphone array. The maximal distance r
s
results
from the structure of the room. Altogether, the posi-
tion of each sound source is assumed being located in-
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
340

Sound Source
(a) 3D view: Bounds [r
s
,r
s
] for radius r.
Sound Source
(b) XY-Plane: Bounds [θ
s
,θ
s
] for az-
imuth θ.
Sound Source
(c) XZ-Plane: Bounds [φ
s
,φ
s
] for ele-
vation φ.
Figure 6: Segment cone.
side a cone segment con
s
([φ
s
,φ
s
],[θ
s
,θ
s
],[r
s
,r
s
]) ∈ R
3
visualized in Figure 6a.
It is quite important to underline that, due to front-
back confusion, the sound sources may not be in-
cluded in this area. As a conclusion, the area of
the cone segment can not directly be used to infer
the sound source positions. Instead, the time differ-
ences resulting from points inside the segment cone
x
c
∈ con
s
and the position of a pair of microphones
can be used to solve this problem by computing the
CSP in Section 5. As a result we obtain an interval
[
(s)
t
(n)
i
,
(s)
t
(n)
i
] which describes the minimal and max-
imal time difference for each microphone pair i ac-
cording to the cone segment for a single sound source
s. There, the calculation is given as:
(s)
t
(n)
i
=
1
c
(||x
(n)
m
P
i,1
− x
c
||
2
− ||x
(n)
m
P
i,2
− x
c
||
2
),
(s)
t
(n)
i
= min
x
c
(s)
t
(n)
i
,
(s)
t
(n)
i
= max
x
c
(s)
t
(n)
i
.
(10)
However, even this interval may not include the true
TDoA in a real application due to the discrete sam-
pling of the microphone signals. For instance, a signal
reaches at t
1
= 0.95 ms the first and at t
2
= 0.3 ms the
second microphone. By selecting the sampling time
t
s
= 0.2 ms of the acoustic signal, both values can not
be perceived accurately. Instead, we build an interval
as follows:
[a] = [t
1
−t
s
,t
1
+t
s
] = [0.75, 1.15]
[b] = [t
2
−t
s
,t
2
+t
s
] = [0.1, 0.5].
As a result the time difference is calculated as follows:
[a] − [b] =
[t
1
−t
2
− 2 ·
1
f
s
,t
1
−t
2
+ 2 ·
1
f
s
] =
[0.25,1.05].
Therefore, it is guaranteed, that the time difference
is between 0.25 ms and 1.05 ms. To enable a com-
parison to real applications, the sampling frequency
usually is in the range of 8000 to 96000 Hz resulting
in a sampling time of 0.01 ms to 0.125 ms.
We use these description of modeling uncertain-
ties to extend the interval of time differences as fol-
lows:
(s)
t
(n)
i
= [
(s)
t
(n)
i
−
2
f
s
,
(s)
t
(n)
i
+
2
f
s
] =
[
(s)
t
(n)
i
− ∆t
e
,
(s)
t
(n)
i
+ ∆t
e
].
Here, ∆t
e
describes the extension of the interval,
which we denote as TDoA sampling extension.
8 SIMULATION AND
EXPERIMENTAL RESULTS
We validated our approach using simulated and real
data. Various simulations were conducted showing
the capabilities of our approach. First we showed
that the solution of our approach contains in all cases
the true sound source position if we are using ground
truth data. Next, we conducted various experiments
showing the influence of different parameters to the
solution of our approach. Furthermore we showed the
feasibility of our approach to handle systematic errors
(inaccurate robot localization). Finally, we performed
a experiment showing the feasibility of our approach
in a real environment.
8.1 Simulation Results
We evaluated our approach using simulated data using
Gazebo (Koenig and Howard, 2004) and implemented
our interval-based Sound Source Mapping (IB-SSM)
using the IBEX library (Ninin, 2015). In order to ne-
glect the influence on the used SSL approach we used
simulated direction measurements. These directions
are used to calculate the TDoA in Equation (10). For
all experiments in this Section we used a fixed con-
figuration of 8 microphones leading to n
p
=
8
2
= 28
microphone pairs (cf. Fig. 1b).
Interval-based Sound Source Mapping for Mobile Robots
341

In the first experiment we tested the feasibility of
our approach using ground truth data. In 1000 trials
we placed randomly 1-10 sound sources in the virtual
environment (7.6 m ×5.5 m ×2 m) and conducted
measurements at 1-30 positions. Fig. 7 shows a single
scenario.
In order to calculate the cone segment in Equa-
tion (10) we set the minimal and maximal distance
between the measurement and the sound sources po-
sitions to [r
s
,r
s
] = [0.5 m,9.6 m] based on the dimen-
sion of the environment and the microphone configu-
ration.
Figure 7: Measurement positions (blue), sound source po-
sitions (red), estimated interval boxes (yellow).
For all tests, we noticed that our method includes
all true sound positions.
In the second experiment, we evaluated the influ-
ence of different parameters on the accuracy of our
approach. After solving the CSP from Section 5 we
obtain a list of boxes. However, we do not get any as-
signment between these boxes and the sound sources.
2D plane
Projected bounds
for s
1
Projected bounds
for s
2
Sound source
s
1
Sound source
s
2
Estimation of sound position
using Interval boxes
Figure 8: Approach to extract corresponding boxes to a
sound source.
In order to calculate the accuracy of our approach
we cluster these boxes. First, we project the boxes to
the XY plane and perform morphological methods to
obtain neighboring areas. Next, we calculate bounds
which contain these separate areas. In the last step,
we add up the volume of all interval boxes which cor-
responding to these bounds.
(a) Accuracy ε = 0.3. (b) Accuracy ε = 0.05.
Figure 9: Influence on the accuracy of SIVIA. Measurement
positions (blue), sound source positions (red), solution of
IB-SSM (yellow).
We focused on the following parameters:
• n
l
: Number of measurement positions
• d : Distance between measurement position and
sound source
• ε : Accuracy of the brand and bound algorithm
SIVIA used for solving the CSP
• ∆t
e
: TDoA sampling extension
To simplify the evaluation in this work, we did not fo-
cus on different microphone configurations. For the
following experiment we conducted measurements
located on a circle and placed a single sound source
in the center at a height of 1 m. We varied the to-
tal amount of measurement positions n
l
from 1 to 20,
the radius of the circle d from 0.5 m to 2 m and the
accuracy ε of SIVIA between 0.1 and 0.3. In simple
terms, ε specifies the dimension of the interval boxes
showing in Fig. 9. The calculated TDoA from Section
7 needs to be extended by the TDoA sampling exten-
sion ∆t
e
in Equation (11). We selected a minimal sam-
pling frequency f
s
of 8000 Hz resulting in a sampling
time t
s
of 0.125 ms. Therefore, we selected the TDoA
sampling extension ∆t
e
between 0 ms and 2/ f
s
= 0.25
ms. For all combination of these aforementioned pa-
rameters we calculated the total volume of the inter-
val boxes and the calculation time of our IB-SSM al-
gorithm using the final contractor from Equation (7).
The results are visualized in Fig. 10.
Fig. 10a and Fig. 10b show that more measure-
ment positions lead to a more accurate solution but
the calculation time increases. However, at a certain
point, only a small improvement is possible. It can be
seen that the distance between the robot and the sound
source is important. Measurements at two positions
with a distance of 0.5 m to the sound source are lead-
ing to a more accurate solution than 20 measurements
point from a distance of 1 m. As a result, selecting op-
timal measurement positions should be evaluated in
following works. Furthermore, Fig. 10c and Fig. 10d
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
342

(a) (b)
(c) (d)
(e) (f)
Figure 10: Dependency of the total volume of all interval
boxes and the measurement time due to the number of mea-
surements (a) + (b), the accuracy of SIVIA (c) + (d) and the
TDoA sampling extension (e) + (f).
show the influence on the volume and the calculation
time caused by the accuracy ε. For d = 2 m a smaller
ε (higher accuracy) results in a large improvement.
The volume decreases from 7.6 to 0.2 cm
3
. However,
the calculation time rises up from 3.1 to 12.7 seconds.
For d = 0.5 m the improvement is not large (from 0.4
to 0.0129 cm
3
) and the calculation time is nearly con-
stant (from 1.06 to 1.36 seconds). As a result, a trade-
off between the accuracy and the calculation time has
to be made. Last, Fig. 10e and Fig. 10f show the in-
fluence on the volume and the calculation time caused
by the TDoA sampling offset ∆t
e
. For a sampling fre-
quency of 8000 Hz (∆t
e
= 0.25 ms) and a sampling
frequency of 96000 Hz (∆t
e
= 0.02 ms) the volume
of the interval boxes for d = 2 m differs between 7.9
cm
3
and 12.7 cm
3
for d = 0.5 m between 1.49 cm
3
and 0.40 cm
3
. The calculation time is slowly rising
for increasing ∆t
e
.
In the last experiment, we modeled a systematic
localization error of 0.15 m in both x and y (plane
of the ground). We selected n
l
= 20, d = 1 m, ε =
0.3 and ∆t
e
= 0 ms. Furthermore, we extended the
transformation t
map
rob
between the measurement posi-
tion (robot) and the global map from Equation (8) in
(a) Without error modeling. (b) With error modeling.
Figure 11: Systematic error of the localization result. Mea-
surement positions (blue), sound source positions (cyan),
estimated interval boxes (yellow).
both dimension with a bound of 0.15 m. In the first
test, we did not consider the localization error from
Section 6 in our approach. Following, in the second
test we took this error into account. It can be seen
in Fig. 11a, that without consideration of systematic
errors the true solution is not within the calculated in-
terval boxes. In contrast, by considering uncertainties
with intervals the true solution is included but the vol-
ume is 12 times larger, see Fig. 11b.
8.2 Experimental Results
In this experiment, we provided a proof of concept,
showing our approach is applicable in a real environ-
ment. We restricted our evaluation on one single ac-
tive sound source. For this purpose, we used loud
speaker of a phone emitting speech.
The experiment was conducted in a room (11.7 m
x 6 m) using a KUKA youBot equipped with a mi-
crophone array (IntRoLab 8SoundUSB) with 8 mi-
crophones sampled with 44100 Hz as shown in Fig.
12. We used the ODAS
1
framework (Open em-
beddeD Audition System) for estimating the sound
source directions. The SRP-PHAT-HSDA algorithm
with a M3K method is applied (Grondin and Michaud,
2019). We used gmapping, an openSLAM imple-
mentation (Grisetti et al., 2007) and amcl (Adaptive
Monte-Carlo localization) to localize the robot within
the environment. Both are packages within the Robot
Operating System (ROS) (Quigley et al., 2009). All
algorithm were executed on the hardware of the robot.
First, we restricted our domain as shown in Fig. 13
and assumed a localization error of 0.03 m. We col-
lected for a duration of 5 seconds the tracked direction
estimations using the M3K method. After collection
all measurements at a position we calculated the so-
lution of the sound source mapping. The results are
shown in Fig. 13.
1
http://odas.io
Interval-based Sound Source Mapping for Mobile Robots
343

Figure 12: Experimental equipment.
(a) Start. (b) After measurement 1.
(c) After measurement 2. (d) After measurement 3.
Figure 13: Results of IB-SSM (potential sound sources as
boxes in yellow) in a real environment. One static sound
source is active (white).
At the first position, we selected a large ε to reduce
calculation time. Next, we applied the results from
the evaluation in Section 8.1 and navigated toward the
area of the sound sources and we reduced ε. After
conducting the third measurement we could show that
the true position is included in our calculated solution.
9 CONCLUSION AND FUTURE
WORK
We presented a new approach for estimating the 3D
position of multiple static sound sources in a map by
using interval methods in an efficient manner. As a
result a calculation on a robot at run time is feasible.
We extended our Interval-Based Sound Source Map-
ping (IB-SSM) in order to model uncertainties due to
inaccurate knowledge about the microphone positions
within the map and the auditory signals extracted by
the microphones. Furthermore, we developed an ap-
proach to estimate the TDoA from direction measure-
ments. Our evaluation showed that our approach is
feasible to correctly estimate the positions of emitting
sound sources. In future work we plane to develop
a strategy to selected optimal measurement points in
the environment.
REFERENCES
Argentieri, S., Danes, P., and Soueres, P. (2015). A survey
on sound source localization in robotics: From binau-
ral to array processing methods. Computer Speech &
Language, 34(1):87–112.
Chabert, G. and Jaulin, L. (2009). Contractor programming.
Artificial Intelligence, 173:1079–1100.
Do, H., Silverman, H. F., and Yu, Y. (2007). A real-time srp-
phat source location implementation using stochas-
tic region contraction (src) on a large-aperture micro-
phone array. In Acoustics, Speech and Signal Process-
ing, 2007. ICASSP 2007. IEEE International Confer-
ence on, volume 1, pages I–121. IEEE.
Even, J., Furrer, J., Morales, Y., Ishi, C. T., and Hagita, N.
(2017). Probabilistic 3-d mapping of sound-emitting
structures based on acoustic ray casting. IEEE Trans-
actions on Robotics, 33(2):333–345.
Evers, C., Dorfan, Y., Gannot, S., and Naylor, P. A. (2017).
Source tracking using moving microphone arrays for
robot audition. In Acoustics, Speech and Signal Pro-
cessing (ICASSP), 2017 IEEE International Confer-
ence on, pages 6145–6149. IEEE.
Foy, W. H. (1976). Position-location solutions by taylor-
series estimation. IEEE Transactions on Aerospace
and Electronic Systems, (2):187–194.
Grisetti, G., Stachniss, C., and Burgard, W. (2007).
Improved techniques for grid mapping with rao-
blackwellized particle filters. IEEE transactions on
Robotics, 23(1):34–46.
Grondin, F. and Michaud, F. (2019). Lightweight and opti-
mized sound source localization and tracking methods
for open and closed microphone array configurations.
Robotics and Autonomous Systems, 113:63–80.
Hu, J.-S., Chan, C.-Y., Wang, C.-K., Lee, M.-T., and Kuo,
C.-Y. (2011). Simultaneous localization of a mobile
robot and multiple sound sources using a microphone
array. Advanced Robotics, 25(1-2):135–152.
Jaulin, L., Kieffer, M., Didrit, O., and Walter, E. (2001).
Interval analysis. In Applied interval analysis, pages
11–43. Springer.
Kallakuri, N., Even, J., Morales, Y., Ishi, C., and Hagita,
N. (2013). Probabilistic approach for building audi-
tory maps with a mobile microphone array. In 2013
IEEE International Conference on Robotics and Au-
tomation, pages 2270–2275. IEEE.
Koenig, N. and Howard, A. (2004). Design and use
paradigms for gazebo, an open-source multi-robot
simulator. In 2004 IEEE/RSJ International Confer-
ence on Intelligent Robots and Systems (IROS)(IEEE
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
344

Cat. No. 04CH37566), volume 3, pages 2149–2154.
IEEE.
Langerwisch, M. and Wagner, B. (2012). Guaranteed mo-
bile robot tracking using robust interval constraint
propagation. In International Conference on In-
telligent Robotics and Applications, pages 354–365.
Springer.
Nakamura, K., Nakadai, K., Asano, F., Hasegawa, Y., and
Tsujino, H. (2009). Intelligent sound source localiza-
tion for dynamic environments. In 2009 IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems, pages 664–669. IEEE.
Ninin, J. (2015). Global optimization based on contractor
programming: An overview of the ibex library. In
International Conference on Mathematical Aspects of
Computer and Information Sciences, pages 555–559.
Springer.
Quigley, M., Conley, K., Gerkey, B., Faust, J., Foote, T.,
Leibs, J., Wheeler, R., and Ng, A. Y. (2009). Ros: an
open-source robot operating system. In ICRA work-
shop on open source software, volume 3, page 5.
Kobe, Japan.
Rascon, C. and Meza, I. (2017). Localization of sound
sources in robotics: A review. Robotics and Au-
tonomous Systems, 96:184–210.
Reynet, O., Jaulin, L., and Chabert, G. (2009). Robust tdoa
passive location using interval analysis and contractor
programming. In 2009 International Radar Confer-
ence” Surveillance for a Safer World”(RADAR 2009),
pages 1–6. IEEE.
Sasaki , Y., Ryo, T., and Takemura, H. (2016). Probabilistic
3d sound sources mapping using moving microphone
array. In Intelligent Robots and Systems (IROS), 2016
IEEE/RSJ International Conference on. IEEE.
Sasaki, Y., Thompson, S., Kaneyoshi, M., and Kagami,
S. (2010). Map-generation and identification of
multiple sound sources from robot in motion. In
2010 IEEE/RSJ International Conference on Intelli-
gent Robots and Systems, pages 437–443. IEEE.
Schmidt, R. (1986). Multiple emitter location and signal
parameter estimation. IEEE transactions on antennas
and propagation, (3):276–280.
Sliwka, J., Le Bars, F., Reynet, O., and Jaulin, L. (2011).
Using interval methods in the context of robust local-
ization of underwater robots. In 2011 Annual Meeting
of the North American Fuzzy Information Processing
Society, pages 1–6. IEEE.
Su, D., Nakamura, K., Nakadai, K., and Valls Miro, J.
(2016). Robust sound source mapping using three-
layered selective audio rays for mobile robots. In In-
telligent Robots and Systems (IROS), 2016 IEEE/RSJ
International Conference on. IEEE.
Voges, R. and Wagner, B. (2018). Timestamp offset cal-
ibration for an imu-camera system under interval un-
certainty. In 2018 IEEE/RSJ International Conference
on Intelligent Robots and Systems (IROS), pages 377–
384. IEEE.
Interval-based Sound Source Mapping for Mobile Robots
345
