
Machine Learning Assisted Caching and Adaptive LDPC Coded
Modulation for Next Generation Wireless Communications
Hassan Nooh, Zhikun Zhu and Soon Xin Ng
School of Electronics and Computer Science, University of Southampton, SO17 1BJ, U.K.
http://www.wireless.ecs.soton.ac.uk
Keywords:
Low Density Parity-check Codes, Latent Dirichlet Allocation, Adaptive Modulation and Coding, K-Means
Clustering.
Abstract:
Unmanned Aerial Vehicles (UAVs) constitute a key technology for next generation wireless communications.
Compared to terrestrial communications, wireless systems with low-altitude UAVs are in general faster to
deploy, more flexible and are likely to have better communication channels due to the presence of short-range
Line of Sight (LoS) links. In this contribution, a Latent Dirichlet Allocation (LDA) based machine learning
algorithm was utilized to optimize the content caching of UAVs, while the K-means clustering algorithm
was invoked for optimizing the assignment of mobile users to the UAVs. We further investigated a practical
adaptive Low Density Parity Check (LDPC) coded modulation (ALDPC-CM) scheme for the communication
links between the UAVs and the users. We found that the caching efficiency of each UAV can be boosted
from 50% with random caching to above 90% with the employment of LDA. We also found that the proposed
ALDPC-CM scheme is capable of performing closely to the ideal perfect coding based scheme, where the
mean delay of the former is only about 0.05 ms higher than that of the latter, when the UAV system aims to
minimize both the transmission and request delays.
1 INTRODUCTION
Emerging technologies such as Internet of Things
(IoT) and autonomous vehicles are expected to be
commercialized as their performance requirements
are theoretically met by 5G specifications (Americas,
2018). Various methods of deployment and system ar-
chitectures have been proposed, yet a clear all-round
approach has not been found. Unmanned Aerial Ve-
hicles (UAVs), also referred to as drones, have been
massively employed in various applications during
the past several decades (Valavanis and Vachtsevanos,
2014), especially for military and recreational use.
More specifically, UAVs have been used mainly for
military purposes due to its high cost. However, con-
tinuous development has made it possible to build
low-cost and light-weight UAVs for civil and com-
mercial applications. UAV based wireless commu-
nication seems to be a promising solution to support
connectivity for users outside the infrastructure cov-
erage (Merwaday and Guvenc, 2015), which may be
caused by disasters, shadowing or overloading. Be-
sides, UAVs can relay the blocked signals from the
base station (BS) to users due to its advantage in mo-
bility and flexibility (Zeng et al., 2016). In cellular
networks, each BS covers and serves a specific re-
gion. In order to extend the coverage area of the BS,
the concept of Remote Radio Head (RRH) has been
investigated (Chen et al., 2017). RRH is a transceiver
that is connected to a BS via the wireless or wired in-
terface. Therefore, RRH can be regarded as a relay
node between the BS and the users. In this contribu-
tion, UAVs are employed as our RRHs.
On the other hand, each UAV can be equipped
with limited memory to cache useful contents for fu-
ture user requests, in order to improve the Quality
of Service (QoS). This is referred to as mobile edge
caching (Wang et al., 2017) and machine learning al-
gorithms could be employed to predict user requests
and to perform caching updates. We model the user
preference as a multinomial process based on the La-
tent Dirichlet Allocation (LDA) algorithm (Blei et al.,
2003), which depends on the User-Topics probabil-
ity density function (PDF) and the Topic-Words PDF.
The user preference is simulated according to the 20-
Newsgroups dataset (Lang, 1995) and it is learned by
the LDA algorithm. The learned user preferences are
clustered by the K–means algorithm for the users-to-
Nooh, H., Zhu, Z. and Ng, S.
Machine Learning Assisted Caching and Adaptive LDPC Coded Modulation for Next Generation Wireless Communications.
DOI: 10.5220/0009840500670076
In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - DCNET, OPTICS, SIGMAP and WINSYS, pages 67-76
ISBN: 978-989-758-445-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
67

UAVs allocation. When the user preference is accu-
rately predicted, useful data can be cached. If a user
request is in the UAV’s cached memory, it could be
sent directly to the user from the UAV, without fur-
ther requests to a remote BS. Thus, the user request
delay is reduced.
Low Density Parity Check (LDPC) codes (Gal-
lager, 1963; Guo, 2005) are powerful forward er-
ror correction schemes that have been widely investi-
gated and are considered in the 5G standard. Adaptive
coding and modulation (L. Hanzo, S. X. Ng and T.
Keller, 2005) is another attractive transmission tech-
nology, where a high-rate channel code and a high-
order modulation scheme are employed, for increas-
ing the transmission rate, when the channel quality
is good. By contrast, a low-rate channel code and a
low-order modulation scheme are employed, for im-
proving the transmission reliability, when the chan-
nel quality is poor. In this contribution, an Adaptive
LDPC Coded Modulation (ALDPC-CM) scheme was
investigated and utilized for the UAV-user communi-
cation link. The ALDPC-CM scheme could provide
a near-capacity transmission rate for a given channel
Signal-to-Noise-Ratio (SNR). Hence, a communica-
tion link with high SNR could lead to a lower trans-
mission period (or transmission delay).
The rest of this paper is organized as follows. The
caching model is investigated in Section 2, while our
system model is detailed in Section 3. Our simulation
results are discussed in Section 4, while our conclu-
sions are summarized in Section 5.
2 CACHING MODEL
In this section, the Latent Dirichlet Allocation algo-
rithm is outlined and the user preference model is pre-
sented.
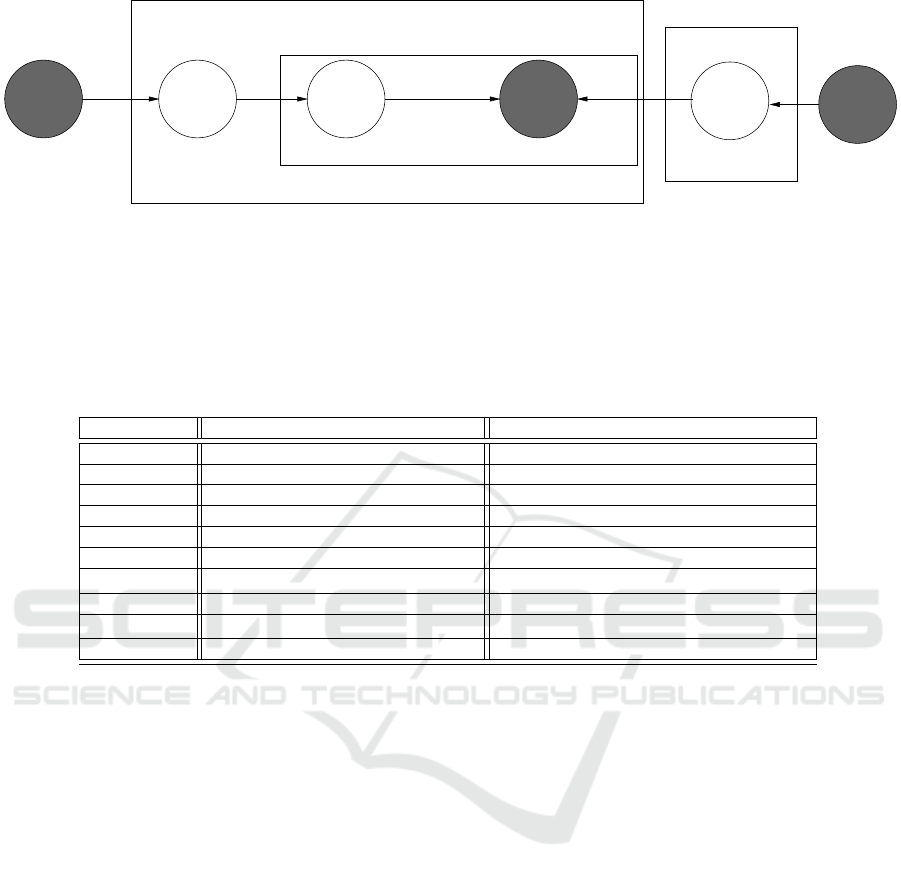
2.1 Latent Dirichlet Allocation
Latent Dirichlet Allocation (LDA) is a generative
probabilistic model (Blei et al., 2003) that character-
izes the document generating process with the graph-
ical model. The grey parameters shown in Fig. 1 are
latent variables and cannot be observed. The remain-
ing variables could be observed with the input data.
LDA algorithm iteratively simulates the generating
process and estimates the latent variables. The gen-
erated data is then evaluated using a cost function.
Additionally, the latent variables are iteratively opti-
mized based on the cost function. Once the model
has converged, it can be used to predict the content of
future user requests.
The LDA model is able to reveal the topic compo-
sition of a document and the word probability that is
related to each topic. It classifies the new document
into different classes and predicts the new words. It
is useful for our system since users that share the
same interest may be gathering around the same ge-
ographical location under specific application scenar-
ios. LDA is a Bag-of-Words (BoW) model that ne-
glects the order of words in the document. In our case,
the order of user requests is not important. Hence,
the LDA algorithm can be employed to perform user
request prediction. More explicitly, LDA is com-
posed of document generation and parameter estima-
tion, where its graphical model is shown in Fig. 1.
The meaning of symbols used in Fig. 1 are presented
in Table 1. In our context, a ‘document’ represents
the ‘content requested by a user’.
We assume that there are a total of |T | = N
T
top-
ics, e.g. cars, movies, weather, news, etc, and they
are controlled by Dirichlet distribution Dir(α). For
each user, their interest topics can be regarded as inde-
pendent identical distributed (i.i.d) random variables
sampled from Dir(α). For example, Bob (Bob ∈ C )
is interested in 40% of news, 10% of cars, 50% of
movies, and 0% for the rest. Then, we can com-
pute the User-Topics distribution of Bob, θ
(d)
. On
the other hand, we have Topic-Contents distribution
of each topic φ
t
for t ∈ T . These distributions are con-
trolled by another Dirichlet distribution Dir(β). Thus,
we can sample from θ
d
and φ
t
to generate a content
w
(d)
i
for Bob. We continue to do this until we have
generated all N
d
contents for each d ∈ C . Likewise,
this model can generate contents for each user. In gen-
eral, the probability that a word blank w is filled by a
term t is given by:
p(w = t) =
∑
k
φ
(k)
(w = t|z = k)θ
(d)
(z = k),
(1)
where
∑
k
θ
(d)
(z = k) = 1.
2.2 User Preference Model
To simulate the user request behaviour and to gener-
ate the related distributions, we performed an LDA
clustering over a text dataset called 20-Newsgroups
dataset, which was first introduced in (Lang, 1995).
It is a popular dataset for experiments in text appli-
cations, which is composed of 20 groups of news.
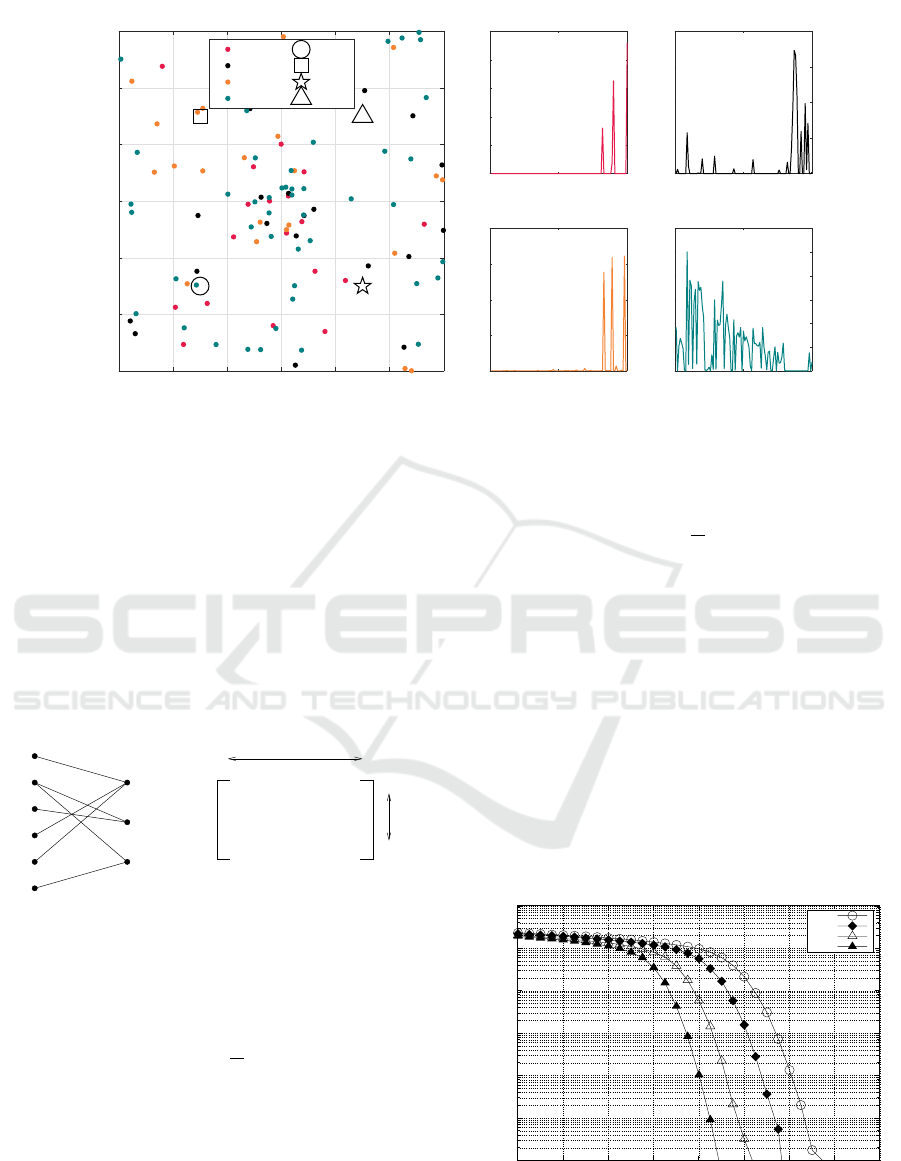
Fig. 2(a) shows the main topics of the dataset. We
need to preprocess the dataset to filter out the stop
words before the LDA algorithm is employed. Then,
we extract n
w
= 1000 significant words from the
dataset to compose a dictionary. Fig. 2(b) shows
the preprocessing of the dataset. Hence, once we
DCNET 2020 - 11th International Conference on Data Communication Networking
68
α
Dirichlet Dirichlet
Cat
Cat
τ
(d)
i
φ
t
t ∈ T
β
d ∈ C
i ∈ 1, 2, ..., N
d
w
(d)
i
θ
(d)
Figure 1: Graphical notation of the LDA algorithm. Each box in the diagram is a ‘for’ loop. From left to right: Dir(α) is
a Dirichlet distribution with parameter α, it generates the topic distribution for each document; θ
(d)
is sampled from Dir(α)
and it represents the topics associated with each document. We then sample from θ
(d)
to get a topic τ
(d)
i
for the word w
(d)
i
.
From right to left: the words associated with each topic φ
t
is sampled from another Dirichlet distribution with parameter β;
we can then generate the word w
(d)
i
according to the sampled topic τ
(d)
i
and the word distribution φ
t
. Note that the grey circle
represents the variables that are latent, N
d
is the word count of the d-th document. C is the category of the documents and T
is the set of topics.
Table 1: Symbol meaning of the LDA algorithm shown in Fig. 1.
Symbols Contents Generation Documents Generation
C User groups Document categories
d ∈ C User Document
i ∈ 1,2,...,N
d
i-th content blank of d i-th word blank of d
Dir(α) Generate User-Topics distributions Generate Document-Topics distributions
Dir(β) Generate Topic-Contents distributions Generate Topic-Words distributions
θ
(d)
User d’s User-Topics distribution Document d’s Document-Topics distribution
τ
(d)
i
i-th content blank’s topic of d i-th word blank’s topic of d
φ
t
Topic t’s Topic-Contents PDF Topic t’s Topic-Words PDF
w
(d)
i
i-th content of d i-th word of d
W Contents Space, w ∈ W Dictionary, w ∈ W
have finished the transform, we should have a n
d
×n
w
sparse matrix, which is 11314 × 1000 for this specific
case. The sparse matrix is then input to the LDA al-
gorithm.
We consider N
u
= 100 users, N
t
= 4 topics and
N
w
= 100 words (contents), as well as N
d
= 4 UAVs
to provide services to the users. The parameters α and
β for Dirichlet distribution are generated based on the
20-Newsgroups dataset. We assign a Topic–Contents
PDF for each topic, and a User–Topics PDF for each
user. Fig. 3(a) shows the Topic–Contents PDFs. It
is clear from Fig. 3(a) that different topics share dis-
tinct top five words, which are marked with red points.
Fig. 3(b) shows the topic distribution for the first 20
users. As can be seen from Fig. 3(b), some users have
a dominant topic amongst the four topics.
The preferred contents by each user may be
different. The user preference is determined by
the User-Topic Probability Density Function (UT-
PDF) and Topic-Content Probability Density Func-
tion (TCPDF). For N
u
= 100 users we have 200 PDFs
as parameters to characterize the user preference.
Again, these parameters are generated according to
the 20-Newsgroup dataset. Fig. 4 shows the user pref-
erence with their dominant topics.
K-means clustering is then performed to match
each user to a UAV, in order to optimize the sys-
tem QoS, which is characterized mathematically as
a function of delay (τ
i
, i ∈ 1,2,...,N
u
). The delay
function for the ith user is determined by two terms,
namely the time to transmit the content to the user
from the UAV (τ
t
i
) and time to request the content (un-
available at the UAV) from the remote BS (τ
r
i
). For a
given request S
i
, the transmit delay τ
t
i
and request de-
lay τ
r
i
are given by Eq. (2) and Eq. (3), respectively.
τ
t
i
= f (SNR,S
i
), (2)
τ
r
i
=
0 S
i
∈ C
d
1 S
i
/∈ C
d
d ∈ 1, 2,..., N
d
, (3)
where C
d
is the contents cached in UAV d, which is
serving user i. For example, the request delay equals
to zero if the UAV has the user request in its memory.
Hence, the system delay for all users can be computed
as:
τ =
N
d
∑
i=1
τ
t
i
+ τ
r
i
, (4)
which is a function of the receive SNR and the re-
quested content. Further analysis on this is carried
out in Section 4.2.
Machine Learning Assisted Caching and Adaptive LDPC Coded Modulation for Next Generation Wireless Communications
69

20 Newsgroups
Religon
Cryptog
raphy
Medicine
Electronics
Space
MAC_ hardware
Windows X
Graphics
Windows misc
Autos
PC_ hardware
Hockey
Motorcycles
Baseball
Rec Computer
Science
Politics
talk
Misc
Misc
Mideast
Guns
Misc
Christian
Atheism
Forsale
(a) The groups of the 20 Newsgroups dataset. The dataset
is composed of 20 newsgroups and they belong to 6 gen-
eral topics. There are a total of n
d
= 11314 documents
in the dataset. Besides, some of the groups are highly
related to each other (i.e., hardware for PC and MAC).
(b) The preprocessing of the input documents. We ex-
tract the first 1000 high frequency words as our dictio-
nary. Then, we use this dictionary to transform each doc-
ument into a sparse vector, where the value of its n-th
element represents the number of repetitions of the n-th
word in the dictionary.
Figure 2: Composition and preprocessing of the 20-
Newsgroup dataset.
3 SYSTEM MODEL
3.1 Rician Fading Channel
The Rician fading channel models a dominant (non-
variant) component amongst the multipath fading
channel components (Goldsmith, 2005). This dom-
inant component can be used to model the Line-of-
Sight (LoS) link between the UAV and its user. The
Rician PDF is given by:
p(r) =
r
σ
2
exp
−
A
2
+ r
2
2σ
2
I
0
A
0
σ
2
, (5)
where A is the peak amplitude of the dominant signal,
I
0
is the zero-order modified Bessel function of the
first kind, K =
A
0
2σ
2
is the Rician factor representing
the ratio of the dominant signal power to the multipath
0 20 40 60 80 100
0
0.1
0.2
0.3
0.4
0.5
Topic: 1
PDF
p(Top
5
)=0.98503
0 20 40 60 80 100
0
0.1
0.2
0.3
0.4
0.5
Topic: 2
PDF
p(Top
5
)=0.64332
0 20 40 60 80 100
0
0.1
0.2
0.3
0.4
0.5
Topic: 3
PDF
p(Top
5
)=0.94064
0 20 40 60 80 100
0
0.1
0.2
0.3
0.4
0.5
Topic: 4
PDF
p(Top
5
)=0.20008
Topic-word PDF
Words/ No.
Probability
(a) Words distribution for all four topics. The top five
frequent words are highlighted in red.
1 2 3 4
0
0.2
0.4
0.6
0.8
1
User: 1
1 2 3 4
0
0.2
0.4
0.6
0.8
1
User: 2
1 2 3 4
0
0.2
0.4
0.6
0.8
1
User: 3
1 2 3 4
0
0.2
0.4
0.6
0.8
1
User: 4
1 2 3 4
0
0.2
0.4
0.6
0.8
1
User: 5
1 2 3 4
0
0.2
0.4
0.6
0.8
1
User: 6
Probability
(b) Topic distribution for the first 6 users.
Figure 3: Generated users Topic–Contents PDFs and User–
Topics PDFs. We assume n
T
= 4 topics and n
C
= 100 con-
tents.
variance. As K → 0 Eq. (5) approaches the Rayleigh
PDF:
p(r) =
r
σ
2
exp
−
r
2
2σ
2
, (6)
which is the commonly used model to describe the
statistical time varying nature of the multipath fading
channel without a dominant component. In a similar
manner, as K → ∞ The Rician PDF approaches the
Gaussian distribution.
3.2 LDPC Codes
Low Density Parity Check (LDPC) codes (Gallager,
1963; D. J. C Mackay, and R. M. Neal, 1997) be-
long to the family of linear block codes, which are
defined by a parity check matrix having M rows and N
columns. The column and row weights are low com-
pared to the dimension M and N of the parity check
matrix H. Fig. 5 shows the bipartite graph (M. R. Tan-
ner, 1981) representation of the parity check matrix.
DCNET 2020 - 11th International Conference on Data Communication Networking
70
0 50 100 150 200 250 300
X (m)
0
50
100
150
200
250
300
Y (m)
Users with associated dominant topics
Topic: 1
Topic: 2
Topic: 3
Topic: 4
Drone
1
Drone
2
Drone
3
Drone
4
0 50 100
Drone 1
0
0.1
0.2
0.3
0.4
0.5
Probability
0 50 100
Drone 2
0
0.05
0.1
0.15
0.2
Probability
0 50 100
Drone 3
0
0.1
0.2
0.3
0.4
Probability
0 50 100
Drone 4
0
0.01
0.02
0.03
0.04
0.05
0.06
Probability
Figure 4: The primary model with user preference. N
d
= 4 UAVs serving N
u
= 100 users within a 300m×300m area.
This graph constitutes of two types of nodes, namely
the message nodes, each of which corresponds to a
column of the parity check matrix, and the check
nodes, each of which corresponds to a row of the ma-
trix. There are lines connecting these two types of
nodes, and each connection corresponds to a non-zero
entry in the parity check matrix of Fig. 5. For exam-
ple, the non-zero entry at the bottom right corner of
the parity check matrix in Fig. 5 corresponds to the
connection between the 6
th
node on the left and the
3
rd
node on the right.
N Message Nodes
1
1
0
0
00
1 1
0 0 0
1 1 0
0 0
1
0
(N−K) Parity Check Nodes
N
N−K
Figure 5: Bipartite graph representation of the parity check
matrix.
The number of information bits encoded by an
LDPC code is denoted by K = N − M, yielding a cod-
ing rate:
R
c
=
K
N
(7)
The modulation rate for an M-ary modulation is given
by:
R
m
= log
2
(M) . (8)
R
m
is the number of modulated bits per symbol, e.g.
for BPSK, QPSK, and 8PSK, we have R
m
equals to 1,
2 and 3 bits, respectively. Hence, the overall rate of
the coded modulation scheme (or information bits per
modulated symbol) can be computed as:
R = R
c
·R
m
=
K
N
·log
2
(M) . (9)
3.3 Adaptive LDPC Coded Modulation
Fig. 6 shows the Bit Error Ratio (BER) versus SNR
performance of an LDPC-coded 8PSK scheme, when
communicating over Rician fading channels. Table 2
depicts the corresponding parameters. The size of the
H is chosen to maintain a code rate of R
c
= 0.5. As
seen from Fig. 6, as the Rician factor K increases, the
BER performance improves because the channel be-
comes more Gaussian like. When K = 0, the channel
becomes a harsh Rayleigh fading channel. We have
chosen a Rician factor of K = 3 for the rest of our
simulations.
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
2 3 4 5 6 7 8 9 10
BER
SNR (dB)
K=0
K=1
K=3
K=10
Figure 6: BER versus SNR performance of LDPC-coded
8PSK scheme, when communicating over Rician fading
channels having a Rician factor of K = {0,1, 3, 10}.
Machine Learning Assisted Caching and Adaptive LDPC Coded Modulation for Next Generation Wireless Communications
71

Table 2: LDPC coding parameters used in Fig. 6.
Parameter Value
Maximum decoding iterations 15
Maximum Frame Size 100 000 bits
Column Weight 3
H Matrix Size 2400 × 1200
In order for a range of data rates to be supported
in the UAV system the rate can be manipulated such
that each modulation supports a throughput value pro-
gressively higher than the previous scheme, as out-
lined below. More specifically, the proposed ALDPC-
CM scheme supports 8 transmission modes as de-
tailed in Table 3. The BER versus SNR performance
of these LDPC coded modulation schemes have been
simulated when communicating over AWGN channel
(Fig. 7), Rician fading channel (Fig. 8) and Rayleigh
fading channels (Fig. 9).
Table 3: Parameters of ALDPC-CM modes.
Modulation
Coding
Rate
Parity Check
Matrix Size
(K × N)
Throughput
(bits/symbol)
BPSK 0.5 2100 × 4200 0.5
4QAM 0.5 2100 × 4200 1
8PSK 2/3 2100 × 3150 2
16QAM 3/4 2100 × 2800 3
32QAM 4/5 2100 × 2625 4
64QAM 5/6 2100 × 2520 5
128QAM 6/7 2100 × 2450 6
256QAM 7/8 2100 × 2400 7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
-5 0 5 10 15 20 25 30 35 40
BER
SNR (dB)
BPSK R=1/2
4QAM R=1/2
8PSK R=2/3
16QAM R=3/4
32QAM R=4/5
64QAM R=5/6
128QAM R=6/7
256QAM R=7/8
Figure 7: BER performance of LDPC coded modulation
when communicating over AWGN channels K = ∞.
Based on the BER curves in Fig. 7, Fig. 8 and
Fig. 9, we extract the SNR thresholds for each of
these LDPC coded modulation schemes at a target
BER of 10
−4
, which are tabulated in in Table 4. The
results displayed on Table 4 are inline with our ex-
pectations based on our prior knowledge of the na-
ture of the respective channels. The AWGN channel
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
-5 0 5 10 15 20 25 30 35 40
BER
SNR (dB)
BPSK R=1/2
4QAM R=1/2
8PSK R=3/4
16QAM R=3/4
32QAM R=4/5
64QAM R=5/6
128QAM R=6/7
256QAM R=7/8
Figure 8: BER performance of LDPC coded modulation
when communicating over Rician fading channels K = 3.
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
0 10 20 30 40
BER
SNR (dB)
BPSK R=1/2
4QAM R=1/2
8PSK R=2/3
16QAM R=3/4
32QAM R=4/5
64QAM R=5/6
128QAM R=6/7
256QAM R=7/8
Figure 9: BER performance of LDPC coded modulation
when communicating over Rayleigh fading channels K = 0.
Table 4: SNR thresholds at BER = 10
−4
for various LDPC
CM schemes. The perfect coding scheme is based on the
channel capacity of the 256QAM scheme.
Modulation
Perfect
Coding
(dB)
AWGN
(dB)
Rician,
K=3 (dB)
Rayleigh
(dB)
BPSK -3 -0.899 -0.236 1.029
4QAM 1 2.092 2.775 4.043
8PSK 6 7.538 8.810 10.829
16QAM 9 10.806 12.332 14.847
32QAM 13 14.564 16.080 18.778
64QAM 16 17.568 19.346 22.413
128QAM 20 20.858 21.418 25.983
256QAM 23 24.026 25.556 29.200
is the best case for all the LDPC coded modulation
schemes followed by the Rician fading channel and
the Rayleigh fading channel. It is also worth pointing
out that the Rician fading channel (K = 3) is closer to
the ideal case of the AWGN channel than the worst
case (Rayleigh fading channel) across all schemes.
Fig. 10 shows a visual presentation of the data pre-
sented in Tables 3 and 4. As seen in Fig. 10, when ac-
tual coding (which has a discrete coding rate) is used,
DCNET 2020 - 11th International Conference on Data Communication Networking
72
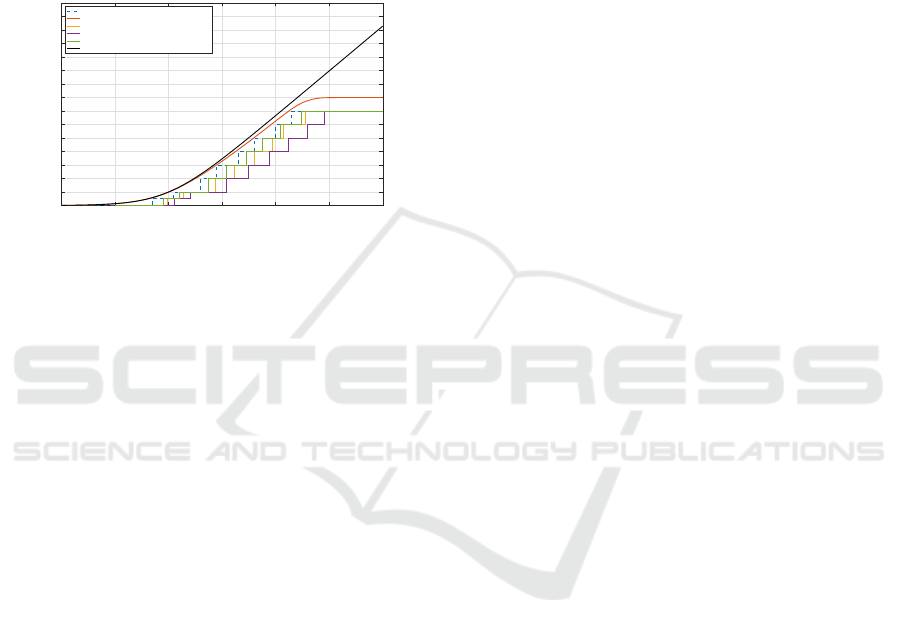
the throughput has a staircase like curve. This is be-
cause when the received SNR is between two thresh-
olds, a lower coded modulation mode is activated. For
example, when the received SNR is above 12.332 dB
but below 16.080 dB (see Table 4), LDPC-16QAM
will be invoked when communicating over the Ri-
cian fading channels. Hence, a constant throughput
of 3 bits/symbol (see Table 3) will be yielded for
a received SNR that is above 12.332 dB but below
16.080 dB.
-20 -10 0 10 20 30 40
SNR (dB)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Capacity (bits/symbol)
Perfect Coding with Discrete Coding Rate
Perfect Coding with Continuous Coding Rate
ALDPC-CM under Rician fading channel, K = 3
ALDPC-CM under Rayleigh fading channel
ALDPC-CM under AWGN channel
Shannon Capacity (Ideal)
Figure 10: Capacity or throughput versus SNR curves of the
ALDPC-CM scheme in comparison with theoretical lim-
its. The Shannon capacity and the two ‘Perfect Coding’
schemes are based on AWGN channels.
4 RESULTS AND DISCUSSIONS
A simulator was created to investigate the overall sys-
tem performance of the proposed UAV based scheme,
incorporating machine learning assisted caching and
ALDPC-CM aided transmission. The mobile users
are served by UAVs, while the UAVs are connected
wirelessly to a Base Station (BS).
The user preferences are estimated by the LDA
algorithm, which classifies the information (word by
word) into a set of topics. The users are then clus-
tered into N
d
groups and each user is allocated to a
UAV. This last step is carried out using the K–means
clustering algorithm. Three user-UAV allocation cri-
teria were considered:
1. max-snr: allocate user to the UAV that would
give the highest received SNR for minimizing the
transmission delay.
2. caching-efficiency: allocate user to the UAV that
is likely to have the requested content, for mini-
mizing the request delay.
3. min-delay: allocate user to the UAV that would
minimize the overall delay (the sum of both trans-
mission and request delay).
4.1 Caching Efficiency
In this section, we investigate the performance of
LDA based caching technique in comparison to a ran-
dom caching benchmark scheme. For most scenar-
ios, only a limited amount of historical user requests
can be accessed. Besides, it is also important to pro-
vide immediate QoS to users once the connection is
established. Hence, the system delay under limited
historical requests is a significant performance indi-
cator. Here, we assume that each user is allocated to
a UAV that has a link with the highest received SNR
(i.e. max-snr criteria). Then, we only examine the ef-
fect of different caching strategies. A perfect coding
scheme with continuous coding rate is assumed in this
subsection.
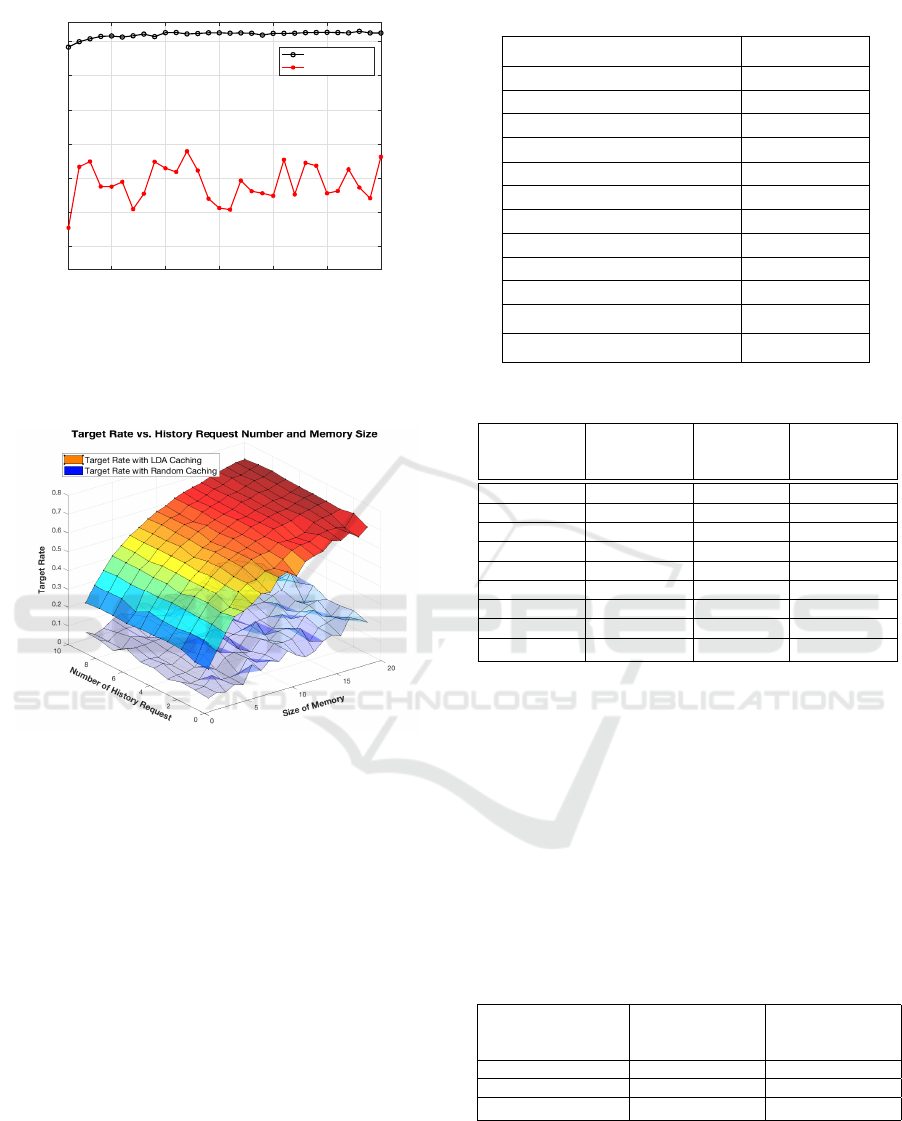
The simulation results for LDA based caching and
random caching with different historical request sizes
are shown in Fig. 11(a), when the UAV’s memory
size is 50% of the total data (i.e. |C
d
| = 50). It
should be noticed that the x-axis in Fig. 11(a), which
is the size of the historical requests, represents the
number of past requests from each user. Not surpris-
ingly the caching efficiency is around 50% for the ran-
dom caching strategy. As shown in Fig. 11(a), the
LDA based approach achieves above 90% caching ef-
ficiency after only 5 historical requests.
Fig. 11(b) shows the influence of both memory
size and the number of historical requests. It can
be observed from Fig. 11(b) that the memory size
is more significant than the number of historical re-
quests, when considering the caching efficiency. This
is because the LDA algorithm learns user preferences
relatively fast when the memory size is big, as shown
in Fig. 11(a). We have shown that the LDA based
caching scheme is significantly more efficient com-
pared to the random caching method. The conver-
gence speed of the LDA algorithm is also fast, espe-
cially when the memory size is big. Having consid-
ered the ideal case with perfect coding here, we will
now investigate the performance of the ALDPC-CM
based scheme in the following section.
4.2 Overall Delay
The simulation parameters used in this section are
given in Table 5. The ALDPC-CM scheme supports
the 8 transmission modes detailed in Table 3, which
have SNR thresholds shown in Table 4. Table 6 shows
the throughput achieved for each coded modulation
mode. Additionally, if the received SNR is lower than
the SNR threshold of the lowest mode (BPSK), then
no transmission (No Tx) will happen. By contrast,
when the received SNR is higher than the highest
Machine Learning Assisted Caching and Adaptive LDPC Coded Modulation for Next Generation Wireless Communications
73
1 5 10 15 20 25 30
Size of History Request (Each User)
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Target Rate
Request Target Rate Under Various Methods
Cache (LDA)
Cache (Count)
(a) Caching efficiency simulation of LDA based and ran-
dom caching strategies under varying size of historical
requests. The system has n
U
= 100 users, n
D
= 4 UAVs,
n
C
= 100 contents, and n
T
= 4 topics. A total of |C
d
| = 50
contents can be cached for each UAV.
(b) Caching efficiency simulation of LDA based and ran-
dom caching strategies under varying size of historical
requests and a range of memory sizes.
Figure 11: Caching efficiency simulation based on perfect
coding scheme that has continuous coding rate.
mode (256QAM), then a throughput of 7 bits/symbol
will be supported, as illustrated in Table 6.
Fig. 12 shows the instantaneous delay and mean
delay of the ALDPC-CM based scheme, for the three
user-UAV allocation criteria considered. The user-
UAV allocation constitutes a trade-off between avail-
able resources. As seen in Fig. 12, minimizing the
transmission delay (max-snr criteria) would give a
lower mean delay compared to minimizing the re-
quest delay (caching-efficiency criteria). Hence, the
transmission delay is more dominant than the re-
quest delay in our system. Furthermore, the min-
delay criteria gives the lowest mean delay as ex-
pected. However, this would require additional com-
putation/overhead for calculating the transmission de-
lay and the request delay.
Table 5: Simulation Parameters.
Parameter Value
No. of UAVs 4
No. of users 50
Total contents, n
C
100
Area served 300 m
2
Drone/UAV height 30 m
Noise PSD -85 dBm
Signal bandwidth 20 MHz
Carrier Frequency 2 GHz
UAV’s memory size, |C
d
| 50
UAV-BS Request delay 2 ms
Maximum user speed 15 m/s
Coded Modulation scheme ALDPC-CM
Table 6: Data rates for various LDPC-CM schemes.
Capacity
Interval
(bits/symbol)
Modulation
Coding
Rate
Throughput
(bits/symbol)
[−∞,0.5] No Tx 0 0
[0.5,1] BPSK 0.5 0.5
[1,2] 4QAM 0.5 1
[2,3] 8PSK 2/3 2
[3,4] 16QAM 3/4 3
[4,5] 32QAM 4/5 4
[5,6] 64QAM 5/6 5
[6,7] 128QAM 6/7 6
[7,+∞] 256QAM 7/8 7
Fig. 13 shows the instantaneous delay compari-
son for the ALDPC-CM based transmission scheme
when considering the three user-UAV allocation crite-
ria. The max-snr criteria may be considered as a good
tradeoff in terms of performance and complexity. Ta-
ble 7 depicts the mean delay values associated with
the instantaneous delay plots shown in Fig. 13 un-
der each criterion. The practical ALDPC-CM based
scheme only invoked an additional mean delay of
1.32 − 1.27 = 0.05 ms compared to the ideal perfect
coding based scheme when the min-delay criteria is
considered, as shown in Table 7.
Table 7: Mean delay comparison over 101 frames.
Criterion
Mean Delay
(ms),
ALDPC-CM
Mean Delay
(ms), Perfect
Coding
max-snr 2.02 1.27
min-delay 1.32 1.27
caching-efficiency 3.16 2.84
DCNET 2020 - 11th International Conference on Data Communication Networking
74
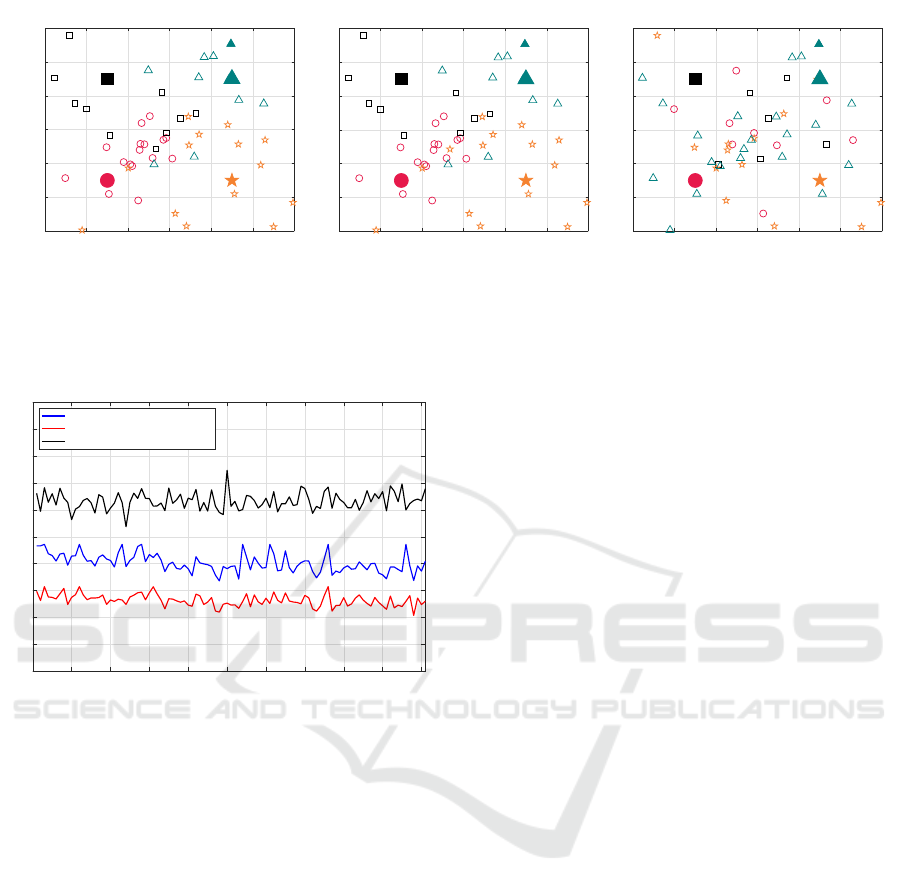
0 50 100 150 200 250 300
X (m)
0
50
100
150
200
250
300
Y (m)
User Assignment According to Maximum SNR
0 50 100 150 200 250 300
0
50
100
150
200
250
300
X (m)
Y (m)
User Assignment According to User Preference
0 50 100 150 200 250 300
X (m)
0
50
100
150
200
250
300
Y (m)
User Assignment According to Minimum Delay
SNR: 11.9 dB, Delay: 1.28 ms
Is Cached: 1, Mean Delay: 1.96 ms
SNR: 11.9 dB, Delay: 0.853 ms
Is Cached: 1, Mean Delay: 1.32 ms
SNR: 11.9 dB, Delay 1.28 ms
Is Cached: 1, Mean Delay: 3.08 ms
Figure 12: An instance of the moving user allocation process under three allocation criteria. The four UAVs are represented
by the four filled-markers, while users allocated to the UAV are denoted by the blank-markers of the same shape and color.
0 10 20 30 40 50 60 70 80 90 100
Frame Index
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Delay (ms)
Instantaneous Delay with LDPC coding
Maximising SNR
Minimising Delay
Maximising Caching Efficiency
Figure 13: Instantaneous delay comparison for the ALDPC-
CM based transmission scheme when considering the three
user-UAV criteria.
5 CONCLUSIONS AND FUTURE
WORK
In this contribution, we have proposed an LDA based
machine learning technique for predicting user re-
quests, which is then investigated for improving the
caching efficiency of UAVs. It was evidenced in
Fig. 11 that the LDA based caching significantly out-
performed the random caching method, where above
90% caching efficiency can be achieved after a short
training based on 5 historical user requests.
We have also implemented an ALDPC-CM
scheme that can support 8 transmission modes on top
of the no transmission mode, as outlined in Table 6.
The Rician fading channel having a Rician factor of
K = 3 was invoked for modeling the LoS link between
the UAV and its serving users. A range of simulations
were done for computing the BER versus SNR curves
of the various LDPC-CM schemes as shown in Fig. 7,
Fig. 8 and Fig. 9. An adaptive scheme was then cre-
ated for maintaining a BER of ≤ 10
−4
while increas-
ing the link throughput as the channel SNR improves,
as depicted in Fig. 10.
After the caching technique and the link-level
transmission were implemented, the K–means algo-
rithm was then utilized for allocating all users to
the UAVs. Three allocation criteria were consid-
ered, where the max-snr criterion aims to minimize
the transmission delay, the caching-efficiency crite-
rion aims to minimize the request delay and the min-
delay criterion aims to minimize the overall delay.
We found that the min-delay criterion would give
the lowest mean delay, while the max-snr criteria
is a good tradeoff when considering the achievable
performance and required complexity, as shown in
Fig. 13. The proposed practical ALDPC-CM based
scheme performed very close to the ideal perfect cod-
ing scheme, as evidenced in Table 7.
For the future work, other machine learning mod-
els such as the Non-negative Matrix Factorization
(NMF) should be comparatively analyzed against our
LDA-based approach for caching optimization. Other
channel coding schemes such as polar codes, trellis
codes and space-time codes can also be utilized in
the link-level transmission. Deep Learning and Re-
inforcement Learning techniques (Ha et al., 2019),
(Bruno et al., 2014) could also be considered for im-
proving the overall performance of the UAV based
system.
REFERENCES
Americas, G. (2018). 5g ultra-reliable and low-latency com-
munication (urllc) to digitize industries and unearth
new use cases. White paper, 5G Americas.
Blei, D. M., Ng, A. Y., and Jordan, M. I. (2003). Latent
Machine Learning Assisted Caching and Adaptive LDPC Coded Modulation for Next Generation Wireless Communications
75

dirichlet allocation. Journal of machine Learning re-
search, 3(Jan):993–1022.
Bruno, R., Masaracchia, A., and Passarella, A. (2014).
Robust adaptive modulation and coding (amc) selec-
tion in lte systems using reinforcement learning. In
2014 IEEE 80th Vehicular Technology Conference
(VTC2014-Fall), pages 1–6.
Chen, M., Challita, U., Saad, W., Yin, C., and Debbah, M.
(2017). Machine learning for wireless networks with
artificial intelligence: A tutorial on neural networks.
arXiv preprint arXiv:1710.02913.
D. J. C Mackay, and R. M. Neal (1997). Near shannon
limit performance of low density parity check codes.
Electronics Letters, 33(6):457–458.
Gallager, R. G. (1963). Low Density Parity Check Codes.
PhD thesis, M.I.T, United States.
Goldsmith, A. (2005). Wireless communications. Cam-
bridge university press.
Guo, F. (2005). Low Density Parity Check Coding. PhD
thesis, University of Southampton, United Kingdom.
Ha, C., You, Y., and Song, H. (2019). Machine learn-
ing model for adaptive modulation of multi-stream in
mimo-ofdm system. IEEE Access, 7:5141–5152.
L. Hanzo, S. X. Ng and T. Keller (2005). Quadra-
ture Amplitude Modulation : From Basics to Adap-
tive Trellis-Coded, Turbo-Equalised and Space-Time
Coded OFDM, CDMA and MC-CDMA Systems.
IEEE Press.
Lang, K. (1995). Newsweeder: Learning to filter netnews.
In Proceedings of the Twelfth International Confer-
ence on Machine Learning, pages 331–339.
M. R. Tanner (1981). A recursive approach to low complex-
ity codes. IEEE Transactions on Information Theory,
27(5).
Merwaday, A. and Guvenc, I. (2015). Uav assisted hetero-
geneous networks for public safety communications.
In Wireless Communications and Networking Confer-
ence Workshops (WCNCW), 2015 IEEE, pages 329–
334. IEEE.
Valavanis, K. P. and Vachtsevanos, G. J. (2014). Handbook
of Unmanned Aerial Vehicles. Springer Publishing
Company, Incorporated.
Wang, S., Zhang, X., Zhang, Y., Wang, L., Yang, J., and
Wang, W. (2017). A survey on mobile edge networks:
Convergence of computing, caching and communica-
tions. IEEE Access, 5:6757–6779.
Zeng, Y., Zhang, R., and Lim, T. J. (2016). Wire-
less communications with unmanned aerial vehi-
cles: opportunities and challenges. arXiv preprint
arXiv:1602.03602.
DCNET 2020 - 11th International Conference on Data Communication Networking
76
